Формула жесткости пружины, как найти коэффициент через массу и длину

Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Особенности работы

Любая пружина представляет собой упругое изделие, которое в процессе эксплуатации подвергается статическим, динамическим и циклическим нагрузкам. Основная особенность этой детали – она деформируется под приложенным извне усилием, а когда воздействие прекращается – восстанавливает свою первоначальную форму и геометрические размеры. В период деформации происходит накопление энергии, при восстановлении – ее передача.

Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность.

Виды пружин

Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.

  • Первые из них без нагрузки имеют нулевой шаг, то есть виток соприкасается с витком. В процессе деформации они растягиваются, их длина увеличивается. Прекращение нагрузки сопровождается возвращением в первоначальную форму – опять витком к витку.
  • Вторые – наоборот, изначально навиваются с определенным шагом между витками, под нагрузкой сжимаются. Соприкосновение витков является естественным ограничителем для продолжения воздействия.

Изначально именно для пружины растяжения было найдено соотношение массы подвешенного на ней груза и изменения ее геометрического размера, которое и стало основой для формулы жесткости пружины через массу и длину.

Какие еще бывают виды пружин

Зависимость деформации от прилагаемой внешней силы справедлива и для других видов упругих деталей: кручения, изгиба, тарельчатых, других. Не важно, в какой плоскости к ним прилагаются усилия: в той, где расположена осевая линия, или перпендикулярной к ней, производимая деформация пропорциональна усилию, под воздействием которого она произошла.

Основные характеристики

Независимо от вида пружин, особенности их работы, связанные с постоянно деформацией, требуют наличия таких параметров:

  • Способности сохранять постоянное значение упругости в течение заданного срока.
  • Пластичности.
  • Релаксационной стойкости, благодаря которой деформации не становятся необратимыми.
  • Прочности, то есть способности выдерживать различные виды нагрузок: статические, динамические, ударные.

Каждая из этих характеристик важна, однако при выборе упругой комплектующей для конкретной работы в первую очередь интересуются ее жесткостью как важным показателем того, подойдет ли она для этого дела и насколько долго будет работать.

Что такое жесткость

Жесткость – это характеристика детали, которая показывает, просто или легко будет ее сжать, насколько большую силу нужно для этого приложить. Оказывается, что возникающая под нагрузкой деформация тем больше, чем больше прилагаемая сила (ведь возникающая в противовес ей сила упругости по модулю имеет то же значение). Потому определить степень деформации можно, зная силу упругости (прилагаемое усилие) и наоборот, зная необходимую деформацию, можно вычислить, какое требуется усилие.

Физические основы понятия жесткость/упругость

Сила, воздействуя на пружину, изменяет ее форму.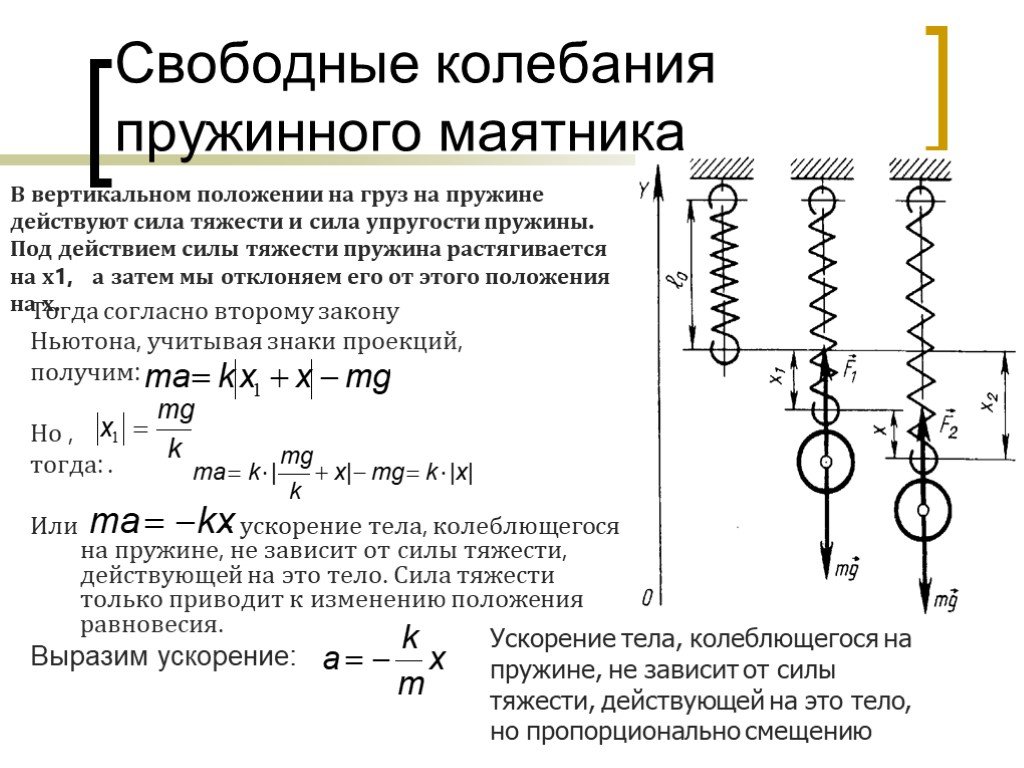 Например, пружины растяжения/сжатия под влиянием внешнего воздействия укорачиваются или удлиняются. Согласно закону Гука (так называется позволяющая рассчитать коэффициент жесткости пружины формула), сила и деформация между собой пропорциональны в пределах упругости конкретного вещества. В противодействие приложенной извне нагрузке возникает сила, такая же по величине и противоположная по знаку, которая направлена на восстановление исходных размеров детали и ее форму.

Природа этой силы упругости – электромагнитная, возникает она как следствие особого взаимодействии между структурными элементами (молекулами и атомами) материала, из которого изготовлена данная деталь. Таким образом, чем жесткость больше, то есть чем труднее упругую деталь растянуть/сжать, тем больше коэффициент упругости. Этот показатель используется, в частности, при выборе определенного материала для изготовления пружин для использования в различных ситуациях.

Как появился первый вариант формулы

Формула для расчета жесткости пружины, которая получила название закона Гука, была установлена экспериментально. В процессе опытов с подвешенными на упругом элементе грузами разной массы замерялась величина его растяжения. Так и выяснилось, что одна и та же испытуемая деталь под разными нагрузками претерпевает различные деформации. Причем подвешивание определенного количества гирек, одинаковых по массе, показало, что каждая добавленная/снятая гирька увеличивает/уменьшает длину упругого элемента на одинаковую величину.

В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).

Так было открыто свойство жесткости, которое, как и формула для определения коэффициента упругости, находит самое широкое применение в любой отрасли промышленности.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или 

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука.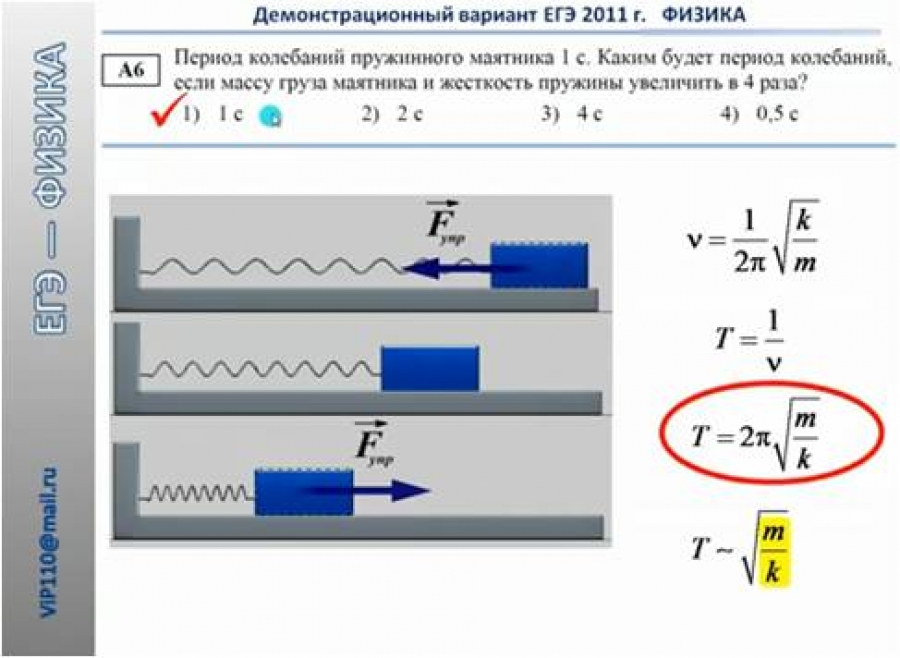 Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

  • Материала, используемого при ее изготовлении.
  • Формы и конструктивных особенностей.
  • Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

Например:

  • Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
  • При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

Особенности расчета жесткости соединений пружин

Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.

При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.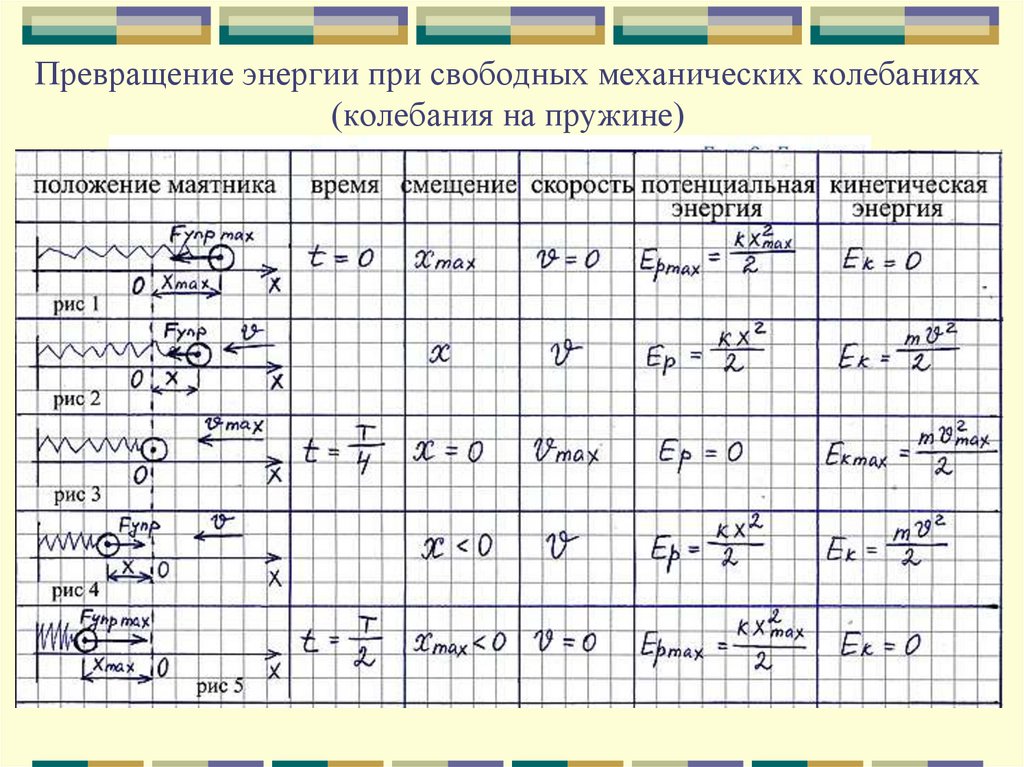

При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.

Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.

Жесткость пружины: формулы и коэффициенты

Пружиной называют объект, способный с помощью деформации, вызванной внешними силами, накапливать и сохранять упругую потенциальную энергию, а после прекращения их воздействия восстанавливаться до прежнего состояния. Реально существующие пружины абсолютно точно восстановить свою прежнюю форму не в состоянии т.к. при внешнем воздействии в той или иной степени нарушается структура их материала, в результате чего возникают так называемые пластичные деформации. Чем они меньшее, тем более качественным считается изделие.

Какие бывают типы пружин

В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.

Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.

Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.

В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.

Основные характеристики пружин

Зная материал и диаметр проволоки, форму её сечения, длину и диаметр пружины, как единого целого, можно с очень высокой достоверностью судить, насколько пружина может сопротивляться попыткам деформировать себя. Существуют также другие характеристики, от которых работоспособность пружины может зависеть очень серьёзно. К таковым относятся усталость материала проволоки, шаг витка, индекс пружины и т. д.

Материал и сила жесткости пружины

Зависимость между этими характеристиками пружин индивидуальная и вычисляется опытным путём. Чаще всего для изготовления металлических пружин используют высокоуглеродистые стали, легированные ванадием, кремнием и марганцем.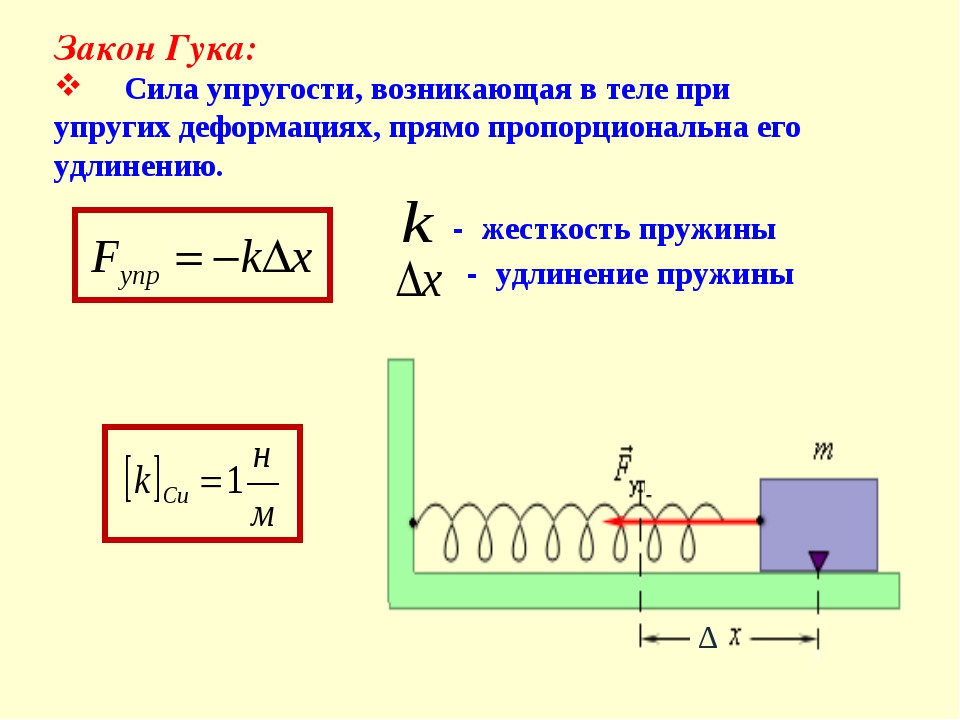 Для изделий, предназначенных для длительной работы в агрессивных средах используют нержавеющую сталь, оловянносвинцовую, бериллиевую и кремнемарганцевую бронзу, различные чугуны, а также некоторые из титановых сплавов.

Небольшие пружины изготавливают из уже закалённой проволоки. Крупные изделия делают из отожжённой стали, а закалку проводят уже после формовки.

Как связана жесткость пружины с диаметром и формой сечения проволоки, из которой она сделана

Чем он меньше, тем пружина более эластична. Способность запасать энергию с уменьшением диаметра тоже становится меньше. Пружины сжатия, как правило, делают из более толстой проволоки.

Следует отметить, что не всегда сечение проволоки для пружин бывает круглым, в пружинах сжатия оно иногда бывает уплощённым. Это обеспечивает лучшую посадку одного витка на другой и делает конструкцию более устойчивой.

Длина и диаметр

Определение

Под длиной пружины понимают её длину в свободном, недеформированном состоянии.

Также следует различать длину собственно изделия и длину проволоки, из которой оно сделано. Это две совершенно разные величины. Не малое значение имеет число витков. В пружинах сжатия, чем их больше, тем выше вероятность соскальзывания изделия с опоры и, как следствие, выхода детали из строя.

О понятии жесткости. Жесткость пружины: формула

Определение

Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.

Посмотрите на закон Гука.

Формула

Fупр = –kx

Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.

k – это и есть жёсткость пружины.

Fупр — сила жесткости или упругости пружины.

x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.

Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.

Закон Гука является одним из основных законов физики.

Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:

Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.  

Имеем два уравнения:

Т. к. Fупр =Fтяж, получаем

Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна

Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как рассчитать жесткость цилиндрической пружины

В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.

С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.

Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.

Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.

Окончательная формула для жёсткости цилиндрической пружины такова:

Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.

Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.

Что такое константа пружины и как рассчитывается формула?

4 июня 2018 г.

Пружины представляют собой упругие механические объекты, которые после деформации, т. е. после растяжения или сжатия, возвращаются к своей первоначальной форме. Они являются необходимым компонентом для самых разных механических устройств. От двигателей, приборов, инструментов, транспортных средств и медицинских инструментов до простых шариковых ручек знакомая металлическая катушка стала незаменимым компонентом в современном мире. Широкое использование и применение пружины обусловлено ее способностью накапливать механическую энергию. Его сила пружины является реактивной, которая генерирует механическую энергию. Сколько энергии представлено константой пружины.

Сила пружины — это сила, необходимая или прикладываемая для сжатия или растяжения пружины на любом объекте, прикрепленном к ней.

Когда объект прикладывает силу к пружине, пружина прикладывает к объекту равную и противоположную силу. Он всегда действует так, чтобы возвращать массу обратно в положение равновесия. Постоянная пружины — это характеристика пружины, которая измеряет отношение силы, действующей на пружину, к вызванному ею смещению. Другими словами, он описывает, насколько жесткой является пружина и насколько она будет растягиваться или сжиматься. Пружины с большей жесткостью пружины будут иметь меньшие смещения, чем пружины с меньшей жесткостью пружины при той же добавленной массе.

Определение силы пружины


Сила пружины рассчитывается с использованием закона Гука, названного в честь Роберта Гука, британского физика 17-го века, который разработал формулу в 1660 году, изучая пружины и упругость. Он заметил, что когда к материалу прикладывается сила, материал растягивается или сжимается в ответ на силу. Упругая деформация возникает при снятии напряжения. Это означает, что если материал возвращается к размерам, которые он имел до приложения нагрузки или напряжения, его деформация является обратимой, непостоянной, и он «пружинивает»9. 0003

Формула усилия пружины выражается уравнением: F = – kx. Где F — приложенная сила, k — постоянная пружины, измеряющая, насколько жесткая и прочная пружина пропорционально, а x — расстояние, на которое пружина растягивается или сжимается от своего положения равновесия или покоя, обычно в ньютонах на метр (Н/м). ). Знак минус показывает, что эта сила имеет направление, противоположное силе, растягивающей или сжимающей пружину.

Постоянная пружины — это сила, необходимая для растяжения или сжатия пружины, деленная на расстояние, на которое пружина становится длиннее или короче. Он используется для определения стабильности или нестабильности пружины и, следовательно, системы, для которой он предназначен. В качестве формулы он перерабатывает закон Гука и выражается уравнением: k = – F/x. Где k — жесткость пружины, F — сила, приложенная к x, а x — смещение пружины, выраженное в Н/м.

Закон Гука описывает линейную упругую деформацию материалов только в диапазоне, в котором сила и перемещение пропорциональны. Эластичность пружины вернется к своей первоначальной форме, как только внешняя сила, независимо от массы, будет устранена. Постоянная пружины — это свойство самой пружины, которое показывает линейную зависимость между силой и смещением. Таким образом, количество механической энергии, хранящейся и используемой пружиной, зависит от силы и смещения: чем сильнее натягивается пружина, тем сильнее она тянет назад.

Использование уравнений Spring — физика для старших классов

Все ресурсы по физике для старших классов

6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Справка по физике для старших классов » Движение и механика » Гармоничное движение » Использование уравнений пружины

Пружина с жесткостью пружины сжимается. Какова потенциальная энергия, запасенная в пружине?

Возможные ответы:

Правильный ответ:

Пояснение:

Уравнение для потенциальной энергии пружины: .

Подставьте данные значения расстояния и жесткости пружины, чтобы найти потенциальную энергию.

Помните, поскольку пружина была сжата, ее смещение отрицательное. Результирующая потенциальная энергия будет положительной, так как при освобождении смещение будет происходить вдоль положительной горизонтальной оси.

Сообщить об ошибке

Жесткость пружины .

Какая сила необходима для сжатия ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи используйте закон Гука:

В этой формуле  является жесткостью пружины,   является сжатием пружины и  является необходимой силой. Нам заданы значения жесткости пружины и расстояния сжатия. Используя эти термины, мы можем вычислить силу пружины.

Подставьте полученные значения и решите.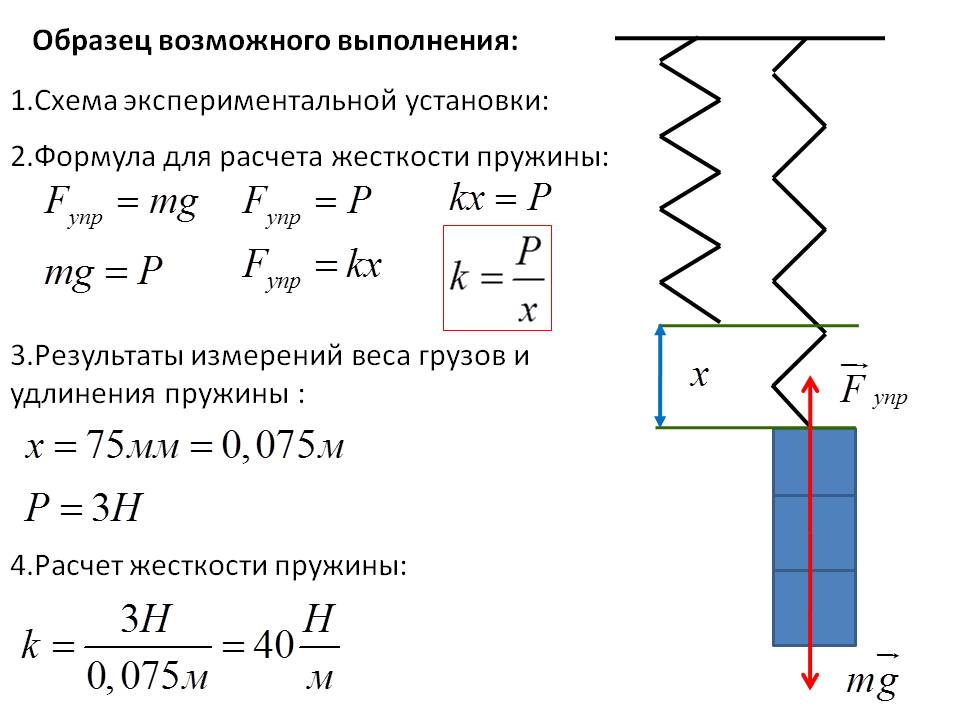

Обратите внимание, что сила отрицательна, потому что она сжимает пружину, давит на спираль. Когда сила сбрасывается, равная и противоположная сила пружины заставит ее растягиваться в положительном направлении.

Сообщить об ошибке

Жесткость пружины .

Если для растяжения пружины используется сила  , каково полное перемещение пружины?

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи используйте закон Гука:

В этой формуле  является жесткостью пружины,   является сжатием пружины и  является необходимой силой. Нам дана постоянная пружины и сила, что позволяет нам найти смещение.

Подставьте полученные значения и решите.

Обратите внимание, что и сила, и смещение положительны, потому что сила растяжения будет тянуть в положительном направлении. Если бы пружина была сжата, изменение расстояния было бы отрицательным.

Сообщить об ошибке

Вертикальная пружина с жесткостью  неподвижна. К концу пружины прикреплен груз. На какое максимальное перемещение может растянуться пружина?

Возможные ответы:

Правильный ответ:

Пояснение:

Лучший способ решить эту проблему — использовать энергию. Обратите внимание, что пружина сама по себе неподвижна. Это означает, что его начальная полная энергия в этот момент равна нулю. Когда груз прикреплен, пружина растягивается, сообщая ей потенциальную энергию пружины ().

Откуда берется эта энергия? Единственное место, откуда он может исходить, это добавление массы. Поскольку система вертикальна, эта масса будет обладать гравитационной потенциальной энергией.

Используйте закон сохранения энергии, чтобы установить эти две энергии равными друг другу:

Мы пытаемся найти смещение, и теперь у нас есть уравнение в терминах нашей переменной.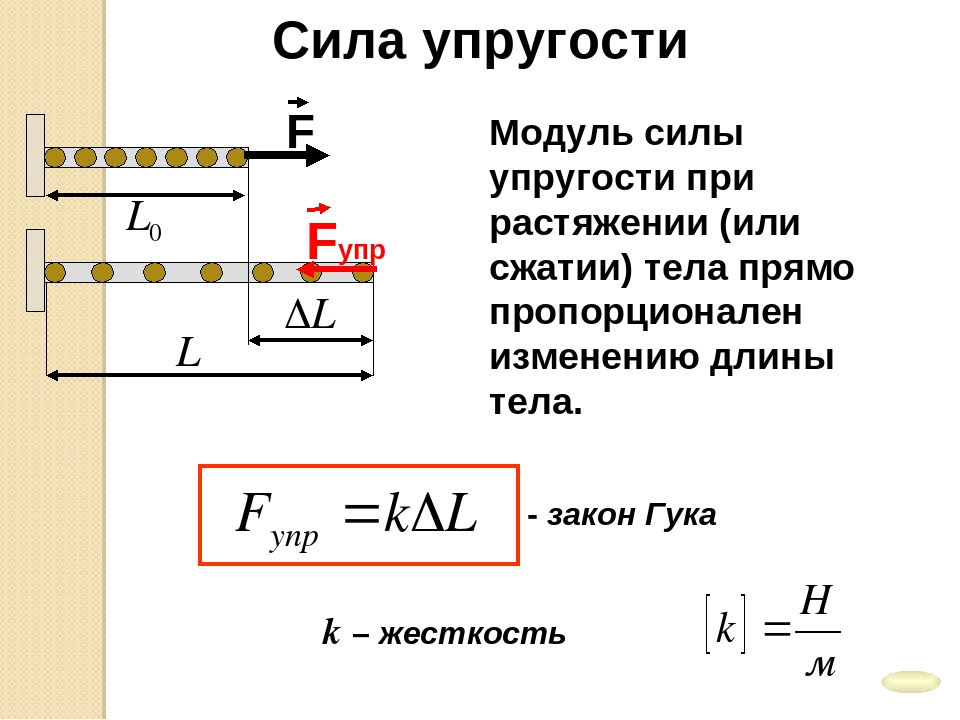

Начните с погружения в обе стороны,  чтобы избавиться от  на правой стороне уравнения.

Нам даны значения жесткости пружины, массы и силы тяжести. Использование этих значений позволит использовать для решения смещения.

Обратите внимание, что смещение будет отрицательным, поскольку пружина растягивается вниз под действием силы тяжести.

Сообщить об ошибке

Какое усилие требуется для сжатия пружины, если ее жесткость равна  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи используйте закон Гука: 

Подставьте полученные значения:

Сообщить об ошибке

Какое усилие требуется для сжатия пружины, если ее жесткость равна  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи используйте закон Гука: 

Подставьте полученные значения:

Сообщить об ошибке

Сколько потенциальной энергии создается при сжатии пружины, если ее жесткость равна  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для потенциальной энергии пружины:

Подключите наши значения и решайте:

, так:

. Отчет о ошибке

. Как много потенциальной энергии. создается при сжатии пружины , если ее жесткость равна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для потенциальной энергии пружины составляет

Подключить наши значения и решать:

, так:

Отчет. пружины. Пружина сжата. Какова максимальная скорость груза, если жесткость пружины равна  ?

Возможные ответы:

Правильный ответ:

Пояснение:

Если мы ищем максимальную скорость, это произойдет, когда вся энергия в системе будет кинетической энергией.

Мы можем использовать закон сохранения энергии, чтобы увидеть .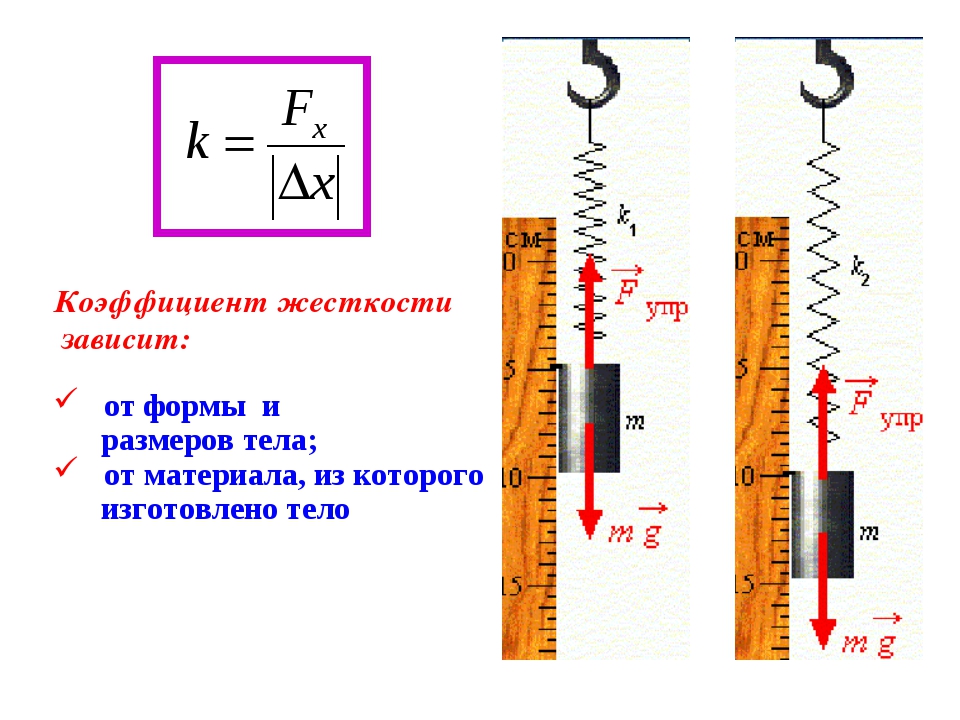 Итак, если мы можем найти начальную потенциальную энергию, мы можем найти конечную кинетическую энергию и использовать ее для определения конечной скорости массы.

Формула потенциальной энергии пружины:

Подключение в наших данных значениях и решайте:

, так:

Формула для кинетической энергии:

С.

Мы можем подставить эту информацию в формулу для кинетической энергии, чтобы найти максимальную скорость:0003

Сообщить об ошибке

Груз помещается на конец пружины. Если пружина сжата, какова будет конечная скорость массы, если пружина имеет жесткость?

Возможные ответы:

Правильный ответ:

Пояснение:

Если мы ищем максимальную скорость, это произойдет, когда вся энергия в системе будет кинетической энергией.