Егэ физика 1 задание теория: Теория по физике для подготовки к ЕГЭ 2023

Прямолинейное движение и движение по окружности

Механическое движение. Относительность механического движения. Система отсчета

Под механическим движением понимают изменение с течением времени взаимного расположения тел или их частей в пространстве: например, движение небесных тел, колебания земной коры, воздушные и морские течения, движение летательных аппаратов и транспортных средств, машин и механизмов, деформации элементов конструкций и сооружений, движение жидкостей и газов и др.

Относительность механического движения

С относительностью механического движения мы знакомы с детства. Так, сидя в поезде и наблюдая за трогающимся с места поездом, стоявшим до этого на параллельном пути, мы часто не можем определить, какой из поездов на самом деле начал двигаться. И здесь сразу следует уточнить: двигаться относительно чего? Относительно Земли, конечно. Потому что относительно соседнего поезда мы начали двигаться независимо от того, какой из поездов начал свое движение относительно Земли.

Относительность механического движения заключается в относительности скоростей перемещения тел: скорости тел относительно разных систем отсчета будут различны (скорость человека, перемещающегося в поезде, пароходе, самолете, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей).

Различными будут и траектории движения тела в разных системах отсчета. Так, например, вертикально падающие на землю капли дождя оставят след в виде косых струй на окне вагона мчащегося поезда. Точно также любая точка на вращающемся пропеллере летящего самолета или спускающегося на землю вертолета описывает окружность относительно самолета и гораздо более сложную кривую — винтовую линию относительно Земли. Таким образом, при механическом движении относительной является также и траектория движения.

Путь, пройденный телом, также зависит от системы отсчета. Возвращаясь все к тому же пассажиру, сидящему в поезде, мы понимаем, что путь, проделанный им относительно поезда за время поездки, равен нулю (если он не передвигался по вагону) или, во всяком случае, намного меньше того пути, который он преодолел вместе с поездом относительно Земли. Таким образом, при механическом движении относительным является также и путь.

Осознание относительности механического движения (т. е. того, что движение тела можно рассматривать в разных системах отсчета) привело к переходу от геоцентрической системы мира Птолемея к гелиоцентрической системе Коперника. Птолемей, следуя наблюдаемому издревле движению Солнца и звезд на небосклоне, в центре Вселенной расположил неподвижную Землю с вращающимися вокруг нее остальными небесными телами. Коперник же считал, что Земля и другие планеты вращаются вокруг Солнца и одновременно вокруг своих осей.

Таким образом, изменение системы отсчета (Земля — в геоцентрической системе мира и Солнце — в гелиоцентрической) привело к гораздо более прогрессивной гелиоцентрической системе, позволяющей решить многие научные и прикладные задачи астрономии и изменить взгляды человечества на Вселенную.

Система координат $X, У, Z$, тело отсчета, с которым она связана, и прибор для измерения времени (часы) образуют систему отсчета, относительно которой рассматривается движение тела.

Телом отсчета называется тело, относительно которого рассматривается изменение положения других тел в пространстве.

Систему отсчета можно выбрать произвольно. При кинематических исследованиях все системы отсчета равноправны. В задачах динамики также можно использовать любые произвольно движущиеся системы отсчета, но удобнее всего инерциальные системы отсчета, так как в них характеристики движения имеют более простой вид.

Материальная точка

Материальная точка — объект пренебрежимо малых размеров, имеющий массу.

Понятие «материальная точка» вводится для описания (с помощью математических формул) механического движения тел. Делается это потому, что описывать движение точки проще, чем реального тела, частицы которого к тому же могут двигаться с разными скоростями (например, при вращении тела или деформациях).

Если реальное тело заменяют материальной точкой, то этой точке приписывают массу этого тела, но пренебрегают его размерами, а заодно пренебрегают различием характеристик движения его точек (скоростей, ускорений и т. д.), если таковое имеется. В каких случаях это можно делать?

Практически любое тело можно рассматривать как материальную точку, если расстояния, проходимые точками тела, очень велики по сравнению с его размерами.

Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении различных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.

Следовательно, если в изучаемом движении тела можно пренебречь его вращением вокруг оси, такое тело можно представить как материальную точку.

Однако при решении задач, связанных с суточным вращением планет (например, при определении восхода Солнца в разных местах поверхности земного шара), считать планету материальной точкой бессмысленно, так как результат задачи зависит от размеров этой планеты и скорости движения точек ее поверхности.

Материальной точкой правомерно считать самолет, если требуется, например, определить среднюю скорость его движения на пути из Москвы в Новосибирск. Но при вычислении силы сопротивления воздуха, действующей на летящий самолет, считать его материальной точкой нельзя, поскольку сила сопротивления зависит от размеров и формы самолета.

Если тело движется поступательно, даже если его размеры сопоставимы с расстояниями, которые оно проходит, это тело можно рассматривать как материальную точку (поскольку все точки тела движутся одинаково).

В заключение можно сказать: тело, размерами которого в условиях рассматриваемой задачи можно пренебречь, можно считать материальной точкой.

Траектория

Траектория — это линия (или, как принято говорить, кривая), которую описывает тело при движении относительно выбранного тела отсчета.

Говорить о траектории имеет смысл лишь в том случае, когда тело можно представить в виде материальной точки.

Траектории могут иметь разную форму. О форме траектории иногда удается судить по-видимому следу, который оставляет движущееся тело, например, летящий самолет или проносящийся в ночном небе метеор.

Форма траектории зависит от выбора тела отсчета. Например, относительно Земли траектория движения Луны представляет собой окружность, относительно Солнца — линию более сложной формы.

При изучении механического движения в качестве тела отсчета, как правило, рассматривается Земля.

Способы задания положения точки и описание ее движения

Положение точки в пространстве задается двумя способами: 1) с помощью координат; 2) с помощью радиус-вектора.

Положение точки с помощью координат задается тремя проекциями точки $х, у, z$ на оси декартовой системы координат $ОХ, ОУ, OZ$, связанные с телом отсчета. Для этого из точки А необходимо опустить перпендикуляры на плоскости $YZ$ (координата $х$), $ХZ$ (координата $у$), $ХУ$ (координата $z$) соответственно. Записывается это так: $А(х, у, z)$. Для конкретного случая, $(х=6, у=10. 2, z= 4.5$), точка $А$ обозначается $А(6; 10; 4.5)$.

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси ($х$ на ось $ОХ$ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат $О$ и лежащая на диагонали параллелепипеда, и будет искомой точкой $А$.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: $ОХ$ и $ОУ$. Тогда положение точки на плоскости определяют двумя координатами $х$ и $у$.

Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.

Задание положения точки $А$ с помощью радиус-вектора осуществляется соединением точки $А$ с началом координат $О$. Направленный отрезок $ОА = r↖{→}$ называется радиус-вектором.

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций $r_x, r_у, r_z$ на оси координат $ОХ, ОY, OZ$, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости имеем:

$x=r_x=rcosα,$

$y=r_y=rsinα.$

Здесь $r=|r↖{→}|$ — модуль радиус-вектора $r↖{→}, r_x$ и $r_y$ — его проекции на оси координат, все три величины — скаляры; хжу — координаты точки А.

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор $r↖{→}$ можно также разложить на составляющие по осям $Х$ и $Y$, т. е. представить в виде суммы двух векторов:

$r↖{→}=r↖{→}_x+r↖{→}_y$

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус-вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

$x = x(t),$

$y = y(t),$

$z = z(t).$

Уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

$r↖{→}=r↖{→}(t)$

Уравнение представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений равносильно заданию одного векторного уравнения.

Для каждого случая движения вид уравнений будет вполне определенным. Если траекторией движения точки является прямая линия, движение называется прямолинейным, а если кривая — криволинейным.

Перемещение и путь

Перемещение в механике — это вектор, соединяющий положения движущейся точки в начале и в конце некоторого промежутка времени.

Понятие вектора перемещения вводится для решения задачи кинематики — определить положение тела (точки) в пространстве в данный момент времени, если известно его начальное положение.

На рис. вектор ${М_1М_2}↖{-}$ соединяет два положения движущейся точки — $М_1$ и $М_2$ в моменты времени $t_1$ и $t_2$ соответственно и, согласно определению, является вектором перемещения. Если точка $М_1$ задана радиус-вектором $r↖{→}_1$, а точка $М_2$ — радиус-вектором $r↖{→}_2$, то, как видно из рисунка, вектор перемещения равен разности этих двух векторов, т. е. изменению радиус-вектора за время $∆t=t_2-t_1$:

$∆r↖{→}=r↖{→}_2-r↖{→}_1$.

Сложение перемещений (например, на двух соседних участках траектории) $∆r↖{→}_1$ и $∆r↖{→}_2$ осуществляется по правилу сложения векторов:

$∆r=∆r↖{→}_2+∆r↖{→}_1$

Путь — это длина участка траектории, пройденного материальной точкой за данный промежуток времени. Модуль вектора перемещения в общем случае не равен длине пути, пройденного точкой за время $∆t$ (траектория может быть криволинейной, и, кроме того, точка может менять направление движения).

Модуль вектора перемещения равен пути только при прямолинейном движении в одном направлении. Если направление прямолинейного движения меняется, модуль вектора перемещения меньше пути.

При криволинейном движении модуль вектора перемещения также меньше пути, т. к. хорда всегда меньше длины дуги, которую она стягивает.

Скорость материальной точки

Скорость характеризует быстроту, с которой происходят любые изменения в окружающем нас мире (движение материи в пространстве и времени). Движение пешехода по тротуару, полет птицы, распространение звука, радиоволн или света в воздухе, вытекание воды из трубы, движение облаков, испарение воды, нагрев утюга — все эти явления характеризуются определенной скоростью.

При механическом движении тел скорость характеризует не только быстроту, но и направление движения, т. е. является векторной величиной.

Скоростью $υ↖{→}$ точки называется предел отношения перемещения $∆r↖{→}$ к промежутку времени $∆t$, в течение которого это перемещение произошло, при стремлении $∆t$ к нулю (т. е. производной $∆r↖{→}$ по $t$):

$υ↖{→}={lim}↙{∆t→0}{∆r↖{→}}/{∆t}=r↖{→}_1’$

Составляющие вектора скорости по осям $X, Y, Z$ определяются аналогично:

$υ↖{→}_x={lim}↙{∆t→0}{∆x}/{∆t}=x’; υ_y=y’; υ_z=z’$

Определенное таким образом понятие скорости называют также мгновенной скоростью. Это определение скорости справедливо для любых видов движения — от криволинейного неравномерного до прямолинейного равномерного. Когда говорят о скорости при неравномерном движении, под ней понимают именно мгновенную скорость. Из этого определения непосредственно вытекает векторный характер скорости, поскольку перемещение — векторная величина. Вектор мгновенной скорости $υ↖{→}$ всегда направлен по касательной к траектории движения. Он указывает направление, по которому происходило бы движение тела, если бы с момента времени $t$ на него прекратилось действие любых других тел.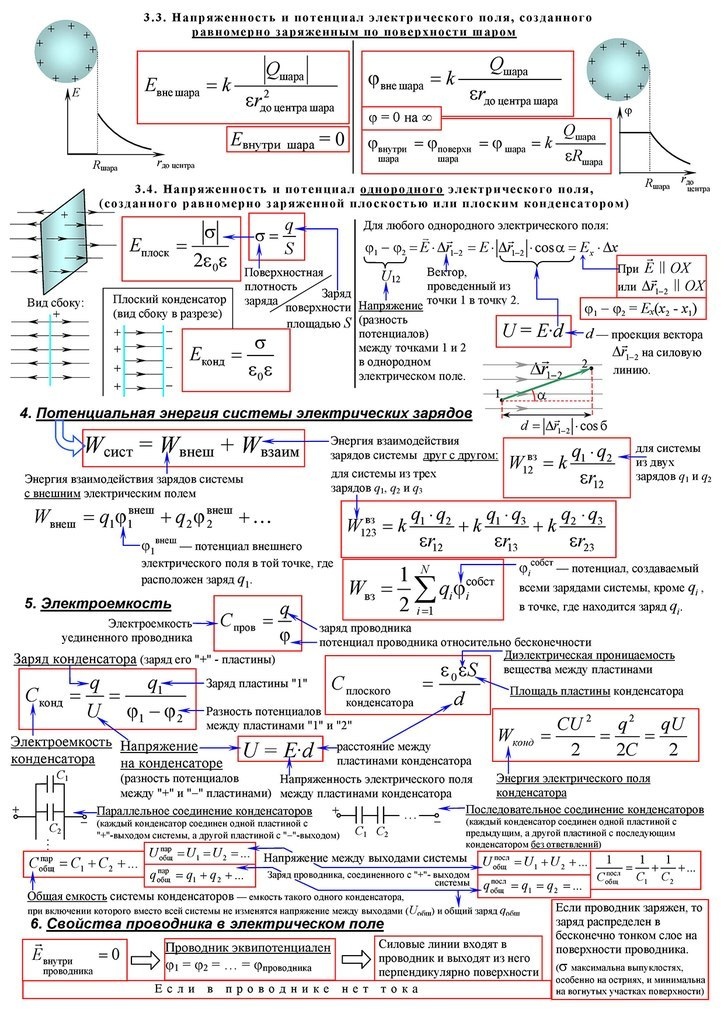

Средняя скорость

Средняя скорость точки вводится для характеристики неравномерного движения (т.е. движения с переменной скоростью) и определяется двояко.

1. Средняя скорость точки $υ_{ср}$ равна отношению всего пройденного телом пути $∆s$ ко всему времени движения $∆t$:

$υ↖{→}_{ср}={∆s}/{∆t}$

При таком определении средняя скорость — скаляр, т. к. пройденный путь (расстояние) и время — величины скалярные.

Такой способ определения дает представление о средней скорости движения на участке траектории (средней путевой скорости).

2. Средняя скорость точки равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло:

$υ↖{→}_{ср}={∆r↖{→}}/{∆t}$

Средняя скорость перемещения — величина векторная.

Для неравномерного криволинейного движения такое определение средней скорости не всегда позволяет определить даже приблизительно реальные скорости на пути движения точки. Например, если точка двигалась по замкнутой траектории в течение некоторого времени, то перемещение ее равно нулю (но скорость явно отличалась от нуля). В этом случае лучше пользоваться первым определением средней скорости.

В любом случае следует различать эти два определения средней скорости и знать, о какой из них идет речь.

Закон сложения скоростей

Закон сложения скоростей устанавливает связь между значениями скорости материальной точки относительно различных систем отсчета, движущихся друг относительно друга. В нерелятивистской (классической) физике, когда рассматриваемые скорости малы по сравнению со скоростью света, справедлив закон сложения скоростей Галилея, который выражается формулой:

$υ↖{→}_2=υ↖{→}_1+υ↖{→}$

где $υ↖{→}_2$ и $υ↖{→}_1$ — скорости тела (точки) относительно двух инерциальных систем отсчета — неподвижной системы отсчета $K_2$ и системы отсчета $K_1$ движущейся со скоростью $υ↖{→}$ относительно $K_2$.

Формула может быть получена путем сложения векторов перемещений.

Для наглядности рассмотрим движение лодки со скоростью $υ↖{→}_1$ относительно реки (система отсчета $K_1$), воды которой движутся со скоростью $υ↖{→}$ относительно берега (система отсчета $K_2$).

Векторы перемещений лодки относительно воды $∆r↖{→}_1$, реки относительно берега $∆r↖{→}$ и суммарный вектор перемещения лодки относительно берега $∆r↖{→}_2$ изображены на рис..

Математически:

$∆r↖{→}_2=∆r↖{→}_1+∆r↖{→}$

Поделив обе части уравнения на интервал времени $∆t$, получим:

${∆r↖{→}_2}/{∆t}={∆r↖{→}_1}/{∆t}+{∆r↖{→}}/{∆t}$

В проекциях вектора скорости на оси координат уравнение имеет вид:

$υ_{2x}=υ_{1x}+υ_x,$

$υ_{2y}=υ_{1y}+υ_y.$

Проекции скоростей складываются алгебраически.

Относительная скорость

Из закона сложения скоростей следует, что если два тела движутся в одной и той же системе отсчета со скоростями $υ↖{→}_1$ и $υ↖{→}_2$, то скорость первого тела относительно второго $υ↖{→}_{12}$ равна разности скоростей этих тел:

$υ↖{→}_{12}=υ↖{→}_1-υ↖{→}_2$

Так, при движении тел в одном направлении (обгон) модуль относительной скорости равен разности скоростей, а при встречном движении — сумме скоростей.

Ускорение материальной точки

Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.

Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖{→}$ по $t$):

$a↖{→}=lim↙{∆t→0}{∆υ↖{→}}/{∆t}=υ↖{→}_t’$

Составляющие $a↖{→} (а_х, а_у, а_z)$ равны соответственно:

$a_x=υ_x’;a_y=υ_y’;a_z=υ_z’$

Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории. 2}$

При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.

Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с² и называют «метр на секунду в квадрате».

Равномерное прямолинейное движение

Движение точки называется равномерным, если за любые равные промежутки времени она проходит равные пути.

Например, если автомобиль за каждую четверть часа (15 мин) проходит 20 км, за каждые полчаса (30 мин) — 40 км, за каждый час (60 мин) — 80 км и т. д., то такое движение считается равномерным. При равномерном движении численная величина (модуль) скорости точки $υ$ — величина постоянная:

$υ=|υ↖{→}|=const$

Равномерное движение может происходить как по криволинейной, так и по прямолинейной траектории.

Закон равномерного движения точки описывается уравнением:

$s=s_0+υt$

где $s$ — расстояние, измеренное вдоль дуги траектории, от некоторой точки на траектории, принятой за начало отсчета; $t$ — время точки в пути; $s_0$ — значение $s$ в начальный момент времени $t=0$.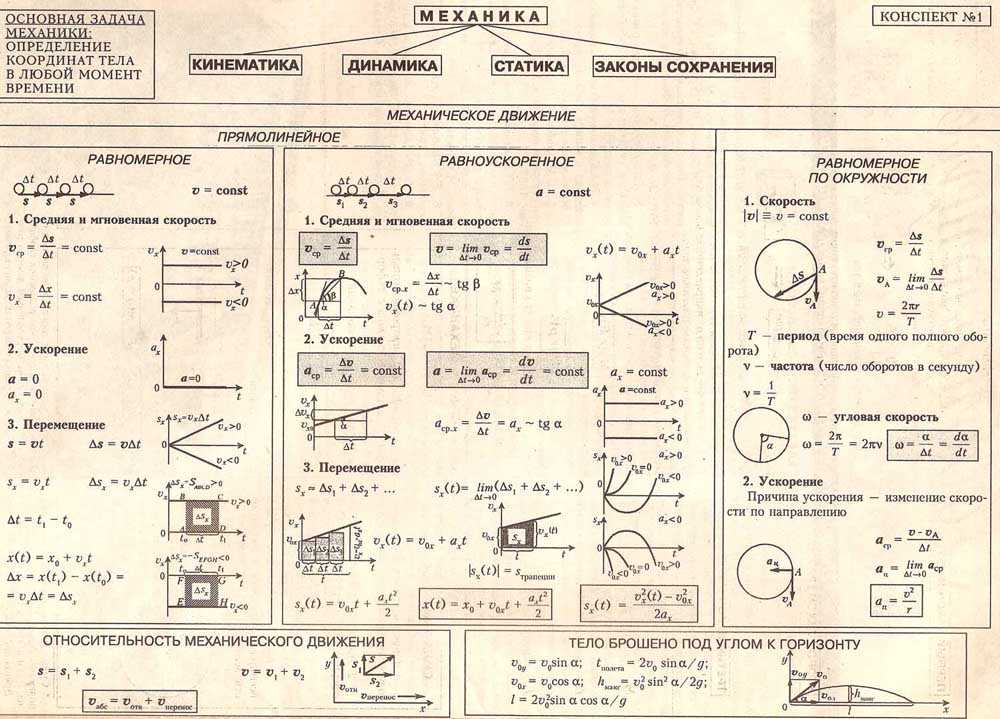

Путь, пройденный точкой за время $t$, определяется слагаемым $υt$.

Равномерное прямолинейное движение — это движение, при котором тело перемещается с постоянной по модулю и направлению скоростью:

$υ↖{→}=const$

Скорость равномерного прямолинейного движения — величина постоянная и может быть определена как отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло:

$υ↖{→}={∆r↖{→}}/{∆t}$

Модуль этой скорости

$υ={|∆r↖{→}|}/{∆t}$

по смыслу есть расстояние $s=|∆r↖{→}|$, пройденное точкой за время $∆t$.

Скорость тела при равномерном прямолинейном движении — это величина, равная отношению пути $s$ ко времени, за которое этот путь пройден:

$υ={s}/{t}$

Перемещение при прямолинейном равномерном движении (по оси X) можно рассчитать по формуле:

$∆x=υ_xt$

где $υ_x$ — проекция скорости на ось X. Отсюда закон прямолинейного равномерного движения имеет вид:

$x=x_0+υ_xt$

Если в начальный момент времени $x_0=0$, то

$x=υ_xt$

График зависимости скорости от времени — прямая, параллельная оси абсцисс, а пройденный путь — это площадь под этой прямой.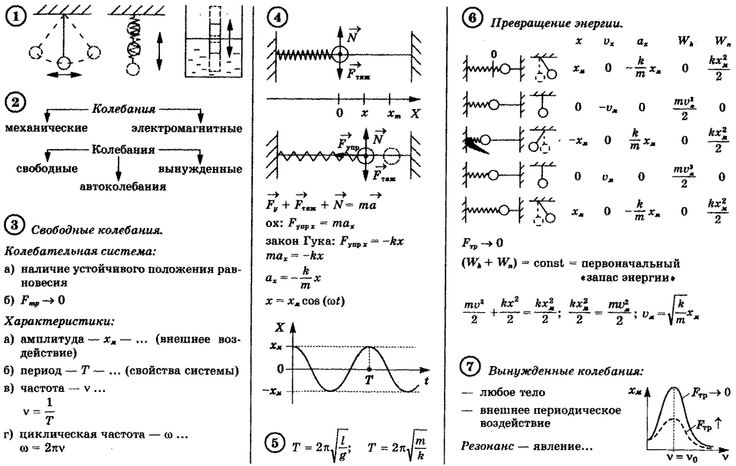

График зависимости пути от времени — прямая линия, угол наклона которой к оси времени $Ot$ тем больше, чем больше скорость равномерного движения. Тангенс этого угла равен скорости.

Скорость, ускорение, равномерное и равноускоренное прямолинейное движение

Основные понятия и законы кинематики

Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.

По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.

Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения

Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение

— это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x₀ + V_xt, где x₀ — начальная координата тела, V_x — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с², не зависящим от массы падающего тела.

Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:

Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название

угловой скорости ω:

Угловая скорость связана с линейной скоростью соотношением

где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν

Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют

центростремительным ускорением, оно направлено по радиусу к центру окружности:

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.

Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).

Или короче, сила действия равна силе противодействия.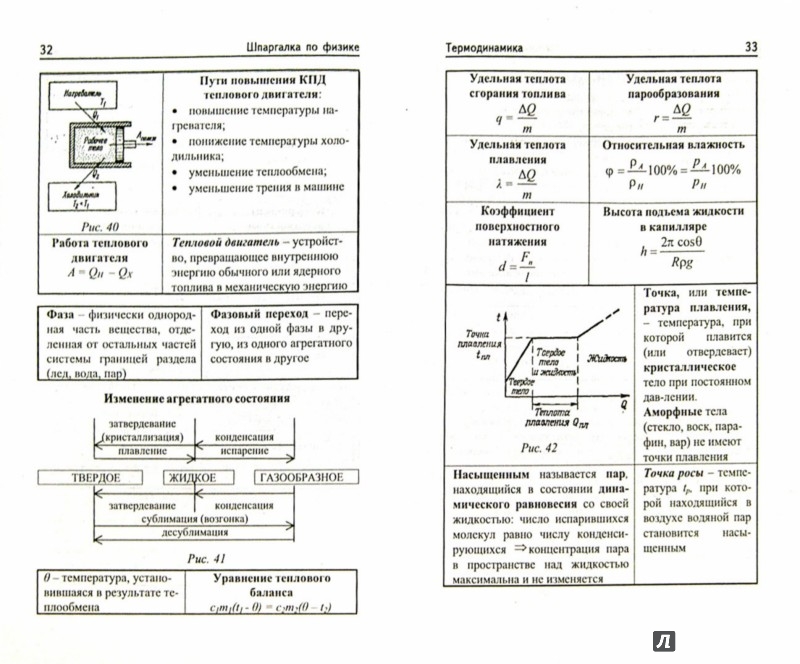 Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.

Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде

где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения

подсчитывается по формуле

где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения

Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.

Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.

Сила тяжести — это сила, с которой все тела притягиваются к Земле:

При неподвижной опоре вес тела равен по модулю силе тяжести:

Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес

Видно, что вес тела больше веса покоящегося тела.

При движении тела с ускорением, направленным вниз, его вес

В этом случае вес тела меньше веса покоящегося тела.

Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.

где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна

1.3. Основные понятия и законы статики и гидростатики

Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).

Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.

Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.

Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:

Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей

где ρ — плотность жидкости, h — глубина проникновения в жидкость.

Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае

Высоты столбов жидкости обратно пропорциональны плотностям:

Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то

Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:

где ρ_жидк — плотность жидкости, в которую погружено тело; V_погр — объём погружённой части тела.

Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.

1.4. Законы сохранения

Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:

Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:

Мощность — это работа, совершённая в единицу времени:

Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле

Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле

где h — высота подъёма

Энергия сжатой пружины:

где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.

Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.

1.5. Механические колебания и волны

Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.

Величина A, равная наибольшему абсолютному значению колеблющейся физической величины x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:

Частота измеряется в с^-1. Эта единица называется герц (Гц).

Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.

Период колебаний математического маятника определяется по формуле

где l — длина маятника.

Период колебаний груза на пружине определяется по формуле

где k — жёсткость пружины, m — масса груза.

Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:

где v — скорость распространения волны.

Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.

AP Физика 1: на основе алгебры – Студенты AP

Не студент?

Посетите AP Central, чтобы получить ресурсы для учителей, администраторов и координаторов.

AP Физика 1: на основе алгебры

Перейти к моей точке доступа

О курсе

Обновление информации о курсе
Колледжи согласны с тем, что разделы 8-10 могут быть удалены из AP Physics 1, поскольку они рассматриваются в AP Physics 2; соответственно, модули 8–10 больше не тестируются в AP Physics 1. С 2021 года экзамены AP Physics 1 сосредоточены исключительно на содержании, охватываемом модулями 1–7.

Узнайте об основных принципах физики, изучая ньютоновскую механику; работа, энергия и мощность; механические волны и звук; и вводные, простые схемы. Вы будете выполнять практическую лабораторную работу по исследованию явлений.

Примечание: Сохраняйте лабораторные журналы и отчеты; колледжи могут попросить вас увидеть их, прежде чем предоставить вам кредит.

Навыки, которым вы научитесь

Эквивалентность и предварительные условия

Эквивалент курса колледжа

Вводный курс колледжа по алгебраической физике в первом семестре

Рекомендуемые предварительные условия

Вы должны пройти курс геометрии и одновременно изучать алгебру II или аналогичный курс.

Экзамен Дата

О модулях

Содержание курса, описанное ниже, организовано в виде общеизучаемых учебных модулей, которые предоставить одну возможную последовательность для курса. Ваш преподаватель может решить организовать курс контента по-разному в зависимости от местных приоритетов и предпочтений.

Содержание курса

Блок 1: Кинематика

Вы познакомитесь с изучением движения.

Темы могут включать:

• Положение, скорость и ускорение
• Представления движения

12%–18% от экзаменационного балла

Модуль 2: Динамика

Вы вернетесь к концепциям, с которыми вы работали в Модуле 1, чтобы исследовать силу, то есть взаимодействие одного объекта с другим объектом.

Темы могут включать:

• Системы
• Гравитационное поле
• Контактные силы
• Первый закон Ньютона
• Третий закон Ньютона и диаграммы свободного тела
• Второй закон Ньютона
• Применение второго закона Ньютона

16–20% от экзаменационного балла

Модуль 3: Круговое движение и гравитация

Вы будете опираться на свое понимание движения и силы, изучая более сложные модели движения, такие как круговая траектория спутника, вращающегося вокруг планеты.

Темы могут включать:

• Векторные поля
• Фундаментальные силы
• Гравитационные и электрические силы
• Гравитационное поле/ускорение силы тяжести на разных планетах
• Инерционная масса против гравитационной
• Центростремительное ускорение против центростремительной силы
• Диаграммы свободного тела для объектов, находящихся в равномерном круговом движении

6–8% от экзаменационного балла

Блок 4: Энергия

Вы узнаете определения и отношения между энергией, работой и силой.

Темы могут включать:

• Открытые и закрытые системы: Энергетика
• Работа и механическая энергия
• Сохранение энергии, принцип работы-энергии и мощность

20–28% от экзаменационного балла

Раздел 5: Импульс

Вы изучите взаимосвязь между силой, временем и импульсом и научитесь использовать закон сохранения импульса для анализа физических ситуаций.

Темы могут включать:

• Импульс и импульс
• Представления изменения импульса
• Открытые и закрытые системы: импульс
• Закон сохранения импульса

12%–18% от экзаменационного балла

Модуль 6: Простое гармоническое движение

Вы будете использовать инструменты, методы и модели, которые вы изучили в предыдущих модулях, для анализа нового типа движения: простого гармонического движения.

Темы могут включать:

• Период простых гармонических осцилляторов
• Энергия простого гармонического осциллятора

4%–6% экзаменационной оценки

Блок 7: Крутящий момент и вращательное движение

Вы изучите движение объекта, вращающегося вокруг оси, и изучите крутящий момент, меру силы, которая может вызвать вращательное движение.

Темы могут включать:

• Вращательная кинематика
• Крутящий момент и угловое ускорение
• Угловой момент и крутящий момент
• Сохранение углового момента

12%–18% от экзаменационного балла

Гл. 1 множественный выбор — физика

Большой выбор

1.1 Физика: определения и приложения

39.

Современную физику лучше всего можно описать как комбинацию каких теорий?

1. квантовая механика и теория относительности Эйнштейна

2. квантовая механика и классическая физика

3. Законы движения Ньютона и классическая физика

4. Законы движения Ньютона и теория относительности Эйнштейна

40.

Что из следующего можно точно изучить с помощью классической физики?

1. сила гравитации в черной дыре

2. движение самолета по небу

3. столкновения субатомных частиц

4. влияние гравитации на течение времени

41.

Что из следующего лучше всего описывает, почему знание физики необходимо для понимания всех других наук?

1. Физика объясняет, как энергия переходит от одного объекта к другому.

2. Физика объясняет, как работает гравитация.

3. Физика объясняет движение объектов, которое можно увидеть невооруженным глазом.

4. Физика объясняет фундаментальные аспекты Вселенной.

42.

Какое отношение лучевая терапия, используемая для лечения больных раком, имеет к физике?

1. Понимание того, как размножаются клетки, связано в основном с физикой.

2. Прогнозы побочных эффектов лучевой терапии основаны на физике.

3. Устройства, используемые для генерации некоторых видов излучения, основаны на принципах физики.

4. Прогнозы продолжительности жизни пациентов, получающих лучевую терапию, основаны на физике.

1,2 Научные методы

43.

Модель металлов со свободными электронами объясняет некоторые важные свойства металлов, предполагая, что электроны металла свободно перемещаются в металле, не отталкивая друг друга. В каком смысле теория свободных электронов основана на модели?

1. Для его использования необходимо изготовить копии металлической проволоки в лаборатории.

2. Он включает в себя анализ воображаемой системы, более простой, чем реальный провод, на который она похожа.

3. Он исследует модель или идеальное поведение, которому должны подражать другие металлы.

4. Он пытается исследовать металл очень реалистичным или модельным способом.

44.

Ученый хочет изучить движение примерно 1000 молекул газа в контейнере, моделируя их как крошечные бильярдные шары, случайным образом отскакивающие друг от друга. Что из следующего необходимо для расчета и хранения данных об их детальном движении?

1. группа гипотез, не поддающихся практической проверке в реальной жизни
2. компьютер, который может хранить и выполнять вычисления на больших наборах данных
3. большое количество экспериментальных результатов по молекулам и их движению
4. набор еще не проверенных гипотез относительно молекул

45.

Когда большое количество экспериментальных данных поддерживает гипотезу, какую гипотезу в конечном итоге можно рассматривать?

1. наблюдение

2. понимание

3. вывод

4. закон

46.

Наблюдая за муравьями возле своего дома, вы замечаете, что рабочие муравьи собираются в определенном месте на вашей лужайке. Что из следующего является поддающейся проверке гипотезой, которая пытается объяснить, почему муравьи собираются в этом конкретном месте на лужайке?

1. Рабочий подумал, что это хорошее место.

2. потому что муравьям, возможно, придется найти место, где королева отложит яйца

3. , потому что там могут лежать частицы пищи

4. , потому что рабочие муравьи должны собираться вместе в одном месте. 9{-3} метра?

   1. 2,0 ​​км

   2. 2,0 ​​мегаметра

   3. 2,0 ​​мм

   4. 2,0 ​​микрометра

   48.

   Предположим, что весы в ванной показывают массу человека как 65 кг с погрешностью 3 процента. Какова неопределенность их массы в килограммах?

   1. а. 2 кг
   2. б. 98 кг
   3. с. 5 кг
   4. д. 0

   49.

   Что из следующего лучше всего описывает переменную?

   1. тренд, демонстрирующий экспоненциальную зависимость

   2. что-то, значение которого может меняться в течение нескольких измерений

   3. мера того, насколько линия графика изменяется по оси Y

   4. то, что остается постоянным при нескольких измерениях

   50.

   Тренер по легкой атлетике только что купил новый секундомер с погрешностью ±0,05 с.