Линейная функция — подготовка к ЕГЭ по Математике

Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.

Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

А что же будет, если ? Мы получим горизонтальную прямую На рисунке показан график функции

Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова.

В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой это не выполняется: значению соответствует бесконечно много значений у.

Если прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции 

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

При получаем, что

При получаем, что

Значит, наша прямая проходит через точки и

Выразив у из уравнения , получим уравнение прямой вида

Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.

Зачем изучать линейную функцию? 

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Формула для равномерного прямолинейного движения: . Пройденное расстояние S прямо пропорционально времени.

Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует или , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.

Спасибо за то, что пользуйтесь нашими публикациями.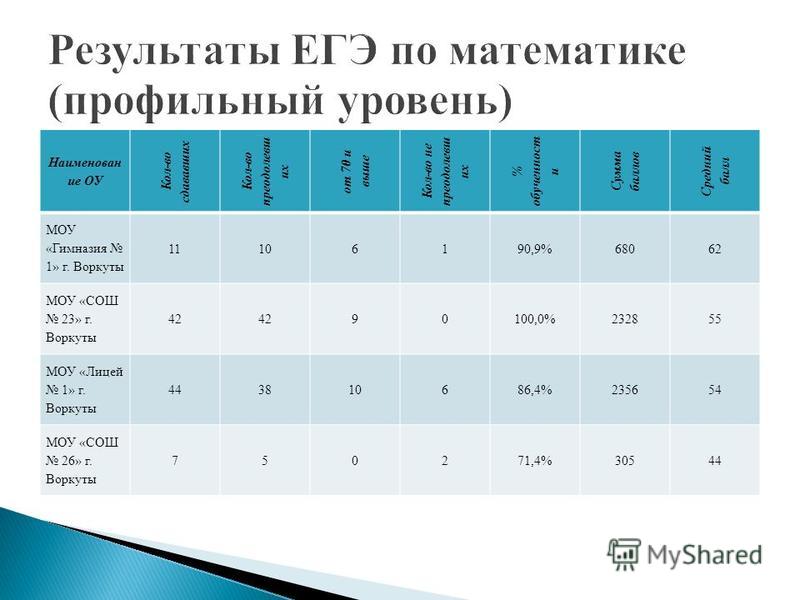 Информация на странице «Линейная функция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 07.04.2023

Задание 9 ЕГЭ по математике базового уровня 2023

Если задание выполнено на отлично, то сможешь получить 1 первичный балл.

На решение отводится примерно 5 минут.

Чтобы решить задание 9 по математике базового уровня нужно знать:

  • Единицы измерения величин

Could not load xLike class!

Установите соответствие между величинами и их возможными значениями:

ВЕЛИЧИНЫВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) Скорость движения велосипедиста

Б) Скорость полета космического корабля

В) Скорость распространения света

Г) Скорость движения улитки

1) 0,4 м/мин

2) 15 км/ч

3) 20 000 км/ч

4) 300 000 км/с

 

В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.

АБВГ
    

 

Обсуждение

Установите соответствие между величинами и их возможными значениями:

ВЕЛИЧИНЫВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) Объем ящика с апельсинами
Б) Объем воды в озере Байкал
В) Объем банки кетчупа
Г) Объем бассейна

1) 110 л
2) 900 м3
3) 0,3 л
4) 18,4 км3

 

В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.

АБВГ
    

Обсуждение

Установите соответствие между величинами и их возможными значениями:

ВЕЛИЧИНЫВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) Масса автобуса
Б) Масса ореха
В) Масса кота
Г) Масса капли воды

1) 6 кг
2) 20 мг
3) 7 г
4) 9 т

 

В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.

АБВГ
    

Обсуждение

Установите соответствие между величинами и их возможными значениями:

ВЕЛИЧИНЫВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) Масса волейбольного мяча

Б) Масса капли дождя

В) Масса взрослого носорога

Г) Масса посудомоечной машины

1) 20 кг
2) 2,4 т
3) 20 мг
4) 800 г

 

В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.

АБВГ
    

Обсуждение

Установите соответствие между величинами и их возможными значениями:

ВЕЛИЧИНЫВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) Расстояние от школы до дома
Б) Расстояние от Земли до Венеры
В) Расстояние от Москвы до Омска
Г) Расстояние между глазами человека

1) 2700 км
2) 190·106 км
3) 60 мм
4) 1 км

 

В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.

АБВГ
    

Обсуждение

Начать

Практический тест FTCE по математике для средних классов 5–9 (2023)

Экзамен FTCE по математике для средних классов 5–9 используется для сертификации кандидатов, которые могут преподавать математику в пятом–девятом классах. Вопросы предназначены для измерения вашего знания математики в этих классах (и немного выше), а также вашего понимания принципов и практики преподавания этой математики учащимся в этом возрастном диапазоне.

Начать тест

 

Учебное пособие FTCE
Карточки FTCE
Тест FTCE

Когда предлагается экзамен FTCE по математике для средних классов 5-9?

Тест доступен круглый год в центрах CBT, расположенных по всему штату Флорида. Его также предлагают в центрах тестирования по всей территории Соединенных Штатов на случай, если вам нужно сдать тест за пределами штата. Несмотря на эту доступность, вам все равно следует планировать встречу как можно раньше, потому что ограниченное количество доступных мест предоставляется в порядке живой очереди.

Прежде чем зарегистрироваться на экзамен, выберите желаемую дату и одну или две альтернативные даты на тот случай, если первый вариант уже занят. При регистрации вам необходимо будет оплатить экзаменационный сбор в размере 150 долларов США.

Сколько времени займет тест?

Общее время пребывания в центре тестирования составит чуть более трех часов. Это включает в себя 30 минут на регистрацию, два с половиной часа на сам тест и около 15 минут после экзамена на то, чтобы администратор собрал материалы и чтобы вы подняли любые вопросы или опасения, которые у вас есть по поводу теста. Например, если во время экзамена произошли какие-либо сбои, которые, по вашему мнению, могли повлиять на вашу успеваемость, вам необходимо сообщить об этом до того, как вы покинете центр тестирования.

Перерывы по расписанию не предусмотрены. Это означает, что вы можете делать перерывы по мере необходимости, но часы не останавливаются, поэтому любые перерывы будут сокращать ваше общее время теста. Учитывая эту политику, сделайте все возможное, чтобы вам не пришлось делать перерыв в течение двух с половиной часов, отведенных на экзамен.

Что еще более важно, 30-минутная регистрация должна пройти до фактической встречи. Если вы опоздаете, чтобы пройти регистрацию до начала экзамена, вас не пустят в экзаменационную комнату. Поэтому, если ваша встреча назначена, скажем, на 10:30, вам нужно прибыть в центр тестирования не позднее 10:00.


Ознакомьтесь с учебным пособием Mometrix по FTCE

Получите практические вопросы, видеоуроки и подробные учебные уроки

Получите учебное пособие


По какому типу математики я буду проходить тестирование?

75 вопросов с несколькими вариантами ответов в тесте охватывают ряд важных математических понятий и принципов обучения. Ниже приведен краткий план вместе с оценкой количества вопросов, которые будут связаны с каждой концепцией и навыком:

  • Знание навыков решения задач и рассуждения – 9-10 вопросов
  • Знание математических манипуляций и моделей и технологии обучения – 4-5 вопросов
  • Знание оценивания по математике – 6-7 вопросов
  • Знание связей между математическими понятиями – 5-6 Вопросы
  • Знание смысла чисел, операций и пропорциональности – 9-10 Вопросы
  • Знание основ алгебры – 10-11 Вопросы
  • Знание алгебраического мышления – 8-9Вопросы
  • Знание анализа данных, статистики и вероятности – 5-6 Вопросы
  • Знание двухмерной геометрии – 11-12 Вопросы
  • Знание измерения и пространственного чувства – 6-7 Вопросы

Какой балл Do I Нужно получить?

Вам необходимо набрать по шкале не менее 200 баллов (из 300 возможных). Это соответствует примерно 54 правильным ответам из 75 вопросов. Это число не должно использоваться в качестве точной цели для вашего обучения, а скорее является приблизительной оценкой того, сколько пространства для маневра у вас есть на экзамене. Другими словами, во время учебы, если вы поставите перед собой цель правильно ответить не менее чем на 60 вопросов во время практических занятий, вы обязательно подготовитесь к получению проходного балла в день экзамена.

Сразу после экзамена вы можете увидеть свой неофициальный балл, чтобы узнать, сдали ли вы экзамен. Если вы не сдадите экзамен с первой попытки, вы можете сдать его повторно, но за каждую последующую попытку вам придется заплатить сбор в размере 220 долларов США. Так что лучше дать себе достаточно времени перед первой попыткой как следует подготовиться.

Как мне подготовиться к тесту?

Большая часть учебного времени должна быть посвящена изучению соответствующей математики и оттачиванию навыков вычисления и математического мышления. Однако вам также следует уделить немного времени ознакомлению со стандартами и общепринятой практикой преподавания математики учащимся в этом возрастном диапазоне.

Все это можно сделать с помощью учебного пособия Mometrix и карточек Mometrix. Эти инструменты помогут вам просмотреть всю необходимую математику, которую вам нужно знать в день экзамена. Они также предоставят множество практических вопросов, которые вы можете использовать для развития своих навыков, поскольку они должны быть применены к тесту.

FTCE Математика для средних классов 5–9 Учебное пособие

Ознакомьтесь с карточками FTCE от Mometrix

Разбейте сложные предметы на понятные понятия

Получите карточки

Академия Mometrix — это совершенно бесплатный ресурс, предоставляемый Mometrix Test Preparation. Если вы найдете пользу от наших усилий здесь, ознакомьтесь с нашим высококачественным учебным пособием FTCE для средних классов по математике 5-9, чтобы поднять свое обучение на новый уровень. Просто нажмите ссылку на учебное пособие FTCE Middle Grades Mathematics 5-9 ниже. Ваша покупка также помогает нам создавать еще больше отличного бесплатного контента для тестируемых.

Тест FTCE

FTCE Средние классы Математика 5–9Практический тест и подготовка

FTCE Math 5-9 Практический тест

Добро пожаловать на нашу страницу пробного теста и подготовки к FTCE по математике для средних классов 5-9. На этой странице мы описываем предметные области и ключевые концепции экзамена FTCE Mathematics 5-9. Это бесплатный ресурс, который мы предоставляем, чтобы вы могли увидеть, насколько вы готовы к официальному экзамену.

В то время как в этом бесплатном руководстве описываются компетенции и домены, полученные на экзамене, наше платное учебное пособие FTCE Mathematics 5-9 охватывает ВСЕ концепции, которые вам нужно знать, и создано для обеспечения вашего успеха! Наша онлайн-математика FTCE 5-9учебное пособие содержит учебные материалы, соответствующие тестированию, с использованием интерактивных пособий, видео, карточек, викторин и практических тестов.

Смогу ли я пройти, используя эту бесплатную статью? Смогу ли я пройти, используя ваше платное учебное пособие?

Если вы воспользуетесь этим руководством и самостоятельно изучите ключевые понятия экзамена FTCE Mathematics 5-9, возможно, вы его сдадите, но зачем рисковать? С нашим платным учебным пособием мы гарантируем, что вы пройдете.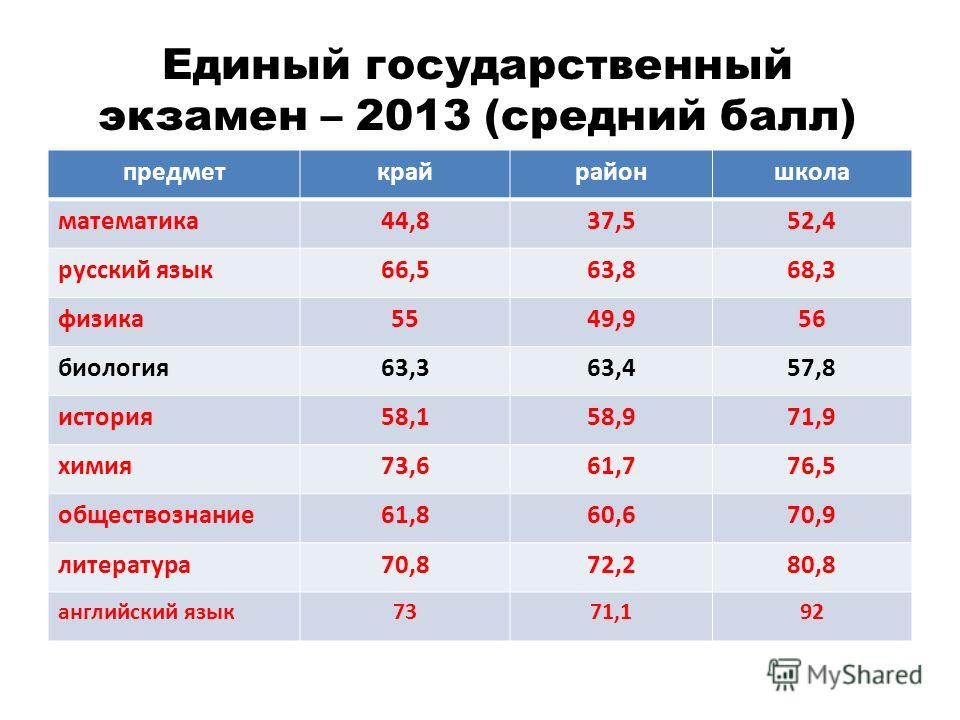

Еще не готовы начать учиться? Это нормально. Продолжайте читать, а когда будете готовы, пройдите наш бесплатный курс FTCE по математике для средних классов 5–9.практические тесты.

В этой статье мы рассмотрим:

  • Информация о тесте FTCE Math 5-9
  • Компетенции FTCE Math 5-9

Информация о тесте FTCE Math 5-9

1 Обзор: 2 

2 Обзор: 003

Флорида учитель Кандидаты на получение сертификата должны пройти этот тест, который охватывает математику для 5-9 классов.

Формат:

Экзамен FTCE по математике для средних классов 5–9 содержит около 75 вопросов с несколькими вариантами ответов. У вас будет два с половиной часа, чтобы сдать экзамен.

Стоимость:

150 долларов США

Оценка:

Чтобы сдать экзамен, необходимо набрать не менее 200 баллов по шкале.

Проходной балл:

Согласно Годовому административному и техническому отчету за 2020 г. , проходной балл составил 45% . Дайте себе достаточно времени для работы над каждой темой, пока не почувствуете себя уверенно в большинстве тем. Составьте учебный план с указанием времени, необходимого для изучения каждой темы, и дней, в которые вы планируете это делать.

Что хотели бы знать испытуемые: 

  • На испытательном полигоне предоставляется научный калькулятор Texas Instruments TI-30X IIS. Экзаменуемые не могут приносить свой собственный калькулятор.
  • Справочный лист для этого теста не предоставляется.
  • Неофициальный статус пройден/не пройден предоставляется сразу после тестирования.
  • Вы не будете оштрафованы за неправильные ответы, поэтому сделайте обоснованное предположение, если вы не уверены.

Информация получена с веб-сайта Национальной серии оценок: https://www.fl.nesinc.com/testPage.asp?test=025

 

Измените свои результаты! Попробуйте бесплатно учебное пособие FTCE (025).

Попробуй перед покупкой

Математика FTCE 5-9 Компетенции

Обзор

Экзамен включает десять компетенций:

  • Решение проблем и рассуждение (13%)
  • Манипуляции, модели и технологии обучения 900 (40%)
  • Оценка по математике (9%)
  • Связи между математическими понятиями (7%)
  • Смысл чисел, операции и пропорциональность (9%)
  • Основы алгебры (14%)
  • Алгебраическое мышление (11%)
  • Анализ данных, статистика и вероятности (7%)
  • Двумерная геометрия (15%)
  • Измерение и пространственное чувство (9 %)

Итак, давайте сначала поговорим о решении проблем и рассуждениях.

Решение проблем и рассуждение

Эта компетенция включает около 10 вопросов с несколькими вариантами ответов, что составляет около 13% всего экзамена.

Эти вопросы проверяют ваши знания стратегий решения задач и математических выражений, а также вашу способность использовать логику и рассуждения.

Давайте поговорим о некоторых концепциях, которые вы, скорее всего, увидите на тесте.

Стратегии обучения: решение задач

Одна из стратегий помощи учащимся средних классов в решении задач, особенно текстовых, состоит в том, чтобы разбить задачу на следующие этапы:

  1. Запишите известную вам информацию.
  2. Запишите, что вам нужно.
  3. Нарисуйте любые соответствующие схемы.
  4. Используйте то, что у вас есть, чтобы работать над тем, что вам нужно.
  5. Обведите решение. Убедитесь, что вы ответили на заданный вопрос и правильно указали единицы измерения.

Другая стратегия решения задач, которая помогает учащимся найти ключевую информацию в задаче, называется C. U.B.E.S:

C обведите важные числа

U подчеркните формулировку вопроса

B

E дополнительная информация

S принцип работы

Дедуктивное рассуждение против индуктивного

Дедуктивное рассуждение, иногда называемое нисходящим рассуждением, начинается с предпосылок, истинность которых известна, и продолжается до логического завершения.

Например, люди дышат воздухом. Дэвид — человек; следовательно, Давид дышит воздухом.

Индуктивное рассуждение, иногда называемое восходящим рассуждением, начинается с конкретных наблюдений и объединяет их, чтобы сделать широкие обобщения.

Например, вы заметили, что Джулия опаздывает на работу. Джулия — подросток; следовательно, вы заключаете, что подростки безответственны.

Выводы, сделанные с помощью индуктивных рассуждений, иногда могут быть ошибочными, но этот тип рассуждений по-прежнему важен. Индуктивное рассуждение чаще всего используется для формирования гипотез, которые затем можно проверить с помощью научного метода.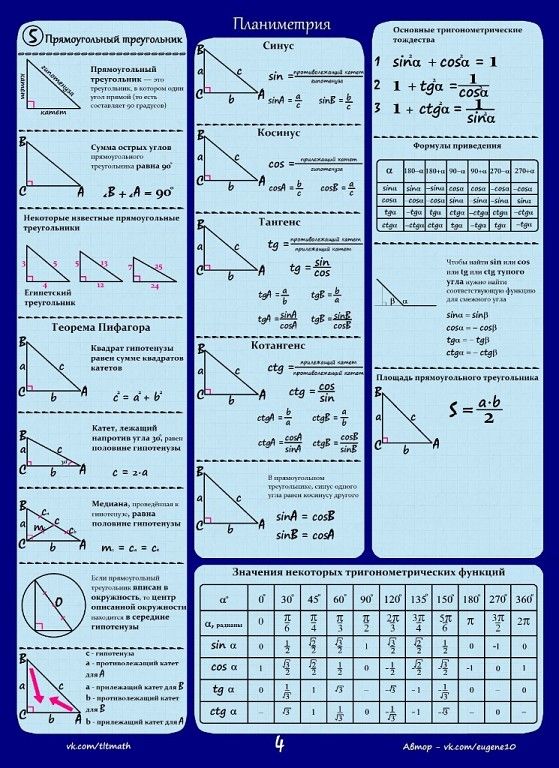

Манипуляции, модели и технологии обучения

Эта компетенция включает около 5 вопросов с несколькими вариантами ответов, что составляет около 6% всего экзамена.

Эти вопросы проверяют ваши знания в области манипулятивных действий, технологий и множественных представлений математических понятий.

Вот некоторые концепции, которые вы можете увидеть на тесте.

Использование моделей

Модели обеспечивают визуальные изображения математических понятий, которые могут помочь запомнить понятия, а также лучше понять их.

Например, ниже приведена модель возведения в квадрат биномиального выражения 5 x – 3:

Графические калькуляторы

В средних классах графические калькуляторы полезны для построения графиков линейных и квадратных уравнений. Они особенно полезны для студентов, чтобы проверить свою работу, как только они поймут, как графически строить такие уравнения вручную.

Графический калькулятор также можно использовать для быстрого поиска статистических измерений из списка данных с помощью функции списка, включая минимум, максимум, среднее значение, медиану, а также верхний и нижний квартили. Это может быть полезно при анализе данных вероятностного моделирования.

Графические калькуляторы наиболее полезны, когда на них не полагаются как на опору для непонимания математических концепций. Поэтому их следует использовать ограниченно.

Один из самых простых способов научить учащихся пользоваться графическим калькулятором — это использовать симулятор онлайн-калькулятора, чтобы они могли следить за тем, как вы последовательно нажимаете кнопки на диаэкране или проекторе.

Assessment

Эта компетенция включает около 7 вопросов с несколькими вариантами ответов, что составляет около 9% всего экзамена.

Эти вопросы проверяют ваши знания в области диагностики потребностей учащихся, интерпретации успеваемости и определения соответствующих оценок.

Давайте поговорим о некоторых конкретных понятиях, которые вам необходимо знать.

Формирующее и итоговое оценивание

Формирующее оценивание проводится регулярно в течение учебного года, чтобы обеспечить постоянную обратную связь и помочь учителям определить концепции, которые необходимо охватить более подробно. Формирующее оценивание также помогает учащимся определить, где их собственное понимание можно улучшить. Формирующее оценивание обычно имеет более низкие ставки и может включать в себя очень неформальные задания, такие как игры, проекты и групповая работа, а также написание краткого изложения основного момента урока в этот день или представление плана работы перед ее написанием.

Суммарное оценивание обычно дается в конце главы, раздела или курса, чтобы определить, сколько учащийся усвоил и усвоил. Эти типы оценок обычно имеют более высокие ставки и включают в себя тесты, викторины, итоговые работы или кумулятивные проекты.

Системы отклика аудитории

Системы отклика аудитории — это технология, которая позволяет учителю очень быстро опрашивать большую группу учащихся. Обычно они включают в себя какой-то портативный инструмент для голосования, который выдается каждому студенту. Затем учащиеся голосуют по теме, а результаты подводятся и отправляются учителю.

Например, учитель может написать на доске вопрос с несколькими вариантами ответов и попросить учеников выбрать a, b, c или d. После того, как учащиеся сделают свой выбор, учитель может в течение нескольких секунд определить, понятна ли концепция большинству учащихся или ее необходимо охватить более подробно.

Связи между математическими понятиями

Эта компетенция включает около 5 вопросов с несколькими вариантами ответов, что составляет около 7% всего экзамена.

Эти вопросы проверяют ваши знания о математических ошибках, взаимосвязях между навыками и распространенных заблуждениях.

Давайте посмотрим на концепцию, которая, скорее всего, появится на тесте.

Распространенные заблуждения в математике

Учащиеся часто путают площадь и периметр, особенно если им задана форма, отличная от прямоугольника. Они пытаются найти площадь фигуры, складывая длины сторон.

При работе с ящичковыми диаграммами распространено заблуждение, что отображаемая медиана на самом деле является средним значением или средним значением данных.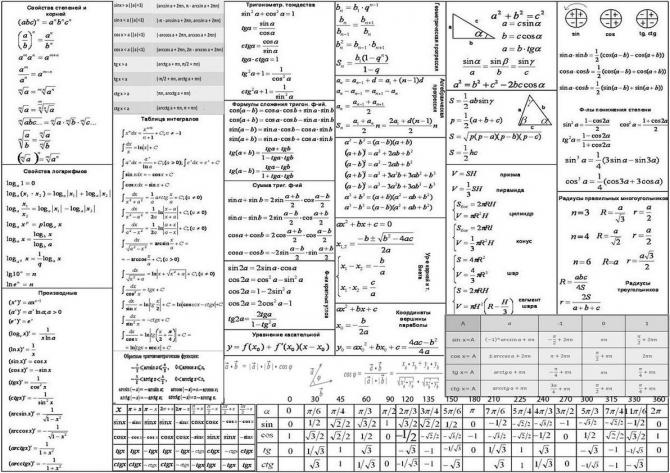

Еще одно распространенное заблуждение состоит в том, что, извлекая квадратный корень из обеих частей уравнения, вы получаете только положительный корень. Студентам очень легко забыть включить как положительный, так и отрицательный корень, даже после того, как их явно этому научили.

Смысл чисел, операции и пропорциональность

Эта компетенция включает около 7 вопросов с несколькими вариантами ответов, что составляет около 9% всего экзамена.

Эти вопросы проверяют ваши знания в области оценок, факторизации, соотношений и относительных величин.

Вот некоторые концепции, которые вы можете увидеть на тесте.

Кубические корни

Кубический корень числа — это значение, которое при трехкратном умножении само на себя дает это число.

Например, кубический корень из 64 равен 4, так как 4*4*4 = 64.

Кубический корень из -729 равен -9, так как -9*-9*-9 = -729.

Кубические корни не всегда являются целыми числами. Например, кубический корень из 21 не является целым числом, поскольку его можно разложить только как 1*21 или 3*7. Однако мы можем сказать, что кубический корень из 21 примерно равен 2,7589.…

GCF и LCM

GCF (наибольший общий делитель) — это наибольший общий делитель для двух чисел.

Например, давайте найдем НОД чисел 18 и 108:

Сначала найдем все множители каждого числа.

18 имеет множители 1, 2, 3, 6, 9, 18.

108 имеет множители 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108.

Факторы общими между этими числами являются 1, 2, 3, 6, 9 и 18.

Наибольший из этих множителей равен 18; следовательно, GCF 18 и 108 равен 18,9.0003

НОК (наименьший общий кратный) — это наименьшее значение, являющееся общим кратным двух чисел.

Например, найдем НОК 6 и 15:

Сначала перечислим кратные каждому числу.

*ПРИМЕЧАНИЕ. Как правило, если вы не знаете, когда прекратить перечисление, продолжайте, пока не получите произведение двух чисел (в данном случае 6*15 = 90). Это число всегда является общим кратным двух; однако оно может не быть наименьшим общим кратным*.0, …

Число, кратное 15, равно 15, 30, 45, 60, 75, 90, …

30, 60 и 90 являются общими кратными 6 и 15; однако, поскольку 30 — наименьшее значение, это LCM.

Основы алгебры

Эта компетенция включает около 11 вопросов с несколькими вариантами ответов, что составляет около 14% всего экзамена.

Эти вопросы проверяют ваши знания шаблонов, неравенств, линейных уравнений и квадратных корней, а также вашу способность упрощать выражения.

Давайте поговорим о некоторых концепциях, которые вы, скорее всего, увидите на тесте.

Решение неравенств

Пример 1:

Решите неравенство 4 x < 2 x + 8. Для этого с обеих сторон вычтем 2 х :

4 х – 2 х < 8

2 х < 8

x < 4

Пример 2

: Решите неравенство ниже: 0278 . Вычтите 10 с обеих сторон:

-7 x ≤ 31 – 10

-7 x ≤ 21

Разделите обе части на -7:

x

*00TENO ≥ 009 : Когда ты умножив или разделив неравенство на отрицательное число, необходимо обратить неравенство (перевернуть знак). *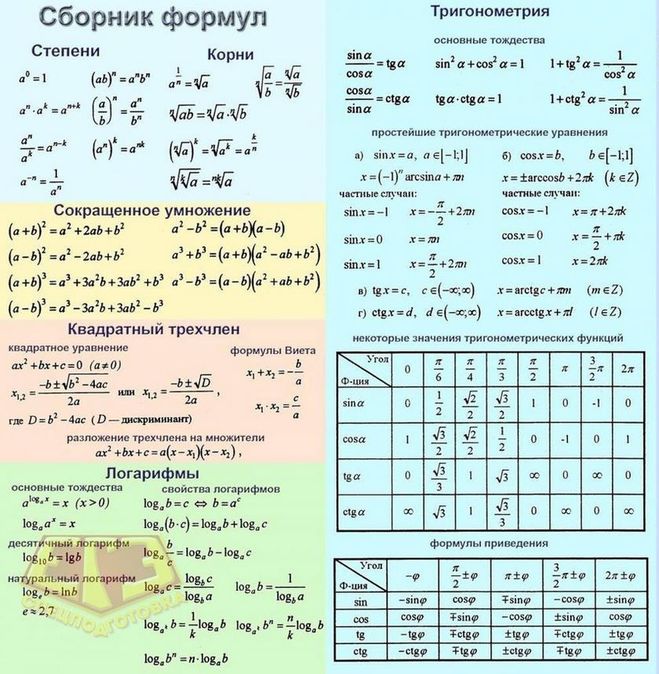

Мы можем представить решение x ≥ -3 на числовой прямой. Поскольку в этом неравенстве используется символ «≥», решение включает значение -3 и все, что больше -3. Итак, заштрихуем справа от -3 на числовой прямой:

Определение уравнения прямой

Уравнение прямой можно определить с помощью двух точек на прямой или с помощью y — точка пересечения и наклон линии.

Эта информация может быть включена в различные формы линейных уравнений:

Форма «точка-уклон»

:

y-y1=m(x-x1)

, где м — уклон, а (x1,y1) — точка на линии.

Форма пересечения уклона

: y = m x + b , где м — уклон, а b — y

-координата концепция

Наклон линии рассчитывается по формуле

м = (y2–y1)/(x2–x1).

Пример 1: Вам дан приведенный ниже график.

Наклон можно рассчитать, используя любые две точки на линии. Мы выберем (2, 0) и (0 , -4):

Используя форму уравнения линии с наклоном точки, y – 0 = 2 ( x – 2).

Пример 2: Учитывая, что линия имеет наклон -8 и точку пересечения y в точке (0, 4), найдите уравнение линии.

В этом случае проще найти уравнение прямой в виде точки пересечения. Мы знаем, что м = -8 и b = 4. Следовательно, y = m x + b = -8 x + 4. Уравнение прямой: y = -8 +

Алгебраическое мышление

Эта компетенция включает около 8 вопросов с несколькими вариантами ответов, что составляет около 11% всего экзамена.

Эти вопросы проверяют ваши знания в области решения систем уравнений и квадратных функций, а также поиска нулей многочленов. Вы также должны знать законы показателей.

Вот некоторые понятия, которые вам необходимо знать.

Факторирование полиномов

Факторинг представляет собой запись полинома как произведения двух других полиномов. Обычно это применяется для упрощения выражения, включающего многочлены, или для нахождения корней многочлена. Существует множество стратегий разложения многочленов на множители, включая разложение наибольшего общего кратного, разложение на множители трехчленов с совершенными квадратами, разложение на множители с помощью группировки и несколько других стратегий.

Давайте рассмотрим несколько примеров.

Законы экспонент

Для a (любое действительное число), b (любое ненулевое действительное число) и n и m (натуральные числа) выполняются следующие свойства. :

Анализ данных, статистика и вероятность

Эта компетенция включает около 5 вопросов с несколькими вариантами ответов, что составляет около 7% всего экзамена.

Эти вопросы проверяют ваши знания статистических показателей, графического представления наборов данных, выборок населения и вероятностей.

Давайте поговорим о концепции, которую вы, скорее всего, увидите на тесте.

Центральная тенденция

Меры центральной тенденции помогают нам определить, как распределяются данные, определяя одно значение примерно в центре данных. Ниже мы рассмотрим несколько показателей центральной тенденции.

Среднее значение набора данных – это среднее значение набора данных. Это можно найти, сложив все значения и разделив их на общее количество значений.

Режим набора данных — это значение, которое чаще всего встречается в наборе данных. В наборе данных может быть более одной моды, если несколько значений встречаются чаще всего.

Медиана набора данных – это среднее значение в наборе, когда точки данных упорядочены от наименьшего к большему. Если имеется четное количество точек данных, точного среднего значения не будет. В этом случае медиана находится путем получения среднего значения двух точек данных, ближайших к середине.

Например, предположим, что возраст группы из десяти учащихся был собран и указан ниже:

9, 11, 13, 11, 8, 7, 13, 9, 9, 12

Среднее значение этого набора данных можно найти, сложив все эти возрасты вместе и разделив на 10, так как есть 10 учеников:

Среднее = (9+11+13+11+8+7+13+9+9+12) /10=10,2

до наивысшего.

7, 8, 9, 9, 9, 11, 11, 12, 13, 13

Теперь мы можем видеть, что мода набора данных равна 9, так как 9 встречается 3 раза, что больше любых других данных точка.

Поскольку набор данных содержит четное количество значений, в середине находятся два значения: 9 и 11. Чтобы найти медиану, необходимо усреднить 9 и 11; поэтому медиана набора данных равна 10.

Двухмерная геометрия

Эта компетенция включает около 11 вопросов с несколькими вариантами ответов, что составляет около 15% всего экзамена.

Эти вопросы проверяют ваши знания геометрических фигур, таких как треугольники, четырехугольники, углы и окружности, включая соответствующие теоремы, а также плоскость координат.

Во время теста может появиться следующее понятие.

Тригонометрические соотношения

Существует 6 тригонометрических соотношений, которые вам следует знать:

Когда заданы x, угол в прямоугольном треугольнике и две стороны, противоположные и примыкающие к углу или гипотенуза, это дает информацию, необходимую для нахождения длины недостающей стороны.

Пример 1

: Найдите гипотенузу треугольника ниже.

Во-первых, подумайте, какое тригонометрическое тождество подходит для использования. Здесь нам дан угол и противолежащая сторона, и мы хотели бы знать гипотенузу. Таким образом, подходящим тождеством триггера является функция синуса, поскольку она включает в себя противоположную сторону и гипотенузу:

Пример 2

: Найдите недостающий угол x прямоугольного треугольника, если вы знаете, что котангенс x = 6.

Теперь найдем угол x , нам нужно использовать функцию арктангенса:

*ПРИМЕЧАНИЕ. Если вы работаете в градусах, убедитесь, что ваш калькулятор находится в режиме градусов при использовании тригонометрических функций.*

Измерение и пространственное чувство

Это компетенция включает около 7 вопросов с несколькими вариантами ответов, что составляет около 9% всего экзамена.

Эти вопросы проверяют ваше знание трехмерных фигур, площади и объема, а также вашу способность конвертировать единицы измерения.