Решите неравенство 15 задание егэ: Логарифмические неравенства — подготовка к ЕГЭ по Математике

Логарифмические неравенства — подготовка к ЕГЭ по Математике

Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.

Давайте повторим, что такое логарифмы:

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

При этом

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)

(Формула для логарифма степени)

Формула перехода к новому основанию:

Алгоритм решения логарифмических неравенств

Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.

И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .

Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение

Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.

Перейдем к практике. Как всегда, начнем с самых простых неравенств.

1. Рассмотрим неравенство log₃x > log₃5.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.

Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»

Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?

Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.

Так почему же мы все-таки «отбрасываем логарифмы»?

Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log₃x₁ > log₃x₂

следует, что x₁ > x₂.

Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.

Итак, x > 5.

Следующее логарифмическое неравенство тоже простое.

2. log₅(15 + 3x) > log₅2x

Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому

Решая эту систему, получим: x > 0.

Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.

15 + 3x > 2x.

Получаем: x > −15.

Итак,

Ответ: x > 0.

А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.

Приведем пример.

3.

Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть

Решая эту систему, получим: x > 4,5.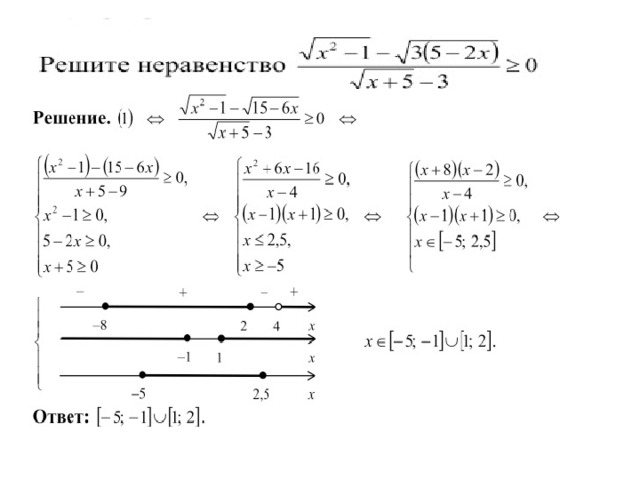

Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента:

И если , то
2x − 9 ≤ x.

Получим, что x ≤ 9.

Учитывая, что x > 4,5, запишем ответ:

x ∈ (4,5; 9].

В следующей задаче логарифмическое неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.

Теперь более сложные неравенства:

4. Решите неравенство

Ответ:

5. Решите неравенство

ОДЗ:

Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.

Сделаем замену

Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!

Ответ:

6.

Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:

Упростим эту систему:

Это область допустимых значений неравенства.

Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что

В данном случае удобно перейти к основанию 4.

Сделаем замену

Упростим неравенство и решим его методом интервалов:

Итак,

Вернемся к переменной x:

Мы добавили условие x > 0 (из ОДЗ).

Ответ:

7. Следующая задача тоже решается с помощью метода интервалов

Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае

Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:

Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:

Видим, что условие (то есть ОДЗ) теперь выполняется автоматически.

Что ж, это упрощает решение неравенства.

Решаем неравенство методом интервалов:

Ответ:

Получилось? Что же, повышаем уровень сложности:

8. Решите неравенство:

Неравенство равносильно системе:

Ответ:

9. Решите неравенство:

Выражение 5^—x2навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:

Поскольку показательная функция принимает только положительные значения, t > 0. Тогда

Неравенство примет вид:

Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, (t − 3) (5⁹ · t − 1) > 0

Если это условие выполнено, то и частное будет положительным.

А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625t − 2)².

Это означает, что 625t − 2 ≠ 0, то есть

Аккуратно запишем ОДЗ

и решим получившуюся систему, применяя метод интервалов.

Итак,

Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:

«Отбросим» логарифмы. Знак неравенства сохраняется.

Перенесем все в левую часть и разложим по известной формуле разности квадратов:

Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.

Получим, что

Вернемся к переменной x

Поскольку

Ответ:

10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.

Запишем ОДЗ:

Воспользуемся формулой и перейдем к основанию 10:

Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию

Эта функция может менять знак в точках, где она равна нулю или не существует.

Выражение lg |x − 3| равно нулю, если |x − 3| = 1, то есть x = 4 или x = 2.

Выражение lg (|x| − 2) равно нулю, если |x| = 3, то есть в точках 3 и −3.

Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.

Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.

Ответ:

11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.

Запишем ОДЗ:

Итак, Это ОДЗ.

Обратите внимание, что .

Это пригодится вам при решении неравенства.

Упростим исходное неравенство:

Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x < 18.

Как же быть? Вспомним, что (x — 18)²=(18 — x)². Тогда:

Вторая ловушка – попроще. Запись означает, что сначала надо вычислить логарифм, а потом возвести полученное выражение в квадрат. Поэтому:

Дальше – всё просто. Сделаем замену

Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда

— не удовлетворяет ОДЗ;

Ответ: 2.

Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье.

Читайте также: Неравенства. Метод замены множителя (метод рационализации)

Логарифмические неравенства повышенной сложности

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Логарифмические неравенства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 09.03.2023

Задание 15 ЕГЭ по математике. Решение дробно-рационального неравенства

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Главная → Видеоуроки →  ЕГЭ по математике. Профильный уровень. Задание 15. Описание видеоурока: Решите дробно-рациональное неравенство. Задание 15. Профильный уровень. Валерий Волков 1 25.01.2019 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования

ЕГЭ по математике Профильный уровень Задание 1     Задание 2 Задание 3     Задание 4 Задание 5     Задание 6 Задание 7     Задание 8 Задание 9     Задание 10 Задание 11     Задание 12 Задание 13     Задание 14 Задание 15     Задание 16 Задание 17     Задание 18 Задание 19     Задание 20 Задание 21 ГИА по математике Задача 1     Задача 2 Задача 3     Задача 4 Задача 5     Задача 6 Задача 7     Задача 8 Задача 9     Задача 10 Задача 11     Задача 12 Задача 13     Задача 14 Задача 15     Задача 16 Задача 17     Задача 18 Задача 19     Задача 20 Задача 21     Задача 22 Задача 23     Задача 24 Задача 25     Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 — 11 класс. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ

3.6 Решение приложений с помощью линейных неравенств — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

• Решение приложений с линейными неравенствами

Будь готов 3.19

Прежде чем начать, пройдите этот тест на готовность.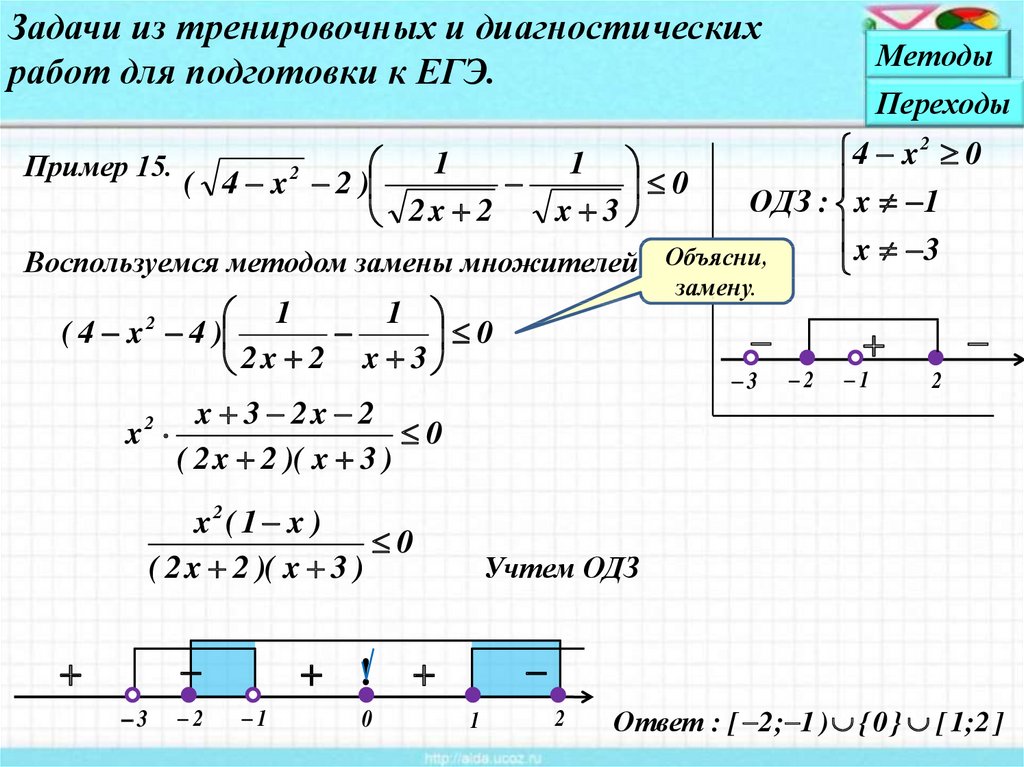

Запишите в виде неравенства: x равно как минимум 30.
Если вы пропустили эту задачу, просмотрите пример 2.77.

Будь готов 3.20

Решите 8−3y<41,8−3y<41.
Если вы пропустили эту проблему, просмотрите пример 2.73.

Решение приложений с линейными неравенствами

Многие жизненные ситуации требуют решения неравенств. На самом деле, приложения неравенства настолько распространены, что мы часто даже не осознаем, что занимаемся алгеброй. Например, сколько галлонов бензина можно заправить в машину за 20 долларов? Доступна ли аренда квартиры? Достаточно ли времени до занятий, чтобы пойти пообедать, поесть и вернуться? Сколько денег должен стоить праздничный подарок каждому члену семьи, не выходя за рамки бюджета?

Метод, который мы будем использовать для решения приложений с линейными неравенствами, очень похож на тот, который мы использовали при решении приложений с уравнениями. Мы прочитаем задачу и убедимся, что все слова поняты. Далее мы определим, что мы ищем, и назначим переменную для ее представления. Мы переформулируем задачу в одном предложении, чтобы ее было легко перевести в неравенство. Затем решим неравенство.

Пример 3,53

Эмма получила новую работу и ей придется переехать. Ее ежемесячный доход составит 5625 долларов. Чтобы снять квартиру, ежемесячный доход Эммы должен как минимум в три раза превышать арендную плату. На какую максимальную арендную плату Эмма может претендовать?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	самая высокая арендная плата, на которую Эмма может претендовать
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть r=r= рента.
Шаг 4. Переведите в неравенство. Сначала напишите предложение, которое дает информацию, чтобы найти его.	Ежемесячный доход Эммы должен как минимум в три раза превышать арендную плату.
Шаг 5. Решить неравенство. Помните, что a>xa>x имеет то же значение, что и x	5,625≥3r1,875≥rr≤1,8755,625≥3r1,875≥rr≤1,875
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Максимальная арендная плата в размере 1875 долларов кажется разумной при доходе в 5625 долларов.
Шаг 7. Ответьте на вопрос полным предложением.	Максимальная арендная плата составляет 1875 долларов.

Стол 3.18

Попробуй 3.105

Алан загружает поддон коробками, каждая из которых весит 45 фунтов. Поддон может безопасно выдерживать не более 900 фунтов. Сколько коробок он может безопасно загрузить на поддон?

Попробуй 3.106

Лифт в многоквартирном доме Йехире имеет табличку с надписью, что максимальный вес составляет 2100 фунтов. Если средний вес одного человека составляет 150 фунтов, сколько человек могут безопасно подняться на лифте?

Иногда приложение требует, чтобы решение было целым числом, но алгебраическое решение неравенства не является целым числом. В этом случае мы должны округлить алгебраическое решение до целого числа. Контекст приложения будет определять, будем ли мы округлять в большую или меньшую сторону. Чтобы проверить такие приложения, мы округлим наш ответ до числа, которое легко вычислить, и убедимся, что это число делает неравенство верным.

Пример 3,54

Дон выиграла мини-грант в размере 4000 долларов на покупку планшетных компьютеров для своего класса. Планшеты, которые она хотела бы купить, стоят 254,12 доллара каждый, включая налог и доставку. Какое максимальное количество планшетов можно купить?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	максимальное количество таблеток Рассвета можно купить
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть n=n= количество таблеток.
Шаг 4. Перевести . Напишите предложение, которое дает информацию, чтобы найти его. Превратите в неравенство.	254,12 долл. США, умноженное на количество планшетов, не превышает 4000 долл. США. 254.12n≤4000254.12n≤4000
Шаг 5. Решить неравенство. Но nn должно быть целым числом таблеток, поэтому округлите до 15.	n≤15,74n≤15,74 n≤15n≤15
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Если округлить цену до 250 долларов, 15 таблеток будут стоить 3750 долларов. , а 16 планшетов обойдутся в 4000 долларов. Так максимум 15 таблеток на $254,12 кажется разумным.
Шаг 7. Ответьте на вопрос полным предложением.	Рассвет можно купить максимум 15 таблеток.

Стол 3.19

Попробуй 3.107

У Энджи есть 20 долларов, чтобы купить коробки сока для дошкольного пикника ее сына. Каждая упаковка коробок сока стоит 2,63 доллара. Какое максимальное количество пачек она может купить?

Попробуй 3.108

Даниэль хочет удивить свою девушку, отметив день рождения в ее любимом ресторане. Ужин будет стоить 42,75 доллара США на человека, включая чаевые и налог. Его бюджет на вечеринку составляет 500 долларов. Какое максимальное количество людей может быть у Даниэля на вечеринке?

Пример 3,55

Пит работает в компьютерном магазине. Его еженедельная оплата будет либо фиксированной, либо 925 долларов, либо 500 долларов плюс 12% от общего объема продаж. Каким должен быть его общий объем продаж, чтобы его вариант с переменной оплатой превышал фиксированную сумму в 9 долларов?25?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	общий объем продаж, необходимый для его варианта с переменной оплатой, чтобы превысить фиксированную сумму в 925 долларов США
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть s=s= общий объем продаж.
Шаг 4. Перевести . Напишите предложение, которое дает информацию, чтобы найти его. Превратите в неравенство. Не забудьте преобразовать проценты в десятичные числа.	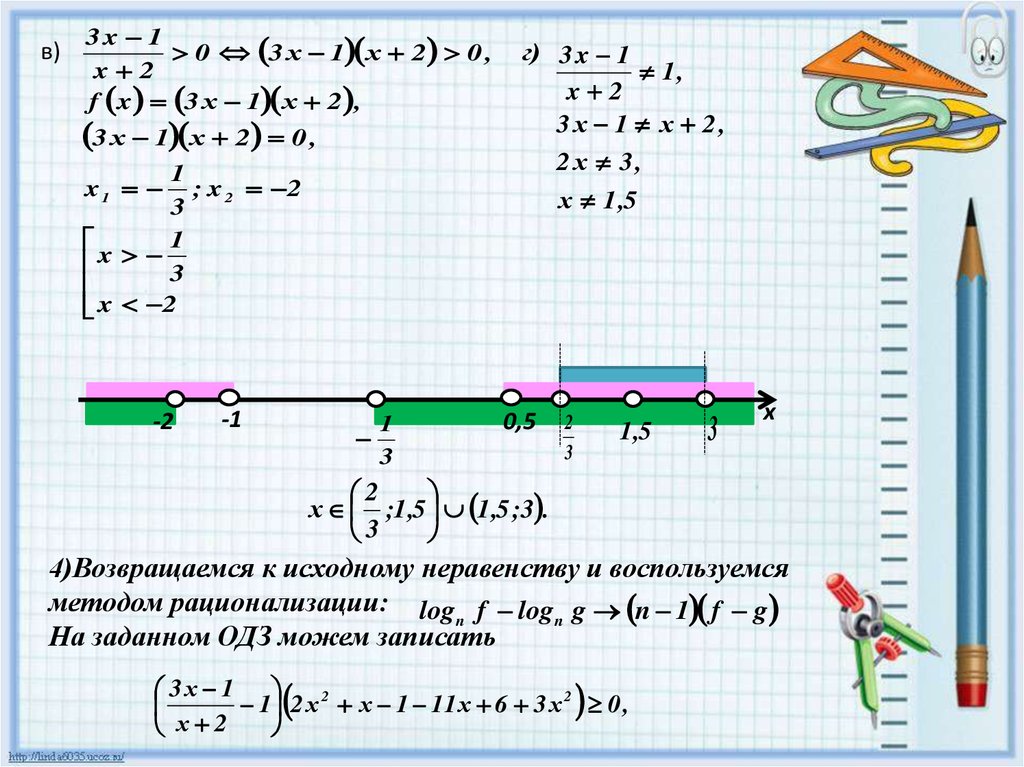500+0,12 с>925500+0,12 с>925
Шаг 5. Решить неравенство.	0,12с>425с>3541,66—0,12с>425с>3541,66—
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Если мы округлим общий объем продаж до 4000 долларов, то увидим, что 500+0,12(4000)=980500+0,12(4000)=980, что больше 925 долларов.
Шаг 7. Ответьте на вопрос полным предложением.	Общая сумма продаж должна превышать 3 541,67 долл. США.

Стол 3.20

Попробуй 3.109

Тиффани только что закончила колледж, и ее новая работа будет приносить ей 20 000 долларов в год плюс 2% от всех продаж. Она хочет зарабатывать не менее 100 000 долларов в год. При каком общем объеме продаж она сможет достичь своей цели?

Попробуй 3.110

Кристиану предложили новую работу с оплатой 24 000 долларов в год плюс 3% от продаж. При каком общем объеме продаж эта новая работа будет приносить больше, чем его нынешняя работа, на которой платят 60 000 долларов?

Пример 3,56

У Серджио и Лизет очень ограниченный бюджет на отпуск. Они планируют арендовать автомобиль у компании, которая берет 75 долларов в неделю плюс 0,25 доллара за милю. Сколько миль они могут проехать и при этом уложиться в свой бюджет в 200 долларов?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	количество миль, которое Серхио и Лизет могут пройти
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть m=m= количество миль.
Шаг 4. Перевести . Напишите предложение, которое дает информацию, чтобы найти его. Перевести в неравенство.	75 долларов плюс умноженное на 0,25 количество миль, меньшее или равное 200 долларам. 75+0,25м≤20075+0,25м≤200
Шаг 5. Решить неравенство.	0,25 м ≤ 125 м ≤ 500 миль 0,25 м ≤ 125 м ≤ 500 миль
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Да, 75+0,25(500)=20075+0,25(500)=200.
Шаг 7. Напишите предложение, отвечающее на вопрос.	Серджио и Лизет могут проехать 500 миль и остаться в рамках бюджета.

Стол 3.21

Попробуй 3.111

Телефонный тариф Талейши стоит 28,80 долларов в месяц плюс 0,20 доллара за текстовое сообщение. Сколько текстовых сообщений она может использовать, чтобы ее ежемесячный счет за телефон не превышал 50 долларов?

Попробуй 3.112

Счет за отопление Рамина составляет 5,42 доллара в месяц плюс 1,08 доллара за тепло. Сколько терм может использовать Рамин, если он хочет, чтобы его счет за отопление составлял не более 87,50 долларов?

Общей целью большинства предприятий является получение прибыли. Прибыль — это деньги, которые остаются после вычета расходов из заработанных денег. В следующем примере мы найдем количество работ, которые мелкий предприниматель должен выполнять ежемесячно, чтобы получать определенную прибыль.

Пример 3,57

У Эллиота есть бизнес по уходу за ландшафтом. Его ежемесячные расходы составляют 1100 долларов. Если он берет 60 долларов за работу, сколько работ он должен выполнить, чтобы получать прибыль не менее 4000 долларов в месяц?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	количество рабочих мест, необходимых Эллиоту
Шаг 3. Назовите то, что мы ищем. Выберите переменную для ее представления.	Пусть j=j= количество заданий.
Шаг 4. Переведите Напишите предложение, которое дает информацию, чтобы найти его.	60 долларов США, умноженное на количество рабочих мест минус 1 100 долларов США, составляет не менее 4 000 долларов США.
Переведем в неравенство.
Шаг 5. Решить неравенство.
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Если бы Эллиот выполнил 90 работ, его прибыль составила бы 60(90)−110060(90)−1100, или 4300$4300. Это более 4000$4000$.
Шаг 7. Напишите предложение, отвечающее на вопрос.	Эллиот должен работать как минимум на 85 работах.

Попробуй 3.

113

У Калеба есть бизнес по присмотру за домашними животными. Он берет 32 доллара в час. Его ежемесячные расходы составляют 2272 доллара. Сколько часов он должен работать, чтобы получать прибыль не менее 800 долларов в месяц?

Попробуй 3.114

Фелисити занимается каллиграфией. Она берет 2,50 доллара за приглашение на свадьбу. Ее ежемесячные расходы составляют 650 долларов. Сколько приглашений она должна написать, чтобы получать прибыль не менее 2800 долларов в месяц?

Иногда жизнь усложняется! Есть много ситуаций, в которых несколько величин влияют на общий расход. Мы должны обязательно учитывать все индивидуальные расходы, когда решаем подобные проблемы.

Пример 3,58

У лучшей подруги Бренды свадьба, и мероприятие продлится 3 дня. У Бренды 500 долларов сбережений, и она может зарабатывать 15 долларов в час, присматривая за детьми. Она рассчитывает заплатить 350 долларов за перелет, 375 долларов за еду и развлечения и 60 долларов за ночь за свою долю в номере отеля. Сколько часов она должна нянчиться, чтобы у нее было достаточно денег, чтобы заплатить за поездку?

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	количество часов, которое Бренда должна присматривать за детьми
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть h=h= количество часов.
Шаг 4. Перевести . Напишите предложение, которое дает информацию, чтобы найти его. Переведите в неравенство.	Расходы должны быть меньше или равны доходам. Стоимость авиабилетов плюс стоимость питания и развлечений и счет отеля должен быть меньше или равен сбережениям плюс сумма, заработанная няней. 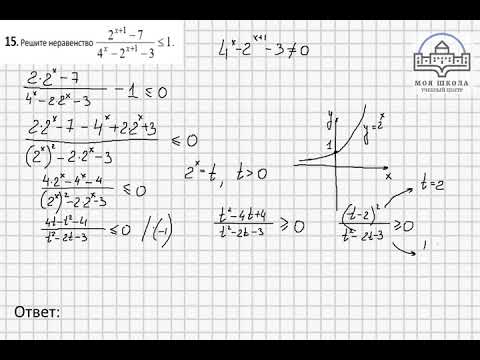$350+$375+$60(3)≤$500+$15ч 350$+$375+$60(3)≤$500+$15ч
Шаг 5. Решить неравенство.	905≤500+15h505≤15h37≤hh≥27905≤500+15h505≤15h37≤hh≥27
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. Подставляем в неравенство 27. 905≤500+15х905≤500+15(27)905≤ 5≤500+15х905≤500+15(27)905≤905
Шаг 7. Напишите предложение, отвечающее на вопрос.	Бренда должна нянчиться не менее 27 часов.

Попробуй 3.115

Малик планирует 6-дневную поездку на летние каникулы. У него есть 840 долларов сбережений, и он зарабатывает 45 долларов в час за репетиторство. Поездка обойдется ему в 525 долларов за перелет, 780 долларов за еду и осмотр достопримечательностей и 95 долларов за ночь в отеле.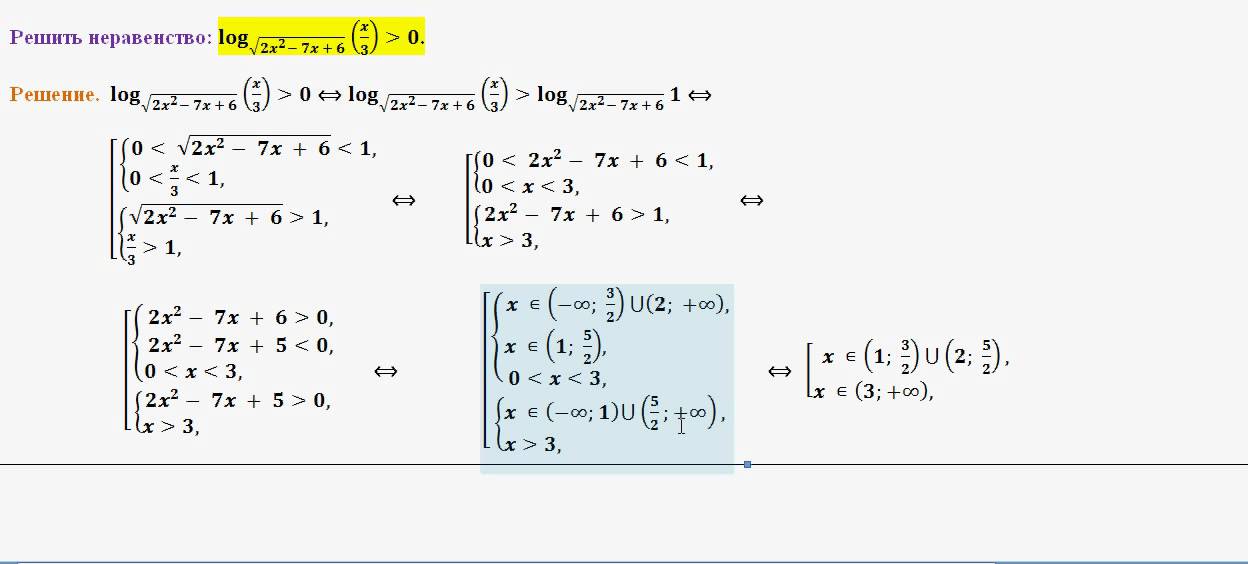 Сколько часов он должен заниматься с репетитором, чтобы иметь достаточно денег для оплаты поездки?

Попробуй 3.116

Джосуе хочет отправиться в 10-дневное путешествие следующей весной. Это будет стоить ему 180 долларов за бензин, 450 долларов за еду и 49 долларов за ночь за мотель. У него есть 520 долларов сбережений, и он может заработать 30 долларов за каждую уборку снега на подъездной дорожке. Сколько подъездных дорог он должен расчистить, чтобы хватило денег на поездку?

Раздел 3.6 Упражнения

Практика ведет к совершенству

Решение приложений с линейными неравенствами

В следующих упражнениях решите.

309.

Мона планирует вечеринку по случаю дня рождения сына, и ее бюджет составляет 285 долларов. Fun Zone взимает 19 долларов за ребенка. Сколько детей она может иметь на вечеринке, не выходя за рамки своего бюджета?

310.

Карлос присматривает квартиры с тремя своими друзьями. Они хотят, чтобы ежемесячная арендная плата не превышала 2360 долларов. Если соседи по комнате поделят арендную плату поровну между четырьмя из них, какова максимальная арендная плата, которую будет платить каждый?

311.

Водное такси имеет максимальную нагрузку 1800 фунтов. Если средний вес одного человека составляет 150 фунтов, сколько человек может безопасно ехать в водном такси?

312.

Марсела регистрируется на занятия в колледже, которые стоят 105 долларов за единицу. Сколько единиц она может взять, чтобы их максимальная стоимость составила 1365 долларов?

313.

Арлин получила подарочную карту на 20 долларов в кафе. Ее любимый напиток со льдом стоит 3,79 доллара. Какое максимальное количество напитков она может купить с помощью подарочной карты?

314.

Тиган любит играть в гольф. В следующем месяце он заложил в бюджет 60 долларов на тренировочное поле. Каждый раз, когда он уходит, это обходится ему в 10,55 доллара за ведро мячей. Какое максимальное количество раз он может посетить тренировочное поле в следующем месяце?

315.

Джони продает кухонные фартуки онлайн по 32,50 доллара за штуку. Сколько фартуков она должна продать в следующем месяце, если хочет заработать не менее 1000 долларов?

316.

Райан берет с соседей 17,50 долларов за то, что они моют их машину. Сколько машин он должен вымыть следующим летом, если его цель — заработать не менее 1500 долларов?

317.

Кешад получает 2400 долларов в месяц плюс 6% от продаж. Его брат зарабатывает 3300 долларов в месяц. На какую сумму от общего объема продаж ежемесячная заработная плата Кешада будет выше, чем ежемесячная заработная плата его брата?

318.

Кимуен нужно зарабатывать 4150 долларов в месяц, чтобы оплачивать все свои расходы. Ее работа приносит ей 3475 долларов в месяц плюс 4% от ее общего объема продаж. Каков минимальный общий объем продаж Кимуен, чтобы она могла оплатить все свои расходы?

319.

Андре предложили работу начального уровня. Компания предложила ему 48 000 долларов в год плюс 3,5% от общего объема продаж. Андре знает, что средняя зарплата за эту работу составляет 62 000 долларов. Каким должен быть общий объем продаж Андре, чтобы его заработок был по крайней мере таким же высоким, как средний заработок за эту работу?

320.

Натали рассматривает два предложения работы. Первая работа будет приносить ей 83 000 долларов в год. Второй заплатит ей 66 500 долларов плюс 15% от ее общего объема продаж. Каким должен быть ее общий объем продаж, чтобы ее зарплата во втором предложении была выше, чем в первом?

321.

Счет Джейка за воду составляет 24,80 доллара в месяц плюс 2,20 доллара за кубический фут (сто кубических футов) воды. Какое максимальное количество ccf может использовать Джейк, если он хочет, чтобы его счет не превышал 60 долларов?

322.

Телефонный план Киоши стоит 17,50 долларов в месяц плюс 0,15 доллара за текстовое сообщение. Какое максимальное количество текстовых сообщений может отправить Киёси, чтобы телефонный счет не превышал 56,50 долларов?

323.

Телевизионный план Марлона стоит 49,99 долларов в месяц плюс 5,49 долларов.за первый фильм. Сколько первых фильмов он может посмотреть, если хочет, чтобы его ежемесячный счет не превышал 100 долларов?

324.

Келлен хочет арендовать банкетный зал в ресторане для детского праздника своей кузины. Ресторан берет 350 долларов за банкетный зал плюс 32,50 доллара на человека за обед. Сколько человек может принять Келлен в душе, если она хочет, чтобы максимальная стоимость составляла 1500 долларов?

325.

Мошде занимается парикмахерским бизнесом из своего дома. Она берет 45 долларов за стрижку и укладку. Ее ежемесячные расходы составляют 9 долларов.60. Она хочет иметь возможность откладывать не менее 1200 долларов в месяц на свой сберегательный счет, чтобы открыть собственный салон. Сколько «стрижек и укладок» она должна сделать, чтобы сэкономить не менее 1200 долларов в месяц?

326.

Noe устанавливает и настраивает программное обеспечение на домашних компьютерах. Он берет 125 долларов за работу. Его ежемесячные расходы составляют 1600 долларов. На скольких работах он должен работать, чтобы получить прибыль не менее 2400 долларов?

327.

Кэтрин — личный повар. Она берет 115 долларов за обед на четверых. Ее ежемесячные расходы составляют 3150 долларов. Сколько обедов на четверых она должна продать, чтобы получить прибыль не менее 1,9 долл.00?

328.

Мелисса делает ожерелья и продает их в Интернете. Она берет 88 долларов за ожерелье. Ее ежемесячные расходы составляют 3745 долларов. Сколько ожерелий она должна продать, чтобы получить прибыль не менее 1650 долларов?

329.

Пятеро чиновников студенческого самоуправления хотят попасть на съезд штата. Это будет стоить им 110 долларов за регистрацию, 375 долларов за транспорт и питание и 42 доллара на человека за отель. На сберегательный счет студенческого самоуправления заложено 450 долларов. Остальную часть денег они могут заработать на автомойке. Если они берут 5 долларов за машину, сколько машин они должны вымыть, чтобы иметь достаточно денег для оплаты поездки?

330.

Цезарь планирует четырехдневную поездку, чтобы навестить своего друга из колледжа в другом штате. Это будет стоить ему 198 долларов на перелет, 56 долларов на местный транспорт и 45 долларов в день на еду. У него есть сбережения в размере 189 долларов, и он может зарабатывать 35 долларов за каждую стрижку газона. Сколько газонов он должен постричь, чтобы хватило денег на поездку?

331.

Алонзо работает мастером по ремонту автомобилей. Он берет 175 долларов за машину. Он планирует переехать из родительского дома и снять свою первую квартиру. Ему нужно будет заплатить 120 долларов США за регистрационные сборы, 9 долларов США.50 за залог и арендную плату за первый и последний месяц в размере 1140 долларов в месяц. У него есть сбережения в размере 1810 долларов. Сколько машин он должен купить, чтобы хватило денег на аренду квартиры?

332.

Ын-Гён работает репетитором и зарабатывает 60 долларов в час. У нее есть 792 доллара сбережений. Она планирует юбилейную вечеринку для своих родителей. Она хотела бы пригласить 40 гостей. Вечеринка обойдется ей в 1520 долларов за еду и напитки и 150 долларов за фотографа. У нее также будет услуга для каждого из гостей, и каждая услуга будет стоить 7,50 долларов. Сколько часов она должна заниматься репетиторством, чтобы хватило денег на вечеринку?

Математика на каждый день

333.

Максимальная нагрузка на сцену В 2014 году в Фуллертоне, штат Калифорния, обрушилась сцена средней школы, когда 250 учеников вышли на сцену для финала музыкального спектакля. Два десятка школьников получили ранения. Сцена могла выдержать максимум 12 750 фунтов. Если предположить, что средний вес студента составляет 140 фунтов, каково максимальное количество студентов, которые могут безопасно находиться на сцене?

334.

Максимальный вес на лодке В 2004 году в порту Балтимора затонуло водное такси, пять человек утонули. Водное такси имело максимальную вместимость 3500 фунтов (25 человек со средним весом 140 фунтов). Средний вес 25 человек в водном такси, когда оно затонуло, составлял 168 фунтов на человека. Каким должно быть максимальное количество людей такого веса?

335.

Свадебный бюджет Адель и Уолтер нашли идеальное место для своего свадебного приема. Стоимость составляет 9 850 долларов США для группы до 100 человек плюс 38 долларов США за каждого дополнительного гостя. Сколько гостей может присутствовать, если Адель и Уолтер хотят, чтобы общая стоимость не превышала 12 500 долларов?

336.

Бюджет на душ Пенни планирует детский душ для своей невестки. Ресторан взимает 950 долларов США за до 25 гостей плюс 31,95 долларов США за каждого дополнительного гостя. Сколько гостей может присутствовать, если Пенни хочет, чтобы общая стоимость не превышала 1500 долларов?

Письменные упражнения

337.

Найдите свой счет за телефон за последний месяц и почасовую зарплату, которую вам платят на работе. (Если у вас нет работы, используйте почасовую оплату, которую вы реально получали бы, если бы у вас была работа). соответствующее неравенство, а затем решить его.

338.

Узнайте, сколько единиц у вас осталось после этого семестра, чтобы достичь своей цели в колледже, и оцените количество единиц, которые вы можете сдать за каждый семестр в колледже. Подсчитайте количество терминов, которое потребуется вам для достижения цели вашего колледжа, написав соответствующее неравенство, а затем решив его.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Графические системы линейных неравенств

Чтобы построить линейный неравенство с двумя переменными (скажем, Икс и у ), сначала получить у один с одной стороны. Затем рассмотрим связанное уравнение, полученное заменой знака неравенства на знак равенства. График этого уравнения представляет собой прямую.

Если неравенство строгое ( < или > ), нарисуйте пунктирную линию. Если неравенство не является строгим ( ≤ или ≥ ), нарисуйте сплошную линию.

Наконец, выберите одну точку, которая не находится ни на одной из прямых ( ( 0 , 0 ) обычно проще всего) и решить, удовлетворяют ли эти координаты неравенству или нет. Если это так, заштрихуйте полуплоскость, содержащую эту точку. Если нет, заштрихуйте другую полуплоскость.

Аналогичным образом изобразите каждое неравенство в системе. Решение система неравенств является областью пересечения всех решений системы.

Пример 1:

Решите систему неравенств, построив график:

у ≤ Икс − 2 у > − 3 Икс + 5

Сначала начертите неравенство у ≤ Икс − 2 . Соответствующее уравнение у «=» Икс − 2 .

Поскольку неравенство ≤ , не строгая, граница сплошная.

Изобразите прямую линию.

Рассмотрим точку, не лежащую на прямой, скажем, ( 0 , 0 ) — и подставить в неравенство у ≤ Икс − 2 .

0 ≤ 0 − 2 0 ≤ − 2

Это неверно. Значит, решение не содержит точки ( 0 , 0 ) . Заштрихуйте нижнюю половину линии.

Точно так же нарисуйте пунктирной линией соответствующее уравнение второго неравенства у > − 3 Икс + 5 имеющее строгое неравенство. Смысл ( 0 , 0 ) не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точку ( 0 , 0 ) .

Решением системы неравенств является область пересечения решений двух неравенств.

Пример 2:

Решите систему неравенств, построив график:

2 Икс + 3 у ≥ 12 8 Икс − 4 у > 1 Икс < 4

Перепишите первые два неравенства с у один с одной стороны.

3 у ≥ − 2 Икс + 12 у ≥ − 2 3 Икс + 4 − 4 у > − 8 Икс + 1 у < 2 Икс − 1 4

Теперь постройте график неравенства у ≥ − 2 3 Икс + 4 . Соответствующее уравнение у «=» − 2 3 Икс + 4 .

Поскольку неравенство ≥ , не строгая, граница сплошная.

Изобразите прямую линию.

Рассмотрим точку, не лежащую на прямой, скажем, ( 0 , 0 ) — и подставить в неравенство.

0 ≥ − 2 3 ( 0 ) + 4 0 ≥ 4

Это неверно. Значит, решение не содержит точки ( 0 , 0 ) . Заштрихуйте верхнюю половину линии.

Аналогичным образом нарисуйте пунктирной линией связанное уравнение второго неравенства у < 2 Икс − 1 4 имеющее строгое неравенство.