Секреты решения задач ЕГЭ по физике

Вариант ЕГЭ по физике состоит из двух частей и включает в себя 32 задания.

В части 1 содержится 24 задания с кратким ответом, в которых ответ записывается в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр.

Часть 2 содержит 8 заданий. Из них два задания с кратким ответом (25 и 26) и шесть заданий (27–32), для которых необходимо привести развернутый и обоснованный ответ.

В первой части – не только формулы и графики. Есть и необычные задания.

В задании 22 вы увидите фотографии или рисунки измерительных приборов. Чтобы сделать это задание, нужно уметь записывать показания приборов при измерении физических величин с учётом абсолютной погрешности измерений.

Задание 23 проверяет умение выбирать оборудование для проведения опыта по заданной гипотезе.

Завершает первую часть задание по астрономии на выбор нескольких утверждений из пяти предложенных.

Вторая часть работы посвящена решению задач: семи расчётных и одной качественной задачи.

Они распределяются по разделам следующим образом: 2 задачи по механике, 2 задачи по молекулярной физике и термодинамике, 3 задачи по электродинамике, 1 задача по квантовой физике.

Задания 25 и 26 – это расчётные задачи с кратким ответом. Задание 25 по молекулярной физике или электродинамике, а задача 26 – по квантовой физике.

Далее идут задания с развёрнутым ответом. Задание 27 – качественная задача, в которой решение представляет собой объяснение какого-либо факта или явления, основанное на физических законах и закономерностях. Качественная задача может быть по любому из разделов курса физики.

Следующие задачи строго распределены по определенным разделам физики.

Задание 28 – по механике или по молекулярной физике,

задание 29 –  по механике,

задание 30 – по МКТ и термодинамике,

задание 31 – по электродинамике,

задание 32 – преимущественно по оптике.

Для расчётных задач высокого уровня сложности (29–32) требуется анализ всех этапов решения. Здесь необходимо пользоваться большим числом законов и формул, вводить дополнительные обоснования в процессе решения. Способ решения задачи надо выбрать самостоятельно.

На нашем сайте размещены статьи по каждой задаче ЕГЭ. В них приведены не только типовые задания ЕГЭ по физике, но и показан подробный ход рассуждений, приводящих к решению задач. Каждое задание сопровождается ссылкой на необходимую теорию.

Рассказано о секретах решения каждой задачи ЕГЭ по физике.

Задание 1  Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.

Задание 2 Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения

Задание 3  Закон сохранения импульса, кинетическая и потенциальные энергии, работа и мощность силы, закон сохранения механической энергии

Задание 4 Механическое равновесие, механические колебания и волны.

 Условие равновесия твёрдого тела, закон Паскаля, сила Архимеда,

Задание 5 Механика. Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков

Задание 6 Механика. Изменение физических величин в процессах. 

Задание 7  Механика. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами.

Задание 8 Основы термодинамики. Тепловое равновесие. Уравнение Клапейрона-Менделеева. Изопроцессы.

Задание 9  Термодинамика. Работа в термодинамике, первый закон термодинамики, КПД тепловой машины

Задание 10  Термодинамика, тепловое равновесие. Относительная влажность воздуха, количество теплоты

Задание 11  Термодинамика и молекулярно-кинетическая теория. Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков.

Задание 12  Термодинамика и молекулярно-кинетическая теория. Изменение физических величин в процессах; установление соответствия между графиками и физическими величинами, между физическими величинами и формулами. 

Задание 13 Электрическое поле, магнитное поле. Принцип суперпозиции электрических полей, магнитное поле проводника с током, сила Ампера, сила Лоренца, правило Ленца

Задание 14  Электричество. Закон сохранения электрического заряда, закон Кулона, конденсатор, сила тока, закон Ома для участка цепи, последовательное и параллельное соединение проводников, работа и мощность тока, закон Джоуля – Ленца

Задание 15  Электричество, магнетизм и оптика. Поток вектора магнитной индукции, закон электромагнитной индукции Фарадея, индуктивность, энергия магнитного поля катушки с током, колебательный контур, законы отражения и преломления света, ход лучей в линзе

Задание 16 Электродинамика. Объяснение явлений; интерпретация результатов опытов, 

представленных в виде таблицы или графиков

Задание 17 Электродинамика и оптика.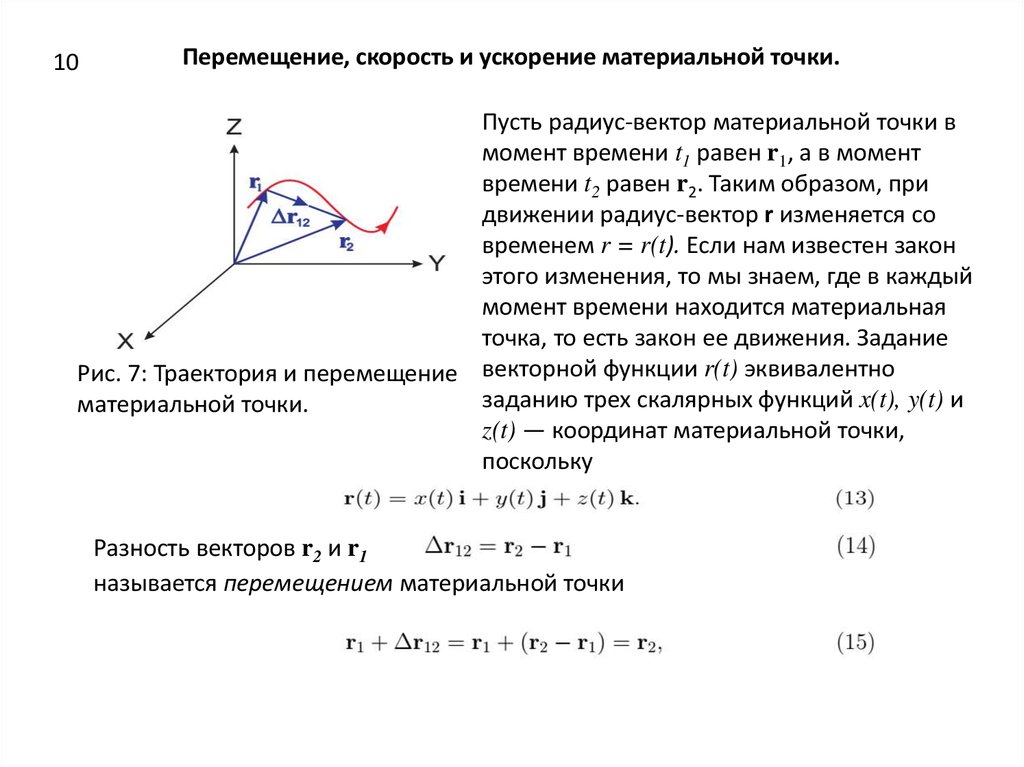 Изменение физических величин в процессах

Задание 18  Электродинамика, оптика, специальная теория относительности. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами

Задание 19 Ядерная физика. Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции.

Задание 20 Линейчатые спектры, фотоны, закон радиоактивного распада.

Задание 21 Квантовая физика. Изменение физических величин в процессах. Установление соответствия 

между графиками и физическими величинами, между физическими величинами и формулами

Задание 22 Механика — квантовая физика, методы научного познания

Задание 23 Механика — квантовая физика, методы научного познания

Задание 24 Элементы астрофизики. Солнечная система, звёзды, галактики

Задание 25 Молекулярная физика, термодинамика, электродинамика. Расчётная задача

Задание 26 Электродинамика, квантовая физика. Расчётная задача

Задание 27 Механика — квантовая физика. Качественная задача

Задание 28 Механика — квантовая физика. Расчётная задача

Задание 29 Механика. Расчетная задача

Задание 30 Молекулярная физика. Расчетная задача

Задание 31 Электродинамика. Расчетная задача

Задание 32 Электродинамика. Квантовая физика. Расчетная задача

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Секреты решения задач ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 07.02.2023

Теория к заданию 1 из ЕГЭ по физике

Архитектор, инженер, программист, технолог — это далеко не полный список специальностей, для которых нужно сдавать экзамен по физике. Задание 1 из ЕГЭ по этому предмету кажется школьникам простым, однако для его решения нужно выучить большой блок теории. Все задачи из первого номера относятся к теме «Движение». Выпускник должен разбираться в видах движения, уметь анализировать графики и знать принцип относительности. Если вы понимаете эту тему и хотите освежить знания перед ЕГЭ, наша статья напомнит вам основные формулы и правила. Также стоит обратить внимание на курсы подготовки к ЕГЭ: там преподаватель объяснит все подробно, с нуля. А чтобы быть уверенным в высоких баллах, можно выбрать комплексную программу, включающую также занятия по русскому языку и профильной математике. 

Кинематика

Путь, траектория, перемещение — понятия, без знания которых не решить задание 1 на ЕГЭ по физике. Подготовка должна начинаться с теории. Когда вы будете хорошо ориентироваться в ней, можно переходить к практике. Наука кинематика, о которой идет речь в первом вопросе, изучает механическое движение тел без описания причин этого движения. А механическим движением называют изменение взаимного расположения тел или их частей в пространстве с течением времени. Для его изучения пользуются системами отсчета. В кинематике это система координат (X, Y, Z), тело отсчета (тело, относительно которого двигаются другие тела) и часы для измерения времени. Форма тел значения не имеет, поэтому в задачах их обозначают материальными точками — объектами, у которых есть масса, а размеры пренебрежимо малые. Не каждое тело может считаться материальной точкой, главное правило — расстояние, которое оно проходит, должно быть намного больше размера. Если мы исследуем скорость самолета на пути из одного города в другой, он является материальной точкой. Если мы определяем сопротивление воздуха в момент полета, нам важна форма, и представить самолет точкой уже нельзя. 

Если материальная точка перемещается в пространстве, у нее есть траектория — это условная линия, описывающая движение.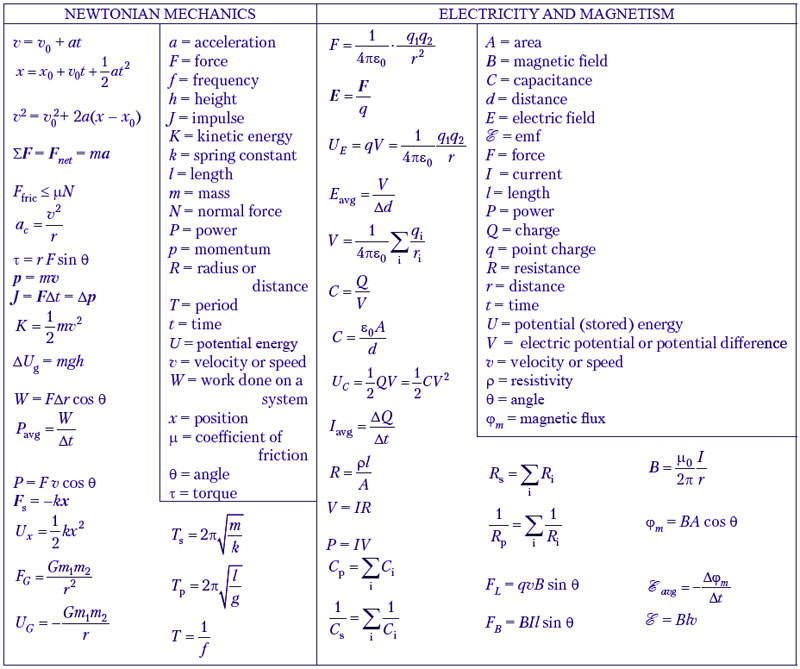 Форма траектории зависит от выбранной системы отсчета, в задачах ЕГЭ траектории обычно рассматривают относительно Земли. Если мы свяжем траекторию с часами, то получим путь — то, что прошло тело за определенный временной промежуток. Путь, как и траектория, может иметь любую форму, но у него есть начальная и конечная точка. Соединив их прямой линией, мы нарисуем вектор перемещения. Он не может быть больше пути, а иногда вовсе равняется нулю (в том случае, когда тело двигалось по замкнутой линии). Теория к заданию 1 из ЕГЭ по физике не будет полной без описания принципа относительности движения. Для этого представим, что мы сидим в поезде и видим еще один на соседнем пути. Сначала наш поезд стоит неподвижно, а потом трогается. Если посмотреть на ситуацию относительно Земли, мы двигаемся: были на станции, а теперь отъехали от нее. Относительно самого поезда мы стоим на месте — как сидели у окна, так и сидим. А если взглянуть на соседний состав? Он постепенно удаляется от нас. 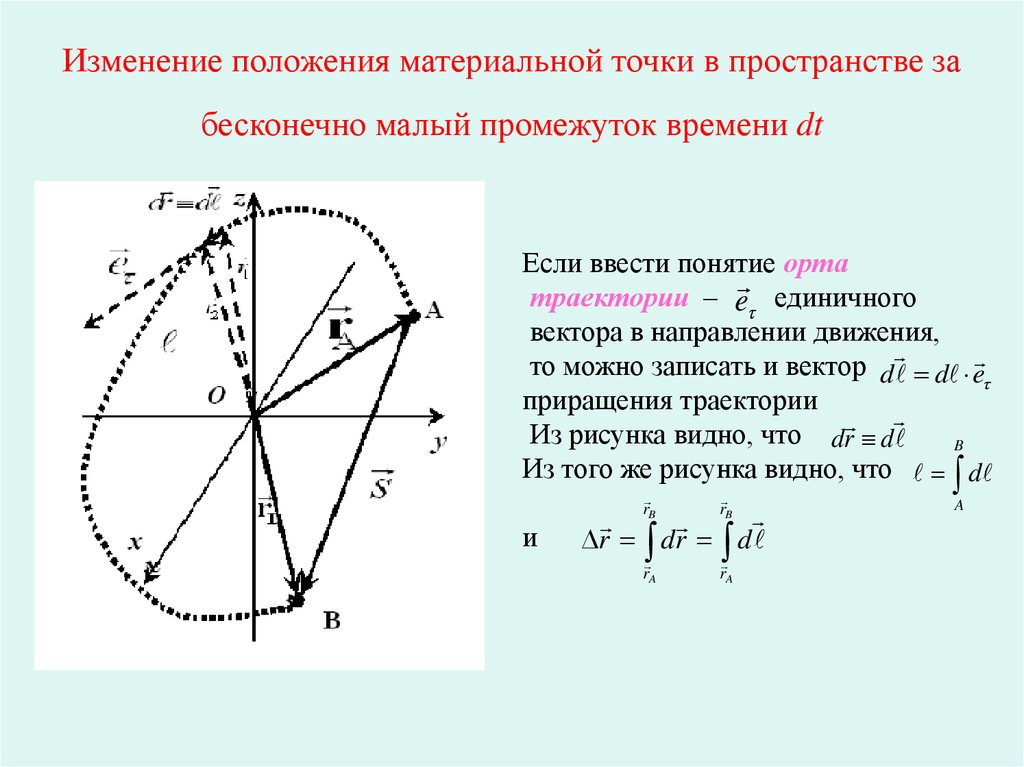Несмотря на то, что он по-прежнему стоит на станции, нам кажется, что он перемещается. Вывод: движение зависит от того, в какой системе координат его изучают. 

Виды движения

От теории мы переходим к решению задач. Чаще всего в них фигурируют два понятия: скорость и ускорение. Скорость — это быстрота и направление перемещения. Средняя скорость перемещения находится по формуле u = s / t, средняя путевая — u = l / t. Здесь u — скорость, l — путь, s — перемещение. Первая величина будет векторной, вторая — скалярной. Существует также мгновенная скорость, то есть скорость в определенной точке. Ее можно найти по графику или из уравнения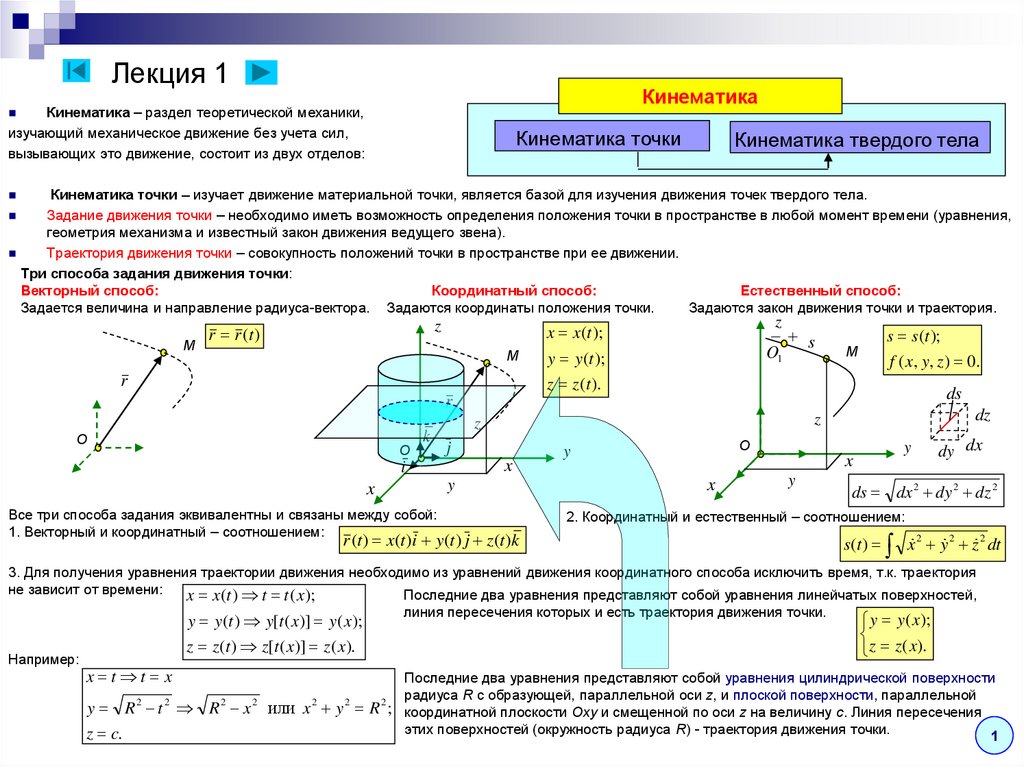

u = u0 + at. a — ускорение, то есть изменение скорости за единицу времени. Это векторная величина, она рассчитывается следующим образом: a = u / t. При ускоренном движении она направлена так же, как и скорость, при замедленном — противоположно ей. В случае с движением по окружности эти величины перпендикулярны. Перечислим несколько формул для задания 1 ЕГЭ по физике, связанных с видами движения: 

  • равномерное прямолинейное: 
  1. x = x0 + ut (x — координата точки в данный момент времени).
  2. s = ut. 
  3. u = const. 
  4. a = 0.
  • прямолинейное равноускоренное:
  1. x = x0 + u0t + аt2 / 2. 
  2. s = u0t + аt2 / 2.
  3. u= uox+ at.
  4. a = const. 
  • движение по окружности (u = const):
  1. T = t / N = 1 / v — период.
  2. v = N / t = 1 / T — частота.
  3. u = l / t = 2πR / T = 2πRv — линейная скорость.
  4. ω = ϕ / t = 2π / T = 2πv — угловая скорость.
  5. a = u2 / R = ω2R = ωu — ускорение.  
  • движение по параболе с ускорением свободного падения: 
  1. x = xo + uoxt + gt2 / 2.
  2. y = yo + uoyt +gt2 / 2.
  3. ux= uox+ gt.
  4. uy= uoy+ gt.
  5. uоx = u0 cosα.
  6. uоy = u0 sinα.

Частные случаи равноускоренного движения под действием силы тяжести

В рамках теории к заданию 1 ЕГЭ по физике нужно знать два частных случая: 

  • движение по вертикали: 
  1. при u0 = 0 высота h = gt2 / 2 и u = gt.
  2. при u0↑ и движении вверх h = u0t — gt2 / 2 и u = u0 – gt.
  3. при u0↑ и движении вниз  h = -u0t + gt2 / 2 и u = -u0 + gt.
  4. при υ0↓ h = u0t + gt2 / 2 и υ = υ0 + gt. 
  • движение тела, брошенного горизонтально: 
  1. h = gt2 / 2 — высота полета.
  2. s = uоt — дальность полета.
  3. υy= gt — скорость относительно оси OY.

Дополнительная информация для частных случаев решения задач

Еще несколько формул для задания 1 ЕГЭ по физике: 

  • модуль вектора: S=sx2+sy2.
  • средняя скорость: uср = (s1 + s2 + … + sn ) / (t1 + t2 + … + tn) = 2u1u2 / (u1 + u2).
  • площадь фигуры равна пройденному пути: S = S1 — S2.
  • физический смысл производной: ux = x΄ и uy = y΄, ах = u΄x = x΄΄ и аy = u΄y = y΄΄.
  • движение колеса без проскальзывания: uпост = uвращ и u = uпост + uвращ.

Пример решения задач

Задача 1: Велосипедисты движутся по уравнениям x1 = 3t и x2 = 12 — t. Найти координату их встречи. 

Решение: В момент встречи велосипедистов их координаты совпадут: x1 = x2, следовательно, 3t = 12 — t. Решив уравнение, найдем, что t = 3 с. Чтобы найти координату, подставим значение в любое из уравнений (для самопроверки лучше подставить в оба): x1 = 3 • 3 = 9. 

Ответ: 9. 

Задача 2: Первую половину пути супермен пролетел со скоростью 30 км/ч, вторую — со скоростью 50 км/ч. Найти среднюю скорость супермена. 

Решение: Нам известны две скорости: u1 и u2, поэтому мы можем воспользоваться формулой uср = 2u1u2 / u1 + u2 = 2 • 30 • 50 / (30 + 50) = 37,5 км/ч.  

Ответ: 37,5. 

Теперь вы знаете больше теории для ЕГЭ по физике в 2020 году. Задание 1 только кажется очень простым, в нем бывают нетипичные задачи, поэтому стоит уделить внимание его разбору. Грамотно подготовиться к ЕГЭ вам помогут курсы ЦМДО «Уникум» . На них вы разберете каждую тему из экзамена, переходя от простого к сложному. Много времени преподаватели уделяют решению задач, объяснению сложных моментов. Но независимо от того, какой способ подготовки вы выберете, мы желаем вам удачи, высоких баллов и поступления в вуз мечты.

Кинематические уравнения: Примеры задач и решений

Ранее в Уроке 6 были представлены и обсуждены четыре кинематических уравнения. Для использования с этими уравнениями была представлена ​​полезная стратегия решения проблем, и были приведены два примера, иллюстрирующие использование этой стратегии. Затем было обсуждено и проиллюстрировано применение кинематических уравнений и стратегии решения задач к свободному падению. В этой части Урока 6 будет представлено несколько примеров задач.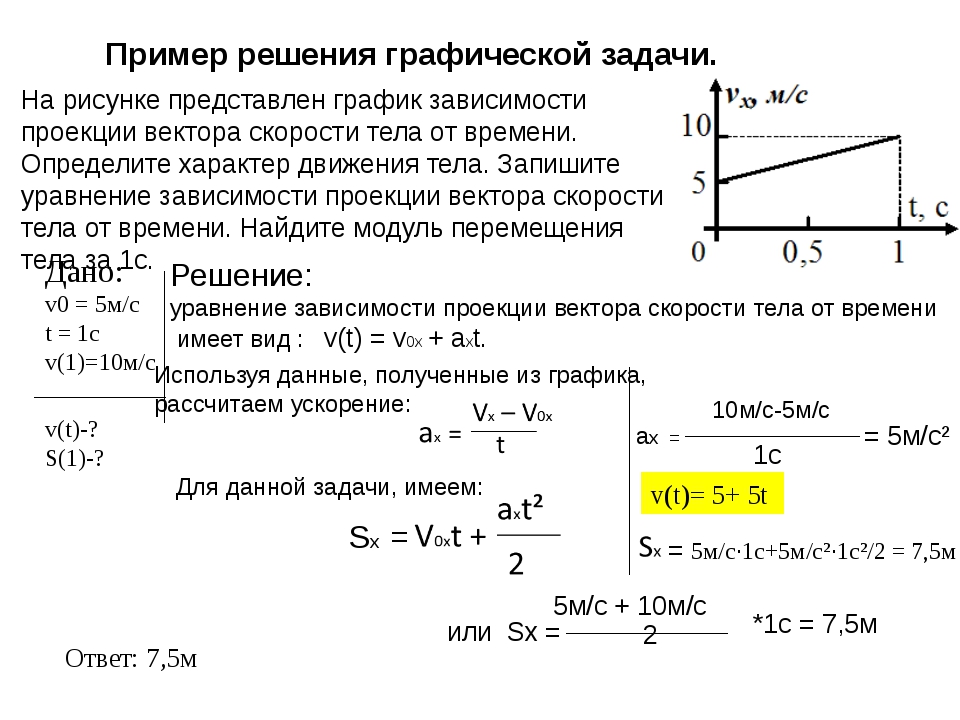 Эти задачи позволяют любому изучающему физику проверить свое понимание использования четырех кинематических уравнений для решения задач, связанных с одномерным движением объектов. Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.

Проверьте свое понимание

  1. Самолет разгоняется по взлетно-посадочной полосе со скоростью 3,20 м/с 2 в течение 32,8 с, пока, наконец, не оторвется от земли. Определить расстояние, пройденное до взлета.
  2. Автомобиль трогается с места и равномерно ускоряется за время 5,21 секунды на расстояние 110 м. Определить ускорение автомобиля.
  3. Аптон Чак едет на Гигантской капле в Большой Америке. Если Аптон будет свободно падать в течение 2,60 с, какова будет его конечная скорость и как далеко он упадет?
  4. Гоночный автомобиль равномерно ускоряется с 18,5 м/с до 46,1 м/с за 2,47 секунды. Определить ускорение автомобиля и пройденный путь.
  5. Перо падает на Луну с высоты 1,40 метра. Ускорение свободного падения на Луне равно 1,67 м/с 2 . Определите время падения пера на поверхность Луны.

    См. решение ниже.


  6. Сани с реактивным двигателем используются для проверки реакции человека на ускорение. Если сани с ракетным двигателем разгоняются до скорости 444 м/с за 1,83 секунды, то каково ускорение и какое расстояние проходят сани?
  7. Велосипед равномерно ускоряется из состояния покоя до скорости 7,10 м/с на пути 35,4 м. Определить ускорение велосипеда.
  8. Инженер проектирует взлетно-посадочную полосу для аэропорта. Из самолетов, которые будут использовать аэропорт, наименьшая скорость ускорения, вероятно, составит 3 м/с 2 . Взлетная скорость этого самолета составит 65 м/с. Предполагая это минимальное ускорение, какова минимальная допустимая длина взлетно-посадочной полосы?
  9. Автомобиль, движущийся со скоростью 22,4 м/с, останавливается за 2,55 с. Определить расстояние заноса автомобиля (считая ускорение равномерным).
  10. Кенгуру способен прыгать на высоту 2,62 м. Определить скорость взлета кенгуру.
  11. Если у Майкла Джордана вертикальный прыжок 1,29 м, то какова его скорость взлета и время зависания (общее время, чтобы подняться вверх до пика и затем вернуться на землю)?
  12. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Разгоняясь через ствол винтовки, пуля проходит расстояние 0,840 м. Определить ускорение пули (ускорение считать равномерным).
  13. Бейсбольный мяч подбрасывается прямо в воздух и имеет время зависания 6,25 с. Определите высоту, на которую поднимается мяч, прежде чем он достигнет своей вершины. (Подсказка: время подъема на пик составляет половину общего времени зависания.)
  14. Смотровая площадка высотного небоскреба на высоте 370 м над ул. Определите время, за которое монета свободно упадет с палубы на улицу.

    См. решение ниже.


  15. Пуля, летящая со скоростью 367 м/с, застревает в комке влажной глины. Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)
  16. Камень брошен в глубокий колодец, и слышно, как он ударяется о воду через 3,41 с после падения. Определить глубину скважины.
  17. Однажды было зафиксировано, что Jaguar оставил следы заноса длиной 290 метров. Предполагая, что Ягуар занесло до остановки с постоянным ускорением -3,90 м/с 2 , определите скорость Ягуара до начала заноса.
  18. Самолет имеет скорость взлета 88,3 м/с, и для достижения этой скорости требуется 1365 м. Определить ускорение самолета и время, необходимое для достижения этой скорости.
  19. Драгстер разгоняется до скорости 112 м/с на расстоянии 398 м. Определить ускорение (предположим равномерным) драгстера.
  20. С какой скоростью в милях/ч (1 м/с = 2,23 мили/ч) должен быть брошен предмет, чтобы он достиг высоты 91,5 м (эквивалентно одному футбольному полю)? Примите пренебрежимо малое сопротивление воздуха.

Решения вышеуказанных проблем

  1. Дано:

    а = +3,2 м/с 2

    т = 32,8 с

    v i = 0 м/с

    Найти:

    д = ??
    d = v i *t + 0,5*a*t 2

    d = (0 м/с)*(32,8 с)+ 0,5*(3,20 м/с 2 )*(32,8 с) 2

    д = 1720 м

    Вернуться к проблеме 1

     

  2. Дано:

    д = 110 м

    т = 5,21 с

    v i = 0 м/с

    Найти:

    а = ??
    d = v i *t + 0,5*a*t 2

    110 м = (0 м/с)*(5,21 с)+ 0,5*(а)*(5,21 с) 2

    110 м = (13,57 с 2 )*a

    а = (110 м)/(13,57 с 2 )

    а = 8,10 м/с 2

    Вернуться к задаче 2

     

  3. Дано:

    а = -9,8 м

    т = 2,6 с

    v i = 0 м/с

    Найти:

    д = ??

    v f = ??

    d = v i *t + 0,5*a*t 2

    d = (0 м/с)*(2,60 с)+ 0,5*(-9,8 м/с 2 )*(2,60 с) 2

    d = -33,1 м (- указывает направление)

    v f = v i + a*t

    v f = 0 + (-9,8 м/с 2 )*(2,60 с)

    v f = -25,5 м/с (- указывает направление)

    Вернуться к проблеме 3

     

  4. Дано:

    v i = 18,5 м/с

    v f = 46,1 м/с

    т = 2,47 с

    Найти:

    д = ??

    а = ??

    а = (Дельта v)/t

    а = (46,1 м/с — 18,5 м/с)/(2,47 с)

    а = 11,2 м/с 2

    д = v i *t + 0,5*a*t 2

    d = (18,5 м/с)*(2,47 с)+ 0,5*(11,2 м/с 2 )*(2,47 с) 2

    d = 45,7 м + 34,1 м

    д = 79,8 м

    (Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2*a*d)

    Вернуться к задаче 4

     

  5. Дано:

    v i = 0 м/с

    d = -1,40 м

    а = -1,67 м/с 2

    Найти:

    т = ??
    d = v i *t + 0,5*a*t 2

    -1,40 м = (0 м/с)*(t)+ 0,5*(-1,67 м/с 2 )*(t) 2

    -1,40 м = 0+ (-0,835 м/с 2 )*(t) 2

    (-1,40 м)/(-0,835 м/с 2 ) = t 2

    1,68 с 2 = т 2

    т = 1,29 с

    Вернуться к проблеме 5

     

  6. Дано:

    v i = 0 м/с

    v f = 444 м/с

    т = 1,83 с

    Найти:

    а = ??

    д = ??

    а = (Дельта v)/t

    а = (444 м/с — 0 м/с)/(1,83 с)

    а = 243 м/с 2

    d = v i *t + 0,5*a*t 2

    d = (0 м/с)*(1,83 с)+ 0,5*(243 м/с 2 )*(1,83 с) 2

    d = 0 м + 406 м

    д = 406 м

    (Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2*a*d)

    Вернуться к задаче 6

     


     

  7. Дано:

    v i = 0 м/с

    v f = 7,10 м/с

    д = 35,4 м

    Найти:

    а = ??
    v f 2 = v i 2 + 2*a*d

    (7,10 м/с) 2 = (0 м/с) 2 + 2*(а)*(35,4 м)

    50,4 м 2 /с 2 = (0 м/с) 2 + (70,8 м)*a

    (50,4 м 2 /с 2 )/(70,8 м) = а

    а = 0,712 м/с 2

    Вернуться к задаче 7

     

  8. Дано:

    v i = 0 м/с

    v f = 65 м/с

    а = 3 м/с 2

    Найти:

    д = ??
    v f 2 = v i 2 + 2*a*d

    (65 м/с) 2 = (0 м/с) 2 + 2*(3 м/с 2 )*d

    4225 м 2 /с 2 = (0 м/с) 2 + (6 м/с 2 )*d

    (4225 м 2 /с 2 )/(6 м/с 2 ) = d

    д = 704 м

    Вернуться к задаче 8

     

  9. Дано:

    v i = 22,4 м/с

    v f = 0 м/с

    т = 2,55 с

    Найти:

    д = ??
    d = (v i + v f )/2 *t

    d = (22,4 м/с + 0 м/с)/2 * 2,55 с

    d = (11,2 м/с)*2,55 с

    д = 28,6 м

    Вернуться к задаче 9

     

  10. Дано:

    а = -9,8 м/с 2

    v f = 0 м/с

    д = 2,62 м

    Найти:

    v i = ??
    v f 2 = v i 2 + 2*a*d

    (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(2,62 м)

    0 м 2 /с 2 = v i 2 — 51,35 м 2 /с 2

    51,35 м 2 /с 2 = v i 2

    v i = 7,17 м/с

    Вернуться к проблеме 10

     

  11. Дано:

    а = -9,8 м/с 2

    v f = 0 м/с

    д = 1,29 м

    Найти:

    v i = ??

    т = ??

    v f 2 = v i 2 + 2*a*d

    (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(1,29 м)

    0 м 2 /с 2 = v i 2 — 25,28 м 2 /с 2

    25,28 м 2 /с 2 = v i 2

    v i = 5,03 м/с

    Чтобы найти время зависания, найдите время до пика и удвойте его.

    v f = v i + a*t

    0 м/с = 5,03 м/с + (-9,8 м/с 2 )*t до

    -5,03 м/с = (-9,8 м/с 2 )*t до

    (-5,03 м/с)/(-9,8 м/с 2 ) = t up

    t до = 0,513 с

    время зависания = 1,03 с

    Вернуться к задаче 11

     

  12. Дано:

    v i = 0 м/с

    v f = 521 м/с

    d = 0,840 м

    Найти:

    а = ??
    против f 2 = v i 2 + 2*a*d

    (521 м/с) 2 = (0 м/с) 2 + 2*(а)*(0,840 м)

    271441 м 2 /с 2 = (0 м/с) 2 + (1,68 м)*a

    (271441 м 2 /с 2 )/(1,68 м) = a

    а = 1,62*10 5 м/с 2

    Вернуться к задаче 12

     

  13. Дано:

    а = -9,8 м/с 2

    v f = 0 м/с

    т = 3,13 с

    Найти:

    д = ??
    1. (ПРИМЕЧАНИЕ: время выхода на пик траектории составляет половину общего времени зависания — 3,125 с. )

    Первое использование: v f  = v i  + a*t

    0 м/с = v i  + (-9,8 м/с 2 )*(3,13 с)

    0 м/с = v i  — 30,7 м/с

    v i = 30,7 м/с (30,674 м/с)

    Теперь используйте: v f 2  = v i 2  + 2*a*d

    (0 м/с) 2  = (30,7 м/с) 2  + 2*(-9,8 м/с 2 )*(d)

    0 м 2 /с 2 = (940 м 2 /с 2 ) + (-19,6 м/с 2 )*d

    -940 м 2 /с 2  = (-19,6 м/с 2 )*d

    (-940 м 2 /с 2 )/(-19,6 м/с 2 ) = d

    д = 48,0 м

    Вернуться к задаче 13

     

  14. Дано:

    v i = 0 м/с

    d = -370 м

    а = -90,8 м/с 2

    Найти:

    т = ??
    d = v i *t + 0,5*a*t 2

    -370 м = (0 м/с)*(t)+ 0,5*(-9,8 м/с 2 )*(t) 2

    -370 м = 0+ (-4,9 м/с 2 )*(t) 2

    (-370 м)/(-4,9 м/с 2 ) = t 2

    75,5 с 2 = т 2

    т = 8,69 с

    Вернуться к задаче 14

     

     

  15. Дано:

    v i = 367 м/с

    против f = 0 м/с

    d = 0,0621 м

    Найти:

    а = ??
    v f 2 = v i 2 + 2*a*d

    (0 м/с) 2 = (367 м/с) 2 + 2*(а)*(0,0621 м)

    0 м 2 /с 2 = (134689 м 2 /с 2 ) + (0,1242 м)*a

    -134689 м 2 /с 2 = (0,1242 м)*a

    (-134689 м 2 /с 2 )/(0,1242 м) = а

    а = -1,08*10 6 м/с 2

    (Знак — означает, что пуля замедлилась. )

    Вернуться к задаче 15

     

  16. Дано:

    а = -9,8 м/с 2

    т = 3,41 с

    v i = 0 м/с

    Найти:

    д = ??
    d = v i *t + 0,5*a*t 2

    d = (0 м/с)*(3,41 с)+ 0,5*(-9,8 м/с 2 )*(3,41 с) 2

    d = 0 м+ 0,5*(-9,8 м/с 2 )*(11,63 с 2 )

    d = -57,0 м

    (ПРИМЕЧАНИЕ: знак — указывает направление)

    Вернуться к задаче 16

     

  17. Дано:

    а = -3,90 м/с 2

    v f = 0 м/с

    д = 290 м

    Найти:

    в и = ??
    v f 2 = v i 2 + 2*a*d

    (0 м/с) 2 = v i 2 + 2*(-3,90 м/с 2 )*(290 м)

    0 м 2 /с 2 = v i 2 — 2262 м 2 /с 2

    2262 м 2 /с 2 = v i 2

    v i = 47,6 м/с

    Вернуться к задаче 17

     

  18. Дано:

    v i = 0 м/с

    v f = 88,3 м/с

    д = 1365 м

    Найти:

    а = ??

    т = ??

    v f 2 = v i 2 + 2*a*d

    (88,3 м/с) 2 = (0 м/с) 2 + 2*(а)*(1365 м)

    7797 м 2 /с 2 = (0 м 2 /с 2 ) + (2730 м)*a

    7797 м 2 /с 2 = (2730 м)*a

    (7797 м 2 /с 2 )/(2730 м) = а

    а = 2,86 м/с 2

    v f = v i + a*t

    88,3 м/с = 0 м/с + (2,86 м/с 2 )*t

    (88,3 м/с)/(2,86 м/с 2 ) = t

    t = 30,8 с

    Вернуться к задаче 18

     

  19. Дано:

    v i = 0 м/с

    v f = 112 м/с

    д = 398 м

    Найти:

    а = ??
    v f 2 = v i 2 + 2*a*d

    (112 м/с) 2 = (0 м/с) 2 + 2*(а)*(398 м)

    12544 м 2 /с 2 = 0 м 2 /с 2 + (796 м)*a

    12544 м 2 /с 2 = (796 м)*a

    (12544 м 2 /с 2 )/(796 м) = а

    а = 15,8 м/с 2

    Вернуться к проблеме 19

     

  20. Дано:

    а = -9,8 м/с 2

    v f = 0 м/с

    д = 91,5 м

    Найти:

    v i = ??

    т = ??

    Сначала найдите скорость в м/с:

    v f 2 = v и 2 + 2*а*д

    (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(91,5 м)

    0 м 2 /с 2 = v i 2 — 1793 м 2 /с 2

    1793 м 2 /с 2 = v i 2

    v i = 42,3 м/с

    Теперь конвертируем из м/с в мили/ч:

    v i = 42,3 м/с * (2,23 мили/ч)/(1 м/с)

    v i = 94,4 миль/ч

    Вернуться к задаче 20

 

Следующий раздел:

AP Физика 1: Кинематика Множественный выбор практики Questions_crackap.

com

1. В секции 5 графика зависимости скорости от времени объект

А. Ускорение движения в положительном направлении

B. замедление движения в положительном направлении

C. Ускорение движения в отрицательном направлении

D. Замедление движения в отрицательном направлении

2. Бейсбольный мяч брошен прямо вверх. Чему равно ускорение мяча в высшей точке?

А. г , вниз

Б. г , вниз

C. г вверх

D. г , вверх

3. Сколько времени потребуется автомобилю, начиная с состояния покоя и равномерно ускоряясь по прямой со скоростью 5 м/с 2 , чтобы преодолеть расстояние 200 м ?

А. 9,0 с

Б. 10,5 с

С. 12,0 с

D. 15,5 с

4. Камень падает со скалы и ударяется о землю со скоростью удара 30 м/с. Какой высоты был утес?

А. 20 м

Б. 30 м

С. 45 м

D. 60 м

5. Камень брошен горизонтально с начальной скоростью 10 м/с с моста. Если предположить, что сопротивление воздуха пренебрежимо мало, сколько времени понадобится камню, чтобы удариться о воду на глубине 80 м ниже моста?

А. 1 с

Б. 2 с

С. 4 с

D. 8 с

6. Футбольный мяч, покоящийся на земле, ударяют ногой с начальной скоростью 10 м/с под углом 30°. Рассчитайте его полное время полета, считая сопротивление воздуха пренебрежимо малым.

А. 0,5 с

Б. 1 с

С. 2 с

D. 4 с

7. Камень брошен горизонтально с начальной скоростью 30 м/с с моста. Найдите общую скорость камня, когда он войдет в воду через 4 с, считая, что сопротивлением воздуха можно пренебречь.

А. 30 м/с

Б. 40 м/с

С. 50 м/с

D. 60 м/с

8. Какое из следующих утверждений верно относительно движения идеального снаряда, запущенного под углом 45° к горизонту?

A.