|
Название |
Ссылка |
Описание |
|
ЕГЭ. Математика |
https://uchebnik.mos.ru/my_materials/material_view/composed_documents/19924233 |
ЭУП предназначен для подготовки к решению задач второй части ЕГЭ с развёрнутым ответом по математике (профильный уровень) |
|
ЕГЭ. Математика. Уравнения |
https://uchebnik.mos.ru/my_materials/material_view/composed_documents/10396967 |
ЭУП предназначен для подготовки к решению задач по теме «Уравнения», в частности, задачи 13 второй части ЕГЭ с развёрнутым ответом по математике (профильный уровень) |
|
11 класс. |
https://uchebnik.mos.ru/my_materials/material_view/lesson_templates/210183 |
Урок повторения по теме «Тригонометрические уравнения», задачи 13 второй части ЕГЭ с развёрнутым ответом по математике (профильный уровень) |
|
11 класс. Тригонометрические выражения |
https://uchebnik.mos.ru/my_materials/material_view/lesson_templates/213830 |
Урок обобщающего повторения по теме «Тригонометрические выражения». На уроке повторяются основные тригонометрические формулы и их применение |
|
11 класс. Решение задач на определение вероятностей |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/197442 |
В уроке рассматривается решение задач на вычисление вероятностей (правила вычисления вероятности различных событий). |
|
Решение задач. Средняя линия треугольника |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/1566157 |
Решение планиметрических задач на среднюю линию треугольника. |
|
10 класс. Геометрия. Решение задач. Призма и пирамида |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/102276 |
Решение задач, связанных с призмой и пирамидой |
|
Решение задач на нахождение объёма пирамиды и конуса |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/106023 |
Урок можно использовать для повторения темы «Объем пирамиды и конуса», задача 8 ЕГЭ |
|
Объём прямоугольного параллелепипеда |
https://uchebnik. |
Урок можно использовать для повторения темы «Прямоугольный параллелепипед и его объём», задача 8 ЕГЭ |
|
Свойства логарифмов и не только |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/87968 |
Урок направлен на повторение темы «Логарифмы. свойства логарифмов», задача 8 ЕГЭ, задача 10 ЕГЭ |
|
Правила размещения и перестановки в задачах на вычисление вероятностей |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/186022 |
Урок направлен на повторение темы «Вероятность. Применение теории вероятностей в реальной жизни», задача 4 ЕГЭ |
|
Решение задач «Угол между плоскостями» |
https://uchebnik. |
Урок направлен на повторение темы «Угол между плоскостями», задача 14 ЕГЭ |
|
Обобщающий урок «Объёмы тел» |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/105424 |
Урок направлен на повторение темы «Объёмы тел», задача 8 ЕГЭ |
|
Обобщающий урок «Понятие производной» |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/25904 |
Урок направлен на повторение темы «Понятие производной. Применение производной», задача 7 ЕГЭ |
|
|
https://uchebnik. |
Урок направлен на повторение темы «Угол между прямой и плоскостью», задача 14 ЕГЭ |
|
Обобщающий урок «Применение производной к исследованию функции» |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/215223 |
Урок помогает отработать навыки применения производной к исследованию функции, задачи 12 (профильный уровень), позволяет рассмотреть применение производной в реальных ситуациях |
|
10 класс. Геометрия. Решение задач. Пирамида 1 |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/103500 |
Урок может быть использован для подготовки к выполнению задания 8 первой части и заданию 14 второй части ЕГЭ по математике (профильный уровень) |
|
10 класс. |
https://uchebnik.mos.ru/catalogue/material_view/lesson_templates/103644 |
Урок может быть использован для подготовки к выполнению задания 8 первой части и заданию 14 второй части ЕГЭ по математике (профильный уровень) |
как сдать часть 2 ЕГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Татьяна Петрова,
аспирантка механико-математического факультета МГУ им. Ломоносова,
преподаватель математики учебного центра Challenge
Задание № 9
Что требуетсяВыполнить вычисления и преобразования.
ОсобенностиЭто задача на вычисление значения числового или буквенного выражения. Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.
Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.
Нужно знать базовые формулы и уметь их применять.
Задание № 10
Что требуетсяРешить задачу с прикладным содержанием.
ОсобенностиВнимательно читайте условие и старайтесь его понять. Следите, чтобы единицы измерения были приведены к одному виду. Выражайте ту или иную переменную в общем виде и только потом подставляйте числовые значения. Не спешите считать в лоб, пробуйте сокращать.
Не спешите считать в лоб, пробуйте сокращать.
Задание № 11
Что требуетсяРешить текстовую задачу.
ОсобенностиВсего существует шесть типов текстовых задач. Они могут быть на движение, на совместную работу, на проценты, на смеси, растворы и сплавы, на прогрессии, на оптимальный выбор и целые числа. Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.
| Задачи на движение | \(S = V \cdot t\) |
| Задачи на совместную работу | \(A = p \cdot t\) |
| Задачи на смеси, растворы и сплавы | \(C = \frac{V_{1}}{ V} \cdot 100\%\) |
Обратите внимание, что формулы в задачах на движение и на работу очень похожи. Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
Задание № 12
Что требуетсяНайти наибольшее или наименьшее значение функции.
ОсобенностиЗдесь требуется уметь находить производную функции, а также исследовать функцию с помощью производной. Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.
СоветыВыучите базовую таблицу производных, а также формулы производной произведения, частного и композиции функций. Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Задание № 13
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое уравнение, уравнение с радикалом или смешанное уравнение, содержащее одновременно логарифмы, модули, радикалы.
ОсобенностиДля решения любого уравнения существует два основных правила. Во-первых, решение всегда должно начинаться с нахождения ОДЗ — области допустимых значений, то есть всех значений переменной, при которых это уравнение имеет смысл. Во-вторых, нужно помнить основные методы решения уравнений и уметь применять их. Как правило, решение данной задачи требует замены, позволяющей свести уравнение к квадратному.
СоветыДля решения тригонометрических уравнений важно знать формулы приведения и знаки тригонометрических функций на четвертях окружности. Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Задание № 14
Что требуетсяРешить стереометрическую задачу.
ОсобенностиЭто задача на построение сечения многогранника и нахождение его площади, а также на нахождение расстояний и углов в пространстве, нахождение объемов различных многогранников и круглых тел (цилиндр, конус, шар). Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).
Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).
В этой задаче, как правило, два пункта. В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.
Задание № 15
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое (в том числе с переменным основанием) неравенство, неравенство с радикалом, смешанное неравенство, содержащее одновременно логарифмы, модули, радикалы.
ОсобенностиЗдесь необходимо свести сложное неравенство к простейшему. Часто для этого используются замены показательных и тригонометрических функций (не забывайте про ограничения!). Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.
СоветыМетод решения логарифмических неравенств опирается на монотонность логарифмической функции. Помните, что если у логарифма переменное основание, то нужно рассматривать два случая: а) основание лежит в диапазоне от 0 до 1 (функция убывает), б) основание больше единицы (функция возрастает). Если основание переменное, то можно избавиться от перебора случаев, перейдя к новому, постоянному основанию.
В логарифмических неравенствах внимательно следите за областью допустимых значений, применяя формулы действий с логарифмами, она может как расширяться, так и сужаться. И если первую ситуацию легко исправить, то вторая приведет к потере решений, что недопустимо.
Задание № 16
Что требуетсяРешить планиметрическую задачу.
ОсобенностиПод этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.
Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.
Необходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.
И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.
| Площадь треугольника через высоту и основание | \(S = \frac{1}{2}a \cdot h_{a}\) |
| Площадь треугольника через две стороны и угол между ними | \(S = \frac{1}{2}a \cdot b \cdot \sin \alpha\) |
| Площадь треугольника через радиус вписанной окружности | \(S = p \cdot r\), где \(p = \frac{a+b+c}{2}\), \(r\) — радиус вписанной окружности |
| Площадь треугольника через радиус описанной окружности | \(S = \frac{a \cdot b \cdot c}{4R}\), где \(R\) — радиус описанной окружности |
| Формула Герона | \(S = {\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p = \frac{a+b+c}{2}\) |
Задание № 17
Что требуетсяРешить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор.
ОсобенностиЗадача на злобу дня, которая появилась на ЕГЭ только в последние годы. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.
Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.
Внимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтоб подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.
Задание № 18
Что требуетсяРешить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.
Эти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика.
СоветыЧтобы подготовиться к заданиям с параметрами, я рекомендую решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов». Также хочется дать лайфхак для уравнений с двумя неизвестными: как правило, там спрятана геометрическая фигура, построй ее и получишь честное графическое решение.
Задание № 19
Что требуетсяРешить задачу на числа и их свойства.
Это самая сложная задача экзамена, олимпиадного уровня, она оценивается в четыре первичных балла. Тем не менее материал для ее решения школьники проходят еще в 6-8 классе. Задание требует хорошего логического мышления и математической культуры.
СоветыПовторите основные признаки делимости целых чисел, вспомните понятия «НОК/НОД», выучите формулы арифметической и геометрической прогрессии. «Прорешайте» типовые задания из сборника Г.И. Вольфсона и М.Я. Пратусевича «Арифметика и алгебра». Последние два задания (№ 18 и № 19) — это прямая заявка на 100 баллов.
Реальный ЕГЭ 29 мая 2019, задание 17 — Решения вариантов ЕГЭ по математике: 2017, 2018, 2019, 2020
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся)
Пусть — размер выданного кредита, — число месяцев, под понимаем число меньшее 1, например для 1% .
Ежемесячная выплата равна постоянная часть переменная часть номер месяца с конца
Общая сумма выплат равна:
Полная выплата в нашем случае равна:
У нас полная выплата , т.е.
Ответ: %
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.
 ),
), получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки «Ященко 36 вариантов 2019»,
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru
Курс по решению задачи 17 егэ по математике онлайн в Красногорске | Услуги
В заданиях ЕГЭ по математике профильного уровня в № 17 выпускнику необходимо решить задачу по финансовой математике. Она относится к повышенному уровню сложности и оценивается в три первичных балла. Экономические задачи в ЕГЭ встречаются следующих типов: 1) банковская задача о кредитах; 2) банковская задача о вкладах; 3) акции и другие ценные бумаги; 4) задачи на оптимальный выбор. Для успешного решения подобных задач требуется не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям. Курс по финансовой математике решения задач № 17 ЕГЭ профильного уровня содержит следующие разделы:
Для успешного решения подобных задач требуется не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям. Курс по финансовой математике решения задач № 17 ЕГЭ профильного уровня содержит следующие разделы:
Ⅰ Банковские задачи на кредиты
Рассматриваются задачи на нахождение ежегодной платы, задачи на нахождение суммы кредита, на вычисление процентной ставки, а также задачи на нахождение количества лет выплаты кредита.
Ⅱ Банковские задачи на вклады
Решаются задачи на нахождение срока вклада, вычисление процентной ставки по вкладу,нахождения суммы вклада и нахождение ежегодной суммы пополнения вклада.
Ⅲ Акции и другие ценные бумаги Данный раздел затрагивает понятие акций и других ценных бумаг и то, как они могут приносить доход. Все условия получения дохода, как правило, описаны в самой задаче.
Ⅳ Задачи на оптимизацию Это особый блок, позволяющий максимизировать одну целевую функцию при учете данных в условии ограничений. Основные типы задач, решаемых в этом блоке: 1) оптимизация работы на производстве с учетом цен на рынке товара и факторов производства; 2) многозаводское производство (включая разные заводы, отели и другие рабочие пространства; 3) транспортная задача.
Основные типы задач, решаемых в этом блоке: 1) оптимизация работы на производстве с учетом цен на рынке товара и факторов производства; 2) многозаводское производство (включая разные заводы, отели и другие рабочие пространства; 3) транспортная задача.
Ⅴ Итоговый раздел Посвящен решению задания № 17 из вариантов ЕГЭ 2020 года.
Приглашаю учащихся 11-ого класса на курс по решению задания №17 ЕГЭ профильного уровня 2020 г. Возможны индивидуальные занятия по скайпу по цене 600р. за час.
ЕГЭ по математике — это несерьёзно / Newtonew: новости сетевого образования
Подготавливая материалы для нашего спецпроекта по ЕГЭ по информатике, я не удержался и скачал с сайта ФИПИ демо-версии по математике. Как многие из вас уже, наверное, слышали, школьники теперь могут сдавать два варианта ЕГЭ по математике: базовый и профильный. В общем-то, идея хорошая, ибо зачем, к примеру, гуманитарию знать интегралы и производные в совершенстве, или, скажем, высшую математику. Однако то, что я увидел, меня убило. И я бы хотел обратиться с восклицанием в сторону составителей: вы офигели. Я, конечно, понимаю, что уровень знаний наших школьников оставляет желать лучшего, но не настолько же.
Однако то, что я увидел, меня убило. И я бы хотел обратиться с восклицанием в сторону составителей: вы офигели. Я, конечно, понимаю, что уровень знаний наших школьников оставляет желать лучшего, но не настолько же.
Я хотел бы сразу договориться о следующем:
- Я не хочу обсуждать в данной статье, плохо ЕГЭ или хорошо. Это тема отдельного разговора.
- Статья имеет несколько разделов: вначале — комментарии к задачам по базовому и профильному уровням, а уже затем — выводы. Пожалуйста, дочитайте до конца.
- Отдельно хотелось бы попросить не обижаться учителей математики. Я уверен, что среди них есть много хороших, но к остальным у меня много «плохих» вопросов. Слишком много.
Давайте взглянем внимательнее на те задачи, которые предлагают решить после одиннадцати лет изучения математики в школе.
Базовый уровень
Для решения предлагается 20 задач. В прошлом году для получения удовлетворительной оценки было необходимо решить 7 задач. 7 задач, Карл! Но, может, эти задачи действительно хорошие и неочевидные? Давайте взглянем на них.
7 задач, Карл! Но, может, эти задачи действительно хорошие и неочевидные? Давайте взглянем на них.
Начнём с задачи 1. Вычислить: \(\cfrac{2}{5}+\cfrac{1}{4}+2\)
Дроби, Карл, в ЕГЭ пришли дроби! Ну ладно, может, первая задача действительно проходная, совсем простенькая, для затравочки. Давайте возьмём что-нибудь из середины. Например, 6-ую задачу:
ФИПИ
Федеральный институт педагогических измерений
Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
Высшая математика, Карл! Серьёзно, неужели для того, чтобы научиться складывать числа (что лично я умел делать в 3-4 года), нужно 11 лет изучать математику по 3 или больше часа в день? А я скажу так: если ребёнок доучился до 11-го класса и не может решить эту задачу, то у меня один простой вопрос к учителю, завучам и директору школы: ребята, вы что, совсем? Эту задачу обязан уметь решать каждый первоклассник. Ну, максимум, во втором классе. Тут нечему учить — тут просто нужно понимать, что такое рубли, что такое копейки и как складывать два числа.
Ну, максимум, во втором классе. Тут нечему учить — тут просто нужно понимать, что такое рубли, что такое копейки и как складывать два числа.
Может, мы опять попали на «проходную» задачу? Давайте возьмём что-нибудь ещё. Например, задачу 11.
Беру свои слова назад. По сравнению с этой задачей прошлая — вершина математической мысли. Неужели нам нужно обучать детей одиннадцать лет математике, чтобы они могли ткнуть на графике в самую высокую точку в промежутке? Неужели недостаточно, блин, одного урока, чтобы объяснить это раз и навсегда всем детям? Как это можно не объяснить? Учителя, ответьте!
Вдумчивый читатель, наверное, скажет: там же есть задачи на проверку знания формул. Типа, ну хоть чему-то мы научили ребёнка, хоть запоминать формулы и воспроизводить их на память (хотя это, конечно, не дело и это — не задача математики). Действительно, в ЕГЭ присутствуют задачи, в которых нужно знать некоторые формулы, точнее, даже не формулы, а определения. 2-x-6=0\).
2-x-6=0\).
Вот тут надо воскликнуть: так вот же где она, математика, в формулах. Спешу огорчить: дружелюбные составители все необходимые формулы вставили в инструкции:
Инструкция к демо-версии ЕГЭ 2016 по математике, базовый уровень. Формулы с логарифмами
Источник: Официальный сайт ФИПИ
То есть, вы поняли весь цимес задания? Мне не надо помнить формулы, мне не надо знать их, мне не надо помнить условия, мне не надо помнить и понимать определения. Мне просто надо уметь подставлять циферки вместо буковок. То, чему учится ребёнок за два часа с помощью приложения Dragonbox Algebra. Я бы предложил составителям добавить в самом начале ещё и таблицу с ответами, чтоб уж наверняка не было неуспевающих учеников!
В завершение я хочу, чтобы вы испытали настоящую гордость за наш уровень образования. Внимание, встречайте самую сложную задачу № 20:
Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м.
Высота дерева 10м. Через сколько дней улитка впервые окажется на вершине дерева?
— ФИПИДемо-версия ЕГЭ-2016 по математике, базовый уровень
Где-то я это уже видел… Ах да, в книге Перельмана (или чём-то подобном) для детей 10-11 лет, в качестве простой тренировки мозга. Значит, вот так оценивает государство уровень современных непрофильных выпускников.
Ну что же, может, в профильном экзамене дела обстоят по-другому.
Профильный уровень
Первое отличие — тут уже нет формул в Инструкции. И на том спасибо. Начнём с первой проходной задачи:
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
— ФИПИДемо-версия ЕГЭ-2016 по математике, профильный уровень
Что нужно знать и уметь для решения этой задачи? Логическое мышление? Умение мыслить аналитически? Знание методов решения задач? Или помнить сложные формулы? Нет, Карл, нет. {x-5}=81\)
{x-5}=81\)
Вы думаете, что для решения этой задачи нужно помнить формулы или логарифмы? Нет, достаточно просто вспомнить, в какой же это степени тройка даёт 81: в первой — 3, во второй — 9, в третьей — 27, в четвёртой — 81. Вот оно, четвёртая степень. Значит, x=9. Всё. И это — профильный уровень ЕГЭ 11 класса?
Или другой пример: в задаче 9 нужно найти значение синуса, если дано значение косинуса. Серьёзно, эти задачки должны щёлкать как орешки в церковно-приходской школе, а не решать на ЕГЭ.
Рассмотрим одну из последних задач повышенной сложности.
31 декабря 2013 г. Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
— ФИПИДемо-вариант ЕГЭ-2016 по математике, профильный уровень
До чего мы с вами дожили? Одна из сложнейших задач ЕГЭ — на решение линейного уравнения.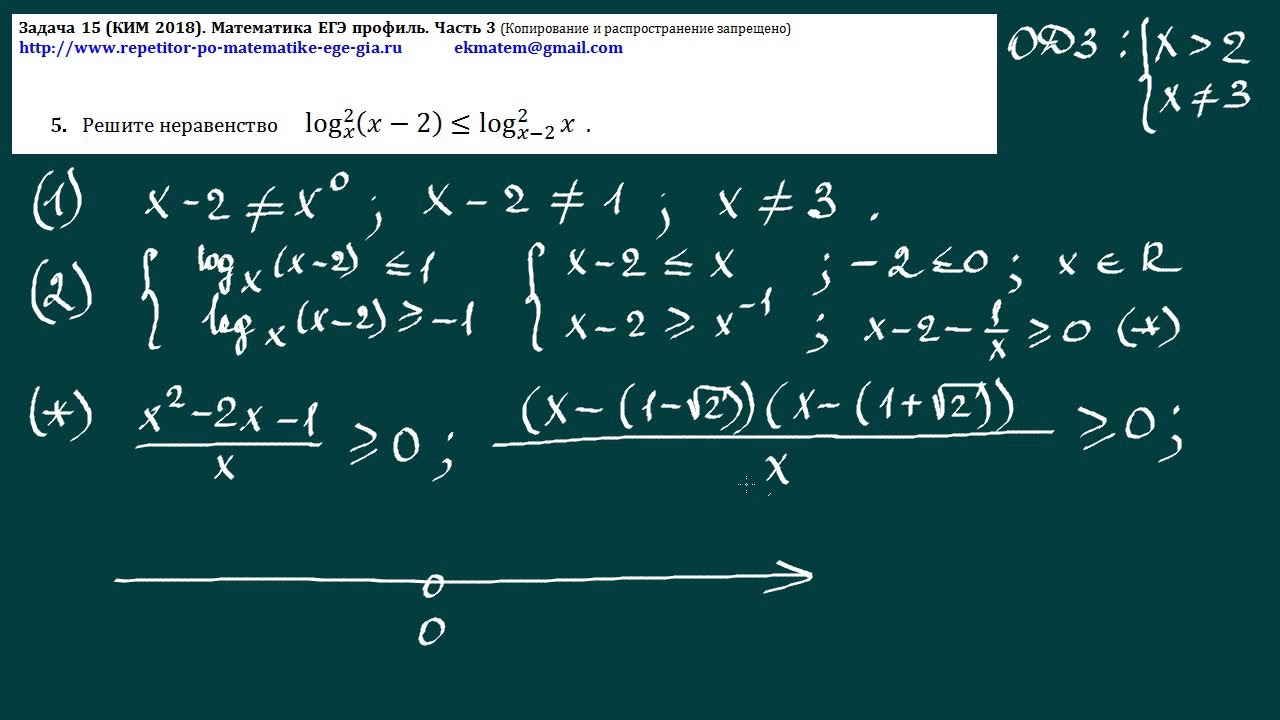 Предлагаю читателю самостоятельно решить за пару минут эту задачу и восхититься её непревзойдённой сложностью. Решая её в первый раз, я даже перепроверил себя по ответу — не слишком ли всё просто, не ошибся ли я. Нет, не ошибся. И это печально.
Предлагаю читателю самостоятельно решить за пару минут эту задачу и восхититься её непревзойдённой сложностью. Решая её в первый раз, я даже перепроверил себя по ответу — не слишком ли всё просто, не ошибся ли я. Нет, не ошибся. И это печально.
Даже две последние задачи (18 и 19), которые должны быть самыми сложными, решаются за 10 и 5 минут соответственно (графически и путём обычных логических размышлений). Но эти задачи уже требуют простейшего навыка абстрактного мышления (действительно простейшего, никак сложных рассуждений от противного, цепочек силлогизмов, мега-замен и/или хитрых ходов).
Вопросы
В результате у меня возникло два глобальных вопроса:
Вопрос 1. Почему государство создаёт столь простые варианты ЕГЭ, следуя в угоду тренду хороших показателей? Какая ценность в том, что все сдадут ЕГЭ на уровне 2-3 класса церковно-приходской школы? Что они хотят проверить таким экзаменом?
Математика — это прежде всего обучение абстрактному мышлению, построению логических цепочек и рассуждений, умению формализовать различные процессы, навыку моделирования реальных физических, экономических и других задач. Это то, что мы хотим видеть на выходе. Чтобы, давая задачу программисту о вычислении расстояния маршрута, руководитель не добавлял в задачу ссылку на теорему Пифагора. Чтобы студент-химик мог сам сделать N%-ный раствор, без гугления и помощи старших друзей-товарищей. Чтобы потребитель мог оценить навскидку переплату по кредиту. Чтобы «прикидки в уме» были с точностью хотя бы до порядка. Чтобы экономист/студент финансового вуза мог посчитать с первого раза НДФЛ. Я готов мириться с тем, что в Инструкции добавляют формулы, ведь, в конце концов, в реальной жизни есть Интернет, где это можно подсмотреть. Но я не готов мириться с тем, чтобы государственная итоговая аттестация за 11 классов математики сводилась к подстановке чисел вместо букв.
Это то, что мы хотим видеть на выходе. Чтобы, давая задачу программисту о вычислении расстояния маршрута, руководитель не добавлял в задачу ссылку на теорему Пифагора. Чтобы студент-химик мог сам сделать N%-ный раствор, без гугления и помощи старших друзей-товарищей. Чтобы потребитель мог оценить навскидку переплату по кредиту. Чтобы «прикидки в уме» были с точностью хотя бы до порядка. Чтобы экономист/студент финансового вуза мог посчитать с первого раза НДФЛ. Я готов мириться с тем, что в Инструкции добавляют формулы, ведь, в конце концов, в реальной жизни есть Интернет, где это можно подсмотреть. Но я не готов мириться с тем, чтобы государственная итоговая аттестация за 11 классов математики сводилась к подстановке чисел вместо букв.
Почему нельзя сказать: «Да, у нас системный кризис в образовании. Мы собираем через месяц 50 лучших педагогов страны, 50 лучших учителей в мире, 50 родителей, 50 детей, 50 работодателей, 50 преподавателей вузов, 50 чиновников и пр. Садимся и за две недели работы создаём план, устраивающий все стороны. С постепенным внедрением «от и до». И с чёткими, конкретными результатами. А затем будет максимальная политическая и экономическая воля для внедрения решений. Никаких отклонений, никаких отговорок, никаких задержек». Под таким подходом, как мне кажется, подпишутся практически все стороны, готовые к конструктивному диалогу.
Садимся и за две недели работы создаём план, устраивающий все стороны. С постепенным внедрением «от и до». И с чёткими, конкретными результатами. А затем будет максимальная политическая и экономическая воля для внедрения решений. Никаких отклонений, никаких отговорок, никаких задержек». Под таким подходом, как мне кажется, подпишутся практически все стороны, готовые к конструктивному диалогу.
Вопрос 2. Уважаемые учителя математики! Как так получилось, что ваши дети не сдают столь простой экзамен? Я всё понимаю, сам нахожусь по эту же сторону баррикад и готов понять, почему они не умеют вычислять пределы, считать сложные производные и интегралы, не умеют решать задачи на формулы условной вероятности и теорему Байеса. Но, уважаемые учителя:
- Как так случилось, что дети просто-напросто не умеют складывать дроби?
- Как так получилось, что существуют дети, не решающие квадратное уравнение с формулой-записанной-в-инструкции-сверху?
- Как так получилось, что умение посмотреть на график считается чем-то, к чему надо готовиться?
- Как так получилось, что вы жалуетесь на то, что детей требуется теперь готовить к ЕГЭ, при наличии задач, к которым не то, что готовиться не надо, а которые можно давать в качестве примеров отстающим детям, которые не могут решить задачи.

- Как так получилось, что теорема Пифагора стала задачей повышенной сложности?
Есть ещё много «как так получилось». И, знаете, сравнивая вклад государства и ваш в падение уровня математики, я бы сказал, что именно вы стали тем звеном, из-за которого государству приходится понижать уровень. Не было бы 25% не набравших минимальный балл, не было бы ЕГЭ церковно-приходского (базового) уровня. Скажите просто — КАК? Я, как учитель информатики, действительно не понимаю. Я учу детей информатике, и, вы не поверите, средняя задача по информатике в ЕГЭ на порядки сложнее задачи по математике. И, вы опять не поверите, они их решают. Все. Все те, кому я ставлю хотя бы 3.
Почему вам стало всё равно? Почему вы не хотите заставлять их понять хотя бы базу? Я всё понимаю: да, зарплаты низкие, да, нагрузка большая, да, много бумажек. Да, мир меняется, меняются поколения, меняется формат и форма. Меняются технологии, за которыми всё время приходится поспевать. Но проявите хоть какую-никакую ответственность. Хороший учитель сможет объяснить даже с мелом и доской. Начните учить. Или уходите.
Хороший учитель сможет объяснить даже с мелом и доской. Начните учить. Или уходите.
23 ноября 2015, 15:15
Мнение автора может не совпадать с позицией редакции.
Данная статья распространяется по лицензии Creative Commons.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
вопросов 1Если журнал x (1/8) = — 3/2, то x равенA. — 4 B. 4 C. 1/4 D 10 вопросов 220% из 2 равноA. 20 B. 4 C. 0,4 D. 0,04 вопросов 3Если журнал 4 (x) = 12, то журнал 2 (x / 4) равноA.  11 11 B. 48 C. -12 D. 22 Вопросы 4Население страны увеличивалось в среднем на 2% в год с 2000 по 2003 год.Если бы население этой страны на 31 декабря 2003 г. составляло 2000000, то на 1 января 2000 г. население этой страны с точностью до тысячи было быA. 1 846 000 B. 1 852 000 C. 1 000 000 Д. 1 500 000 Вопросы 5f — квадратичная функция, график которой представляет собой раскрывающуюся вверх параболу с вершиной на оси x. График новой функции g, определенной как g (x) = 2 — f (x — 5), имеет диапазон, определенный интерваломA. [-5, + infinity) B.[2, + бесконечность) C. (- бесконечность, 2] D. (- бесконечность, 0] Вопросы 6f — функция, такая что f (x) <0. График новой функции g, определенной формулой g (x) = | f (x) | является отражением графика f График новой функции g, определенной формулой g (x) = | f (x) | является отражением графика f A. на оси y B. на оси x C. на прямой y = x D. на прямой y = — Икс Вопросы 7Если график y = f (x) преобразовать в график 2y — 6 = — 4 f (x — 3), точка (a, b) на графике y = f (x) станет точка (A, B) на графике 2y — 6 = — 4 f (x — 3), где A и B равныA.A = a — 3, B = b B. A = a — 3, B = b C. A = a + 3, B = -2 b D. A = a + 3, B = -2 b + 3 Вопросы 8Когда парабола, представленная уравнением y — 2x 2 = 8 x + 5, перемещается на 3 единицы влево и на 2 единицы вверх, новая парабола имеет вершину вA.  (-5, -1 ) (-5, -1 ) B. (-5, -5) C. (-1, -3) D. (-2, -3) Вопросы 9Графики двух линейных уравнений ax + by = c и bx — ay = c, где ни один из коэффициентов a, b, c не равен нулю,A.параллельны B. пересекаются в точке (0,0) C. пересекаются в двух точках D. перпендикулярно Вопросы 10Графики двух уравнений y = ax 2 + bx + c и y = A x 2 + B x + C, так что a и A имеют разные знаки и что величины b 2 — 4 ac и B 2 — 4 AC отрицательны,A.  пересекаются в двух точках пересекаются в двух точках B. пересекаются в одной точке C. не пересекаются с D. ни один из вышеперечисленных Вопросы 11Для x больше или равного нулю и меньше или равного 2π, sin x и cos x уменьшаются на интервалахА.(0, π / 2) B. (π / 2, π) C. (π, 3 π / 2) D. (3 π / 2, 2 π) Вопросы 12Три решения уравнения f (x) = 0 равны -2, 0 и 3. Следовательно, три решения уравнения f (x — 2) = 0 равныA. — 4, -2 и 1 B. -2, 0 и 3 C. 4, 2 и 5 D. 0, 2 и 5 Вопросы 13Три решения уравнения f (x) = 0 — 4, 8 и 11. Следовательно, три решения уравнения уравнение f (2 x) = 0 равноA.  — 2, 4 и 11/2 — 2, 4 и 11/2 B.- 8, 16 и 22 C. — 4, 8 и 11 D. 2, 19/2 и 7/2 Вопросы 14Школьный комитет состоит из 2 учителей и 4 учеников. Количество различных комитетов, которые могут быть сформированы из 5 учителей и 10 студентов, составляетA. 10 B. 15 C. 2100 D. 8 Вопросы 15Пять разных книг (A, B, C, D и E) размещаются на полке. Книги C и D должны располагаться первой и второй справа от полки. Количество различных порядков, в которых можно расположить книги A, B и E, составляетA.5! Б. 3! С. 2! Д. 3! * 2! Вопросы 16Среднее значение набора данных равно 10, а его стандартное отклонение равно 1. Если мы добавим 5 к каждому значению данных, то среднее и стандартное отклонение станут Если мы добавим 5 к каждому значению данных, то среднее и стандартное отклонение станут A. Среднее значение = 15, стандартное отклонение = 6 B. среднее значение = 10, стандартное отклонение = 6 C. среднее значение = 15, стандартное отклонение = 1 D. среднее значение = 10, стандартное отклонение = 1 Вопросы 17Были записаны экзаменационные баллы всех 500 студентов, и было определено, что эти баллы были распределены нормально.Если оценка Джейн на 0,8 стандартного отклонения выше среднего, то сколько, с точностью до ближайшей единицы, ученики набрали больше баллов, чем Джейн?A. 394 B. 250 C. 400 D. 106 Вопросы 18Если f (x) — нечетная функция, то | f (x) | равноA. нечетная функция B.  четная функция четная функция C. ни нечетная, ни четная D. четная и нечетная Вопросы 19Период | грех (3x) | равноA. 2 π B. 2 π / 3 C. π / 3 D. 3 π Вопросы 20Когда металлический шарикоподшипник помещается в цилиндрический контейнер радиусом 2 см, высота воды внутри контейнера увеличивается на 0.6 см. Радиус шарикового подшипника с точностью до десятых долей сантиметра равенA. 1 см B. 1,2 см C. 2 см D. 0,6 см Вопросы 21Период 2 sin x cos x равенA. 4 π 2 B.  2 π 2 π C. 4 π D. π Вопросы 22Вероятность того, что электронное устройство, произведенное компанией, не функционирует должным образом, равна 0,1. Если куплено 10 устройств, то вероятность с точностью до тысячных, что 7 устройств исправно работают, составляетА.0,057 B. 0,478 C. 0,001 D. 0 Ответы на поставленные выше вопросы1b, 2c, 3d, 4a, 5c, 6b, 7d, 8a, 9d, 10c11b, 12d, 13a, 14c, 15b, 16c, 17d, 18b, 19c, 20b 21d, 22a. Дополнительные ссылки и ссылки по математическим вопросам и задачамматематическим вопросам и задачам с подробными решениями. |
Как решить вирусную математическую задачу 2019
Вот оно появилось в Твиттере, как жестокая насмешка:
Этот контент импортирован из Twitter.Вы можете найти то же содержимое в другом формате или найти дополнительную информацию на их веб-сайте.
Каждые несколько месяцев Интернет пожирает себя какой-нибудь вирусной загадкой или иллюзией, каждая из которых выводит из себя больше, чем предыдущая. И так, как по маслу, эта сводящая с ума математическая задача стала вирусной, следуя великой традиции таких травмирующих событий, как «Платье» и «Янни / Лорел».
Загадки такого рода преднамеренно предназначены для разделения и подчинения, и, как и ожидалось, кажущаяся простая проблема, поставленная в оскорбительном твите — 8 ÷ 2 (2 + 2) — на практике вызвала гражданскую войну в офисе Popular Mechanics . которыми мы также делимся с нашими (бывшими) друзьями в журналах Runner’s World и Bicycling .
➗ Вы любите сложные математические задачи. И мы тоже. Решим их вместе.
Естественно, мы обратились к Slack, чтобы устранить наши различия. Вот горячая беседа между редакторами, которые перестали делать хоть какое-то подобие реальной работы в течение дня, чтобы решить уравнение, созданное, чтобы сбить с толку четвероклассников — и нажить много врагов в процессе, — за которым следует понимание реальных математиков и физиков, которые неохотно откликнулись на наш запрос за комментарий, чтобы раз и навсегда разрешить яростные математические дебаты.
Война слабаков, часть I
Дерек Колл, видеопродюсер: 8 разделить на 8 равно 1.
Джефф Денгейт, Runner’s World главный бегун: PEMDAS. 16.
Бобби Ли, редактор тестов (и трехкратный олимпийский велосипедист): Я езжу на велосипедах
Пэт Хайне, видеопродюсер: . .. она пишет PEMDAS, а затем PEDMAS
.. она пишет PEMDAS, а затем PEDMAS
Matt: Вы явно не слушали
Pat: Я не слушал…я была занята исправлением своей математики.
Дерек: Когда они изобретают математику заново?
Мэтт: хорошо, Дерек, видео для тебя
Пат: если у тебя 16, это потому, что ты не знаешь разницы между скобками и скобками.
Википедия
Морган Петруни, редактор тестирования: Я согласен с Дереком и не согласен с YouTube. Что, если вы хотите проделать долгий путь и использовать свойство распределения, а сначала распространить 2? Вы бы сделали: 8 / (4 + 4) = 1.
Или свойство распределения вдруг перестало действовать?
Я бы сказал, что это доказывает, что 1 правильный.
Дерек: Я доверяю Морган, потому что в это десятилетие у нее был урок математики.
Pat: Википедия говорит, что вы ненавидите Америку, если получаете 16.
Википедия
Дэн Роу, редактор теста: Верно, но это умножение / деление, а не умножение, а затем деление
Морган: НО умножение с круглыми скобками превосходит деление.Так что у вас все еще остается 8/2 (4). Так что сначала вам нужно сделать 2х4. По крайней мере, так меня учили.
Дэн: умные люди из Беркли говорят, что это слишком двусмысленно, чтобы говорить; PEMDAS — это не столько математическое соглашение, сколько метод обучения. но этот человек не умеет писать четкие уравнения
Билл Стрикленд, редакторский директор : СДЕЛАЙТЕ ЭТО СОДЕРЖАНИЕ!
инстаграм-история с нашими сотрудниками обсуждают?
можно назвать известного математика?
Бобби: Это похоже на разговор, который относится к сегменту «Не моя работа» Подожди, подожди, не говори мне
Кэти Фогель, редактор социальных сетей: сейчас опрашивает нашу аудиторию IG по этому поводу. ..
..
Pat: Уравнение написано не в соответствии со стандартами ISO, что оставляет неоднозначность интерпретации, и настоящий ответ заключается в том, что нам нужно научить лучше писать математику.
Неоднозначный PEMDAS
Неоднозначные проблемы, порядок операций, PEMDAS, BEMDAS, BEDMAS
он же … то, что сказал Тейлор, но из Гарварда
Морган: он же … научить распределительному свойству вместо случайных сокращений
Pat: Если написано в соответствии со стандартом ISO, ответ — 1.
Пэт Хайне
Эндрю Дэниэлс, редактор с практическими рекомендациями: честно говоря, мы могли бы опубликовать эту слабую ветку слово в слово, а затем попросить ученого вмешаться и обучить нас
Кэти Фогель: Из нашей аудитории IG …
Кэти Фогель / Instagram
Кит Фокс, редактор специальных проектов: Разве здесь не вопрос и двусмысленность, когда исчезают круглые скобки? Мол, остаются ли парены после того, как вы сделаете 2 + 2? Или они исчезнут, как только вы сначала решите мини-уравнение внутри скобок. Я говорю, что они никуда не денутся. Я в команде 1
Я говорю, что они никуда не денутся. Я в команде 1
Я также не посещал математические классы более 10 лет
Тревор Рааб, фотограф: Мой вопрос в том, к какому сценарию реального мира это применимо к
Брэд Форд, редактор теста: Класс математики?
Тревор: ах, классический учись математике, чтобы научиться больше заниматься математикой
Бобби: школа — не настоящий мир
Морган: Создание горячих и поляризующих офисных дискуссий
Брэд: Бобби, скажи это шестикласснику.
Бобби: Сейчас я буду работать над подготовкой аргументации
Тейлор: У вас есть, что, 11 лет, чтобы усовершенствовать его
Бобби: время на моей стороне
это код для: Я могу отложить это на очень долгое время
Пат: , который является кодом для «спроси свою мать»
Бобби: она любит утверждать, что она хороша в математике. Она может пожалеть о том дне, когда хвасталась этим
Она может пожалеть о том дне, когда хвасталась этим
Pat: «Это не поможет мне выиграть миллионы долларов, играя в Fortnite, хотя»
Краткое заявление Майка Брина, сотрудника по общественной информации Американского математического общества , Чья работа — «рассказывать людям, насколько хороша математика»
В соответствии с порядком операций вы сначала решаете то, что указано в скобках.Это дает вам 4. Затем, в PEMDAS, умножение и деление имеют равный приоритет, поэтому вы должны делать первое, что происходит слева направо. Итак, сначала вы должны разделить 8 на 2, то есть 4. Таким образом, получится 16 в соответствии с классическим порядком операций.Но то, как это написано, неоднозначно. В математике очень часто возникают двусмысленности. Математики стараются делать правила как можно точнее. По строгому порядку действий вы получите 16, но я бы не стал бить кого-нибудь линейкой по запястью, если он скажет 1.
The Slack War, часть II
Эндрю: ууууу мальчик
я только что разговаривал по телефону с американским математическим обществом
какие американские горки это оказывается
мой человек микрофон с AMS чья работа — прямо отвечать на подобные вопросы, говорит, что ответ такой . ..
..
Брэд: 42
Тайлер Дасвик, помощник редактора функций: тайно лучший ответ здесь
Эндрю: ШЕСТНАДЦАТЬ
Эндрю, минуты спустя: почему никто не реагирует должным образом на эту новость
Брэд: Потому что он неправ.
Trevor: но разве это не противоречит PEMDAS?
Эндрю: он говорит (и мне придется вернуться к стенограмме), что при использовании * традиционного * порядка операций ответ будет 16
Мэтт Филлипс, старший редактор теста: Эндрю, у моего брата есть Имеет докторскую степень по теоретической физике и пишет статьи с такими названиями, как… «Угловая зависимость для ν ‘, j’-разрешенных состояний в F + h3 → HF (ν’, j ‘) + H реактивном рассеянии с использованием нового источника пучка атомного фтора» I может посмотреть, хочет ли он взвесить…
Андрей: да! пожалуйста, сделайте [Примечание редактора: брат Мэтта не ответил. ]
]
Тейлор: есть ли способ, которым 1 также является правильным ответом для этого?
Тревор: PEMDAS
Эндрю: Я также отправлю запрос своему физику, который также только что ответил на вопрос POP о том, как прыгнуть с движущегося поезда
Тейлор: tbh это было бы было бы здорово, если бы мы смогли найти экспертов, которые не согласны.
Тревор: подождите, вернул мою интерпретацию PEMDAS к 16
вот почему я пошел в художественную школу
Тейлор: Я спросил моего друга [УДАЛЕНО], кто такой собирается закончить университет с докторской степенью по статистике из [УДАЛЕНО] и имеет три или четыре степени магистра математики
, и я так рад сообщить, что она на моей стороне
Тейлор Ройек
Дерек: [УДАЛЕНО] побеждает
Эндрю: но что [УДАЛЕНО] было ответом ??!
Тейлор: нет ответа, фальшивый вопрос, созданный, чтобы разжечь возмущение
Билл: может быть, наш умный подход таков: математика не субъективна, никто не пишет математику так, вот что не так
Тейлор: она только начинает
Тейлор Ройек
Комплект: Похоже, [УДАЛЕНО] нужно написать потную математику. Take
Take
Эндрю: daaaaang [УДАЛЕНО]
go off
Бобби: нет, мы на что-то наткнулись!
Прощальный выстрел от Ретта Аллена, доктора философии.D., доцент кафедры физики Университета Юго-Восточной Луизианы, вынесший окончательный вердикт и решительно закрывший нас всех
Это математическая версия вопроса: «Какого цвета это платье? Синий и черный или золотой и белый? »Я отвечу, что сначала вы ставите скобки, так что получается:
8/2 * 4
Затем вы идете слева направо.
8/2 равно 4, поэтому это
4 * 4
Теперь вы получаете 16.
Конечно, это не математика. Это условность.У нас есть соглашения о том, как писать эти вещи, точно так же, как у нас есть соглашения о том, как писать что-то по буквам. Но все же есть разные условности. Некоторые люди пишут это как «серый», а другие как «серый».Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Вот так:
8 / (2 * (2 + 2)), если это то, что вы пытаетесь сделать. Таким образом, никто не ошибется.
Футболки Popular Mechanics на Amazon
Футболка с обложки Popular Mechanics, апрель 1940 г.
Футболка Popular Mechanics Январь 1951 на обложке
Футболка с обложки журнала Popular Mechanics, июль 1982 года
Футболка с обложки Popular Mechanics, октябрь 1943 года
Футболка на обложке Popular Mechanics, март 1936 года
Футболка с обложки Popular Mechanics, июнь 1935 года
Футболка с обложки Popular Mechanics, ноябрь 1923 года
Футболка на обложке Popular Mechanics Ноябрь 1922 года
Футболка с обложки Popular Mechanics, январь 1994
Футболка на обложке Popular Mechanics, апрель 1915 года
Футболка с обложки Popular Mechanics, январь 1931 года
Футболка с обложки журнала Popular Mechanics, июнь 1926 года
Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.
Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.
Новейшие математические задачи со словами
Задачи со словами по математике
Эльза арендует автомобиль на выходные, она может выбрать один из двух планов: первый план имеет начальную плату в размере 51,98 доллара и стоит дополнительно 0,12 доллара за милю, второй план имеет начальную плату в размере… более
кошка добралась до дома?
Есть кошка в поезде, где ее дом находится в 16 милях, кошка пробегает 2 мили в один день, на следующий день кошка пробегает 3 мили, а на следующий день кошка пробегает 11 миль. сколько миль проехал … более
Пожалуйста, ответьте быстро
В моей сумке 1/3 четвертинки — это то же самое, что и 2/5 десятицентовика. 2 т — 0,2 син т. Находить…
более
2 т — 0,2 син т. Находить…
более
Справка по проблеме исчисления слов
Скорость объекта, движущегося по линии, в момент времени t секунд равна v (t) = 2cos (πt), а расстояние измеряется в метрах. Положение объекта в момент нуля секунд составляет 2 метра. Найдите ускорение … более
Математическая задача со словами
Мне нужна помощь с вопросом, связанным с комплексными числами.Возникает вопрос: рассмотрим комплексное число: 𝑧 = 3 — 3 𝑖. Оцените: (i) 𝐼𝑚 (𝑧) (ii) | 𝑧 | (iii) 𝐴𝑟𝑔 (𝑧)
Математическая задача со словами
У Шайны было немного конфет, чтобы дать своим троим детям. Сначала она взяла восемь штук для себя, а затем поровну разделила остальное между своими детьми. Каждый ребенок получил четыре штуки. сколько штук …
более
Каждый ребенок получил четыре штуки. сколько штук …
более
ОЖИДАЕМАЯ СТОИМОСТЬ ИГРОВОЙ КОЛЕСО ВОПРОС
Предположим, вы поставили 1 доллар на красное колесо рулетки.Есть 18 красных чисел и 20 не красных чисел (включая зеленые 0 и 00). Вы выигрываете 1 доллар, если выпадает красное число, и теряете 1 доллар, если другое … более
При затемнении возвращается слово справка по проблеме
Г-н К. стригает газон за 24 минуты. Мистер Z косит за 36 минут. Вопрос в том, через сколько минут у мистера Z будет вдвое больше газонов, чем у мистера К. Как решить эту проблему с помощью уравнения… более
Справка по проблеме Word
Кофейник с температурой 100 градусов Цельсия ставят в комнату с температурой 20 градусов Цельсия. Кофе остывает до 50 градусов по Цельсию за час. Найдите T (t), …
более
Кофе остывает до 50 градусов по Цельсию за час. Найдите T (t), …
более
Справка по задаче с предварительным исчислением
Некий прямоугольный треугольник имеет площадь 65 квадратных дюймов.Длина одного катета треугольника на один дюйм меньше гипотенузы. Пусть x представляет длину гипотенузы. Напишите стороны треугольника … более
Задача предварительного исчисления слов
Предположим, что среднее количество автомобилей, прибывающих к главным воротам парка развлечений, равно 10 в минуту, в то время как среднее количество автомобилей, проезжающих через ворота в минуту, равно… более
Задача предварительного исчисления слов
Прямоугольный кусок картона размером 12 на 18 дюймов должен быть превращен в коробку с открытым верхом, вырезав квадраты одинакового размера с каждого угла и загнув стороны.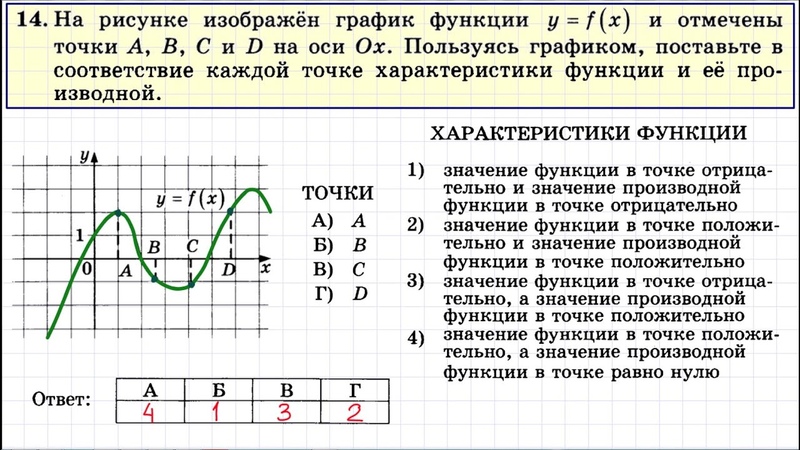 Пусть x представляет …
более
Пусть x представляет …
более
Как решить эту проблему
общая длина 4 синих знамен и 5 желтых знамен составляет 49 метров.общая длина 2 синих баннеров и 1 желтого баннера составляет 17 метров, все баннеры одного цвета имеют одинаковую длину. найти… более
21 сложнейший математический вопрос для ACT
Вы учились и теперь готовы к математическому разделу ACT (уф!). Но готовы ли вы ответить на самые сложные математические вопросы, которые предлагает ACT? Вы хотите точно знать, почему эти вопросы так сложны и как лучше всего их решать? Если вы настроены на этот высший балл (или вам просто очень любопытно посмотреть, какие будут самые сложные вопросы), то это руководство для вас.
Мы собрали, по нашему мнению, 21 самый сложный вопрос, который ACT задавал студентам за последние 10 лет, со стратегиями и ответами на каждый из них. . Все это настоящие вопросы по математике ACT, поэтому их понимание и изучение — один из лучших способов улучшить свой текущий результат ACT и выбить его из общего ряда в день экзамена.
. Все это настоящие вопросы по математике ACT, поэтому их понимание и изучение — один из лучших способов улучшить свой текущий результат ACT и выбить его из общего ряда в день экзамена.
Краткий обзор математического раздела ACT
Как и все тематические разделы ACT, математический раздел ACT представляет собой один законченный раздел, который вы будете изучать сразу.Это всегда будет второй раздел теста, и у вас будет 60 минут, чтобы ответить на 60 вопросов .
ACT размещает свои вопросы в порядке возрастания сложности . Как правило, вопросы 1-20 считаются «легкими», вопросы 21-40 — «средней сложности», а вопросы 41-60 — «сложными».
АСТ классифицирует «легкий» и «сложный» на основании того, сколько времени требуется среднему учащемуся, чтобы решить задачу, а также процент учащихся, ответивших на вопрос правильно. Чем быстрее и точнее средний ученик решает задачу, тем «легче» это. Чем больше времени требуется на решение проблемы и чем меньше людей ответят на нее правильно, тем «сложнее» проблема.
Чем больше времени требуется на решение проблемы и чем меньше людей ответят на нее правильно, тем «сложнее» проблема.
(Примечание: мы помещаем слова «легкий» и «сложный» в кавычки по какой-то причине — у всех разные математические сильные и слабые стороны, поэтому не все сочтут «легкий» легким или «сложный» вопрос трудным. Эти категории усреднены для многих студентов по определенной причине, и не каждый студент вписывается в эту точную форму.)
С учетом всего сказанного, , за очень немногими исключениями, самые сложные математические задачи ACT будут сгруппированы в дальнем конце теста. Помимо того, что эти вопросы попадают в тест, у этих вопросов есть еще несколько общих черт. Вскоре мы рассмотрим примеры вопросов, способы их решения, а также общие черты этих вопросов.
Но сначала: следует ли
сосредоточиться на самых сложных математических вопросах прямо сейчас? Если вы только начинаете подготовку к учебе, обязательно остановитесь и найдите время, чтобы пройти полный практический тест, чтобы определить свой текущий уровень баллов и процентиль. Самый лучший способ оценить свой текущий уровень — просто пройти ACT, как если бы он был реальным, соблюдая строгий график и работая без остановки (мы знаем — не самый захватывающий способ потратить четыре часа, но он очень поможет в долгосрочной перспективе. пробег). Так что распечатайте один из бесплатных практических тестов ACT, доступных в Интернете, а затем сядьте и сдавайте все сразу.
Самый лучший способ оценить свой текущий уровень — просто пройти ACT, как если бы он был реальным, соблюдая строгий график и работая без остановки (мы знаем — не самый захватывающий способ потратить четыре часа, но он очень поможет в долгосрочной перспективе. пробег). Так что распечатайте один из бесплатных практических тестов ACT, доступных в Интернете, а затем сядьте и сдавайте все сразу.
После того, как вы получите хорошее представление о своем текущем уровне и процентиле, вы можете установить контрольные точки и цели для получения окончательного результата ACT.Если вы в настоящее время набираете баллы в диапазоне от 0 до 16 или от 17 до 24, вам лучше сначала ознакомиться с нашими руководствами по использованию ключевых математических стратегий, включающих числа и ответы, которые помогут поднять ваш счет до того уровня, в котором вы хочу. Только после того, как вы попрактикуетесь и успешно улучшите свои баллы по вопросам 1-40, вы можете начать пытаться решать самые сложные математические задачи в тесте.
Если, однако, вы уже набрали 25 или больше баллов и хотите проверить свои способности на реальном ACT, то обязательно переходите к остальной части этого руководства.Если вы стремитесь к совершенству (или близкому к нему), вам нужно знать, как выглядят самые сложные математические вопросы ACT и как их решать. И, к счастью, мы здесь для этого.
Готово, готово …
21 сложнейший математический вопрос для ACT
Теперь, когда вы уверены, что вам следует попробовать эти сложные математические вопросы, давайте приступим к делу! Ответы на эти вопросы находятся в отдельном разделе ниже, так что вы можете пройти их все сразу, не испортившись.
# 1:
# 2:
# 3:
# 4:
# 5:
# 6:
# 7:
# 8:
# 9:
# 10:
# 11:
# 12:
# 13:
# 14:
# 15:
# 16:
# 17:
# 18:
# 19:
# 20:
# 21:
Разочарованы вашими результатами ACT? Хотите улучшить свой результат ACT на 4+ балла? Загрузите наше бесплатное руководство по 5 основным стратегиям, которые вам понадобятся при подготовке, чтобы значительно улучшить свой результат ACT. 2 + bt + c $), является параболой, и нам предлагается описать, что происходит, когда мы меняем c (точку пересечения по оси y).
2 + bt + c $), является параболой, и нам предлагается описать, что происходит, когда мы меняем c (точку пересечения по оси y).
Из того, что мы знаем о функциях и переводах функций, мы знаем, что изменение значения c сдвинет всю параболу вверх или вниз, что изменит не только точку пересечения оси y (в данном случае это называется «пересечение h»), но и также максимальная высота параболы, а также ее точка пересечения по оси x (в данном случае это называется точкой пересечения t). Вы можете увидеть это в действии, когда мы увеличим значение точки пересечения оси Y нашей параболы.
Все варианты I, II и III верны.
Наш окончательный ответ: K, I, II и III
# 2: Сначала давайте составим уравнение, которое нам говорят: произведение $ c $ и $ 3 $ равно $ b $.
$ 3c = b $
Теперь мы должны изолировать c, чтобы мы могли добавить его значение к 3.
$ 3c = b $
$ c = b / 3
$ Наконец, добавим это значение к 3.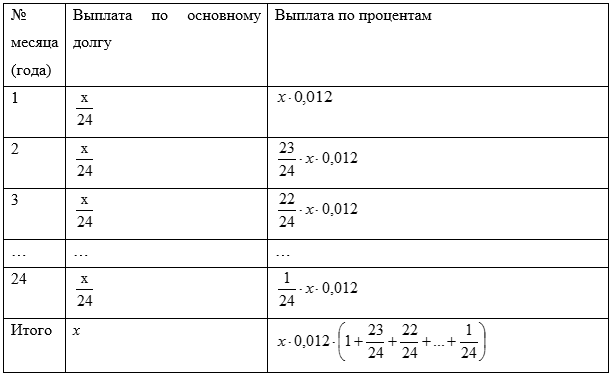
$ c + 3 = {b / 3} + 3
$Наш окончательный ответ: E , $ b / 3 + 3 $
[Примечание: поскольку в этой задаче используются переменные как в задаче, так и в вариантах ответа — ключевой особенности вопроса с PIN-кодом — вы всегда можете использовать стратегию добавления цифр для решения вопроса.]
# 3: Поскольку в этом вопросе используются переменные как в задаче, так и в вариантах ответа, вы всегда можете использовать PIN-код для ее решения.2 − x} $.
# 4: Прежде чем делать что-либо еще, убедитесь, что вы преобразовали все свои измерения в одну и ту же шкалу. Поскольку мы работаем в основном с дюймами, преобразуйте стол с диаметром 3 фута в стол с диаметром $ (3) (12) = (36) $ дюйма.
Теперь мы знаем, что скатерть должна вешать дополнительные 5 + 1 $ дюймов на с каждой стороны , поэтому наша полная длина скатерти по любой прямой будет:
$ 1 + 5 + 36 + 5 + 1 = 48 $ дюймов.
Наш окончательный ответ — K , 48.
# 5: Положение значений a (перед синусом и косинусом) означает, что они определяют амплитуду (высоту) графиков. Чем больше значение a, тем выше амплитуда.
Поскольку высота каждого графика больше 0, мы можем исключить варианты ответов C, D и E.
Поскольку $ y_1 $ выше, чем $ y_2 $, это означает, что $ y_1 $ будет иметь большую амплитуду. График $ y_1 $ имеет амплитуду $ a_1 $, а график $ y_2 $ имеет амплитуду $ a_2 $, что означает, что $ a_1 $ будет больше, чем $ a_2 $.2} = 2 $), поэтому наше выражение будет иметь следующий вид:
$ = {sinx} / {sinx} + {cosx} / {cosx} $
Или, другими словами:
$ = 1 + 1 $
$ = 2
$Наш окончательный ответ: H , 2.
# 7: Благодаря работе с вложенными функциями мы знаем, что должны работать наизнанку. Таким образом, мы должны использовать уравнение для функции g (x) в качестве нашего входного значения для функции $ f (x) $.
$ f (g (x)) = 7x + b
$Теперь мы знаем, что эта функция проходит через координаты (4, 6), поэтому давайте заменим наши значения x и y для этих данных.(Помните: имя функции — в данном случае $ f (g (x)) $ — действует как наше значение y).
$ 6 = 7 (4) + b $
36 $ = 7 (4) +
b $$ 36 = 28 + b $
8 долларов =
бразильских долларовНаш окончательный ответ: A , b = 8.
# 8: Если вы освежили основы ведения журнала, то знаете, что $ log_b (m / n) = log_b (m) −log_b (n) $. Это означает, что мы можем работать в обратном порядке и преобразовать наше первое выражение в:
$ log_2 (24) -log_2 (3) = log_2 (24/3)
$$ = log_2 (8)
$ Мы также знаем, что журнал, по сути, спрашивает: «До какой степени нужно поднять базу, чтобы достичь этого определенного значения?» В данном конкретном случае мы спрашиваем: «В какой степени нужно возвести 2 до 8?» На что ответ — 3. 2} $
2} $
$ √ {16 + 25}
$6.2} $
$ √ {16 + 4}
$4,5
Наибольшее (и действительно наибольшее ) значение модуля находится в точке $ z_1 $
.Наш окончательный ответ — F , $ z_1 $.
# 10: Для такой задачи вы можете не знать, что такое рациональное число, но вы все равно сможете решить ее, просто взглянув на любой ответ, который кажется подходящим с другими минимум . Все варианты ответов A, B, C и D дают нецелые значения, когда мы извлекаем их квадратный корень, но вариант ответа E является исключением.
долл. США √ {64/49}
долл. СШАСтановится:
долл. США √ {64} / √ {49}
долл. США$ 8/7 $
Рациональное число — это любое число, которое может быть выражено как дробь двух целых чисел, и это единственный вариант, который подходит под определение. Или, если вы не знаете, что такое рациональное число, вы можете просто увидеть, что это единственный ответ, который дает целочисленные значения после того, как мы взяли корень, что выделяет его из толпы.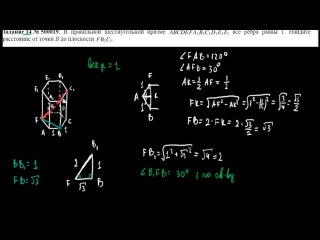
Наш окончательный ответ: E , √ {64/49} $
# 11: Поскольку мы работаем с числами в тройных цифрах, наши числа с хотя бы одним 0 будут иметь этот 0 либо в разряде единиц, либо в разряде десятков (или в обоих, хотя они будут учитываться только один раз).
Мы знаем, что наши числа являются инклюзивными, поэтому наше первое число будет 100 и будет включать все числа от 100 до 109. На данный момент это дает нам 10 чисел.
Отсюда мы видим, что первые 10 чисел 200, 300, 400, 500, 600, 700, 800 и 900 также будут включены, что даст нам всего:
$ 10 * 9 $
90 пока.
Теперь мы также должны включить каждое число, которое заканчивается на 0. Для первых 100 (, а не , включая 100, которые мы уже подсчитали!), У нас будет:
110, 120, 130, 140, 150, 160, 170, 180, 190
Это дает нам еще 9 чисел, которые мы также можем расширить, включив еще 9 в числа 200, 300, 400, 500, 600, 700, 800 и 900. Это дает нам всего:
Это дает нам всего:
$ 9 * 9 $
81
Теперь давайте сложим наши итоги (все числа с цифрой единиц 0 и все числа с цифрой десятков 0) вместе:
90 долл. США + 81 долл. США 90 165 долл. США
171
Всего 900 чисел от 100 до 999 включительно, поэтому наша окончательная вероятность будет:
$ 171/900 $
Наш окончательный ответ — D , 171 $ / 900 $
# 12: Во-первых, превратите данное уравнение для прямой q в правильную форму пересечения наклона.
$ −2x + y = 1 $
$ y = 2x + 1 $
Теперь нам говорят, что углы, которые образуют прямые, совпадают. Это означает, что наклоны линий будут противоположны друг другу [Примечание: перпендикулярные линии имеют противоположные обратные наклоны , поэтому НЕ путайте эти понятия!].
Поскольку мы уже установили, что наклон прямой $ q $ равен 2, прямая $ r $ должна иметь наклон -2.
Наш окончательный ответ — F , -2
# 13: Если вы помните свои правила тригонометрии, вы знаете, что $ tan ^ {- 1} (a / b) $ — это то же самое, что сказать $ tanΘ = a / b $. 2}}
2}}
# 14: Самый простой способ решить этот вопрос — использовать ПИН-код и просто выбрать число для нашего $ x $ и найти соответствующее ему значение $ y $. После этого мы можем проверить наши варианты ответов, чтобы найти правильный.
Итак, если бы мы сказали, что $ x $ было 24 (Почему 24? Почему нет!), Тогда наше значение $ t $ было бы 2, наше значение $ u $ было бы 4, а наше значение y было бы 42 $. И $ x − y $ будет $ 24-42 = -18 $
.Теперь давайте проверим наши варианты ответов.
С первого взгляда мы видим, что варианты ответа H и J будут положительными, а вариант ответа K равен 0.Таким образом, мы можем устранить их все.
Мы также можем видеть, что $ (t − u) $ будет отрицательным, а $ (u − t) $ — нет, поэтому вполне вероятно, что F — наш ответ. Давайте проверим это полностью, чтобы убедиться.
$ 9 (t − u)
$$ 9 (2–4) $
$ 9 (−2) $
$ −18 $
Успех!
Наш окончательный ответ — F, $ 9 (t − u) $
# 15: В таком вопросе единственный способ ответить на него — это последовательно выбрать варианты ответов.
Вариант ответа A никогда не будет , поскольку $ y <−1 $. Поскольку $ x $ положительно, дробь всегда будет $ \ positive / \ negative $, что дает нам отрицательное значение.
Вариант ответа B: не всегда правильный, так как у нас может быть небольшое значение $ x $ (например, $ x = 3 $) и очень большое отрицательное значение для $ y $ (например, $ y = −100 $). . В этом случае $ {| x |} / 2 $ будет меньше $ | y | $.
Вариант ответа C действительно всегда верно, так как $ {\ a \ positive \ number} / 3-5 $ может быть или не быть положительным числом, но оно всегда будет больше, чем $ {\ a \ negative \ number} / 3−5 $, который будет становиться все более отрицательным.2 + mx + n = 0 $, что означает, что когда мы разлагаем наше уравнение на множители, мы должны получить квадрат.
Мы также знаем, что наши значения для $ x $ всегда будут напротив значений внутри фактора. (Например, если наш факторинг дал нам $ (x + 2) (x − 5) $, наши значения для $ x $ были бы $ -2 $ и $ + 5 $). 2 + 6x + 9 $
2 + 6x + 9 $
$ m $ в нашем уравнении стоит вместо 6, что означает, что $ m = 6 $.
Наш окончательный ответ — C , 6.
# 17: Самый простой способ решить эту проблему (и ключевой способ избежать ошибок с алгеброй) — просто подставить свои собственные числа для $ a $, $ r $ и $ y $. Если не усложнять, предположим, что сумма ссуды $ a $ равна 100 долларам, процентная ставка $ r $ равна 0,1, а продолжительность ссуды $ y $ составляет 2 года. Теперь мы можем найти наш начальный $ p $.
$ p = {0.5ary + a} / 12y $
$ p = {0,5 (100) (0.1) (2) +100} / {12 (2)} 90 165 долл. США
$ п = 110/24 $
$ p = 4,58 $
Теперь, если мы оставим все остальное нетронутым, но удвоим сумму кредита (значение в долларах), мы получим:
$ p = {0.5ary + a} / 12y $
$ p = {0,5 (200) (0,1) (2) +200} / {12 (2)}
долл. США$ p = 220/24
$$ п = 9,16 $
Когда мы удвоили наше значение $ a $, наше значение $ p $ также удвоилось.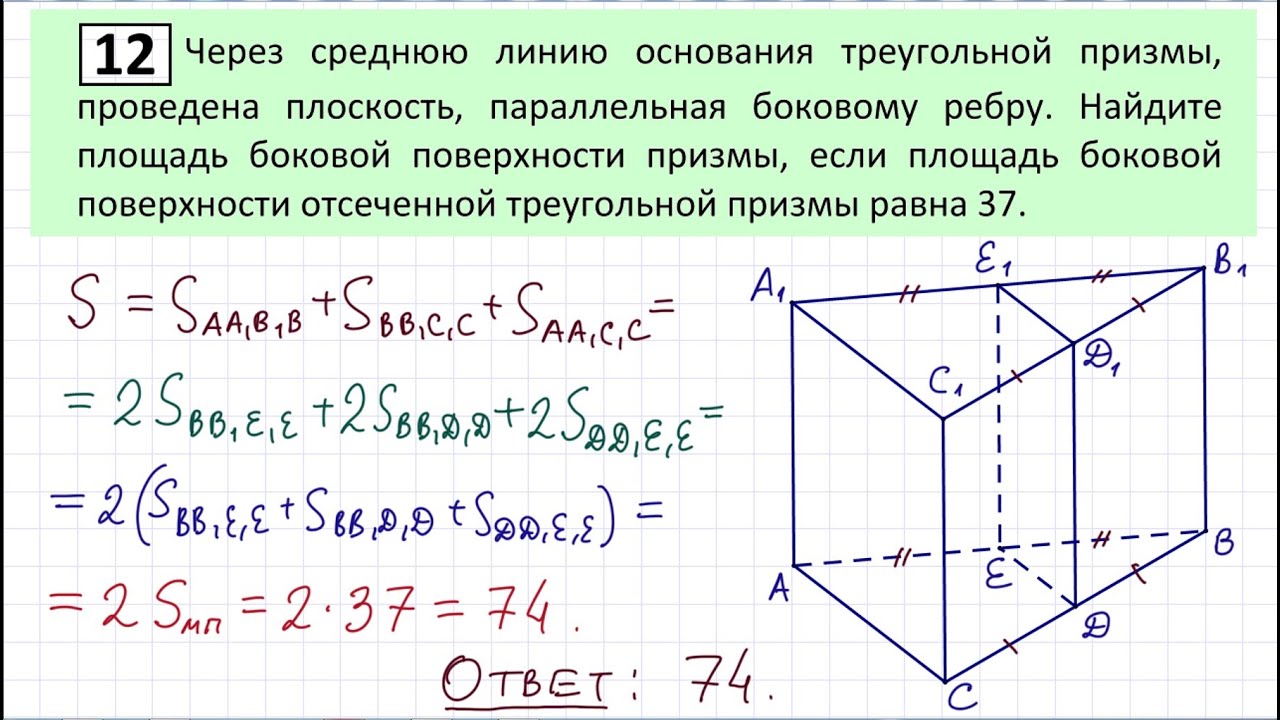
Наш окончательный ответ: D , $ p $ умножается на 2.
# 18: Если бы мы составили прямоугольный треугольник из нашей диаграммы, мы могли бы увидеть, что у нас был бы треугольник с длинами ног 8 и 8, что сделало бы его равнобедренным прямоугольным треугольником.
Это означает, что полная длина $ \ ov {EF} $ (гипотенуза нашего прямоугольного треугольника) будет $ 8√2 $. Теперь $ \ ov {ED} $ составляет $ 1/4 $ длины $ \ ov {EF} $, что означает, что $ \ ov {ED} $ составляет:
$ {8√2} / 4
$И катеты меньшего прямоугольного треугольника также будут на $ 1/4 $ размера катетов большего треугольника. Таким образом, наш меньший треугольник будет иметь длину ног 8/4 = 2
долларов.Если мы прибавим 2 как к нашей координате x, так и к нашей координате y от точки E, мы получим:
$ (6 + 2,4 + 2)
$$ (8,6)
$Наш окончательный ответ: G , $ (8,6) $
# 19: Во-первых, чтобы решить неравенство, мы должны подойти к нему как к уравнению с одной переменной и вычесть 1 из обеих частей выражения
$ −5 <1−3x <10 $
$ −6 <−3x <9 $
Теперь мы должны разделить каждую сторону на $ -3 $. Однако помните, что всякий раз, когда мы умножаем или делим неравенство на отрицательное, неравенство обозначается ОБРАТНО. Итак, теперь мы получим:
Однако помните, что всякий раз, когда мы умножаем или делим неравенство на отрицательное, неравенство обозначается ОБРАТНО. Итак, теперь мы получим:
$ 2> x> −3 $
А если расставить по порядку, то получится:
$ −3 Наш окончательный ответ: H , $ −3 # 20: Единственное различие между нашими графиками функций — это горизонтальный сдвиг, что означает, что наше значение b (которое будет определять вертикальный сдвиг синусоидального графика) должно быть 0. Просто используя эту информацию, мы можем исключить любой вариант ответа, кроме A, поскольку это единственный ответ с $ b = 0 $. Для удобства на этом можно остановиться. Наш окончательный ответ: A , $ a <0 $ и $ b = 0 $ Advanced ACT Math Примечание. Важное слово в вопросах ACT Math — «должен», как в «] что-то] должно быть истинным». Если в вопросе нет этого слова, то ответ должен быть верным только для конкретного случая (то есть может быть истинным. В этом случае большую часть времени для горизонтального смещения графика влево требуется $ a> 0 $. Однако, поскольку $ sin (x) $ — периодический график, $ sin (x + a) $ сдвинется по горизонтали влево, если $ a = -π / 2 $, что означает, что по крайней мере для одного значения константы $ a $, где $ a <0 $, ответ A верно. Напротив, нет обстоятельств, при которых графики могли бы иметь такое же максимальное значение (как указано в тексте вопроса), но иметь константу $ b ≠ 0 $. Однако, как мы указывали выше, на реальном ACT, как только вы придете к выводу, что $ b = 0 $ и заметите, что только один вариант ответа имеет это как часть его, вы должны остановиться на этом.Не отвлекайтесь и не тратьте больше времени на этот вопрос на приманку $ a <0 $! # 21: У вас может возникнуть соблазн решить этот вопрос о неравенстве абсолютных значений как обычно, выполнив два вычисления и затем решив как уравнение с одной переменной. Однако в этом случае обратите внимание на тот факт, что наше абсолютное значение предположительно должно быть на меньше , чем отрицательное число.Абсолютное значение всегда будет положительным (поскольку это мера расстояния, а отрицательного расстояния не существует). Это означает, что было бы буквально невозможно, чтобы уравнение абсолютного значения было меньше -1. Наш окончательный ответ — K , пустое множество, поскольку никакое число не удовлетворяет этому уравнению. Ух! Вы добрались до финиша — вперед! Теперь, наконец, прежде чем мы перейдем к самим вопросам, важно понять, что делает эти сложные вопросы «сложными».«Поступая таким образом, вы сможете понять и решить похожие вопросы, когда вы увидите их в день тестирования, а также получите лучшую стратегию для выявления и исправления ваших предыдущих математических ошибок ACT. В этом разделе мы рассмотрим, что общего в этих вопросах , и дадим примеры для каждого типа. В следующем разделе мы дадим вам все 21 самый сложный вопрос, а также ответим на каждый вопрос, включая те, которые мы используем здесь в качестве примеров. Некоторые из причин, по которым самые сложные математические вопросы являются самыми сложными математическими вопросами, заключаются в том, что эти вопросы выполняют следующие функции: Как видите, этот вопрос касается комбинации функций и точек координатной геометрии. Многие из самых сложных вопросов ACT Math в первую очередь проверяют только одну базовую математическую концепцию.Их усложняет то, что вам нужно выполнить несколько шагов, чтобы решить проблему. (Помните: чем больше шагов вам нужно предпринять, тем легче где-то напортачить!) Хотя это может звучать как простой вероятностный вопрос, вы должны просмотреть длинный список чисел с 0 в качестве цифры. Еще одна причина, по которой вопросы, которые мы выбрали, так сложны для многих студентов, заключается в том, что они сосредоточены на предметах, с которыми вы, вероятно, мало знакомы.Например, многие студенты менее знакомы с алгебраическими и / или тригонометрическими функциями, чем с дробями и процентами, поэтому большинство функциональных вопросов считаются задачами «высокой сложности». Многие студенты пугаются функциональных проблем, потому что они не знакомы с этими типами вопросов. Некоторые из самых сложных вопросов ACT не столько сложны математически, сколько их просто сложно декодировать.Тем более, что вы приближаетесь к концу математического раздела, может быть легко устать и неправильно истолковать или неправильно понять, какой именно вопрос даже просит вас найти. Этот вопрос знакомит студентов с совершенно чужеродной математической концепцией и может занять ограниченное время. Помните: если вопрос расположен в самом конце математического раздела, это означает, что многие студенты, вероятно, сделают в нем ошибки.Обращайте внимание на эти вопросы, которые могут создать ложное впечатление, будто они легкие, чтобы заманить вас на поиски ответов на приманку. Будь осторожен! Этот вопрос может показаться легким, но из-за того, как он задается, многие студенты попадутся на один из ответов на приманку. Более сложные вопросы ACT Math, как правило, используют много разных переменных — как в вопросе, так и в выборе ответов — или представляют гипотетические предположения.(Примечание: лучший способ решить эти типы вопросов — вопросы, которые используют несколько целых чисел как в задаче, так и в вариантах ответа, — это использовать стратегию вставки чисел. Работа с гипотетическими сценариями и переменными почти всегда сложнее, чем с числами. А теперь представьте себе что-нибудь вкусненькое и успокаивающее в награду за всю эту тяжелую работу. ACT — это долгий путь; Чем больше вы привыкнете к нему раньше времени, тем лучше вы почувствуете себя в день тестирования.А знание того, как отвечать на самые сложные вопросы, которые когда-либо задавали тестировщики, сделает вашу ACT менее сложной. Если вы считаете, что эти вопросы были легкими , не стоит недооценивать влияние адреналина и усталости на вашу способность решать свои математические задачи. Во время учебы старайтесь следовать указаниям по времени (в среднем одна минута на один вопрос по математике ACT) и старайтесь проходить полные тесты, когда это возможно. Это лучший способ воссоздать реальную среду тестирования, чтобы вы могли подготовиться к реальной сделке. Если вы почувствовали, что эти вопросы были сложными , обязательно укрепите свои математические знания, ознакомившись с нашими индивидуальными руководствами по математическим темам для ACT. Там вы увидите более подробные объяснения рассматриваемых тем, а также более подробную разбивку ответов. Почувствовали, что эти вопросы оказались сложнее, чем вы ожидали? Взгляните на все темы, затронутые в математическом разделе ACT, а затем отметьте, в каких разделах у вас были особые трудности.Затем взгляните на наши индивидуальные руководства по математике, которые помогут вам укрепить любую из этих слабых сторон. Не хватает времени на математический раздел ACT? Наше руководство, которое поможет вам опередить время, поможет вам вовремя ответить на эти математические вопросы. Хотите набрать наивысший балл? Ознакомьтесь с нашим руководством о том, как получить идеальные 36 в математическом разделе ACT, написанном отличным бомбардиром. Хотите улучшить свой результат ACT на 4 балла? Посетите наши лучшие в своем классе онлайн-классы подготовки к ACT.Мы гарантируем возврат ваших денег , если вы не улучшите свой результат ACT на 4 или более балла. Наши классы полностью онлайн, и их ведут эксперты ACT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую индивидуальную программу, которой вы будете следовать, чтобы вы никогда не запутались, что изучать дальше. Попробуйте без риска сегодня: MATH 087 Авторизоваться Панель приборов Календарь Входящие История Помощь ПОСЛЕ ОКОНЧАНИЯ ВРЕМЯ РАБОТЫ ВЕЛИКОЛЕПНОГО ЛЕТА ФИНАЛ будет отдан ПОНЕДЕЛЬНИК,
14 МАЯ, 14:15 — 17: 00, JAVITS 102 Q Здесь размещены 3 РЕШЕНИЯ Лекции 13, 14 РАЗМЕЩЕНА ВАЖНОЕ ИЗМЕНЕНИЕ в Syllabus: ЗАКЛЮЧИТЕЛЬНАЯ ПРАКТИКА ПЯТНИЦА, 4 мая в JAVITS 102 Кафедра новой информатики, каб. 208; CONCRETE MATHEMATICS Мы рассмотрим все или части глав 1-5 книги Конкретная математика Если время позволяет мы будет охватывать избранные темы по классической Дискретной математике В этом случае я предоставлю конспекты лекций и комплекты
Задачи, и вы можете использовать любую книгу по дискретной математике в качестве дополнительной
чтение Будет промежуточная практика,
три теста с одним вопросом, промежуточный и финальный
экзамен Также будут назначены наборы
домашние задания учащиеся должны решать и учиться для
тесты Все тесты ЗАКРЫТО, ЗАМЕТКИ и ЗАКРЫТО
КНИГА Есть 6 наборов домашних заданий ОЦЕНКИ за викторины и тесты
будет зависеть от формы, внимания к деталям и тщательности
ваши письменные решения. Курс будет очень внимательно следовать книге, и в частности, мы
будет охватывать некоторые или все следующие главы и темы Глава 1: Повторяющиеся проблемы Глава 2: Суммы Глава 3. Целочисленные функции Глава 4: Теория чисел Глава 5: Биномиальные коэффициенты стр. 153-204 Глава 6: Специальные номера стр. 243-264 (чтение) ДОМАШНЕЕ ЗАДАНИЕ 1, Глава 1: Проблемы на страницах 17-20. ДОМАШНЕЕ ЗАДАНИЕ 2, Глава 2, часть первая: Проблемы на страницах 62-63. ДОМАШНЕЕ ЗАДАНИЕ 2, Глава 2, часть вторая: Проблемы на страницах 63-66. ДОМАШНЕЕ ЗАДАНИЕ 3, Глава 3: Проблемы на страницах 96-101. ДОМАШНЕЕ ЗАДАНИЕ 4, Глава 4: Проблемы на страницах 144 — 149. ДОМАШНЕЕ ЗАДАНИЕ 5, Глава 5: Проблемы на страницах 230 — 235. ДОМАШНЕЕ ЗАДАНИЕ 6, Дискретная математика — опубликованы некоторые задачи — подробнее на
приходи Это предварительное расписание Q1: понедельник, 12 февраля ПРАКТИКА MIDTERM : Пятница, 9 марта Это классный тест, разработанный для вашей ПРАКТИКИ.Будет исправлена ТОЛЬКО одна проблема Весенние каникулы: март 12–18 СЕРЕДИНА: ПЯТНИЦА, 23 марта в JAVITS 101 Q2: Понедельник, 9 апреля Q3: пятница, 27 апреля ЗАКЛЮЧИТЕЛЬНАЯ ПРАКТИКА ПЯТНИЦА, 4 мая в JAVITS 102 Общее представление с расслабленным основанием ГЛАВА 2 Решения для домашних заданий Можно ли получить области Zn с n изогнутыми линиями, когда
угол на каждом зиге 30 градусов? Ответ: Здесь нам понадобится 12 таких изогнутых линий, когда первые
происходит перекрытие. Глава 1, Проблема на страницах 11-12 ДОМАШНЕЕ ЗАДАНИЕ 4
ПРОБЛЕМЫ 10 Примеры Проблемы ЗАДАЧИ СО СЛОВАМИ требует практики в переводе словесного языка на алгебраический язык.См. Урок 1, Задача 8. Тем не менее, проблемы со словами делятся на разные типы. Ниже приведены некоторые примеры. Пример 1. ax ± b = c . Все проблемы, подобные следующей, в конечном итоге приводят к уравнению в такой простой форме. Джейн потратила 42 доллара на обувь. Это было на 14 долларов меньше, чем вдвое, чем она потратила на блузку. Сколько была кофточка? Решение. У каждой проблемы со словом неизвестный номер.В этой проблеме цена кофточки. Всегда позволяйте x представлять неизвестное число. То есть пусть на вопрос ответит x . Тогда пусть x будет тем, сколько она потратила на блузку. В задаче говорится, что «Это», то есть 42 доллара, было на 14 долларов меньше, чем удвоенное значение x . Вот уравнение: Блузка стоила 28 долларов. Пример 2. В классе б мальчиков. Это в три раза больше, чем в четыре раза девушек. Сколько девочек в классе? Решение. Опять же, пусть x представляет неизвестное число, которое вас просят найти: пусть x будет количеством девушек. (Хотя b неизвестно — это произвольная константа — это не то, что вас просят найти.) В задаче указано, что «Это» — b — на три больше, чем в четыре раза x : Решение здесь не число, потому что оно будет зависеть от значения b . Это тип «буквального» уравнения, очень распространенного в алгебре. Пример 3. Целое равно сумме частей. Сумма двух чисел равна 84, и одно из них на 12 больше, чем другое. Какие два числа? Решение. В этой задаче нам предлагается найти два числа.Следовательно, мы должны позволить x быть одним из них. Пусть тогда x будет первым числом. Нам говорят, что второе число больше 12, x + 12. В задаче указано, что их сумма равна 84: = 84 Линия над x + 12 — это символ группировки, который называется vinculum . Это избавляет нас от написания скобок. У нас: Это первое число. Следовательно, другой номер — x + 12 = 36 + 12 = 48. Сумма 36 + 48 равна 84. Пример 4.Сумма двух последовательных чисел составляет 37. Какие они? Решение . Два последовательных числа равны 8 и 9 или 51 и 52. Пусть тогда x будет первым числом. Тогда число после него будет x +1. В задаче указано, что их сумма равна 37: = 37 Два числа — 18 и 19. Пример 5. Одно число на 10 больше другого. Сумма, состоящая из удвоенного меньшего и трехкратного большего, равна 55.Какие два числа? Решение. Пусть x будет меньшим числом. Тогда большее число на 10 больше: x + 10. В проблеме говорится: Это меньшее число. Чем больше число, тем больше на 10: 15. Пример 6. Разделите 80 долларов между тремя людьми так, чтобы у второго было вдвое больше, чем у первого, а у третьего было на 5 долларов меньше, чем у второго. Решение . Опять же, нас просят найти более одного числа. Мы должны начать с того, что допустим, что x будет тем, сколько получает первый человек. Затем второй получает вдвое больше, 2 x . А третий получает на 5 долларов меньше, 2 x — 5. Их сумма 80 $: Вот сколько получает первый человек. Следовательно, второй получает Сумма 17, 34 и 29 на самом деле равна 80. Пример 7.Нечетные числа. Сумма двух подряд идущих нечетных чисел равна 52. Какие два нечетных числа? Решение . Во-первых, четное число кратно 2: 2, 4, 6, 8 и так далее. В алгебре принято представлять четное число как 2 n , где, вызывая переменную n , понимается, что n будет принимать целые числа: n = 0, 1, 2 , 3, 4 и т. Д. Нечетное число на 1 больше (или на 1 меньше) четного.Итак, представим нечетное число как 2 n + 1. Пусть 2 n + 1 будет первым нечетным числом. Далее будет еще 2 — это будет 2 n + 3. В задаче указано, что их сумма 52: Теперь мы решим это уравнение для n , а затем заменим решение в 2 n + 1, чтобы найти первое нечетное число.У нас: Следовательно, первое нечетное число 2 · 12 + 1 = 25.Итак, следующее 27. Их сумма 52. Проблемы Задача 1. У Джули 50 долларов, что на восемь долларов больше, чем у Джона. Сколько у Джона? (Сравните Пример 1.) Во-первых, что вы позволите представить x ? Чтобы увидеть ответ, наведите указатель мыши на цветную область. Неизвестный номер — сколько у Джона. Что такое уравнение? 2 x + 8 = 50. Вот решение: x = 21 Проблема 2. Карлотта потратила на рынке 35 долларов. Это было на семь долларов меньше, чем в три раза больше, чем она потратила в книжном магазине; сколько она там потратила? Вот уравнение. 3 x — 7 = 35 Вот решение: x = 14 Проблема 3.Есть b черных шариков. Это на четыре больше, чем в два раза больше красных шариков. Сколько там красных шариков? (Сравните Пример 2.) Вот уравнение. 2 x + 4 = b Вот решение: Проблема 4. Джанет потратила 100 долларов на книги. Это было на тыс. долларов меньше, чем в пять раз больше, чем она потратила на обед.Сколько она потратила на обед? Вот уравнение. 5 x — k = 100 Вот решение: Задача 5. Целое равно сумме частей. Сумма двух чисел равна 99, и одно из них на 17 больше, чем другое. Какие два числа? (Сравните Пример 3.) Вот уравнение. Вот решение: Задача 6. Класс из 50 учеников делится на две группы; в одной группе на восемь меньше, чем в другой; сколько в каждой группе? Вот уравнение. Вот решение: Проблема 7.Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа? Вот уравнение. x + 5 x = 72, Вот решение: x = 12. 5 x = 60. Задача 8. Сумма трех последовательных чисел равна 87; кто они такие? (Сравните Пример 4.) Вот уравнение. Вот решение: 28, 29, 30. Задача 9. Группа из 266 человек состоит из мужчин, женщин и детей. Мужчин в четыре раза больше, чем детей, а женщин в два раза больше, чем детей. Сколько их там? (Чему вы приравняете x — количеству мужчин, женщин или детей?) x + 4 x + 2 x = 266 Вот решение: х = 38.4 x = 152. 2 x = 76, Задача 10. Разделите 79 долларов между тремя людьми так, чтобы у второго было в три раза больше, чем у первого, а у третьего было на два доллара больше, чем у второго. (Сравните Пример 6.) Вот уравнение. Вот решение: 11, 33, 35 долларов. Задача 11. Разделите 15,20 доллара между тремя людьми так, чтобы у второго было на доллар больше, чем у первого, а у третьего — на 2,70 доллара больше, чем у второго. Вот уравнение. Вот решение: 3,50 доллара США, 4,50 доллара США, 7,20 доллара США. Задача 12. Два последовательных нечетных числа таковы, что три раза первое будет на 5 больше, чем в два раза больше второго.Что это за два нечетных числа? (см. Пример 7, где мы представляем нечетное число как 2 n + 1.) Решение . Пусть первое нечетное число будет 2 n + 1. Тогда следующий 2 n + 3 — потому что будет еще 2. Задача состоит в следующем: Следовательно, первое нечетное число — 2 · 4 + 1 = 9. Следующее — 11. )
) (Для получения дополнительной информации об этом ознакомьтесь с нашим руководством, посвященным уравнениям абсолютных значений).
(Для получения дополнительной информации об этом ознакомьтесь с нашим руководством, посвященным уравнениям абсолютных значений). Что общего у самых сложных вопросов по математике ACT?

# 1: Проверьте несколько математических понятий одновременно
# 2: требуется несколько шагов
 Это оставляет место для ошибок в расчетах.
Это оставляет место для ошибок в расчетах. # 3: Используйте понятия, с которыми вы менее знакомы
# 4: Дайте вам запутанные или многословные сценарии для проработки

# 5: Кажется обманчиво простым
# 6: Включите несколько переменных или гипотетических факторов
 )
) На вынос

Что дальше?

MATH 087 F17 1255 — ОСНОВЫ АЛГЕБРЫ
Приборная панель
Закрывать
Осень 2017 г.
Посмотреть ленту курса Скоро
Просмотр календаря cse547, ams547 Дискретная математика
cse547, ams547 Дискретная математика
ОБЩИЕ НОВОСТИ:
Вторник, 22 мая, 13:00 —
16:00
Спасибо за то, что вы хорошие ученики!
FINAL решает проблемы
из всех викторин, hmks и тестов
ФИНАЛ будет содержать 5
Вопросы — по одному из каждой главы и один дополнительный зачетный вопрос
Согласно ПРАВИЛАМ университета, мы ДОЛЖНЫ ПРОЙТИ ОКОНЧАТЕЛЬНЫЙ экзамен во время ФИНАЛЬНОЙ НЕДЕЛИ
Я дам вам ЗАКЛЮЧИТЕЛЬНУЮ ПРАКТИКУ (дополнительно
кредит) от 4 мая
Это классный, дополнительный кредитный тест, разработанный для вашего
УПРАЖНЯТЬСЯ. ТОЛЬКО одна проблема будет
исправлено
ТОЛЬКО одна проблема будет
исправлено
ВСЕ ОЦЕНКИ указаны на ЧЕРНОЙ ДОСКЕ
. Свяжитесь с техническим специалистом, если вам нужна дополнительная информация или нужно обсудить
оценка
Я перечислю имена, которые исправляют какой тест, когда вы их будете сдавать
Класс соответствует:
понедельник, пятница 13:00 — 14:20
PM Место:
ЯВИТС 101 Профессор:
Анита Василевская
телефон: 632-8458
электронная почта: anita @ cs.stonybrook.edu
Часы работы: Среда 19:00 — 20:00, пятница 15:30 — 16:30 и
по предварительной записи
электронная почта: [email protected]
Часы работы: Среда, пятница
10:00 — 11:30, по предварительной записи
Расположение офиса: 2217 Old CS Building TA: Рахул Верма
электронная почта: rahul.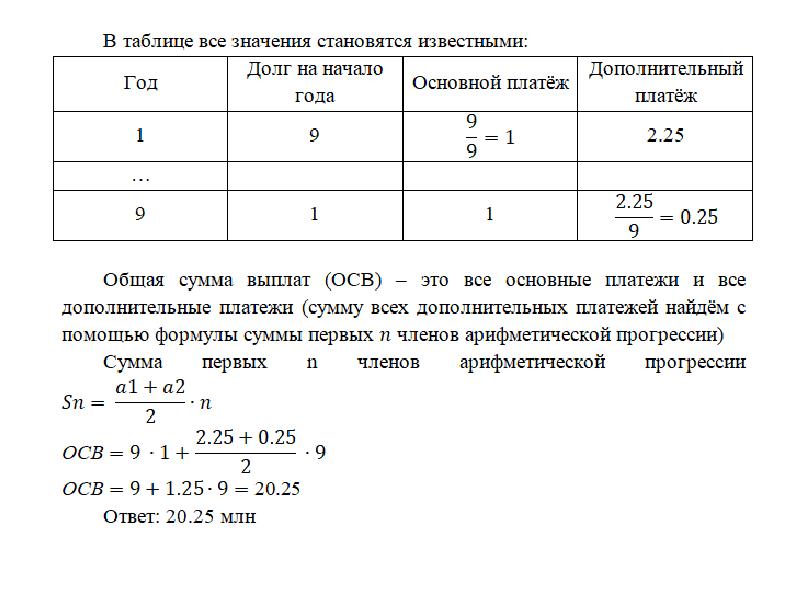 [email protected]
[email protected]
Часы работы: Среда, Четверг
13: 00–14: 00, по предварительной записи
Расположение офиса: 2217 Old CS Building Учебник курса
Фонд информатики
Graham, Knuth, Patashnik
Addison-Wesley, Second or Third Edition Описание курса
Курс будет очень подробно охватывать учебник Общая информация о курсе
Полные решения всех задач размещены в курсе
webpage
Книга также содержит большинство решений, но они не
полная
Если во время теста обнаруживается, что студент использует записи или книгу, он / она
получит АВТОМАТИЧЕСКИ 0pts для данного теста.
Не все из них могут быть выполнены. Не собираются и не оцениваются .
Вы будете проверены на домашние задания, связанные с материалом, представленным в классе.
Некоторые решения (очень короткие) домашних заданий также находятся в
учебник.
Студенты несут ответственность за разработку и написание подробно
решения , объясняющие все используемые шаги и методы, как есть
сделано в наших конспектах лекций.Мы будем
охватить некоторые из таких подробных решений в классе
. ВСЕ они РАЗМЕЩАЮТСЯ на нашей веб-странице, чтобы вы могли изучить их.
как их написать.
КОМПОНЕНТЫ ДЛЯ ОЦЕНКИ
3 викторины — 25 баллов каждое
Промежуточное обучение — 25 баллов
Среднесрочное обучение — 100 баллов
Финальное — 100 баллов
ВЫЧИСЛЕНИЕ ЗАКЛЮЧИТЕЛЬНОЙ ОЦЕНКИ Вы можете заработать
до 300 баллов + x дополнительных баллов = 300 + x баллов во время
семестр.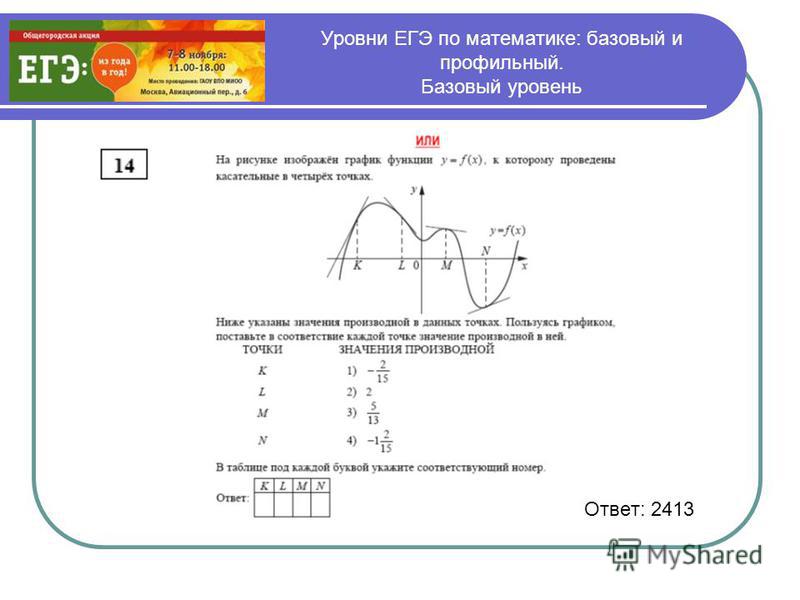
Оценка будет определяться следующим образом: количество заработанных
баллы, разделенные на 3 =% оценки.
Оценка в% переводится в буквенную оценку в стандартной
способ, как описано в курсе SYLLABUS
Ни один из классов не будет изогнутым
Записи оценок студентов хранятся на BLACKBOARD
Свяжитесь с техническим специалистом для получения дополнительной информации СОДЕРЖАНИЕ КУРСА
Если позволит время, затронет некоторые выбранные темы
по дискретной математике
— рекламироваться ПРОБЛЕМЫ ПО ДОМУ

Напишите внимательно подробное решение задач 2, 6, 7, 8, 9, 11,
12, 14, 15, 16, 19, 18, 20,
напишите подробности из стр. 12-13, где обсуждаются циклические свойства J (n).
и ложное предположение, что J (n) = n / 2,
записывают детали двоичных решений pp 15-16 в обобщенные
повторение.
Напишите и представьте подробное решение задач 5, 6, 7, 8, 9,
10, 11, 13, 14, 15, 16,
Напишите и представьте подробное решение задач 16, 18, 19, 20,
21, 23, 24, 25, 26, 27, 29, 30, 31.
Напишите и представьте подробное решение проблем 10, 11, 12, 14,
16, 17, 19, 20, 23, 28, 31, 33, 35, 36.
Напишите и представьте подробное решение проблем 2, 6, 14, 15,
45.
Напишите и представьте подробное решение задач 2, 4, 6, 7, 8,
15, 16, 17, 18, 35, 43, 45.
Изменения и обновления, если таковые будут, будут опубликованы в разделе НОВОСТИ
Midterm охватывает задачи из домашних заданий 1 и 2 (главы
1 и 2) плюс содержание и проблемы в слайдах лекций, которые
были охвачены в классе до Практика Среднесрочная
Это классный, дополнительный кредитный тест, разработанный для вашего
УПРАЖНЯТЬСЯ. ТОЛЬКО одна проблема будет
исправлено
ТОЛЬКО одна проблема будет
исправлено
ФИНАЛ охватывает задачи из всех викторин, hmks и тестов
ЗАГРУЗИТЬ
Syllabus
Syllabus Slides СЛАЙДЫ ЛЕКЦИЙ
Лекция 1
Лекция 2
Лекция 3
Лекция 4
Лекция 4a: Глава 1, Задача 20
Лекция 5
Лекция 6
Лекция 7
Лекция 8
Лекция 8a
Лекция 9a
Лекция 9b
161650 110008 Лекция
Лекция 12
Лекция 13: Глава 5, часть 1
Лекция 14: ОБЗОР ЗАКЛЮЧИТЕЛЬНОГО Некоторые прошлые тесты и викторины
2017 ВИКТОРИНА 1
2017 ПРАКТИЧЕСКАЯ ПРОГРАММА
2017 ПРОМЕЖУТОЧНАЯ ПРОГРАММА
ВИКТОРИНА 2017 2
ВИКТОРИНА 2017 3
ВИКТОРИНА 2017
ПРОБЛЕМЫ для практики Финал
2017 КРАТКИЙ ОБЗОР
FOR FINAL
Старый
Обзор заключительных слайдов
Написание математических текстов Более старые МАТЕРИАЛ
Конспект лекции к главе 1 РЕШЕНИЯ ДЛЯ ДОМАШНИХ ПРОБЛЕМ: ГЛАВА 1
Исправленное решение вопроса 19, глава 1: Это потому, что полный круг составляет 360
градусов, а каждый зиг — 30 градусов. Итак, до n = 11 получим Zn
регионы. На 12-й изогнутой линии он будет перекрываться одним из
предыдущие строки, чтобы указать области Zn.
Это потому, что полный круг составляет 360
градусов, а каждый зиг — 30 градусов. Итак, до n = 11 получим Zn
регионы. На 12-й изогнутой линии он будет перекрываться одним из
предыдущие строки, чтобы указать области Zn.
Глава 1, Проблема 2
Глава 1, Проблема 6
Глава 1, Проблема 7
Глава 1, Проблема 8
Глава 1, Проблема 9
Глава 1, Проблемы 14, 2
Глава 1, Проблема 16 Старый
Глава 1, Проблема 16
Обобщение
Глава 1, Проблемы 18, 19
Глава 1, Проблема 20
Глава 1, Проблема 20, решение 2 РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ДОМАШНЕГО ЗАДАЧИ: ГЛАВА 2
Глава 2, Проблема
6 Исправлено
Глава 2, Проблема 11
Глава 2, Проблемы 13, 14
Глава 2, Проблема 15
Глава 2, Проблема 19
Глава 2, Проблемы 20,
21 Исправлено
Глава 2, проблема 23
Глава 2, проблема 29 полное решение
Глава 2, Проблема 29, краткое решение
Глава 2, проблема 29
Глава 2, проблема 31 РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ДОМАШНЕГО ЗАДАЧИ: ГЛАВА 2
Глава 2, Проблемы 5,7
Глава 2, Проблема 8
Глава 2, Проблемы 9, 10
Глава 2, Проблемы 16, 17
Глава 2, Проблемы 27,29
Глава 2, Проблема 29
Глава 2 , Краткое решение проблемы 29 РЕШЕНИЕ ДОМАШНИХ ПРОБЛЕМ: ГЛАВА 3
Глава 3, проблема 10, 12
Глава 3, проблема 11
Глава 3, проблема 14
Глава 3, проблема 16
Глава 3, проблема 17
Глава 3, проблема 19, 20
Глава 3, проблема 23
Глава 3, проблема 28
Глава 3, проблема 31
Глава 3, проблема 33, 36
Глава 3, проблема 35 РЕШЕНИЯ ДОМАШНИХ ПРОБЛЕМ: ГЛАВА 4
Глава 4, проблема 2, 14
Глава 4, проблема 6
Глава 4, проблема 14
Глава 4, проблема 15
Глава 4, проблема 45 ПРОБЛЕМЫ ДЛЯ ДОМАШНЕГО ЗАДАНИЯ: РЕШЕНИЕ 5
Глава 5, Решение проблемы 2
Глава 5, Решение проблемы 3
Глава 5, Решение проблемы 4
Глава 5, Решение проблем 4, 6
Глава 5, Решение проблемы 7
Глава 5, Решение проблемы 8
Глава 5, Решение проблемы 8 2
Глава 5, Решение проблемы 14
Глава 5, Решение проблемы 15
Глава 5, Проблема 16, Глава 4
Проблема 15 Решение
Глава 5, Проблемы 15, 43 Решение
Глава 5, Решение проблемы 17
Глава 5, Решение проблемы 18
Глава 5, Проблемы 18, 45 Решение
Глава 5, Решение проблемы 35
Глава 5, Проблема 74 Решение ОПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ МАТЕМАТИКИ: ДОМАШНЕЕ ЗАДАНИЕ 4 ПРОБЛЕМЫ
Descrete Mathenatics
Определения 1
Определения дискретной математики 2
Определения дискретной математики 3
Определения дискретной математики 3
ДОМАШНИЕ 4 ПРОБЛЕМЫ РЕШЕНИЯ ПРЕДЫДУЩИЕ ИСПЫТАНИЯ ДЛЯ ИЗУЧЕНИЯ ЗАКЛЮЧИТЕЛЬНО
Практика Среднесрочная 1
Среднесрочная 1
Практика Среднесрочная 2
Среднесрочная 2
ЗАКЛЮЧИТЕЛЬНАЯ ПРАКТИКА КОММЕНТАРИИ К СТАРЫМ ЛЕКЦИЯМ (рукописные)
Лекция 3
Лекция 4
Лекция 5
Лекция 6
Лекция 7 Исправлено
pg (119-123a)
Лекция 7
Лекция 8
Лекция 9
Лекция 9a (Глава 2, Бесконечные суммы 1)
Лекция 9а (Глава 2, Бесконечные суммы 1
СЛАЙДЫ)
Лекция 9б (Глава 2, Бесконечные суммы
2)
Лекция 10
Лекция 11
Лекция 12
Лекция 13
Лекция 14
Лекция 15
Лекция 16 6
50 Лекция ДОПОЛНИТЕЛЬНЫЕ СЛАЙДЫ
Глава 2 Метод 5
Немного практики Проблемы с обзором в среднесрочной перспективе 1
СПЕКТР ТЕОРЕМЫ ДОКАЗАТЕЛЬСТВО Заявление об академической честности
Каждый студент должен добросовестно преследовать свои академические цели и
лично несет ответственность за все представленные работы. Представляя
работа другого человека как твоя всегда неправильна. Любые подозреваемые
о случае академической нечестности будет сообщено в Академическую
Судебная власть. Для получения более полной информации об академических
честность, включая категории академической нечестности, пожалуйста
см. веб-сайт академической судебной системы по адресу Academic Веб-сайт судебной системы
Представляя
работа другого человека как твоя всегда неправильна. Любые подозреваемые
о случае академической нечестности будет сообщено в Академическую
Судебная власть. Для получения более полной информации об академических
честность, включая категории академической нечестности, пожалуйста
см. веб-сайт академической судебной системы по адресу Academic Веб-сайт судебной системы Заявление об учебной программе Университета Стоуни-Брук
Если у вас есть физическая, психологическая, медицинская или учебная
инвалидность, которая может повлиять на вашу курсовую работу, пожалуйста, свяжитесь с
Служба поддержки лиц с ограниченными возможностями по телефону (631) 632-6748 или по вопросам инвалидности Служба поддержки Веб-сайт Они определят вместе с вами
какие приспособления необходимы и уместны. Вся информация
и документация конфиденциальна. Студенты, которым требуется помощь
во время экстренной эвакуации рекомендуется обсудить свои потребности
со своими профессорами и Службой поддержки инвалидов. За
информацию о процедурах и информации можно найти на следующем веб-сайте: Инвалидность Веб-сайт службы поддержки
Вся информация
и документация конфиденциальна. Студенты, которым требуется помощь
во время экстренной эвакуации рекомендуется обсудить свои потребности
со своими профессорами и Службой поддержки инвалидов. За
информацию о процедурах и информации можно найти на следующем веб-сайте: Инвалидность Веб-сайт службы поддержки Общее описание курса:
Курс будет состоять из двух частей: Конкретная математика в том виде, в каком она представлена.
в учебнике и по конкретной математике есть «контролируемый
манипулирование (некоторыми) математическими формулами с использованием набора
приемы решения задач »(учебники введение).Мы будем
охватить часть или весь материал из глав 1-5 книги.
Первоначальный учебник был расширением «Предварительных математических упражнений»
книги Кнута ИСКУССТВА КОМПЬЮТЕРНОГО ПРОГРАММИРОВАНИЯ. Конкретная математика
должен (и, надеюсь, поможет) помочь вам в искусстве письма
программы, или думать о них.
Вторая часть курса будет охватывать некоторые выбранные темы в
Теория чисел и классическая дискретная математика, если раз
разрешения. Задачи со словами — Полный курс алгебры

2 x -14 = 42. 2 x = 42 + 14 (Урок 9) = 56. x = 56
2 = 28. 4 x + 3 = б . Следовательно, 4 x = б — 3 x = б — 3
4. 2 x = 84–12 = 72. x = 72
2 = 36. 2 x = 37 — 1 = 36. x = 36
2 = 18. 2 x + 3 ( x + 10) = 55. Это означает 2 x + 3 x + 30 = 55.Урок 14. . 5 x = 55–30 = 25. x = 5. 5 x = 80 + 5 x = 85
5 = 17. 2 x = 34. А третий получает 2 x -5 = 29. 2 n + 1 + 2 n + 3 = 52. 4 n + 4 = 52 4 n = 48 n = 12.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами! Let x = Количество детей.Тогда 4 x = Количество мужчин. И 2 x = Количество женщин. Вот уравнение: 3 (2 n + 1) = 2 (2 n + 3) + 5. Это означает: 6 n + 3 = 4 n + 6 + 5. 2 n = 8. n = 4.

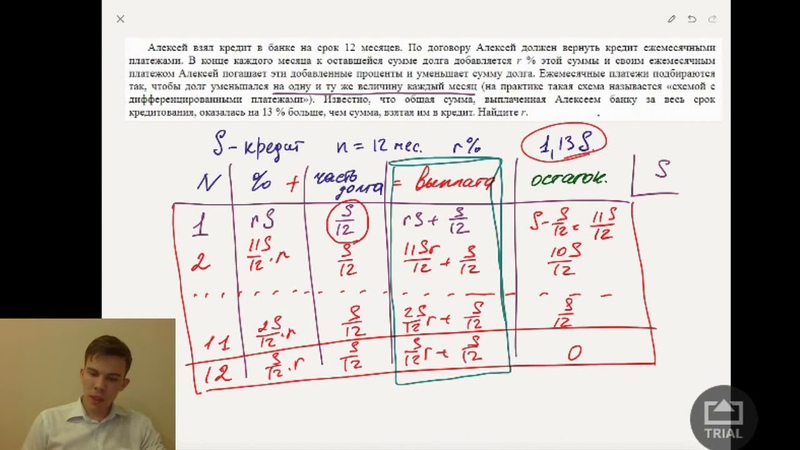 Тригонометрические уравнения
Тригонометрические уравнения

 mos.ru/catalogue/material_view/lesson_templates/120055
mos.ru/catalogue/material_view/lesson_templates/120055 mos.ru/catalogue/material_view/lesson_templates/11896
mos.ru/catalogue/material_view/lesson_templates/11896
 Высота дерева 10м. Через сколько дней улитка впервые окажется на вершине дерева?
Высота дерева 10м. Через сколько дней улитка впервые окажется на вершине дерева?
 Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Вот так:
Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Вот так:
Leave A Comment