Егэ по математике профильный уровень 2019 задание 14: Задачи 14 ЕГЭ профильная математика

Задачи 14 ЕГЭ профильная математика



Задачи 14 ЕГЭ профильная математика

MATHM >> ЕГЭ >> ЕГЭ профиль >>

задача 14

ЗАДАЧА 14
сортировка
по темам

Сложность 1
Сложность 2
Сложность 3

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ЕГЭ, более сложные встретятся если «не повезло».

Сложность 1 (легкие задачи)

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

Сложность 2 (средние по сложности задачи)

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

Сложность 3 (сложные задачи)

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

ЕГЭ.

Задание 14. Стереометрия — Сайт Трушина Б.В.

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по стереометрии, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

• Все ролики с заданием 14 
• Все ролики по стереометрии
• Мини-курс «Задачи по стереометрии на ЕГЭ по математике (задача №14)»
• Мини-курс «Векторный метод в пространстве»

Как решать стереометрию

Теорема о трёх перпендикулярах

Как найти объем. Принцип Кавальери

Видеоразборы задач

В треугольной пирамиде $SABC$ $SB=SC=AC=AB=\sqrt{17}$, $SA= BC = 2\sqrt5$.
а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
б) Найдите расстояние между прямыми $BC$ и $SA$.

 

В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3\sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.
а) Докажите что угол $ANO$ — прямой.
б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.

 

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 2. Точка $M$ — середина ребра $AA_1$.
а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.
б) Найдите расстояние между прямыми $MB$ и $B_1C$.

 

На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
а) Докажите, что угол $C_1BA$ прямой.
б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.

 

Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $\alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что $DM : MD_1 = 2 : 1$.
б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.

 

Длина диагонали куба $ABCDA_1B_1C_1D_1$ равна 3. На луче $A_1C$ отмечена точка $P$ так, что $A_1P = 4$.
a) Докажите, что грань $PBDC_1$ — правильный тетраэдр.
б) Найдите длину отрезка $AP$.

 

Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$, содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб. 
a) Докажите, что грань $ABCD$ — квадрат. 
б) Найдите угол между плоскостями $\alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.

 

В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна 6, а боковое ребро $AA_1$ равно 3. На ребре $AB$ отмечена точка $K$ так, что $AK = 1$. Точки $M$ и $L$ — середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $\gamma$ параллельна прямой $AC$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $BM$ перпендикулярна плоскости $\gamma$;
б) Найдите расстояние от точки $C$ до плоскости $\gamma$.

 

Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $\alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что $DM : MD_1 = 2 : 1$.
б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.

 

Подборка заданий прошлых лет

1. В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3\sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.
   а) Докажите что угол $ANO$ — прямой.
   б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.
   (ЕГЭ-2019, досрочная волна, резервный день)
2. В треугольной пирамиде $SABC$ $SB=SC=AC=AB=\sqrt{17}$, $SA= BC = 2\sqrt5$.
   а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
   б) Найдите расстояние между прямыми $BC$ и $SA$.
   (ЕГЭ-2019, досрочная волна)
3. В треугольной пирамиде $SABC$ $SB=SC=\sqrt{17}$, $AB=AC=\sqrt{29}$, $SA= BC = 2\sqrt5$.
   а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
   б) Найдите угол между прямой $SA$ и плоскостью $SBC$.
   (ЕГЭ-2019, досрочная волна)
4. Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $\alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.
   а) Докажите, что $DM : MD_1 = 2 : 1$.
   б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.
   (ЕГЭ-2018, досрочная волна)
5. В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны~2. Точка $M$ — середина ребра $AA_1$.
   а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.
   б) Найдите расстояние между прямыми $MB$ и $B_1C$.
   (ЕГЭ-2018, досрочная волна, резервный день)
6. На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
   а) Докажите, что угол $C_1BA$ прямой.
   б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.
   (ЕГЭ-2018, основная волна)
7. На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра. {\circ}$.
   б) Найдите расстояние между прямыми $AC$ и $BC_1$.
   (ЕГЭ-2018, основная волна)
8. На ребре $AB$ правильной четырёхугольной пирамиды $SABCD$ с основанием $ABCD$ отмечена точка $Q$, причём $AQ:OB=1:2$. Точка $P$ — середина ребра $AS$.
   а) Докажите, что плоскость $DPQ$ перпендикулярна плоскости основания пирамиды.
   б) Найдите площадь сечения $DPQ$, если площадь сечения $DSB$ равна 6.
   (ЕГЭ-2018, основная волна, резервный день)
9. В правильном тетраэдре $ABCD$ точка $H$ — центр грани $ABC$, а точка $M$ — середина ребра $CD$.
   а) Докажите, что прямые $AB$ и $CD$ перпендикулярны.
   б) Найдите угол между прямыми $DH$ и $BM$.
   (ЕГЭ-2018, основная волна, резервный день)
10. Основанием прямой четырехугольной призмы $ABCDA_1B_1C_1D_1$ является ромб $ABCD$, $AB = AA_1$.
    а) Докажите, что прямые $A_1C$ и $BD$ перпендикулярны.
    б) Найдите объем призмы, если $A_1C = BD = 2$.
    (ЕГЭ-2017, основная волна, резервный день)
11. В правильной четырехугольной пирамиде $SABCD$ все ребра равны 5. На ребрах $SA$, $AB$, $BC$ взяты точки $P$, $Q$, $R$ соответственно так, что $PA = AQ = RC = 2$.
    а) Докажите, что плоскость $PQR$ перпендикулярна ребру $SD$.
    б) Найдите расстояние от вершины $D$ до плоскости $PQR$.
    (ЕГЭ-2017, основная волна, резервный день)
12. В треугольной пирамиде $PABC$ с основанием $ABC$ известно, что $AB = 17$, $PB = 10$, $\cos \angle PBA = \dfrac{32}{85}$. Основанием высоты этой пирамиды является точка $C$. Прямые $PA$ и $BC$ перпендикулярны.
    а) Докажите, что треугольник $ABC$ прямоугольный.
    б) Найдите объем пирамиды $PABC$.
    (ЕГЭ-2017, основная волна, резервный день)
13. Ребро куба $ABCDA_1B_1C_1D_1$ равно 6. Точки $K$, $L$ и $M$ — центры граней $ABCD$, $AA_1D_1D$ и $CC_1D_1D$ соответственно.
    а) Докажите, что $B_1KLM$ — правильная пирамида.
    б) Найдите объём $B_1KLM$.
    (ЕГЭ-2017, основная волна)
14. В треугольной пирамиде $SABC$ известны боковые рёбра: $SA = SB = 7$, $CS = 5$. Основанием высоты этой пирамиды является середина медианы $CM$ треугольника $ABC$. Эта высота равна 4.
    а) Докажите, что треугольник $ABC$ равнобедренный.
    б) Найдите объём пирамиды $SABC$.
    (ЕГЭ-2017, основная волна)
15. Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали боковых граней $AA_1B_1B$ и $BB_1C_1C$ равны 15 и 9 соответственно, $AB = 13$.
    а) Докажите, что треугольник $BA_1C_1$ прямоугольный.
    б) Найдите объём пирамиды $AA_1C_1B$.
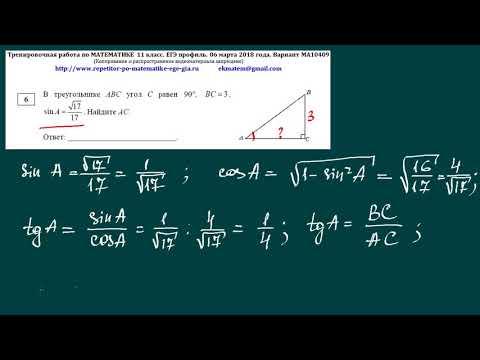
    (ЕГЭ-2017, основная волна)
16. Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Прямые $CA_1$ и $AB_1$ перпендикулярны.
    а) Докажите, что $AA_1 = AC$.
    б) Найдите расстояние между прямыми $CA_1$ и $AB_1$, если $AC = 6$, $BC = 3$.
    (ЕГЭ-2017, основная волна)
17. На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$ соответственно, причём $AM:MB = CN:NB = 1:3$. Точки $P$ и $Q$ — середины сторон $DA$ и $DC$ соответственно.
    а) Доказать, что $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
    б) Найти отношение объемов многогранников, на которые плоскость $PQM$ разбивает пирамиду.
    (ЕГЭ-2017, основная волна)
18. Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$ содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб.
    а) Докажите, что грань $ABCD$ — квадрат.
    б) Найдите угол между плоскостями $\alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.
    (ЕГЭ-2017, досрочная волна)
19. В правильной треугольной призме $ABCA_1B_1C_1$ сторона $AB$ основания равна 12, а высота призмы равна 2. На рёбрах $B_1C_1$ и $AB$ отмечены точки $P$ и $Q$ соответственно, причём $PC_1 = 3$, а $AQ = 4$. Плоскость $A_1PQ$ пересекает ребро $BC$ в точке $M$.
    а) Докажите, что точка $M$ является серединой ребра $BC$.
    б) Найдите расстояние от точки $B$ до плоскости $A_1PQ$.
    (ЕГЭ-2016, основная волна)
20. На рёбрах $DD_1$ и $BB_1$ куба $ABCDA_1B_1C_1D_1$ с ребром 12 отмечены точки $P$ и $Q$ соответственно, причём $DP = 10$, а $B_1Q = 4$. Плоскость $A_1PQ$ пересекает ребро $CC_1$ в точке $M$.
    а) Докажите, что точка $M$ является серединой ребра $CC_1$.
    б) Найдите расстояние от точки $C_1$ до плоскости $A_1PQ$.
    (ЕГЭ-2016, основная волна)
21. В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна $2\sqrt{3}$, а высота $SH$ пирамиды равна 3. Точки $M$ и $N$ — середины рёбер $CD$ и $AB$, соответственно, а $NT$ — высота пирамиды $NSCD$ с вершиной $N$ и основанием $SCD$.
    а) Докажите, что точка $T$ является серединой $SM$.
    б) Найдите расстояние между $NT$ и $SC$.
    (ЕГЭ-2016, основная волна)
22. В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3\sqrt2$. На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $\gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.
    а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $\gamma$;
    б) Найдите расстояние от точки $B_1$ до плоскости $\gamma$.
    (ЕГЭ-2016, основная волна)
23. В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.
    а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.
    б) Найдите расстояние от точки $M$ до плоскости $SBC$.
    (ЕГЭ-2016, основная волна)
24. В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.
    а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.
    б) Найдите объём тетраэдра $MNBB_1$.
    (ЕГЭ-2016, досрочная волна)
25. В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3\sqrt2$. На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $\gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.
    а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $\gamma$;
    б) Найдите расстояние от точки $B_1$ до плоскости $\gamma$.
    (ЕГЭ-2016, основная волна)
26. В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.
    а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.
    б) Найдите расстояние от точки $M$ до плоскости $SBC$.
    (ЕГЭ-2016, основная волна)
27. В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.
    а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.
    б) Найдите объём тетраэдра $MNBB_1$.
    (ЕГЭ-2016, досрочная волна)
28. Дана правильная треугольная призма $ABCA_1B_1C_1$, все рёбра которой равны 6. Через точки $A$, $C_1$ и середину $T$ ребра $A_1B_1$ проведена плоскость.
    а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
    б) Найдите угол между плоскостью сечения и плоскостью $ABC$.
    (ЕГЭ-2016, досрочная волна)
29. В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB = 6$, а боковое ребро $AA_1 = 4\sqrt3$. На рёбрах $AB$, $A_1D_1$ и $C_1D_1$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = A_1N = C_1K = 1$.
    а) Пусть $L$ — точка пересечения плоскости $MNK$ с ребром $BC$. Докажите, что $MNKL$ — квадрат.
    б) Найдите площадь сечения призмы плоскостью $MNK$.
    (ЕГЭ-2016, досрочная волна)
30. В правильной треугольной пирамиде $SABC$ сторона основания $AB$ равна 24, а боковое ребро $SA$ равно 19. Точки $M$ и $N$ — середины рёбер $SA$ и $SB$ соответственно. Плоскость $\alpha$ содержит прямую $MN$ и перпендикулярна плоскости основания пирамиды.
    а) Докажите, что плоскость $\alpha$ делит медиану $CE$ основания в отношении $5 : 1$, считая от точки $C$.
    б) Найдите площадь многоугольника, являющегося сечением пирамиды $SABC$ плоскостью $\alpha$.
    (ЕГЭ-2015, основная волна)
31. В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 4. На его ребре $BB_1$ отмечена точка $K$ так, что $KB = 3$. Через точки $K$ и $C_1$ проведена плоскость $\alpha$, параллельная прямой $BD_1$.
    а) Докажите, что $A_1P: PB_1 = 2:1$, где $P$ — точка пересечения плоскости $\alpha$ с ребром $A_1B_1$.
    б) Найдите угол наклона плоскости $\alpha$ к плоскости грани $BB_1C_1C$.
    (ЕГЭ-2015, досрочная волна)

Онлайн-игры и рабочие листы по математике, разработанные экспертами по математике

Приложение для студентов

Smart & Fun

Компания Matific серьезно относится к тому, чтобы сделать математику увлекательной. Учащиеся продвигаются по своей индивидуальной траектории обучения, выполняют назначенную работу и учатся в многопользовательских играх.

Игра в роли ученика

Математические задания для K-6

Лучшие в мире

Более 1500 математических заданий по учебной программе K-6, разработанных экспертами в области образования. От концептуального понимания до свободного владения языком — Matific поможет вам.

Изучение занятий

Инструменты для преподавателей и родителей

Простой, но мощный

Педагоги и родители имеют доступ к мощным инструментам, которые обеспечивают контроль, понимание и позволяют вмешиваться.

Просмотр функций

Индивидуальный и адаптивный план обучения

Математические задания для K-6 классов с строгим педагогическим подходом, разработанным экспертами в области образования.

Исследуйте деятельность

Опыт учителя

Экономия вашего времени

Учителя просто поощряют своих учеников использовать Matific в течение 30 минут в неделю, и Matific выделит то, что они знают, и области для улучшения в режиме реального времени. Еженедельные обновления также будут отправляться учителям, чтобы информировать их об успехах учеников.

Необходимый контент

Если преподаватели хотят охватить определенный контент, они могут просто поручить этот контент учащимся заполнить его, и он будет легко интегрирован в их рабочий процесс. Для учителя, который планирует заранее, назначенный ему рабочий график может быть легко составлен на несколько месяцев вперед.

Узнать больше

Студенческий опыт

Игровые занятия со строгой педагогикой

Учащиеся работают с нашим интерактивным и увлекательным контентом. Matific учит критическому мышлению, решению проблем и снижает математическую тревожность. Наш тщательно подобранный педагогический контент наполнен увлекательным путешествием открытий.

Индивидуальные пути обучения

Путь, по которому учатся учащиеся, охватывает полный учебный план по темам и навыкам, составленным с учетом их конкретных пробелов в знаниях и потребностей. Студенты также могут практиковать определенные навыки в специальной тренировочной зоне.

Домашнее или школьное задание четко обозначено

Если учитель поставил перед ним конкретную работу, она представлена ​​в разделе «Домашнее задание» или «Школьное задание», которое должен выполнить ребенок.

Опыт для родителей

Сделайте изучение математики легким для вас и увлекательным для вашего ребенка

Родители поощряют своих детей играть в Matific 30 минут в неделю, а Matific позаботится об остальном.

Поддержите индивидуальные потребности вашего ребенка в обучении

Родительская зона позволяет родителям следить за прогрессом своего ребенка в режиме реального времени с любого устройства. Родители получают представление о том, в чем их ребенок преуспевает, и нужна ли им помощь в определенных навыках. Еженедельные обновления также будут отправляться родителям, чтобы информировать их об успехах их ребенка.

Узнать больше

Матифик Воркс

• Улучшает результаты на

  34%

  Использование Matific в классе повышает успеваемость учащихся.

  Университет Западного Сиднея

• Зацепление привода для

  89%

  Учителя рекомендуют Matific своим коллегам и продолжают использовать его на уроках.

  Вирджиния, США

• Увеличивает процент на

  31%

  Студенты с большей вероятностью согласятся с тем, что они «хотят изучать математику».

  Тамил Наду, Индия

Педагогические принципы Matific

Сильной стороной Matific являются педагогические принципы из 5 пунктов, разработанные экспертами из Стэнфорда, Гарварда, Беркли и Института Эйнштейна.

Изучите нашу педагогику

Полностью интегрирован в вашу образовательную экосистему

Нам доверяют миллионы пользователей по всему миру

«Matific — это фантастический инструмент для интуитивного обучения математике и приобщения детей к научному мышлению».

Профессор Аарон Чехановер

Лауреат Нобелевской премии

«Гораздо интереснее для наших студентов, чем другие онлайн-платформы, и нам нравится, как вопросы были адаптированы к способностям студентов».

Начальная школа Темплтона

«Matific очень прост в использовании, и нашим ученикам понравилось его использовать. Родители также были очень впечатлены тем, чему их дети учились и что использовали».

Государственная школа Флагстоун

Раскрытие детского математического потенциала

Посмотреть блог Matific

Используйте Matific на любом устройстве

Начните работу с Matific, попробуйте бесплатно

Matific — обладатель множества наград

Герой Курса | Владейте учебным часом

Доступ к 100 миллионам учебных материалов по конкретным курсам.

Знакомство с решениями и пояснениями из учебника

Позвольте нам шаг за шагом помочь вам разобраться с вопросами в вашем учебнике. Мы добавляем новые учебники каждую неделю.

Просмотреть учебники

Вы педагог? Узнать больше

Найти учебные ресурсы

Для конкретного курса

Учебные документы для всех ваших классов

Популярные курсы

Помощь с домашними заданиями 24/7 от экспертов в предметной области

Пошаговые объяснения

Мы разберем это для вас

Быстрые ответы

Мы вылечим вас всего за 15 минут

Помощь с домашним заданием

Новый

Решения для учебников

Новый

Получите пошаговые объяснения, проверенные преподавателями

© Этот учебник можно приобрести на сайте www. amazon.com

.

Бухгалтерский учет колледжа, главы 1-27

© Этот учебник можно приобрести на сайте www.amazon.com

Анатомия и физиология человека Хоула

© Этот учебник можно приобрести на сайте www.amazon.com

.

Микробиология: введение

© Этот учебник можно приобрести на сайте www.amazon.com

Анатомия и физиология: единство формы и функции

Просмотрите учебники

Начните работу с Course Hero

Получите бесплатный доступ

Загрузите свои учебные документы для бесплатного доступа к другим учебным документам в нашей библиотеке.

Получите бесплатный доступ

Подпишитесь на мгновенный доступ

Выберите свой план — от 9,95 долларов США в месяц.

Получить мгновенный доступ

Студент первого поколения жонглирует семьей, финансами и колледжем

Студент-спортсмен находит цель за пределами поля

36 вещей, которые вы должны знать о своем соседе по комнате, чтобы год прошел без конфликтов

Совместное использование личного пространства может быть непростой задачей. Секрет гармоничной жизни заключается в построении эмпатии и доверия.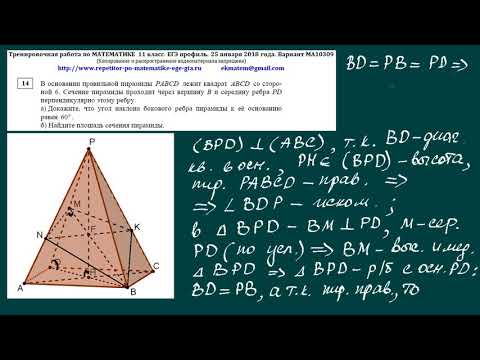 Вот 36 вопросов, предназначенных для этого.

Как извлечь максимальную пользу из учебника (за наименьшее количество времени)

Так много слов, так мало учебных часов. Прежде чем браться за книги, прочтите эти 6 советов и приемов, которые помогут вам более эффективно разобраться во всем этом тексте.

Не сдаете тренировочные тесты? Вот почему вам следует

Исследования показывают, что этот метод обучения, которым часто пренебрегают, может помочь превратить пассивно усвоенную информацию в истинное понимание. Вот почему это работает.

Вы в правильном майоре? 6 вопросов, которые нужно задать перед тем, как

Предугадывать свою специальность совершенно нормально. Но какие признаки вам действительно нужны, чтобы пересмотреть свой выбор?

Почему вы прокрастинируете (Потому что: неврология)

Прокрастинация — это плохая привычка или заложенная черта характера? Не ждите ни минуты, чтобы узнать, что говорит наука.