Задание №7. Производная. Поведение функции. Первообразная
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке
Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой в точке
При значения выражений и равны.
При этом производная функции равна угловому коэффициенту касательной, то есть .
Из второго уравнения находим или Первому уравнению удовлетворяет только .
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.
Мгновенная скорость движущегося тела является производной от его координаты по времени.
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени получим:
.
Ответ: 3.
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция возрастает.
Если , то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| 0 | 0 |
5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.
Производная функции в точках максимума и минимума функции Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.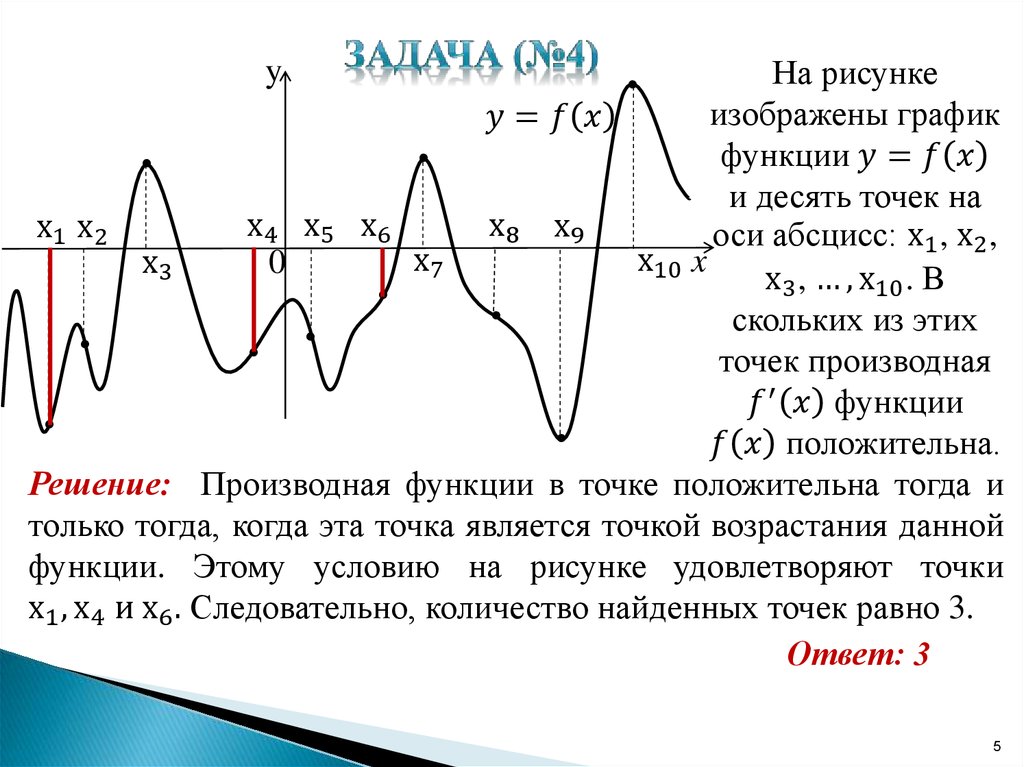
На отрезке производная функции положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции
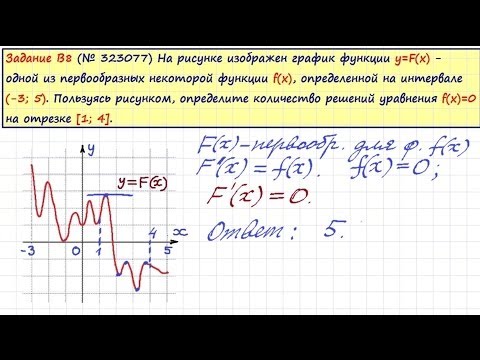
10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
Функция для которой является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.
Это точки максимума и минимума функции На отрезке таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 07.02.2023
Задание №7 ЕГЭ по математике профильного уровня с решением
В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.
В большинстве случаев достаточно просто определения понятий и понимания значений производной.
Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
Алгоритм решения:
- Рассматриваем график функции.
- Ищем точки, в которых функция убывает.
- Подсчитываем их количество.
- Записываем ответ.
Решение:
1. На графике функция периодически возрастает, периодически убывает.
2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.
3. В этих интервалах лежат точки x3, x4, x5, x9. Таких точек 4.
Таких точек 4.
Ответ: 4.
Второй вариант задания (из Ященко, №4)
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Алгоритм решения:
- Рассматриваем график функции.
- Рассматриваем поведение функции в каждой из точек и знак производной в них.
- Находим точки в наибольшим значением производной.
- Записываем ответ.
Решение:
1. Функция имеет несколько промежутков убывания и возрастания.
2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.
3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.
Производная имеет наибольшее значение.
Ответ: 2.
Третий вариант задания (из Ященко, №21)
Прямая является касательной к графику функции . Найдите а.
Алгоритм решения:
- Приравняем уравнения касательной и функции.
- Упрощаем полученное равенство.
- Находим дискриминант.
- Определяем параметр а, при котором решение единственное.
- Записываем ответ.
1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:
2. Упрощаем равенство, перенеся все слагаемые в одну сторону:
3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.
4. Получаем:
Ответ: 4.
ib-math-ai-sl-syllabus — Googlesuche
AlleBilderBücherVideosMapsNewsShopping
suchoptionen
[PDF] Математика: приложения и руководство по интерпретации — erhs. la ibdp_mathematics-application…
la ibdp_mathematics-application…
План программы. 23. Предварительные учебные темы. 24. Содержание программы. 26. Оценка. 72. Оценка в дипломной программе. 72. План оценки — SL.
Откройте для себя IBDP Math AI & AA HL/SL Syllabus 2021 — Sev7n
sev7n.co.in › math-ai-aa-hl-sl-syllabus-ibdp-2021
Цели и задачи программы IBDP Math AI & AA HL/SL: ; Функции, 21, 32 ; Геометрия и тригонометрия, 25, 51; Статистика и вероятность, 27, 33; Исчисление …
Предназначено для студентов, интересующихся математикой, инженерно-физическими науками и некоторыми видами экономики: Предназначено для студентов…
Занимается математическими задачами и исследует реальные и абстрактные приложения: Занимается решением реальных математических задач проблемы …
Цели и задачи-Развитие прочных навыков математического мышления: Цели и задачи-Развитие сильных навыков практического применения…
Основная область — Упор на алгебраические методы: Основная область — Моделирование и статистика
[PDF] Дипломная программа международного бакалавриата Subject Brief
www. ibo.org › contentassets › subject-brief-dp-math-applications-and…
ibo.org › contentassets › subject-brief-dp-math-applications-and…
Математика: приложения и интерпретация и Математика: анализ и подходы имеют 60 часов общего содержания. Силлабусный компонент. Рекомендуемое обучение …
[PDF] Математика: приложения и интерпретация Программа SL и курс …
zso13.edu.gdansk.pl › getfile › Программа по математике – приложения и…
IB WORLD SCHOOL 1309 (ZSO13 Gdańsk) . Математика: приложения и интерпретация SL программа и курс обучения. (на основе математики: приложения и …
The Complete IB Math Syllabus SL / HL 2021 (обновлено) — TestprepKart
www.testprepkart.com › ib › blog-single ›
25.11.2021 · Темы, изучаемые в Math AI SL · Числа и алгебра (16 часов) · Функции (31 час) · Геометрия и тригонометрия (18 часов) · Вероятность и … AI (SL и HL) – YouTube
www.youtube.com › смотреть
25.11.2021 · Скачать бесплатные электронные книги IB по математике, банки вопросов и статьи за прошлый год: https://www . ..
..
Dauer: 7:54
Прислан: 25.11.2021
[PDF] Программа курса для IB Math Applications & Interpretations SL
wl.apsva.us › загрузки › сайты › 2019/08 › Wright-SY21-IB-AI-syllabus
IB Test: все учащиеся сдают двухдневный экзамен IB Math Studies в мае 2021 года. Государственные школы Арлингтона ( APS) оплачивает экзаменационные сборы для всех классов IB.
Полная программа IB по математике SL / HL 2021 | ibvilla.com
ibvilla.com › математика-приложения-интерпретация…
Новый учебный план IB Mathematics Analysis and Approaches & Application and Interpretation 2022 можно найти здесь. Все о математике AA/AI HL/SL и университете …
[PDF] Mathematics SL guide — Berlin Cosmopolitan School
www.cosmopolitanschool.de › uploads › 2018/10 › dp-math-sl-guide
Международная организация бакалавриата (известная как IB) предлагает три высших — … Математика SL справочник. План силлабуса. Учебный план. Силлабусный компонент.
Силлабусный компонент.
IB Math AI SL Notes (обновлено в 2023 г.) — Nail IB Библиотека. Адам Нажа. 30 часов. 17 разделов. 113 лекций.
ähnliche sucalfragen
Математические приложения и интерпретация
IB Математика AI SL Темы
IB Math AA SL Примечания
IB Математика
IB Maths AA
Математика Oxford Mathematics и интерпретация SL. Образование : Математическая оценка OSAS : Оценка учащихся : Штат Орегон
- 2022-23 OSAS Mathematics Test Blueprint
- Обзор изменений в проекте OSAS по математике на 2021–2022 годы
В этом документе содержится краткая информация об изменениях в схеме итогового оценивания по математике OSAS на 2021–2022 административный год. Для конкретных сравнений между приоритетными и вспомогательными кластерами в рамках каждой заявки см. Инструмент сравнения математических схем. Оценки штата Орегон по предметным областям и классам/эталонным уровням.
Оценки штата Орегон по предметным областям и классам/эталонным уровням.
- Пешеходные переходы теста OSAS по математике (заявления, цели, стандарты и дескрипторы уровня достижений)
Эти документы согласовывают требования и цели теста OSAS по математике с математическими стандартами штата Орегон K-12. Заявления и цели можно использовать для разработки уроков в классе и школьных оценок. Кроме того, эти документы содержат дескрипторы уровня достижений, которые служат руководством для понимания отчетов по тестам OSAS по математике.
3 класс, 4 класс, 5 класс, 6 класс, 7 класс, 8 класс, средняя школа
- Smarter Content Explorer
На следующем веб-сайте представлены интерактивные связи между математическими стандартами штата Орегон K-12 и оценочными требованиями и целевыми показателями. Дополнительные ресурсы находятся на веб-сайте: рекомендации по доступности, критерии оценки и многое другое. Для получения дополнительной информации о навигации и использовании веб-сайта см. Видео об умном обозревателе контента.
Видео об умном обозревателе контента. -
Таблица использования ресурсов для оценки
В этом документе представлено параллельное сравнение учебных тестов, практических тестов и промежуточных оценок, чтобы помочь учителям решить, какой инструмент лучше всего соответствует их потребностям. - Разработка и дизайн Содержание и спецификации предметов
переводят математические стандарты штата Орегон K-12 в рамки оценки и фактические данные. - Математический конструкционный словарь
Краткий справочный документ, который включает в себя словарь конструктов для 3–8 классов и старшей школы, полученный из спецификаций пункта 1. - Орегон Оценочные задания по математике
Включает в себя критерии оценки выполнения заданий для использования при подготовке к тесту OSAS по математике.
4 балла за задание, 3 балла за задание, 2 балла за задание, 1 балл за задание
- Руководство по прочтению вслух для OSAS ELA и тестов по математике (английский) (испанский)
Читатели тестов на людях должны использовать эти рекомендации для учащихся, использующих Read Поддержка вслух или чтения вслух на испанском языке.
 Рекомендации для
Использование подробно описано в Руководстве по доступности штата Орегон.
Рекомендации для
Использование подробно описано в Руководстве по доступности штата Орегон.
Орегон предлагает более 85 блоков промежуточных оценок по математике (IAB), которые предназначены для включения в учебный процесс. Большинство IAB состоят из 8–15 пунктов, на выполнение которых у большинства студентов уходит примерно 30–45 минут. Другими отличительными чертами промежуточных оценок штата Орегон являются:
- IAB полностью соответствуют глубине и широте стандартов штата Орегон
- IAB предоставляют меньшие пакеты контента, которые можно использовать по мере необходимости для корректировок «точно в срок»
- IAB обеспечивают частое и гибкое использование
- IAB могут быть легко встроены в карты математических единиц (узнайте, как!)
- Промежуточные элементы включают все доступные ресурсы, доступные в итоговых оценках штата Орегон
- IAB могут использоваться учащимися вне 9-го класса0112
- IAB напрямую подключаются к следующим шагам обучения в Инструментах для учителей
Для получения дополнительной информации посетите веб-страницу промежуточной оценки ODE.
- OSAS Mathematics Sample and Training Tests Примеры и обучающие тесты
по математике позволяют учащимся и преподавателям предварительно ознакомиться с тестовыми вопросами.
-
Образцы заданий OSAS
На этом сайте представлены примеры тестовых вопросов, используемых в тесте OSAS по математике. Учителя, родители, учащиеся, администраторы и лица, определяющие политику, могут выполнять эти тестовые задания точно так же, как с ними сталкиваются учащиеся.Эти образцы заданий не предназначены для использования в качестве практических тестов, но преподаватели могут использовать их, чтобы лучше понять, как Суммативное оценивание штата Орегон измеряет знания и навыки, необходимые для поступления в колледж и карьеры.
- Понимание результатов учащихся
- Результаты оценки
В отчетах на этой странице показан процент учащихся, которые соответствуют или превышают стандарты успеваемости, действовавшие в течение учебного года, результаты которого сообщаются.
- Доступ к отчетам о целевых показателях
Отчеты о целевых показателях показывают успеваемость групп учащихся по целевым показателям на уровне класса по сравнению с уровнем знаний, а также то, какие из этих целевых показателей являются относительными сильными и слабыми сторонами. Справочный документописывает требования к вариантам оценивания Essential Skills, включая требования к разработке, администрированию и подсчету оценок.
- Требования к выпускникам по основным навыкам
Включает дополнительные ресурсы для поддержки требований основных навыков.
- Руководство по оценке основных навыков
Включает официальные руководства по подсчету очков для основных навыков.
- Базовые математические навыки
Включает дополнительные ресурсы для поддержки требований к базовым навыкам математики.
В штате Орегон Требования к оценке успеваемости гласят, что школьные округа должны ежегодно проводить одну или несколько оценок успеваемости для всех учащихся с 3 по 8 классы и старшей школы по математике, научным исследованиям, устной и письменной речи.
Оценка успеваемости должна быть стандартизированной мерой (например, деятельность, упражнение, задача или образец работы, оцениваемые с помощью общего инструмента оценки, такого как официальное руководство штата или другое руководство по оценке, принятое школьным округом), которое встроено в школу. учебный план и оценивает применение знаний и навыков учащихся. Образцы работ, оцениваемые с использованием официального руководства штата по подсчету очков, являются лишь одним из примеров приемлемой оценки производительности. Округа обладают значительной гибкостью при планировании оценок эффективности, которые будут использоваться для выполнения этого требования.
В дополнение к обязательным областям школьным округам рекомендуется рассмотреть возможность проведения местной оценки успеваемости в других областях навыков в соответствии с местной учебной программой. Например, округа могут выбрать администрирование местных оценок эффективности в любой из других областей, таких как анализ социальных наук.
Руководство по оценке основных навыков и эффективности
В этом справочном документе описываются требования к администрированию Local Performance Assessment.
Руководство по подсчету баллов и формы обратной связи
Для оценки успеваемости на местном уровне школьные округа могут разработать на местном уровне руководство по подсчету баллов, чтобы предоставить учащимся обратную связь, или они могут использовать Руководство штата по подсчету баллов.
- Руководство по подсчету очков для решения задач по математике
Включает руководство по подсчету баллов штата и языковые версии для учащихся на испанском и английском языках
- Форма обратной связи средней школы
Форма обратной связи приведена в соответствие с Руководством по оценке состояния
- K-8 Форма обратной связи
Форма обратной связи приведена в соответствие с руководством по оценке состояния
Примеры заданий и оцениваемые работы учащихся
Другие ресурсы
Связь
2023 OSAS ELA и тренинг по подсчету итоговых тестов по математике
Департамент образования штата Орегон заинтересован в участии преподавателей заданий по английскому языку и математике для итогового теста штата Орегон
- Зарегистрируйтесь в Oregon Math Educator Update, периодическом информационном бюллетене, рассылаемом Департаментом образования штата Орегон, чтобы получать регулярные обновления и ссылки на возможности математики в нашем штате.

Профессиональное обучение
- Использование Desmos в экзаменах OSAS по математике и естественным наукам
Используйте эти ресурсы, чтобы подготовить учащихся к использованию калькулятора Desmos, встроенного в итоговые экзамены штата Орегон по математике и естественным наукам.- Слайд-презентация
- Поиски графического калькулятора, используемого в школьных тестах
- Охота за научным калькулятором, используемым в 7-8 классах
- Калькуляторы для тестирования Desmos
- Understanding Proficiency: Performance Tasks
Ресурсы, помогающие преподавателям глубже понять Общие базовые стандарты штата Орегон путем анализа работы учащихся над исполнительскими заданиями. Центральное место в этих ресурсах занимают примеры реальных работ учащихся над примерами заданий по английскому языку и математике. - Assessment Professional Learning
Ресурсы, помогающие преподавателям и администраторам повысить грамотность оценивания и отточить свою практику в рамках сбалансированной системы оценивания.
- Веб-страница математических стандартов и учебных пособий
- Орегонский математический проект
- Племенная история, общие уроки математики по истории
- Орегонские учебные материалы
Сеть лидеров математики штата Орегон – это сообщество практикующих математиков, которые вместе работают над внедрением и поддержкой преподавания и обучения математике в штате Орегон. В число участников входят руководители учителей, TOSA, администраторы программ, преподаватели колледжей и партнеры по математическому сообществу. Эмпирическое правило: если вы идентифицируете себя как лидер по математике, вы им являетесь!
Мы встречаемся практически каждый месяц, чтобы поддерживать друг друга в личном и профессиональном плане, задавая критические вопросы, сотрудничая в решении практических проблем и делясь своей работой. Поскольку эта сеть охватывает весь штат, темы нашего сотрудничества, как правило, определяются потребностями округа.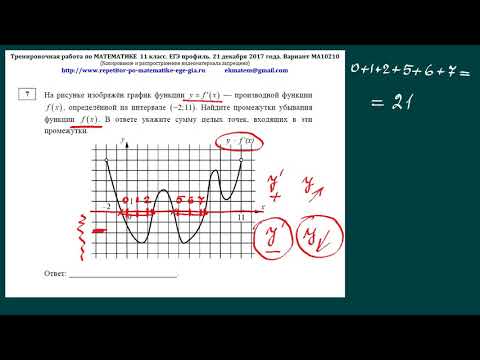

 Оценки штата Орегон по предметным областям и классам/эталонным уровням.
Оценки штата Орегон по предметным областям и классам/эталонным уровням. Видео об умном обозревателе контента.
Видео об умном обозревателе контента.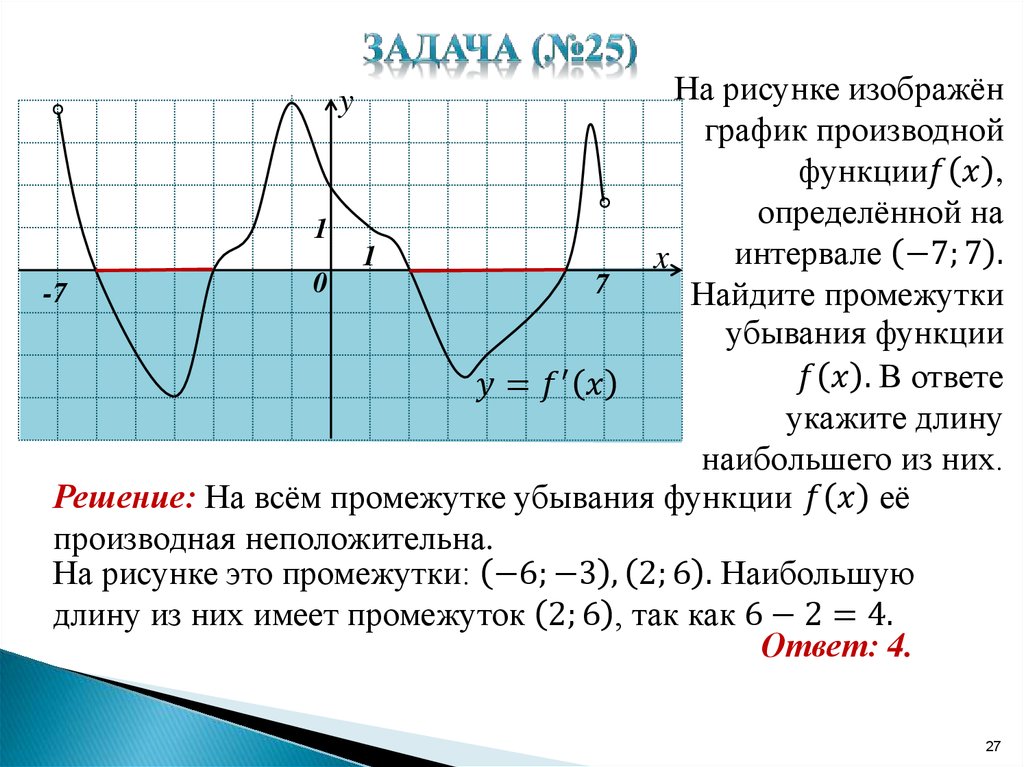 Рекомендации для
Использование подробно описано в Руководстве по доступности штата Орегон.
Рекомендации для
Использование подробно описано в Руководстве по доступности штата Орегон.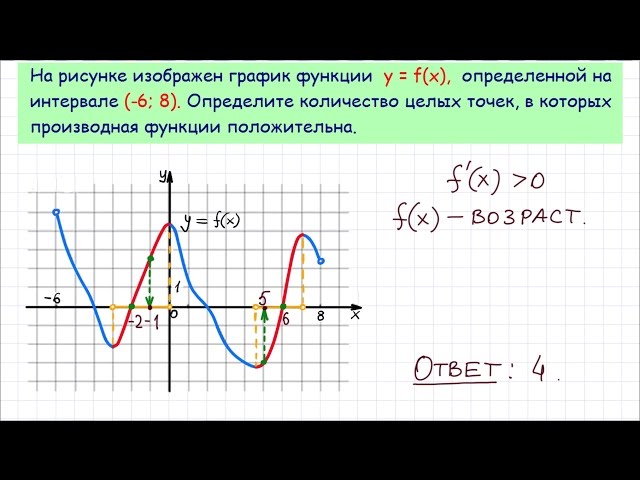

Leave A Comment