Концы двух пересекающихся отрезков AC и BD лежат на двух параллельных плоскостях, причем расстояние между точками одной плоскости равны. Докажите, что: а) AD||BC б)один из углов четырехугольника ABCD равен 130 град., найдите остальные углы.
Последние вопросы
Геометрия
6 минут назад
Задача за 10 класс по геометрииГеометрия
16 минут назад
Помогите задача по геометрии 10 классГеометрия
31 минут назад
Помогите пожалуйста с геометрией 7 класс!! СРОЧНО! С дано и решение, пожалуйста, не только ответГеометрия
32 минут назад
Допоможіть будь ласка. Знайдіть довжину невідомого відрізка x .
( Найдите длину неизвестного отрезка x )
Знайдіть довжину невідомого відрізка x .
( Найдите длину неизвестного отрезка x )Геометрия
46 минут назад
Пожалуйста помогите с геометрией!!!!!! Прошу!!! Дано и решениеГеометрия
1 час назад
Настоящий треугольник невозможно было бы увидеть ибо его стороны, будучи идеальными отрезками не обладали бы толщиной?Геометрия
1 час назад
Геометрия 7 класс. Равнобедренные треугольники.Геометрия
1 час назад
Расстояние между скрещивающимися прямымиГеометрия
1 час назад
Помогите пожалуйста! контрольная по геометрииГеометрия
1 час назад
Помогите!! контрольная работа по геометрии. пожалуйста
пожалуйстаГеометрия
1 час назад
Помогите!! контрольная по геометрии. срочно1 час назад
3. Дано прямокутник ABCD зі сторонами AB = 6 см, ВС = 8 см, AM — перпендикуляр до площини прямокутника. Пряма MC нахилена до площини прямокутника під кутом 60°. Знайдіть тангенс кута, який утворює площина MDC із площиною прямокутника. 4. Трикутник А1 B1 C1 є ортогональною проєкцією трикутника АВС зі сторонами 4 см, 13 см і 15 см. Знайдіть кут між площинами трикутників, якщо трикутник А1 В1 С1 прямокутний з катетами 6 см і 4√2 см. Допоможіть будь ласкаГеометрия
1 час назад
 Знайдіть зовнішній кут трикутника при вершині С.СРОЧНООО
Знайдіть зовнішній кут трикутника при вершині С.СРОЧНОООГеометрия
1 час назад
Геометрия 7 класс. Равнобедренный треугольник.Геометрия
1 час назад
Объясните пожалуйста и помогите..
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
1 hour 1 day 100 years
1.
 2. Параллельность прямых и плоскостей в пространстве
2. Параллельность прямых и плоскостей в пространстве1.2. Параллельность прямых и плоскостей в пространстве
С понятием «параллельность» вы познакомились при изучении планиметрии. Там оно относилось лишь к прямым. Выход в пространство, изменение «статуса» плоскости вынуждает нас не только уточнить определения некоторых понятий, но и расширить область их применения.
Определение 1
Две плоскости в пространстве называются параллельными, если они не имеют общих точек.
Определение 2
Прямая и плоскость в пространстве называются параллельными, если они не имеют общих точек.
Определение 3
Как видим, первые два определения расширяют «зону действия» понятия «параллельность», а третье — уточняет старое определение. Ведь в пространстве две прямые могут и не принадлежать одной плоскости.
Определение 4
Две прямые, не принадлежащие одной плоскости, называются скрещивающимися.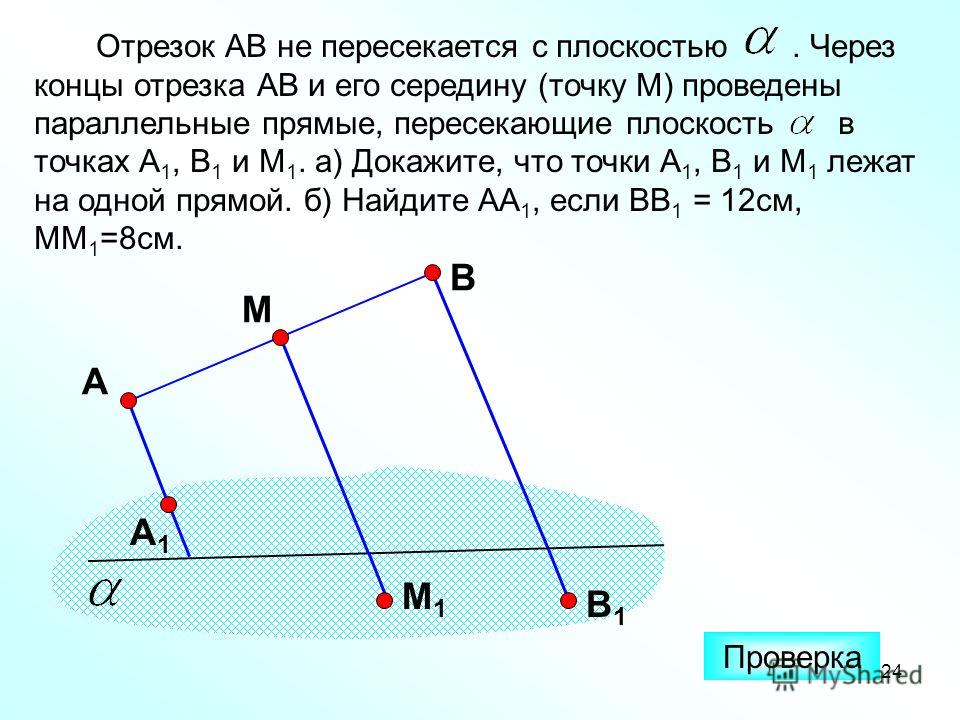
Рис. 17
На рисунке 17 изображена треугольная пирамида ABCD. Прямые AB и DC, AC и BD, AD и BC являются скрещивающимися, поскольку точки A, B, C и D не лежат в одной плоскости. Таким образом, противоположные рёбра треугольной пирамиды попарно скрещиваются (т. е. они лежат на скрещивающихся прямых).
Сформулируем и докажем несколько теорем о свойствах и признаках параллельности в пространстве.
Теорема 1.2 (о прямой, параллельной плоскости)
Если прямая l параллельна плоскости a, то любая плоскость, проходящая через l и пересекающая плоскость a, пересекает её по прямой, параллельной l.
Рис. 18
Доказательство. Пусть плоскость b проходит через прямую l и пересекается с плоскостью a по прямой m (рис. 18). Поскольку прямая l параллельна плоскости a, она не может пересекаться с прямой m. Значит, эти прямые, согласно определению 3, параллельны. ▼
Теорема 1.3 (о двух параллельных плоскостях)
Если две плоскости параллельны, то любая плоскость, пересекающая одну из них, пересекает также и вторую, причём получившиеся при пересечении прямые параллельны.
Рис. 19
Доказательство. Рассмотрим две параллельные плоскости a и b. Пусть M — некоторая точка плоскости b (рис. 19, а). Рассмотрим плоскость l, проходящую через точку M. Пусть эта плоскость пересекает обе данные плоскости. Прямые, по которым плоскость l пересекает a и b, не могут пересечься, следовательно, являются параллельными.
Осталось доказать, что плоскость l, если она не совпадает с плоскостью b, непременно пересекается с плоскостью a. Предположим, что это не так (рис. 19, б). Возьмём любую точку K в плоскости a и проведём через точки M и K некоторую плоскость j так, чтобы она не содержала прямой, по которой пересекаются плоскости b и l. Это всегда можно сделать. Плоскость j пересекает все три плоскости a, b и l. В соответствии с только что доказанным получим, что в плоскости j через точку M проходят две прямые, параллельные одной и той же прямой (прямые, по которым плоскость j пересекает плоскости b и l, параллельны прямой, по которой пересекаются плоскости j и a), что противоречит известному нам свойству плоскости (свойство 4, § 5.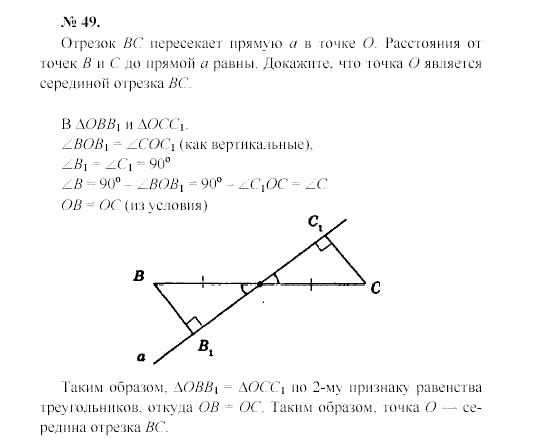
В теореме 1.3 содержится утверждение, которое выделим отдельно.
Через любую точку пространства, не лежащую в данной плоскости, проходит не более одной плоскости, параллельной данной.
Это утверждение аналогично свойству параллельных прямых на плоскости.
Теорема 1.4 (признак параллельности прямой и плоскости)
Если прямая, не лежащая в плоскости, параллельна какой-то прямой этой плоскости, то она параллельна и самой плоскости.
Рис. 20
Доказательство. Пусть прямая k, не лежащая в плоскости a, параллельна прямой m этой плоскости (рис. 20). Согласно определению две прямые k и m лежат в одной плоскости (обозначим эту плоскость через b) и не пересекаются. Это означает, что прямая k не может пересечься с плоскостью a, так как если они пересекаются, то точка их пересечения должна принадлежать плоскости b. Отсюда следует, что прямые k и m пересекаются, что противоречит условию теоремы.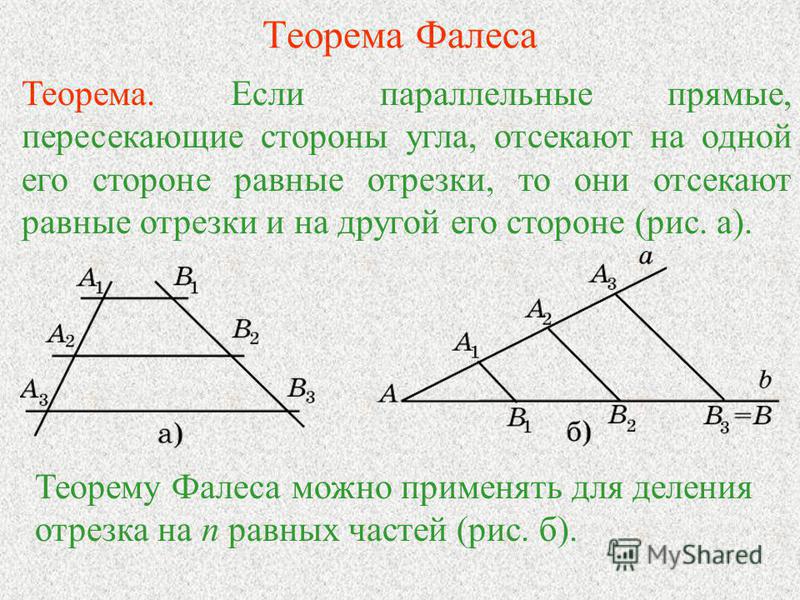
Теорема 1.5 (признак параллельности двух плоскостей)
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.
Рис. 21
Доказательство. Пусть пересекающиеся прямые k и m плоскости a соответственно параллельны прямым kʹ и mʹ плоскости b (рис. 21). Предположим, что эти плоскости пересекаются. Обозначим прямую, по которой они пересекаются, через n. Эта прямая пересекается хотя бы с одной из заданных прямых плоскости a. Пусть прямая n пересекается с прямой k. Но прямая k параллельна плоскости b (см. теорему 1.4) и не может пересекаться ни с какой прямой этой плоскости. Полученное противоречие доказывает теорему. ▼
Теперь мы можем уточнить утверждение, сделанное после доказательства теоремы 1.3.
Через любую точку пространства, не принадлежащую данной плоскости, проходит единственная параллельная ей плоскость.
В самом деле, чтобы провести параллельную плоскость, нам достаточно построить две прямые, проходящие через точку и параллельные двум прямым в данной плоскости.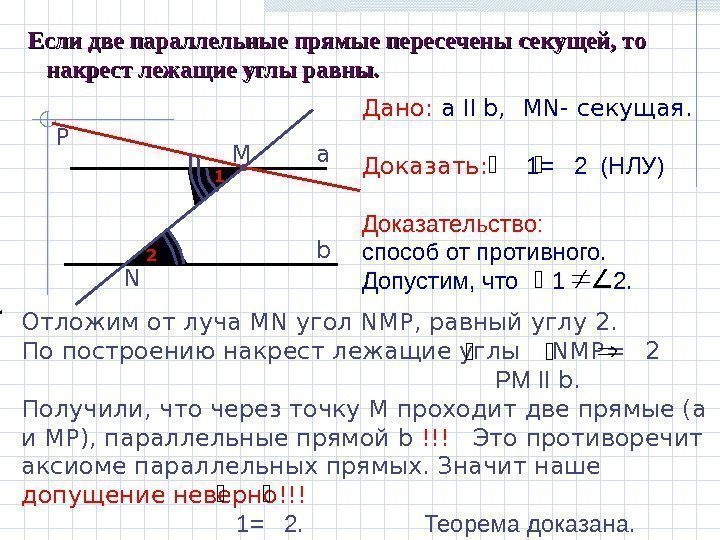
Теорема 1.6 (о двух плоскостях, проходящих через параллельные прямые)
Пусть a и b — две параллельные прямые. Рассмотрим две пересекающиеся плоскости a и b, проходящие соответственно через прямые a и b и не совпадающие с плоскостью, содержащей эти прямые. Тогда линия пересечения плоскостей a и b параллельна прямым a и b.
Доказательство. По признаку параллельности прямой и плоскости (теорема 1.4) прямая a параллельна плоскости b (a ∥ b), а прямая b параллельна плоскости a (b ∥ a). Теперь по теореме 1.2 линия пересечения плоскостей a и b параллельна как прямой a, так и b. ▼
Теорема 1.7 (о транзитивности понятия параллельности для прямых)
Если каждая из двух различных прямых параллельна третьей, то и сами эти прямые параллельны.
(Понятие «транзитивность» в математике означает перенос некоторого свойства: если рассматриваемое свойство выполняется для пары a и b и для пары b и c, то оно выполняется и для пары a и c. В данном случае a, b и c — это прямые, поэтому рассматриваемое свойство — параллельность прямых. При этом мы дополнительно требуем, чтобы a и c не совпадали.)
При этом мы дополнительно требуем, чтобы a и c не совпадали.)
Рис. 22
Доказательство. Пусть три прямые a, b и c таковы, что a ∥ b и c ∥ b. Надо доказать, что a ∥ c.
Возьмём на прямой c произвольную точку M (рис. 22). Рассмотрим плоскости a и b: плоскость a проходит через прямую a и точку M, плоскость b — через прямые b и c. Обозначим через c1 линию пересечения a и b. По теореме 1.6 имеем: c1 ∥ a и c1 ∥ b. Но так как в плоскости b через точку M проходит единственная прямая, параллельная b, то прямая c1 совпадает с прямой c. Теорема доказана. ▼
Задачи, задания, вопросы |
1(в). Пусть A, B, C и D — четыре точки, не лежащие в одной плоскости. (В этой главе для краткости иногда используется выражение: «ABCD — треугольная пирамида». Здесь важно лишь то, что точки A, B, C и D не лежат в одной плоскости.) Докажите, что прямая AB параллельна плоскости, проходящей через середины AD, BD и CD. |
2(в). Пусть A, B, C и D — четыре точки, не лежащие в одной плоскости. |
3.В пространстве проведены две параллельные прямые и пересекающие эти прямые две параллельные плоскости. Докажите, что четыре точки пересечения прямых и плоскостей служат вершинами параллелограмма. |
4(в). Пусть A, B, C и D — четыре точки в пространстве. Докажите, что середины отрезков AB, BC, CD и DA служат вершинами параллелограмма. |
5.Пусть A — некоторая точка пространства, не лежащая в плоскости a, M — произвольная точка плоскости a. Найдите геометрическое место середин отрезков AM. |
6.Найдите геометрическое место середин всевозможных отрезков, концы которых лежат в двух параллельных плоскостях. |
7(в). Пусть A, B, C и D — четыре точки пространства, не лежащие на одной прямой. Докажите, что отрезок, соединяющий середины AB и CD, пересекается с отрезком, соединяющим середины AD и BC. |
8(т). В пространстве проведены четыре прямые, не лежащие в одной плоскости, но при этом никакие две из них не являются скрещивающимися. Докажите, что все эти прямые проходят через одну точку либо параллельны. |
9(в). Докажите, что через любую из двух скрещивающихся прямых можно провести плоскость, параллельную другой прямой. |
10(п). Рассмотрим две скрещивающиеся прямые a и b. Проведём через a плоскость, параллельную b, а через b — плоскость, параллельную a. Возьмём точку M, не лежащую в проведённых плоскостях. Докажите, что две плоскости, проходящие через прямую a и точку M, а также через прямую b и точку M, пересекаются по прямой, пересекающей a и b. (Этот факт даёт способ построения прямой, проходящей через данную точку пространства и пересекающей две заданные скрещивающиеся прямые.) |
11.Рассмотрим прямоугольник ABCD и точку E, не лежащую в его плоскости. |
12(т). Пусть A, B, C и D — четыре точки, не лежащие в одной плоскости. Через точку пересечения медиан треугольника ABC проведена плоскость, параллельная прямым AB и CD. В каком отношении эта плоскость делит медиану к стороне CD в треугольнике ACD ? |
13.В каком отношении плоскость, проходящая через точки пересечения медиан треугольников ABC, ABD и BCD, делит отрезок BD (ABCD — пирамида)? |
14(тв). В треугольниках ACD и ADB проведены соответственно медианы AM и DN. На этих медианах взяты точки E и F так, что прямая EF параллельна BC. Найдите отношение EF : BC (ABCD — пирамида). |
15(т). В пирамиде ABCD точки M, F и K — середины BC, AD и CD соответственно. На прямых AM и CF взяты точки P и Q так, что PQ параллельна BK. Найдите отношение PQ : BK. |
16(т). |
17.Может ли сечение параллелепипеда быть правильным пятиугольником? |
18.Плоскость проходит через середины рёбер AB и AC пирамиды ABCD и делит ребро BD в отношении 1 : 3. В каком отношении эта плоскость делит ребро CD ? |
19(пт). Докажите, что если две пересекающиеся плоскости параллельны некоторой прямой, то и линия их пересечения параллельна этой же прямой. |
20(т). Дан параллелепипед ABCDA1B1C1D1 (рис. 23). На рёбрах AD, A1D1 и B1C1 взяты соответственно точки M, L и K так, что B1K = A1L, AM = A1L. Известно, что KL = 2. Найдите длину отрезка, по которому плоскость KLM пересекает параллелограмм ABCD. |
Рис. |
Видео с вопросами: Определение отношения между сегментами прямых в пространстве
Стенограмма видео
Рассмотрим прямоугольный параллелепипед 𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻, где 𝐴𝐵 не равно 𝐵𝐶 не равно 𝐴𝐸. Что можно сказать об отрезке 𝐸𝐹 и отрезке 𝐹𝐺? Что можно сказать об отрезке 𝐴𝐸 и отрезке 𝐶𝐺? Что можно сказать об отрезке 𝐵𝐷 и отрезке 𝐷𝐻? Что можно сказать об отрезке 𝐵𝐷 и отрезке 𝐴𝐶?
В этом вопросе мы рассматриваем взаимосвязь между двумя отрезками линии в трехмерной форме. Итак, давайте рассмотрим возможные отношения, которые могут иметь две линии в пространстве. Это, а именно, они могут быть параллельными, перпендикулярными, ни параллельными, ни перпендикулярными, или косыми.
Давайте посмотрим, как на самом деле будет выглядеть каждое из этих четырех различных отношений. Во-первых, давайте подумаем, что произойдет, если две линии на самом деле находятся в одной плоскости. Тогда у нас могут быть две параллельные линии. Или если линии пересекаются под углом 90 градусов, то они будут перпендикулярны. Или, конечно, эти две линии на одной плоскости могут пересекаться под углом, отличным от 90 градусов. И поэтому мы можем сказать, что они были бы ни параллельны, ни перпендикулярны.
Или, конечно, эти две линии на одной плоскости могут пересекаться под углом, отличным от 90 градусов. И поэтому мы можем сказать, что они были бы ни параллельны, ни перпендикулярны.
Таким образом, у нас остается последний тип отношений, который представляет собой две наклонные линии. Важно помнить о наклонных линиях: они могут существовать только в трех измерениях. Они также не пересекаются. Допустим, например, у нас есть линия на плоскости. Тогда другая строка, которая наклонена к первой строке, может выглядеть так. Итак, по мере прохождения каждой части этого вопроса мы рассмотрим различные сегменты линий и рассмотрим отношения между ними. Тот факт, что это прямоугольный параллелепипед, очень важен для определения отношений между этими отрезками.
Первая часть спрашивает, что можно сказать об отрезке 𝐸𝐹 и отрезке 𝐹𝐺? Эти два отрезка линии выделены на кубоиде. Что ж, поскольку это прямоугольный параллелепипед, мы знаем, что каждая грань будет прямоугольником. И лицо будет в одной плоскости. Мы также знаем, что прямоугольники имеют четыре угла по 90 градусов. Следовательно, мы можем дать ответ в форме утверждения о том, что можно сказать о двух заданных отрезках прямой, так это то, что они перпендикулярны.
Мы также знаем, что прямоугольники имеют четыре угла по 90 градусов. Следовательно, мы можем дать ответ в форме утверждения о том, что можно сказать о двух заданных отрезках прямой, так это то, что они перпендикулярны.
Во второй части этого вопроса мы рассматриваем отрезки 𝐴𝐸 и 𝐶𝐺. Эти два отрезка лежат на противоположных гранях прямоугольной призмы. Мы знаем, что они не пересекаются, и мы знаем, что они не перпендикулярны. На самом деле эти два отрезка параллельны. На данный момент это может сбить с толку, поскольку мы знаем, что они находятся на противоположных гранях. Ну почему же мы не говорим, что эти две линии косые? И ответ заключается в том, что на самом деле мы можем сказать, что все эти четыре точки лежат в одной плоскости, плоскости, которая проходит через точки 𝐴, 𝐶, 𝐺 и 𝐸. Так как эти два отрезка лежат в одной плоскости и они параллельны, то мы даем ответ, что они параллельны.
В третьей части этого вопроса спрашивается, что можно сказать об отрезке 𝐵𝐷 и отрезке 𝐷𝐻? Мы знаем, что отрезок 𝐵𝐷 и отрезок 𝐷𝐻 — это отрезки, расположенные на перпендикулярных гранях призмы. И они пересекаются в точке 𝐷. Следовательно, отрезок 𝐵𝐷 и отрезок 𝐷𝐻 должны быть перпендикулярны.
И они пересекаются в точке 𝐷. Следовательно, отрезок 𝐵𝐷 и отрезок 𝐷𝐻 должны быть перпендикулярны.
В последней части этого вопроса нас спрашивают об отрезке 𝐵𝐷 и отрезке 𝐴𝐶. Обратите внимание, что отрезка 𝐴𝐶 не было на исходной диаграмме, но мы можем добавить его. Конечно, мы можем видеть, что эти два отрезка на самом деле образуют диагонали граней этого прямоугольного параллелепипеда. Тогда мы также можем сказать, что эти два отрезка лежат в одной плоскости. Мы знаем, что эти два отрезка не будут параллельны, и они были бы перпендикулярны только в том случае, если бы грань была квадратной. Но так как нам дано в вопросе, что сторона 𝐴𝐵 не равна 𝐵𝐶, то мы знаем, что это прямоугольник.
Поскольку два отрезка лежат в одной плоскости, они не будут перекошены. Следовательно, мы можем дать ответ на заключительную часть этого вопроса, что они не параллельны и не перпендикулярны.
Наклонные линии — определение, значение, формула, примеры
Наклонные линии — это пара прямых, которые не пересекаются и не параллельны друг другу. Наклонные линии могут существовать только в измерениях выше 2D-пространства. Они должны быть некомпланарными, что означает, что такие линии существуют в разных плоскостях. В двухмерном пространстве две линии могут быть как пересекающимися, так и параллельными друг другу. Таким образом, в двумерном пространстве никогда не может существовать косых линий.
Наклонные линии могут существовать только в измерениях выше 2D-пространства. Они должны быть некомпланарными, что означает, что такие линии существуют в разных плоскостях. В двухмерном пространстве две линии могут быть как пересекающимися, так и параллельными друг другу. Таким образом, в двумерном пространстве никогда не может существовать косых линий.
Перекосные линии можно встретить во многих реальных ситуациях. Предположим, есть линия на стене и линия на потолке. Если эти прямые не параллельны друг другу и не пересекаются, то они могут быть косыми, так как лежат в разных плоскостях. Эти линии бесконечно продолжаются в двух направлениях. В этой статье мы узнаем больше о косых линиях, их примерах и о том, как найти кратчайшее расстояние между ними.
| 1. | Что такое наклонные линии? |
| 2. | Наклонные линии в 3D |
| 3. | Формула наклонных линий |
4. | Расстояние между наклонными линиями |
| 5. | Часто задаваемые вопросы о наклонных линиях |
Что такое наклонные линии?
Прежде чем изучать наклонные линии, нам нужно знать три других типа линий. Они даны следующим образом:
- Пересекающиеся линии. Если две или более линий пересекаются друг с другом в определенной точке и лежат в одной плоскости, то они называются пересекающимися линиями.
- Параллельные линии. Если две линии никогда не пересекаются, даже если они бесконечно расширены, и лежат в одной плоскости, то они называются параллельными линиями.
- Копланарные линии — Копланарные линии лежат в одной плоскости.
Наклонные линии Определение
Наклонные линии — это пара непересекающихся, непараллельных и некомпланарных линий. Это означает, что косые линии никогда не могут пересекаться и не параллельны друг другу. Чтобы линии существовали в двух измерениях или в одной плоскости, они могут быть либо пересекающимися, либо параллельными. Поскольку это свойство не относится к наклонным линиям, следовательно, они всегда будут некомпланарными и существуют в трех или более измерениях.
Поскольку это свойство не относится к наклонным линиям, следовательно, они всегда будут некомпланарными и существуют в трех или более измерениях.
Наклонные линии Пример
В реальной жизни у нас могут быть разные типы дорог, например шоссе и эстакады в городе. Эти дороги считаются лежащими в разных плоскостях. Линии, проведенные на таких дорогах, никогда не пересекаются и не параллельны друг другу, образуя косые линии.
Наклонные линии в 3D
Наклонные линии всегда будут существовать в трехмерном пространстве, поскольку эти линии обязательно не компланарны. Предположим, у нас есть трехмерная твердая форма, как показано ниже. Нарисуем одну линию на треугольной грани и назовем ее «а». Мы также рисуем одну линию на четырехугольной грани и называем ее «b». И a, и b не лежат в одной плоскости. Если мы продолжим «а» и «b» бесконечно в обоих направлениях, они никогда не пересекутся и не параллельны друг другу. Таким образом, «a» и «b» являются примерами наклонных линий в 3D. В трехмерном пространстве, если есть небольшое отклонение параллельных или пересекающихся линий, это, скорее всего, приведет к перекосу линий.
В трехмерном пространстве, если есть небольшое отклонение параллельных или пересекающихся линий, это, скорее всего, приведет к перекосу линий.
Наклонные линии в кубе
Куб является примером объемной формы, существующей в трех измерениях. Чтобы найти косые линии в кубе, мы делаем три шага.
- Шаг 1: Найдите линии, которые не пересекаются друг с другом.
- Шаг 2: Проверьте, не параллельны ли эти пары линий.
- Шаг 3: Затем проверьте, являются ли эти непересекающиеся и непараллельные линии некомпланарными. Если да, то выбранная пара прямых является косой линией.
Предположим, у нас есть куб, как показано ниже:
Мы видим, что прямые CD и GF не пересекаются и не параллельны. Кроме того, они не лежат в одной плоскости. Таким образом, CD и GF — косые прямые.
Диагонали сплошных фигур также могут быть включены при поиске наклонных линий.
Формула наклонных линий
В двумерном пространстве нет скрещивающихся линий.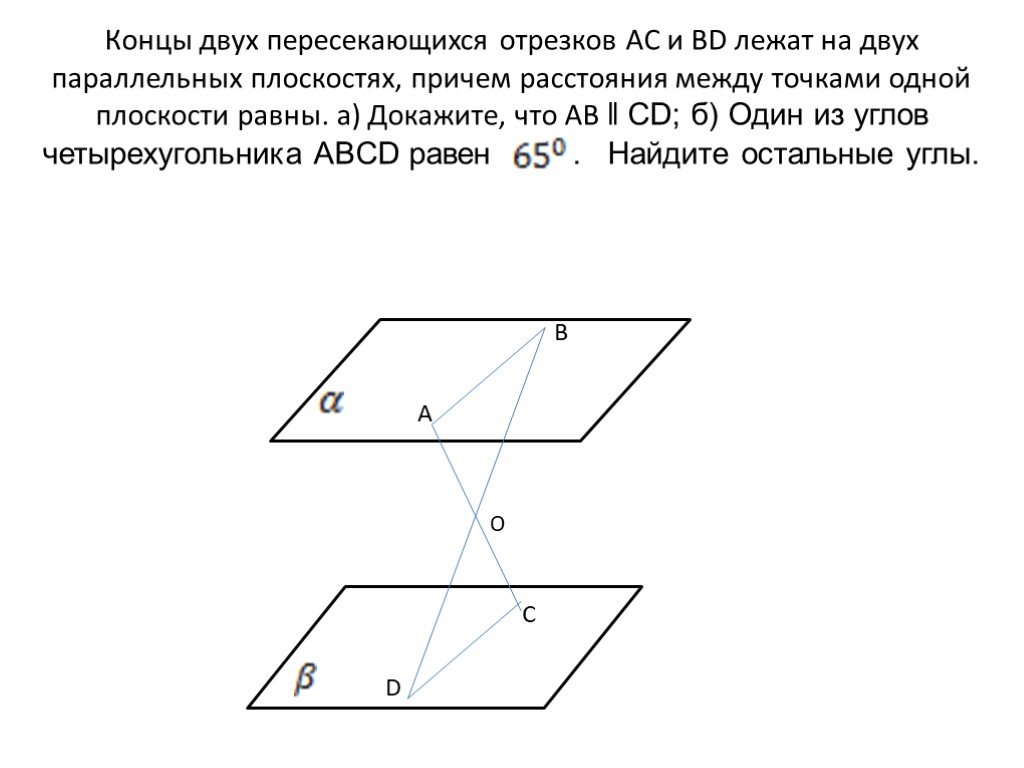 В трех измерениях у нас есть формулы для нахождения кратчайшего расстояния между наклонными линиями с использованием векторного метода и декартова метода. Чтобы определить угол между двумя наклонными линиями, процесс немного сложен, поскольку эти линии не параллельны и никогда не пересекаются друг с другом.
В трех измерениях у нас есть формулы для нахождения кратчайшего расстояния между наклонными линиями с использованием векторного метода и декартова метода. Чтобы определить угол между двумя наклонными линиями, процесс немного сложен, поскольку эти линии не параллельны и никогда не пересекаются друг с другом.
Угол между двумя наклонными линиями
Предположим, у нас есть две наклонные линии PQ и RS. Возьмите точку O на RS и проведите из этой точки линию, параллельную PQ, с именем OT. Угол SOT даст меру угла между двумя наклонными линиями.
Расстояние между наклонными линиями Формула
Чтобы найти расстояние между двумя наклонными линиями, мы должны провести линию, перпендикулярную этим двум линиям. Мы можем представить эти прямые в декартовой и векторной форме, чтобы получить различные формы формулы для кратчайшего расстояния между двумя выбранными наклонными прямыми.
Допустим, у нас есть две линии сдвига P1 и P2. Мы изучим методы нахождения расстояния между двумя наклонными линиями в следующем разделе.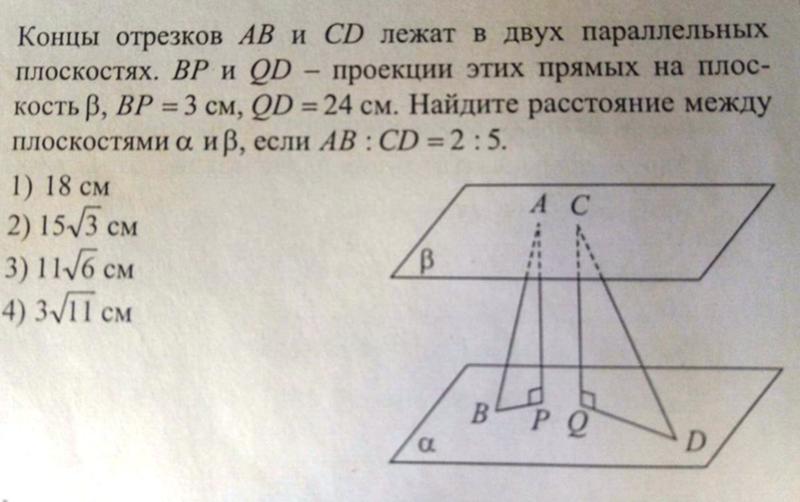
Векторная форма P1: \(\overrightarrow{l_{1}} = \overrightarrow{m_{1}} + t.\overrightarrow{n_{1}}\)
Векторная форма P2: \(\overrightarrow{l_{2}} = \overrightarrow{m_{2}} + t.\overrightarrow{n_{2}}\)
Здесь E = \(\overrightarrow{m_{1}} \) — точка на прямой P1, а F = \(\overrightarrow{m_{2}}\) — точка на P2. \(\overrightarrow{m_{2}}\) — \(\overrightarrow{m_{1}}\) — вектор из E в F. Здесь \(\overrightarrow{n_{1}}\) и \( \overrightarrow{n_{2}}\) представляют направление линий P1 и P2 соответственно. t — значение действительного числа, определяющего положение точки на прямой. Единичный вектор нормали к P1 и P2 задается как:
n = \(\frac{\overrightarrow{n_{1}}\times\overrightarrow{n_{2}}}{|\overrightarrow{n_{1}}\times\overrightarrow{n_{2}}|} \)
Кратчайшее расстояние между P1 и P2 есть проекция EF на эту нормаль. Таким образом, это дается как
d = |\(\frac{(\overrightarrow{n_{1}}\times\overrightarrow{n_{2}})(\overrightarrow{m_{2}}-\overrightarrow{m_ {1}})}{|\overrightarrow{n_{1}}\times\overrightarrow{n_{2}}|}\)|
Декартова форма
Рассмотрим симметричные уравнения прямых P1 и P2, чтобы найти кратчайшее расстояние между ними. {1/2}}\)
{1/2}}\)
Расстояние между наклонными линиями
Расстояние между наклонными линиями можно определить, проведя линию, перпендикулярную обеим линиям. Мы можем использовать вышеупомянутые векторные и декартовы формулы, чтобы найти расстояние.
Расстояние между двумя наклонными линиями
В зависимости от типа приведенных уравнений мы можем применить любую из двух формул расстояния, чтобы найти расстояние между двумя наклонными линиями. Мы можем использовать параметрические уравнения линии или симметричные уравнения, чтобы найти расстояние.
Кратчайшее расстояние между двумя наклонными линиями
Кратчайшее расстояние между двумя наклонными линиями определяется линией, перпендикулярной этим двум линиям, а не любой линией, соединяющей обе наклонные линии.
Векторное уравнение задается следующим образом: d = |\(\frac{(\overrightarrow{n_{1}}\times\overrightarrow{n_{2}})(\overrightarrow{a_{2}}-\overrightarrow{a_ {1}})}{|\overrightarrow{n_{1}}\times\overrightarrow{n_{2}}|}\)| используется, когда линии представлены параметрическими уравнениями 9{1/2}}\) используется, когда линии обозначаются симметричными уравнениями.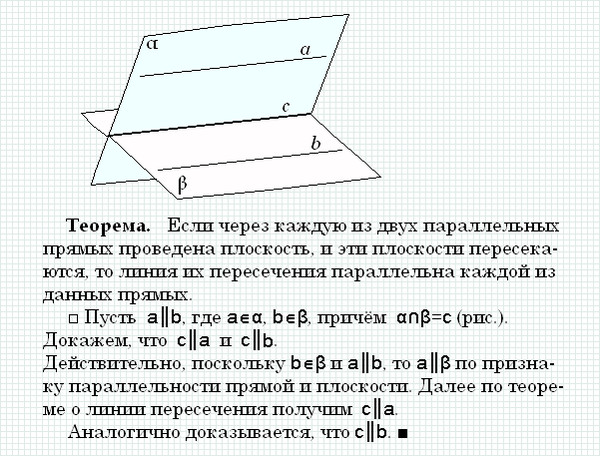
- Векторное перекрестное произведение
- Определение плоскости
- 3D-фигуры
Важные замечания по наклонным линиям
- Непересекающиеся, непараллельные и некомпланарные прямые являются наклонными.
- Наклонные линии могут существовать только в трех или более измерениях. Таким образом, у нас не может быть косых линий в двумерном пространстве.
- Формула для расчета кратчайшего расстояния между наклонными линиями может быть представлена как в векторной, так и в декартовой форме.
Часто задаваемые вопросы о наклонных линиях
Что такое наклонные линии с примерами?
В трехмерном пространстве, если есть две прямые линии, которые не параллельны и не пересекаются, а также лежат в разных плоскостях, они образуют наклонных линий . Примером может служить брусчатка перед домом, проходящая по его длине и диагонали на крыше того же дома.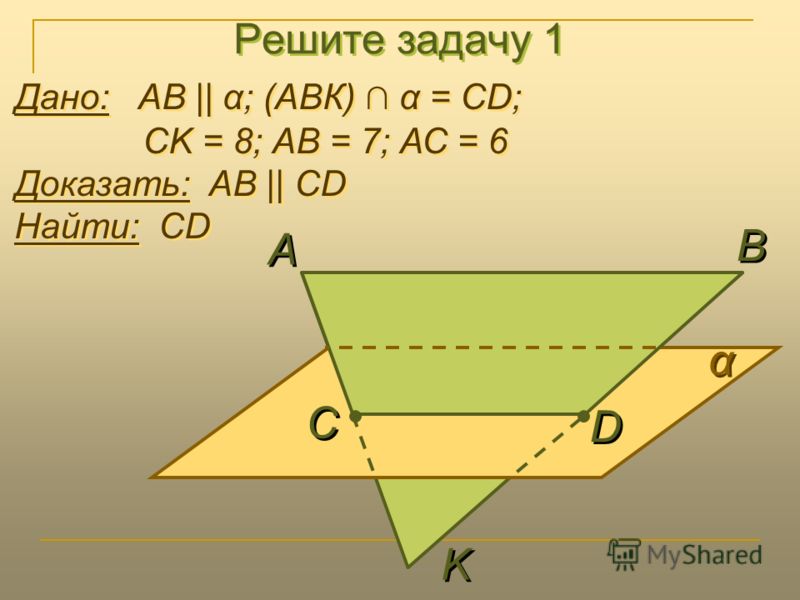
Являются ли параллельные линии наклонными линиями?
Согласно определению, наклонные линии не могут быть параллельными, пересекающимися или лежащими в одной плоскости. Таким образом, параллельные прямые не являются скрещивающимися.
Наклонные линии равноудалены?
Поскольку косые прямые не параллельны друг другу, то, даже если они не пересекаются ни в одной точке, они не будут равноудалены друг от друга.
Наклонные линии не компланарны?
Прямые, лежащие в одной плоскости, могут быть параллельны друг другу или пересекаться в одной точке. Таким образом, чтобы две прямые можно было классифицировать как наклонные, они должны быть непересекающимися и непараллельными. Как следствие, косые линии всегда некомпланарны.
Как найти наклонную линию?
Сначала мы проверяем, лежат ли заданные линии в трехмерном пространстве. Далее проверяем, параллельны ли они друг другу. Если они не параллельны, мы определяем, пересекаются ли эти две прямые в любой заданной точке.

 Знайдіть довжину невідомого відрізка x .
( Найдите длину неизвестного отрезка x )
Знайдіть довжину невідомого відрізка x .
( Найдите длину неизвестного отрезка x )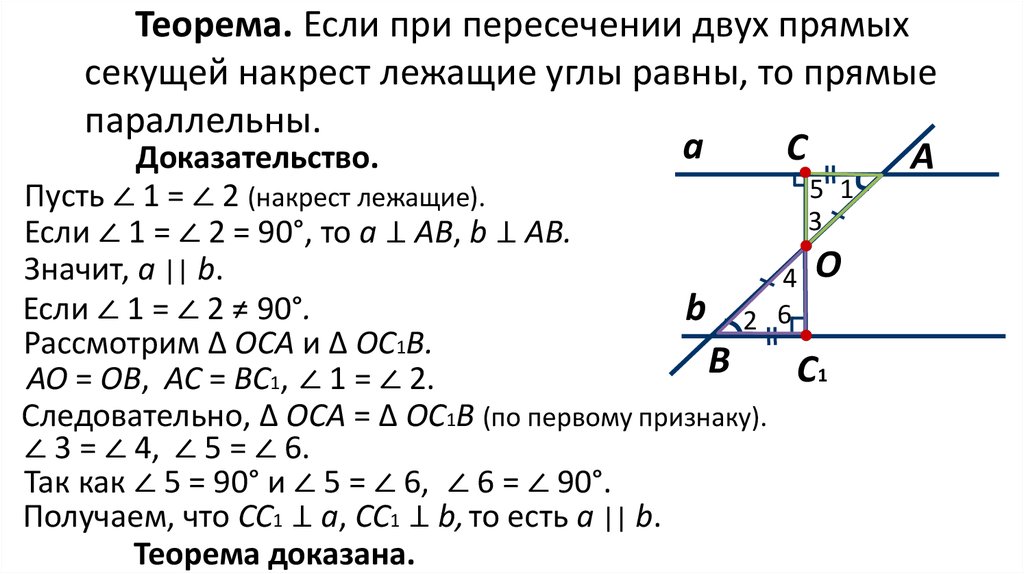 пожалуйста
пожалуйста Знайдіть зовнішній кут трикутника при вершині С.СРОЧНООО
Знайдіть зовнішній кут трикутника при вершині С.СРОЧНООО Докажите, что плоскость, проходящая через середины AD, BD и CD, параллельна плоскости ABC.
Докажите, что плоскость, проходящая через середины AD, BD и CD, параллельна плоскости ABC. При этом каждый из этих отрезков делится точкой пересечения пополам.
При этом каждый из этих отрезков делится точкой пересечения пополам. Пусть плоскости ABE и CDE пересекаются по прямой l, а плоскости BCE и ADE — по прямой p. Найдите угол между прямыми l и p.
Пусть плоскости ABE и CDE пересекаются по прямой l, а плоскости BCE и ADE — по прямой p. Найдите угол между прямыми l и p.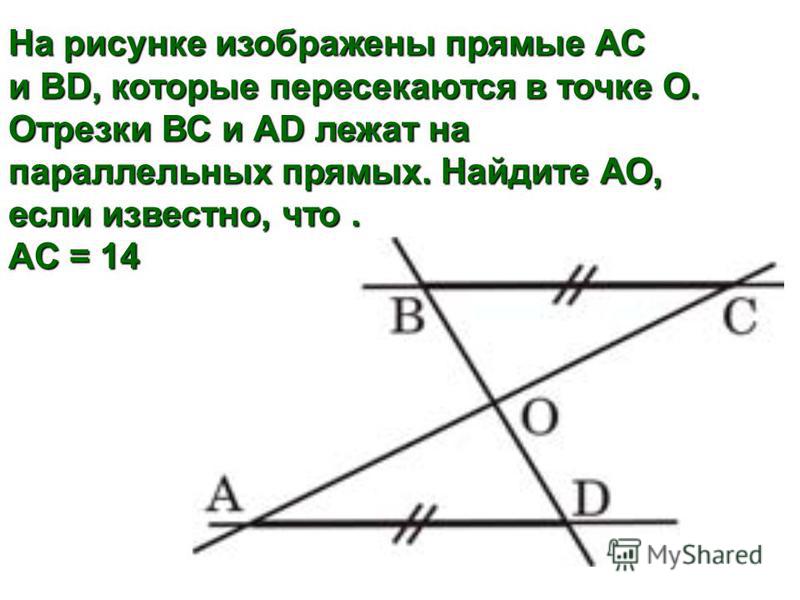 Известно, что параллелепипед — это шестигранник, ограниченный тремя парами параллельных плоскостей. Покажите, что если сечение параллелепипеда плоскостью является многоугольником с числом сторон, большим трёх, то у этого многоугольника есть параллельные стороны.
Известно, что параллелепипед — это шестигранник, ограниченный тремя парами параллельных плоскостей. Покажите, что если сечение параллелепипеда плоскостью является многоугольником с числом сторон, большим трёх, то у этого многоугольника есть параллельные стороны. 23
23
Leave A Comment