Задание №7 ЕГЭ по математике профильного уровня

Производная и первообразные функции

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

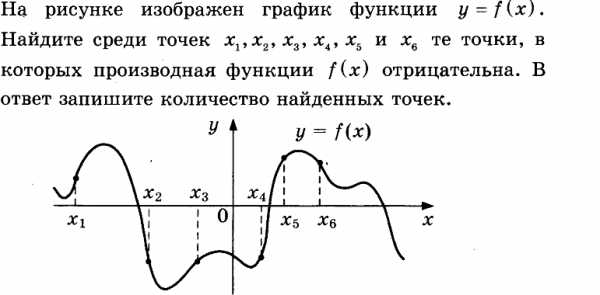
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

Алгоритм решения:
  1. Рассматриваем график функции.
  2. Ищем точки, в которых функция убывает.
  3. Подсчитываем их количество.
  4. Записываем ответ.
Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x3, x4, x5, x9. Таких точек 4.

Ответ: 4.

Второй вариант задания (из Ященко, №4)

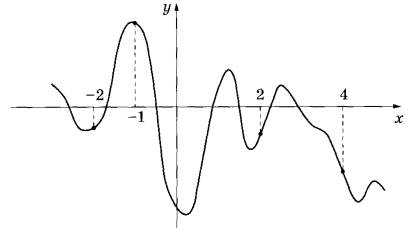
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Алгоритм решения:
  1. Рассматриваем график функции.
  2. Рассматриваем поведение функции в каждой из точек и знак производной в них.
  3. Находим точки в наибольшим значением производной.
  4. Записываем ответ.
Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

Третий вариант задания (из Ященко, №21)

Прямая  является касательной к графику функции . Найдите а.

Алгоритм решения:
  1. Приравняем уравнения касательной и функции.
  2. Упрощаем полученное равенство.
  3. Находим дискриминант.
  4. Определяем параметр а, при котором решение единственное.
  5. Записываем ответ.
Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

 

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:

Ответ: 4.

spadilo.ru

Разбор задания № 7 по математике ЕГЭ профильный уровень.

Автор Багменова Т. А. учитель математики МБОУ СОШ № 14 г. Новочеркасска Ростовской области.

При решении заданий на применение производной при подготовке к ЕГЭ встречается большое разнообразие заданий, что наталкивает на необходимость разбить задания на группы сопроводив теоретическим материалом по теме «Производная».

Хочу поделиться моими наработками при подготовке учащихся к решению задания №7 профильного уровня.

Рассмотрим примеры заданий № 7 по теме «Производная» профильного уровня по математике, разбив их на группы.

1. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если производная функции больше нуля для всех x принадлежащих [a;b], то функция возрастает на [a;b], а если производная функции меньше нуля, то она убывает на этом отрезке.

Примеры:

1)

Решение.

В точках и точках функция убывает, следовательно производная функции в этих точках отрицательна.

Ответ: 2.

2)

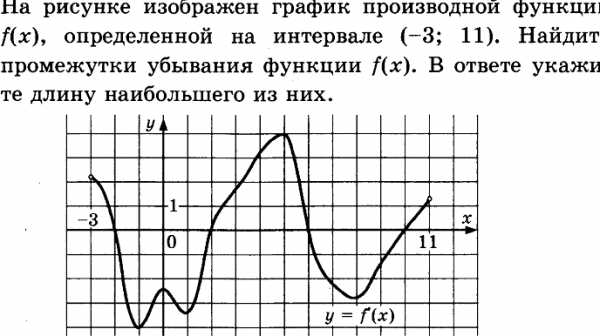
Решение.

На промежутках (-2;2), (6;10) производная функции отрицательна, следовательна функция на этих промежутках убывает. Длина и того и другого промежутка 4.

Ответ: 4.

3)

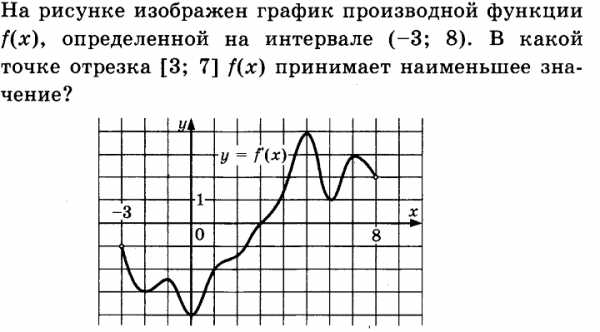
Решение.

На отрезке [3;7] производная функции положительна, следовательна функция на этом промежутке возрастает, следовательно наименьшее значение функция принимает в точке 3.

Ответ: 3.

4)

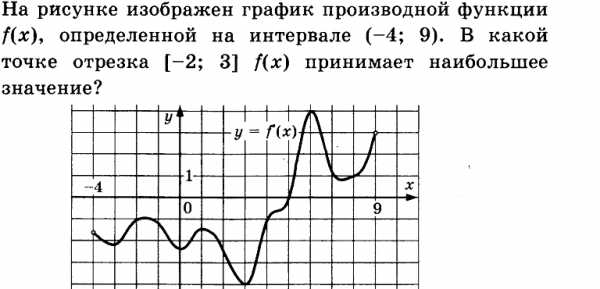
Решение.

На отрезке [-2;3] производная функции отрицательна, следовательна функция на этом промежутке убывает, следовательно наибольшее значение функция принимает в точке -2.

Ответ: -2.

2. Если в точке производная функции меняется знак с «-» на «+», то это точка минимума функции; если в точке производная функции меняется знак с «+» на «-», то это точка максимума функции.

Пример:

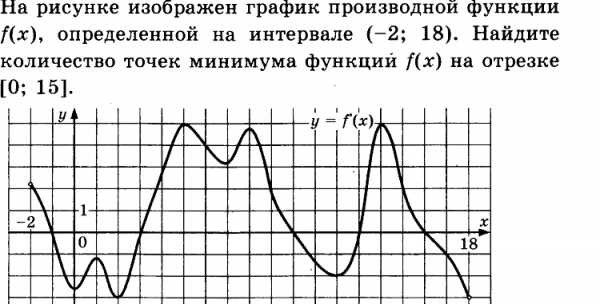
Решение.

В точке х=3; х=13 производная функции меняется знак с «-» на «+», следовательно это точки минимума функции.

Ответ: 2.

3. Условие(x)=0 является необходимым условием экстремума дифференцируемой функции f(x). Так как в точках пересечения графика производной функции с осью Ох производная функции равна нулю, то данные точки являются точками экстремума.

Пример:

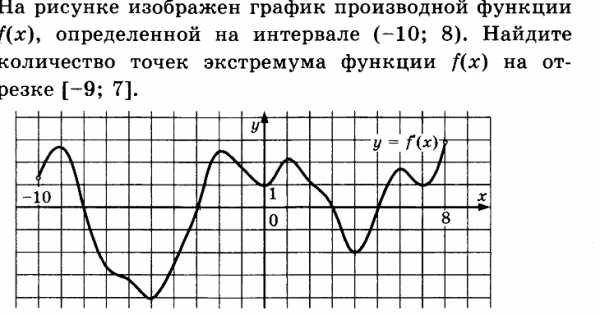
Решение.

Точек пересечения графика производной функции с осью Ох на заданном отрезке 4, следовательно точек экстремума 4.

Ответ: 4.

4. Производная функции равна нулю в точках экстремума функции. В данной задаче это точки где функция переходит с возрастания на убывания или наоборот.

Пример:

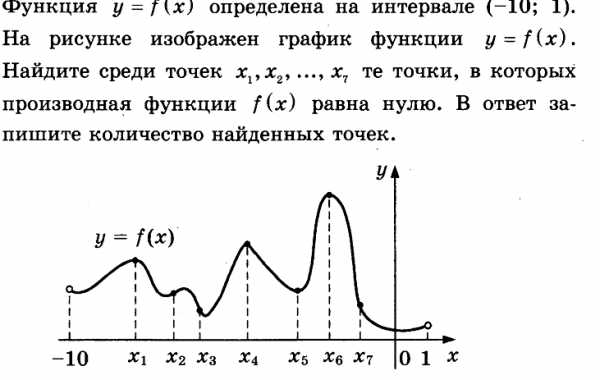
Решение.

В точках производная равна нулю.

Ответ: 4.

5. Найти значение производной функции в точке , это значит найти тангенс угла наклона касательной к оси Ох или к прямой параллельной оси Ох. Если угол наклона касательной к оси Ох острый, то тангенс угла положительный, если угол наклона касательной к оси Ох тупой, то тангенс угла отрицательный.

Пример:

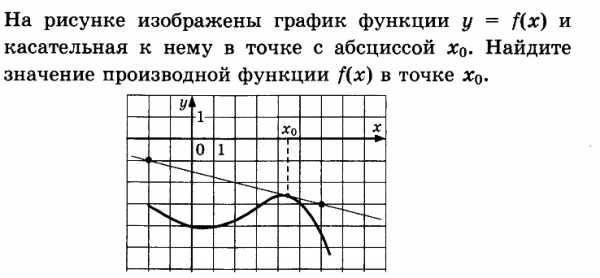
Решение.

Построим прямоугольный треугольник, у которого гипотенуза будет лежать на касательной, а один из катетов лежит на оси Ох или на прямой параллельной оси Ох, затем посчитаем длины катетов и вычислим тангенс острого угла прямоугольного треугольника. Противолежащий катет равен 2, прилежащий катет равен 8, следовательно тангенс острого угла прямоугольного треугольника равен 0,25. Угол наклона касательной к оси Ох тупой, следовательно тангенс угла наклона касасательной отрицательный, следовательно значение производной функции в точке равно -0,25.

Ответ: — 0,25.

6. 1) Угловые коэффициенты параллельных прямых равны.

2) Значение производной функции f(

x) в точке равно угловому коэффициенту касательной к графику функции y= f(x) в точке (; f()).

Пример.

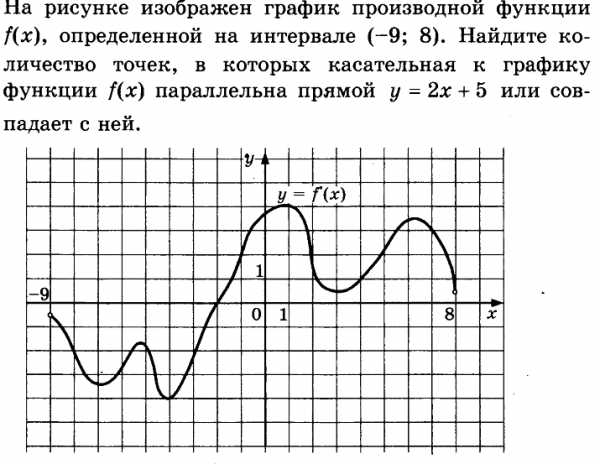
Решение.

Угловой коэффициент прямой равен 2. Так как значение производной функции f(x) в точке равно угловому коэффициенту касательной к графику функции y= f(x) в точке (;f()), то найдем точки, в которых производная функции f(x) равна 2. Таких точек на данном графике 4. Следовательно количество точек в которых касательная к графику функции f(x) параллельна данной прямой или совпадает с ней равно 4.

Ответ: 4.

Используемая литература:

  1. Колягин Ю. М., Ткачева М. В., Федорова Н. Е. и др. Алгебра и начала математического анализа (базовый и углубленный уровень). 10 кл. – Просвещение. 2014 г.

  2. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровень. Под редакцией И. В. Ященко.- М.: Издательство «Экзамен»,-2016.-640с.

infourok.ru

Тест 7 задание ЕГЭ 2019 математика профильный уровень.

Седьмое задание ЕГЭ 2018 математика

Лимит времени: 0

Информация

Седьмое задание ЕГЭ 2018 математика

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 6

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

  • Мастера это люди, и ты тоже человек, и,если ты хочешь стать таким же как они, ты уже на пути к этому.

Ваш результат был записан в таблицу лидеров
  1. С ответом
  2. С отметкой о просмотре

matematikaprosta.ru

Материал для подготовки к ЕГЭ (ГИА) по математике (11 класс) на тему: Задание №7 (часть 1) ЕГЭ Профильный уровень | скачать бесплатно

По теме: методические разработки, презентации и конспекты

Материалы для подготовки к ЕГЭ ( профильный уровень, задание 9)

Представлены материалы для подготовки к ЕГЭ (профильный уровень ) заданий на вычисление объема и площади поверности различных многогранников….

Задание №19 (ЕГЭ профильный уровень)

Карточка с заданиями типа №19 (ЕГЭ профильный уровень)…

ЕГЭ – 2017. №1 — 5. Профильный уровень. Задания для проведения зачетов и ответы.

Зачеты  определяют  готовность выпускников к сдаче ЕГЭ профильного уровня в заданиях тестовой части.Зачеты составлены по всем возможным прототипам с использованием заданий сайта Дмитрия Гущи…

Теория для решения заданий №1 — №12 профильный уровень ЕГЭ

Данный материал служит основой для отработки навыков решения заданий №1 — №12 профильного уровня ЕГЭ…

Разработка методических рекомендаций по подготовке учащихся к заданиям №9, №13 КИМ ЕГЭ (профильный уровень)

В работе даны методические рекомендации по подготовке учащихся к заданиям №9, №13 КИМ ЕГЭ (профильный уровень). Также представлены планы-конспекты трех уроков: «Числовая окружность», «П…

Математический тренажер Подготовка к ЕГЭ (профильный уровень) Модуль «Начала математического анализа» Задание 9.

Подготовка к ЕГЭ (профильный уровень)Модуль «Начала математического анализа»Задание 9….

ЕГЭ Профильный уровень. Задание 8.

Карточки-задания по материалам Открытого банка ЕГЭ по математике. Профильный уровень….

nsportal.ru