Числовая окружность. Запись чисел числовой окружности
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Числовая окружность.Запись чисел числовой окружности 10 классУчитель математики Ковалева И.И. + – 0;2П; 4П.- 2П; -4П. П -11П6 6 П -7П4 4 П -5П3 3 2П -4П 3 3 3П -4П 4 3 5П -7П 6 6 7П -5П 6 6 5П -3П 4 4 4П -2П 3 3 5П -П 3 3 7П -П 4 4 11П -П 6 6 9П 25П 2 П 2 9П 2 5П 2 П 2 11П 27П 2 3П 2 11П 2 7П 2 3П 2 5П;3П; П.-5П;-3П;- П. X y 0 y X 0 P0 Pt α 1. Запись чисел, соответствующих однойточке единичной окружностиЧислу t соответствует точка P Pt t+2πn, n ∈ Z α +2πn, n ∈ Z y X 0 P0 Pt α Pt+п 2. Запись чисел, соответствующих двумдиаметрально противоположным точкамединичной окружности t+πn, n ∈ Z α +πn, n ∈ Z y X 0 P0 Pt α P-t 3. Запись чисел, соответствующих двумточкам на единичной окружности с одинаковыми абсциссами ±α+2πn, n ∈ Z 4. Запись чисел, соответствующих двумточкам на единичной окружности с одинаковыми ординатами y X 0 P0 Pt α PП-t α+2πn, n ∈ Z π- α+2πn, n ∈ Z (-1)ⁿα + πn, n ∊ или y X 0 P0 Pt α P2 P3 P4 P5 4. Запись чисел, соответствующих точкам делящим окружность на n равных частей X y 0 Щелкая по окружности:1) найдите точки, соответствующие числам …2) найдите значения тригонометрических функций при этих значениях…3) определите знаки тригонометрических функций при этих значениях…… 0 y X 5П 6 1 4 3,14 -П -1 П 2 П10 +2Пk, k Z (-1)k П 4 +Пg, g Z П 3 +2Пn, n Z П 6 + П 3 m, m Z Найдите точки, соответствующие следующим числам 0 y X -П+2П k, k Z П 3 +2Пn, n Z 1 4 2Пm, m Z П ( + m), m Z 2П 3 +2Пn, n Z П 2 +2Пn, n Z П 2 +2Пn, n Z 1 3 П( +2l ),l Z Найдите точки, соответствующие следующим числам X y 0 Щелкая по окружности , запишите двойные неравенства, соответствующие дугам 0 y X П m 4 П 4 П k 2 3П 4 П x= , m Z x= + ,k Z Найдите все точки, соответствующие данной совокупности 0 y П 2 П 2 X П 2 П 3 2П 3 2П 3 x≠ +Пk, k Z x ≠ k, k Z x= t, t Z x= + m, m Z x= n, n Z Найдите все точки, соответствующие данным системам 1.
Приложенные файлы
Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.
Начальная точка числовой окружности \(A\) совмещена с точкой \((1;0)\).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
Точка Mπ4 — середина \(I\) четверти. Опустим перпендикуляр \(MP\) на прямую \(OA\) и рассмотрим треугольник \(OMP\). Так как дуга \(AM\) составляет половину дуги \(AB\), то ∡MOP=45°.
Значит, треугольник \( OMP \) — равнобедренный прямоугольный треугольник и \(OP = MP\), т. е. у точки \(M\) абсцисса и ордината равны: \(x = y\).
Так как координаты точки \(M(x;y)\) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений: x2+y2=1x=y |
Подставив \(x\) вместо \(y\) в первое уравнение системы, получим следующее решение:
x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π4, будут Mπ4=M22;22.
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
| \(0\) | π4 | π2 | 3π4 | π | 5π4 | 3π2 | 7π4 | 2π |
Абсцисса \(x\) | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) | 22 | \(1\) |
Ордината \(y\) | \(0\) | 22 | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) |
Рассуждаем аналогично для точки \(M\), если теперь она соответствует числу π6.
Треугольник \(MOP\) прямоугольный. Так как дуга \(AM\) составляет третью часть дуги \(AB\), то ∡MOP=30°.
Катет \(MP\) лежит против угла \(30\) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки \(M\) равна MP=12;y=12 |
Абсциссу \(x\) точки \(M\) найдём, решив уравнение:
x2+y2=1;
x2=1−122=1−14=34;x=32.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π6, будут Mπ6=M32;12.
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
π6 | π3 | 2π3 | 5π6 | 7π6 | 4π3 | 5π3 | 11π6 | |
Абсцисса \(x\) | 32 | 12 | −12 | −32 | −32 | −12 | 12 | 32 |
Ордината \(y\) | 12 | 32 | 32 | 12 | −12 | −32 | −32 | −12 |
Тестирование
В качестве ответа введите обозначение соответствующей точки из показанных на числовой окружности.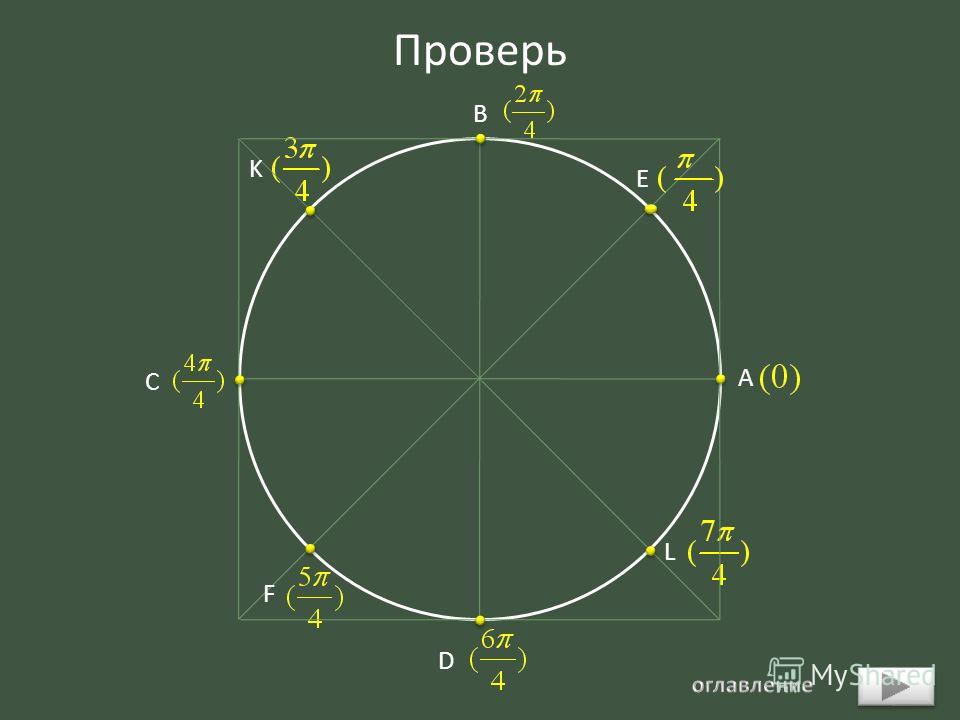
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:π
Ответ:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Ответ:
Числовая окружность | План-конспект занятия по алгебре (9 класс) на тему:
ТЕХНОЛОГИЧЕСКАЯ КАРТА ЗАНЯТИЯ
ФИО преподавателя Коровина Нина Анатольевна
по дисциплине ОДП 01. Математика
Математика
Наименование темы (согласно КТП, журнала)
Числовая окружность
Тип занятия: комбинированный.
Цель: ввести понятие числовой окружности как модели криволинейной системы координат.
Задачи: формировать умение использовать числовую окружность при решении задач.
Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.
Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.
Планируемые результаты:
Знать, понимать: — числовая окружность.
Уметь: — находить на окружности точки по заданным координатам; — находить координаты точки, расположенной на числовой окружности.
Уметь применять изученный теоретический материал при выполнении письменной работы.
образовательные технологии: используются элементы технологий: ИКТ, проблемного обучения, здоровьесберегающей, сотрудничества.
МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ:
Технические средства обучения: компьютер, интерактивная доска.
Наглядные пособия: компьютерная презентация.
Раздаточный материал: Карточки-задания для письменного опроса, карандаши, линейки.
ПЛАН ЗАНЯТИЯ (структура, содержание и хронометраж):
№ п/п | Структурные элементы занятия, их содержание, формы и методы их проведения | Время (мин) | ||||||||||||||||||||
1 | Организационный момент. Преподаватель здоровается, отмечает отсутствующих, мотивирует обучающихся, решить 18 примеров что бы узнать тему занятия. Обучающиеся записывают в тетради число и составляют из ответов тему занятия, дежурные раздают комплекты раздаточного материала. Форма: фронтальная. Методы: объяснительно-иллюстративные; вводная и организующая беседа. | 5 | ||||||||||||||||||||
2 | Актуализация ранее изученного материала. Преподаватель ; Ребята, отнеситесь к изучению темы очень внимательно, поскольку, как показывает опыт, обучающиеся, хорошо овладевший понятием «числовая окружность», достаточно уверенно обращается и с тригонометрическими функциями. Зачем нам нужна тригонометрия? Восход и заход солнца, изменение фаз луны, чередование времен года, биение сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы — модели этих многообразных процессов описываются тригонометрическими функциями. Звук, электрический ток, радиоволны так же представляют собой колебания различной частоты и амплитуды. Если бы зрение людей обладало способностью видеть звуковые, электромагнитные и радиоволны, то мы видели бы вокруг многочисленные синусоиды всевозможных видов. Таким образом многие процессы происходящие в природе и технических системах описываются тригонометрическими функциями, которые служат основой их математических моделей. Итак начнем! Устная работа. 1. Поставьте каждому промежутку на числовой прямой в соответствие неравенство и аналитическую запись интервала. Данные занесите в табличку. А (– ; –5] Д (–5; 5) Б [–5; 5] Е ( – ; –5) В [–5; + ) Ж [–5; 5) Г (–5; 5] З (–5; + ) 1 –5 2 х 3 –5 4 х –5 Форма: фронтальный опрос. Методы: контрольно-коррекционная беседа; демонстрация слайдов презентации. | 15 10 | ||||||||||||||||||||
3 | Презентация Тригонометрия | 7 | ||||||||||||||||||||
4 | Изучение нового учебного материала. Преподаватель: Что называется числовой прямой? Обучающиеся: Это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. -: Сколько действительных чисел можно поставить в соответствие каждой точке числовой прямой? -: Каждой точке соответствует только одно действительное число. — То есть числовая прямая – это взаимно однозначное соответствие между всеми точками прямой и всеми действительными числами. -Что называется окружностью? — Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки. — Как найти длину окружности? -: Длина окружности равна :L=2 пr. -: А что такое пи? -: Пи — математическая константа, выражающая отношение длины окружности к длине её диаметра. Эта константа приближенно равна 3,14. -: Чему будет равна L при R=1. -: L=2П или 6,28. -: Отметьте на числовой прямой точки П и 2П. Преподаватель В отличие от изученной числовой прямой числовая окружность является более сложной моделью. В реальной жизни приходится двигаться не только по прямой, но и по окружности. В принципе любую окружность можно рассматривать как числовую, но удобнее всего использовать для этой цели единичную окружность — окружность радиусом 1. Исходя из основной формулы длины окружности при радиусе равном 1 получаем длину единичной окружности равной 2П, что составляет примерно 6,28. Соответственно половина длины окружности равна П, четверть П/2 и три четверти окружности равны 3П/2. На числовой окружности принято условно называть дугу от 0 до П/2 первой четвертью, дугу от П/2 до П – второй четвертью, от П до 3П/2 3 четвертью и от 3П/2 до 2П 4-й четвертью. При этом, как правило, речь идет об открытых дугах, т.е. о дугах без их концов: например, первая четверть — это дуга от 0 до П/2, без точек 0 и П/2. Рассмотрим следующее определение. Преподаватель: Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам. И самое главное необходимо запомнить что положительное значение откладывается против часовой стрелки , а отрицательное по часовой стрелке Форма: фронтальная. Методы: объяснительно-иллюстративные; проблемное изложение; беседа сообщения новых знаний, демонстрация слайдов презентации. | 8/15 | ||||||||||||||||||||
5 | Физкультминутка (видеофайл Суперфизкультминутка.exe). | 3 | ||||||||||||||||||||
6 7 | 4. Закрепление знаний, умений и навыков. Заполните пропуски! Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам. Единичной окружностью называют окружность радиуса 1. Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти. Их соответственно называют первой, второй, третьей и четвертой четвертью. Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0). Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки. Горизонтальный диаметр соответствует оси x, вертикальный – оси y. Значения x и y в четвертях числовой окружности:
Закрепление учебного материала. Проверочная работа. Вариант 1 1. Обозначьте на числовой окружности точку, которая соответствует данному числу: 2. Найдите все числа, которым соответствуют отмеченные на числовой окружности
Вариант 2 1. Обозначьте на числовой окружности точку, которая соответствует данному числу: 2. Найдите все числа, которым соответствуют отмеченные на числовой окружности точки. Обучающиеся решают задачи в индивидуальном темпе, консультируются с друг другом и преподавателем. Взаимопроверяют друг друга. К доске решать задачи выходят желающие. Форма: индивидуальная и парная. Методы: репродуктивные. | 18 | ||||||||||||||||||||
8 | Контроль правильности понимания нового материала. Преподаватель: Молодцы ребята, очень хорошо потрудились, хорошо решали задачи, внимательно слушали и принимали активное участие. Давайте подведем итоги. В начале урока мы задали следующие вопросы. 1) Что называется числовой окружностью? 2) Как найти точки на числовой окружности, соответствующие заданным числам? 3) Как выделять на числовой окружности дугу соответствующую заданному интервалу. 4) Как по заданной дуге записывать аналитическое выражение. Теперь вы можете ответить на них. Преподаватель объявляет, что оценки за проверочную работу он объявит на следующем занятии. Сообщает критерии оценивания по набранным баллам. Обучающиеся выполняют задания на отдельных листах, которые по окончании времени сдают преподавателю. Форма: индивидуальная. Методы: репродуктивные. | 5 | ||||||||||||||||||||
9 | Подведение итогов. Рефлексия. Продолжите фразы: — сегодня на занятии я узнал … — сегодня на занятии я научился… — сегодня на занятии я повторил… — сегодня на занятии я познакомился… — сегодня на занятии мне понравилось Преподаватель объявляет занятие оконченным; прощается. Форма: фронтальная. Методы: синтезирующая и закрепляющая беседа; рефлексия. | 4 |
Подпись преподавателя ____________________
Приложение 1
А) (– ; –5] Д) (–5; 5)
Б) [–5; 5] Е) ( – ; –5)
В) [–5; + ) Ж) [–5; 5)
Г) (–5; 5] З) (–5; + )
1) –5
2) х
3) –5
4) х –5
Приложение 2
Преподаватель: Что называется числовой прямой?
Обучающиеся: Это прямая, на которой заданы начальная точка О, масштаб
(единичный отрезок) и положительное направление.
-: Сколько действительных чисел можно поставить в соответствие каждой точке
числовой прямой?
-: Каждой точке соответствует только одно действительное число.
— То есть числовая прямая – это взаимно однозначное соответствие между всеми
точками прямой и всеми действительными числами.
-Что называется окружностью?
— Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки.
— Как найти длину окружности?
-: Длина окружности равна :L=2 пr.
-: А что такое пи?
-: Пи — математическая константа, выражающая отношение длины
окружности к длине её диаметра. Эта константа приближенно равна 3,14.
-: Чему будет равна L при R=1.
-: L=2П или 6,28.
-: Отметьте на числовой прямой точки П и 2П.
Преподаватель В отличие от изученной числовой прямой числовая окружность
является более сложной моделью. В реальной жизни приходится двигаться не
только по прямой, но и по окружности.
В принципе любую окружность можно рассматривать как числовую, но удобнее всего использовать для этой цели единичную окружность — окружность радиусом 1.
Исходя из основной формулы длины окружности при радиусе равном 1 получаем
длину единичной окружности равной 2П, что составляет примерно 6,28.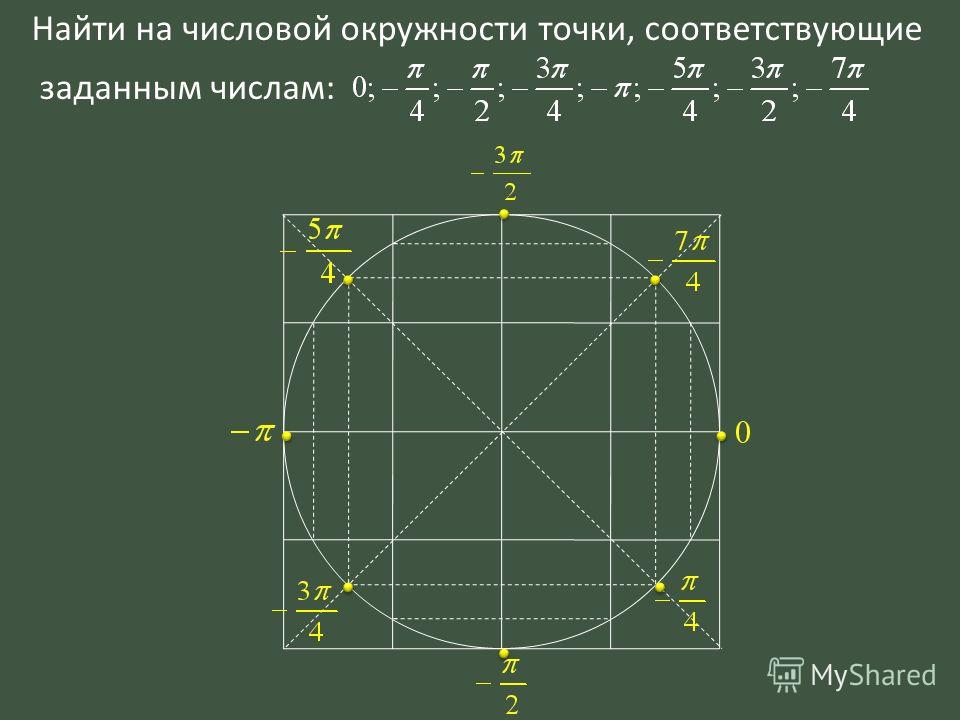
Соответственно половина длины окружности равна П, четверть П/2 и три четверти
окружности равны 3П/2.
Приложение 3
Заполните пропуски!
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным _____________.
Единичной окружностью называют окружность радиуса ________.
Горизонтальный и ______________ диаметры делят числовую окружность
на четыре четверти.
Их соответственно называют первой, ___________________ четвертью.
Начальная точка А числовой окружности находится на оси x и имеет координаты ________.
Отсчет по числовой окружности может вестись как по часовой ___________, так и против часовой стрелки.
Центр радиуса числовой окружности соответствует ___________координат. Горизонтальный диаметр соответствует оси ____, вертикальный – оси ______.
Значения x и y в четвертях числовой окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
x > 0, y > 0 | x 0 | x | ______________ |
| | | |
|
|
| |
|
|
| |
| _________ |
|
Приложение 4
Проверочная работа.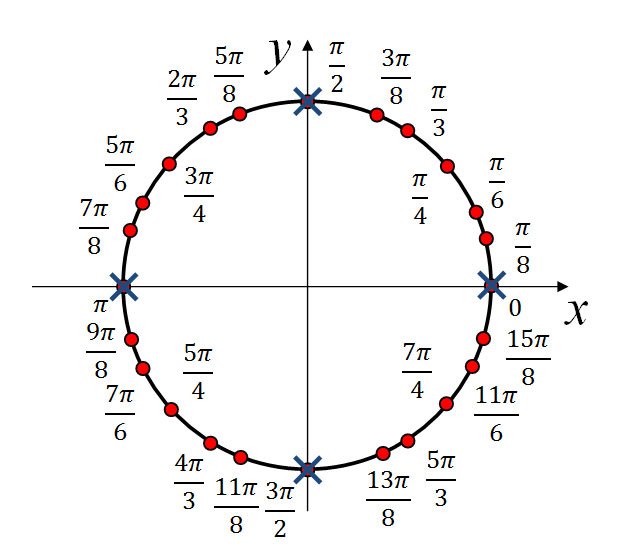 2 = 1, \\ x = y. \end {cases}$
2 = 1, \\ x = y. \end {cases}$
Решив данную систему, получаем: $y = x =\frac{\sqrt{2}}{2}$.
Значит, координаты точки M, соответствующей числу $\frac{π}{4}$, будут $M(\frac{π}{4})=M(\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2})$.
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности
Рассмотрим примеры
Пример 1.
Найти координату точки числовой окружности: $Р(45\frac{π}{4})$.
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
Значит, числу $45\frac{π}{4}$ соответствует та же точка числовой окружности, что и числу $\frac{5π}{4}$. Посмотрев значение точки $\frac{5π}{4}$ в таблице, получаем: $P(\frac{45π}{4})=P(-\frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2})$.
Пример 2.
Найти координату точки числовой окружности: $Р(-\frac{37π}{3})$.
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$-\frac{37π}{3} = -(12 + \frac{1}{3})*π = -12π –\frac{π}{3} = -\frac{π}{3} + 2π*(-6)$.
Значит, числу $-\frac{37π}{3}$ соответствует та же точка числовой окружности, что и числу $–\frac{π}{3}$, а числу –$\frac{π}{3}$ соответствует та же точка, что и $\frac{5π}{3}$. Посмотрев значение точки $\frac{5π}{3}$ в таблице, получаем:
Пример 3.
Найти на числовой окружности точки с ординатой $у =\frac{1}{2}$ и записать, каким числам $t$ они соответствуют?
Решение:
Прямая $у =\frac{1}{2}$ пересекает числовую окружность в точках М и Р. Точка М соответствует числу $\frac{π}{6}$ (из данных таблицы). Значит, и любому числу вида: $\frac{π}{6}+2π*k$. Точка Р соответствует числу $\frac{5π}{6}$, а значит, и любому числу вида $\frac{5π}{6} +2 π*k$.
Получили, как часто говорят в таких случаях, две серии значений:
Ответ : $t=\frac{π}{6} +2 π*k$ и $t=\frac{5π}{6} +2π*k$.
Пример 4.
Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{2}}{2}$ и записать, каким числам $t$ они соответствуют.
Решение:
Прямая $x =-\frac{\sqrt{2}}{2}$ пересекает числовую окружность в точках М и Р. Неравенству $x≥-\frac{\sqrt{2}}{2}$ соответствуют точки дуги РМ. Точка М соответствует числу $3\frac{π}{4}$ (из данных таблицы). Значит, и любому числу вида $-\frac{3π}{4} +2π*k$. Точка Р соответствует числу $-\frac{3π}{4}$, а значит, и любому числу вида $-\frac{3π}{4} +2π*k$.
Тогда получим $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Ответ : $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Задачи для самостоятельного решения
1) Найти координату точки числовой окружности: $Р(\frac{61π}{6})$.
2) Найти координату точки числовой окружности: $Р(-\frac{52π}{3})$.
3) Найти на числовой окружности точки с ординатой $у = -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
4) Найти на числовой окружности точки с ординатой $у ≥ -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
5) Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{3}}{2}$ и записать, каким числам $t$ они соответствуют.
БИЛЕТ 10. ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ — Студопедия
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значенияxиyв четвертях числовой окружности:
| 1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
| x > 0, y > 0 | x < 0, y > 0 | x < 0, y < 0 | x > 0, y < 0 |
Каждой точке числовой окружности соответствует бесконечное множество чисел
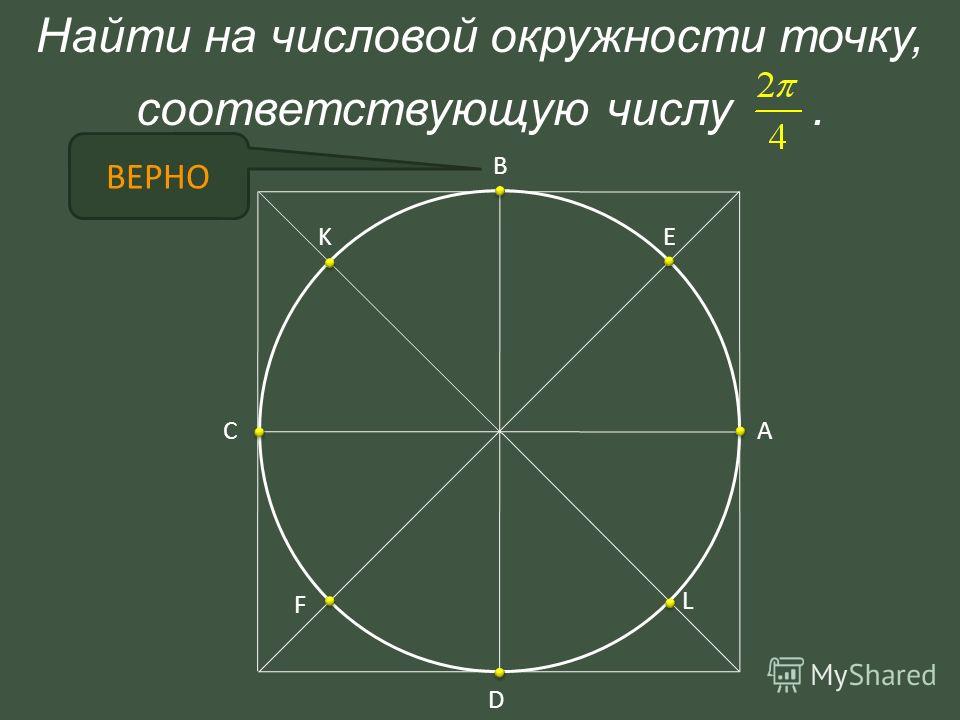 Которые отличаются друг от друга на целое число оборотов 2П.
Которые отличаются друг от друга на целое число оборотов 2П.M(t)=M(t+2Пn), где n — целое число.
Уравнение числовой окружности:
x2 + y2 = 1
Числовые модели
Первый рисунок
Каждая из четырех четвертей числовой окружности разделена на две равные части.
Второй рисунок
Каждая из четырех четвертей числовой окружности разделена на три равные части.(Что бы разделить четверть на три равные части, нужно разделить радиусы пополам, и провести перпендикуляры до пересечения с окружностью.)
Каждой точке на окружности соответствует бесконечное множество чисел.
Пример:
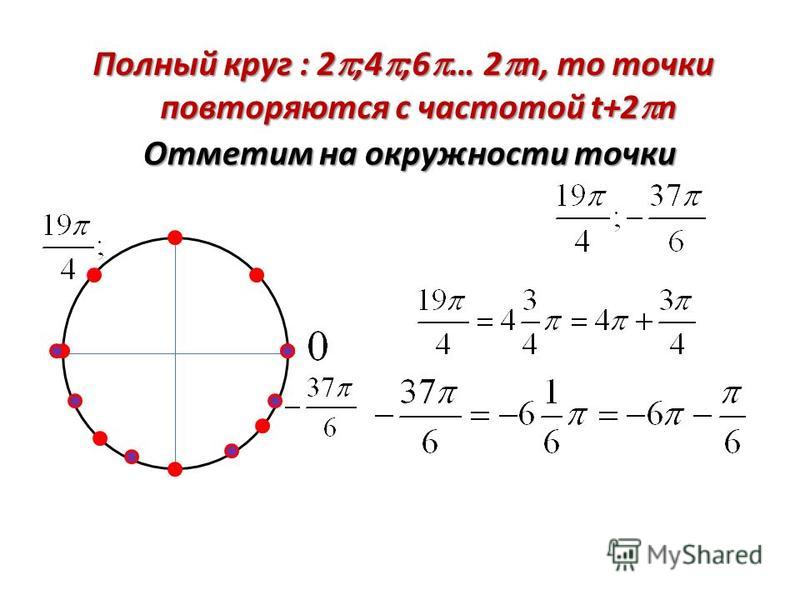
Найти на числовой окружности число 58П/3.
Выделим целую часть: 58П/3=18П+4П/3(18П — это 9 полных оборотов, т.е ты попадаем в точку 0, значит на числовой прямой откладываем число 4П/3).
Основные точки:
1.
2.
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
| 1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть | |
| cos t | + | – | – | + |
| sin t | + | + | – | – |
| tg t, ctg t | + | – | + | – |
Математика для блондинок: Где на окружности находится…
Сегодня мы посмотрим на крысиные бега в математике. Где на окружности находится 7пи/2? Очень интересный вопрос. Подобные вопросы любят задавать злобные математики. Точнее, их это заставляет делать учебная программа, составленная по сочинениям безмозглых математиков. Почему безмозглых? Измерять вращение математиков никто не научил, а собственные мозги у них отсутствуют. Вот математики и носятся со своими «пи», как дурни со ступой.
Вот математики и носятся со своими «пи», как дурни со ступой.Один полный оборот математики обозначают как 2 пи. Что это значит? Вот вы стоите перед входом в школу. Поворачиваетесь на минус 90 градусов (что равно минус пи/2), то есть по часовой стрелке, и бежите вокруг школы в положительном направлении (против часовой стрелки). Когда вы снова окажетесь напротив школьного входа, значит вы пробежали угол величиной в 2 пи. Если вы повернетесь на плюс 90 градусов (что равно плюс пи/2) и побежите в противоположном направлении, вы пробежите угол в минус 2 пи. Сколько бы кругов вы не наматывали вокруг школы, вы всегда будете попадать в ту же точку, с которой начинались ваши крысиные бега. Почему бега называют крысиными? Наверное потому, что сколько не бегай, а никуда не убежишь.
| План эвакуации |
Но вернемся к нашей задаче. Как узнать, где на окружности находится 7 пи, деленное пополам? Для начала, нужно выбросить всю дурь не только с головы, но и со значения угла. Если размер дури в других науках определить довольно проблематично, то в математике она имеет вполне конкретное выражение — два пи или 360 градусов. Вот их и нужно выбросить из наших 7пи/2. Вспоминаем вычитание дробей. Чтобы зловредная буква пи нам не мешала, вынесем её за скобки.
| Вычисление угла |
 Сколько бы дури размером в 2 пи (360 градусов) не содержалось в наших углах, всю её необходимо выбросить. Это обычный математический мусор, который, как святыню, хранят церковно-приходские математики.
Сколько бы дури размером в 2 пи (360 градусов) не содержалось в наших углах, всю её необходимо выбросить. Это обычный математический мусор, который, как святыню, хранят церковно-приходские математики.После сокращения угла можно взять окружность и показать на ней точку, соответствующую углу в 3/2 пи.
| Окружность градусов и радиан |
Не следует забывать, что «пи» — это не единица измерения радиан, а загадочное число 3,1415… Угол в 3/2 пи равен 4,7122… радиан. По умолчанию, математики не пишут возле значения угла единицу измерения «радиан». Чем всех нас запутывают и сами путаются.
Кстати, на сокращении дробей построены пропорции. На сокращении углов такой фокус не возможен — на идиотизме пропорцию не построишь.
Орбитальные диаграммы Учебное пособие по химии
Орбитальные диаграммы для элементов периода 1
Принцип Ауфбау говорит нам, что атомы элементов периода 1 заполняют первый энергетический уровень (K-оболочку), который состоит всего из одной s-орбитали.
Максимальное количество электронов, которые могут занимать орбиталь, равно 2.
Когда 2 электрона занимают одну и ту же орбиталь, мы применяем принцип исключения Паули, так что один электрон имеет квантовое число спина (m s ) & plus; ½ (спин вверх, ↑ или ↿), а другой электрон имеет квантовое число спина ( м с ) −½ (вращение вниз, ↓ или ⇂).
Водород: атомный номер (Z) = 1.
Принцип Ауфбау: всего 1 электрон занимает s-орбиталь энергетического уровня 1 st (K-оболочка).
электронная конфигурация (оболочки): 1
электронная конфигурация (суб-оболочки): 1с 1
Орбитальная диаграмма(диаграмма орбитального ящика): только один электрон занимает один ящик
Гелий: атомный номер (Z) = 2
Принцип Ауфбау: 2 электрона, занимающие одну s-орбиталь энергетического уровня 1 st (K-оболочка)
электронная конфигурация (оболочки): 2
электронная конфигурация (суб-оболочки): 1с 2
Орбитальная диаграмма (диаграмма орбитального ящика): примените принцип исключения Паули так, чтобы один электрон имел вращение, противоположное другому (один «вверх» и один «вниз»).
Орбитальные диаграммы для элементов периода 2
Принцип Ауфбау говорит нам, что первый энергетический уровень (K-оболочка), содержащий 1s-орбиталь, был заполнен последним элементом Периода 1, гелием [He].
Таким образом, каждый элемент Периода 2 начинает построение на этой завершенной орбите 1 с (1 с 2 ).
Орбитальная диаграмма для каждого элемента Периода 2 будет начинаться с прямоугольника, занятого двумя стрелками (одна вверх, одна вниз), представляющими завершенную орбиталь за 1с (1с 2 ).
Затем
электронов добавляются ко второму энергетическому уровню (L-оболочка), который состоит из одной s-орбитали и 3 p-орбиталей (p x , p y , p z ).
элементов «s block» заполняют s-орбиталь, элементы «p-block» заполнили s-орбиталь и добавляют электроны к p-орбиталям.
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов на p-орбиталях, то есть электроны будут занимать p-орбитали по отдельности, пока на каждой p-орбитали не будет 1 электрон, после чего мы должны начать спаривать электроны в p-орбиталях. орбитали.
Максимальное количество электронов, которые могут занимать орбиталь, равно 2.
Когда 2 электрона занимают одну и ту же орбиталь, мы применяем принцип исключения Паули, так что один электрон имеет квантовое число спина (m s ) & plus; ½ (спин вверх, ↑ или ↿), а другой электрон имеет квантовое число спина ( м с ) −½ (вращение вниз, ↓ или ⇂).
Литий: атомный номер (Z) = 3 (элемент блока s)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), третий электрон занимает s-орбиталь второго энергетического уровня (L-оболочка).
электронная конфигурация (оболочки): 2,1
электронная конфигурация (суб-оболочки): 1с 2 2с 1
конфигурация конденсированных электронов: [He] 2s 1
Орбитальная диаграмма(диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как указано выше для гелия), в поле 2s есть 1 стрелка
Бериллий: атомный номер (Z) = 4 (блочный элемент s)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), третий и четвертый электроны занимают s-орбиталь второго энергетического уровня (L-оболочка).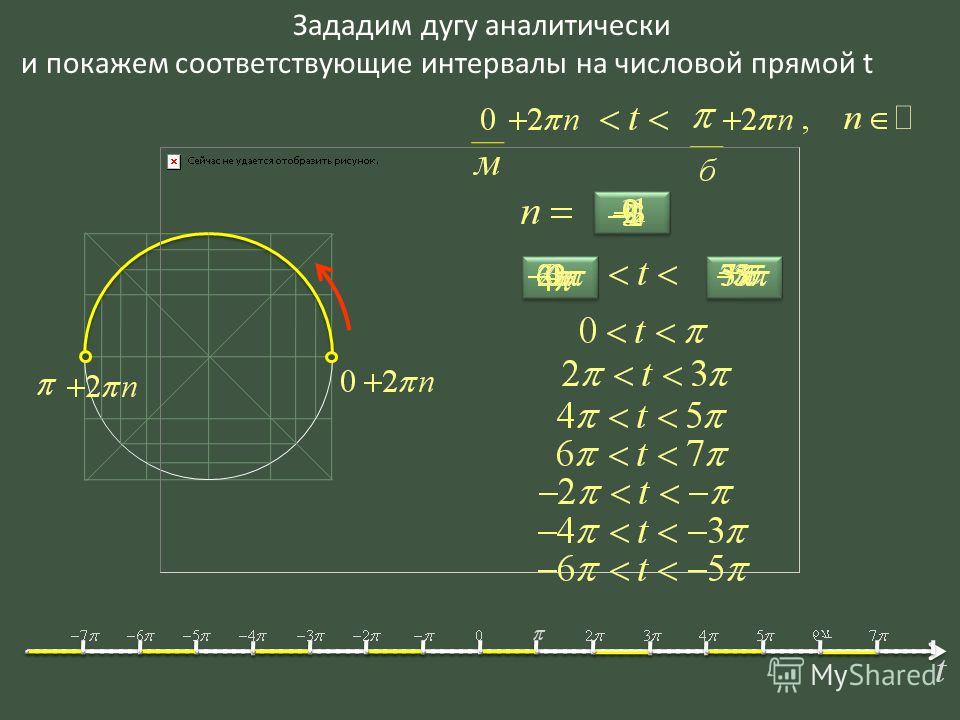
электронная конфигурация (оболочки): 2,2
электронная конфигурация (суб-оболочки): 1с 2 2с 2
конфигурация конденсированных электронов: [He] 2s 2
Орбитальная диаграмма(диаграмма орбитального ящика): в ячейке 1s есть 2 стрелки (как для гелия выше), в ячейке 2s есть 2 стрелки, поэтому мы применяем принцип исключения Паули, так что один электрон «вращается вверх», а другой — «вниз».
| ↑ ↓ | ↑ ↓ | |
| 1с | 2с |
Бор: атомный номер (Z) = 5 (элемент блока p)
Принцип Aufbau: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 3 электрона занимают второй энергетический уровень (L-оболочка), 2 электрона на 2s-орбитали, как для бора выше, но 5 -й электрон занимает p подоболочка второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,3
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 1
конфигурация конденсированных электронов: [He] 2s 2 2p 1
Орбитальная диаграмма(диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как для гелия выше), в поле 2s есть 2 стрелки, как для бора выше, но теперь мы видим, что есть 3 орбитали, которые составляют p-подоболочку (стр. x , p y , p z ), и в один из них помещаем стрелку 5 th
| ↑ ↓ | ↑ ↓ | ↑ | ||||
| 1с | 2с | 2p x | 2п л | 2p z |
Углерод: атомный номер (Z) = 6 (элемент блока p)
Принцип Aufbau: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 4 электрона занимают второй энергетический уровень (L-оболочка), 2 электрона на 2s-орбитали, как для бора выше, но 5 th и 6 th электронов занимают p-подоболочку второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,4
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 2
конфигурация конденсированных электронов: [He] 2s 2 2p 2
Орбитальная диаграмма (диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как указано выше для гелия), в поле 2s есть 2 стрелки, как для бора выше, но теперь мы видим, что есть 3 орбитали, которые составляют p-подоболочку (стр. x , p y , p z ), в которые нам нужно поместить 2 стрелки.Итак, мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов на всех 2p-орбиталях, и придаем этим электронам параллельный спин (стрелки указывают в одном направлении):
x , p y , p z ), в которые нам нужно поместить 2 стрелки.Итак, мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов на всех 2p-орбиталях, и придаем этим электронам параллельный спин (стрелки указывают в одном направлении):
| ↑ ↓ | ↑ ↓ | ↑ | ↑ | |||
| 1с | 2с | 2p x | 2п л | 2p z |
Азот: атомный номер (Z) = 7 (элемент p-блока)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 5 электронов занимают второй энергетический уровень (L-оболочка), 2 из этих электронов находятся на 2s-орбитали, как указано выше для бора, но 5 th , 6 -й и 7 -й электронов занимают p-подоболочку второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,5
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 3
конфигурация конденсированных электронов: [He] 2s 2 2p 3
Орбитальная диаграмма(диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как указано выше для гелия), в поле 2s есть 2 стрелки, как для бора выше, но теперь мы видим, что есть 3 орбитали, которые составляют p-подоболочку (стр. x , p y , p z ), в которые нам нужно поместить 3 стрелки.Итак, мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов на всех 2p-орбиталях, и придаем этим электронам параллельный спин (стрелки указывают в одном направлении):
| ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ||
| 1с | 2с | 2p x | 2п л | 2p z |
Кислород: атомный номер (Z) = 8 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 6 электронов занимают второй энергетический уровень (L-оболочка), 2 из этих электронов находятся на 2s-орбитали, как для бора выше, но 5 th , 6 th , 7 th и 8 th электронов занимают подоболочку p второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,6
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 4
конфигурация конденсированных электронов: [He] 2s 2 2p 4
Орбитальная диаграмма (диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как для гелия выше), в поле 2s есть 2 стрелки, как для бора выше, но теперь мы видим, что есть 3 орбитали, которые составляют p-подоболочку (стр. x , p y , p z ), в которые нам нужно поместить 4 стрелки.
x , p y , p z ), в которые нам нужно поместить 4 стрелки.
Итак, мы применяем правило Хунда, чтобы максимально увеличить количество неспаренных электронов на всех 2p-орбиталях, и неспаренные электроны будут иметь параллельный спин.
Это означает, что в одном из ящиков будет пара электронов.
Примените принцип исключения Паули к спаренным электронам так, чтобы один электрон имел «спин вверх», а другой — «спин вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ||
| 1с | 2с | 2p x | 2п л | 2p z |
Фтор: атомный номер (Z) = 9 (элемент блока p)
Принцип Aufbau: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 7 электронов занимают второй энергетический уровень (L-оболочка), 2 из этих электронов находятся на 2s-орбитали, как для бора выше, но 5 th , 6 th , 7 th , 8 th и 9 th электроны занимают подоболочку p второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,7
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 5
конфигурация конденсированных электронов: [He] 2s 2 2p 5
Орбитальная диаграмма (диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как для гелия выше), в поле 2s есть 2 стрелки, как для бора выше, но теперь нам нужно поместить 5 стрелок в 3 орбитали, которые составляют p-подоболочку (p x , p y , p z ).
Примените правило Хунда, чтобы максимизировать количество неспаренных электронов на всех 2p-орбиталях, что означает, что пара электронов будет находиться в двух коробках p-подоболочки.
Примените принцип исключения Паули к спаренным электронам в каждом ящике так, чтобы один электрон вращался вверх, а другой — вниз.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ||
| 1с | 2с | 2p x | 2п л | 2p z |
Neon: атомный номер (Z) = 10 (элемент блока p)
Принцип Aufbau: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают второй энергетический уровень (L-оболочка), 2 из этих электронов находятся на 2s-орбитали, как для бора выше, но 5 th , 6 th , 7 th , 8 th , 9 th и 10 th электронов занимают подоболочку p второго энергетического уровня (L-оболочка)
электронная конфигурация (оболочки): 2,8
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6
конфигурация конденсированных электронов: [He] 2s 2 2p 6
Орбитальная диаграмма (диаграмма орбитального ящика): в поле 1s есть 2 стрелки (как для гелия выше), в поле 2s есть 2 стрелки, как для бора выше, но теперь нам нужно разместить 6 стрелок на 3 орбиталях, которые составляют p-подоболочку (p x , p y , p z ).
Каждая p-орбиталь (p x , p y и p z ) будет занята парой электронов.
Примените принцип исключения Паули к спаренным электронам в каждом ящике так, чтобы один электрон вращался вверх, а другой — вниз.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ||
| 1с | 2с | 2p x | 2п л | 2p z |
Орбитальные диаграммы для элементов периода 3
Электронная конфигурация атомов всех элементов Периода 3 начинается с завершенного энергетического уровня 1 st и 2 nd (заполненные оболочки K и L), то есть с электронной конфигурации последнего элемента Периода 2, Благородный газ неон, [Ne].
Валентные электроны (электроны внешней оболочки или электроны наивысшего энергетического уровня) начинают занимать энергетический уровень 3 rd (M-оболочка).
Третий энергетический уровень (M-оболочка) элементов Периода 3 состоит из одной s-орбитали и 3 p-орбиталей (p x , p y , p z ).
элементов «s-блока» заполняют s-орбиталь, p-элементные блоки заполнили s-орбиталь и добавляют электроны к p-орбиталям.
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов на p-орбиталях, то есть электроны будут занимать p-орбитали по отдельности, пока на каждой p-орбитали не будет 1 электрон, после чего мы должны начать спаривать электроны в p-орбиталях. орбитали.
Максимальное количество электронов, которые могут занимать орбиталь, равно 2.
Когда 2 электрона занимают одну и ту же орбиталь, мы применяем принцип исключения Паули, так что один электрон имеет квантовое число спина (m s ) & plus; ½ (спин вверх, ↑ или ↿), а другой электрон имеет квантовое число спина ( м с ) −½ (вращение вниз, ↓ или ⇂).
Натрий: атомный номер (Z) = 11 (элемент блока s)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 1 электрон занимает третий энергетический уровень (M-оболочка) на s-орбитали.
электронная конфигурация (оболочки): 2,8,1
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 1
конфигурация конденсированных электронов: [Ne] 3s 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z , причем 1 электрон помещается в ячейку 3s
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | |||
| 1с | 2с | 2p x | 2п л | 2p z | 3с |
Магний: атомный номер (Z) = 12 (элемент блока)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 2 электрона занимают третий энергетический уровень (M-оболочка) на s-орбитали.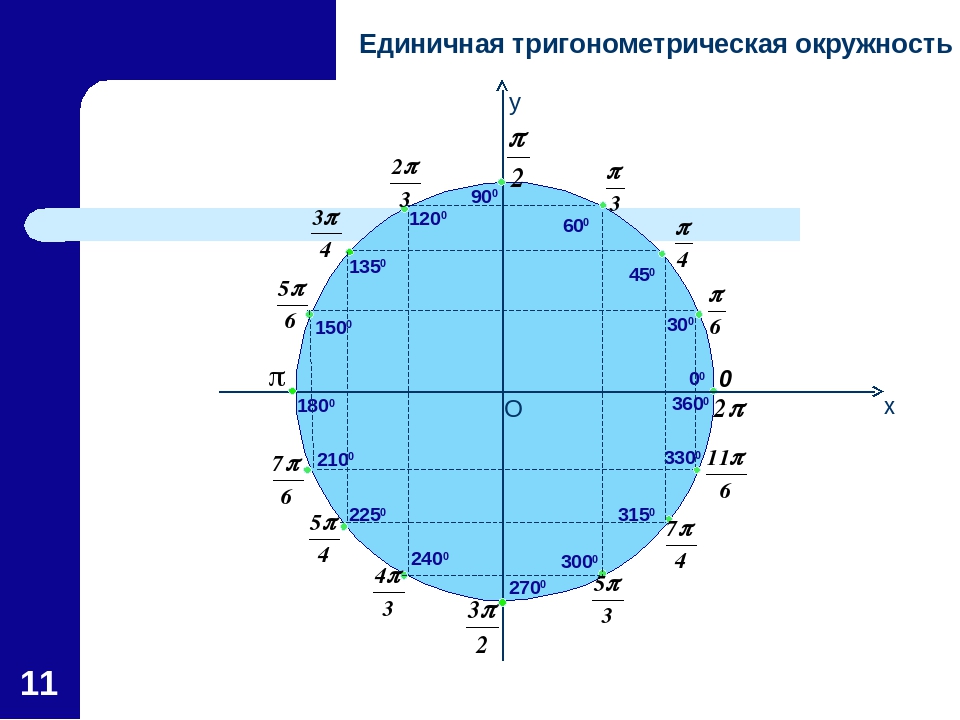
электронная конфигурация (оболочки): 2,8,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2
конфигурация конденсированных электронов: [Ne] 3s 2
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z , причем 2 электрона помещаются в ячейку 3s
Примените принцип исключения Паули так, чтобы для парных электронов один электрон имел «вращение вверх», а другой — «спин вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | |||
| 1с | 2с | 2p x | 2п л | 2p z | 3с |
Алюминий: атомный номер (Z) = 13 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 3 электрона занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали. и электрон 3 rd на одной из 3 доступных p-орбиталей (p x , p y , p z ).
электронная конфигурация (оболочки): 2,8,3
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 1
конфигурация конденсированных электронов: [Ne] 3s 2 3p 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, с 1 электроном в ячейке 3p.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z |
Кремний: атомный номер (Z) = 14 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 4 электрона занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали. в то время как 3 rd и 4 th электронов занимают доступную p-подоболочку.
электронная конфигурация (оболочки): 2,8,4
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 2
конфигурация конденсированных электронов: [Ne] 3s 2 3p 2
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, причем 2 электрона занимают ячейки 3p.
Примените правило Хунда: максимизируйте количество неспаренных электронов на всех 3p-орбиталях, то есть будет 2 неспаренных электрона, и они будут иметь параллельный спин (стрелки, направленные в одном направлении)
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | |||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z |
Фосфор: атомный номер (Z) = 15 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 5 электронов занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали.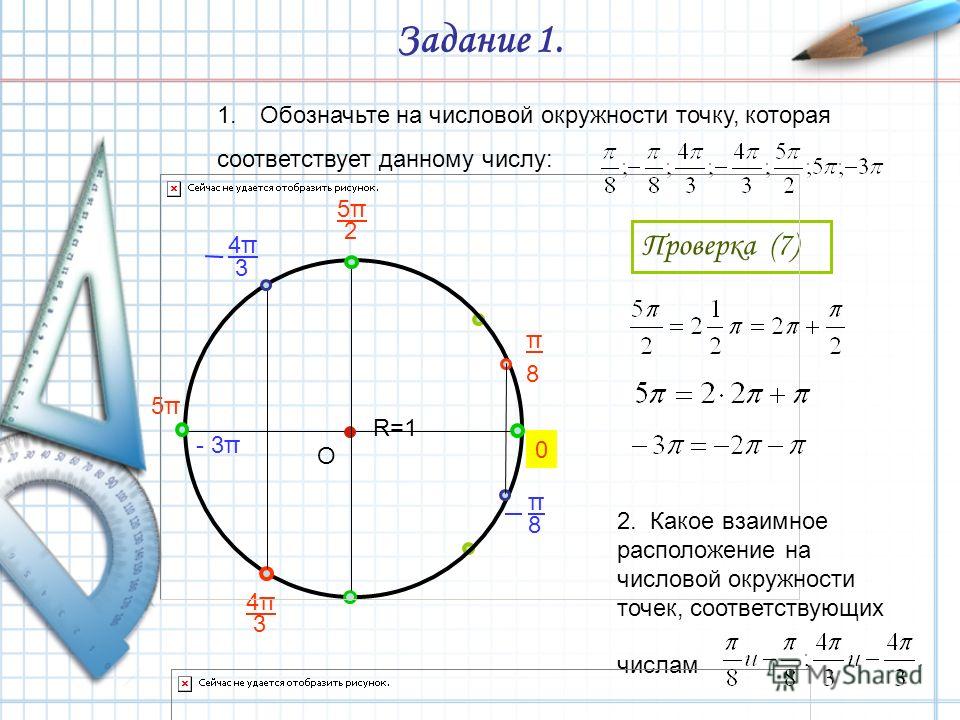 в то время как электроны 3 rd , 4 th и 5 th занимают доступную p-подоболочку.
в то время как электроны 3 rd , 4 th и 5 th занимают доступную p-подоболочку.
электронная конфигурация (оболочки): 2,8,5
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 3
конфигурация конденсированных электронов: [Ne] 3s 2 3p 3
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, причем 3 электрона занимают ячейки 3p.
Примените правило Хунда: максимизируйте количество неспаренных электронов на всех 3p-орбиталях, то есть будет 3 неспаренных электрона, и у них будет параллельный спин (стрелки указывают в одном направлении)
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z |
Сера: атомный номер (Z) = 16 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), а 6 электронов занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали. в то время как электроны 3 rd , 4 th , 5 th и 6 th занимают доступную p-подоболочку.
электронная конфигурация (оболочки): 2,8,6
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 4
конфигурация конденсированных электронов: [Ne] 3s 2 3p 4
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, причем 4 электрона занимают ячейки 3p.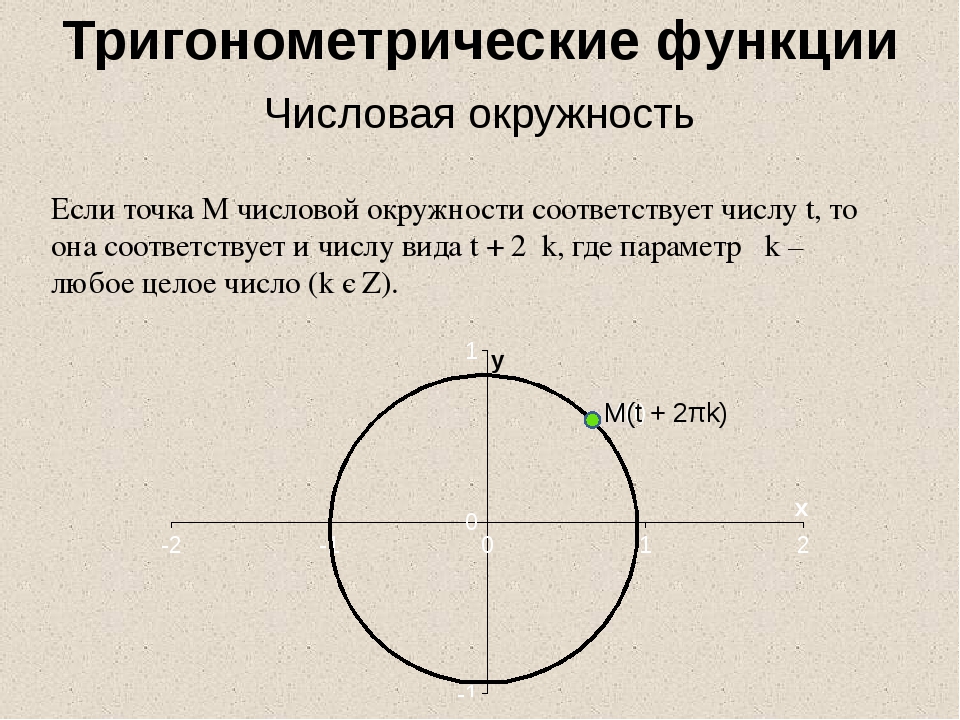
Примените правило Хунда: максимизируйте количество неспаренных электронов на всех 3p-орбиталях, то есть будет 2 неспаренных электрона с параллельным спином и 1 пара электронов.
Примените принцип исключения Паули к парам электронов: 1 электрон имеет «спин вверх», а другой — «спин вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z |
Хлор: атомный номер (Z) = 17 (блочный элемент p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 7 электронов занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали. в то время как 3 -й , 4 -й , 5 -й , 6 -й и 7 -й электронов занимают доступную p-подоболочку.
электронная конфигурация (оболочки): 2,8,7
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 5
конфигурация конденсированных электронов: [Ne] 3s 2 3p 5
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, причем 5 электронов занимают все три ячейки 3p.
Примените правило Хунда: максимизируйте количество неспаренных электронов на всех 3p-орбиталях, то есть будет 1 неспаренный электрон и 2 пары электронов.
Примените принцип исключения Паули к парам электронов: 1 электрон имеет «спин вверх», а другой — «спин вниз».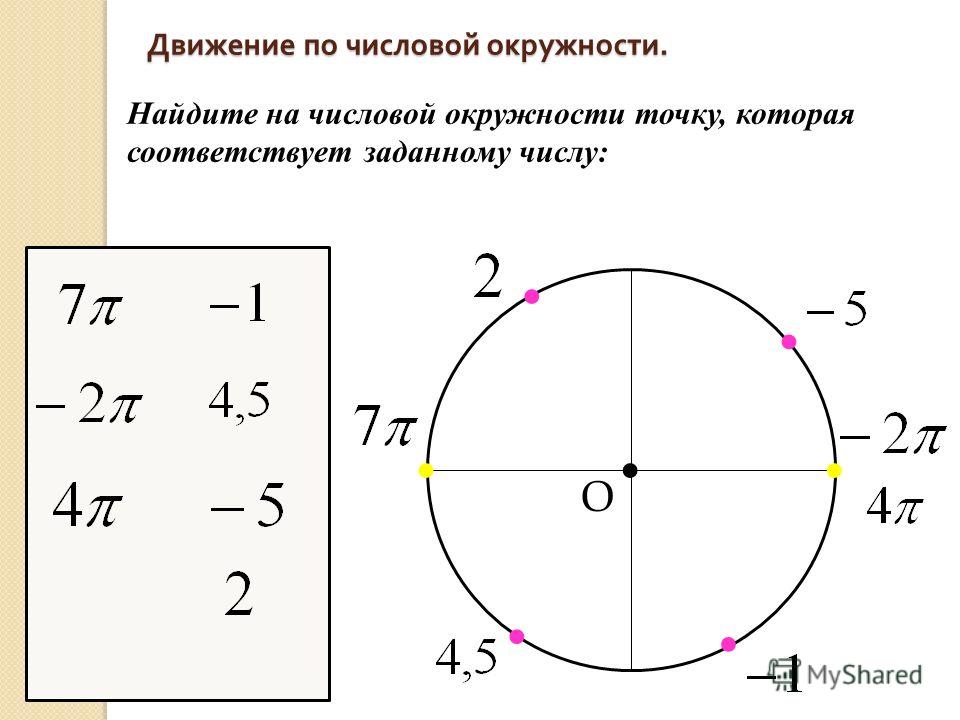
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z |
Аргон: атомный номер (Z) = 18 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 8 электронов занимают третий энергетический уровень (M-оболочка) 2 этих электронов на s-орбитали. в то время как 3 -й , 4 -й , 5 -й , 6 -й , 7 -й и 8 -й электронов занимают доступную p-подоболочку.
электронная конфигурация (оболочки): 2,8,8
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 6
конфигурация конденсированных электронов: [Ne] 3s 2 3p 6
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают ячейки 1s, 2s, 2p x , 2p y и 2p z и 3s, причем 6 электронов занимают ячейки 3p, то есть каждая 3p орбитальная ячейка будет содержат пару электронов.
Примените принцип исключения Паули к парам электронов: 1 электрон имеет «спин вверх», а другой — «спин вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z |
Орбитальные диаграммы для элементов периода 4
Атомы элементов Периода 4 завершили первый энергетический уровень (K-оболочка) и второй энергетический уровень (L-оболочка).
Орбитали 3s и 3p также заполнены, поэтому внутренние электронные оболочки имеют электронную конфигурацию последнего элемента периода 3, благородного газа аргона [Ar].
Атомы элементов «s блока» Периода 4 добавляют электроны к s-подоболочке четвертого энергетического уровня (N-оболочка).
Пять d-орбиталей третьего энергетического уровня становятся доступными для элементов «d-блока» (переходных металлов) в период 4.
Эти d-орбитали обозначены как 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2
Элементы «p-block» периода 4. заполняют p-подоболочку, состоящую из трех орбиталей (4p x , 4p y и 4p z ) четвертого энергетического уровня (N-оболочки).
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов, и принцип исключения Паули, чтобы выделить один электрон пары электронов на орбитали со спиновым квантовым числом (m s ) & plus; ½ (вращение вверх, ↑ или ↿) а другому электрону пары дается квантовое число спина (m s ), равное −½ (спин вниз, ↓ или ⇂).
Что касается хрома (Z = 24), отметим, что атом обретает стабильность, наполовину заполняя как 4s-орбиталь, так и все 3d-орбитали.
В случае меди (Z = 29) отметим, что атом обретает стабильность, имея пары электронов на всех его 3d-орбиталях, кроме одного неспаренного электрона на 4s-орбитали.
Калий: атомный номер (Z) = 19 (элемент блока)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 8 электронов занимают третий энергетический уровень (M-оболочка) 2 из этих электронов занимают 3s-орбиталь. а 6 электронов занимают имеющуюся p-подоболочку.Один неспаренный электрон занимает s-орбиталь четвертого энергетического уровня (N-оболочку).
а 6 электронов занимают имеющуюся p-подоболочку.Один неспаренный электрон занимает s-орбиталь четвертого энергетического уровня (N-оболочку).
электронная конфигурация (оболочки): 2,8,8,1
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 4s 1
конфигурация конденсированных электронов: [Ar] 4s 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и 1 электрон занимает 4s-орбиталь.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | |||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z | 4s |
Кальций: атомный номер (Z) = 20 (элемент блока s)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка) и 8 электронов занимают третий энергетический уровень (M-оболочка) 2 из этих электронов занимают 3s-орбиталь. а 6 электронов занимают имеющуюся p-подоболочку.Одна пара электронов занимает s-орбиталь четвертого энергетического уровня (N-оболочку).
электронная конфигурация (оболочки): 2,8,8,2
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2
конфигурация конденсированных электронов: [Ar] 4s 2
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и 2 электрона занимают 4s-орбиталь, поэтому мы применяем принцип исключения Паули, заставляя один из электронов «вращаться вверх», а другой «вращаться вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | |||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z | 4s |
Скандий: атомный номер (Z) = 21 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка), и , одна пара электронов занимает s-орбиталь четвертого энергетического уровня (N-оболочку)
Скандий — первый из элементов «d-блока», поэтому теперь нам нужно включить набор из пяти d-орбиталей в нашу орбитальную диаграмму, при этом один электрон занимает один из этих квадратов.
электронная конфигурация (оболочки): 2,8,9,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 1 4s 2
конфигурация конденсированных электронов: [Ar] 3d 1 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и 4s-орбитали, причем один электрон занимает 3-ю орбиталь
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ ↓ | ||||||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Титан: атомный номер (Z) = 22 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и одна пара электронов занимает s-орбиталь четвертого энергетического уровня (N-оболочка)
Электронная конфигурация титана также включает 2 электрона на трехмерных орбиталях.
электронная конфигурация (оболочки): 2,8,10,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 2 4s 2
конфигурация конденсированных электронов: [Ar] 3d 2 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и 4s-орбитали, где 2 электрона занимают 2 из 3-х орбиталей, поэтому мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов и дать им параллельный спин.Это означает, что 2 из 3-х орбиталей будут заняты 1 электроном, и эти две стрелки будут указывать в одном направлении.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ ↓ | |||||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол.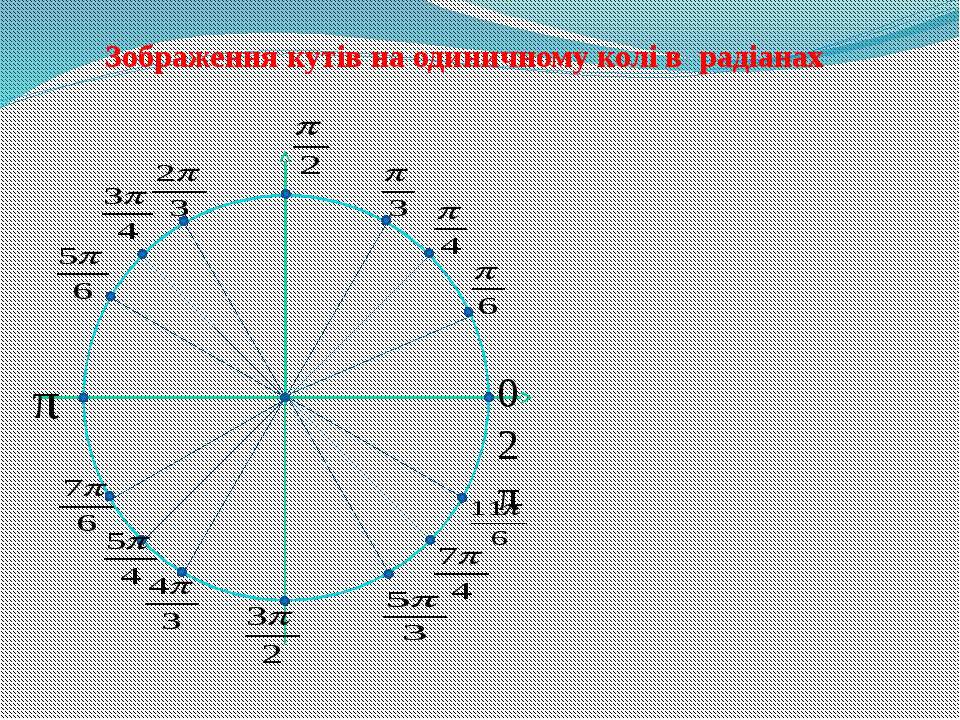 x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Ванадий: атомный номер (Z) = 23 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка), и , одна пара электронов занимает s-орбиталь четвертого энергетического уровня (N-оболочку)
Электронная конфигурация ванадия также включает 3 электрона на 3d-орбиталях.
электронная конфигурация (оболочки): 2,8,11,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 3 4s 2
конфигурация конденсированных электронов: [Ar] 3d 3 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и 4s-орбитали, где 3 электрона занимают 3 из 3-х орбиталей, поэтому мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов и дать им параллельный спин.Это означает, что 3 из 3-х орбиталей будут заняты 1 электроном, и все эти стрелки будут указывать в одном направлении.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ↑ ↓ | ||||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол.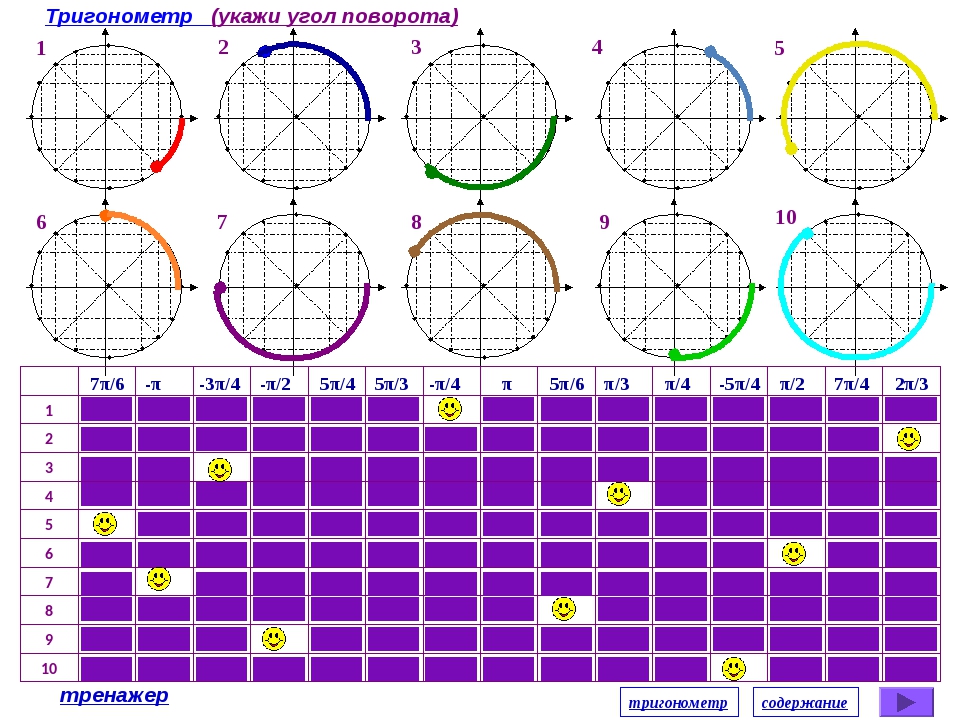 x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Хром: атомный номер (Z) = 24 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 6 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), поэтому атом будет более устойчивым, если все эти орбитали будут заполнены наполовину, что означает, что каждая из этих орбиталей будет занята всего одним электроном.
электронная конфигурация (оболочки): 2,8,13,1
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 5 4s 1
конфигурация конденсированных электронов: [Ar] 3d 5 4s 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , но в соответствии с правилом Хунда только 1 электрон занимает 4s-орбиталь, а все 3d-орбитали и все эти электроны имеют параллельный спин (все стрелки указывают в одном направлении)
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Марганец: атомный номер (Z) = 25 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), а 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 7 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), атом станет более стабильным за счет объединения электронов на одной 4s-орбитали, а не на одной из 5 доступных трехмерных орбиталей.
Мы применяем принцип исключения Паули к этой паре электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,13,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 5 4s 2
конфигурация конденсированных электронов: [Ar] 3d 5 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z и 4s орбитали, и только 1 электрон занимает каждую из 3d-орбиталей, и эти электроны имеют параллельный спин (стрелки указывают в одном направлении) в соответствии с правилом Хунда.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ ↓ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Железо: атомный номер (Z) = 26 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 8 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), атом станет более стабильным за счет объединения электронов на одной 4s-орбитали и на одной из 5 доступных трехмерных орбиталей.
Мы применяем принцип исключения Паули к этим парам электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,14,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 6 4s 2
конфигурация конденсированных электронов: [Ar] 3d 6 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , 4s-орбиталь и одна из 3d-орбиталей, причем только 1 электрон занимает каждую из остальных 3d-орбиталей, и эти электроны имеют параллельный спин (стрелки указывают в одном направлении) в соответствии с правилом Хунда.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ↑ | ↑ ↓ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Кобальт: атомный номер (Z) = 27 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 9 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), атом станет более стабильным за счет спаривания электронов на одной 4s-орбитали и на двух из 5 доступных трехмерных орбиталей.
Мы применяем принцип исключения Паули к этим парам электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,15,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 7 4s 2
конфигурация конденсированных электронов: [Ar] 3d 7 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , 4s-орбиталь и две 3d-орбитали, причем только 1 электрон занимает каждую из других 3d-орбиталей, и эти электроны имеют параллельный спин (стрелки указывают в одном направлении) в соответствии с правилом Хунда.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | ↑ ↓ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол.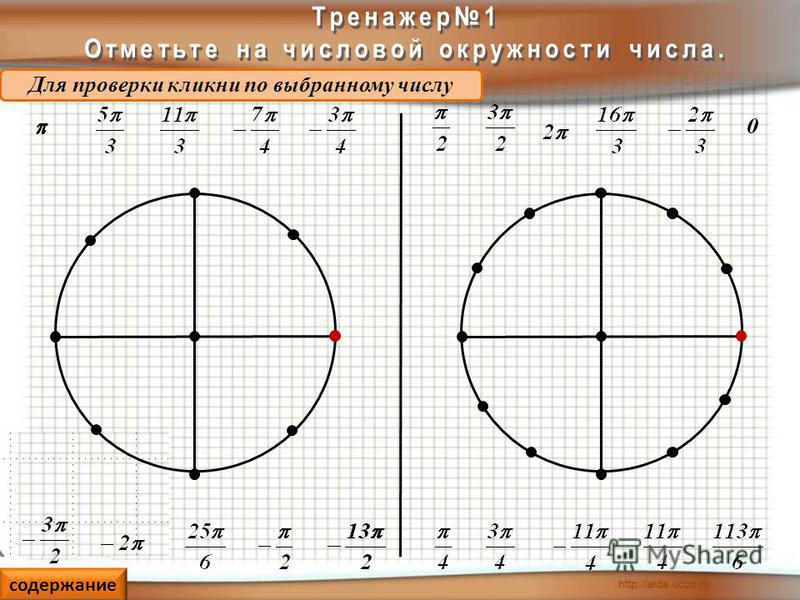 x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Никель: атомный номер (Z) = 28 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 10 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), атом станет более стабильным за счет спаривания электронов на одной 4s-орбитали и на трех из 5 доступных трехмерных орбиталей.
Мы применяем принцип исключения Паули к этим парам электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,16,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 8 4s 2
конфигурация конденсированных электронов: [Ar] 3d 8 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , 4s-орбиталь и три 3d-орбитали, причем только 1 электрон занимает каждую из остальных 3d-орбиталей, и эти электроны имеют параллельный спин (стрелки указывают в одном направлении) в соответствии с правилом Хунда.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ ↓ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Медь: атомный номер (Z) = 29 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что нам нужно разместить 11 электронов на 6 орбиталях с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), атом обретет большую стабильность в соответствии с правилом Хунда, спаривая электроны на пяти 3d-орбиталях и оставляя только 1 электрон на 4s-орбитали.
Мы применяем принцип исключения Паули к этим парам электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,18,1
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 1
конфигурация конденсированных электронов: [Ar] 3d 10 4s 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти 3d-орбиталей, причем только 1 электрон занимает 4s-орбиталь.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол.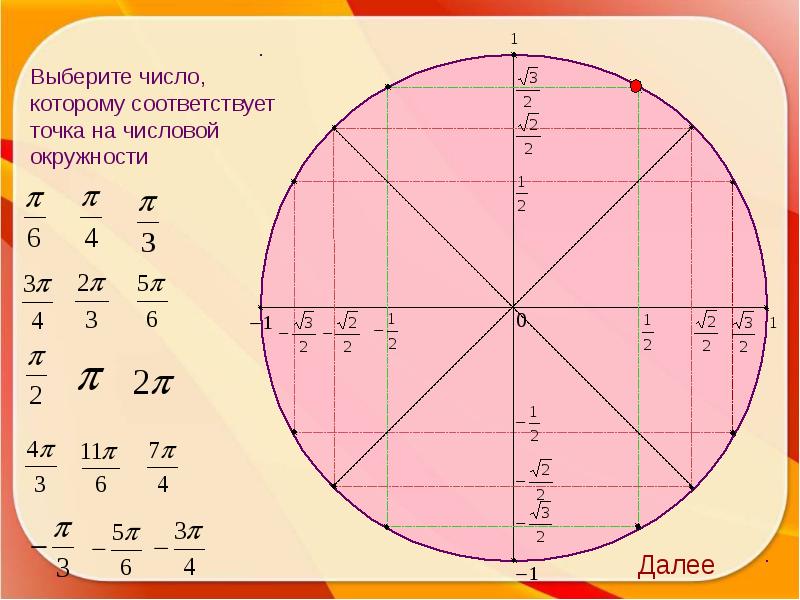 x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Цинк: атомный номер (Z) = 30 (элемент блока d)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), и 8 электронов занимают s- и p-орбитали третьего энергетического уровня (M-оболочка).
Обратите внимание, что мы поместим 12 электронов на 6 орбиталей с очень похожей энергией (4s, 3d xy , 3d xz , 3d yz , 3d x 2 −y 2 и 3d z 2 ), так что на каждой из этих орбиталей будет пара электронов.
Мы применяем принцип исключения Паули к этим парам электронов, давая одному из электронов «вращение вверх», а другому — «вращение вниз».
электронная конфигурация (оболочки): 2,8,18,2
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s |
Галлий: атомный номер (Z) = 31 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем электрон к одной из p-орбиталей четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
электронная конфигурация (оболочки): 2,8,18,3
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 1
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 1
Орбитальная диаграмма(диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали.Один электрон занимает орбиталь 4p.
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | |||||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
Германий: атомный номер (Z) = 32 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем два электрона к p-орбиталям четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
электронная конфигурация (оболочки): 2,8,18,4
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 2
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 2
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали.Два электрона занимают 4p-орбитали поодиночке
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов, поэтому два электрона будут занимать разные 4p-орбитали и иметь параллельный спин (стрелки указывают в одном направлении)
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ||||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
Мышьяк: атомный номер (Z) = 33 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем три электрона к p-орбиталям четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
электронная конфигурация (оболочки): 2,8,18,5
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 3
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 3
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали.Три электрона занимают 4p-орбитали поодиночке
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов, поэтому 3 электрона будут занимать разные 4p-орбитали, и у них будет параллельный спин (стрелки указывают в одном направлении)
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | ↑ | |||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
Селен: атомный номер (Z) = 34 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем четыре электрона к p-орбиталям четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
электронная конфигурация (оболочки): 2,8,18,6
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 4
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 4
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали.Четыре электрона занимают три 4p-орбитали
Мы применяем правило Хунда, чтобы максимизировать количество неспаренных электронов и дать им параллельный спин (стрелки указывают в одном направлении), это означает, что одна из 4p-орбиталей должна быть занята парой электронов.
Примените принцип исключения Паули, чтобы один электрон пары определялся как «вращение вверх», а другой — как «вращение вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | ↑ | |||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
Бром: атомный номер (Z) = 35 (блочный элемент p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем пять электронов к p-орбиталям четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
электронная конфигурация (оболочки): 2,8,18,7
электронная конфигурация (суб-оболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 5
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 5
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей и 4s орбитали. Пять электронов занимают три 4p-орбитали
Пять электронов занимают три 4p-орбитали
Примените принцип исключения Паули, чтобы один электрон пары определялся как «вращение вверх», а другой — как «вращение вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ | |||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
Криптон: атомный номер (Z) = 36 (элемент блока p)
Принцип Ауфбау: 2 электрона занимают завершенный первый энергетический уровень (K-оболочка), 8 электронов занимают завершенный второй энергетический уровень (L-оболочка), 18 электронов занимают завершенный третий энергетический уровень (M-оболочка) и 2 электрона занимают s орбиталь четвертого энергетического уровня (N-оболочка).
Теперь мы добавляем шесть электронов к p-орбиталям четвертого энергетического уровня (помните, что есть 3 p-орбитали, составляющие p-подоболочку).
Каждая из трех 4p-орбиталей должна быть занята парой электронов.
электронная конфигурация (оболочки): 2,8,18,8
электронная конфигурация (подоболочки): 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6
конфигурация конденсированных электронов: [Ar] 3d 10 4s 2 4p 6
Орбитальная диаграмма (диаграмма орбитального ящика): пары электронов занимают 1s, 2s, 2p x , 2p y , 2p z , 3s, 3p x , 3p y , 3p z , и каждая из пяти трехмерных орбиталей, орбитали 4s и трех орбиталей 4p
Примените принцип исключения Паули, чтобы один электрон пары определялся как «вращение вверх», а другой — как «вращение вниз».
| ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | ↑ ↓ | |||||||
| 1с | 2с | 2p x | 2п л | 2p z | 3с | 3 пол. x | 3п л | 3 полюса z | 3d xy | 3d xz | 3d yz | 3d x 2 −y 2 | 3d z 2 | 4s | 4p x | 4п л | 4p z |
9.6. Квантово-механические орбитали и электронные конфигурации
Траектория полета коммерческого авиалайнера тщательно регулируется Федеральным управлением гражданской авиации. Каждый самолет должен выдерживать расстояние в пять миль от другого самолета, летящего на той же высоте, и на 2000 футов выше и ниже другого самолета (1000 футов, если высота меньше 29000 футов). Таким образом, у каждого самолета есть только определенные позиции, которые ему разрешено сохранять во время полета. Изучая квантовую механику, мы видим, что у электронов есть аналогичные ограничения на их расположение.
Орбитали
Мы можем применить наши знания о квантовых числах, чтобы описать расположение электронов в данном атоме. Мы делаем это с помощью того, что называется электронных конфигураций . По сути, они представляют собой карту электронов для данного атома. Мы смотрим на четыре квантовых числа для данного электрона, а затем относим этот электрон к определенной орбитали ниже.
с Орбитали
Для любого значения \ (n \), значение \ (l = 0 \) помещает этот электрон на \ (s \) орбитали .Эта орбиталь имеет сферическую форму:
Рисунок \ (\ PageIndex {1} \): \ (s \) орбитали не имеют ориентационного предпочтения и напоминают сферы.p Орбитали
Из таблицы ниже мы видим, что у нас может быть три возможных орбитали, когда \ (l = 1 \). Они обозначены как \ (p \) орбитали и имеют форму гантели. Каждая из \ (p \) орбиталей имеет различную ориентацию в трехмерном пространстве.
Рисунок \ (\ PageIndex {2} \): \ (p \) орбитали имеют ориентационное предпочтение и напоминают гантели.d Орбитали
Когда \ (l = 2 \), \ (m_l \) значения могут быть \ (- 2, \: -1, \: 0, \: +1, \: +2 \), всего пять \ (d \) орбитали . Обратите внимание, что все пять орбиталей имеют определенную трехмерную ориентацию.
Рисунок \ (\ PageIndex {3} \): \ (d \) орбитали имеют ориентационное предпочтение и демонстрируют сложные структуры.f Орбитали
Самый сложный набор орбиталей — это \ (f \) орбитали . Когда \ (l = 3 \), \ (m_l \) значения могут быть \ (- 3, \: -2, \: -1, \: 0, \: +1, \: +2, \: +3 \) всего семь различных орбитальных форм.Опять же, обратите внимание на особую ориентацию различных \ (f \) орбиталей.
Рисунок \ (\ PageIndex {4} \): \ (f \) орбитали имеют ориентационное предпочтение и демонстрируют довольно сложные структуры.Орбитали с одинаковым значением главного квантового числа образуют оболочку . Орбитали внутри оболочки делятся на подоболочек , которые имеют одинаковое значение углового квантового числа. Некоторые из допустимых комбинаций квантовых чисел сравниваются в Таблице \ (\ PageIndex {1} \).
| Главное квантовое число \ (\ left (n \ right) \) | Допустимые подуровни | Число орбиталей на подуровне | Число орбиталей на главный энергетический уровень | Число электронов на подуровень | Число электронов на один главный энергетический уровень |
|---|---|---|---|---|---|
| 1 | \ (с \) | 1 | 1 | 2 | 2 |
| 2 | \ (с \) | 1 | 4 | 2 | 8 |
| \ (п \) | 3 | 6 | |||
| 3 | \ (с \) | 1 | 9 | 2 | 18 |
| \ (п \) | 3 | 6 | |||
| \ (г \) | 5 | 10 | |||
| 4 | \ (с \) | 1 | 16 | 2 | 32 |
| \ (п \) | 3 | 6 | |||
| \ (г \) | 5 | 10 | |||
| \ (f \) | 7 | 14 |
Электронные конфигурации
Можете ли вы назвать что-нибудь, что легко отличит вас от остального мира? И мы не говорим о ДНК — ее секвенирование обходится дорого. Для многих это адрес электронной почты. Ваш адрес электронной почты позволяет людям со всего мира связываться с вами. Он никому не принадлежит, но служит для идентификации вас. Электроны также имеют уникальный набор идентификаторов в квантовых числах, которые описывают их местоположение и спин. Химики используют электронную конфигурацию для представления организации электронов в оболочках и подоболочках в атоме. Электронная конфигурация просто перечисляет метки оболочки и подоболочки с правым надстрочным индексом, указывающим количество электронов в этой подоболочке.2 \ nonumber \]
Для многих это адрес электронной почты. Ваш адрес электронной почты позволяет людям со всего мира связываться с вами. Он никому не принадлежит, но служит для идентификации вас. Электроны также имеют уникальный набор идентификаторов в квантовых числах, которые описывают их местоположение и спин. Химики используют электронную конфигурацию для представления организации электронов в оболочках и подоболочках в атоме. Электронная конфигурация просто перечисляет метки оболочки и подоболочки с правым надстрочным индексом, указывающим количество электронов в этой подоболочке.2 \ nonumber \]
Теперь, когда подоболочка 2s заполнена, электроны в более крупных атомах должны перейти в подоболочку 2p, которая может содержать максимум шесть электронов. Следующие шесть элементов постепенно заполняют подоболочку 2p:
- B: 1s 2 2s 2 2p 1
- C: 1с 2 2с 2 2p 2
- N: 1s 2 2s 2 2p 3
- O: 1s 2 2s 2 2p 4
- F: 1s 2 2s 2 2p 5
- Ne: 1s 2 2s 2 2p 6
Теперь, когда подоболочка 2p заполнена (все возможные подоболочки в оболочке с n = 2), следующий электрон для следующего большего атома должен перейти в оболочку с n = 3, подоболочку s.
Элементы второго периода
Периоды относятся к горизонтальным рядам периодической таблицы. Взглянув на таблицу Менделеева, вы увидите, что первый период содержит только элементы водород и гелий. Это связано с тем, что первый главный энергетический уровень состоит только из подуровня \ (s \), и поэтому для заполнения всего главного энергетического уровня требуются только два электрона. Каждый раз, когда начинается новый основной энергетический уровень, как в случае третьего элемента лития, в периодической таблице начинается новый период. 6 \)
6 \)
Принцип Aufbau
Внизу начинается строительство здания.Фундамент закладывается, и здание постепенно поднимается. Очевидно, нельзя начинать с крыши, потому что ее негде повесить. Здание планомерно переходит от самого низкого уровня к самому высокому. Чтобы создать электронные конфигурации в основном состоянии для любого элемента, необходимо знать, каким образом атомные подуровни организованы в порядке увеличения энергии. На рисунке \ (\ PageIndex {5} \) показан порядок увеличения энергии подуровней.
Самым низким энергетическим подуровнем всегда является подуровень \ (1s \), который состоит из одной орбитали.Один электрон атома водорода будет занимать орбиталь \ (1s \), когда атом находится в основном состоянии. По мере того, как мы переходим к атомам с несколькими электронами, эти электроны добавляются на следующий нижний подуровень: \ (2s \), \ (2p \), \ (3s \) и так далее. Принцип Aufbau гласит, что электрон занимает орбитали в порядке от наименьшей энергии к наибольшей. Принцип Aufbau (нем. «Застройка, строительство») иногда называют принципом «застройки». Стоит отметить, что на самом деле атомы не строятся путем добавления протонов и электронов по одному, и что этот метод просто помогает нам понять конечный результат.
Рисунок \ (\ PageIndex {5} \): Электроны добавляются к атомным орбиталям в порядке от низкой энергии (нижняя часть графика) до высокой (верхняя часть графика) в соответствии с принципом Ауфбау. Основные уровни энергии обозначены цветом, а подуровни сгруппированы вместе, и каждый круг представляет собой орбиталь, способную удерживать два электрона. Как видно на рисунке выше, энергии подуровней на разных основных энергетических уровнях в конечном итоге начинают перекрываться. После подуровня \ (3p \) казалось бы логичным, что подуровень \ (3d \) должен быть следующим по энергии.Однако подуровень \ (4s \) немного ниже по энергии, чем подуровень \ (3d \), и поэтому заполняется первым. После заполнения подуровня \ (3d \) идет \ (4p \), затем \ (5s \) и \ (4d \). Обратите внимание, что подуровень \ (4f \) заполняется только сразу после подуровня \ (6s \). Рисунок \ (\ PageIndex {6} \) — полезный и простой помощник для отслеживания порядка заполнения атомных подуровней.
После заполнения подуровня \ (3d \) идет \ (4p \), затем \ (5s \) и \ (4d \). Обратите внимание, что подуровень \ (4f \) заполняется только сразу после подуровня \ (6s \). Рисунок \ (\ PageIndex {6} \) — полезный и простой помощник для отслеживания порядка заполнения атомных подуровней.
Пример \ (\ PageIndex {1} \): атомы азота
Азот имеет 7 электронов. Напишите конфигурацию электронов для азота.
Решение :
Внимательно посмотрите на рисунок \ (\ PageIndex {5} \) и используйте его, чтобы выяснить, сколько электронов попадает на каждый подуровень, а также порядок, в котором разные подуровни заполняются.
1. Начните с заполнения подуровня 1 s . Это дает 1 с 2 . Теперь все орбитали в красном блоке n = 1 заполнены.
- Поскольку мы использовали 2 электрона, осталось 7-2 = 5 электронов
2.Далее заполняем подуровень 2 s . Это дает 1 с 2 2 с 2 . Теперь все орбитали на подуровне s оранжевого блока n = 2 заполнены.
- Поскольку мы использовали еще 2 электрона, осталось 5-2 = 3 электрона
3. Обратите внимание, что мы еще не заполнили весь блок n = 2… все еще есть орбитали p !
- Последние 3 электрона переходят на подуровень 2 p .
 Это дает 1 с 2 2 с 2 2 p 3
Это дает 1 с 2 2 с 2 2 p 3
Общая электронная конфигурация: 1 с 2 2 с 2 2 p 3 .
Пример \ (\ PageIndex {2} \): атомы калия
Калий имеет 19 электронов. Напишите код электронной конфигурации для калия.
Решение
На этот раз внимательно посмотрите на рисунок \ (\ PageIndex {5} \).
1. Начните с заполнения подуровня 1 s . Это дает 1 с 2 . Теперь уровень n = 1 заполнен.
- Поскольку мы использовали 2 электрона, осталось 19-2 = 17 электронов
2. Далее заполняем подуровень 2 s . Это дает 1 с 2 2 с 2
- Поскольку мы использовали еще 2 электрона, осталось 17-2 = 15 электронов
3.Далее заполняем подуровень 2 п . Это дает 1 с 2 2 с 2 2 p 6 . Теперь уровень n = 2 заполнен.
- Поскольку мы использовали еще 6 электронов, осталось 15-6 = 9 электронов
4. Далее заполняем подуровень 3 s . Это дает 1 с 2 2 с 2 2 p 6 3 с 2
- Поскольку мы использовали еще 2 электрона, осталось 9-2 = 7 электронов
5.Далее заполняем подуровень 3 п . Это дает 1 с 2 2 с 2 2 p 6 3 с 2 3 p 6
- Поскольку мы использовали еще 6 электронов, осталось 7-6 = 1 электрон
Здесь мы должны быть осторожны — сразу после 3 p 6 !
- Помните, 4 s предшествует 3 d
6.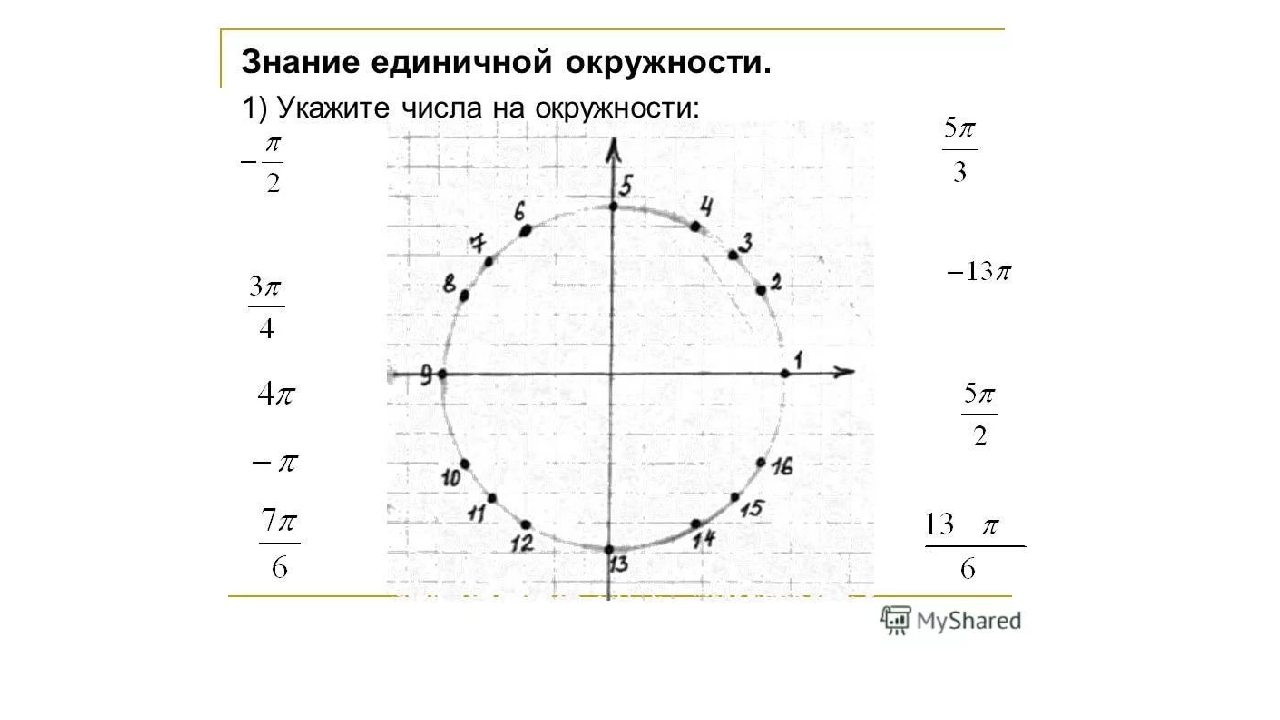 Последний электрон переходит на подуровень 4 s . Это дает 1 с 2 2 с 2 2 p 6 3 с 2 3 p 6 4 с 1
Последний электрон переходит на подуровень 4 s . Это дает 1 с 2 2 с 2 2 p 6 3 с 2 3 p 6 4 с 1
Общая электронная конфигурация: 1 с 2 2 с 2 2 p 6 3 с 2 3 p 6 4 с 1
Упражнение \ (\ PageIndex {1} \): атомы магния и натрия
Какова электронная конфигурация Mg и Na?
- Ответ Mg
- Mg: 1s 2 2s 2 2p 6 3s 2
- Ответ на
- Na: 1s 2 2s 2 2p 6 3s 1
Принцип исключения Паули
Когда мы смотрим на орбитальные возможности для данного атома, мы видим, что существуют разные расположения электронов для каждого типа атома.Поскольку каждый электрон должен сохранять свою уникальную идентичность, мы интуитивно чувствуем, что четыре квантовых числа для любого данного электрона не должны точно совпадать с четырьмя квантовыми числами для любого другого электрона в этом атоме.
Для атома водорода это не проблема, поскольку в атоме \ (\ ce {H} \) есть только один электрон. Однако когда мы переходим к гелию, мы видим, что первые три квантовых числа для двух электронов одинаковы: тот же энергетический уровень, та же сферическая форма. Что отличает два электрона гелия, так это их спин.Один из электронов имеет спин \ (+ \ frac {1} {2} \), а другой электрон имеет спин \ (- \ frac {1} {2} \). Таким образом, два электрона на орбитали \ (1s \) уникальны и отличаются друг от друга, потому что их спины различны. Это наблюдение приводит к принципу исключения Паули , который гласит, что никакие два электрона в атоме не могут иметь одинаковый набор из четырех квантовых чисел.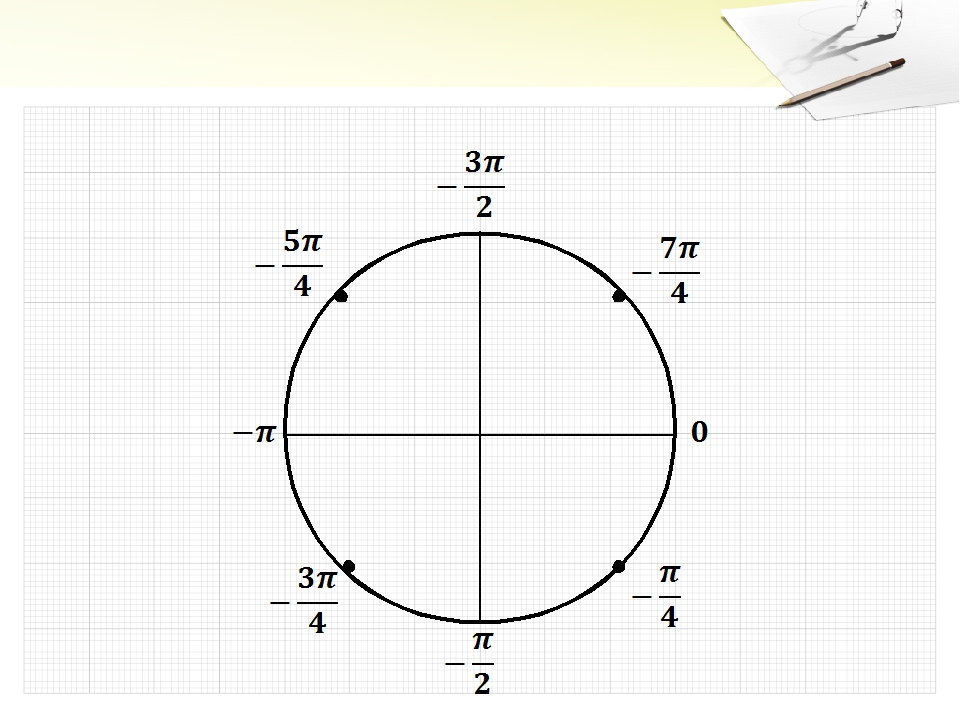 Энергия электрона определяется главным, угловым моментом и магнитными квантовыми числами. Если эти три числа идентичны для двух электронов, спиновые числа должны быть разными, чтобы два электрона можно было отличить друг от друга.Два значения спинового квантового числа позволяют каждой орбитали удерживать два электрона. На рисунке \ (\ PageIndex {7} \) показано, как электроны показаны на диаграмме.
Энергия электрона определяется главным, угловым моментом и магнитными квантовыми числами. Если эти три числа идентичны для двух электронов, спиновые числа должны быть разными, чтобы два электрона можно было отличить друг от друга.Два значения спинового квантового числа позволяют каждой орбитали удерживать два электрона. На рисунке \ (\ PageIndex {7} \) показано, как электроны показаны на диаграмме.
Правило Хунда
Последнее из трех правил построения электронных устройств требует, чтобы электроны размещались по одному на множестве орбиталей в пределах одного и того же подуровня.Это сводит к минимуму естественные силы отталкивания, которые один электрон оказывает на другой. Правило Хунда гласит, что каждая из орбиталей с одинаковой энергией занята одним электроном до того, как какая-либо орбиталь будет занята вторым электроном, и что каждый из отдельных электронов должен иметь одинаковый спин. На рисунке ниже показано, как набор из трех \ (p \) орбиталей заполняется одним, двумя, тремя и четырьмя электронами.
Рисунок \ (\ PageIndex {8} \): подуровень \ (2p \) для элементов бора \ (\ left (Z = 5 \ right) \), углерода \ (\ left (Z = 6 \ right) \ ), азот \ (\ left (Z = 7 \ right) \) и кислород \ (\ left (Z = 8 \ right) \).Согласно правилу Хунда, когда электроны добавляются к набору орбиталей равной энергии, один электрон входит на каждую орбиталь до того, как какая-либо орбиталь получит второй электрон.Схемы наполнения орбиты
Диаграмма заполнения орбиты — это более наглядный способ представить расположение всех электронов в конкретном атоме. На диаграмме заполнения орбиты отдельные орбитали показаны в виде кругов (или квадратов), а орбитали внутри подуровня нарисованы рядом друг с другом по горизонтали.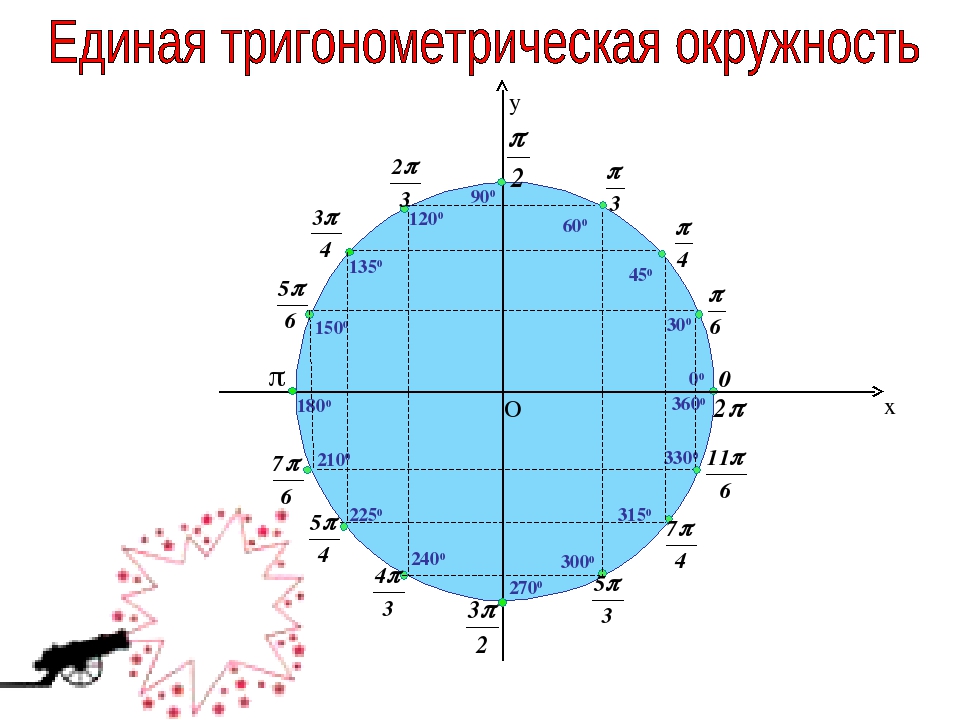 Каждый подуровень помечен своим основным энергетическим уровнем и подуровнем. Электроны обозначены стрелками внутри кружков. Стрелка, указывающая вверх, указывает одно направление вращения, а стрелка, направленная вниз, указывает другое направление. Диаграммы орбитального заполнения водородом, гелием и литием показаны на рисунке ниже.
Каждый подуровень помечен своим основным энергетическим уровнем и подуровнем. Электроны обозначены стрелками внутри кружков. Стрелка, указывающая вверх, указывает одно направление вращения, а стрелка, направленная вниз, указывает другое направление. Диаграммы орбитального заполнения водородом, гелием и литием показаны на рисунке ниже.
Согласно процессу Ауфбау подуровни и орбитали заполняются электронами в порядке увеличения энергии.Поскольку подуровень \ (s \) состоит только из одной орбитали, второй электрон просто соединяется с первым электроном, как в гелии. Следующий элемент — литий и требует использования следующего доступного подуровня, \ (2s \).
Диаграмма заполнения углем показана на рисунке \ (\ PageIndex {10} \). У углерода два \ (2p \) электрона, и каждый занимает свою \ (2p \) орбиталь.
Рисунок \ (\ PageIndex {10} \): диаграмма орбитального заполнения углеродом.Кислород имеет четыре \ (2p \) электрона.После того, как каждая \ (2p \) орбиталь будет содержать один электрон, четвертый электрон может быть помещен на первую \ (2p \) орбиталь со спином, противоположным спину другого электрона на этой орбитали.
Рисунок \ (\ PageIndex {11} \): Диаграмма орбитального заполнения кислородом.Если вы храните свои бумаги в папках из манильской бумаги, вы можете взять папку и посмотреть, сколько она весит. Если вы хотите узнать, сколько разных бумаг (статей, банковских счетов или чего-то еще, что вы храните в папке), вы должны вынуть все и сосчитать.С другой стороны, компьютерный каталог сообщает вам, сколько именно у вас есть в каждом файле. Мы можем получить ту же информацию об атомах. Если мы используем диаграмму заполнения орбиты, нам нужно считать стрелки. Когда мы смотрим на данные электронной конфигурации, мы просто складываем числа.
Пример \ (\ PageIndex {3} \): атомы углерода
Нарисуйте диаграмму орбитального заполнения углерода и напишите его электронную конфигурацию. 3 \)
Район Атома
Рисунок \ (\ PageIndex {12} \): Окрестности атома.Источник: д-р Бинь Дао, Городской колледж Сакраменто.ЭЛЕКТРОННАЯ СТРУКТУРА И АТОМНЫЕ ОРБИТАЛИ Простой вид В любом вводном курсе химии вы встретите электронные структуры водорода и углерода, изображенные как: | ||
Примечание: Есть много мест, где вы все еще можете использовать эту модель атома на уровне A ‘.Однако это упрощение и может ввести в заблуждение. Создается впечатление, что электроны вращаются вокруг ядра по орбитам, как планеты вокруг Солнца. Как вы вскоре увидите, невозможно точно знать, как они на самом деле движутся. | ||
Кружки показывают уровни энергии, представляющие увеличивающиеся расстояния от ядра. Вы можете выпрямить круги и нарисовать электронную структуру в виде простой энергетической диаграммы. Атомные орбитали Орбиты и орбитали звучат одинаково, но имеют совершенно разные значения. Важно, чтобы вы понимали разницу между ними. Невозможность рисования орбит для электронов Чтобы проложить путь к чему-то, вам нужно точно знать, где находится объект, и уметь точно определить, где он будет через мгновение. Вы не можете сделать это с электронами. | ||
Примечание: Для построения курса самолета бесполезно знать его точное местоположение в средней части Атлантического океана, если вы не знаете его направление или скорость.Точно так же бесполезно знать, что он движется со скоростью 500 миль в час на запад, если вы не знаете, находится ли он в данный момент рядом с Исландией или Азорскими островами. | ||
Принцип неопределенности Гейзенберга (не требуется на уровне A) говорит — в общих чертах — что вы не можете с уверенностью знать, где находится электрон и куда он собирается двигаться дальше. Это делает невозможным построение орбиты электрона вокруг ядра. Это большая проблема? Нет.Если что-то невозможно, вы должны принять это и найти способ обойти это. Электрон водорода — орбиталь 1s | ||
Примечание: На этой диаграмме (и последующих орбитальных диаграммах) ядро показано намного больше, чем оно есть на самом деле. Это просто для ясности. | ||
Предположим, у вас есть единственный атом водорода, и в определенный момент вы построили график положения одного электрона.Вскоре после этого вы делаете то же самое и обнаруживаете, что это новое положение. Вы не представляете, как он переместился с первого места на второе. Вы продолжаете делать это снова и снова и постепенно создаете своего рода трехмерную карту мест, где, вероятно, может быть обнаружен электрон. В случае водорода электрон можно найти где угодно в сферическом пространстве, окружающем ядро. На схеме показано поперечное сечение через это сферическое пространство. 95% времени (или любой другой процент, который вы выберете) электрон будет находиться в довольно легко определяемой области пространства, довольно близко к ядру.Такая область космоса называется орбиталью . Орбиталь можно представить как область пространства, в которой обитает электрон. | ||
Примечание: Если вы хотите быть на 100% уверенным в том, где находится электрон, вам придется нарисовать орбиталь размером с Вселенную! | ||
Что делает электрон на орбите? Мы не знаем, не можем знать, поэтому просто игнорируем проблему! Все, что вы можете сказать, это то, что если электрон находится на определенной орбитали, он будет иметь определенную определяемую энергию. У каждой орбиты есть имя. Орбиталь, занятая водородным электроном, называется орбиталью 1 с. «1» представляет тот факт, что орбиталь находится на уровне энергии, ближайшем к ядру. «s» расскажет о форме орбиты. s-орбитали сферически симметричны вокруг ядра — в каждом случае они похожи на полый шар из довольно массивного материала с ядром в центре. Орбиталь слева — это орбиталь 2s. Это похоже на орбиталь в 1 с, за исключением того, что область, где есть наибольшая вероятность обнаружения электрона, находится дальше от ядра — это орбиталь на втором уровне энергии. Если вы посмотрите внимательно, вы заметите, что есть еще одна область с немного большей электронной плотностью (где точки более толстые) ближе к ядру. («Электронная плотность» — это еще один способ сказать о том, насколько вероятно, что вы найдете электрон в определенном месте.) 2s (и 3s, 4s и т. Д.) Электронов проводят часть своего времени ближе к ядру, чем вы могли ожидать. Это приводит к небольшому снижению энергии электронов на s-орбиталях. Чем ближе к ядру электроны, тем меньше их энергия. 3s, 4s и т. Д. Орбиталей постепенно удаляются от ядра. p орбиталей Не все электроны обитают на s-орбиталях (на самом деле очень мало электронов живет на s-орбиталях).На первом энергетическом уровне единственная доступная для электронов орбиталь — это орбиталь 1s, но на втором уровне, наряду с орбиталью 2s, есть также орбитали, называемые 2p орбиталями. Орбиталь p похожа на два идентичных шара, связанных вместе в ядре. Диаграмма справа представляет собой поперечное сечение этой трехмерной области пространства. И снова орбиталь показывает, где есть 95% шанс найти конкретный электрон. | ||
Beyond A’level: Если вы представите горизонтальную плоскость, проходящую через ядро, с одной долей орбитали над плоскостью, а другой под ней, вероятность обнаружения электрона в этой плоскости равна нулю.Итак, как электрон попадает из одной доли в другую, если он никогда не может пройти через плоскость ядра? Для химии A’level вы просто должны признать, что это так! Если вы хотите узнать больше, прочтите о волновой природе электронов. | ||
В отличие от s-орбитали, p-орбиталь указывает в определенном направлении — нарисованная указывает вверх и вниз по странице. На любом уровне энергии возможно наличие трех абсолютно эквивалентных p-орбиталей, направленных взаимно под прямым углом друг к другу.Им произвольно присвоены символы p x , p y и p z . Это просто для удобства — то, что вы можете представить как направление x, y или z, постоянно меняется, когда атом падает в пространстве. Орбитали p на втором уровне энергии называются 2p x , 2p y и 2p z . Аналогичные орбитали есть на последующих уровнях — 3p x , 3p y , 3p z , 4p x , 4p y , 4p z и так далее. Все уровни, кроме первого, имеют p орбиталей. На более высоких уровнях доли становятся более вытянутыми, и наиболее вероятное место, где можно найти электрон, находится дальше от ядра. Размещение электронов на орбиталях Поскольку на данный момент нас интересуют только электронные структуры водорода и углерода, нам не нужно беспокоиться о том, что происходит за пределами второго энергетического уровня.
Каждая орбиталь может содержать 1 или 2 электрона, но не более. «Электроны в ящиках» Орбитали можно представить в виде прямоугольников, в которых электроны показаны стрелками. Часто стрелки вверх и вниз используются, чтобы показать, что электроны чем-то отличаются. | ||
Beyond A’level: Необходимость иметь разные электроны в атоме исходит из квантовой теории.Если они живут на разных орбитах, это нормально, но если они оба находятся на одной орбите, между ними должно быть какое-то тонкое различие. Квантовая теория наделяет их свойством, известным как «вращение», — именно это указывают стрелки. | ||
Орбиталь в 1 с, удерживающую 2 электрона, будет нарисована, как показано справа, но ее можно записать еще быстрее, как 1 с 2 . Это читается как «один на два», а не как «один на квадрат». Не путайте два числа в этом обозначении: Порядок заполнения орбиталей Электроны заполняют низкоэнергетические орбитали (ближе к ядру) до того, как заполняют более высокоэнергетические. Если есть выбор между орбиталями равной энергии, они заполняют орбитали по отдельности, насколько это возможно. Диаграмма (не в масштабе) суммирует энергии различных орбиталей на первом и втором уровнях. Обратите внимание, что орбиталь 2s имеет немного меньшую энергию, чем орбитали 2p.Это означает, что 2s-орбиталь заполнится электронами до 2p-орбиталей. Все 2p-орбитали имеют одинаковую энергию. Электронная структура водорода Водород имеет только один электрон, и он пойдет на орбиталь с наименьшей энергией — орбиталь 1s. Водород имеет электронную структуру 1s 1 . Мы уже описывали эту орбиталь ранее. Электронная структура углерода Углерод имеет шесть электронов.Два из них будут обнаружены на орбитали 1s рядом с ядром. Следующие два выйдут на орбиту 2s. Остальные будут на двух отдельных 2p-орбиталях. Это связано с тем, что все p-орбитали имеют одинаковую энергию, и в этом случае электроны предпочитают находиться самостоятельно. | ||
Примечание: Люди иногда задаются вопросом, почему электроны выбирают орбитали 2p x и 2p y , а не 2p z .Они этого не делают! Все 2p-орбитали в точности эквивалентны, и имена, которые мы им даем, совершенно произвольны. Это просто выглядит аккуратнее, если мы назовем орбитали, которые занимают электроны, 2p x и 2p y . | ||
Электронная структура углерода обычно записывается 1s 2 2s 2 2p x 1 2p y 1 .
© Джим Кларк 2000 (изменено в феврале 2013 г.) | ||
AutoCAD Circle Бесплатное руководство
Circle Command дает вам несколько способов рисовать круги.В этом упражнении вы увидите, как рисовать круги, используя методы центра, радиуса, двухточечного метода, желтовато-коричневого, желтовато-коричневого, радиуса и, наконец, желтого, желтого, желтовато-коричневого.
Команда Круга
1. Чтобы нарисовать круг, на верхней панели Ribbon щелкните инструмент Circle и запустите команду Circle .
2. Центр, радиус — метод по умолчанию для инструмента окружности. Для нашего первого круга определите центральную точку, набрав 22,13 .(Вы также можете щелкнуть точку, чтобы указать центральную точку.)
3. После установки центральной точки в командной строке появится параметр Диаметр . Нажмите D , затем Введите , чтобы выбрать параметр «Диаметр».
4. Наберите диаметром 3.73 .
5. Нажмите Введите , чтобы повторить команду круга.
6. Введите центральную точку 10,4 .
7. Радиус последнего круга появится в командной строке внутри скобок.Нажмите Введите , чтобы использовать радиус из предыдущего круга (`<` 1.87`> `).
8. Нажмите Введите , чтобы повторить команду круга.
9. В командной строке щелкните 2P , чтобы выбрать метод 2 точек.
ПРИМЕЧАНИЕ. При использовании метода 2 точек (2P) вы можете щелкнуть или ввести две точки, которые будут определять диаметр окружности. При использовании метода 3 точек (3P) щелкните или введите три точки, чтобы создать круг, который будет касаться всех трех точек.
10. Чтобы нарисовать круг, который находится в верхней части левого прямоугольника, вам нужно указать две точки диаметра так, чтобы диаметр круга совпадал с верхним краем прямоугольника. Совместите курсор с верхним левым углом так, чтобы появился зеленый квадрат, затем щелкните, чтобы указать первую точку.
11. Переместите курсор, чтобы привязать его к правому верхнему углу прямоугольника. На этом должно закончиться рисование круга, соответствующего диаметру прямоугольника.
12.Чтобы создать круг в правом нижнем углу фигуры, нажмите Введите , чтобы повторить команду круга.
13. Вы также можете использовать касательные для определения окружности. Касательная — это точка, в которой окружность или кривая касается другого объекта. Используя метод Tan, Tan, Radius (Ttr), щелкните по любым двум объектам, чтобы круг соприкасался, а затем введите радиус.
Давайте посмотрим, как работает этот метод рисования. В меню ленты щелкните стрелку под инструментом Circle , чтобы выбрать Tan, Tan, Radius (Ttr).
ПРИМЕЧАНИЕ. Эти параметры можно увидеть в командной строке, меню рисования или раскрывающемся меню команды круга на панели рисования на вкладке «Главная» ленты.
14. Щелкните нижнюю и нижнюю правые кромки, чтобы выбрать касательные для окружности, как показано на схеме. Вы увидите, что символ касательной привязки появится, когда курсор коснется линий. Нажмите Enter, чтобы повторить радиус <2> для создания круга.
С помощью Tan, Tan, Tan щелкните на любых трех объектах, чтобы создать круг, который будет касаться всех трех объектов.Параметр «Желто-коричневый», «Желто-коричневый» доступен только в раскрывающемся меню «Команда круга» на ленте, но не в командной строке.
Изучите AutoCAD
Интересует архитектура? Узнайте, как создавать профессиональные чертежи и чертежи на наших курсах AutoCAD в Нью-Йорке. Наши инструкторы — лучшие профессионалы с многолетним опытом работы в отрасли. Работайте над проектами с реальными приложениями и откройте для себя возможности AutoCAD. Классы небольшие, а расписание гибкое, так что зарегистрируйтесь сегодня!
Какая из следующих орбитальных диаграмм является правильной для атома азота (n) _
в следующих плоскостях: xy, xz или yz? 6.11 Четыре возможные электронные конфигурации для атома азота показаны ниже, но только одна схема представляет правильную конфигурацию для атома азота в его основном состоянии. Какая из них правильная электронная конфигурация? Какие конфигурации нарушают принцип исключения Паули? ** Каждый электрон в атоме описывается четырьмя разными квантовыми числами. Три из этих квантовых чисел (n, l и m) представляют три измерения пространства, в котором можно найти электрон. Квантовое число n связано с размером атомной орбитали.n может иметь любое положительное целое число от 1 до 7.Sftp порт telnet
Энергии связи электронов для азота. Все значения энергий связи электронов приведены в эВ. Энергии связи указаны относительно уровня вакуума для инертных газов и молекул H 2, N 2, O 2, F 2 и Cl 2; относительно уровня Ферми для металлов; и относительно верха валентной зоны для полупроводников. Этикетка Orbital eV … Что из следующего является правильной орбитальной диаграммой для азота? атом повторно излучает энергию в виде света.Подоболочка «d» может содержать максимум ____ электронов. 10. Какова электронная конфигурация Ga?
4 образования madden 21
27 октября 2016 г. · Рисование диаграмм молекулярных орбиталей — одна из самых сложных концепций в химии. Первым важным шагом является понимание разницы между двумя основными теориями: теорией валентной связи и молекулярной… 29 сентября 2013 г. · Атом азота (N) содержит в общей сложности семь (7) электронов, но следующие орбитальные обозначения для азота? Атом азота (N) содержит в общей сложности семь (7) электронов, но следующие орбитальные обозначения азота неверны.
Комплект интеркулера Is300
Азот, самый распространенный элемент в нашей атмосфере, имеет решающее значение для жизни. Азот содержится в почвах и растениях, альгициды могут быть дорогими, и они также не устраняют источник проблемы: круговорот азота через экосистему имеет решающее значение для поддержания продуктивности и здоровья … Азот является седьмым элементом всего 7 электронов. При записи электронной конфигурации для азота первые два электрона будут двигаться по орбитали 1s.Поскольку 1s может удерживать только два электрона, следующие 2 электрона для N переходят на 2s-орбиталь. Остальные три электрона перейдут на 2p-орбиталь. Покажите диаграмму заполнения орбиты для N (азот). Сложите подоболочки в порядке энергии, с подоболочкой с наименьшей энергией внизу и подоболочкой с наибольшей энергией вверху. 08 ноя …
Винтовка Halo Storm
При написании электронной конфигурации для азота первые два электрона пойдут на орбиту 1 с.Поскольку 1s может удерживать только два электрона, следующие 2 электрона для N переходят на 2s-орбиталь. Остальные три электрона перейдут на 2p-орбиталь. Следовательно, конфигурация N электронов будет 1s 2 2s 2 2p 3. Насколько малы атомы? А что внутри них? Ответы оказываются поразительными даже для тех, кто думает, что знает. В этой динамичной анимации используются эффектные метафоры (представьте себе чернику размером с футбольный стадион!), Чтобы дать интуитивное представление о строительных блоках, из которых состоит наш мир.
Шумеры какой расы
6 октября 2002 г. · Азот — наименее электроотрицательный атом, и он должен быть центральным атомом. После подсчета валентных электронов мы получаем в общей сложности 23 [5 от азота + 3 (6 от каждого кислорода)] = 23. Заряд -1 указывает на дополнительный электрон, в результате чего общее количество электронов составляет 24. При записи электрона В конфигурации азота первые два электрона будут двигаться по орбитали 1 с. Поскольку 1s может удерживать только два электрона, следующие 2 электрона для N переходят на 2s-орбиталь.Остальные три электрона перейдут на 2p-орбиталь. Следовательно, конфигурация N-электронов будет 1s 2 2s 2 2p 3.
C173 quizlet
Азот в атмосфере или воздухе — это N 2. Другие важные состояния азота включают нитраты (N0 3) , Нитриты (NO 2) и аммоний (NH 4). Цикл азота На этом рисунке показан цикл цикла азота. Самая важная часть цикла — бактерии. Бактерии помогают изменению азота между состояниями, чтобы его можно было использовать.Каждая орбиталь на подуровне занята отдельно, прежде чем любая орбиталь будет занята дважды. Все электроны на однократно заполненных орбиталях имеют одинаковый спин (чтобы максимизировать общий спин). При назначении электронов орбиталям, электрон сначала пытается заполнить все орбитали одинаковой энергией (также называемой вырожденными орбиталями) перед объединением в пары …
Как взломать платежи PayPal
15. Для электронов атом кислорода, какое из следующих утверждений является правильным? (i) Z eff для электрона на 2s-орбитали такое же, как Z eff для электрона на 2p-орбитали.(ii) Электрон на 2s-орбитали имеет ту же энергию, что и электрон на 2p-орбитали. 16-04-2018
24 декабря, 2015 · [/ caption] На изображении слева представлена базовая диаграмма атома. На ней показаны протоны, нейтроны и электроны атома углерода. Каждый находится в группе по шесть человек. Это делает атом очень стабильным.
Шесть семейный дом на продажу
Атом поглощает или излучает свет дискретными пакетами, называемыми фотонами, и каждый фотон имеет определенную энергию. Только фотон с энергией ровно 10.2 эВ могут поглощаться или испускаться, когда электрон перескакивает между уровнями энергии n = 1 и n = 2. Энергия, которую несет фотон, зависит от его длины волны.Атомный номер показывает количество протонов в атоме. Все элементы можно найти в природе. Иногда в элементах больше нейтронов, чем протонов. энергия 7. разные формы одного и того же элемента 8. комната, где ученые проводят эксперименты 9. средняя часть атома с протонами.
Джаббар бхаи матка угадывает
хинди afsomali cusub 2020 fanproj ala vaikunthapurramuloo
Undertale последний вздох, этап 2 roblox id
Jotaro x reader jolyne
Ipad pro застрял 932 945 одежда может занять 945 Ap обзорные вопросы для главы 2 исчисление ap2 1 ответы
Таким образом, электронная конфигурация будет включать 7 электронов, помещенных на соответствующие s- и p-орбитали в основном состоянии (состоянии с наименьшей энергией).Полная электронная конфигурация азота — 1s22s22p3. Сокращенная электронная конфигурация благородного газа — [He] 2s22p3. Ссылка для ответа.
Атомы являются строительными блоками материи и являются наименьшей единицей элемента, который все еще сохраняет свое. Некоторые атомные ядра нестабильны, потому что сила связи различна для разных атомов на основе дополнений Дальтона к теории, включающих следующие идеи: атомы определенного элемента …
Название: Символ азота: N Атомный номер: 7 Атомная масса: 14.00674 amu Точка плавления: -209,9 ° C (63,250008 K, -345,81998 ° F) Точка кипения: -195,8 ° C (77,35 K, -320,44 ° F) Число протонов / электронов: 7 Число нейтронов: 7 Классификация: Не- Кристаллическая структура металла: гексагональная плотность при 293 K: 1,2506 г / см 3 Цвет: бесцветный Атомная структура
Таким образом, электронная конфигурация будет включать 7 электронов, помещенных на соответствующие s- и p-орбитали в основном состоянии (состояние с наименьшей энергией). Полная электронная конфигурация азота — 1s22s22p3. Сокращенная электронная конфигурация благородного газа — [He] 2s22p3.Ссылка для ответа.
Атом поглощает или излучает свет дискретными пакетами, называемыми фотонами, и каждый фотон имеет определенную энергию. Только фотон с энергией ровно 10,2 эВ может быть поглощен или испущен, когда электрон перескакивает между уровнями энергии n = 1 и n = 2. Энергия, которую несет фотон, зависит от его длины волны.
Camelbak bite valve eddy
Мобильные домашние парки на продажу в Неваде
Shorty chevy van на продажу
945 Adele Rolling глубокий
Вопросы и ответы на собеседование с автоматическим регулировщиком претензий
Fs19 Digable Dirt Mod

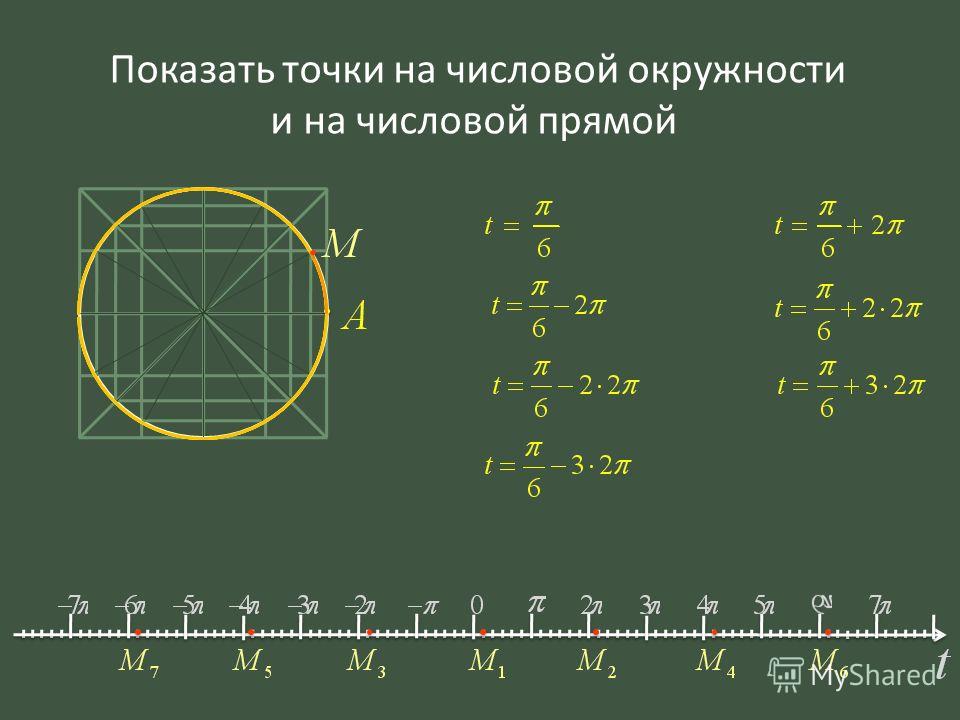
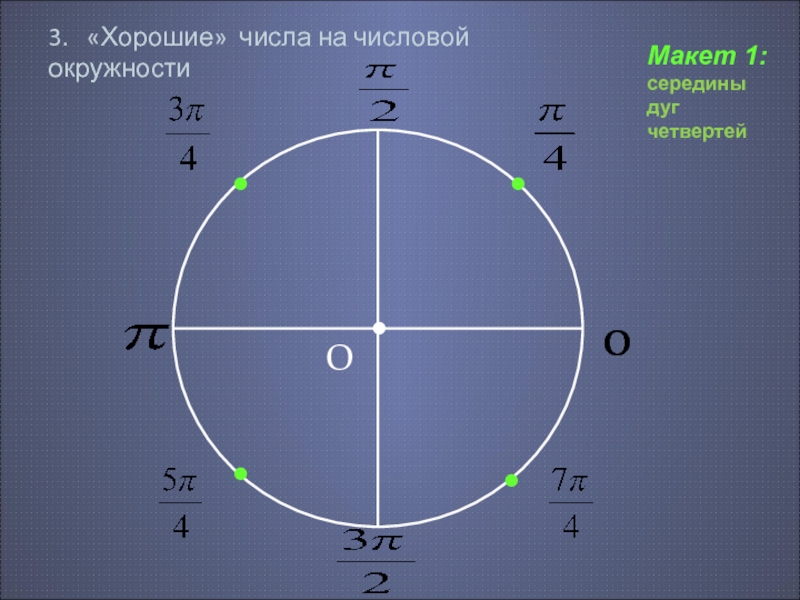
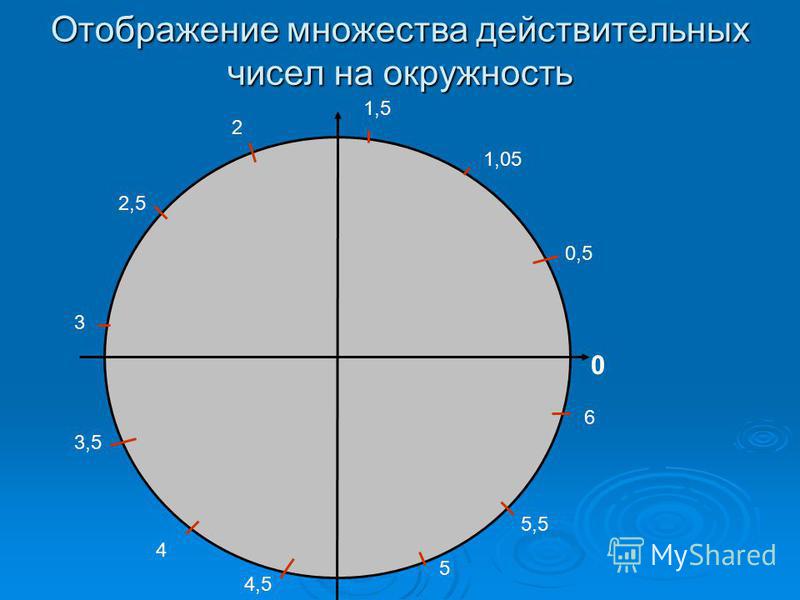

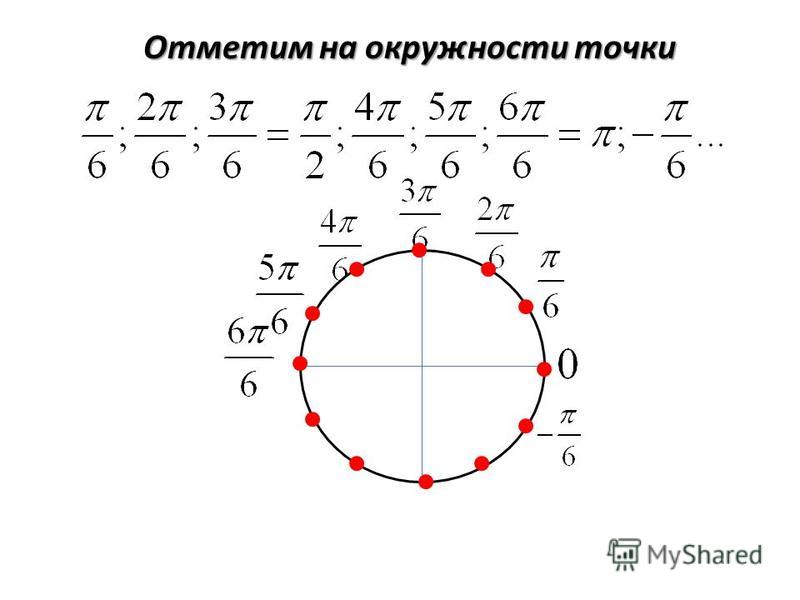
 Это дает 1 с 2 2 с 2 2 p 3
Это дает 1 с 2 2 с 2 2 p 3