поверхность многогранника — это… Что такое поверхность многогранника?
- поверхность многогранника
- мат. polyhedral surface
Большой англо-русский и русско-английский словарь. 2001.
- поверхность мишени
- поверхность нагрева
Смотреть что такое «поверхность многогранника» в других словарях:
ВЫПУКЛАЯ ПОВЕРХНОСТЬ — область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… … Математическая энциклопедия
Перекатывание многогранников — Теория перекатывания многогранников (построена Виктором Матизеном в 1979 г.) изучает сеть перекатывания выпуклого многогранника (СПМ) множество следов его вершин, рёбер и граней при всевозможных перекатываниях по плоскости через… … Википедия
картографическая проекция — математически определённое отображение поверхности земного шара, эллипсоида (или глобуса) на плоскость карты. Проекция устанавливает соответствие между географическими координатами точки (широтой В и долготой L) и её прямоугольными координатами… … Географическая энциклопедия
Проекция Димаксион — Развёртка карты Димаксион с земной поверхностью в виде единого массива суши … Википедия
Изгибаемый многогранник — Многогранник (точнее многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело) … Википедия
Многогранник — В Викисловаре есть статья «многогранник» … Википедия
Многогранники — Многогранник поверхность составленная из многоугольников, а также тело ограниченное такой поверхностью.
 Содержание 1 Три варианта определения 2 Вариации и обобщения 3 Использование … Википедия
Содержание 1 Три варианта определения 2 Вариации и обобщения 3 Использование … ВикипедияПолиэдр — Многогранник поверхность составленная из многоугольников, а также тело ограниченное такой поверхностью. Содержание 1 Три варианта определения 2 Вариации и обобщения 3 Использование … Википедия
ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия
огранка — и; ж. 1. к Огранить. О. алмазов. У вас камни в огранку принимают? 2. Характер шлифовки, обработки граней; совокупность граней чего л. Замечательная о.! Видна рука мастера. Сложная о. Хрустальный бокал с изящной огранкой. * * * огранка 1) Придание … Энциклопедический словарь
Эйлерова характеристика — или характеристика Эйлера Пуанкаре характеристика топологического пространства. Эйлерова характеристика пространства обычно обозначается . Содержание 1 Определения 2 Свойства … Википедия
Урок 13. многогранник — Геометрия — 10 класс
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
- Определение многогранника и его элементов;
- Виды многогранников;
- Многогранник как модель реального объекта;
- Теорема Эйлера для многогранников.
Глоссарий по теме
Многогранник
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Основная литература:
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Дополнительная литература:
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Часть 1 // Квант. 2001. № 5. С. 7—12. http://www.etudes.ru/data/localdocs/dolbilin_kvant1.pdf
Часть 2 // Квант. 2001. № 6. С. 3—10. http://www.etudes.ru/data/localdocs/dolbilin_kvant2.pdf
Теоретический материал для самостоятельного изучения
Понятие многогранника
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
А)
Б)
Рисунок 1 – разные подходы к определению многоугольника
По аналогии с первым толкованием понятия многоугольника рассматривается следующее толкование понятия многогранника. Многогранник — поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. В данной трактовке многогранник можно называть еще многогранной поверхностью.
Многогранник — поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. В данной трактовке многогранник можно называть еще многогранной поверхностью.
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
Примеры многогранников
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Элементы многогранника
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Виды многогранников
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Утверждение. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600.
Пояснить данное утверждение поможет рисунок 4. “Разрежем” многогранник вдоль его ребер и все его грани с общей вершиной расположим так, чтобы они оказались в одной плоскости. Видим, что сумма всех плоских углов действительно меньше 360
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
1) отрезок
2) плоскость
3) точка
4) луч
5) многоугольник
6) многогранник
7) прямая
8) трапеция
Решение
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Ответ: 2467
Задание 2. Сопоставьте геометрическим фигурам их вид
А) плоская фигура
Б) пространственная фигура
В) Многогранник
Решение
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
|
Некоторые пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников. |
|
|
Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника. Многоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника:ABC, DEF, ABED, BCFE, ACFD – грани; AB, BC, AC, DE, EF, DF, AD, BE, CF – рёбра; A, B, C, D, E, F – вершины многогранника ABCDEF. Теорема Эйлера для многогранников: Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство: V – R + G = 2. |
|
|
Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы. Основания призмы равны и лежат в параллельных плоскостях. Боковые рёбра призмы равны и параллельны. Поверхность призмы состоит из двух оснований и боковой поверхности. Боковая поверхность любой призмы состоит из параллелограммов, у каждого из которых две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми рёбрами. Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы. Призма называется п-угольной, если её основание – п-угольник. АВСA1В1С1 – треугольная призма; ΔАВС и ΔA1В1С1 – основания; АA1, ВВ1, СС1 – боковые рёбра; АA1В1В, АA1С1С, ВВ1С1С – боковые грани; A1О – высота призмы; α – угол наклона бокового ребра к основанию призмы. |
|
|
Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной. Боковые грани прямой призмы – прямоугольники. Боковое ребро прямой призмы является её высотой. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы: Sб = Pосн·АА1. Прямая призма называется правильной, если её основания являются правильными многоугольниками. |
|
|
Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. В частности, параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими, через два боковых ребра, не принадлежащих одной грани: ВВ1D1D – диагональное сечение. Если в произвольной наклонной призме провести сечение, перпендикулярное боковым рёбрам и пересекающее все боковые рёбра, и площадь этого сечения обозначить S⊥, а периметр – Р⊥, тогда:
Sб = Р⊥·АА1;
V = S⊥·АА1. В прямой призме: S⊥= Sосн; Р⊥= Pосн· В любой призме площадь полной поверхности считается как сумма площади боковой поверхности и удвоенной площади основания: Sп = Sб + 2·Sосн. |
|
|
Призма, в основании которой лежит параллелограмм, называется параллелепипедом. У параллелепипеда все грани – параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. У параллелепипеда противолежащие грани параллельны и равны. Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. Точка пересечения диагоналей параллелепипеда является его центром симметрии. |
|
|
Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник. Все грани прямоугольного параллелепипеда являются прямоугольниками. Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами. У прямоугольного параллелепипеда три измерения. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений: d² = a² + b² + c². В прямоугольном параллелепипеде верно:
Sп = 2·(ab+bc+ac); V = abc. |
|
|
В прямоугольном параллелепипеде, как и во всяком параллелепипеде, есть центр симметрии – точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно парам противолежащих граней. На первом рисунке, приведённом выше, показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме трёх названных. Если же у параллелепипеда два линейных размера равны, то есть он является правильной четырёхугольной призмой, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на втором рисунке. |
|
|
Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Диагональ куба в квадратный корень из трёх раз больше его стороны: В кубе верно:
Sп = 6·a², Sп = 2·d², |
|
|
Четыре сечения куба являются правильными шестиугольниками (одно из них показано на рисунке) – эти сечения проходят через центр куба перпендикулярно четырём его диагоналям. У куба девять плоскостей симметрии:
|
|
|
|
Пирамидой (например, SABCDE) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) – основания пирамиды, точки (S), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки (SA, SB, SC, SD, SE), соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания (пятиугольник ABCDE) и боковых граней. Каждая боковая грань – треугольник. ΔSAB, ΔSBC, ΔSCD, ΔSDE, ΔSEA – боковые грани. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром. α – угол наклона бокового ребра SA пирамиды к плоскости её основания; β – угол наклона боковой грани (SED) пирамиды к плоскости её основания. Основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и только тогда, когда выполняется одно из условий:
Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и только тогда, когда выполняется одно из условий:
Объём пирамиды равен трети произведения площади основания на высоту пирамиды: V = 1/3·Sоснh. Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания: Sп = Sб + Sосн. Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды. |
|
|
|
|
Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части: пирамиду, подобную данной (SA1В1С1) и многогранник, называемый усеченной пирамидой (AВСA1В1С1). Грани усеченной пирамиды, лежащие в параллельных плоскостях (ΔАВС и ΔA1В1С1), называются основаниями, остальные грани (АA1В1В, АA1С1С, ВВ1С1С) называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции. Высота усеченной пирамиды (ОО1) – это расстояние между плоскостями её оснований. Если S1 и S2 – площади оснований усечённой пирамиды и h – её высота, то для объёма усеченной пирамиды верно: |
|
|
Пирамида (например, SABCD) называется правильной, если ее основанием является правильный многоугольник (ABCD – квадрат), а основание высоты совпадает с центром этого многоугольника (О – центр описанной и вписанной окружностей основания). Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны. Боковые грани правильной пирамиды – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды (SL), проведенная из ее вершины к стороне основания, называется апофемой. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему: Sб = ½Pосн·SL. |
|
|
Усеченная пирамида (например, АВСDA1В1С1D1), которая получается из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды (АA1В1В, АA1С1С, DD1С1С, АA1D1D) – равные равнобокие трапеции; их высоты называются апофемами. |
|
|
Тетраэдр Куб Октаэдр
Додекаэдр Икосаэдр |
|
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны. У куба (правильный гексаэдр) все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами. У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра. У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра. У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер. |
|
Многогранники — урок. Геометрия, 9 класс.
Всё, что мы с вами изучали ранее, относится к такому разделу геометрии, как планиметрия.
Планиметрия — это раздел геометрии, изучающий двумерные фигуры, то есть фигуры, которые можно расположить в одной плоскости. Фигуры, изучаемые планиметрией: точка, отрезок, прямоугольник, квадрат, окружность и т.д.
Предметы, которые нас окружают, не всегда являются плоскими, чаще реальные объекты занимают некоторую часть пространства.
Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Фигуры, изучаемые стереометрией: куб, шар, конус, параллелепипед, пирамида и т.д.
Это слово \(στερεομετρία\) происходит от древнегреческих слов «stereos» — объёмный, пространственный и «metria» — измерение.
Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
Грани — это многоугольники, из которых состоит многогранник. Две соседние грани не могут лежать в одной плоскости.
Две соседние грани не могут лежать в одной плоскости.
Рёбра многогранника— это стороны граней, а вершины — это концы рёбер.
Диагональ многогранника — это отрезок, который соединяет две вершины, не принадлежащие одной грани.
Многогранники бывают выпуклыми и невыпуклыми.
Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани. На рисунке выпуклый многогранник — октаэдр. У октаэдра восемь граней, все грани — правильные треугольники.
На рисунке — невыпуклый (вогнутый) многоугольник. Если рассмотреть, например, плоскость треугольника \(EDC\), то, очевидно, часть многоугольника находится по одну сторону, а часть — по другую сторону этой плоскости.
Для дальнейших определений введём понятие параллельных плоскостей и параллельных прямых в пространстве и перпендикулярности прямой и плоскости.
Две плоскости называются параллельными, если они не имеют общих точек.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Прямую называют перпендикулярной к плоскости, если она перпендикулярна к любой прямой в этой плоскости.
Теперь можем ввести определение призмы.\(n\)-угольной призмой называют многогранник, составленный из двух равных \(n\)-угольников, лежащих в параллельных плоскостях, и \(n\)-параллелограммов, которые образовались при соединении вершин \(n\)-угольников отрезками параллельных прямых.
Равные \(n\)-угольники называют основаниями призмы.
Стороны многоугольников называют рёбрами оснований.
Параллелограммы называют боковыми гранями призмы.
Параллельные отрезки называют боковыми рёбрами призмы.
Призмы бывают прямыми и наклонными.
Если основания прямой призмы — правильные многоугольники, то такую призму называют правильной.
У прямых призм все боковые грани — прямоугольники. Боковые рёбра прямой призмы перпендикулярны к плоскостям её оснований.
Если из любой точки одного основания провести перпендикуляр к другому основанию призмы, то этот перпендикуляр называют высотой призмы.
На рисунке — наклонная четырёхугольная призма, в которой проведена высота B1E.
В прямой призме каждое из боковых рёбер является высотой призмы.
На рисунке — прямая треугольная призма. Все боковые грани — прямоугольники, любое боковое ребро можно называть высотой призмы. У треугольной призмы нет диагоналей, так как все вершины соединены рёбрами.
На рисунке — правильная четырёхугольная призма. Основания призмы — квадраты. Все диагонали правильной четырёхугольной призмы равны, пересекаются в одной точке и делятся в этой точке пополам.
Четырёхугольная призма, основания которой — параллелограммы, называется параллелепипедом.
Вышеупомянутую правильную четырёхугольную призму можно также называть прямым параллелепипедом.
Если основания прямого параллелепипеда — прямоугольники, то этот параллелепипед — прямоугольный.
На рисунке — прямоугольный параллелепипед. Длины трёх рёбер с общей вершиной называют измерениями прямоугольного параллелепипеда.
Например, AB, AD и AA1 можно называть измерениями.
Так как треугольники ABC и ACC1 — прямоугольные, то, следовательно, квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:
AC12=AB2+AD2+AA12.
Если через соответственные диагонали оснований провести сечение, получится то, что называют диагональным сечением призмы.
В прямых призмах диагональные сечения являются прямоугольниками. Через равные диагонали проходят равные диагональные сечения.
На рисунке — правильная шестиугольная призма, в которой проведены два разных диагональных сечения, которые проходят через диагонали с разными длинами.
Основные формулы для расчётов в прямых призмах
1. Боковая поверхность Sбок.=Pосн.⋅H, где \(H\) — высота призмы. Для наклонных призм площадь каждой боковой грани определяется отдельно.
2. Полная поверхность Sполн.=2⋅Sосн.+Sбок.. Эта формула справедлива для всех призм, не только для прямых.
3. Объём V=Sосн.⋅H. Эта формула справедлива для всех призм, не только для прямых.
\(n\)-угольная пирамида — многогранник, составленный из \(n\)-угольника в основании и \(n\)-треугольников, которые образовались при соединении точки вершины пирамиды со всеми вершинами многоугольника основания.
\(n\)-угольник называют основанием пирамиды.Треугольники — боковые грани пирамиды.
Общая вершина треугольников — вершина пирамиды.
Рёбра, выходящие из вершины — боковые рёбра пирамиды.
Перпендикуляр от вершины пирамиды к плоскости основания называют высотой пирамиды.
На рисунке — шестиугольная пирамида \(GABCDEF\), проведена высота пирамиды \(GH\).
Пирамиду, в основании которой правильный многоугольник, и высота соединяет вершину пирамиды с центром правильного многоугольника, называют правильной.
У правильной пирамиды все боковые грани — равные равнобедренные треугольники. Если провести высоты этих треугольников, то они также будут равны.
Высоту боковой грани правильной пирамиды называют апофемой.
На рисунке — правильная четырёхугольная пирамида. Высота пирамиды \(KO\) проведена от вершины \(K\) к центру основания \(O\).
Высота боковой грани \(KN\) — апофема.
Если у правильной треугольной пирамиды все боковые грани — равносторонние треугольники (равные с основанием), то такую пирамиду называют правильным тетраэдром:
ΔABC=ΔABD=ΔACD=ΔBCDп.
Если у многоугольника в основании есть диагонали, то через эти диагонали и вершину пирамиды можно провести диагональное сечение.
На рисунке проведено диагональное сечение правильной четырёхугольной пирамиды.
Основные формулы для расчётов в правильных пирамидах
1. Боковая поверхность Sбок.=Pосн.⋅h3, где \(h\) — апофема. Для пирамид, которые не являются правильными, необходимо определить отдельно поверхность каждой боковой грани.
2. Полная поверхность Sполн.=Sосн.+Sбок.. Эта формула справедлива для всех пирамид, не только для правильных.
3. Объём V=13⋅Sосн.⋅H, где \(H\) — высота пирамиды. Эта формула справедлива для всех пирамид, не только для правильных.
4.1. Основные понятия
Определение 4.1.Многогранником в трехмерном пространстве называется совокупность конечного числа плоских многоугольников такая, что
- каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым по этой стороне;
- от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя по очереди от одного многоугольника к другому, смежному с ним.
Многоугольники, из которых состоят многогранники, называются гранями, их стороны – ребрами, а их вершины – вершинами многогранника.
Определение понятия «многогранник» в пространстве зависит от того, как на плоскости определять понятие «многоугольник». Если под многоугольником понимать плоские замкнутые ломаные (хотя бы и пересекающиеся), то приходим к первому определению многогранника. Чаще, однако, придерживаются другого определения многоугольника и, соответственно, многогранника. Под многоугольником понимается часть плоскости, ограниченная ломаными. С этой точки зрения, многогранник есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое тоже называется многогранником; отсюда возникает третья точка зрения на многогранники, как на геометрические тела, причем допускается существование у этих тел «дырок». На рисунке 4.1.1 приведены некоторые примеры многогранников.
На рисунке 4.1.1 приведены некоторые примеры многогранников.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников-граней.
Обозначения: V — объем; Формула Эйлера N − L + F = 2 N — число вершин, L — число ребер, F — число граней выпуклого многогранника.
| |
| |
|
|
|
|
|
|
Правильные многогранники Многогранник называется правильным, если все его грани — равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны. Существует пять различных правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр). Обозначения: | |
|
|
|
|
|
|
|
|
|
|
Урок 1: Многогранники — 100urokov.ru
План урока:
Понятие многогранника
Теорема Эйлера
Призма
Типичные задачи на призмы
Понятие многогранника
Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.
Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.
Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».
Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.
Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника. Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу.
Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:
На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.
А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.
Теорема Эйлера
У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?
Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:
4 + 4 — 6 = 2
Если выполнить такие же действия для параллелепипеда, то снова получится двойка:
6 + 8 — 12 = 2
Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:
Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.
Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?
Решение. Запишем теорему Эйлера:
Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?
Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:
Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?
Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:
Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?
Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?
Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:
Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:
Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.
Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.
Призма
Пусть в некоторой плос-ти α есть n-угольник с вершинами А1, А2, А3,…, Аn. Пусть в другой плос-ти β, которая параллельна α, есть равный ему многоуг-к В1В2В3…Вn, причем отрезки А1В1, А2В2, А3В3…, АnВn параллельны друг другу:
В результате мы получили геометрическую фигуру, которую именуют призмой. Многоуг-ки А1А2А3…Аn и В1В2В3…Вn именуются основаниями призмы, а все остальные грани – это боковые грани призмы. Можно доказать, что боковые грани – это параллелограммы. Действительно, в четырехуг-ке А1А2В2В1 стороны А1В1 и А2В2 параллельны по условию. Также они равны по теореме 12 из этого урока. Это и значит, что А1А2В2В1 – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:
Также они равны по теореме 12 из этого урока. Это и значит, что А1А2В2В1 – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:
Ребра призмы, не принадлежащие основанию, именуются боковыми ребрами призмы. Ясно, что любые два соседних ребра параллельны, ведь они являются сторонами параллелограммами. Но тогда по свойству транзитивности параллельности получается, что вообще любые два боковых ребра параллельны. Если из какой-нибудь точки основания построен перпендикуляр к противоположному основанию, то он именуется высотой призмы:
Естественно, что высота перпендикулярна обоим основаниям. Возможна ситуация, когда высота падает не на основание, а на какую-нибудь точку плос-ти основания, не находящуюся внутри него. Ясно, что все высоты призмы имеют одинаковую длину независимо от того, через какие точки они проведены, ведь высота по своей сути – это расстояние между плос-тями оснований.
Особый интерес вызывают призмы, где боковые ребра и основания перпендикулярны друг другу. Такие призмы именуются прямыми. Ясно, что у них боковые грани оказываются уже не просто параллелограммами, а уже прямоуг-ками. При этом любое боковое ребро одновременно является и высотой. Все остальные призмы именуют наклонными.
Если в основании призмы находится n-угольник, то призму называют n-угольной. В частности, в основании треугольной призмы лежит треуг-к, в основании десятиугольной призмы находится десятиугольник и т. д. Наконец, в особую группу выделяют прямые призмы, основаниями которых представляют собой правильные многоуг-ки. Их так и именуют – правильные призмы.
Если сложить площадь всех граней призмы, то получится сумма, которую именуют площадью полной поверхности призмы. Обычно ее обозначают как Sполн. Если же складываются только площади боковых граней, то в сумме получается площадь боковой поверхности призмы, обозначаемая как Sбок. Если площадь основания призмы обозначить как Sосн., то справедлива будет очевидная формула:
Если площадь основания призмы обозначить как Sосн., то справедлива будет очевидная формула:
Действительно, пусть есть прямая призма с основаниями А1А2…Аn и B1B2…Bn:
Так как ее боковые ребра перпендикулярны основаниям, то они должны быть перпендикулярны и тем ребрам, которые образуют основания. Это значит, каждая боковая грань – это прямоуг-к. При этом боковые ребра – это одновременно и высоты призмы. Тогда площадь боковых граней вычисляется так:
Отметим наконец, что параллелепипед можно считать частным случаем призмы, а прямоугольный параллелепипед – частным случаем прямой призмы.
Типичные задачи на призмы
Призмы нередко встречаются в заданиях ЕГЭ, поэтому важно уметь решать задачи, в которых используются эти фигуры.
Задание. Сколько диагоналей имеет n-угольная призма?
Решение. В любом многограннике диагональ соединяет точки, не лежащие на одной грани. Каждая вершина призмы принадлежит одному из оснований, причем в n-угольной призме каждому основанию принадлежат n вершин.
Возьмем произвольную вершину на одном из оснований и посчитаем, сколько диагоналей из нее можно провести. Если соединять ее отрезками с другими вершинами, принадлежащему тому же основанию, то получатся диагонали грани, но не диагонали призмы (зеленые линии на рисунке):
Значит, остается только провести прямые к тем вершинами, которые лежат в другом основании. Так как в другом основании находятся n вершин, то и отрезков будет ровно n. Однако три из них не будут диагоналями (показаны на рисунке синим цветом), так как будут либо являться одним из ребер призмы либо одной из диагоналей. Получается, что из вершины можно провести (n – 3) диагоналей. Так как в основании находятся n вершин, то всего можно построить n•(n– 3) диагоналей.
Ответ: n•(n – 3) диагоналей.
Задание. Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?
Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?
Решение. Выполним построение по условию задачи:
Здесь сечение проведено через ребро В1С1 и противолежащую ей вершину А. Призма правильная, поэтому ее основания ∆АВС и ∆А1В1С1 – это равносторонние треуг-ки, и все их стороны равны 8 см. По определению правильная призма обязательно ещё и прямая. Тогда боковые грани – прямоуг-ки.
∆АВВ1 – прямоугольный, с помощью теоремы Пифагора мы можем вычислить его гипотенузу АВ1:
Аналогично можно вычислить, что и диагональ АС1 также равна 10 см. Вообще в правильных призмах все грани – это равные друг другу прямоуг-ки, поэтому и диагонали у них одинаковы.
Длина ребра В1С1 составляет 8 см. Получается, нам надо вычислить площадь равнобедренного ∆АВ1С1 с основанием 8 см и боковыми сторонами 10 см. Это можно сделать множеством способов. Самый простой из них заключается в использовании формулы Герона. Для ее применения сначала вычислим полупериметр ∆АВ1С1:
Задание. В основании призмы находится равносторонний ∆АВС. Ребро АА1 образует одинаковые углы с ребрами АС и АВ. Докажите, что ребра АА1 и ВС перпендикулярны и что СС1В1В – прямоуг-к.
Решение. Выполняем построение:
По условию ∠А1АВ и ∠А1АС одинаковы. Проведем диагонали А1В и А1С. В итоге мы получим ∆А1АВ и А1АС. У них есть АА1 – общая сторона, стороны АВ и АС одинаковы (ведь ∆АВС – равносторонний), а углы между ними одинаковы. Значит, ∆А1АВ и А1АС равны, и тогда диагонали А1В и А1С одинаковы.
Получается, что точка А1 равноудалена вершин В и С. Аналогично и точка А равноудалена от В и С, ведь АВ и АС одинаковы. Это значит, что и А1, и А лежат на серединных перпендикулярах, проведенных к отрезку ВС:
Обозначим середину ВС как Н, тогда НА1 и НА – серединные перпендикулярны. То есть ВС⊥АН и ВС⊥А1Н. Но это значит (по признаку перпендикулярности прямой и плос-ти), что ВС перпендикулярен всей плос-ти АНА1. Из этого вытекает, что ВС⊥АА1, ч. т. д.
Осталось показать, что грань СС1В1В – это прямоуг-к. Так как ВВ1||АА1, и ВС⊥АА1, то и ВС⊥ВВ1. Значит в параллелограмме СС1В1В (напомним, что в призме все боковые грани – параллелограммы) есть прямой угол. Это значит, что он является прямоуг-ком, ч. т. д.
Задание. Призма АВСА1В1С1 – наклонная. Известно, что АС = АВ = 13 и ВС = 10. Боковые ребра призмы образуют с основанием АВС угол 45°. Проекция точки А1 на плос-ть АВС совпадает с точкой пересечения медиан в ∆АВС. Какова площадь грани СС1В1В?
Решение. Снова выполняем построение:
Здесь О – это проекция точки А1 и одновременно точка пересечения медиан. H– середина отрезка ВС, то есть АН – как раз одна из медиан. Заметим, что так как ∆АВС равнобедренный, и ВС – это его основание, то АН одновременно является и высотой, то есть ∠ВНА = 90°. Раз Н – середина ВС, то ВН будет вдвое короче ВС:
Напомним, точка пересечения медиан делит их в отношении 2:1, поэтому мы можем найти ОА:
Понятно, что ОА – это проекция прямой ОА на плос-ть АВС. Тогда угол между ребром АА1 и плос-тью АВС, по условию равный 45° – это ∠ОАА1.
Из прямоугольного ∆АОА1 с помощью тригонометрии мы найдем длину ребра АА1:
Теперь покажем, что грань СС1В1В – прямоуг-к. Ясно, что ОА1⊥ВН, ведь ОА1 – перпендикуляр ко всей плос-ти АВС. Но также ВН⊥АН. Значит, ВН перпендикулярен плос-ти АОА1, и, в частности, перпендикулярен ребру АА1. Но тогда и ВВ1⊥ВН, ведь ВВ1||АА1. Значит, грань СС1В1В – прямоуг-к, ведь в ней есть прямой угол. Для нахождения площади прямоуг-ка надо перемножить две его смежные стороны:
Задание. Ребро при основании правильной 6-угольной призмы имеет длину 23, а боковое ребро равно 50. Вычислите площадь поверхности призмы (и полную, и боковую).
Решение.
Сначала найдем площадь и периметр основания. Формулы для правильных многоуг-ков мы уже изучали:
Здесь а – сторона шестиугольника, R и r – радиусы описанной и вписанной окружности, n– число сторон шестиугольника. Во второй формуле мы использовали известный факт, что длина стороны правильного 6-угольника совпадает с радиусом описанной около него окружности.
Далее вычисляем площадь боковой поверхности:
Добавив к этому значению удвоенную площадь поверхности основания, найдем и полную площадь призмы:
Задание. В правильной треугольной призме АВСА1В1С1, у которой все ребра одинаковы и равны единице, вычислите угол между гранью АВС и сечением АСВ1:
Решение. Вспомним, что для нахождения угла между плос-тями необходимо построить в этих плос-тях перпендикуляры к линии их пересечения, причем эти перпендикуляры должны падать на одну и ту же точку.
Пересекаются плос-ти АВС и АСВ1 по грани АС. Заметим, что и ∆АВС, и ∆АСВ1 – равнобедренные, причем у них общее основание АС. Действительно, АВ = ВС, так как в основании правильной призмы лежит равносторонний треуг-к, а АВ1 = СВ1, так как это диагонали равных граней АВВ1А1 и ВСС1В1.
Если мы отметим середину отрезка АС (например, точкой Н) и соединим ее с В и В1, то мы получим две медианы НВ и НВ1, которые одновременно будут и высотой. Это значит, что именно ∠ВНВ1 и будет искомым углом между плос-тями:
Осталось найти ∠ВНВ1. Длину ВВ1 мы уже знаем, она составляет 1.
АН вдвое короче АС:
Теперь заметим, что ∆НВВ1 – прямоугольный, поэтому для него можно использовать тригонометрию:
Задание. Найдите угол между прямыми А1D и СD1 в правильной призме, показанной на рисунке:
Все ребра этой призмы равны единице.
Решение. Сначала внимательно рассмотрим верхнее основание призмы. Так как оно представляет собой правильный многоуг-к, то вокруг него можно описать окружность. Обозначим центр этой окружности как О и проведем радиусы к вершинам:
Так как в правильном шестиуг-ке радиус описанной окружности равен стороне шестиугольника, то получается, что ∆А1ОВ1, ∆В1ОС1 и ∆С1ОD1 – равносторонние. Тогда ∠А1ОВ1, ∠B1OC1 и ∠С1ОD1 составляют по 60°. Тогда ∠А1ОD1 равен 180°, то есть точки А1, О и D1 находятся на одной прямой А1D1. Также заметим, что эта прямая параллельна ребру В1С1, ведь ∠D1OC1и ∠ОС1B1 являются накрест лежащими для этих прямых (при секущей ОС1) и при том они одинаковы. Так как отрезки А1О и D1O как стороны равносторонних треуг-ков равны 1, то
Теперь вернемся к призме:
Так как А1D1||В1С1 и В1С1||ВС, то и А1D1||ВС. Это значит, что через А1D1 и ВС можно провести плос-ть, в которой будут лежать и интересующие нас прямые А1В и СD1. Для нахождения угла между ними надо рассмотреть четырехуг-к А1D1CB. Раз А1D1||ВС, то этот четырехуг-к является трапецией.
Далее найдем длину А1В. Для этого используем ∆АВА1:
Аналогично из ∆СDD1 можно определить, что СD1 имеет такую же длину. Это значит, что А1D1CB – равнобедренная трапеция.
Теперь рассмотрим отдельно эту трапецию, чтобы найти искомый угол:
Опустим из вершин трапеции В и С перпендикуляры на А1D1. В итоге получим прямоуг-к ВСРН, где
Сегодня мы более детально изучили понятие многогранника и познакомились с новой геометрической фигурой – призмой. Призма довольно часто встречается в задаче С2 на ЕГЭ. Также мы узнали о теореме Эйлера, из которой вытекают некоторые важные факты. Один из них заключается в том, что не бывает выпуклых многогранников, у которых ни одна грань не является треуг-ком, четырехуг-ком или пятиуг-ком.
Как найти площадь многогранника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Что такое многогранник? — Определение, факты и пример
Многогранник
Многогранник — это трехмерное тело, образованное соединением многоугольников.
Слово «многогранник» происходит от двух греческих слов: поли, означающее «много», и «эдрон», обозначающее поверхность.
Многогранники определяются количеством граней, которые у них есть.
Пример многогранника
Части многогранника
Каждый многогранник состоит из трех частей:
- Грань: плоские поверхности, составляющие многогранник, называются его гранями. Эти грани представляют собой правильные многоугольники.
- Кромка: области, где две плоские поверхности встречаются и образуют линейный сегмент, называются кромками.
- Вершина: это точка пересечения ребер многогранника. Вершину также называют углом многогранника. Множественное число вершин называется вершинами.
Имена многогранников основаны на количестве граней, которые у них есть:
Имя | №лиц |
Тетраэдр | Многогранник с 4 гранями. |
Пентаэдр | 5-гранный многогранник. |
Шестигранник | Шестигранный многогранник. |
Гептаэдр | Семи гранный многогранник. |
Октаэдр | Многогранник с 8 гранями. |
Нонаэдр | 9-гранный многогранник. |
Декаэдр | Многогранник с 10 гранями |
Виды многогранника
Правильный многогранник
Правильный многогранник состоит из правильных многоугольников.Такие твердые тела также известны как «платоновые твердые тела»
.
Неправильный многогранник
Неправильный многогранник состоит из многоугольников разной формы, в которых все компоненты не одинаковы. Это означает, что все стороны неправильного многогранника не равны.
Некоторые из правильных многоугольников описаны в таблице ниже:
Многогранники в быту
Примеры | Изображения |
Дома / Постройки: Большинство домов вокруг нас многогранники, так как они сделаны из плоских поверхностей. | |
Призма A: призма состоит из трех прямоугольников, соединенных вместе треугольными основаниями | |
Футбольный мяч или футбольный мяч | |
Пирамиды: Многогранник с четырьмя сторонами является тетраэдром и также называется пирамидой. |
Интересные факты о многограннике
Если мы знаем количество граней и вершину многогранника, количество ребер можно вычислить с помощью «формулы многогранника» или «формулы Эйлера».
F + V = E — 2
, где F, V и E представляют количество граней, ребер и вершин многогранника соответственно.
1.5.3: Сети и площадь поверхности
Давайте воспользуемся сетками, чтобы найти площадь поверхности многогранников.
Сводка
Сеть пирамиды имеет один многоугольник, который является основанием. Остальные многоугольники — треугольники. Здесь показаны пятиугольная пирамида и ее сетка.
Рисунок \ (\ PageIndex {6} \)Сеть призмы имеет две копии многоугольника, который является основанием.Остальные многоугольники — прямоугольники. Здесь показаны пятиугольная призма и ее сетка.
Рисунок \ (\ PageIndex {7} \)В прямоугольной призме есть три пары параллельных и идентичных прямоугольников. Основанием может быть любая пара этих одинаковых прямоугольников.
Рисунок \ (\ PageIndex {8} \)Поскольку сеть показывает все грани многогранника, мы можем использовать ее, чтобы найти площадь его поверхности. Например, сетка прямоугольной призмы показывает три пары прямоугольников: 4 единицы на 2 единицы, 3 единицы на 2 единицы и 4 единицы на 3 единицы.
Рисунок \ (\ PageIndex {9} \)Площадь поверхности прямоугольной призмы составляет 52 квадратных единицы, потому что \ (8 + 8 + 6 + 6 + 12 + 12 = 52 \).
Глоссарий
Определение: Основание (призмы или пирамиды)
Слово с основанием может также относиться к грани многогранника.
У призмы два идентичных основания, расположенных параллельно. У пирамиды одно основание.
Призма или пирамида названы в честь формы их основания.
Рисунок \ (\ PageIndex {10} \): Рисунок слева помечен пятиугольной призмой.Сверху и внизу расположены два одинаковых пятиугольника. Каждая вершина пятиугольника соединена вертикальным сегментом с соответствующей вершиной других пятиугольников. Каждый пятиугольник заштрихован, и основание слова указывает на каждый из них. Фигура справа помечена шестиугольной пирамидой. Внизу находится шестиугольник, заштрихованный зеленым. Из точки над шестиугольником проходят 6 сегментов, каждый из которых соединен с вершиной шестиугольника.Определение: лицо
Каждая плоская сторона многогранника называется гранью.Например, у куба 6 граней, и все они квадратные.
Определение: Net
Сеть — это двумерная фигура, которую можно сложить в многогранник.
Вот сетка для куба.
Рисунок \ (\ PageIndex {11} \)Определение: Многогранник
Многогранник — это замкнутая трехмерная форма с плоскими сторонами. Когда у нас более одного многогранника, мы называем их многогранниками.
Вот несколько рисунков многогранников.
Рисунок \ (\ PageIndex {12} \)Определение: призма
Призма — это тип многогранника, у которого есть два основания, которые являются идентичными копиями друг друга.Основания соединяются прямоугольниками или параллелограммами.
Вот несколько чертежей призм.
Рисунок \ (\ PageIndex {13} \)Определение: Пирамида
Пирамида — это разновидность многогранника с одним основанием. Все остальные грани представляют собой треугольники, и все они пересекаются в одной вершине.
Вот несколько рисунков пирамид.
Рисунок \ (\ PageIndex {14} \)Определение: Площадь поверхности
Площадь поверхности многогранника — это количество квадратных единиц, покрывающих все грани многогранника без зазоров и перекрытий.
Например, если каждая грань куба имеет площадь 9 см 2 , то площадь поверхности куба равна \ (6 \ cdot 9 \), или 54 см 2 .
Многогранник — Типы многогранников — Названные, Выпуклые, Многоугольники и Куб
Многогранник — это трехмерная замкнутая поверхность или твердое тело, ограниченное плоскостью фигуры, называемые многоугольниками .
Слово многогранник происходит от греческого префикса поли- , что означает «многие», и корневого слова hedron , которое означает «поверхность».»Многогранник — это твердое тело, границы которого состоят из плоскостей. Многие обычные объекты в мире вокруг нас имеют форму многогранников. Куб можно увидеть повсюду, от игральных костей до радиочасов; коробки для компакт-дисков и палочки с маслом находятся в форма многогранников называется параллелепипедами. Пирамиды являются разновидностью многогранников, как и геодезических купола . Большинство форм, образующихся в природе, имеют неправильную форму. Однако за интересным исключением кристаллы растут в математически совершенные и часто сложные многогранники.
Ограничивающие многоугольники многогранника называются гранями. Отрезки линии, вдоль которых встречаются грани, называются ребрами. Точки пересечения концов ребер (представьте себе угол коробки с хлопьями) — это вершины. Вершины через тело многогранника соединяются воображаемой линией, называемой диагональю.
Многогранник считается выпуклым, если диагональ содержит только точки внутри многогранника. Выпуклые многогранники также известны как многогранники Эйлера и могут быть определены уравнением E = v + f — e = 2, где v — количество вершин, f — число граней, а e — количество граней.Пересечение плоскости и многогранника называется сечением многогранника. Поперечные сечения выпуклого многогранника — это все выпуклые многоугольники.
Многогранники классифицируются и именуются в соответствии с количеством и типом граней. Многогранник с четырьмя сторонами — это тетраэдр , но его также называют пирамидой . Шестигранный куб еще называют шестигранником. Многогранник с шестью прямоугольниками в качестве сторон также имеет много названий — прямоугольный параллелепипед, прямоугольный , призма или прямоугольник.
Многогранник, у которого все грани представляют собой правильные многоугольники, конгруэнтные друг другу, у которого все многогранные ангелы равны и у которого одинаковое количество граней пересекаются в каждой вершине, называется правильным многогранником. Существует только пять правильных многогранников: тетраэдр (четыре треугольных грани), куб (шесть квадратных граней), октаэдр (восемь треугольных граней — представьте себе две пирамиды, помещенные снизу вниз), додекаэдр (12 пятиугольных граней) и икосаэдр. (20 треугольных граней).
Другие общие многогранники лучше всего описать как такие же, как и один из ранее названных, у которого часть его обрезана или усечена плоскостью.Представьте, что вы срезаете углы куба, чтобы получить, например, многогранник, состоящий из треугольников и квадратов.
Формула многогранника Эйлера | plus.maths.org
Июнь 2007 г.
Леонард Эйлер, 1707 — 1783
Давайте начнем с представления главного героя этой истории — формулы Эйлера:
В — E + F = 2.Хотя это может показаться простой, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками , которые очаровывали математиков более 4000 лет.На самом деле я могу пойти дальше и сказать, что формула Эйлера говорит нам нечто очень глубокое о форме и пространстве. Формула носит имя знаменитого швейцарского математика Леонарда Эйлера (1707–1783), которому в этом году исполнилось бы 300 лет.
Что такое многогранник?
Прежде чем мы исследуем, что говорит нам формула Эйлера, давайте рассмотрим многогранники более подробно. Многогранник — это твердый объект, поверхность которого состоит из ряда плоских граней , которые сами по себе ограничены прямыми линиями.Каждая грань представляет собой многоугольник , замкнутую форму на плоской 2-мерной плоскости, состоящую из точек, соединенных прямыми линиями.
Рис. 1. Знакомые треугольник и квадрат являются многоугольниками, но многоугольники могут иметь и более неправильную форму, как показано справа.
В многоугольниках не разрешается иметь отверстия, как показано на рисунке ниже: левая фигура здесь является многоугольником, а правая — нет.
Рис. 2: Фигура слева — многоугольник, а фигура справа — нет, потому что в ней есть «дыра».
Многоугольник называется правильным , если все его стороны имеют одинаковую длину и все углы между ними одинаковы; треугольник и квадрат на рисунке 1 и пятиугольник на рисунке 2 правильные.
Многогранник — это то, что вы получаете, когда перемещаетесь на одно измерение вверх. Это замкнутый твердый объект, поверхность которого состоит из множества многоугольных граней. Мы называем стороны этих граней ребрами — две грани пересекаются вдоль каждого из этих ребер. Назовем углы граней вершинами , так что любая вершина лежит как минимум на трех разных гранях.Чтобы проиллюстрировать это, вот два примера известные многогранники.
Рис. 3. Знакомый куб слева и икосаэдр справа. Многогранник состоит из многоугольных граней , их стороны известны как ребер , а углы — как вершин .
Многогранник состоит из одной части. Например, он не может состоять из двух (или более) в основном отдельных частей, соединенных только ребром или вершиной. Это означает, что ни один из следующих объектов не является истинным многогранником.
Рисунок 4: Эти объекты не являются многогранниками, потому что они состоят из двух отдельных частей, которые встречаются только на ребре (слева) или вершине (справа).
Что нам говорит формула?
Теперь мы готовы посмотреть, что формула Эйлера говорит нам о многогранниках. Посмотрите на многогранник, например куб или икосаэдр, посчитайте количество вершин, которые у него есть, и назовите это число V . У куба, например, 8 вершин, поэтому V = 8 .Затем посчитайте количество ребер многогранника и назовите это число E . У куба 12 ребер, поэтому в случае куб E = 12 . Наконец, посчитайте количество лиц и назовите его F . В случае с кубом F = 6 . Теперь формула Эйлера говорит нам, что
В — E + F = 2;или, говоря словами: количество вершин минус количество ребер плюс количество граней равно двум.
В случае с кубом мы уже видели, что V = 8, E = 12 и F = 6 .Итак,
V — E + F = 8 — 12 + 6 = 14 — 12 = 2, что и должно быть согласно формуле Эйлера. Если мы теперь посмотрим на икосаэдр, мы обнаружим, что V = 12, E = 30 и F = 20 . Сейчас,
V — E + F = 12-30 + 20 = 32-30 = 2, как мы и ожидали.Формула Эйлера верна для куба и икосаэдра. Оказывается, довольно красиво, что это верно для почти для каждого многогранника . Единственные многогранники, для которых это не работает, — это те, в которых есть отверстия, как показано на рисунке ниже.
Рис. 5. В многограннике сквозное отверстие. Формула Эйлера в этом случае не выполняется.
Эти многогранники называются непростыми , в отличие от многогранников без отверстий, которые называются простыми . Непростые многогранники, возможно, не первое, что приходит в голову, но их много, и мы не можем избежать того факта, что формула Эйлера не работает ни с одним из них. Однако даже этот неловкий факт стал частью совершенно новой теории о космосе. и форма.
Сила формулы Эйлера
Каждый раз, когда математики сталкиваются с инвариантным признаком, свойством, истинным для целого класса объектов, они знают, что натолкнулись на что-то хорошее. Они используют его, чтобы исследовать, какими свойствами может обладать отдельный объект, и для определения свойств, которые должны иметь все они. Формула Эйлера может сказать нам, например, что не существует простого многогранника с ровно семь граней. Вам не нужно садиться с картоном, ножницами и клеем, чтобы узнать это — формула — это все, что вам нужно.Аргумент, показывающий, что не существует семигранного многогранника, довольно прост, так что взгляните на него, если вам интересно.
Используя аналогичным образом формулу Эйлера, мы можем обнаружить, что не существует простого многогранника с десятью гранями и семнадцатью вершинами. Призма, показанная ниже, в основе которой лежит восьмиугольник, имеет десять граней, но число вершин здесь шестнадцать. Пирамида, имеющая 9-гранное основание, также имеет десять граней, но имеет десять вершин. Но формула Эйлера говорит нам, что ни один простой многогранник не имеет ровно десять граней и семнадцать вершин.
Рисунок 6: Оба этих многогранника имеют десять граней, но ни у одного из них нет семнадцати вершин.
Именно такие соображения приводят нас к, вероятно, самому прекрасному открытию из всех. Он включает Платоновых тел , хорошо известный класс многогранников, названный в честь древнегреческого философа Платона, в трудах которого они впервые появились.
Рисунок 7: Платоновы тела. Слева направо мы видим тетраэдр с четырьмя гранями, куб с шестью гранями, октаэдр с восемью гранями, додекаэдр с двенадцатью гранями и икосаэдр с двадцатью гранями.
Хотя их симметричная элегантность сразу бросается в глаза, когда вы смотрите на приведенные выше примеры, на самом деле не так просто описать это словами. Оказывается, это описывается двумя особенностями. Во-первых, у Платоновых тел нет ни шипов, ни провалов, поэтому они имеют красивую округлую форму. Другими словами, это означает, что всякий раз, когда вы выбираете две точки в Платоновом теле и рисуете прямая линия между ними, этот кусок прямой линии будет полностью заключен в твердое тело — Платоново твердое тело называется выпуклым .Вторая особенность, называемая регулярностью , заключается в том, что все грани твердого тела представляют собой правильные многоугольники с одинаковым количеством сторон и одинаковое количество ребер выходит из каждой вершины твердого тела.
Куб правильный, так как все его грани квадратные и из каждой вершины выходит ровно три ребра. Вы можете сами убедиться, что тетраэдр, октаэдр, икосаэдр и додекаэдр тоже правильные.
Теперь вы можете задаться вопросом, сколько существует различных Платоновых Тел.С момента открытия куба и тетраэдра математиков настолько привлекла элегантность и симметрия Платоновых тел, что они искали больше и пытались перечислить их все. Здесь на помощь приходит формула Эйлера. Вы можете использовать ее, чтобы найти все возможности для числа граней, ребер и вершины правильного многогранника. Вы обнаружите, что на самом деле существует только пять различных правильных выпуклых многогранников! Это очень удивительно; в конце концов, количество различных правильных многоугольников не ограничено, так почему мы должны ожидать здесь ограничения? Пять Платоновых Тел — это тетраэдр, куб, октаэдр, икосаэдр и додекаэдр, показанные выше.
Доказательство
Рене Декарт,
(1596–1650)
Игра с различными простыми многогранниками покажет вам, что формула Эйлера всегда верна. Но если вы математик, этого недостаточно. Вам понадобится доказательство, водостойкий логический аргумент, который показывает, что это действительно работает для всех многогранников, включая те, которые у вас никогда не будет времени проверить.
Адриан-Мари Лежандр, (1752 — 1833)
Несмотря на название формулы, на самом деле не Эйлер придумал первое полное доказательство.Его история сложна, насчитывает 200 лет и включает в себя некоторых из величайших математиков, в том числе Рене Декарта (1596–1650), самого Эйлера, Адриана-Мари Лежандра (1752–1833) и Огюстена-Луи Коши (1789–1857).
Огюстен-Луи Коши, (1789 — 1857)
Интересно отметить, что все эти математики использовали очень разные подходы для доказательства формулы, каждый из которых поражал своей изобретательностью и проницательностью. Тем не менее, это доказательство Коши, и я хотел бы дать вам здесь представление.Его метод состоит из нескольких этапов и шагов. Первый этап включает построение так называемой сети .
Создание сети
Представьте, что вы держите свой многогранник одной стороной вверх. Теперь представьте, что вы «удаляете» только эту грань, оставляя края и вершины вокруг нее позади, так что у вас есть открытая «коробка». Затем представьте, что вы можете держаться за коробку и отодвинуть края отсутствующей грани друг от друга. Если вы потянете их достаточно далеко, коробка расплющится и превратится в сеть точек и линий. в плоской плоскости.Приведенная ниже серия диаграмм иллюстрирует этот процесс применительно к кубу.
Рисунок 8: Превращение куба в сеть.
Как вы можете видеть на диаграмме выше, каждая грань многогранника становится областью сети, окруженной ребрами, и это то, что мы будем называть гранью сети. Это внутренних лиц сети. Также существует внешняя грань , состоящая из области вне сети; это соответствует той грани, которую мы удалили из многогранника.Итак, у сети есть вершины, прямые края и многоугольные грани.
Рисунок 9: Сеть имеет грани, ребра и вершины.
При формировании сети вы не добавляли и не удаляли вершины, поэтому сеть имеет то же количество вершин, что и многогранник — V . Сеть также имеет такое же количество ребер — E — что и многогранник. Теперь о лицах; все грани многогранника, кроме «недостающей», оказываются «внутри» сети. Отсутствующее лицо стало внешним лицом, которое тянется по всей сети.Итак, включая внешнюю грань, в сети насчитывается F граней. Таким образом, вы можете использовать сеть , а не сам многогранник, чтобы найти значение V — E + F . Теперь мы продолжим преобразование нашей сети, чтобы упростить вычисление этого значения.
Преобразование сети
Есть три типа операций, которые мы можем выполнять в нашей сети. Мы представим три этапа с их участием.
Шаг 1 Мы начинаем с рассмотрения полигональных граней сети и спрашиваем: существует ли грань с более чем тремя сторонами? Если есть, мы рисуем диагональ, как показано на схеме ниже, разделяя лицо на две меньшие грани.
Рисунок 10: Разделение граней.
Мы повторяем это с выбранной гранью до тех пор, пока грань не будет разбита на треугольники.
Рис. 11: В итоге у нас остались треугольные грани.
Если есть еще одна грань с более чем тремя сторонами, мы используем Шаг 1 для этой грани, пока она тоже не будет разбита на треугольные грани. Таким образом, мы можем разбить каждую грань на треугольные грани и получить новую сеть, все грани которой треугольные. Мы проиллюстрируем этот процесс, показав, как преобразовать сеть, созданную из куба.
Рисунок 12: Вот что происходит с сетью куба, когда мы неоднократно выполняем Шаг 1.
Мы возвращаемся к шагу 1 и смотрим на сеть, которую мы получаем после выполнения шага 1 только один раз. Теперь, нарисовав диагональ, мы добавили одно ребро. Наше исходное лицо стало двумя лицами, поэтому мы добавили одно к количеству лиц. Мы не изменили количество вершин. Теперь сеть имеет V, вершин, E + 1 ребер и F + 1 граней. Так как же V — E + F изменилось после того, как мы выполнили шаг 1 один раз? Используя то, что мы знаем об изменениях в V, , E и F , мы можем увидеть, что V — E + F превратилось в V — (E + 1) + (F + 1) .Теперь у нас
V — (E + 1) + (F + 1) = V — E — 1 + F + 1 = V — E + F.Итак, V — E + F имеет не изменено после шага 1! Поскольку каждое использование шага 1 оставляет V — E + F неизменным, оно остается неизменным, когда мы достигаем нашей новой сети, состоящей полностью из треугольников! Влияние на V — E + F при преобразовании сети, созданной из куба, показано в таблице ниже.
| Круглый | В | E | F | V — E + F |
| (а) | 8 | 12 | 6 | 2 |
| б) | 8 | 13 | 7 | 2 |
| (в) | 8 | 14 | 8 | 2 |
| г | 8 | 15 | 9 | 2 |
| д) | 8 | 16 | 10 | 2 |
| (ж) | 8 | 17 | 11 | 2 |
Теперь мы представляем шаги 2 и 3.Они будут удалять грани с внешней стороны сети, шаг за шагом уменьшая количество лиц. Как только мы начнем это делать, сеть, вероятно, больше не будет представлять собой многогранник, но важное свойство сети сохранится.
Шаг 2 Проверяем, есть ли в сети грань, которая имеет только одно ребро с внешней гранью. Если это так, мы удаляем эту грань, удаляя одно общее ребро. Область, которая была покрыта выбранной нами гранью, становится частью внешней грани, и сеть имеет новую границу.Это проиллюстрировано приведенной ниже схемой для сети, построенной из куба.
Рис. 13: Удаление граней с одной внешней кромкой.
Теперь возьмем V , E и F как числа вершин, ребер и граней, которые имела сеть, состоящая из треугольных граней, до того, как мы выполнили шаг 2. Теперь посмотрим, как число V — E + F изменился после того, как мы выполнили Шаг 2 один раз. Мы удалили одно ребро, поэтому наша новая сеть имеет E — 1 ребер.Мы не трогали вершины в всего, так что у нас осталось V вершин. Грань, которую мы использовали для шага 2, была объединена с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в V — (E — 1) + (F — 1) и
. V — (E — 1) + (F — 1) = V — E + 1 + F — 1 = V — E + F.Итак, еще раз V — E + F не изменился.
Step 3 Мы проверяем, есть ли у нашей сети грань, которая имеет два общих ребра с внешней гранью.Если это так, мы удаляем эту грань, удаляя как эти общие ребра, так и их общую вершину, так что снова область, принадлежащая нашей выбранной грани, становится частью внешней грани. Это проиллюстрировано ниже в случае сети, сделанной из куба, после выполнения шага 2. дважды.
Рисунок 14: Удаление граней с двумя внешними кромками.
Как и раньше, возьмем V , E и F в качестве количества вершин, ребер и граней сети, с которой мы начинаем.Каким образом шаг 3 повлиял на число V — E + F ? Мы удалили одну вершину — ту, которая находится между двумя ребрами, — теперь осталось V — 1 вершин. Мы удалили два ребра, так что теперь есть E — 2 кромок. Наконец, наша выбранная грань слилась с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в (V — 1) — (E — 2) — (F — 1) и
. (V — 1) — (E -2) + (F — 1) = V — 1 — E + 2 + F — 1 = V — E + F.Итак, еще раз V — E + F не изменился.
Секрет доказательства заключается в выполнении последовательности шагов 2 и 3 для получения очень простой сети. Напомним, что мы неоднократно использовали шаг 1 для создания сети только с треугольными гранями. Эта сеть определенно будет иметь грань, которая имеет ровно одно ребро с внешней гранью, поэтому мы берем эту грань и выполняем Шаг 2. Мы можем выполнить Шаг 2 на нескольких гранях, по одной, пока не появится появится грань, имеющая два ребра с внешней гранью.Затем мы можем выполнить шаг 3, используя это лицо. Мы продолжаем выполнять шаги 2 и 3 и продолжаем удалять лица таким образом.
При этом необходимо соблюдать два важных правила. Во-первых, мы всегда должны выполнять Шаг 3, когда это возможно; если есть выбор между Шагом 2 и Шагом 3, мы всегда должны выбирать Шаг 3. В противном случае сеть может разбиться на отдельные части. Во-вторых, мы должны удалять лица только по одному. Если мы этого не сделаем, мы можем закончить тем, что края сами по себе будут торчать наружу. лицо, и у нас больше не будет нормальной сети.Чтобы проиллюстрировать процесс, мы выполним несколько шагов в сети куба, продолжая с того места, где мы оставили его на последней диаграмме.
Рисунок 15: Применение нашего алгоритма к сети куба.
Теперь мы можем задать себе один или два вопроса. Прекращается ли когда-нибудь этот процесс удаления лиц, и если да, то с чем мы остались? Небольшое размышление покажет вам, что он должен остановиться — мы можем удалить только конечное число граней и ребер — и что когда это произойдет, у нас останется один треугольник.Вы можете увидеть несколько диаграмм, описывающих весь процесс для сети, образованной из додекаэдра (напомним, что это было одно из Платоновых тел, представленных ранее).
Теперь посмотрите на количество вершин, ребер и граней, присутствующих в нашей окончательной сети — единственном треугольнике. У нас V = 3 , E = 3 и F = 2 — мы все равно должны включить внешнюю грань. Сейчас
V — E + F = 3 — 3 + 2 = 2.На протяжении всего процесса, начиная с полного многогранника и заканчивая треугольником, значение V — E + F не менялось.Итак, если V — E + F = 2 для конечной сети, мы также должны иметь V — E + F = 2 для самого многогранника! Доказательство закончено!
За многогранниками
Я закончу упоминанием некоторых следствий формулы Эйлера за пределами мира многогранников. Я начну с очень малого: компьютерных чипов. Компьютерные микросхемы — это интегральные схемы, состоящие из миллионов мельчайших компонентов, связанных миллионами проводящих дорожек. Они напоминают наши сети выше, , за исключением , которые обычно невозможно разложить в плоскости. без некоторых проводящих дорожек — краев — пересечения.Крестовины — плохая вещь в схемотехнике, поэтому их количество должно быть уменьшено, но найти подходящее расположение — непростая задача. Формула многогранника Эйлера с ее информацией о сетях является важным ингредиентом в поиске решений.
Теперь перейдем к самому большому: нашей Вселенной. До сих пор космологи не пришли к единому мнению о его точной форме. Основным для их рассмотрения является топология , , математическое исследование формы и пространства. В 19 веке математики обнаружили, что все поверхности в трехмерном пространстве по существу характеризуются количеством отверстий, которые у них есть: наши простые многогранники не имеют отверстий, т.е. пончик имеет одно отверстие и т. д.Формула Эйлера не работает для многогранников с дырками, но математики обнаружили захватывающее обобщение. Для любого многогранника V — E + F ровно в 2 минус 2 раза больше количества отверстий! Оказывается, это число, называемое эйлеровой характеристикой , имеет решающее значение для изучения всех трехмерных поверхностей, а не только многогранников. Формулу Эйлера можно рассматривать как катализатор совершенно нового мышления о форме и пространстве.
Об авторе
Аби выросла на севере Англии и переехала на юг, чтобы изучать математику в Имперском колледже в Лондоне и Королеве Марии в Лондонском университете.Сейчас она преподает математику в Открытом университете. Главный математический интерес Аби — теория групп. При написании этой статьи ей очень понравилось исследовать тайны формулы Эйлера.
Первоначально опубликовано 1 июня 2007 г.
Многогранник | Encyclopedia.com
Многогранник — это замкнутое трехмерное твердое тело, полностью ограниченное по крайней мере четырьмя многоугольниками, два из которых не находятся в одной плоскости. Многоугольники — это плоские двухмерные фигуры (плоскости), ограниченные прямыми сторонами.Квадрат и треугольник — два примера многоугольников.
Количество сторон каждого многоугольника является основным отличительным признаком многогранников друг от друга. Некоторые общие многоугольники — это треугольник (с тремя сторонами), четырехугольник (с четырьмя сторонами), пятиугольник (с пятью сторонами), шестиугольник (с шестью сторонами), семиугольник (с семью сторонами) и восьмиугольник (с восемью сторонами). стороны).
Правильный многоугольник, как и квадрат, имеет равные внутренние углы и равные длины сторон.Многоугольник считается неправильным, если его внутренние углы не равны или если длины его сторон не равны.
Каждый многоугольник многогранника называется гранью. Прямая сторона, пересекающая две грани, называется ребром. Точка, в которой встречаются три или более ребра, называется вершиной. На рисунке ниже показаны эти особенности куба, который представляет собой хорошо известный многогранник, состоящий из шести квадратных граней.
Связь между количеством вершин ( v ), граней ( f ) и ребер ( e ) задается уравнением v + f — e = 2.Например, куб имеет 8 вершин, 6 граней и 12 ребер, что дает 8 + 6 — 12 = 2. Значение v + f — e для многогранника называется эйлеровой характеристикой поверхности многогранника. в честь швейцарского математика Леонарда Эйлера (1707–1783). Используя эйлерову характеристику и зная две из трех переменных, можно вычислить третью переменную.
Платоновы и архимедовы тела
Существует множество групп многогранников, классифицируемых по определенным характеристикам — слишком много, чтобы обсуждать их здесь.Одна общая группа известна как Платоновы тела, названные так потому, что ее пять членов появились в трудах греческого философа Платона. Платоновы тела входят в большую группу, известную как правильные многогранники, в которой многоугольники каждого из них правильные и конгруэнтные (то есть все многоугольники одинаковы по размеру и форме, а все ребра одинаковы по длине) и характеризуются одинаковыми количество полигонов, пересекающихся в каждой вершине.
На иллюстрации ниже изображены пять Платоновых тел (слева направо): тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Тетраэдр состоит из четырех треугольных граней и представлен как {3, 3}, в котором первые 3 указывают, что каждая грань состоит из трех сторон, а вторые 3 указывают, что три грани пересекаются в каждой вершине. Куб, иногда называемый шестигранником, имеет шесть квадратных граней и представлен как {4, 3}. Октаэдр состоит из восьми равносторонних треугольников и состоит из двух одинаковых квадратных пирамид, основанных на основании. Октаэдр представлен как {3, 4}. Додекаэдр состоит из пяти сторон каждой грани и трех пятиугольников, пересекающихся в каждой из двадцати вершин многогранника.Он представлен {5, 3}. Икосаэдр состоит из пяти равносторонних треугольников вокруг каждой вершины. Он содержит равносторонние равносторонние треугольники с двадцатью гранями и двенадцатью вершинами и описывается как {3, 5}.
Архимедовы тела. Другая распространенная группа многогранников — это архимедовы тела, в которых появляются два или более различных типа многоугольников. Каждая грань представляет собой правильный многоугольник, и вокруг каждой вершины появляются одинаковые многоугольники в той же последовательности. Например, усеченный додекаэдр состоит из последовательности пятиугольник-пятиугольник-треугольник.
Сетки
Многогранник можно «раскрыть» вдоль некоторых его краев до тех пор, пока его поверхность не расплющится, как коврик. Полученная карта, похожая на выкройку портнихи, называется сеткой. Сеть содержит все грани многогранника, некоторые из которых разделены угловыми промежутками. Поскольку сетка представляет собой плоский узор, который затем можно сложить по краям и связать вместе, чтобы восстановить исходный многогранник, сетка, таким образом, позволяет легко создавать базовые многогранники из бумаги. Построение моделей многогранников может облегчить изучение геометрических понятий.
см. Также Сети.
Уильям Артур Аткинс с
Филип Эдвард Кот
Библиография
Хендерсон, Кеннет Б. Современная геометрия: ее структура и функции. Сент-Луис: Webster Division McGraw-Hill Book Company, 1962.
Что такое многогранник — определение, типы и примеры
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что».«Студенты могут изучить огромное количество интерактивных рабочих листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
Введение в многогранники Что такое многогранники?Многогранник — это трехмерная фигура с плоскими гранями, прямыми краями и острыми углами или вершинами.
Слово «многогранник» происходит от греческих слов poly , что означает «много», и hedron , что означает «поверхность».
Таким образом, многогранник означает множество плоских поверхностей, соединенных вместе, чтобы образовать трехмерную форму.
Множественное число многогранника — это многогранника.
В зависимости от количества граней многоугольника в многограннике они подразделяются на различные формы многогранников.
Различные формы многогранников также определяются их основанием многоугольника.
Наша жизнь вращается вокруг многогранников, поскольку мы живем в трехмерном мире.
Например, кирпичи, игральные кости, офисные столы, дома и т. Д. — все это примеры многогранников.
Фигуры многогранниковПо количеству многоугольных граней и оснований многогранники подразделяются на различные формы многогранников.
Существует три основных категории многогранников.
- Семейство призм
- Семья пирамид
- Платоновы тела
Они снова в основном делятся на два типа — правильные многогранники и неправильные многогранники.
Правильные многогранникиМногогранник, все грани которого являются правильными многоугольниками и конгруэнтны друг другу, и имеют одинаковое количество граней, пересекающихся в каждой вершине, известен как правильный многогранник .
В правильном многограннике все многогранные углы равны.
неправильные многогранникиМногогранник с неправильными многоугольными гранями, которые не совпадают друг с другом, и в котором многогранные углы не равны, называется неправильным многогранником .
Вогнутый многогранникЕсли отрезок прямой, соединяющий две точки, лежит на выпуклой поверхности многогранника, он называется Вогнутым многогранником .
Выпуклый многогранникЕсли отрезок прямой, соединяющий две точки, лежит на внутренней поверхности многогранника, он называется выпуклым многогранником .
- Сделайте эти фигуры, используя простой лист бумаги.Это поможет визуализировать твердые формы.
- Используя геотвердое тело, проведите пальцем по каждой форме, чтобы понять концепцию граней, ребер и вершин.
Правильные многогранники или платоновы тела выпуклые с одинаковым количеством граней, пересекающихся в каждой вершине, и сторонами, которые равны.
Это 5 правильных многогранников.3 \ end {align} \)
Икосаэдр- У этого многогранника 20 граней.
- Каждая грань имеет форму равностороннего треугольника.
- Имеет 30 ребер.
- У него 12 вершин и 5 ребер, пересекающихся в каждой вершине.
Множественное число многогранника — это многогранника, или многогранника.
Наиболее часто встречающиеся многогранники:
Обычные многогранники
Примеры из реальной жизни
Призмы, египетские пирамиды, ульи, бриллианты — вот некоторые из реальных примеров многогранников.
CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку Многогранник , используя интерактивные симуляции и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!
Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Подсчет граней, вершин и ребер
грани многогранников — это плоские стороны индивидуальной многогранной геометрии.
Края указывают, где встречаются две или более граней.
вершины обозначают углы.
Подсчет лицПосмотрите на фигуру ниже.
Сколько лиц вы можете сосчитать?
Вы видите, что у него лицо сверху, снизу, слева, справа, спереди и сзади?
В этом примере мы можем наблюдать 8 лиц.
Счетные кромкиТеперь посчитаем ребра в указанном выше многограннике.
Мы видим, что у фигуры 18 ребер.
Подсчет вершинВы можете заметить, что у этой формы 12 вершин.
ОтношенияСуществует взаимосвязь между количеством граней, ребер и вершин в многограннике.
Мы можем представить эту взаимосвязь в виде математической формулы.
Это соотношение известно как Формула Эйлера .
где,
F = Количество граней
V = Количество вершин
E = Количество ребер
Формула многогранникаВ показанном ниже моделировании вы можете исследовать взаимосвязь между гранями, вершинами и ребрами тетраэдра, используя формулу Эйлера.
Важные примечания
- Многогранник — это трехмерная форма с плоскими гранями, прямыми краями и острыми вершинами.
- Обычно они встречаются в виде призм, пирамид и платоновых тел.
- Пять правильных многогранников или платоновых тел: Тетраэдр, Куб, Октаэдр, Додекаэдр и Икосаэдр.
- Подсчитав количество граней, вершин и ребер многогранника, мы можем связать их формулой Эйлера F + V — E = 2
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath.Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.
Решенные примеры многогранников
В каком из следующих правильных многогранников 3 пятиугольника пересекаются в каждой вершине?
(а)
(б)
(в)
Решение:
(a) Этот многогранник состоит из трех пятиугольников, пересекающихся в каждой вершине.
(b) Этот многогранник имеет 2 прямоугольника и один семиугольник, пересекающиеся в каждой вершине.
(c) У этого многогранника 3 треугольника, пересекающихся в вершине.
| \ (\ следовательно \) 3 пятиугольника пересекаются в каждой вершине в (a) |
Мэри считала ребра, грани и вершины многогранника.
Она утверждает, что есть 12 вершин, 5 граней и 10 ребер.
Она сделала ошибку?
Решение:
Используя формулу Эйлера, мы можем проверить, правильно ли она их посчитала.
По ее словам, количество лиц 5
Количество вершин 12
Количество ребер 10
Подставляя эти числа в формулу Эйлера:
\ [F + V-E = 2 \]
\ [5 + 12-10 = 2 \]
\ [7 \ neq 2 \]
| \ (\ следовательно \) Мэри сделала ошибку при подсчете. |
Что из перечисленного является платоновыми телами?
(а) Цилиндр
(б) Конус
(в) Октаэдр
(d) Треугольная призма
Решение:
Обычно встречаются платоновы тела или правильные многогранники:
- Тетраэдр
- Куб
- Октаэдр
- Додекаэдр
- Икосаэдр
| \ (\ следовательно \) (c) Октаэдр |
Какова площадь поверхности многогранника внизу?
(а) \ (6 \: e ^ 2 \)
(б) \ (2 \ sqrt {3} \: e ^ 2 \)
(с) \ (\ sqrt {3} \: e ^ 2 \)
(г) \ (3 \ sqrt {25 + 10 \ sqrt {5}} \: e ^ 2 \)
Решение:
(c) Площадь поверхности Тетраэдра равна \ (\ sqrt {3} \: e ^ 2 \)
| \ (\ следовательно \) SA тетраэдра = \ (\ sqrt {3} \: e ^ 2 \) |
По дороге домой из школы Генри нашел твердое тело с шестью гранями, шестью вершинами и десятью ребрами.
Определите этот многогранник.
Решение:
Из рисунка выше видно, что заданным параметрам удовлетворяет только пятиугольная пирамида.
| \ (\ следовательно \) Генри нашел пятиугольную пирамиду. |
Практические вопросы по многогранникам
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Образцы материалов олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике, вы можете нажать здесь
Часто задаваемые вопросы (FAQ)
1.Сколько граней у многогранника?
В зависимости от количества плоских сторон многогранника на основе многоугольника, мы можем подсчитать количество граней.
Мы также можем найти количество граней, используя формулу Эйлера, F + V — E = 2, если мы знаем количество ребер и вершин.
2. Является ли сфера многогранником?
Нет, сфера — это криволинейная поверхность, в то время как многогранники имеют только прямые и плоские поверхности.
3. Является ли призма многогранником?
Да, это многогранник.
У призмы плоские грани, прямые края и острые вершины.
Треугольная призма, прямоугольная призма и пятиугольная призма подпадают под многогранники.

 Содержание 1 Три варианта определения 2 Вариации и обобщения 3 Использование … Википедия
Содержание 1 Три варианта определения 2 Вариации и обобщения 3 Использование … Википедия Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.


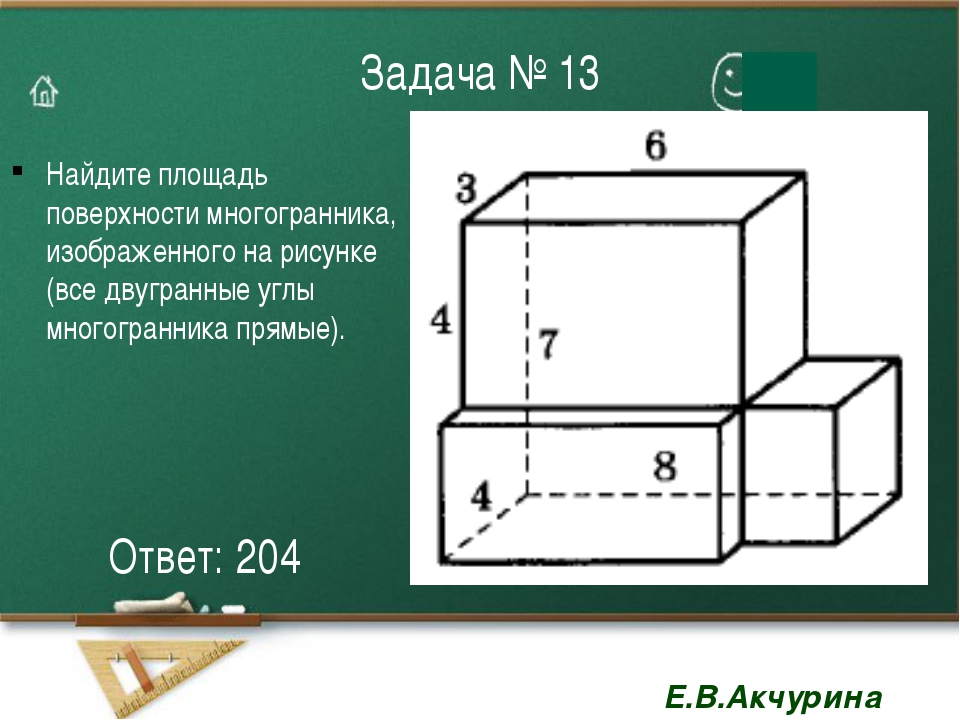 Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:
Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:

 Тетраэдр имеет четыре вершины и шесть ребер
Тетраэдр имеет четыре вершины и шесть ребер
Leave A Comment