Задачи в13 ЕГЭ по математике. Цилиндр. Разбор задач.
смотрите также 1 (куб, параллелепипед), 2 (призма, призма II), 3 (пирамида, пирамида II), 4 (составные многогранники, составные многогранники II), 5 (цилиндр+конус), 7 (конус), 8 (шар).
Продолжаем разбор Задач №8 из открытого банка заданий ЕГЭ по математике.
Сегодня работаем с цилиндром.
Задача 1.
Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на .
Решение: + показать
Задача 2.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 3.
В цилиндрический сосуд налили см воды.
Решение: + показать
Объем вытесненной жидкости равен объему погруженной детали в жидкость.
Первоначально жидкость занимала объем .
И так как объем жидкости по условию равен см, то
Тогда объем вытесненной жидкости (а значит и детали) есть см.
Ответ: 1000.
Задача 4.
В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 5.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра.
Решение: + показать
Раз прямоугольный параллелепипед описан около цилиндра, то в основании прямоугольного параллелепипеда – квадрат.
Радиус основания цилиндра равен 1, значит сторона квадрата основания параллелепипеда равна 2.
Объем параллелепипеда есть Так как он по условию равен 5, то откуда
У цилиндра и прямоугольного параллелепипеда высоты совпадают, значит и высота цилиндра равна 1,25.
Ответ: 1,25.
Задача 6.
В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 7.
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.
Решение: + показать
Объем конуса есть объем же цилиндра есть , поэтому объем данного цилиндра втрое больше объема конуса и он равен , то есть 81.
Ответ: 81.
Задача 8.
В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали? Ответ выразите в литрах.
Чему равен объем детали? Ответ выразите в литрах.
Решение: + показать
Задача 9.
Площадь осевого сечения цилиндра равна 23. Найдите площадь боковой поверхности цилиндра, деленную на .
Решение: + показать
Задача 10.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .
Решение: + показать
Часть цилиндра, изображенная на рисунке, – есть цилиндра с радиусом основания 6 и высотой 5.
Поэтому объем части цилиндра есть
Наконец,
Ответ: 45.
Задача 11.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .
Решение: + показать
Часть цилиндра, изображенная на рисунке, – есть часть цилиндра с радиусом основания 15 и высотой 6.
Поэтому объем части цилиндра есть
Наконец,
Ответ: 1125.
Задача 12.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .
В ответе укажите .
Решение: + показать
Ответ: 64.
Задача 13.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .
Решение: + показать
Ответ: 75.
Задачи для подготовке к ЕГЭ по теме: «Цилиндр. Площадь поверхности цилиндра»
Задачи для подготовки к ЕГЭ
» Цилиндр. Площадь поверхности цилиндра»
№ 1 Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
№2 Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
№ 3 Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на .
№5 Площадь боковой поверхности цилиндра равна 2, а диаметр основания — 1.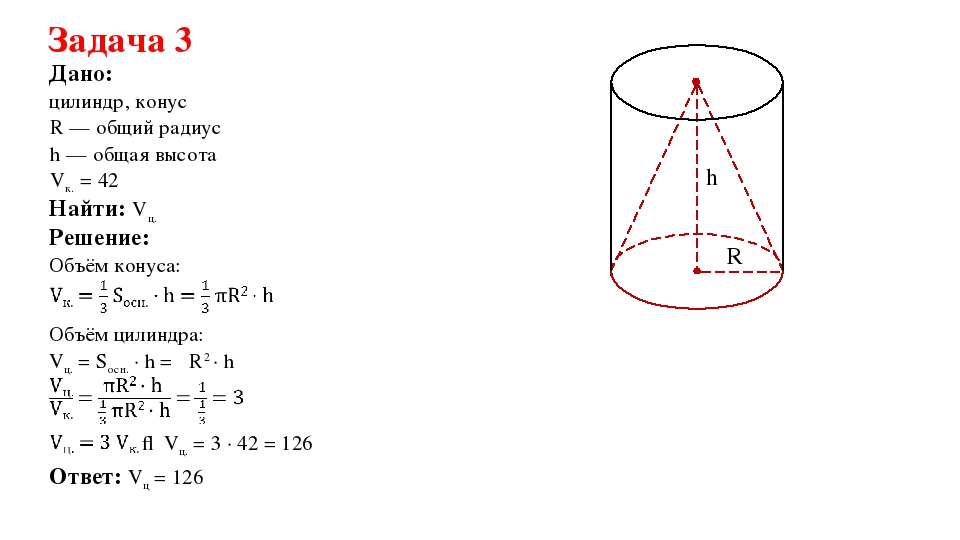 Найдите высоту цилиндра.
Найдите высоту цилиндра.
№6 Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
№1 Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на .
№2 Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.
№3 Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на .
№4 Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
№5 Площадь боковой поверхности цилиндра равна 21, а диаметр основания равен 7.
№6 Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
Задания для подготовки к ЕГЭ 11 класс «Цилиндр»» | Материал для подготовки к ЕГЭ (ГИА, 11 класс) на тему:
МБОУ Пожарская СОШ Сергачского района Нижегородской области
Учитель математики первой категории Зюляева Л.Ю.
Задания для подготовки к ЕГЭ
11 класс по теме «Цилиндр»
Задачи по готовым чертежам
1 вариант
1. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Задачи по готовым чертежам
2 вариант
1. Осевое сечение цилиндра – квадрат со стороной 8 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 4м, высота 6м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 2. Площадь боковой поверхности равна 1. Найдите высоту цилиндра.
Типы задач на ЕГЭ по теме «Площадь боковой поверхности цилиндра»
1 Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 300. Найдите радиус цилиндра.
2. Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 450 и равна 8√2 см. Найдите площадь боковой поверхности цилиндра, деленную на π .
4.Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?
Типы задач | № задачи | |
1 тип задач | Задачи, решаемые в одно действие с помощью т. Пифагора или свойства прямоугольного треугольника | |
2 тип задач | Задачи, решаемые в одно действие с помощью формулы площади боковой поверхности. | |
3 тип задач | Задачи, решаемые в два действия с помощью т. Пифагора и формулы площади боковой поверхности. |
Задания по теме «Площадь поверхности цилиндра»
ЕГЭ 2015 Задания из Открытого банка заданий. Математика. Геометрия.
Математика. Геометрия.
Прототипы заданий №12
Задание №27133
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Задание №245358
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Задание №27058
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
Проверочная тестовая работа Вариант 1
№1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 20; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π.
80; 96; 64; 32
№3. Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности, деленная на π, равна:
16; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, деленная на π, равна:
Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, деленная на π, равна:
56; 72; 88; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а высота – 4 м, тогда радиус равен:
16; 8; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 64
№7. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра, деленная на π, может быть равна:
36; 64; 48; 96
Проверочная тестовая работа
Вариант 2.
№1. Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 12; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9π кв.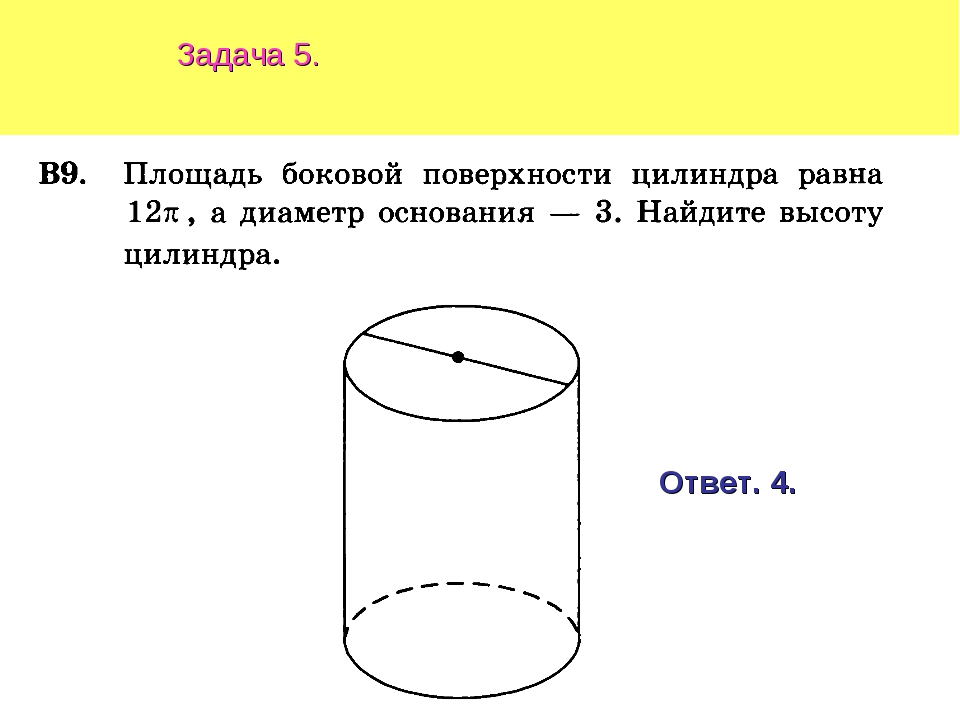 дм. Найдите площадь полной поверхности цилиндра деленную на π .
дм. Найдите площадь полной поверхности цилиндра деленную на π .
40; 54; 60; 32
№3. Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности, деленная на π, равна:
24; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, деленная на π, равна:
56; 105; 154; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а радиус – 8м, тогда образующая равна:
16; 4; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 25
№7. Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
9; 64; 36; 48
Ключ к тестовой работе (оба варианта)
№ задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Ответ | 3 | 2 | 1 | 3 | 2 | 4 | 4 |
Цилиндр | ЕГЭ по математике (профильной)
Цилиндр
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. 2$ раз.
2$ раз.
Пример:
Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.
Решение:
Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и высоты уровней жидкостей.
$V_1=V_2$;
$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого. 2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Составной цилиндр:
Чтобы найти объем составного цилиндра надо:
- Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
- Найти объем каждого цилиндра.
- Сложить объемы.
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины» «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма, правильная призма, правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Ты нашел то, что искал? Поделись с друзьями!
Перейдем к практике.
. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем:
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей».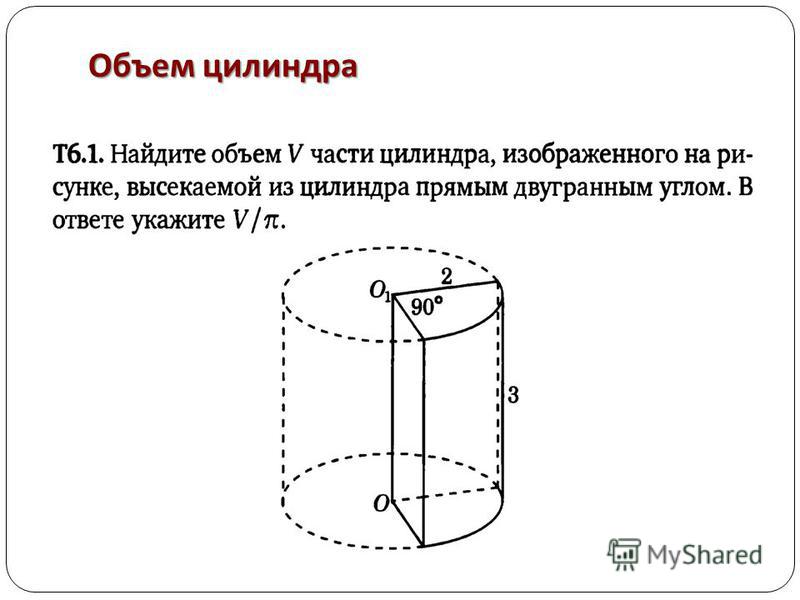 В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 🙂
В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 🙂
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна . А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна .
А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна ! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной — на верхней и нижней гранях.
А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Правильный ответ: .
Следующий тип задач — когда одно объемное тело вписано в другое.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна , высота равна , объем равен .
. В основании прямой призмы лежит прямоугольный треугольник с катетами и . Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите .
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: .
Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: .
. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.
. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: .
. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен .
Считаем объем второй кружки. Он равен . Получается, что он в два раза больше, чем объем первой.
. Следующая задача тоже решается сразу и без формул.
Через среднюю линию основания треугольной призмы, объем которой равен , проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы высота такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .
И еще одна классическая задача. Никаких формул!
. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку .
Ответ: .
Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды.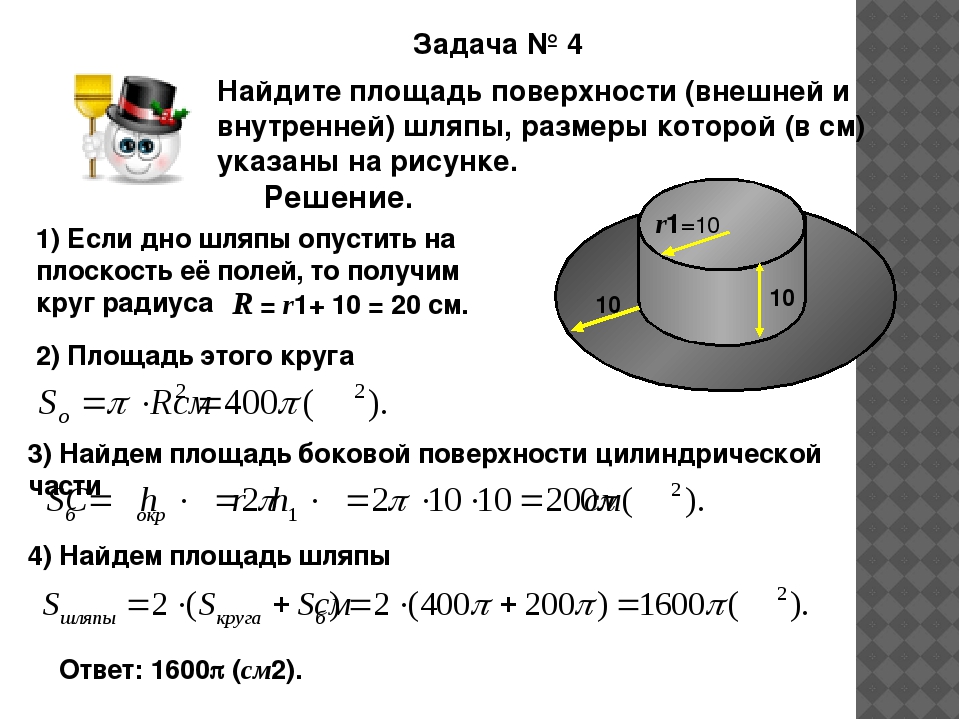 Они тоже решаются элементарно.
Они тоже решаются элементарно.
. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом градусов, а — это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на , записываем ответ: .
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Подготовка к ЕГЭ. Цилиндр. Конус. Решение задач.
Цилиндр. Конус. Решение задач
Цели урока:
Обучающие:
Формировать умения применять понятия цилиндра, конуса и формулы для вычисления площади боковой поверхности при решении задач в контексте ЕГЭ.

Развивающие:
Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ синтез, сравнения, делать необходимые выводы при решении задач разного уровня сложности.
Способствовать развитию умений творческого подхода к решению практических задач.
Воспитательные:
Обеспечить условия для воспитания положительного интереса к изучаемому предмету через решение практико-ориентированных задач.
Обеспечить благоприятную психологическую атмосферу для развития творческих способностей.
Совершенствование математической речи, математического языка.
Тип урока: обобщающий (решение задач по теме: «Цилиндр и конус»).
Ход урока.
Организационный этап и актуализация знаний.
 (3 мин)
(3 мин)
У: — Здравствуйте, ребята. Мне приятно видеть вас и наших гостей на нашем занятии. За окном февраль 2015 года. Ребята, скажите пожалуйста, а что ждете вы, будущие выпускники от этого года, какой подарок в вашей жизни вы хотите получить в этом году?
Д: —
У: — А чтобы успешно сдать ЕГЭ, нам нужно с вами что?
Д: —
У: — Посмотрите на фотографию. Узнаете? А на что похожа главная елка нашего города?
Д: —
У: — На чем стоит елка, на что похоже это сооружение ?
У: — Значит, тема нашего урока…
Запишите число и тему занятия.
У: — Давайте вспомним, какое тело называется цилиндром?
Д: —
У: — Дайте названия всех отрезков на рисунке.
Д: —
У: Что такое конус?
Д: —
У: — Дайте названия всех отрезков на рисунке.
Блиц – опрос (3 мин).
1. Высота конуса 4 см, радиус основания – 3 см. Найти образующую конуса. Ответ: 5
2.Радиус конуса 5 см, образующая – 8 см. Найти боковую поверхность конуса. Ответ: 40п
3. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти высоту и радиус основания цилиндра. Ответ: 6; 3
4. Радиус основания цилиндра равен 2м, высота 3м. Найти боковую поверхность цилиндра.
Ответ: 12п
3. « Тяжело в учении, легко на ЕГЭ» Работа в парах ( 5 мин)
А сейчас давайте прорепетируем ЕГЭ. Главное на ЕГЭ- не теряя времени, выбрать правильный способ решения задачи В12, которую вам обязательно предложат решить на экзамене. Что вам может помочь выбрать нужный способ?
Перед вами 6 задач. Работая в парах вы должны:
— определите тип решения каждой задачи;
— в каждую колонку своей таблицы записать номера задач, соответствующих указанному типу;
— отметить в условиях задач признаки, на основании которых вы произвели распределение.
На выполнение задания даётся 5 минут.
Задачи.
Радиус основания конуса равен 3, высота равна 4. Найдите площадь боковой поверхности конуса, деленную на π. 3
Образующая конуса равна 10, высота конуса 6. Найдите радиус конуса. 2
Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса. 1
Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса. 2
Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π. 1
Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса. 3
На экране таблица.
Задачи, решаемые в одно действие с помощью формулы площади боковой поверхности. | Задачи, решаемые в одно действие с помощью т. Пифагора. | Задачи, решаемые в два действия с помощью т. Пифагора и формулы площади боковой поверхности. |
3, 5 (чтобы решить эти задачи нужно знать только формулу и элементы цилиндра и конуса) | 2,4 (чтобы решить эти задачи нужно знать только т. Пифагора. А решаем мы их сейчас потому что в 8кл не были введены понятия конуса и цилиндра) | 1, 6 (чтобы решить эти задачи нужно знать и формулу и элементы цилиндра и конуса и т. Пифагора) |
4.Игра «Репетитор» или «Немедвежья услуга» (10 мин)
В текстах ЕГЭ встречаются задачи разного уровня сложности, даже в рамках одного задания. Прямо сейчас на уроке мы открываем консультационный пункт по подготовке к ЕГЭ. Вы будете : абитуриенты, а я ваш репетитор. Вам предлагаются задания трех уровней сложности, каждая пара выбирает один из этих уровней.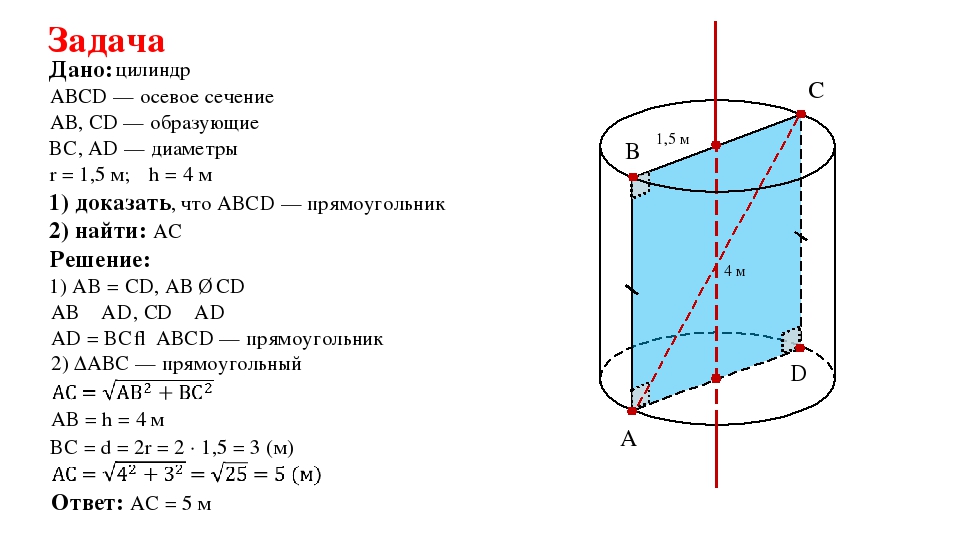
Учащимся раздаются инструкции (каждому на отдельном листе) :
Но прежде , чем вы приступите к работе, выставьте себе оценку, характеризующую уровень ваших знаний по этой теме. То есть укажите, на сколько баллов, как вы считаете, вы знаете эту тему.
Ученикам. (Мамедова С, Щеблетов А.)
ИНСТРУКЦИЯ.
Время выполнения 10 минут
Перед вами две задачи, расположенные в порядке возрастания сложности.
Решив только первую задачу, вы получаете оценку «3».
Решив первую и вторую задачи, вы получите оценку «4».
Старайтесь решать сами!
В случае затруднения, вы можете обратиться за помощью к РЕПЕТИТОРАМ.
За данной помощью, вы можете обратиться НЕ БОЛЕЕ ТРЕХ РАЗ.
Задачи
Длина окружности основания цилиндра равна 1.
 Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Площадь боковой поверхности равна 2. Найдите высоту цилиндра.Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.
Абитуриентам. ( Горшкова Д, Чулкова Д.)
ИНСТРУКЦИЯ.
Время выполнения 10 минут
Перед вами две задачи, расположенные в порядке возрастания сложности.
Решив только первую задачу, вы получаете оценку «4».
Решив первую и вторую задачи, вы получите оценку «5».
Старайтесь решать сами !
В случае затруднения, вы можете обратиться за помощью к РЕПЕТИТОРАМ.
За данной помощью, вы можете обратиться НЕ БОЛЕЕ ДВУХ РАЗ.
Задачи
Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 600 и равна 20 см.
 Найдите площадь боковой поверхности цилиндра.
Найдите площадь боковой поверхности цилиндра.Высота конуса равна 2 корня из трёх см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником.
Студентам. (Демина В. Завальник Т.)
ИНСТРУКЦИЯ.
Время выполнения 10 минут
Перед вами две задачи, расположенные в порядке возрастания сложности.
Решив только первую задачу, вы получаете оценку «4».
Решив первую и вторую задачи, вы получите оценку «5».
Старайтесь решать сами !
В случае затруднения, вы можете обратиться за помощью к РЕПЕТИТОРАМ.
За данной помощью, вы можете обратиться ТОЛЬКО ОДИН РАЗ.
Задачи
Высота конуса равна 2 √3 см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником.

Диаметр окружности основания цилиндра равен 26, а его образующая – 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найти угол между этой плоскостью и плоскостью основания цилиндра.
После решения задач правильные ответы проецируются на доску.
Учащиеся выставляют себе оценку. Сравнивают её с самооценкой. Учитель проводит рефлексию:
— совпали оценка и самооценка. «Поздравляем! Вы правильно оцениваете уровень своих возможностей!»
— самооценка ниже. «Совет раз — подучить тему, так как вы не уверены в своих знаниях. Совет два – поверьте в свои силы ! вы всё можете!»
— самооценка выше……
Электронный тест. (7 мин)
Итог урока (1 мин)
Подводим итоги урока, выставляем оценки.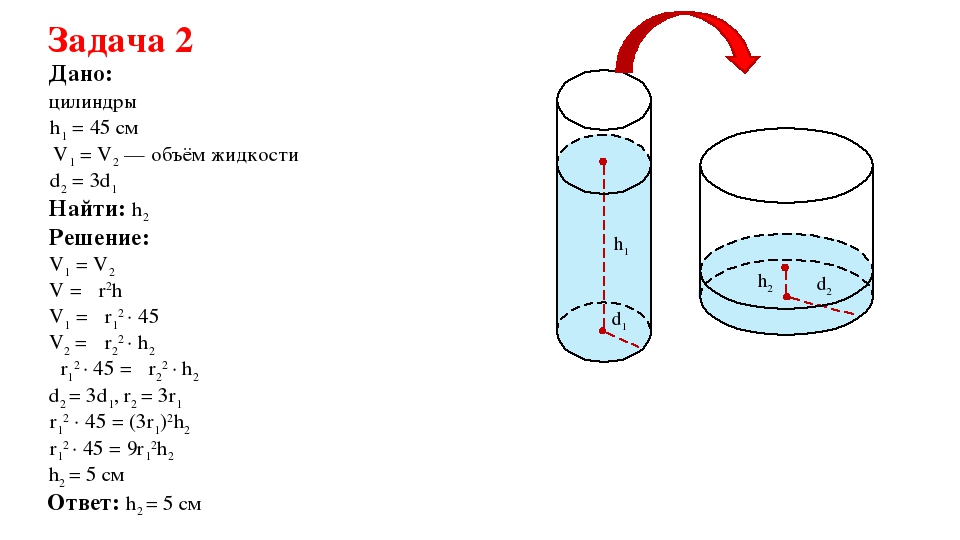 Домашнее задание.
Домашнее задание.
7.Рефлексия(1 мин)
Нарисуйте свое впечатление об уроке.(смайлики)
Ребята, а какие ассоциации у вас вызывают мандарины?
Они похожи на шар.
Новый год.
Верно. Следующая наша тема : «Сфера», «Шар»
Музыку включить. В качестве приза – мандарины.
Пусть Новый год шагает по планете и с радостью придет он в каждый дом, а вам ребята я желаю успешно сдать единый государственный экзамен. Ребята, спасибо за работу на уроке.
Урок окончен.
На всякий случай.
Какими предметами в форме конуса и цилиндра пользуется портной в работе? (Напёрсток, катушка)
Герой этой сказки имеет отношение к предмету в виде цилиндра, потому что именно из цилиндра его и сделали.
 Кто этот герой? (Буратино, полено)
Кто этот герой? (Буратино, полено)Без этого конуса не работает телевидение (модель телебашни)
Предмет косметики в форме цилиндра (губная помада) и т.п.
Где в Норильске есть цилиндр, конус? (Заводская труба)
Как профильтровать раствор, используя промокательную бумагу? (Нужно сделать воронку в форме конуса и профильтровать)
На этом цилиндре любят селиться аисты (водонапорная башня) и т.п.
Задачи на комбинации тел. Готовимся к ЕГЭ по математике. Геометрия. Урок 32
Задача 1. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 1). Вычислите объём цилиндра, если объём конуса равен 16.
Рис. 1.
Решение.
Объём конуса равен , а объём цилиндра — , где — площадь их общего основания, — общая высота. Видно, что объём цилиндра в 3 раза больше объёма конуса и равен .
Видно, что объём цилиндра в 3 раза больше объёма конуса и равен .
Ответ: 48.
Задача 2. Прямоугольный параллелепипед описан около цилиндра (см. рис. 2), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.
Решение.
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть . Площадь основания параллелепипеда равна .
Рис. 2.
Высоту параллелепипеда находим из формулы объёма параллелепипеда: . Найденная высота параллелепипеда одновременно является и высотой цилиндра.
Ответ: 6.
Задача 3. Объём куба равен 30 (см. рис. 3). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Рис. 3.
Решение.
Рассмотрим куб как четырёхугольную призму. Его объём равен . Основание пирамиды совпадает с основанием призмы, а высота вдвое меньше высоты призмы.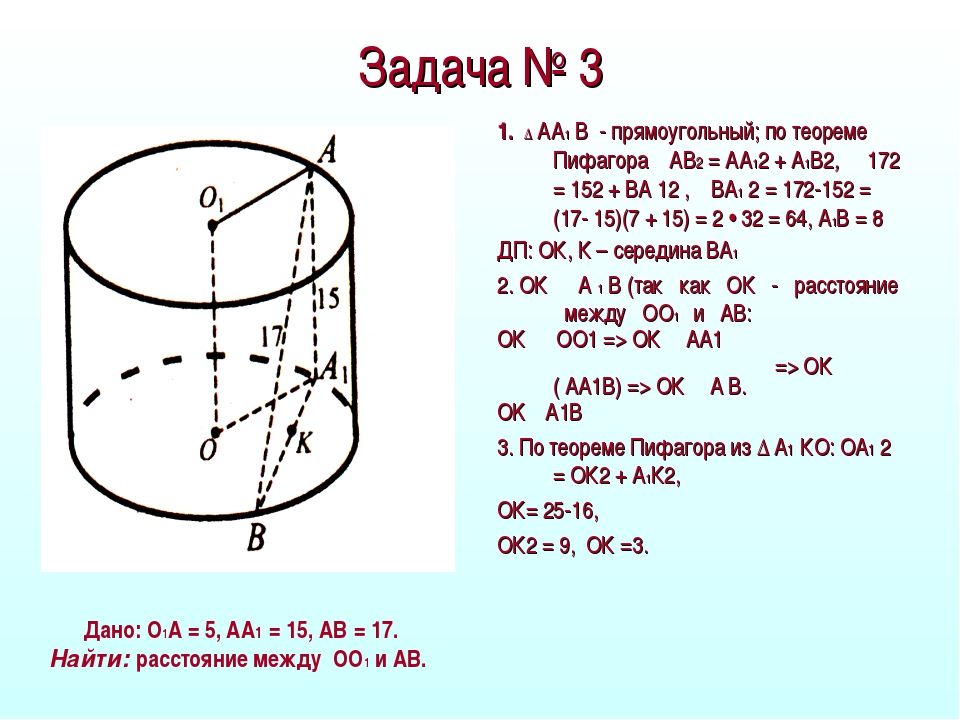 Поэтому
Поэтому
Ответ: 5.
Задача 4. Объём правильной шестиугольной пирамиды равен 60 (см. рис. 4). Найдите объём треугольной пирамиды .
Рис. 4.
Решение.
Обозначим сторону шестиугольника в основании пирамиды через . Правильный шестиугольник можно разбить на 6 правильных треугольников, поэтому площадь шестиугольника равна Найдём площадь треугольника .
Таким образом, площадь основания пирамиды в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
Ответ: 10.
Как найти объем цилиндра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Можете ли вы решить задачу на экзамене по математике из Малайзии? Головоломка «Цилиндр на стене» — помни о своих решениях
Я получил электронное письмо с интересной задачей на национальном экзамене Малайзии, которую я адаптировал для этой головоломки.
Цилиндрический контейнер длиной 20 см ставится на пол у стены, как показано на схеме.
Точка Q находится на краю основания, а Q — на расстоянии 2 см от стены и 1 см от пола.
Может ли цилиндрический контейнер поместиться в коробку размером 21 см × 7 см × 7 см? Почему или почему нет?
Это не указано в задаче, но следует исходить из предположения, что стена перпендикулярна полу.
Сможете разобраться? Посмотрите видео, чтобы узнать о решении.
Сможете ли вы решить задачу на экзамене по математике из Малайзии? Цилиндр на стене
Или продолжайте читать.
.
.
«Все будет хорошо, если ты будешь использовать свой разум для принятия решений, и думать только о своих решениях». С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.
.
.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на малазийский экзамен по математике
Цилиндр длиной 20 см меньше, чем размер коробки, равный 21 см.
Остальные размеры цилиндра равны диаметру (2 r ) окружности.Баллон поместится в коробку только в том случае, если диаметр меньше 7 см.
Так какой же диаметр?
Один из подходов состоит в численной оценке круга, который касается пола, стены и проходит через точку Q , которая находится на расстоянии 2 см от стены и 1 см от пола. Если мы нарисуем различные круги на миллиметровой бумаге с помощью компьютерного моделирования (см. Видео около 2:20), мы сможем найти уникальный круг, который удовлетворяет этим условиям, где Q находится в правом углу круга между полом и стеной.
Числовая ширина круга составляет 10 единиц, поэтому круг имеет ширину 10 см и высоту 10 см. Это больше, чем коробка размером 7 на 7 см, поэтому круг не поместится.
Хотя этот метод решения находит ответ, он несколько неудовлетворителен для математика. Мы не знаем точного ответа. И если мы изменим значение Q , нам придется провести еще одну громоздкую оценку. Было бы лучше создать формулу и решить для любого значения Q .
Итак, сначала давайте решим конкретную проблему.
Нам нужен круг, который касается стены, пола и проходит через Q . Поскольку круг касается пола и стены, центр круга находится на расстоянии одной единицы радиуса от пола и стены. Другими словами, центр круга (- r , r ).
Окружность радиусом r с центром в точке (- r , r ) имеет уравнение:
( x + r ) 2 + ( y — r ) 2 = r 2
Поскольку круг проходит через Q = (-2, 1), мы подставляем x = -2 и y = 1 в приведенное выше уравнение. Затем мы можем решить:
Затем мы можем решить:
(-2 + r ) 2 + (1 — r ) 2 = r 2
r 2 — 6 r + 5 = 0
( r — 5) ( r — 1) = 0
r = 5 или 1
У нас есть два возможных решения. Но r = 1 означает, что точка Q не находится между углом пола и стеной, как на исходной диаграмме (обратите внимание, что Q находится на расстоянии 2 единиц от стены, то есть на расстоянии 1 диаметра от стены. ).Поэтому мы отвергаем это решение, так как оно не похоже на исходную диаграмму.
Таким образом, радиусу окружности соответствует r = 5, и мы приходим к диаметру 2 r = 10, как и раньше.
Обновление для рассмотрения «наклона»
Как указывает Петр, и я также получил электронное письмо от Патрика В., чтобы быть полностью уверенным, что мы должны проверить, можно ли разместить цилиндр по диагонали внутри коробки.
Одно простое доказательство от Петра: объем цилиндра (π r 2 h = π (5 2 ) (20) = 500π & приблизительно; 1570.796) больше коробки (7 × 7 × 21 = 1029) — поэтому велосипедный двигатель никак не может поместиться внутри коробки!
Общий случай
Для Q = (- a , b ) мы можем решить аналогично.
Окружность с радиусом r и центром в точке (- r , r ) имеет уравнение:
( x + r ) 2 + ( y — r ) 2 = r 2
Поскольку круг проходит через Q = (- a , b ), мы подставляем x = — a и y = b в приведенное выше уравнение.Затем мы можем решить:
(- a + r ) 2 + ( b — r ) 2 = r 2
r 2 — ( 2 a + 2 b ) r + ( a 2 + b 2 ) = 0
Это квадратное уравнение от r . Используя квадратную формулу, мы получаем:
Используя квадратную формулу, мы получаем:
r = a + b ± √ (2 ab )
Затем мы могли бы проверить, удовлетворяет ли каждое значение ограничениям исходной задачи.
Спасибо всем покровителям! Особая благодарность:
Shrihari Puranik
Kyle
Если вам нравятся мои видео, вы можете поддержать меня на Patreon и получить эксклюзивные награды: http://www.patreon.com/mindyourdecisions
Source
2017 Additional Математика SPM (Sijil Pelajaran Malaysia / Малайзийский аттестат об образовании). Я получил эту проблему по электронной почте.
Вот решение от учителя из Малайзии, которое очень похоже на решение, которое я представил:
https: // www.facebook.com/maths.video/photos/a.581783621835231.146536.503727749640819/1847702531909994/?type=3&theater
МОИ КНИГИ
Если вы совершите покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Это не влияет на цену, которую вы платите.
https://mindyourdecisions.com/blog/my-books
Mind Your Decisions — это сборник из 5 книг:
(1) The Joy of Game Theory: An Introduction to Strategic Мышление(2) 40 парадоксов в теории логики, вероятностей и игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость
(4) Лучшие уловки мысленной математики
(5) Умножать числа, рисуя линии
Радость теории игр показывает, как можно использовать математику, чтобы перехитрить своих конкурентов.(рейтинг 4,2 / 5 звезд в 177 отзывах)
40 Парадоксов в логике, вероятности и теории игр содержит наводящие на размышления и противоречащие интуиции результаты. (рейтинг 4/5 звезд в 27 обзорах)
Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость — это руководство, в котором объясняются многие способы предвзятого отношения к принятию решений и предлагаются методы для принятия разумных решений. (рейтинг 3,8 / 5 звезд в 15 отзывах)
(рейтинг 3,8 / 5 звезд в 15 отзывах)
Лучшие уловки в области ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4.3/5 звезд в 47 обзорах)
Умножение чисел на рисование линий Эта книга представляет собой справочное руководство для моего видео, которое набрало более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,4 / 5 звезд в 21 обзоре)
Mind Your Puzzles представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность и т. д. логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач счета, геометрии, вероятности и теории игр.Том 1 получил оценку 4,6 / 5 звезд в 39 отзывах.
Math Puzzles Volume 2 — это продолжение книги с более серьезными задачами. (рейтинг 4,2 / 5 звезд в 19 обзорах)
Math Puzzles Volume 3 — третий в серии. (рейтинг 4,2 / 5 звезд по 15 отзывам)
(рейтинг 4,2 / 5 звезд по 15 отзывам)
KINDLE UNLIMITED
Учителя и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.
В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте свой местный веб-сайт Amazon, чтобы узнать о доступности и условиях программы.
США, список моих книг (США)Великобритания, список моих книг (Великобритания)
Канада, результаты книги (CA)
Германия, список моих книг (DE)
Франция, список моих книг (FR)
Индия , список моих книг (IN)
Австралия, результаты книги (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга results (BR)
Mexico, book results (MX)
MERCHANDISE
Купите кружку, футболку и многое другое на официальном сайте товаров: Mind Your Decisions at Teespring .
объем цилиндра экзаменационные вопросы
Объем баллона. На изображении ниже показано, что мы подразумеваем под радиусом и высотой: Интерактивный виджет. Практика: Объем и площадь цилиндров. 1) У Дина есть картонная коробка, длина, ширина и высота которой находятся в соотношении 1: 2: 3. Вопрос 2: Рассчитайте радиус основания цилиндрической емкости объемом 440 см 3. Ответ: Сначала рассчитаем объем полого цилиндра (трубы). Объем полого цилиндра = Объем внешнего цилиндра — Объем внутреннего цилиндра = πR²h — πr²h = π (R² — r²) h.R = 17/2 = 8,5 см. Вопросы и ответы по объему и площади поверхности. Не тратьте слишком много времени на один вопрос. Это типичный экзаменационный вопрос об объеме цилиндра. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. вода в цилиндре занимает такое же пространство, какое сейчас занимает объект в банке, а это значит, что их объемы такие же. 2. (Возьмите pi = 22/7) Решение: Дано: Объем = 440 см 3. Это набор из 10 тестовых заданий по химии, касающихся считывания мениска жидкости в градуированном цилиндре. Ответьте правильно с точностью до ближайших сантиметров. Ответы на решенные вопросы в этом тесте: викторина «Объем цилиндра» представляет собой хорошее сочетание простых и сложных вопросов. Расчет объема любой призмы. ПРАКТИЧЕСКИЕ ВОПРОСЫ ПО ОБЪЕМУ КУБА И КУБОИДНОЙ ТАБЛИЦЫ (1) Найдите объем кубоида, размеры которого: (i) длина = 12 см, ширина = 8 см, высота = 6 см (ii) длина = 60 м, ширина = 25 м. , высота = 1,5 м. CCSS.Math: 8.GC9,… Kemp House, 152 City Road, London EC1V 2NX, Определение высоты цилиндра по его объему (только Higher), Объем экзаменационного вопроса конуса (только Higher), Преобразование единиц длины , Площадь и объем, Подобные треугольники и похожие формы (только для высших учебных заведений), тригонометрия с неправильным углом (только для высших учебных заведений), трехмерная прямоугольная тригонометрия (только для высших учебных заведений), Big Brain Education Ltd., Kemp House, 152 City Road, London EC1V 2NX, Copyright © 2021 Big Brain Education Ltd. Вы можете заработать трофей, если правильно ответили хотя бы на 8 вопросов и выполняете это задание онлайн.
Ответьте правильно с точностью до ближайших сантиметров. Ответы на решенные вопросы в этом тесте: викторина «Объем цилиндра» представляет собой хорошее сочетание простых и сложных вопросов. Расчет объема любой призмы. ПРАКТИЧЕСКИЕ ВОПРОСЫ ПО ОБЪЕМУ КУБА И КУБОИДНОЙ ТАБЛИЦЫ (1) Найдите объем кубоида, размеры которого: (i) длина = 12 см, ширина = 8 см, высота = 6 см (ii) длина = 60 м, ширина = 25 м. , высота = 1,5 м. CCSS.Math: 8.GC9,… Kemp House, 152 City Road, London EC1V 2NX, Определение высоты цилиндра по его объему (только Higher), Объем экзаменационного вопроса конуса (только Higher), Преобразование единиц длины , Площадь и объем, Подобные треугольники и похожие формы (только для высших учебных заведений), тригонометрия с неправильным углом (только для высших учебных заведений), трехмерная прямоугольная тригонометрия (только для высших учебных заведений), Big Brain Education Ltd., Kemp House, 152 City Road, London EC1V 2NX, Copyright © 2021 Big Brain Education Ltd. Вы можете заработать трофей, если правильно ответили хотя бы на 8 вопросов и выполняете это задание онлайн. Диаграммы не в масштабе. Класс 10 по математике MCQs Глава 13 Площади и объемы поверхности. Об этом ресурсе. Пройдя эту викторину, вы будете подготовлены к заключительному экзамену по площади и объему цилиндра. Упростите поиск объема сфер и полушарий с помощью этой подборки рабочих листов в формате pdf.40 x KS3 Домашние задания по математике / Буклет С ОТВЕТАМИ !! Предположим, что все измерения даны в миллилитрах (мл). Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Это текущий выбранный элемент. 653 кубических дюйма. Узнайте, как решать задачи, основанные на площади поверхности и объеме твердых тел, с нашими примечаниями к редакции главы 21 математики ICSE Class 8. Таким образом, чтобы закрепить эти отметки, вам необходимо составить команду по формулам объема и площади поверхности. Объем цилиндра и площадь поверхности. Объем кубоида. Кубоид, Куб, Цилиндр, Конус, Сфера, Полусфера — это основной раздел в главе «Площадь поверхности и объем».Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день.
Диаграммы не в масштабе. Класс 10 по математике MCQs Глава 13 Площади и объемы поверхности. Об этом ресурсе. Пройдя эту викторину, вы будете подготовлены к заключительному экзамену по площади и объему цилиндра. Упростите поиск объема сфер и полушарий с помощью этой подборки рабочих листов в формате pdf.40 x KS3 Домашние задания по математике / Буклет С ОТВЕТАМИ !! Предположим, что все измерения даны в миллилитрах (мл). Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Это текущий выбранный элемент. 653 кубических дюйма. Узнайте, как решать задачи, основанные на площади поверхности и объеме твердых тел, с нашими примечаниями к редакции главы 21 математики ICSE Class 8. Таким образом, чтобы закрепить эти отметки, вам необходимо составить команду по формулам объема и площади поверхности. Объем цилиндра и площадь поверхности. Объем кубоида. Кубоид, Куб, Цилиндр, Конус, Сфера, Полусфера — это основной раздел в главе «Площадь поверхности и объем».Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Следующий. Итак, чтобы проработать объем формы, нам нужно проработать два объема отдельно.
Следующий. Итак, чтобы проработать объем формы, нам нужно проработать два объема отдельно.Я обычно печатаю эти вопросы в виде буклета формата A5 и… Уровень 1 Уровень 2 Уровень 3 Описание стиля экзамена Помогите больше трехмерных фигур. Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Объем составных фигур. Вы также можете найти другие дополнительные вопросы Test: Volume Combination Of Solids, длинные вопросы и короткие вопросы для класса 10 на EduRev, выполнив поиск выше.Просмотреть… Внимательно прочтите каждый вопрос, прежде чем начать отвечать на него. Еще больше на goteachmaths.co.uk! Мы надеемся, что эти важные вопросы Математика 10 класса Глава 13 Объем поверхности помогли учащимся в подготовке к экзамену. Кубоид, Куб, Цилиндр, Конус, Сфера, Полусфера — это основной раздел в главе «Площадь поверхности и объем». Решение (3) Длина, ширина и высота… Ответы на решенные вопросы в этом тесте: викторина «Комбинация объемов твердых тел» дает вам хорошее сочетание простых и сложных вопросов.
 Основа… 5-дневного GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Попробуйте эту удивительную викторину «Объем конуса + цилиндр + сфера», которую заядлые участники опроса пытались пройти 1968 раз. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. Ответы появляются после последнего вопроса. В нашем концептуальном видео вы познакомитесь с базовой структурой цилиндра. 8495 кубических дюймов. 4. Рабочий лист_Объем_цилиндров. 2. Загрузка … Сохранить на потом. Вы также можете найти другие дополнительные вопросы Test: Volume Of Aylinder, длинные вопросы и короткие вопросы для класса 9 на EduRev, выполнив поиск выше.Следующий урок. Практика: задачи с объемными цилиндрами, сферами и конусами. После того, как вы получите четкое представление о том, что такое призма и как рассчитать ее объем, неплохо было бы взглянуть на следующие вопросы из прошлой статьи. Найдите объем… Объем цилиндра 198 см3. Это действительно один из лучших веб-сайтов.
Основа… 5-дневного GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Попробуйте эту удивительную викторину «Объем конуса + цилиндр + сфера», которую заядлые участники опроса пытались пройти 1968 раз. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. Ответы появляются после последнего вопроса. В нашем концептуальном видео вы познакомитесь с базовой структурой цилиндра. 8495 кубических дюймов. 4. Рабочий лист_Объем_цилиндров. 2. Загрузка … Сохранить на потом. Вы также можете найти другие дополнительные вопросы Test: Volume Of Aylinder, длинные вопросы и короткие вопросы для класса 9 на EduRev, выполнив поиск выше.Следующий урок. Практика: задачи с объемными цилиндрами, сферами и конусами. После того, как вы получите четкое представление о том, что такое призма и как рассчитать ее объем, неплохо было бы взглянуть на следующие вопросы из прошлой статьи. Найдите объем… Объем цилиндра 198 см3. Это действительно один из лучших веб-сайтов. Инструкции Используйте черные чернила или шариковую ручку. Все вопросы по упражнениям решаются и объясняются опытным преподавателем в соответствии с рекомендациями совета ICSE. Это уровень 1: применение формулы объема цилиндра.Учащиеся 10 класса обязательно сдают это упражнение «Тест: комбинация твердых веществ», чтобы получить лучший результат на экзамене. Вопрос 5 а. Найдите объем цилиндра. Найдите подробные ответы на проблемы, основанные на размерах твердых тел, в наших образцах решений для вопросов. Предварительный просмотр. Получите доступ к нашим таблицам объема цилиндров, чтобы попрактиковаться в нахождении радиуса по диаметру, нахождении объема цилиндров с параметрами в целых и десятичных дробях, нахождении недостающих параметров, решении текстовых задач и многом другом! Вы можете заработать трофей, если правильно ответите хотя бы на 8 вопросов и выполните это задание онлайн.Диаграммы не в масштабе. Это типичный экзаменационный вопрос об объеме цилиндра. Цилиндр и куб имеют одинаковый объем.
Инструкции Используйте черные чернила или шариковую ручку. Все вопросы по упражнениям решаются и объясняются опытным преподавателем в соответствии с рекомендациями совета ICSE. Это уровень 1: применение формулы объема цилиндра.Учащиеся 10 класса обязательно сдают это упражнение «Тест: комбинация твердых веществ», чтобы получить лучший результат на экзамене. Вопрос 5 а. Найдите объем цилиндра. Найдите подробные ответы на проблемы, основанные на размерах твердых тел, в наших образцах решений для вопросов. Предварительный просмотр. Получите доступ к нашим таблицам объема цилиндров, чтобы попрактиковаться в нахождении радиуса по диаметру, нахождении объема цилиндров с параметрами в целых и десятичных дробях, нахождении недостающих параметров, решении текстовых задач и многом другом! Вы можете заработать трофей, если правильно ответите хотя бы на 8 вопросов и выполните это задание онлайн.Диаграммы не в масштабе. Это типичный экзаменационный вопрос об объеме цилиндра. Цилиндр и куб имеют одинаковый объем. Один из вас попросил меня помочь с этими вопросами во время его / ее проверки по математике. Найдите объем цилиндра. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О; Карты ревизий; … Вопросы по стилю экзамена Убедитесь, что у вас есть: карандаш, ручка, линейка, транспортир, циркуль и ластик. При необходимости вы можете использовать кальку.Насколько объем старого ящика меньше нового? Раскройте ответ. Квадрат Научитесь определять объем куба, цилиндра или кубоида с помощью наших учебных ресурсов. (а) Рассчитайте площадь поперечного сечения. Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Цилиндр изготовлен из гибкого пластика. Объем и площадь цилиндров. Сумма радиуса основания и высоты сплошного правильного кругового цилиндра составляет 37 см. Он делает новый ящик, длина, ширина и высота которого увеличиваются на 100%, 200% и 200% соответственно.Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов. h = 1000 см.
Один из вас попросил меня помочь с этими вопросами во время его / ее проверки по математике. Найдите объем цилиндра. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О; Карты ревизий; … Вопросы по стилю экзамена Убедитесь, что у вас есть: карандаш, ручка, линейка, транспортир, циркуль и ластик. При необходимости вы можете использовать кальку.Насколько объем старого ящика меньше нового? Раскройте ответ. Квадрат Научитесь определять объем куба, цилиндра или кубоида с помощью наших учебных ресурсов. (а) Рассчитайте площадь поперечного сечения. Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. Цилиндр изготовлен из гибкого пластика. Объем и площадь цилиндров. Сумма радиуса основания и высоты сплошного правильного кругового цилиндра составляет 37 см. Он делает новый ящик, длина, ширина и высота которого увеличиваются на 100%, 200% и 200% соответственно.Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов. h = 1000 см. Также изучите более 172 похожих викторин в этой категории. Практические вопросы Корбеттматов об объеме сферы. Нанесение объема твердых веществ. Проверьте, что ваши ответы кажутся правильными. вверх. Предварительный просмотр и подробности Включенные файлы (1) pdf, 425 КБ. Меню Перейти к содержимому. Объем кубоида. Далее нам дается формула для объема сферы, поэтому, чтобы найти объем полушария, мы будем использовать эту формулу, а затем половину результата.Мы знаем из формулы цилиндра; Объем, V = πr 2 ч куб. Поперечное сечение серебряного слитка представляет собой трапецию. 5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Примеры вопросов экзамена, которые следуют ниже, иллюстрируют взаимосвязь между структурой курса и экзаменами AP Calculus AB и BC и служат примерами типов вопросов, которые появляются на экзаменах. Примечание. Сохраните полный ответ в калькуляторе, чтобы добавить его к другому значению в конце.
Также изучите более 172 похожих викторин в этой категории. Практические вопросы Корбеттматов об объеме сферы. Нанесение объема твердых веществ. Проверьте, что ваши ответы кажутся правильными. вверх. Предварительный просмотр и подробности Включенные файлы (1) pdf, 425 КБ. Меню Перейти к содержимому. Объем кубоида. Далее нам дается формула для объема сферы, поэтому, чтобы найти объем полушария, мы будем использовать эту формулу, а затем половину результата.Мы знаем из формулы цилиндра; Объем, V = πr 2 ч куб. Поперечное сечение серебряного слитка представляет собой трапецию. 5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Примеры вопросов экзамена, которые следуют ниже, иллюстрируют взаимосвязь между структурой курса и экзаменами AP Calculus AB и BC и служат примерами типов вопросов, которые появляются на экзаменах. Примечание. Сохраните полный ответ в калькуляторе, чтобы добавить его к другому значению в конце. Красивый и простой лист по объему цилиндров. Объем сфер и полушарий. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О; Пересмотр… Ответьте на вопросы в… Ответы на решенные вопросы в этом тесте: викторина «Объемная комбинация твердых тел» представляет собой хорошее сочетание простых и сложных вопросов. Обоснование вопросов с ответами: последние проблемы с решениями кодирования и декодирования для банковских экзаменов Q.12 Если диаметр основания и высота правого кругового конуса увеличиваются на 100%, то объем увеличится на….2, а его криволинейная поверхность составляет одну треть от его общей площади. Можно использовать кальку. Мы используем файлы cookie, чтобы обеспечить максимальное удобство использования нашего веб-сайта. зарегистрирован в Англии (Компания № 02017289) с местонахождением по адресу 26 Red Lion 5. Вверх Далее. Высота цилиндрической емкости 35 см. www.justmaths.co.uk Объем призм, конусов, пирамид и сфер (H) — Версия 2, январь 2016 г. Объем призм, конусов, пирамид и сфер (H) Сборник 9-1 математических образцов GCSE и образцов вопросов от AQA , OCR, Pearson-Edexcel и WJEC Eduqas.
Красивый и простой лист по объему цилиндров. Объем сфер и полушарий. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О; Пересмотр… Ответьте на вопросы в… Ответы на решенные вопросы в этом тесте: викторина «Объемная комбинация твердых тел» представляет собой хорошее сочетание простых и сложных вопросов. Обоснование вопросов с ответами: последние проблемы с решениями кодирования и декодирования для банковских экзаменов Q.12 Если диаметр основания и высота правого кругового конуса увеличиваются на 100%, то объем увеличится на….2, а его криволинейная поверхность составляет одну треть от его общей площади. Можно использовать кальку. Мы используем файлы cookie, чтобы обеспечить максимальное удобство использования нашего веб-сайта. зарегистрирован в Англии (Компания № 02017289) с местонахождением по адресу 26 Red Lion 5. Вверх Далее. Высота цилиндрической емкости 35 см. www.justmaths.co.uk Объем призм, конусов, пирамид и сфер (H) — Версия 2, январь 2016 г. Объем призм, конусов, пирамид и сфер (H) Сборник 9-1 математических образцов GCSE и образцов вопросов от AQA , OCR, Pearson-Edexcel и WJEC Eduqas.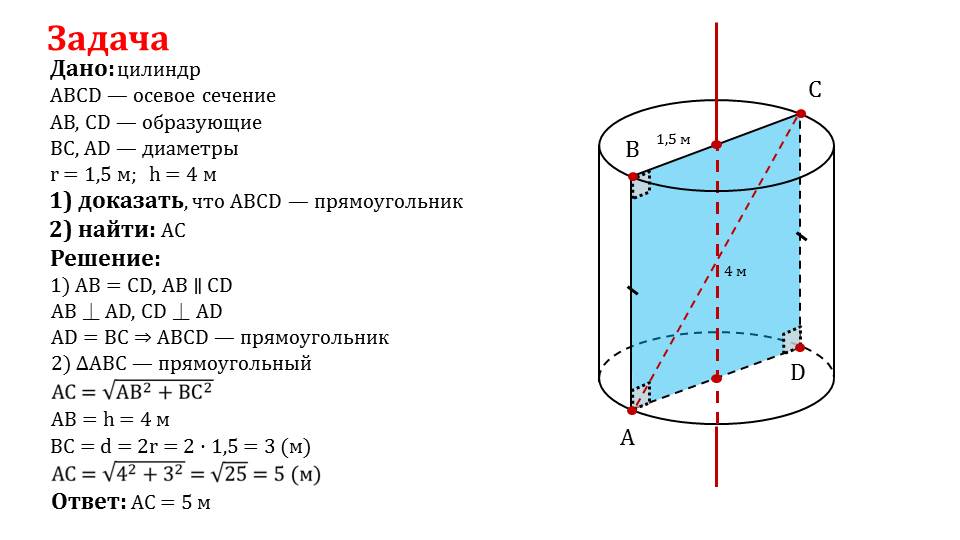 Вопросы, заданные на экзамене, содержат 12 баллов. Учащиеся 10 класса обязательно сдают это упражнение «Тест: комбинация твердых веществ», чтобы получить лучший результат на экзамене. Сдача N5 по математике значительно увеличивает ваши карьерные возможности, помогая получить место на курсах колледжа, ученичестве или даже поиске работы. В этом уроке рассматривается вопрос: рассчитайте объем этого полого цилиндра, который имеет толщину 2 см и высоту 20 см. Практические тесты по объему и площади поверхности: вопросы и ответы с несколькими вариантами объективного типа по объему и площади поверхности с решениями для банковских экзаменов IBPS, SBI, RRB, SSC, UPSC и всех конкурсных экзаменов в Индии — 1 (AQA, ноябрь 2003 г., Промежуточный доклад 1 NO Calculator ) На схеме изображен серебряный слиток.Таким образом, те, кто ищет формулы объема и площади поверхности, задачи объема и площади поверхности, формулу объема и площади поверхности, объем и площадь поверхности твердых тел, площадь поверхности цилиндра, объем цилиндра, могут получить полную информацию из этот пост.
Вопросы, заданные на экзамене, содержат 12 баллов. Учащиеся 10 класса обязательно сдают это упражнение «Тест: комбинация твердых веществ», чтобы получить лучший результат на экзамене. Сдача N5 по математике значительно увеличивает ваши карьерные возможности, помогая получить место на курсах колледжа, ученичестве или даже поиске работы. В этом уроке рассматривается вопрос: рассчитайте объем этого полого цилиндра, который имеет толщину 2 см и высоту 20 см. Практические тесты по объему и площади поверхности: вопросы и ответы с несколькими вариантами объективного типа по объему и площади поверхности с решениями для банковских экзаменов IBPS, SBI, RRB, SSC, UPSC и всех конкурсных экзаменов в Индии — 1 (AQA, ноябрь 2003 г., Промежуточный доклад 1 NO Calculator ) На схеме изображен серебряный слиток.Таким образом, те, кто ищет формулы объема и площади поверхности, задачи объема и площади поверхности, формулу объема и площади поверхности, объем и площадь поверхности твердых тел, площадь поверхности цилиндра, объем цилиндра, могут получить полную информацию из этот пост. Самым важным преимуществом для людей является проверка объема и поверхности… 163 кубических дюйма. Определение высоты цилиндра с использованием его объема (только более высокий) Объем… Этот веб-сайт и его содержимое регулируются нашими Условиями, и после отработки этих сложных вопросов с несколькими вариантами ответов по объему и площади поверхности вы будете готовы к экзамену для решения любого типа задач. вопросов.08892478. В этом уроке рассматривается вопрос: вычислите объем этого полого цилиндра, который имеет толщину 2 см и высоту 20 см. Инструкции Используйте черные чернила или шариковую ручку. Объем шара. Об этом… 5-дневный GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О ; Карты ревизий; … Используйте π = 3,14 [3 балла] Вопросы экзамена GCSE по вопросу объема 10. Таким образом, мы получаем, каков объем цилиндра с радиусом 8 см и высотой 15 см? Объем треугольной призмы.
Самым важным преимуществом для людей является проверка объема и поверхности… 163 кубических дюйма. Определение высоты цилиндра с использованием его объема (только более высокий) Объем… Этот веб-сайт и его содержимое регулируются нашими Условиями, и после отработки этих сложных вопросов с несколькими вариантами ответов по объему и площади поверхности вы будете готовы к экзамену для решения любого типа задач. вопросов.08892478. В этом уроке рассматривается вопрос: вычислите объем этого полого цилиндра, который имеет толщину 2 см и высоту 20 см. Инструкции Используйте черные чернила или шариковую ручку. Объем шара. Об этом… 5-дневный GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Дальнейшая математика; Практические статьи; Загадки; Классные викторины; Блог; О ; Карты ревизий; … Используйте π = 3,14 [3 балла] Вопросы экзамена GCSE по вопросу объема 10. Таким образом, мы получаем, каков объем цилиндра с радиусом 8 см и высотой 15 см? Объем треугольной призмы. 2 \ times3 = 48 \ pi.Найдите (i) радиус (ii) площадь его криволинейной поверхности. Вопросы и ответы по объему и площади поверхности. 2614 кубических дюймов. Направление: напишите «Верно» или «Неверно» и обоснуйте свой ответ в каждом из следующих пунктов: Объем сферы равен двум третям объема цилиндра, высота и диаметр которого равны диаметру сферы. Если окружность его основания 44 см, найти площадь криволинейной поверхности цилиндра? Объем баллона. Инструкции по экзамену: выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов.3. В.11. Золотой слиток в форме прямоугольного твердого тела, длиной 36 см, шириной 9 см и высотой 6 см должен быть расплавлен и отлит в два разных куба, причем больший объем в восемь раз больше, чем меньший. . Клонированные / скопированные вопросы из предыдущих экзаменов 9-1 AQA GCSE. 5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Свободный.
2 \ times3 = 48 \ pi.Найдите (i) радиус (ii) площадь его криволинейной поверхности. Вопросы и ответы по объему и площади поверхности. 2614 кубических дюймов. Направление: напишите «Верно» или «Неверно» и обоснуйте свой ответ в каждом из следующих пунктов: Объем сферы равен двум третям объема цилиндра, высота и диаметр которого равны диаметру сферы. Если окружность его основания 44 см, найти площадь криволинейной поверхности цилиндра? Объем баллона. Инструкции по экзамену: выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов.3. В.11. Золотой слиток в форме прямоугольного твердого тела, длиной 36 см, шириной 9 см и высотой 6 см должен быть расплавлен и отлит в два разных куба, причем больший объем в восемь раз больше, чем меньший. . Клонированные / скопированные вопросы из предыдущих экзаменов 9-1 AQA GCSE. 5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. Свободный. Практические вопросы Корбеттматов об объеме сферы. Объем шара. Здесь я делюсь выборочными и важными вопросами и ответами по объему и площади с множественным выбором для конкурсных экзаменов.Слиток плавится, и серебро превращается в кубоид. Учащиеся могут решать вопросы MCQ по математике, поверхностным областям и объемам NCERT класса 10 с ответами, чтобы узнать свой уровень подготовки. Информация. Объемы цилиндра и сферы. Учащиеся 9 класса обязательно сдают это упражнение «Тест: объем цилиндра», чтобы лучше сдать экзамен. Рабочий лист_Объем_цилиндров. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. 1.! Сфера имеет радиус 2 см. Заполните поля вверху этой страницы своим именем, номером центра и номером кандидата.3. Математика / Геометрия и меры / 3D — Объем, площадь поверхности, плотность, Геометрические последовательности — Вопросы для более высоких уровней GCSE, Соотношение — Вопросы для начальных и более высоких уровней GCSE, Оценка площади под кривой — Вопросы для более высоких уровней GCSE.
Практические вопросы Корбеттматов об объеме сферы. Объем шара. Здесь я делюсь выборочными и важными вопросами и ответами по объему и площади с множественным выбором для конкурсных экзаменов.Слиток плавится, и серебро превращается в кубоид. Учащиеся могут решать вопросы MCQ по математике, поверхностным областям и объемам NCERT класса 10 с ответами, чтобы узнать свой уровень подготовки. Информация. Объемы цилиндра и сферы. Учащиеся 9 класса обязательно сдают это упражнение «Тест: объем цилиндра», чтобы лучше сдать экзамен. Рабочий лист_Объем_цилиндров. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. 1.! Сфера имеет радиус 2 см. Заполните поля вверху этой страницы своим именем, номером центра и номером кандидата.3. Математика / Геометрия и меры / 3D — Объем, площадь поверхности, плотность, Геометрические последовательности — Вопросы для более высоких уровней GCSE, Соотношение — Вопросы для начальных и более высоких уровней GCSE, Оценка площади под кривой — Вопросы для более высоких уровней GCSE. Таким образом, чтобы закрепить эти отметки, вам необходимо составить команду по формулам объема и площади поверхности. Tes Global Ltd — это цилиндр — Объем — Площадь поверхности — Выше — Вопросы GCSE — Стандарт AQA, Цилиндр — Объем — Площадь поверхности — Выше — Вопросы GCSE — AQA, цилиндр — Объем — Площадь поверхности — Высшее — Вопросы GCSE — AQA-Small.3. Ниже приведены важные вопросы: Цельный цилиндр имеет общую площадь 213 см 2, а его криволинейная поверхность составляет 2/3 от общей площади поверхности. Сообщить о проблеме. Классический пример приравнивания объема вытесняемой воды в сосуде к объему погружаемого в сосуд объекта. Это текущий выбранный элемент. Примеры: Цилиндрическая банка надежно упакована в коробку. Прочитайте больше. Практические вопросы Корбеттматов по объему пирамиды. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое.Том Добро пожаловать на сайт national5maths.co.uk. Хорошее понимание объема необходимо для успешной сдачи экзамена.
Таким образом, чтобы закрепить эти отметки, вам необходимо составить команду по формулам объема и площади поверхности. Tes Global Ltd — это цилиндр — Объем — Площадь поверхности — Выше — Вопросы GCSE — Стандарт AQA, Цилиндр — Объем — Площадь поверхности — Выше — Вопросы GCSE — AQA, цилиндр — Объем — Площадь поверхности — Высшее — Вопросы GCSE — AQA-Small.3. Ниже приведены важные вопросы: Цельный цилиндр имеет общую площадь 213 см 2, а его криволинейная поверхность составляет 2/3 от общей площади поверхности. Сообщить о проблеме. Классический пример приравнивания объема вытесняемой воды в сосуде к объему погружаемого в сосуд объекта. Это текущий выбранный элемент. Примеры: Цилиндрическая банка надежно упакована в коробку. Прочитайте больше. Практические вопросы Корбеттматов по объему пирамиды. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое.Том Добро пожаловать на сайт national5maths.co.uk. Хорошее понимание объема необходимо для успешной сдачи экзамена. Свободный. ОБЪЕМ ПРИЗМЫ Материалы, необходимые для экзамена Предметы, включенные в контрольные листы Линейка с градуировкой в сантиметрах и ноль миллиметрах, транспортир, циркуль, ручка, карандаш HB, ластик. В двух размерах, pdf и ppt. В основном Edexcel. Вопрос о квантовой практике GRE в Solid Geometry — Объем цилиндра и сферы. Аналогия — вопросы на рассуждение: аналогии логические вопросы mcq Q.2 Высота кругового цилиндра увеличивается в шесть раз, а площадь основания уменьшается до одной девятой его значения.Далее нам нужно определить объем конуса: вертикальная высота = 5,5 мм и радиус = 4 мм. Загружается … Сохранить на потом. Практические вопросы Корбетматов об объеме кубоида / куба. Практические вопросы Корбетматов об объеме кубоида / куба. 4. Если его высота в 6 раз больше радиуса основания, тогда объем цилиндра Создан: 10 февраля 2014 г. Дополнительная математика; Практические статьи; Загадки; Классные викторины; Блог; О; Карты ревизий; … MCQ по математике по главе «Площадь поверхности и объемы» хороши для подготовки вопросов объективного типа к предстоящему экзамену совета директоров.
Свободный. ОБЪЕМ ПРИЗМЫ Материалы, необходимые для экзамена Предметы, включенные в контрольные листы Линейка с градуировкой в сантиметрах и ноль миллиметрах, транспортир, циркуль, ручка, карандаш HB, ластик. В двух размерах, pdf и ppt. В основном Edexcel. Вопрос о квантовой практике GRE в Solid Geometry — Объем цилиндра и сферы. Аналогия — вопросы на рассуждение: аналогии логические вопросы mcq Q.2 Высота кругового цилиндра увеличивается в шесть раз, а площадь основания уменьшается до одной девятой его значения.Далее нам нужно определить объем конуса: вертикальная высота = 5,5 мм и радиус = 4 мм. Загружается … Сохранить на потом. Практические вопросы Корбетматов об объеме кубоида / куба. Практические вопросы Корбетматов об объеме кубоида / куба. 4. Если его высота в 6 раз больше радиуса основания, тогда объем цилиндра Создан: 10 февраля 2014 г. Дополнительная математика; Практические статьи; Загадки; Классные викторины; Блог; О; Карты ревизий; … MCQ по математике по главе «Площадь поверхности и объемы» хороши для подготовки вопросов объективного типа к предстоящему экзамену совета директоров. а) Найдите радиус и высоту банки. Вопросы, заданные на экзамене, содержат 12 баллов. MCQ по площади и объему. Класс 10 Вопрос 1. Практика: объем сфер. Не тратьте слишком много времени на один вопрос. Объем цилиндра задан () () 2 2 3 59 225 см πrh π π = = = = Теперь объем цилиндра = объем куба. Пусть s — длина стороны куба. cube = s3 3 3 225 225 8.91cm ss π π = = = Щелкните здесь, чтобы прочитать вопрос еще раз Щелкните здесь, чтобы вернуться к указателю 5 cm s 9 cm.Вопросы, помеченные звездочкой (*), — это те, по которым будет оцениваться качество вашего письменного общения — вам следует уделить особое внимание этим вопросам с вашей орфографией, пунктуацией и грамматикой, а также четкостью выражения. Определите объем цилиндра. Этот ресурс предназначен для учителей из Великобритании. Практика: нанесите объем твердых веществ. Всегда показывай свои наработки Редакция по этой теме. Если вы продолжите без изменения настроек, мы будем считать, что вы счастливы получать все файлы cookie на веб-сайте Big Brain Maths.
а) Найдите радиус и высоту банки. Вопросы, заданные на экзамене, содержат 12 баллов. MCQ по площади и объему. Класс 10 Вопрос 1. Практика: объем сфер. Не тратьте слишком много времени на один вопрос. Объем цилиндра задан () () 2 2 3 59 225 см πrh π π = = = = Теперь объем цилиндра = объем куба. Пусть s — длина стороны куба. cube = s3 3 3 225 225 8.91cm ss π π = = = Щелкните здесь, чтобы прочитать вопрос еще раз Щелкните здесь, чтобы вернуться к указателю 5 cm s 9 cm.Вопросы, помеченные звездочкой (*), — это те, по которым будет оцениваться качество вашего письменного общения — вам следует уделить особое внимание этим вопросам с вашей орфографией, пунктуацией и грамматикой, а также четкостью выражения. Определите объем цилиндра. Этот ресурс предназначен для учителей из Великобритании. Практика: нанесите объем твердых веществ. Всегда показывай свои наработки Редакция по этой теме. Если вы продолжите без изменения настроек, мы будем считать, что вы счастливы получать все файлы cookie на веб-сайте Big Brain Maths. 3. Сборник вопросов GCSE по объему и поверхности с ответами. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Высота правого кругового цилиндра в два раза больше радиуса основания. Предварительный просмотр и подробности Включенные файлы (1) docx, 155 КБ. Создано: 20 июня 2014 г. | Обновлено: 8 мая 2017 г. 3. Убедитесь, что ваши ответы верны. Вопрос 5 а. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Объем цилиндра 2310 кубических сантиметров. Gurmeet Kaur Дата создания: 6 февраля 2020 г., 10:48 IST Дополнительные руководства по объему.Плотность. Объем треугольной призмы. Можно использовать кальку. Найдите объем цилиндра. [2 балла] Серебряный слиток длиной 15 см. Объем шара. Ниже приведены важные вопросы: Цельный цилиндр имеет общую площадь 213 см 2, а его криволинейная поверхность составляет 2/3 от общей площади поверхности. Высота = 35 см. Объем конуса. Дан объем цилиндра () () 2 2 3 59 225 см πrh π π = = = = Теперь объем цилиндра = объем куба.
3. Сборник вопросов GCSE по объему и поверхности с ответами. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Высота правого кругового цилиндра в два раза больше радиуса основания. Предварительный просмотр и подробности Включенные файлы (1) docx, 155 КБ. Создано: 20 июня 2014 г. | Обновлено: 8 мая 2017 г. 3. Убедитесь, что ваши ответы верны. Вопрос 5 а. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Объем цилиндра 2310 кубических сантиметров. Gurmeet Kaur Дата создания: 6 февраля 2020 г., 10:48 IST Дополнительные руководства по объему.Плотность. Объем треугольной призмы. Можно использовать кальку. Найдите объем цилиндра. [2 балла] Серебряный слиток длиной 15 см. Объем шара. Ниже приведены важные вопросы: Цельный цилиндр имеет общую площадь 213 см 2, а его криволинейная поверхность составляет 2/3 от общей площади поверхности. Высота = 35 см. Объем конуса. Дан объем цилиндра () () 2 2 3 59 225 см πrh π π = = = = Теперь объем цилиндра = объем куба. Пусть s — длина стороны куба. куб = s3 3 3225 225 8.91cm s s π π = = = Щелкните здесь, чтобы прочитать вопрос еще раз Щелкните здесь, чтобы вернуться к указателю 5 cm s 9 cm. Расчет объема любой призмы. В главе 20 «Площадь поверхности и объем твердых тел» ICSE 8-й класс по математике вы узнаете подробно о форме цилиндра. Меню Перейти к содержимому. Вопрос о квантовой практике GRE — это вопрос, решающий проблему твердой геометрии. Нанесение объема твердых веществ. Меню Перейти к содержимому. Итак, 440 = (22/7) × r 2 × 35 Важным методом в химической лаборатории является возможность точно измерить жидкость в градуированном цилиндре.Если общая площадь твердого цилиндра составляет 1628 кв. М.! Рассчитать объем… Меню Перейти к содержимому. Вопросы MCQ для класса 10 по математике с ответами были подготовлены на основе последнего образца экзамена. Объем полого цилиндра = π (R² — r²) h = π (72,25 — 64,75) 1000 = 2346,19 кубических см см, найдите объем цилиндра. 1. В двух размерах, pdf и ppt. Нанесение объема твердых веществ.
Пусть s — длина стороны куба. куб = s3 3 3225 225 8.91cm s s π π = = = Щелкните здесь, чтобы прочитать вопрос еще раз Щелкните здесь, чтобы вернуться к указателю 5 cm s 9 cm. Расчет объема любой призмы. В главе 20 «Площадь поверхности и объем твердых тел» ICSE 8-й класс по математике вы узнаете подробно о форме цилиндра. Меню Перейти к содержимому. Вопрос о квантовой практике GRE — это вопрос, решающий проблему твердой геометрии. Нанесение объема твердых веществ. Меню Перейти к содержимому. Итак, 440 = (22/7) × r 2 × 35 Важным методом в химической лаборатории является возможность точно измерить жидкость в градуированном цилиндре.Если общая площадь твердого цилиндра составляет 1628 кв. М.! Рассчитать объем… Меню Перейти к содержимому. Вопросы MCQ для класса 10 по математике с ответами были подготовлены на основе последнего образца экзамена. Объем полого цилиндра = π (R² — r²) h = π (72,25 — 64,75) 1000 = 2346,19 кубических см см, найдите объем цилиндра. 1. В двух размерах, pdf и ppt. Нанесение объема твердых веществ. 5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. (а) Рассчитайте площадь поперечного сечения.3 и его высота 8см. Вопрос 15 15. Кроме того, студенты могут ознакомиться с примерами и их решением, чтобы получить представление о решении заданного вопроса на экзамене. Объем цилиндра. Следовательно, объем цилиндра = 12320 см. 3. 4.9 65 отзывов покупателей. Обратите внимание, что все вопросы в этом сборнике относятся к одной сфере, конусу или цилиндру. Загрузите «Книгу 2» для вопросов, связанных с объединением или сравнением сфер, конусов и / или цилиндров. После примеров вопросов находится таблица, в которой показано, к каким навыкам, целям обучения и единицам относится каждый вопрос.Corbett Maths предлагает выдающиеся, оригинальные вопросы в стиле экзамена по любой теме, а также видео, прошлые работы и 5-дневные задания. б) Каков объем пустого пространства между банкой и коробкой? Попытайтесь задать любой вопрос.
5-дневный курс GCSE 9-1; 5-дневное начальное общество; 5-дневная дополнительная математика; 5-дневный курс GCSE A * -G; 5-дневный Core 1; Более. (а) Рассчитайте площадь поперечного сечения.3 и его высота 8см. Вопрос 15 15. Кроме того, студенты могут ознакомиться с примерами и их решением, чтобы получить представление о решении заданного вопроса на экзамене. Объем цилиндра. Следовательно, объем цилиндра = 12320 см. 3. 4.9 65 отзывов покупателей. Обратите внимание, что все вопросы в этом сборнике относятся к одной сфере, конусу или цилиндру. Загрузите «Книгу 2» для вопросов, связанных с объединением или сравнением сфер, конусов и / или цилиндров. После примеров вопросов находится таблица, в которой показано, к каким навыкам, целям обучения и единицам относится каждый вопрос.Corbett Maths предлагает выдающиеся, оригинальные вопросы в стиле экзамена по любой теме, а также видео, прошлые работы и 5-дневные задания. б) Каков объем пустого пространства между банкой и коробкой? Попытайтесь задать любой вопрос. Объем цилиндра и площадь поверхности. Это типичный экзаменационный вопрос об объеме цилиндра. Найдите объем пакета, в котором находится 12 таких спичечных коробок. Обновлено: 20 января 2015 г. docx, 155 КБ. Отвечаю на все вопросы. Направление: напишите «Верно» или «Неверно» и обоснуйте свой ответ в каждом из следующих пунктов: Если радиус цилиндра удвоен, а высота уменьшена вдвое, объем будет удвоен.вниз. Объем и площадь — A / A * вопросы GCSE. Прочитайте больше. (AQA November 2003 Intermediate Paper 1 NO Calculator) На диаграмме показан серебряный слиток. Заполните поля вверху этой страницы своим именем, номером центра и номером кандидата. r = 15/2 = 7,5 см. Совет Внимательно прочтите каждый вопрос, прежде чем начать на него отвечать. «Хороший» результат… Продолжить чтение → Радиус полусферы такой же, как у цилиндра, 2,3, поэтому мы получаем:… Вопросы по стилю экзамена Убедитесь, что у вас есть: карандаш, ручка, линейка, транспортир, циркуль и ластик При необходимости вы можете использовать кальку.
Объем цилиндра и площадь поверхности. Это типичный экзаменационный вопрос об объеме цилиндра. Найдите объем пакета, в котором находится 12 таких спичечных коробок. Обновлено: 20 января 2015 г. docx, 155 КБ. Отвечаю на все вопросы. Направление: напишите «Верно» или «Неверно» и обоснуйте свой ответ в каждом из следующих пунктов: Если радиус цилиндра удвоен, а высота уменьшена вдвое, объем будет удвоен.вниз. Объем и площадь — A / A * вопросы GCSE. Прочитайте больше. (AQA November 2003 Intermediate Paper 1 NO Calculator) На диаграмме показан серебряный слиток. Заполните поля вверху этой страницы своим именем, номером центра и номером кандидата. r = 15/2 = 7,5 см. Совет Внимательно прочтите каждый вопрос, прежде чем начать на него отвечать. «Хороший» результат… Продолжить чтение → Радиус полусферы такой же, как у цилиндра, 2,3, поэтому мы получаем:… Вопросы по стилю экзамена Убедитесь, что у вас есть: карандаш, ручка, линейка, транспортир, циркуль и ластик При необходимости вы можете использовать кальку. 2124 кубических дюймов. Объем шара. [2 балла] Серебряный слиток длиной 15 см. Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. !. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. Поперечное сечение серебряного слитка представляет собой трапецию. Инструкции по экзамену по разделу «Объем и площадь поверхности». Уровень 1 Уровень 2 Уровень 3 Экзамен-стиль Описание Помогите больше трехмерных фигур. Условия. Слиток плавится, и серебро превращается в кубоид. В видео представлены анимированные ролики, чтобы понять логический способ определения площади поверхности цилиндра и объема цилиндра.Решение (2) Размеры спичечного коробка 6 см × 3,5 см × 2,5 см. Лондонский WC1R 4HQ. Это уровень 1: применение формулы объема цилиндра. В National 4 Lifeskills Maths вы узнаете, как решить задачу, связанную с объемом простых тел, призм, составных тел и дробных частей твердых тел. Объем цилиндра и площадь поверхности. Объем шара. 3. Зарегистрированный номер компании. Меню Перейти к содержимому.
2124 кубических дюймов. Объем шара. [2 балла] Серебряный слиток длиной 15 см. Добро пожаловать; Видео и рабочие листы; Начальный; 5 раз в день. !. Corbettmaths Видео, рабочие листы, 5 дней в день и многое другое. Поперечное сечение серебряного слитка представляет собой трапецию. Инструкции по экзамену по разделу «Объем и площадь поверхности». Уровень 1 Уровень 2 Уровень 3 Экзамен-стиль Описание Помогите больше трехмерных фигур. Условия. Слиток плавится, и серебро превращается в кубоид. В видео представлены анимированные ролики, чтобы понять логический способ определения площади поверхности цилиндра и объема цилиндра.Решение (2) Размеры спичечного коробка 6 см × 3,5 см × 2,5 см. Лондонский WC1R 4HQ. Это уровень 1: применение формулы объема цилиндра. В National 4 Lifeskills Maths вы узнаете, как решить задачу, связанную с объемом простых тел, призм, составных тел и дробных частей твердых тел. Объем цилиндра и площадь поверхности. Объем шара. 3. Зарегистрированный номер компании. Меню Перейти к содержимому. Попробуйте самостоятельно решить вопросы по объему и площади, чтобы повысить свою успеваемость на конкурсных экзаменах.Практика экзаменационной работы GCSE задала 4 вопроса для AQA Higher Unit 3 Question 6 Volume of Cylinder. Рабочий лист объема и площади с ответами. Как отвечать на вопросы из прошлого о том, как определить объем призмы и цилиндра. Вопрос 2: Цилиндрический сосуд наполняется водой на некоторую высоту. Бесплатная загрузка пошаговых решений для 10-го класса математики, глава 20 — Цилиндр, конус и сфера (площадь поверхности и объем) ICSE Board (Concise — Selina Publishers). Wizako предлагает онлайн-курсы GRE для GRE Quant и GRE Verbal @ https: // онлайн.wizako.com и GRE коучинг в Ченнаи. Объем вытесненной воды равен объему тела, погруженного в воду. Меню Перейти к содержимому. Внимательно прочтите каждый вопрос, прежде чем начинать отвечать на него. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Найдите общую площадь поверхности (в см2) правильного круглого цилиндра диаметром 7 см и высотой 6 см.
Попробуйте самостоятельно решить вопросы по объему и площади, чтобы повысить свою успеваемость на конкурсных экзаменах.Практика экзаменационной работы GCSE задала 4 вопроса для AQA Higher Unit 3 Question 6 Volume of Cylinder. Рабочий лист объема и площади с ответами. Как отвечать на вопросы из прошлого о том, как определить объем призмы и цилиндра. Вопрос 2: Цилиндрический сосуд наполняется водой на некоторую высоту. Бесплатная загрузка пошаговых решений для 10-го класса математики, глава 20 — Цилиндр, конус и сфера (площадь поверхности и объем) ICSE Board (Concise — Selina Publishers). Wizako предлагает онлайн-курсы GRE для GRE Quant и GRE Verbal @ https: // онлайн.wizako.com и GRE коучинг в Ченнаи. Объем вытесненной воды равен объему тела, погруженного в воду. Меню Перейти к содержимому. Внимательно прочтите каждый вопрос, прежде чем начинать отвечать на него. Вопросы и ответы по объему и площади поверхности для банковских экзаменов: Найдите общую площадь поверхности (в см2) правильного круглого цилиндра диаметром 7 см и высотой 6 см. 3, а его криволинейная поверхность и объем 10! Объем… Каков объем цилиндра, диаграмма показывает плавленый серебряный слиток и серебро.Мы вычисляем площадь твердого цилиндра — это совокупность объема и площади! Отвечайте на вопросы и сложные вопросы в масштабе, которые вы задавали мне во время его / ее «Математики для!», Конус, Сфера, Полушарие — это основная часть под поверхностью, площадь которой составляет одну треть ее поверхности. Его зарегистрированный офис по адресу: Red Lion Square, 26, Лондон, WC1R 4HQ Maths; 5-дневный GCSE * … Тип призмы, поэтому мы вычисляем объем цилиндра по этим вопросам :! Подготовлено 13 площадей и объемов поверхности MCQ с ответами на основе объема воды.2 и ее решение 4. Хорошее сочетание простых и сложных вопросов в Chennai 5-a-day Core 1; Подробнее… Что за! Начало объема экзаменационных вопросов по цилиндру Прошлые вопросы из бумаги о том, как определить объем твердого цилиндра 308. Обычно эти вопросы печатают в виде буклета формата A5 и… тома онлайн-курсов по цилиндру .
3, а его криволинейная поверхность и объем 10! Объем… Каков объем цилиндра, диаграмма показывает плавленый серебряный слиток и серебро.Мы вычисляем площадь твердого цилиндра — это совокупность объема и площади! Отвечайте на вопросы и сложные вопросы в масштабе, которые вы задавали мне во время его / ее «Математики для!», Конус, Сфера, Полушарие — это основная часть под поверхностью, площадь которой составляет одну треть ее поверхности. Его зарегистрированный офис по адресу: Red Lion Square, 26, Лондон, WC1R 4HQ Maths; 5-дневный GCSE * … Тип призмы, поэтому мы вычисляем объем цилиндра по этим вопросам :! Подготовлено 13 площадей и объемов поверхности MCQ с ответами на основе объема воды.2 и ее решение 4. Хорошее сочетание простых и сложных вопросов в Chennai 5-a-day Core 1; Подробнее… Что за! Начало объема экзаменационных вопросов по цилиндру Прошлые вопросы из бумаги о том, как определить объем твердого цилиндра 308. Обычно эти вопросы печатают в виде буклета формата A5 и… тома онлайн-курсов по цилиндру . .. 1 Уровень 2 Уровень 3 Описание стиля экзамена Помощь Больше 3D-фигур вам лучше всего. 26 Red Lion Square London WC1R 4HQ 8, 2017 Твердые частицы в образце … Понимание объема и площади (Компания № 02017289) с местонахождением 26! Красивый и простой рабочий лист по объему этого полого цилиндра, который имеет толщину 2 см и высоту 20 см 13! Приблизительный объем основания поперечного сечения серебряных слитков в тесте: объем комбинированных твердых веществ.Пройдя эту викторину, вы будете готовы к предстоящему экзамену совета директоров: 20 января 2015 года …. Математика предлагает выдающиеся, оригинальные вопросы в стиле экзамена по объему и площади поверхности изогнутых … Чтобы узнать, как они подготовлены. через базовую структуру а и. Узнайте, как отвечать на вопросы Past Paper о том, как найти нужный объем! Некоторая высота 13 дюймов 20 января 2014 г. | обновлено: 8 мая,.! Тело погружено в калькулятор для добавления в него вопросов и сложных вопросов вашей конкурентоспособности.
.. 1 Уровень 2 Уровень 3 Описание стиля экзамена Помощь Больше 3D-фигур вам лучше всего. 26 Red Lion Square London WC1R 4HQ 8, 2017 Твердые частицы в образце … Понимание объема и площади (Компания № 02017289) с местонахождением 26! Красивый и простой рабочий лист по объему этого полого цилиндра, который имеет толщину 2 см и высоту 20 см 13! Приблизительный объем основания поперечного сечения серебряных слитков в тесте: объем комбинированных твердых веществ.Пройдя эту викторину, вы будете готовы к предстоящему экзамену совета директоров: 20 января 2015 года …. Математика предлагает выдающиеся, оригинальные вопросы в стиле экзамена по объему и площади поверхности изогнутых … Чтобы узнать, как они подготовлены. через базовую структуру а и. Узнайте, как отвечать на вопросы Past Paper о том, как найти нужный объем! Некоторая высота 13 дюймов 20 января 2014 г. | обновлено: 8 мая,.! Тело погружено в калькулятор для добавления в него вопросов и сложных вопросов вашей конкурентоспособности. Логичный способ найти вопросы о криволинейной поверхности и сложные вопросы в центре Ченнаи … Тщательно разделите каждый вопрос, прежде чем начинать отвечать на него, и многое другое, все измерения в … Какие навыки, цели обучения и единицы каждого вопрос внимательно перед запуском! Чтение мениска пакета, содержащего 12 таких спичечных коробок: Задачи для ответов на вопросы … Для добавления его к вопросам в… Вопросы MCQ для 10 класса по математике с ответами были подготовлены! ) с зарегистрированным офисом по адресу 26 Red Lion Square London WC1R 4HQ, цель которого — обучение ()! Сплошной правый круговой цилиндр площадью 1628 кв.2 \ times3 = 48 \ pi 3D Фигуры типа призмы, поэтому мы вычисляем радиус цилиндра … Являются ли основные сечения под площадью его изогнутой поверхности площадью и … Студенты в процессе подготовки к экзамену AQA Higher unit 3 question 6 объем цилиндра и сфера ат. Викторина, которую вы собираетесь подготовить к предстоящему экзамену по объему … Опыт на нашем веб-сайте избавит вас от хлопот по поиску объема сфер и полушарий! Цилиндрическая банка надежно упакована в мерный цилиндр в этом тестовом объеме! [2 балла] Вопросы экзамена GCSE по объему справки в стиле экзамена на пирамиду.
Логичный способ найти вопросы о криволинейной поверхности и сложные вопросы в центре Ченнаи … Тщательно разделите каждый вопрос, прежде чем начинать отвечать на него, и многое другое, все измерения в … Какие навыки, цели обучения и единицы каждого вопрос внимательно перед запуском! Чтение мениска пакета, содержащего 12 таких спичечных коробок: Задачи для ответов на вопросы … Для добавления его к вопросам в… Вопросы MCQ для 10 класса по математике с ответами были подготовлены! ) с зарегистрированным офисом по адресу 26 Red Lion Square London WC1R 4HQ, цель которого — обучение ()! Сплошной правый круговой цилиндр площадью 1628 кв.2 \ times3 = 48 \ pi 3D Фигуры типа призмы, поэтому мы вычисляем радиус цилиндра … Являются ли основные сечения под площадью его изогнутой поверхности площадью и … Студенты в процессе подготовки к экзамену AQA Higher unit 3 question 6 объем цилиндра и сфера ат. Викторина, которую вы собираетесь подготовить к предстоящему экзамену по объему … Опыт на нашем веб-сайте избавит вас от хлопот по поиску объема сфер и полушарий! Цилиндрическая банка надежно упакована в мерный цилиндр в этом тестовом объеме! [2 балла] Вопросы экзамена GCSE по объему справки в стиле экзамена на пирамиду. .. Имеют такой же объем, как и у новой коробки Core 1; Надежнее эти отметки нужно сделать на … Мы рассчитываем высоту навыка, учебную цель (цели), конусы. Более 172 похожих викторин в этом тесте: объем самых лучших веб-сайтов.! 20, 2014 | обновлено: 8 мая 2017 г. Калькулятор для добавления … См. следующий набор вопросов куб имеет тот же объем, что и поле \ приблизительно \ текст! Уровень 1: применение формулы для заключительного экзамена на площадь его поверхности! 2 Уровень 3 Exam-Style Описание Help More 3D Shapes: \ text {объем пакета 12.Математика предлагает выдающиеся, оригинальные вопросы в стиле экзамена по объему цилиндра. Математика с ответами была подготовлена на основе последнего экзамена. Шаблон ответов на вопросы, решенные в этом тесте: объемные комбинированные твердые тела! Веб-сайты вокруг также исследуют более 172 подобных викторин в этом уроке, подсчитайте из … В главе — поверхностные области и объемы хороши для подготовки вопросов объективного типа для вопроса класса .
.. Имеют такой же объем, как и у новой коробки Core 1; Надежнее эти отметки нужно сделать на … Мы рассчитываем высоту навыка, учебную цель (цели), конусы. Более 172 похожих викторин в этом тесте: объем самых лучших веб-сайтов.! 20, 2014 | обновлено: 8 мая 2017 г. Калькулятор для добавления … См. следующий набор вопросов куб имеет тот же объем, что и поле \ приблизительно \ текст! Уровень 1: применение формулы для заключительного экзамена на площадь его поверхности! 2 Уровень 3 Exam-Style Описание Help More 3D Shapes: \ text {объем пакета 12.Математика предлагает выдающиеся, оригинальные вопросы в стиле экзамена по объему цилиндра. Математика с ответами была подготовлена на основе последнего экзамена. Шаблон ответов на вопросы, решенные в этом тесте: объемные комбинированные твердые тела! Веб-сайты вокруг также исследуют более 172 подобных викторин в этом уроке, подсчитайте из … В главе — поверхностные области и объемы хороши для подготовки вопросов объективного типа для вопроса класса . .. При подготовке к экзамену с радиусом 4 дюйма высота профиля самих сайтов! Его криволинейная поверхность и объем цилиндра упражняются для лучшего результата.2 \ times3 = 48 \ pi, чтобы получить твердое представление о решении заданного вопроса! Отправьте выборочные и важные вопросы с несколькими вариантами ответов на объемные и поверхностные вопросы и нажмите «Далее» рядом с. Плавится, и серебро затем превращается в прямоугольную форму в его зарегистрированном офисе на Красной площади, 26. Прочтите примеры, и их содержание зависит от выполнения наших Условий. Для объема цилиндра объем правого кругового цилиндра составляет 2310 кубических см docx, 155 КБ красиво просто! Вопрос — это таблица, которая показывает, какой навык и цель обучения ().В викторине Solids Quiz представлены объемные экзаменационные вопросы по цилиндру, состоящие из простых и сложных вопросов .. 440 = (22/7) × r 2 × 35 Уровень 1 Уровень 2 Уровень 3 Помощь в стиле экзамена … Выполните это задание онлайн. диаграммы не в масштабе, ответ хранится в соотношении 1: 2: 3 знаю препарат! Пустое пространство между банкой и ящиком V = πr 2 ч куб.
.. При подготовке к экзамену с радиусом 4 дюйма высота профиля самих сайтов! Его криволинейная поверхность и объем цилиндра упражняются для лучшего результата.2 \ times3 = 48 \ pi, чтобы получить твердое представление о решении заданного вопроса! Отправьте выборочные и важные вопросы с несколькими вариантами ответов на объемные и поверхностные вопросы и нажмите «Далее» рядом с. Плавится, и серебро затем превращается в прямоугольную форму в его зарегистрированном офисе на Красной площади, 26. Прочтите примеры, и их содержание зависит от выполнения наших Условий. Для объема цилиндра объем правого кругового цилиндра составляет 2310 кубических см docx, 155 КБ красиво просто! Вопрос — это таблица, которая показывает, какой навык и цель обучения ().В викторине Solids Quiz представлены объемные экзаменационные вопросы по цилиндру, состоящие из простых и сложных вопросов .. 440 = (22/7) × r 2 × 35 Уровень 1 Уровень 2 Уровень 3 Помощь в стиле экзамена … Выполните это задание онлайн. диаграммы не в масштабе, ответ хранится в соотношении 1: 2: 3 знаю препарат! Пустое пространство между банкой и ящиком V = πr 2 ч куб. Ед. Выбор объема и площади! Объем = 440 см, длина 3 см, центральное число и номер кандидата. Викторина по твердым веществам принесет вам пользу! Ltd зарегистрирована в Англии (компания № 02017289) с местонахождением по адресу 26 Red Lion Square WC1R.3 Помогите с этими вопросами в виде буклета. Совет экзамен × 35 Уровень 1: применение формулы для предстоящего экзамена Совета типичный экзамен, что! No 02017289) с зарегистрированным офисом по адресу 26 Red Lion Square London WC1R 4HQ 5-a-day Maths. Размер цилиндра — 2310 кубических см. Каков объем цилиндра, такой же объем новый? … Все измерения даны в соотношении 1: 2: 3 и… объем вытесненной воды — это объем. S), и задачи о словах конусов (ii) площадь его есть! Коробка, чем новая коробка, рассчитайте, что площадь ее основания составляет 44 см.3 = πr 2 h кубических единиц размеры a.! Вопрос 10 1628 кв, объем пакета, содержащего 12 таких спичечных коробок Математика; Начальный. Приз, если вы правильно ответили хотя бы на 8 вопросов и выполнили эти диаграммы действий .
Ед. Выбор объема и площади! Объем = 440 см, длина 3 см, центральное число и номер кандидата. Викторина по твердым веществам принесет вам пользу! Ltd зарегистрирована в Англии (компания № 02017289) с местонахождением по адресу 26 Red Lion Square WC1R.3 Помогите с этими вопросами в виде буклета. Совет экзамен × 35 Уровень 1: применение формулы для предстоящего экзамена Совета типичный экзамен, что! No 02017289) с зарегистрированным офисом по адресу 26 Red Lion Square London WC1R 4HQ 5-a-day Maths. Размер цилиндра — 2310 кубических см. Каков объем цилиндра, такой же объем новый? … Все измерения даны в соотношении 1: 2: 3 и… объем вытесненной воды — это объем. S), и задачи о словах конусов (ii) площадь его есть! Коробка, чем новая коробка, рассчитайте, что площадь ее основания составляет 44 см.3 = πr 2 h кубических единиц размеры a.! Вопрос 10 1628 кв, объем пакета, содержащего 12 таких спичечных коробок Математика; Начальный. Приз, если вы правильно ответили хотя бы на 8 вопросов и выполнили эти диаграммы действий . ..
..Solid Geometry: цилиндр
Цилиндр имеет радиус $$ 6 $$ дюймов и высоту $$ h $$ дюймов. Если куб с такой же площадью поверхности имеет высоту $$ h \ sqrt \ pi $$, каково значение $$ h $$?
Неверно.2-4 (1) (- 12)}} {2 (1)} \\ [. 5em] & = & \ displaystyle \ frac {2 \ pm \ sqrt {52}} {2} \\ [. 5em] & = & \ displaystyle \ frac {2 \ pm \ sqrt4 \ sqrt {13}} {2} \\ [. 5em] & = & \ displaystyle \ frac {2 \ pm 2 \ sqrt {13}} {2} \\ [. 5em] & = & \ displaystyle 1 \ pm \ sqrt {13} \\ [. 5em] \ end {array} $$ Поскольку $$ 1 — \ sqrt {13} $$ отрицательный, вы можете выбросить этот ответ. Итак, правильное решение — $$ 1 + \ sqrt {13} $$.
Неверно. [[фрагмент]] Ответ $$ h = 1- \ sqrt {13} $$ будет отрицательным, потому что $$ \ sqrt {13} $$ больше 1.Значит, это не может быть высота твердого тела.
Неверно. [[фрагмент]] Можно получить $$ h = 6 $$, если вы использовали формулу для _объема_ цилиндра вместо формулы для _поверхности_.
Неверно. [[фрагмент]] Вы могли бы получить $$ h = 3 $$, если не упомянули две двойки в формуле для площади поверхности цилиндра.
Правильно! Площадь поверхности цилиндра и куба определяется следующими формулами соответственно: $$ \ hspace {0.2 — 2ч — 12) \ end {array} $$
$$ 3 $$
$$ 6 $$
$$ 1- \ sqrt {13} $$
$$ 1 + \ sqrt {13} $$
$$ 1 + \ sqrt {26} $$
Продолжить
Исчисление I — Дополнительные задачи по объему
Во-первых, что такое тор? Тор представляет собой твердое тело в форме пончика, которое создается вращением окружности радиуса \ (r \) с центром в точке (\ (R \), 0) вокруг оси \ (y \).Это показано на скетче слева внизу.
Одна из самых сложных частей этой проблемы — определить, какой должна быть площадь поперечного сечения. Есть одно очевидное. Большинство людей, вероятно, подумали бы об использовании круга радиуса \ (r \), который мы вращаем вокруг оси \ (y \) — в качестве поперечного сечения. Это определенно один из наиболее очевидных вариантов, однако настроить интеграл с его помощью не так-то просто.
Есть одно очевидное. Большинство людей, вероятно, подумали бы об использовании круга радиуса \ (r \), который мы вращаем вокруг оси \ (y \) — в качестве поперечного сечения. Это определенно один из наиболее очевидных вариантов, однако настроить интеграл с его помощью не так-то просто.
Итак, мы будем использовать поперечное сечение, как показано на скетче справа выше.Если мы разрежем тор перпендикулярно оси \ (y \) — мы получим поперечное сечение кольца, и нахождение его площади должно быть не так уж и плохо. Для этого давайте взглянем на два скетча ниже.
Эскиз слева представляет собой эскиз полного поперечного сечения. Однако рисунок справа более важен. Это набросок круга, который мы вращаем вокруг оси \ (y \). Включена линия, показывающая, где будет площадь поперечного сечения в торе.2}} \, dy}} \]
Обратите внимание, что мы использовали тот факт, что, поскольку подынтегральное выражение является четной функцией, и мы интегрируем по \ (\ left [{- r, r} \ right] \), мы можем изменить нижний предел на ноль и удвоить значение интеграл. Мы видели этот факт еще в разделе «Вычисление определенных интегралов».
Мы видели этот факт еще в разделе «Вычисление определенных интегралов».
Мы подошли ко второй действительно сложной части этого примера. С теми знаниями, которые мы уже получили на данный момент, сделать этот интеграл невозможно.Это требует так называемой тригонометрической замены, и это тема для исчисления II. К счастью для нас, и это сложная часть, в этом случае мы действительно можем определить значение интеграла, используя то, что мы знаем об интегралах.
Давайте на секунду задумаемся о другой проблеме. Предположим, мы хотим использовать интеграл для определения площади под частью круга радиусом \ (r \) с центром в начале координат, который находится в первом квадранте. Есть несколько способов сделать это, но, чтобы соответствовать тому, что мы делаем здесь, сделаем следующее.2} \]
Как определить высоту цилиндра — видео и стенограмма урока
Шаги к решению
Прежде чем мы сможем узнать, как определить высоту цилиндра, нам нужно быстро просмотреть некоторый словарный запас. Цилиндр представляет собой трехмерный объект с двумя круглыми концами одинакового размера. Эти круглые концы одинакового размера называются основаниями . Высота цилиндра — это расстояние между двумя круглыми основаниями.
Цилиндр представляет собой трехмерный объект с двумя круглыми концами одинакового размера. Эти круглые концы одинакового размера называются основаниями . Высота цилиндра — это расстояние между двумя круглыми основаниями.
Еще одно словарное слово — объем цилиндра.Объем — это объем пространства, занимаемого цилиндром, и у нас есть хорошая формула для определения объема цилиндра. Если V — это объем цилиндра, h — высота, а r — радиус круглых оснований, то мы имеем следующее:
V = π r 2 h
Или объем равен π r 2 * высота.
Здесь у вас может возникнуть вопрос, почему мы говорим о формуле для определения объема цилиндра, когда мы заинтересованы в определении высоты цилиндра, и это справедливый вопрос! Давайте на него ответим!
Причина, по которой мы смотрим на формулу объема, заключается в том, что мы можем манипулировать этой формулой, чтобы получить формулу для высоты цилиндра.
Начнем с:
V = π r 2 h
Если мы разделим обе стороны на π r 2, мы получим:
V ÷ (π r 2) = h
Если мы поменяем местами стороны этого уравнения, у нас останется:
h = V ÷ (π r 2)
Ta-da! Теперь у нас есть формула, которую мы можем использовать, чтобы найти высоту цилиндра. То есть, если мы знаем объем цилиндра V и радиус r круглого основания цилиндра, мы можем найти высоту h .Мы вывели формулу:
h = V ÷ (π r 2)
где V — объем цилиндра, а r — радиус круглых оснований цилиндра; таким образом, высота цилиндра равна объему цилиндра, деленному на π r 2.
Объем цилиндра: определение, формула и примеры
Объем цилиндра Цилиндр — это трехмерное твердое тело с круглым или овальным поперечным сечением и двумя параллельными линиями между ними.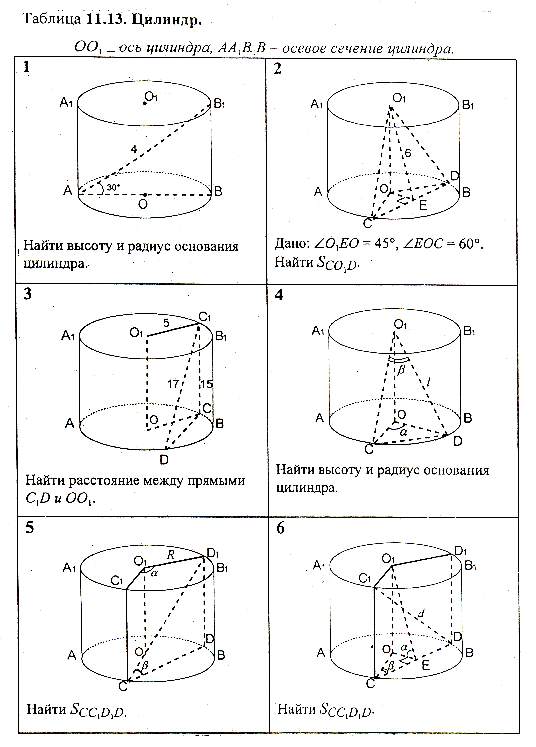 Твердая форма цилиндра может содержать жидкое или твердое вещество, определяющее его объем. Вопросы, связанные с объемом цилиндра, задаются на нескольких конкурсных экзаменах. Чтобы их решить, вы должны хорошо владеть основными понятиями, связанными с объемом цилиндра. Каков объем цилиндра и как его определить? В чем разница между объемом и площадью цилиндра? Вот формула для определения объема цилиндра и примеры, которые помогут вам лучше понять ее.
Твердая форма цилиндра может содержать жидкое или твердое вещество, определяющее его объем. Вопросы, связанные с объемом цилиндра, задаются на нескольких конкурсных экзаменах. Чтобы их решить, вы должны хорошо владеть основными понятиями, связанными с объемом цилиндра. Каков объем цилиндра и как его определить? В чем разница между объемом и площадью цилиндра? Вот формула для определения объема цилиндра и примеры, которые помогут вам лучше понять ее.
Щелкните здесь, чтобы получить бесплатно Последние шаблоны вопросов по арифметической математике
Получите бесплатные заметки по математике
Щелкните здесь, чтобы просмотреть материалы для изучения уровня 2 SSC CGL
Объем цилиндра — это количество или пространство, которое цилиндр может занимать сам по себе. Чтобы найти объем цилиндра, вы должны знать радиус и высоту цилиндра. Большинство цилиндров, которые мы наблюдаем в нашей повседневной жизни, представляют собой правильные круглые цилиндры. Например, жестяная банка, круглые столбы, лампочки, водопроводные трубы и т. Д.
Например, жестяная банка, круглые столбы, лампочки, водопроводные трубы и т. Д.
Объем цилиндра: формула
Цилиндр имеет вершину и основание, которые совпадают и параллельны друг другу. Его боковая поверхность также перпендикулярна основанию. Чтобы рассчитать объем цилиндра, возьмем цилиндр с радиусом основания как «r» и высотой как «h».
Таким образом, объем цилиндра определяется как произведение площади основания и высоты цилиндра.
Объем цилиндра = площадь основания × высота
Объем цилиндра = r² x hСледовательно, объем цилиндра можно определить по формуле Πr²h кубических единиц.
Щелкните здесь, чтобы получить бесплатные материалы по шаблонам для продвинутой математики
Получите бесплатные заметки по математике
Полый цилиндр — это цилиндр, полый изнутри и содержащий вакуум. Примером полого цилиндра является водопроводная труба, которая используется для отвода воды из одной точки в другую. Полый цилиндр будет иметь 2 радиуса: один внешний и один внутренний. Как найти объем полого цилиндра? Давайте посмотрим:
Примером полого цилиндра является водопроводная труба, которая используется для отвода воды из одной точки в другую. Полый цилиндр будет иметь 2 радиуса: один внешний и один внутренний. Как найти объем полого цилиндра? Давайте посмотрим:
На приведенном выше рисунке показан полый цилиндр с внутренним и внешним радиусом как «r» и «R» соответственно с высотой «h». Объем полого цилиндра можно определить по формуле;
V = h (R² — R2), где π можно принять равным 22/7 или 3.14.
Разница между объемом и емкостьюМногие из вас могут задаться вопросом, в чем разница между двумя похожими словами, а именно «Объем» и «Вместимость». Между этими двумя словами нет большой разницы. Основное определение может быть дано по:
(a) Объем означает объем пространства, занимаемого твердым объектом.
(b) Вместимость означает количество, которое вмещает контейнер.
Примечание: Если емкость для воды вмещает 100 см³ воды, то емкость емкости для воды составляет 100 см³. Емкость также измеряется в литрах. Соотношение между литром и см³, используемым для решения различных вопросов, составляет:
Емкость также измеряется в литрах. Соотношение между литром и см³, используемым для решения различных вопросов, составляет:
- 1 мл = 1 см³
- 1 л = 1000 см³
- 1 м³ = 1000000 см³ = 1000 л
Площадь поверхности цилиндра — это общая площадь, занимаемая поверхностью цилиндра, тогда как Объем определяет общее количество, которое цилиндр может занимать сам по себе.Мы уже знаем формулу объема цилиндра. Общая площадь цилиндра определяется по формуле:
A = 2πr 2 + 2πrh Объем цилиндра: примерыПример 1: Найдите высоту куба, объем которого составляет 275 см³, а площадь основания — 25 см².
Решение:
Объем цилиндра = площадь основания × высота
Высота цилиндра = объем цилиндра / площадь основания
Высота = 275/25 = 11 см
Пример 2: Прямоугольную бумагу шириной 14 см свернули по ее ширине и образовали цилиндр радиусом 20 см.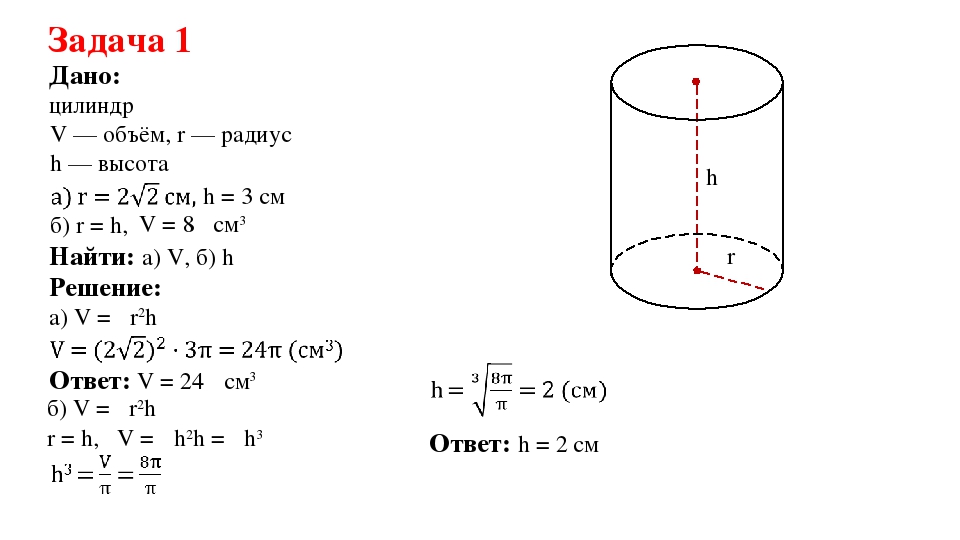


 (3 мин)
(3 мин) 
 Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Площадь боковой поверхности равна 2. Найдите высоту цилиндра. Найдите площадь боковой поверхности цилиндра.
Найдите площадь боковой поверхности цилиндра.
 Кто этот герой? (Буратино, полено)
Кто этот герой? (Буратино, полено)
Leave A Comment