Формулы площади треугольника через синус
Определение и формула площади треугольника через синус
ОПРЕДЕЛЕНИЕТреугольником называется фигура, состоящая из трех вершин и трех сторон.
Существует много формул для вычисления площади треугольника. Если известны длины двух сторон треугольника и угол между этими сторонами, то для вычисления площади треугольника удобно пользоваться следующей формулой
где – стороны треугольника, – угол между сторонами и .
Примеры решения задач
ПРИМЕР 1| Задание | Найти площадь треугольника со сторонами см и см, если угол между этими сторонами равен . |
| Решение | Площадь треугольника будем искать как полупроизведение сторон треугольника на синус угла между ними:
|
| Ответ | см |
| Задание | В треугольнике угол , а сторона на см больше стороны . Найти длины сторон и треугольника, если его площадь равна . |
| Решение | Обозначим сторону через , тогда сторона будет равна . Запишем формулу для площади треугольника
и подставим в нее известные данные:
Преобразуем последнее уравнение и получим квадратное уравнение
Корнями полученного уравнения будут и . По смыслу задачи подходит только первый корень. Тогда см, а см. |
| Ответ |
Площадь треугольника через синус и косинус
I. Площадь треугольника через синус
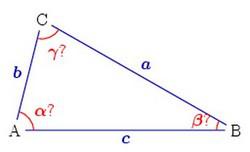Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: 
Подставляем данные в формулу
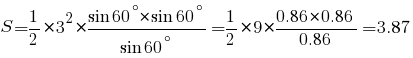
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Как найти площадь треугольника — Лайфхакер
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
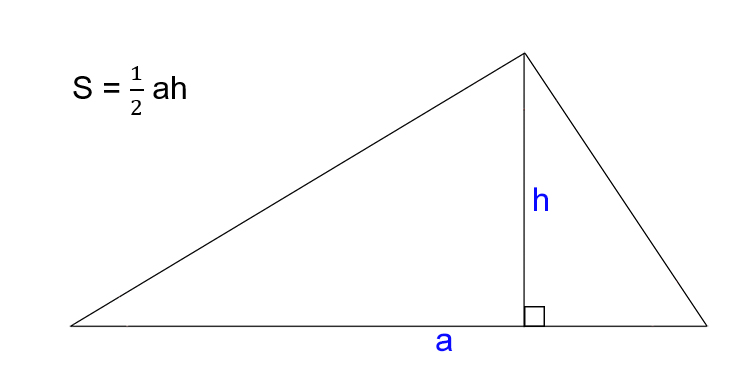
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
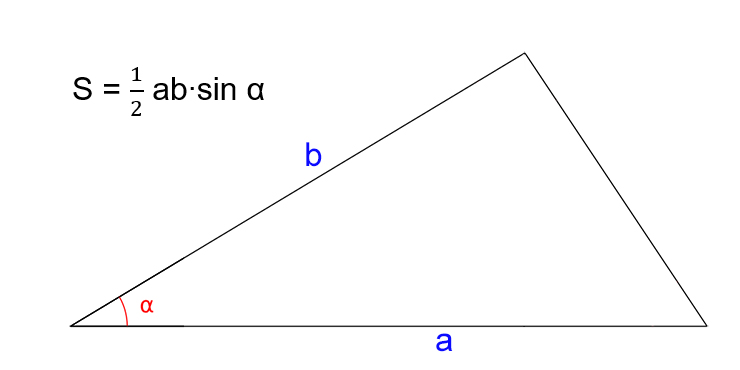
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Сейчас читают 🔥
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
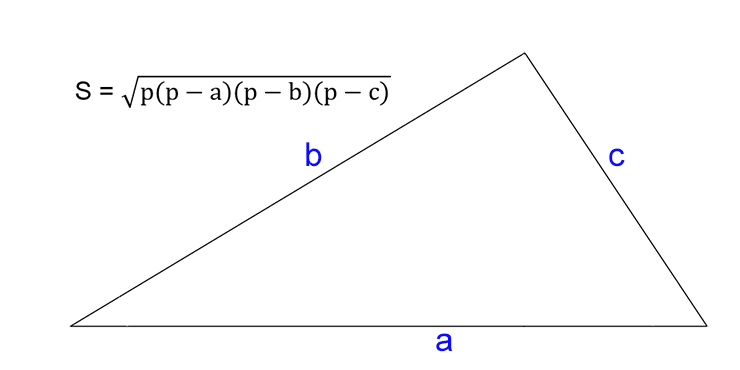
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
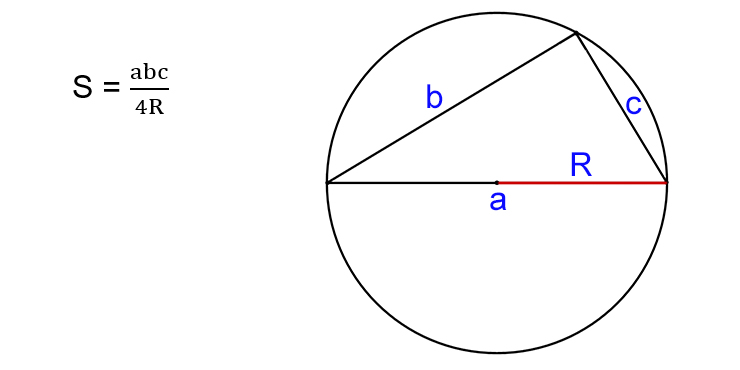
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
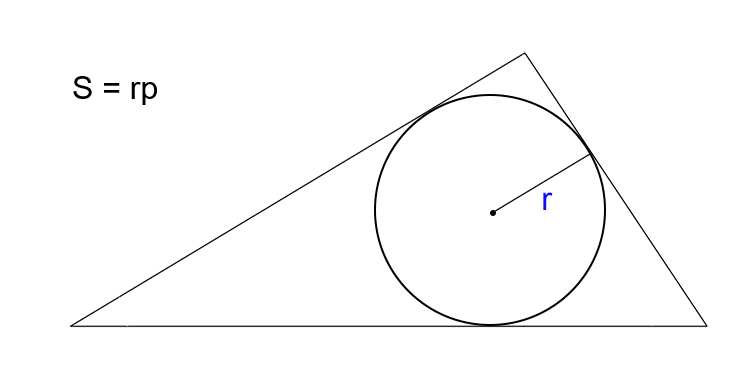
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
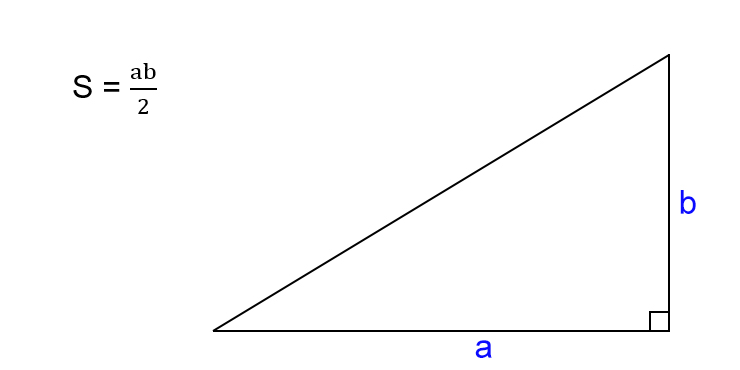
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
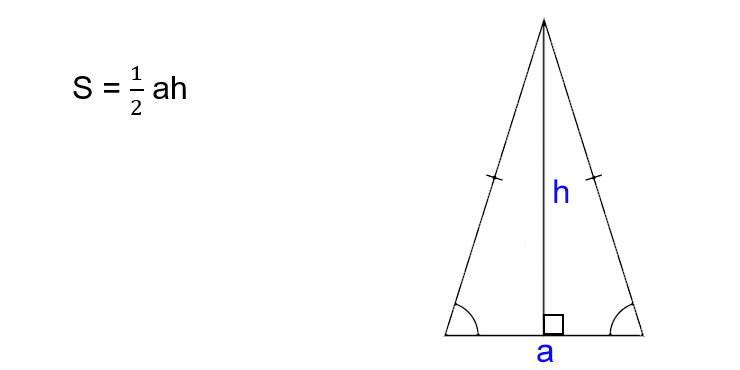
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
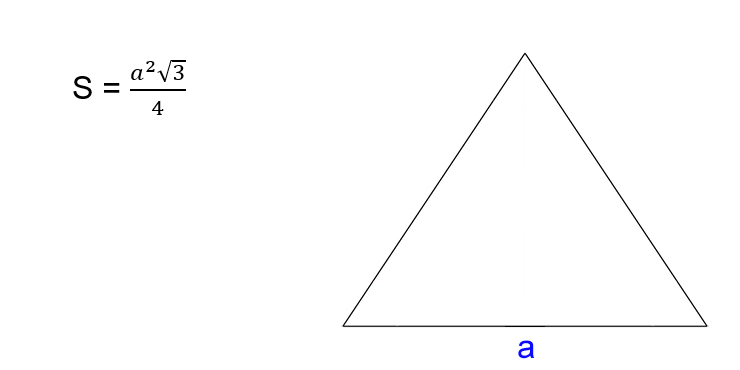
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
Формулы для площади треугольника
Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула площади | Обозначения |
| Произвольный треугольник |  |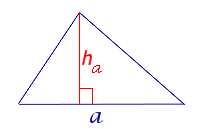
Посмотреть вывод формулы | a – любая сторона, |
 |
Посмотреть вывод формулы | a и b – две любые стороны, | |
 |
Посмотреть вывод формулы Герона | a, b, c – стороны, Формулу называют «Формула Герона» | |
 |
Посмотреть вывод формулы | a – любая сторона, | |
 |
Посмотреть вывод формулы | a, b, c – стороны, | |
 |
Посмотреть вывод формулы | a, b, c – стороны, | |
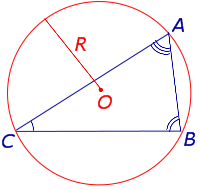 | S = 2R2 sin A sin Посмотреть вывод формулы | A, B, С – углы, | |
| Равносторонний (правильный) треугольник |  |
Посмотреть вывод формулы | a – сторона |
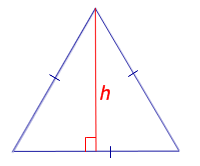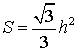 |  Посмотреть вывод формулы | h – высота | |
 |
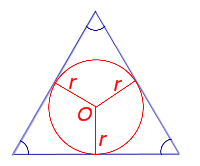Посмотреть вывод формулы | r – радиус вписанной окружности | |
 |
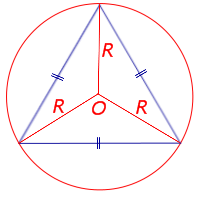Посмотреть вывод формулы | R – радиус описанной окружности | |
| Прямоугольный треугольник |  |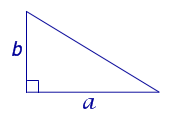
Посмотреть вывод формулы | |
 |
Посмотреть вывод формулы | a – катет, | |
 |
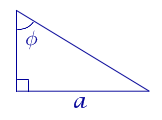Посмотреть вывод формулы | a – катет, | |
 |
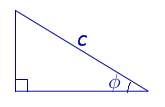Посмотреть вывод формулы | c – гипотенуза, |
.
| Произвольный треугольник | |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Формулу называют «Формула Герона» Посмотреть вывод формулы Герона |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| S = 2R2 sin A sin B sin C где Посмотреть вывод формулы |
| Равносторонний (правильный) треугольник | |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Прямоугольный треугольник | |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Формулу называют «Формула Герона» Посмотреть вывод формулы Герона |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2R2 sin A sin B sin C где Посмотреть вывод формулы |
| Равносторонний (правильный) треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
Вывод формул для площади произвольного треугольника
Утверждение 1. Площадь треугольника можно найти по формуле
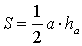
где a – любая сторона треугольника, а ha – высота, опущенная на эту сторону.
Доказательство.
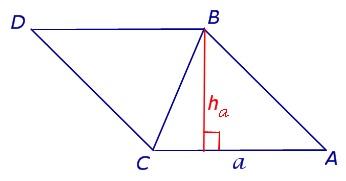
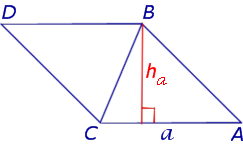
Рис. 1
Достроив треугольник ABC до параллелограммапараллелограмма ABDC (рис. 1), получим
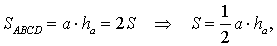
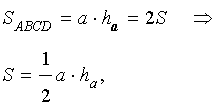
что и требовалось доказать.
Утверждение 2. Площадь треугольника можно найти по формуле
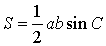
где a и b – две любые стороны треугольника, а С – угол между ними.
Доказательство.
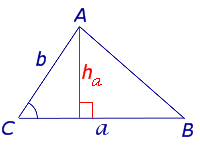
Рис. 2
Поскольку
ha = b sin C ,
то, в силу утверждения 1, справедлива формула
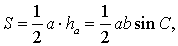
что и требовалось доказать.
Утверждение 3. Площадь треугольника можно найти по формуле
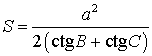
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.
Замечание. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.
Доказательство.
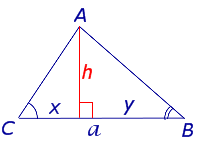
Рис. 3
Поскольку (рис.3)
x = hactg C , y = hactg B ,
то
a = x + y =
= hactg C + hactg B =
= ha( ctg C + ctg B) .
Следовательно,
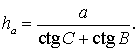
Поэтому
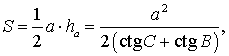
что и требовалось доказать.
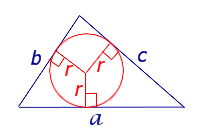
Утверждение 4. Площадь треугольника можно найти по формуле
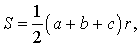
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.
Доказательство.
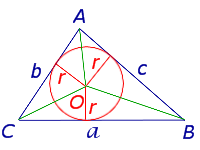
Рис. 4
Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим
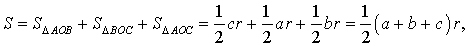
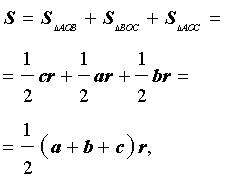
что и требовалось доказать.
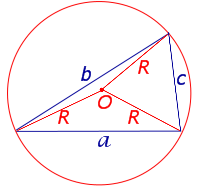
Утверждение 5. Площадь треугольника можно найти по формуле
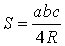
где a, b, c – стороны треугольника, а R – радиус описанной окружности.
Доказательство.
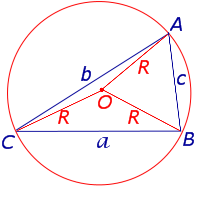
Рис. 5
В силу теоремы синусов справедливо равенство
.
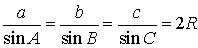Следовательно,
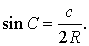
Поэтому
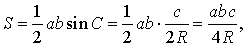
что и требовалось доказать.
Утверждение 6. Площадь треугольника можно найти по формуле:
S = 2R2 sin A sin B sin C ,
где A, B, С – углы треугольника, а R – радиус описанной окружности.
Доказательство.
Рис. 6
В силу теоремы синусов справедливо равенство
.
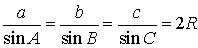Поэтому
a = 2R sin A ,
b = 2R sin B ,
c = 2R sin C ,
В силу утверждения 5
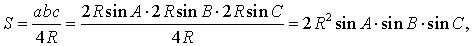
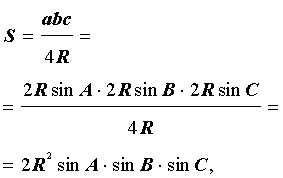
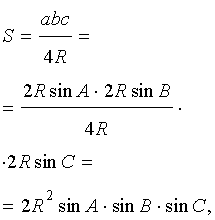
что и требовалось доказать.
Вывод формул для площади равностороннего треугольника
Утверждение 7.
- Если h – высота равностороннего треугольника, то его площадь
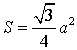
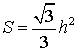
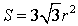
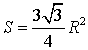
Доказательство.
Рассмотрим рисунок 7.
Рассмотрим рисунок 8.
Рассмотрим рисунок 9.
Рассмотрим рисунок 10.
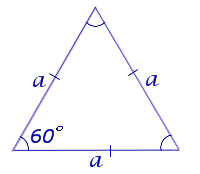
Рис. 7
В силу утверждения 2
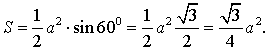
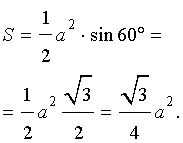
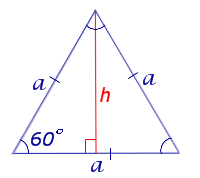
Рис. 8
Поскольку
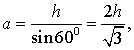
то
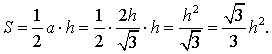
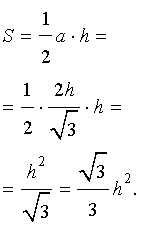
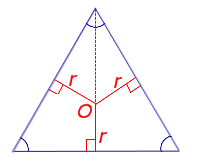
Рис. 9
Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство h = 3r. Следовательно,
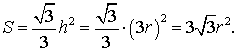
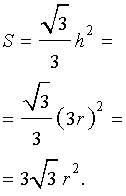
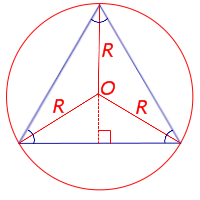
Рис. 10
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство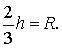 
Следовательно,
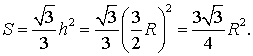
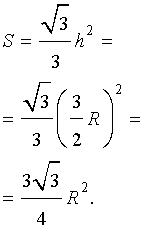
Доказательство утверждения 7 завершено.
Вывод формул для площади прямоугольного треугольника
Утверждение 8.
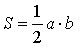
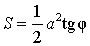
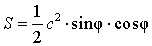
Доказательство.
Рассмотрим рисунок 11.
Рассмотрим рисунок 12.
Рассмотрим рисунок 13.
Рассмотрим рисунок 14.
Рис. 11
В силу утверждения 2
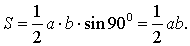
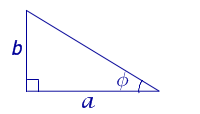
Рис. 12
Поскольку
b = a tg φ ,
то
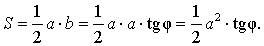
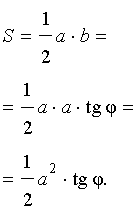
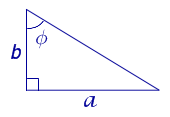
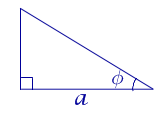
Рис. 13
Поскольку
b = a ctg φ ,
то
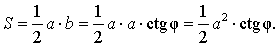
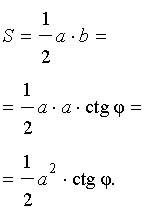
Рис. 14
Поскольку
a = c cos φ ,
b = c sin φ ,
то
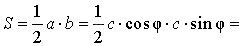
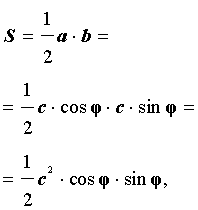
Доказательство утверждения 8 завершено.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
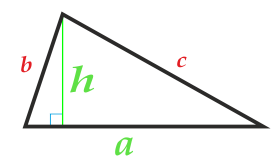
Сторона a
Высота h
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
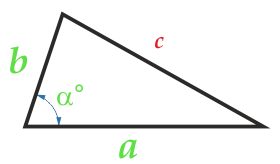
Сторона a
Сторона b
Угол α° между сторонами a и b
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
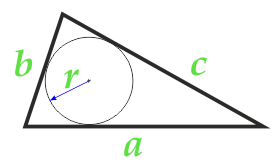
Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
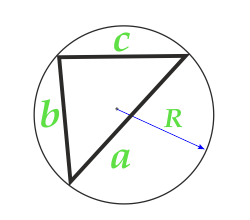
Сторона a
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
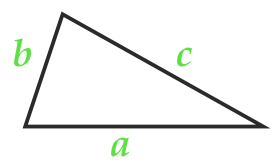
Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника по стороне и двум прилежащим углам
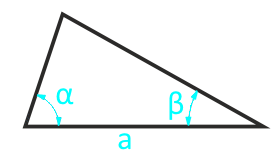
Сторона a
Угол β°
Угол α°
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию
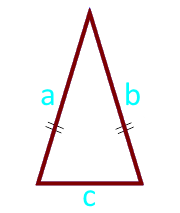
Сторона a (a = b)
Сторона c
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
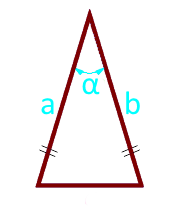
Боковая сторона a (a = b)
Угол α° между боковыми сторонами
9
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними
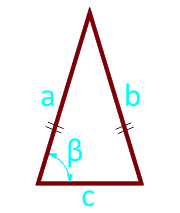
Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной
10
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
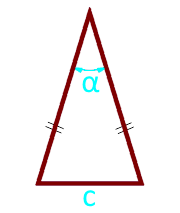
Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
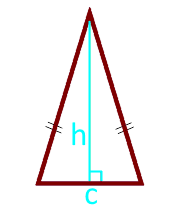
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника по стороне
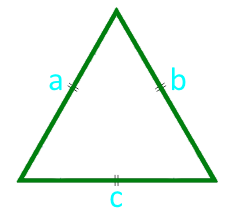
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
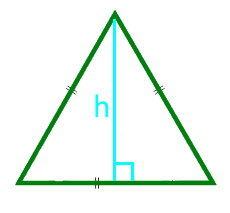
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
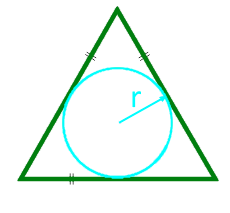
Радиус r вписанной окружности
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам
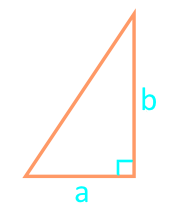
Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
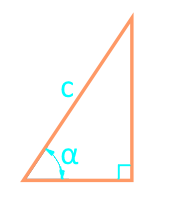
Сторона c
Угол α
18
Площадь прямоугольного треугольника через катет и угол
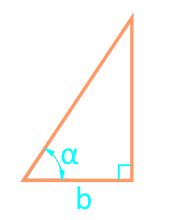
Сторона b
Угол α
19
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
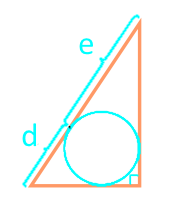
Отрезок d
Отрезок e
20
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность
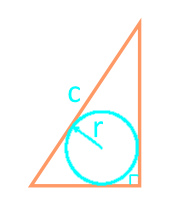
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
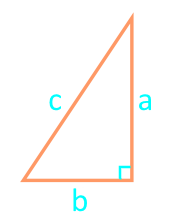
Полупериметр:
Сторона a
Сторона b
Сторона c
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Скачать формулы площади треугольника в виде картинки
Площадь треугольника по двум сторонам
Выясним, как найти площадь треугольника по двум сторонам.
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула площади треугольника по двум сторонам:
Дано:
∆ ABC.
Доказать:
Доказательство:
Проведем в треугольнике ABC высоту BD.
Площадь треугольника
равна половине произведения его стороны на высоту, проведенную к этой стороне:
Рассмотрим треугольник ABD — прямоугольный (так как BD — высота по построению).
По определению синуса острого угла в прямоугольном треугольнике,
Отсюда
Таким образом,
Если в треугольнике ABC
угол A тупой,
то в треугольнике ABD
(как смежные).
По формуле
имеем:
То есть, и в случае тупого угла A выполняется равенство
а значит, верна формула
Что и требовалось доказать.
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь Треугольников
Есть несколько способов найти площадь треугольника.
Знание базы и высоты
Когда мы знаем основание и высоту, это легко.
Это просто половина b раз ч
Площадь = 1 2 чч
(страница «Треугольники» объясняет больше)
Самое главное, чтобы основание и высота были под прямым углом.Поиграйте здесь:
Пример: какова площадь этого треугольника?
(примечание: 12 — высота , , а не длина левой стороны)
Высота = h = 12
Base = b = 20
Площадь = ½ чч = ½ × 20 × 12 = 120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Это можно найти на странице формулы Герона.
Знание двух сторон и включенного угла
Когда мы знаем две стороны и включенный угол (SAS), есть другая формула (фактически три эквивалентные формулы), которую мы можем использовать.
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin
Площадь = 1 2 ca sin B
Это действительно одна и та же формула, только с измененными сторонами и углом.
Пример: Найти площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Мы знаем угол C = 25º, а стороны a = 7 и b = 10.
Итак, начнем:
Площадь = (½) ab sin C
Введите значения, которые мы знаем: ½ × 7 × 10 × sin (25º)
Выполнить работу калькулятора: 35 × 0,4226 …
Площадь = 14,8 с точностью до одного знака после запятой
Как запомнить
Просто подумайте «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол всегда составляет между двумя известными сторонами , называемыми «включенным углом».
Как это работает?
Мы знаем, как найти область, когда мы знаем основание и высоту:
Площадь = ½ × основание × высота
В этом треугольнике:
|
Итак, мы получаем:
Площадь = ½ × (с) × (b × грех A)
Что (проще):
Площадь = 1 2 до н.э. sin
Изменяя метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найти, сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора до н.э. составляет 231 м.
Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы мы знаем:
- AB = c = 150 м,
- г. до н.э. = а = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите значения, которые мы знаем: ½ × 150 × 231 × грех (123º) м 2
Выполнить работу калькулятора: 17,325 × 0.838 … м 2
Площадь = 14 530 м 2
Фермер Джонс имеет 14 530 м 2 земли
,- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классу
- Учебная программа по экономическому классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
Краткое содержание тригонометрических формул
Краткое содержание тригонометрических формулЭти формулы соотносят длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.
Формулы для дуг и секторов окружностей
Можно легко найти как длину дуги, так и площадь сектора для угла θ в окружности радиуса r .
| Длина дуги. Длина дуги равна радиусу r, в раз превышающему угол θ , где угол измеряется в радианах. Чтобы преобразовать градусы в радианы, умножьте количество градусов на π /180. | |
| Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где угол снова измеряется в радианах. |
Формулы для правильных треугольников
Наиболее важные формулы для тригонометрии — это формулы для прямоугольного треугольника. Если θ является одним из острых углов в треугольнике, то синус тета — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а касательная — это отношение противоположная сторона к соседней стороне.
Эти три формулы все вместе известны мнемоническим SohCahToa.Помимо этого, есть важная пифагорейская формула, которая говорит, что квадрат гипотенузы равен сумме квадратов двух других сторон.
Наряду со знанием того, что два острых угла дополняют друг друга, то есть они добавляют к 90 °, вы можете решить любой прямоугольный треугольник:
- Если вы знаете две из трех сторон, вы можете найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Формулы для косых треугольников
Эти формулы работают для любого треугольника, острого, тупого или правильного. Мы будем использовать стандартную запись, в которой три вершины треугольника обозначены заглавными буквами A , B и C , а три противоположные стороны соответственно обозначены строчными буквами a , b и c .
Существуют две важные формулы для косых треугольников.Их называют законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники. В нем говорится, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумма квадратов двух других сторон, минус 2 ab cos & nbsp C , в два раза больше их произведения, умноженного на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Если вы знаете два угла и одну сторону, вы можете найти третий угол и две другие стороны.
- Если вы знаете две стороны и включенный угол, вы можете найти третью сторону и оба других угла.
- Если вам известны две стороны и угол, противоположный одной из них, есть две возможности для угла, противоположного другому (один острый и один тупой), и для обеих возможностей вы можете определить оставшийся угол и оставшуюся сторону.
Формулы площадей для треугольников
Существует три разных полезных формулы для площади треугольника, и какая из них вы используете, зависит от того, какая у вас информация.
| Половина базы умножается на высоту. Это обычный способ использования, поскольку он самый простой, и у вас обычно есть эта информация. Выберите любую сторону для вызова базы b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh . | |
| Формула Герона. Это полезно, когда вы знаете три стороны a , b и c треугольника, и все, что вы хотите знать, это область.Пусть с будет вдвое меньше их суммы, называемой полупериметром . Тогда площадь является квадратным корнем из произведения с , с — a , с — b и с — c . | |
| Формула бокового угла. Используйте это, когда вы знаете две стороны, a и b , и включенный угол, C . Площадь составляет половину произведения двух сторон от синуса включенного угла. |
областей треугольников
Наиболее распространенная формула для нахождения площади треугольника: K = ½ bh , где K — это площадь треугольника, b — основание треугольника, а h — высота. (Буква K используется для области треугольника, чтобы избежать путаницы при использовании буквы A для обозначения угла треугольника.) Полезны три дополнительные категории формул площади.
Две стороны и включенный угол (SAS): Учитывая Δ ABC (рисунок), высота задается как h = c sinA.Следовательно,
Рисунок 1
Контрольные треугольники для формул площади.
Два угла и сторона (AAS) или (ASA): Использование закона синусов и подстановка в предыдущих трех формулах приводит к следующим формулам:
Аналогично,
Три стороны (SSS): Известный греческий философ и математик Герон (или Герой) разработал формулу, которая вычисляет площадь треугольников только по длине трех сторон.Это известно как формула Герона . Если а, b и с являются длинами трех сторон треугольника, а с — это полупериметров , то
и
Одно из многих доказательств формулы Герона начинается с закона косинусов:
Пример 1: (SAS) Как показано на рисунке 2, две стороны треугольника имеют меры 25 и 12.Мера включенного угла составляет 51 °. Найдите площадь треугольника.
Рисунок 2
Чертеж для примера 1.
Используйте формулу SAS:
Пример 2: (AAS и ASA) Найдите площадь треугольника, показанную на рисунке 3.
Рисунок 3
Рисунок для примера 2.
Сначала найдите меру третьего угла треугольника, так как все три угла используются в формуле площади.
Пример 3: (AAS или ASA) Найти площадь равностороннего треугольника с периметром 78.
Если периметр равностороннего треугольника равен 78, то мера каждой стороны равна 26. Нетригонометрическое решение этой задачи дает ответ
Тригонометрическое решение дает тот же ответ.
Пример 4: (SSS) Найти площадь треугольника, если его стороны имеют размеры 31, 44 и 60.
Используйте формулу Герона:
Формула Герона не использует тригонометрические функции напрямую, но тригонометрические функции использовались при разработке и доказательстве формулы.
,
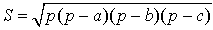
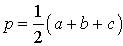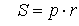
Leave A Comment