Егэ математика база 13 задание: Задание 13 ЕГЭ по математике база

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Подготовка к ЕГЭ по математике

Базовый уровень
Сложные задачи
Доцент кафедры математики и информатики,
эксперт предметной комиссии
ЕГЭ по математике
Савин Владимир Николаевич
2
3
Первичные баллы базового уровня ЕГЭ по
математике переводятся в следующие
школьные оценки:
«2» (неудовлетворительно) — от 0 до 6 баллов
«3» (удовлетворительно) — от 7 до 11 баллов
«4» (хорошо) — от 12 до 16 баллов
«5» (отлично) — от 17 до 20 баллов
4

5. Результаты ЕГЭ 2015

Средний первичный балл 13,52 (максимум 20).
Средний тестовый балл 3,97.
Высокие показатели успешности – выше 80% –
продемонстрированы при решении заданий
1 (вычислительный пример),
3 (решение простейшей задачи на проценты),
6 (решение простейшей задачи на действия с целыми
числами),
9 (знание площадей, длин, масс реальных объектов),
11 (чтение диаграмм, графиков),
12 (решение простейших задач на действия с числами,
получение информации из таблиц),
14 (чтение графика),
18 (логическая)
5

6.

Задание 13В заданиях на объёмы важно помнить, что
при увеличении всех размеров плоской фигуры в k
раз площадь увеличивается в k2 раз,
при увеличении всех размеров объёмного тела в k
раз объём увеличивается в k3 раз,
Если у фигуры два одинаковых основания
(призма, цилиндр, параллелепипед), то объём
V=Sосн*h
Если есть вершина и только 1 основание
(пирамида, конус), то объём в 3 раза меньше
V=Sосн*h/3
6

7. Задание 13

В заданиях на объёмы важно помнить, что
при увеличении всех размеров плоской фигуры в k
раз площадь увеличивается в k2 раз,
при увеличении всех размеров объёмного тела в k
раз объём увеличивается в k3 раз,
Площадь основания второй кружки больше в
22=4 раза, а высота больше в 1,5 раза, значит,
объём больше в 4*1,5= 6 раз.
Ответ. 6
7

8. Задание 13

Даны две кружки
цилиндрической
формы. Первая кружка
вдвое выше второй, а
вторая в четыре раза
шире первой.

Во
сколько раз объём
второй кружки больше
объёма первой?
Ответ: 8
8
Площадь
основания
увеличилась в
42=16 раз, а высота
уменьшилась в 2
раза. Значит, объём
увеличился в
16/2=8раз

9. Задание 13

В сосуд
цилиндрической
формы была налита
вода до уровня 80 см.
Её перелили во второй
цилиндрический сосуд,
у которого радиус
основания в 4 раза
больше, чем у первого.
На каком уровне будет
вода во втором сосуде?
Ответ дайте в
сантиметрах.
9
Решение.
Так как площадь основания
увеличится в 4*4=16 раз, то
высота жидкости уменьшится
в 16 раз и станет равна
80/16=5см.
Ответ: 5

10. Задание 13

Пирамида Хеопса имеет форму
правильной
четырёхугольной
пирамиды, сторона основания
которой равна 230 м, а высота
— 147 м. Сторона основания
точной музейной копии этой
пирамиды равна 23 см. Найдите
высоту музейной копии. Ответ
дайте в сантиметрах.

Ответ: 14,7
10
Основание Высота
Оригинал
230 м
147 м
Копия
23 см
x см

11. Задание 14

Это задания на
производные,
возрастание,
убывание функций
Для записи ответов
удобно заранее
построить таблицу
для ответов:
11
Функция f(x)
Производная f’(x)
Возрастает ↗
Положительна или 0
f’(x) ≥ 0
Убывает ↘
Отрицательна или 0
f’(x) ≤ 0
А
Б
В
Г

12. Задание 14 Сравнение производных

На рисунке изображён график
функции, к которому проведены
касательные в четырёх точках.
Ниже указаны значения
производной в данных точках.
Пользуясь графиком, поставьте
в соответствие каждой точке
значение производной в ней.
Производная положительна (№2 и 3),
Ответ. 2143
12
если функция возрастает, то есть в
точках K и N.
В точке K касательная сильнее
наклонена, значит, в точке К модуль
производной больше, поэтому K=п.2)
N=п.

3)
В точке L наклон круче, чем в точке M,
значит, модуль отрицательной
производной больше в точке L. Но
4>0,5, значит, L=п.1)

13. Задание 14 Возрастание — убывание

1
13
2
3
4
Можно идти методом исключения.
А: 1 не выполнено, 2 выполнено (февраль и март) А=п.2
Б: п.1, 3 не выполнено. Б = п.4
В =п.1; Г=п.3 (последний пункт всё равно нужно проверять)
Ответ. 2413

14. Задание 14 Возрастание — убывание

14
А: п.1,2,4 не выполнены, значит, А=п.3
Б=п.4
В= п.1
Г=п.2
Ответ. 3412

15. Задание 17 Решение неравенств

Решаем в произвольном порядке.
А)
; x>1 – п.2)
Б) –x > 1;
x < –1 – п.4
В) методом интервалов
Значит, В=п.3
Г) методом интервалов
Г= п.1
15
Ответ. 2431

16. Задание 17 Округление чисел

А=п.4
1=3/3 < 4/3 < 6/3=2
Б=п.1
В=п.3
1/0,35 = 1/ (35/100) = 100 / 35 > 70/35=2
100 / 35 < 105 /35 = 3; Г=п.

2
Ответ. 4132
16

17. Задание 17 Сравнение чисел

1 < m <2 (*)
1) –2< –m< –1 прибавим 6:
4<6 –m<5, значит, N=п.1
2) Все части неравенства * положительны, поэтому
1 < m2 <4 , значит, M=п.2
3) Отнимем 1 от всех частей неравенства *: 0 < m < 1, значит, L=п.3
4) 1 < 2/m < 1/2 –0,5 < – 2/m < –1 , значит, K=п.4
Ответ. 4321
17

18. Задание 18 Пересекающиеся множества (формула)

В
Элементы не входящие ни в одно множество
Множество В – это пересечение множеств А и Б. Тогда Общее
количество элементов в множествах А и Б равно:
Кол(А+Б) = Кол (А) + Кол (Б) – Кол (В)
Различные варианты ответов получаются изменением Кол(В)
от минимально возможного до максимально возможного
18

19. Задание 18 Пересекающиеся множества (пример)

Обе
сети
Элементы не входящие ни в одно множество
19
Кол(F+В) = Кол (F) + Кол (В) – Кол (обе)
10<25<30.
1)10+25=35>30, поэтому все могут быть пользователями
2)35 –30=5, поэтому действительно найдутся 5 человек в обоих сетях
3)25>10, поэтому не могут все из Facebook быть Вконтакте
4)Это верно, так как Вконтакте 10 человек
Ответ.

20. Задание 18 Сравнение (пример)

В городе Z в 2013 г. мальчиков родилось больше, чем девочек. Мальчиков чаще всего называли Андрей, а
девочек — Мария. Выберите утверждения, которые следуют из приведённых данных.
Среди рождённых в 2013 г. в городе Z:
1) девочек с именем Мария больше, чем с именем Светлана.
2) мальчиков с именем Николай больше, чем с именем Аристарх.
3) хотя бы одного из родившихся мальчиков назвали Андреем.
4) мальчиков с именем Андрей больше, чем девочек с именем Мария.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
20
1) Мария самое популярное имя, значит, их больше, чем Марий. Верно.
2) Про эти имена нет информации, значит, утверждение не следует из условия.
3) Мальчиков больше, чем девочек, значит, есть мальчики и среди них Андреев
больше всего, значит, утверждение верно.
4) Это неверно, так как количество различных имён неизвестно. Например,
100 мальчиков из них 20 Андреев и по 10 других имён.

При это 50 девочек,
их них 30 Марий и и по 10 других имён
Ответ. 13

21. Задание 18 Сравнение (пример)

Так как максимум 75, то утверждение верно
2) Сравнения баллов в тексте нет, так что это не
следует из условия задачи
3) Распределение баллов в тексте не описывается,
поэтому п.3 не верен
4) Минимум 36 ≥ 35, поэтому утверждение верно.
Ответ. 14
1)
21

22. Задание 18 Сравнение

П>М>Д
Д<C
1) Магнитофон и стол дороже доски, но не сказано насколько
поэтому нельзя сравнить, а, значит, утверждение неверно
2) Верно
3) Верно
4) И принтер, и стол дороже доски, но не сказано насколько,
поэтому они могут стоить одинаково. Утверждение неверно.
Ответ. 23
22

23. Задание 19 Признаки делимости

Число называется простым, если оно делится только на 1 и само на себя.
Первые простые числа нужно запомнить: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
(все простые числа невозможно запомнить, так как их бесконечно много)
Признаки делимости на числа:
Число 2
3
4
5
Признак
Последняя
цифра –
чётная
(0,2,4,6,8)
Число
6
9
10
11
Признак
Делится
на 2 и на
3
Сумма
цифр
числа
делится
на 9
После
дняя
цифра
0
Разность суммы цифр на нечётных
местах и суммы цифр на чётных
местах делится на 11
23
Сумма
цифр
числа
делится
на 3
1) Число из последних двух цифр
делится на 4
2) Сумма числа единиц +
удвоенного числа десятков
делится на 4
Последняя
цифра 0
или 5

24.

Задание 19Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма
квадратов цифр делится на 3, но не делится на 9.
Решение. Сумма цифр постоянна. Порядок цифр неважен. Поэтому цифры будем
брать в возрастающем порядке. Остаток от деления числа на 3 и на 9 совпадает с
остатком суммы цифр этого числа
659 не проверяем, так как цифры совпадают с 569, значит, последняя цифра не 9.
Пробуем последнюю цифру 8.
Цифры
24
Сумма
Сумма
Остаток при
квадратов делении на 3
Остаток при
делении на 9
299
20
166
1
4
389
20
154
1
1
479
20
146
2
2
569
20
142
1
7
488
20
144
0
0
578
20
138
0
Ответ: 578
Примечание. Есть ещё ответы 587, 758, 785, 857, 875.
3

25. Задание 19

Приведите пример трёхзначного натурального числа
большего 400, которое при делении на 6 и на 5 даёт равные
ненулевые остатки и первая слева цифра которого является
средним арифметическим двух других цифр.

В ответе укажите
ровно одно такое число.
Если число делится на 5*6=30, то оно делится на 5 и 6.
Попробуем числа 30n+k, где k от 0 до 4.
Например 420. 4 это среднее 2 и 6, но 426 делится на 6, но не
на 5. Далее 450. 4 это среднее 5 и 3, значит, нам подойдёт 453.
Проверка. 453:5=90 (ост.3), 453:6 = 75 (ост.3)
(5+3) / 2 = 4
Ответ. 453
Примечание. Возможны также ответы 573 (ост.3), 693 (ост.3)
Есть ещё 480 (ост.0), но оно не подходит, так как в условии
говорится, что остатки ненулевые.
25

26. Задание 19 Остатки от деления

Приведите пример трёхзначного натурального
числа, большего 600, которое при делении на 4, на 5 и
на 6 даёт в остатке 3 и цифры которого расположены
в порядке убывания слева направо. В ответе укажите
ровно одно такое число.
Решение. Возьмём число на 3 меньше искомого,
оно делится на 4, 5, 6, значит, делится на их НОК
(наименьшее общее кратное), то есть 22*3*5=60,
значит, наше число 60n+3.

Начинаем с 600, пока не
выполнится условие: 603, 663, 723, 783, 843 –
последнее подходит
Ответ. 843
Примечание. Ответ 963 также является верным
26

27. Задание 19

Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и
получили второе четырёхзначное число. Затем из первого числа вычли второе и
получили 4536. Приведите ровно один пример такого числа.
Решение. Число кратно 5, значит, это abc0 или abc5, но 0cba – трехзначное
число, значит было число abc5, а получилось 5cba.
a
bc5
–
5c b a
4 536, значит, abc5 = 5cba + 4536, поэтому цифра a не меньше 9, значит a
=9.
9bc5 = 5cb9 + 4536.
36+9=45, значит, с=b+4 или с = b +4 –10=b –6
Если с=b+4, то в следующий разряд ничего не переносится и получается b
=с+5, чего быть не может (с больше и меньше b одновременно)
с =b – 6 (единица переносится в следующий разряд), тогда b = c+5+1, что
совпадает с предыдущим условием. Осталось выбрать b и с, например, b = 6;
c=0.

Проверка. 9605 – 5069 = 4536 верно
Ответ. 9605
Примечание. Есть ещё ответы 9715, 9825, 9935
27

28. Задание 20 На смекалку (пример 1)

Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м.
Через сколько дней улитка впервые окажется на вершине дерева?
Решение. Лучше сделать таблицей, указывая все состояния (на какой высоте будет улитка после
каждого действия)
№ дня
1
2
3
4
5
6
7
8
Вечер (после дня)
3
4
5
6
7
8
9
10
Утро (после ночи)
1
2
3
4
5
6
7
9
Значит, улитка впервые окажется на вершине дерева через 8 дней.
Ответ. 8
Примечание. Популярна следующая ошибка: на 3 – 2 = 1 м в день поднимается улика, значит,
10/1=10 дней. Однако, в данном случае улитка через 10 дней СПУСТИТСЯ на вершину дерева,
значит, она должна раньше была подняться. Такое решение неверно.
28

29. Задание 20 На смекалку (пример 2)

В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.

У Николы были только серебряные монеты. После посещений обменного пункта
серебряных монет у него стало меньше, золотых не появилось, зато появилось 90
медных. На сколько уменьшилось количество серебряных монет у Николы?
Решение. Выделяем особые моменты:
1. При каждом обмене добавляется 1 медная монета, значит, всего было 90 обменов.
2. В итоге нет золотых монет, значит их нужно сразу разменивать, но 5 золотых не
имеет общих множителей с 4, значит нужно сначала сделать 4 обмена 2 типа:
4*7=28 серебряных монет меняется на 20 золотых и 4 медных, а затем 5 обменов 1го типа: 20 золотых меняется на 5*5=25 серебряных и 5 медных.
В итоге за 4+5=9 обменов мы из 28 серебряных получаем 25 серебряных (на 3
меньше, чем было) и 4+5=9 медных.
Так как нужно сделать 90 обменов (см.п.1), то нужно провести 90/9=20 обменов по
п.2, тогда количество серебряных монет уменьшится на 3*10=30 монет.
Ответ: 30
29

30. Задание 20 На смекалку (пример 3)

В корзине лежат 25 грибов: рыжики и грузди.

Известно, что среди любых 11 грибов имеется хотя
бы один рыжик, а среди любых 16 грибов хотя бы
один груздь. Сколько рыжиков в корзине?
Решение. Смотрим по самому плохому варианту, так
как среди 11 точно есть один рыжик, значит, не
рыжиков (груздей) не наберётся больше 10.
Аналогично, не груздей (рыжиков) не больше 15.
р+г ≤ 25, но так как р+г=25 по условию, то г=10, р=15
Ответ. 15
30

31. Полезные ссылки

http://www.fipi.ru/content/otkrytyy-bank-zadaniy-
ege
http://practice.opengia.ru/ — официальный (ФИПИ)
генератор вариантов базовых заданий (с таймером и
возможностью многократной проверки правильности
ответов)
http://alexlarin.net/ege/baza/main.html альтернативный генератор вариантов базовых
заданий (неофициальный сайт, без ответов)
http://mathb.ege.sdamgia.ru/test?a=catlistwstat
– список рассмотренных задач (неофициальный сайт,
с ответами и решенями)
31

32. Генератор заданий fipi.ru

http://practice.

opengia.ru/
32

33. СПАСИБО ЗА ВНИМАНИЕ!

33
Доцент кафедры математики и информатики,
эксперт предметной комиссии
ЕГЭ по математике
Савин Владимир Николаевич

как сдать ЕГЭ по профильной математике — Учёба.ру

Что нужно делать школьнику, чтобы получить 100 баллов?

Чтобы получить 100 баллов, надо любить и понимать математику (быть математиком — по сути, по настроению, по образу жизни). Если школьник рассматривает математику как второстепенный предмет, как предмет, который просто необходимо сдать, например, когда речь идет о поступлении на экономические направления, он не сможет получить 100 баллов ни при каком раскладе. Максимальный балл требует, чтобы человек всем своим «нутром и состоянием своего мозга» был ориентирован на математику. Потому что есть задачи, которые требуют четкого, хорошего логического мышления и владения абсолютно всем материалом. В нужный момент необходимо выудить необходимые знания и применить их для решения задачи. Есть такие задачи, на которые натаскать по принципу «делай вот так» просто нельзя (например, задача № 19). Даже если школьник прекрасно знает математику, 100 баллов получить очень сложно. Это единичные случаи.

По вашему опыту преподавания, какие разделы математики самые сложные и вызывают наибольшие затруднения?

Сегодня для школьника самое сложное — это геометрия. К сожалению, культура геометрии в школе просто отсутствует. И еще, конечно, задачи с параметрами. Старшеклассники их панически боятся. Но ученик, который понимает математику, и с этими задачами справляется. Для их решения требуется именно понимание, а все необходимые для этого знания изложены в курсе школьной математики.

А вообще, в любой теме есть простой материал (азы), который лежит в основе задач из первой части ЕГЭ, и сложный материал, который лежит в основе задач второй части. Думаю, что если есть желание, то каждый в состоянии освоить азы любой темы из школьной программы по математике, а вот более глубокое понимание этих тем и умение решать сложные задачи по силам не всем.

Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов

А какие темы можно назвать самыми простыми?

Обычно школьники легко решают линейные и квадратные уравнения, но только в том случае, если в них нет параметра. Так что по темам «Линейная функция» и «Квадратичная функция» есть простые задачи, а есть сложные. И так по любой теме. Можно сформулировать простую задачу, а можно такую, что никто не решит.

Простыми темами можно считать те, на большинство задач по которым можно школьника натаскать. Простая задача — это гарантированно правильно решенная. А про ЕГЭ (особенно про задачи первой части) так вообще нельзя говорить. Например, школьник знает, как решить задачу, но допускает арифметическую ошибку или невнимательно читает условие (ищет одну величину, а для ответа надо еще что-то с ней сделать). В итоге получается неверный ответ. И задача не решена. И не важно, простая она была или сложная.

Присутствует ли на ЕГЭ по математике фактор везения? Возможно ли получить высокий балл, если знаешь предмет на более скромный результат?

Да, это возможно, но только если речь идет о результате в районе 75 баллов или меньше. Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов. Там нужно решать сложные задачи из второй части, а они требуют четкого обоснования решения, что для большинства является непосильным. Здесь должна быть стабильность.

А можно завалить экзамен, если знаешь предмет очень хорошо?

Элементарно. Арифметические ошибки, невнимательное чтение условия задачи и просто паника. Все это приводит талантливых учеников к более скромным результатам.

Что же делать? Есть «формула успеха», которая поможет подготовиться к ЕГЭ по математике?

Учить математику! Не натаскиваться по вариантам ЕГЭ, а систематически учить темы, разбираться, стараться понять. Тогда до многих задач школьник дойдет сам, своим умом, а это и есть залог успешной подготовки и высоких баллов. Математика — это, в первую очередь, понимание, а потом уже формулы и схемы решения. При подготовке методом натаскивания потолок — это 75 баллов. Одна и та же задача, сформулированная просто «с другого конца», натасканного ребенка деморализует. Он не может узнать знакомую задачу, а разобраться в «новой» сам не в состоянии.

Вот, например, задача № 17. Когда она появилась в вариантах диагностических работ, детям в школе начали давать формулы для ее решения. И школьники заучивали эти формулы, сопротивляясь попыткам учителей объяснить, откуда они взялись. Многие действовали методом «я знаю формулу и по ней буду решать». А на самом экзамене в условие внесли незначительное изменение, и ни одна из выученных формул не подходила. Как получить ту, которая позволит решить задачу, дети не знали. Вроде бы решили все 120 вариантов задания № 17, а на ЕГЭ дали 121-й вариант. В итоге те, кто не разбирался, задачу не решили.

Надо выбросить калькулятор и научиться считать без него

До ЕГЭ по математике осталось 3,5 месяца. Как вы посоветуете выпускникам распределить время, чтобы подготовиться наилучшим образом?

Во-первых, выбросить калькулятор и научиться считать без него. Во-вторых, повторить теорию и выучить формулы (именно сейчас, а не перед экзаменом): то есть подготовить базу, а дальше решать задачи. Можно решать из сборников вариантов ЕГЭ, но, к сожалению, там их не очень много и они часто повторяются.

Каждый ребенок ставит для себя определенную планку в зависимости от того, куда собирается поступать и как знает предмет. Если говорить о заданиях второй части ЕГЭ, то во время подготовки необходимо прежде всего обратить внимание на задачи № 13, № 15 и № 17. Их можно научиться решать. Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.

Задачи № 18 и № 19 — это, конечно, уже очень высокий уровень, но попробовать можно. Если эти задачи идут хорошо, то я не думаю, что надо тратить оставшееся время на курсы. Лучше решить больше задач самостоятельно. Если же возникают проблемы или неуверенность, что вы все решаете верно, не откладывая обращайтесь за помощью. Эффективная стратегия на этот период — решать, решать и решать!

Задание № 10	Задача легкая. Здесь важно внимательно читать условие. Внимание на единицы измерения! Все величины подставлять в одних единицах измерения.
Задание № 11	Текстовая задача. Не считаю ее сложной. Обратите внимание на вопрос задачи, что именно спрашивают в условии и в каких единицах измерения необходимо записать ответ. Часто школьники пишут скорость не того пешехода или производительность не той трубы.
Задания № 13, № 15	Задания решаемые, но должна быть база по всем темам алгебры. Особенное внимание необходимо обратить на область определения (в особенности это касается логарифма, тангенса и котангенса). Нужно уметь применять те тождественные преобразования, которые помогут решить задачу, а не заведут в тупик, и знать все формулы наизусть.
Задания № 14, № 16	Задачи по геометрии. Самое сложное в них — это умение доказать. Для этого школьник должен владеть всем материалом планиметрии и стереометрии, знать все теоремы и следствия из них, уметь их доказывать. И еще важен чертеж! Он может либо стать эффективным инструментом и подсказать правильный ход решения, либо, если сделан некорректно, помешать решению задачи.
Задание № 17	Несложная задача. Это задание на умение формализовать текстовую задачу, то есть записать условие задачи в виде уравнений или неравенств (этого же требует и решение задачи № 11). На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики.
Задание № 18	Для решения этой задачи необходимо отличное владение предметом. Поможет ее решить знание свойств элементарных функций, умение исследовать функции и строить их графики. Все это есть в школьном курсе математики.
Задание № 19	Это задача для тех, кому интересна математика. В ходе решения может возникнуть необходимость обратиться к любому разделу предмета из программы любого класса. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование.

23 Увлекательные математические игры для детей, которые помогут развить новые математические навыки в классе

Игра в математические игры в классе стала способом сделать уроки математики или обзоры по математике более увлекательными, особенно для учащихся, которым сложно решать математические задачи.

Так же, как существует множество полезных математических веб-сайтов, существуют математические онлайн- и оффлайн-задачи, подходящие для этой работы. Математические игры в классе могут выступать в качестве настраиваемых входных и выходных билетов, а также в качестве занятий в середине класса. Вы можете легко добавить их в свои планы уроков и использовать для математических обзоров.

Если вы учитель математики с 1 по 8 класс, вот 20 математических игр для детей, в которые можно играть с компьютером и без него:

1. Prodigy Math

Подпишитесь на Prodigy Math — учебный план -согласованная математическая игра — чтобы вовлечь класс в процесс закрепления содержания урока и закрепления основных навыков — дома или в школе .

Бесплатный для школ и учителей, он заимствует элементы из ролевых игр (RPG), поскольку игроки соревнуются в математических дуэлях с игровыми персонажами. Чтобы выиграть, они должны ответить на ряд математических задач.

Как учитель, вы можете настроить эти вопросы, чтобы дополнить учебный материал. В игре также используются принципы адаптивного обучения и дифференцированного обучения для корректировки содержания с учетом проблемных мест каждого учащегося.

Вот пример математической игры в действии. Допустим, вы только что познакомили свой класс с математической концепцией, такой как дроби, на уровне 2-го класса. Создав задание для всего класса, вы можете попросить учащихся войти в Prodigy и начать играть самостоятельно или в небольших группах. Развлекаясь, играя в Prodigy Math, они будут отвечать на вопросы, соответствующие заданию и их способностям.

У вас также будет доступ к панели управления учителя, которая предоставляет вам бесплатные отчеты и данные об успеваемости каждого ученика, помогая вам выявлять и устранять пробелы в обучении всего за несколько кликов!

Уровень класса: 1-8 классы

Создайте бесплатную учетную запись учителя за считанные секунды!

2. Around the Block

Play Around the Block как умственное задание, используя только мяч, чтобы отработать практически любой математический навык. Сначала составьте список вопросов, связанных с навыком. Во-вторых, пусть ученики встанут в круг. Наконец, дайте одному ученику мяч и зачитайте вслух вопрос из вашего списка.

Учащиеся должны передать мяч по часовой стрелке по кругу, и тот, кто начал с ним, должен ответить на вопрос, прежде чем получить его снова. Если учащийся ответил неправильно, вы можете передать мяч однокласснику для следующего вопроса. Если студент отвечает правильно, он или она выбирает следующего участника.

Уровень класса: 3-8 классы

3. Математический бейсбол

Разделите свой класс на две команды, чтобы играть в математический бейсбол — еще одно задание, которое дает вам полный контроль над вопросами, на которые отвечают учащиеся. Одна команда начинает с битой, подсчитывая баллы, выбирая вопросы на одну, две или три базы.

Вы будете задавать вопросы, сложность которых зависит от их ценности. Если команда летучих мышей отвечает неправильно, защищающаяся команда может ответить правильно, чтобы заработать аут. После трех аутов поменяйте сторону. Играйте до тех пор, пока одна из команд не сделает 10 пробежек.

Уровень: 3–8 классы

4. Игра «Прыгающие суммы»

Дайте учащимся возможность передвигаться по классу, играя в «Прыгающие суммы», развивая математические мышцы в уме. Для подготовки используйте этикетки и маркер, чтобы нанести на пляжный мяч целые числа, десятичные дроби или дроби.

Передайте мяч одному ученику, который прочитает вслух этикетку, касаясь одним из своих больших пальцев. Этот ученик бросает мяч однокласснику и так далее. Каждый учащийся должен прочитать число на своей этикетке, добавив его или умножив на сумму или произведение, которое указал предыдущий учащийся.

Вызов? Достигните максимально возможного числа за отведенное время.

Уровень класса: 3–8 классы

5. Гонка математических фактов

Продолжайте сочетать математику с физической активностью в этом динамичном упражнении на беглость чтения фактов. Разделите учащихся на группы в конце класса, разместив перед каждой группой лист с сеткой. К листу подбегает один учащийся от каждой команды, записывая ответ в соответствующую сетку.

Чтобы попрактиковаться в умножении, например, ученик должен написать 12 в сетке, где встречаются третья строка и четвертый столбец. Учащийся возвращается к своей команде после ответа, позволяя члену группы подбежать к листу. Участник группы может заполнить другую сетку или, при необходимости, исправить предыдущий ответ.

Этот процесс повторяется до тех пор, пока команда не выиграет, правильно заполнив свой лист.

Уровень класса: 2–5 классы

6. Математические факты Бинго

Упражнения на беглость речи включают , играя в эту версию бинго. Во-первых, создайте карты бинго, которые содержат ответы на разные таблицы умножения. Во-вторых, раздайте их учащимся и убедитесь, что у них есть отдельный лист для расчетов. Наконец, вместо того, чтобы звонить по номерам, сформулируйте уравнения, такие как 8 × 7.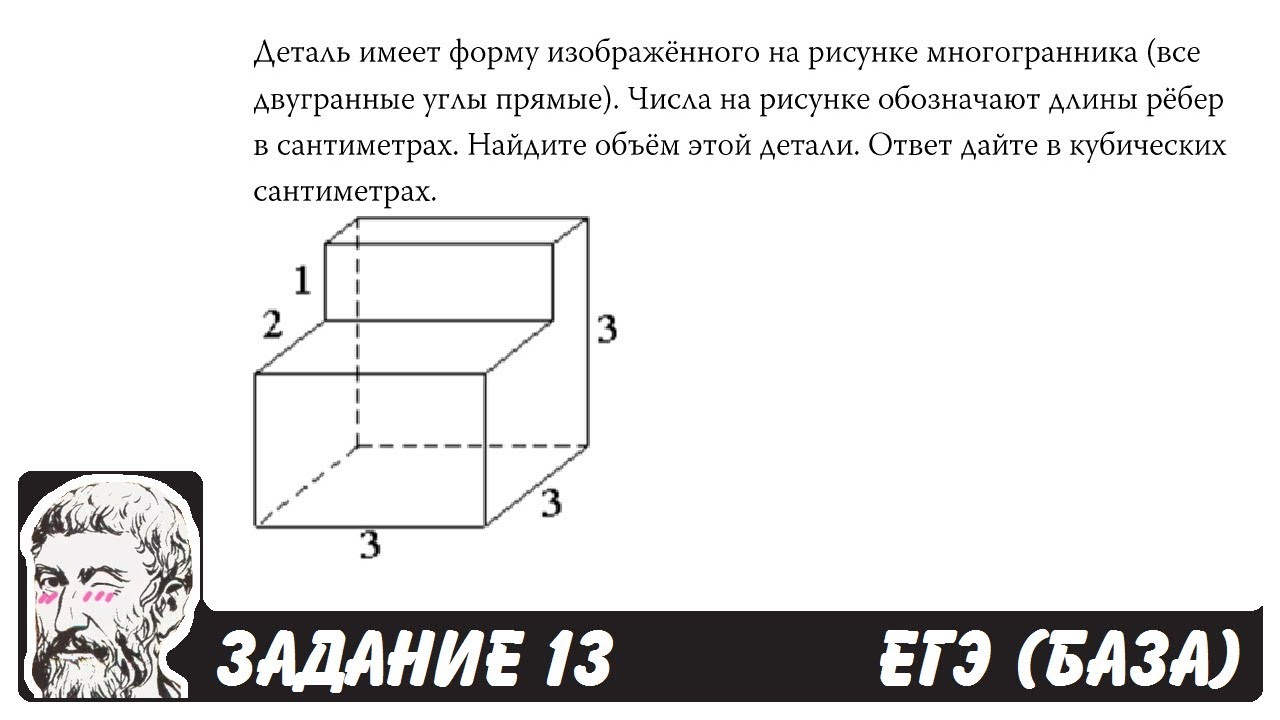 Определив, что произведение равно 56, они могут отметить число, если оно есть на их карточках.

Уровень класса: 3–6 классы

7. «Математика — это весело»

Привлеките учащихся начальной школы, указав им игр и головоломок на веб-сайте «Математика — это весело». Идеально подходит в качестве учебной станции или для занятий с использованием устройств один на один. Игры варьируются от сложной классической математики, такой как судоку, до упражнений на счет для младших школьников. В последней категории используются краткие предложения и мультяшные персонажи, что облегчает усвоение материала этими учащимися.

Уровень: 1-5 классы

8. 101 и аут

Сыграйте несколько раундов 101 и аут как забавный способ закончить урок математики. Как следует из названия, цель состоит в том, чтобы набрать как можно больше очков, не превышая 101. Вам нужно разделить свой класс пополам, раздав каждой группе кости вместе с бумагой и карандашом.

Группы по очереди бросают кости, разрабатывая стратегию подсчета числа по номинальной стоимости или умножения его на 10. Например, учащиеся, выбрасывающие шестерку, могут сохранить это число или превратить его в 60. Эта игра быстро становится соревновательной, повышая азарт уровень в вашем классе математики.

Уровень: 2-6 классы

9. Бег на один метр

Запустите эту быструю игру, чтобы улучшить восприятие и понимание измерения. Объедините учащихся в небольшие группы, раздайте им измерительные палочки. Затем они осматривают комнату в поисках двух-четырех предметов, длина которых, по их мнению, составляет один метр.

Через несколько минут группы измеряют предметы и записывают, насколько близки были их оценки. Хотите больше испытаний? Дайте им отметку в сантиметрах вместо метра и попросите перевести результаты в микрометры, миллиметры и т. д.

Уровень обучения: 3-5 классы

10.

Back-to-Back

Выявите конкурентоспособность своего класса. Просто не забудьте сгруппировать учеников с одинаковым уровнем навыков. Спина к спине включает в себя пару одноклассников, стоящих у доски с мелом в руке, лицом друг к другу.

Третий учащийся говорит «Числа вверх», требуя, чтобы каждый участник написал число на доске в пределах указанного диапазона. Затем третий ученик называет сумму или произведение двух чисел. Используя эту информацию, участник выигрывает, называя номер другого первым.

Уровень класса: 2–6 классы

11. Математика Крестики-нолики

Учащиеся объединяются в пары, чтобы соревноваться друг с другом, отрабатывая различные математические навыки в этом варианте игры в крестики-нолики.

Подготовьте, разделив лист на квадраты — три по вертикали и три по горизонтали. Не оставляйте их пустыми. Вместо этого заполните поля вопросами, проверяющими различные способности. Выигрывает тот, кто первым свяжет три крестика или нолика, правильно ответив на вопросы.

Вы можете использовать эту игру в качестве обучающей станции, обновляя необходимые навыки при подготовке к новому контенту. Кроме того, вы можете попробовать это на всем классе, разместив квадраты на доске и разделив класс на две соревнующиеся команды.

Уровень обучения: 1-8 классы

P.S. Крестики-нолики можно легко изменить в соответствии с вашим классом и планами уроков, ознакомьтесь с этой версией ниже:

12. Получите математику

Посетите веб-сайт Get the Math вместе со своими учениками, чтобы решить увлекательные задачи, каждая из которых связана с использованием математики в различных профессиях и реальных ситуациях. Он в первую очередь предназначен для старшеклассников или тех, кто заканчивает среднюю школу.

На веб-сайте размещены видеоролики с участием молодых специалистов, которые объясняют, как они используют математику в своих областях, таких как дизайн одежды и разработка видеоигр.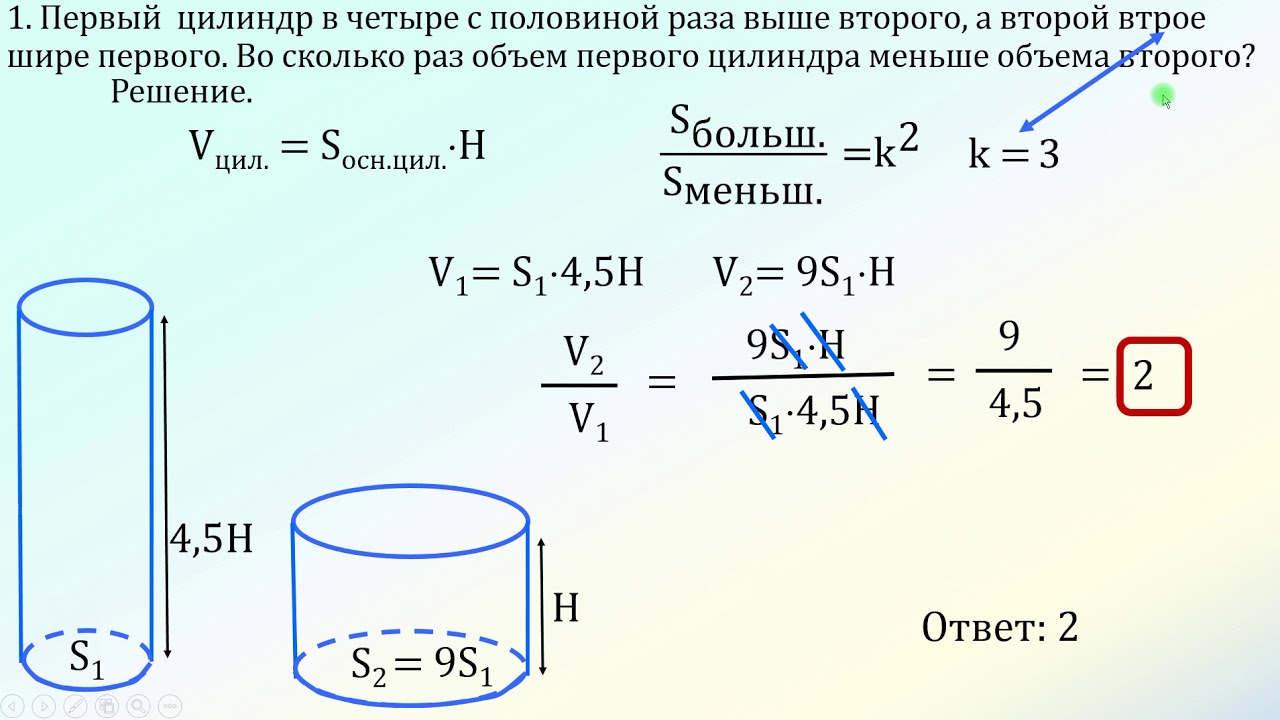 После просмотра вы можете давать задания своему классу, которые включают в себя игры.

Например, один основан на использовании материалов с разной ценой и размерами для создания рубашки менее чем за 35 долларов США.

Уровень: 6-й класс и выше

13. Саймон Сэйс: Геометрия

Обратитесь к кинестетическим учащимся, играя в эту версию Саймона Сэйса, и в процессе улучшите их понимание базовой геометрии.

Играя за Саймона, все ваши команды должны требовать, чтобы ученики изображали углы и формы, двигая руками. Например, попросите их составить углы разной степени, а также параллельные и перпендикулярные линии. Постоянно ускоряйте свои команды — и меняйте, исходят ли они от Саймона или нет — пока не останется только один ученик, который станет победителем.

Уровень класса: 2–3 классы

14. Математические полезные вещи

Попробуйте математические полезные вещи для увлекательных интерактивных заданий и онлайн-уроков. Бесплатный веб-сайт привлекает самых разных учащихся, предлагая головоломки, статьи и текстовые задачи.

Просматривая содержимое сайта, учащиеся могут, например, прочитать заполненное примерами пошаговое руководство о том, как упорядочивать десятичные дроби. Затем они могут проверить свои навыки, выполняя упражнения и задачи. Вы также можете использовать веб-сайт для создания пользовательских рабочих листов. Развлечение для класса, полезное для учителя.

Уровень обучения: 4–8 классы

15. Initials

Добавьте игровой процесс к обзорам контента, играя в Initials. Раздайте каждому учащемуся уникальный лист с задачами, относящимися к общему навыку или теме. Вместо того, чтобы сосредотачиваться на своих листах, ученики ходят по комнате, чтобы решить вопросы своих одноклассников.

Но есть загвоздка. Студент может заполнить только один вопрос на листе, подписавшись рядом с ответом своими инициалами. Работая вместе для достижения индивидуальной, но совместной цели, учащиеся должны укреплять доверие и работать в команде.

Уровень: 3–8 классы

16. Встань, сядь

Игра «Встань, сядь» как упражнение для ума, регулируя сложность в соответствии с возрастом ученика и уровнем навыков. Принцип игры прост: вы выбираете число, и ученики должны стоять, если ответ на уравнение, которое вы читаете вслух, совпадает с этим числом. Если это не так, они остаются сидеть в кругу. Вы можете изменить требования к репутации по мере необходимости.

Например, вы можете предложить учащимся встать, если ответ:

Больше 10
Четное число
Число, кратное трем

Вы также можете чередовать сложение с вычитанием и с умножения на разделение.

Уровень класса: 1-5 классы

17. 100s

Соберите свой класс в круг, чтобы сыграть 100s как для быстрой разминки перед уроком. Вы дадите учащимся набор чисел на выбор — например, от пяти до максимум 20 — по мере того, как они по очереди складывают вслух по часовой стрелке. Ученик, набравший или сдавший 100, выбывает. Вы начнете заново, пока не останется только один участник.

Несмотря на то, что игра проста, вы можете изменить способ игры в соответствии с навыками ваших учеников. Например, им, возможно, придется умножать на четыре вместо сложения на пять.

Уровень класса: 2-8 классы

18. Война

Дайте учащимся математическую интерпретацию традиционной карточной игры, играя в эту версию «Войны». Для начала объедините учеников в пары и дайте каждому по колоде карт. Затем присвойте следующие значения:

Туз — 1
От двойки до 10 — номинал
Валет — 11
Дама — 12
Король — 13

9000 7 Правила игры будут зависеть от класса, который вы преподаете, и навыков, которые вы строим. Например, ученики младших классов будут разыгрывать две карты, вычитая меньшее число из большего. Учащиеся старших классов могут умножать числа, обозначая определенную масть как имеющую отрицательные целые числа. Тот, у кого самая высокая рука, выигрывает все четыре карты.

Уровень класса: 2-8 классы

19. Национальная библиотека виртуальных манипуляций

Предложите учащимся посетить онлайн Национальную библиотеку виртуальных манипуляций, чтобы получить доступ к действиям, которые включают цифровых математических манипуляций, таких как монеты и блоки. Целью онлайн-библиотеки, созданной Университетом штата Юта, является привлечение студентов. Он делает это, предоставляя учителям задания, поскольку есть манипулятивные задания, предназначенные для учащихся всех классов, включая среднюю школу.

Например, задание по геометрии в 6-м классе включает использование геодосок для иллюстрации понятий площади, периметра и рациональных чисел. Идеально подходит для занятий с использованием устройств один на один, вы также можете использовать веб-сайт как собственную учебную станцию.

Уровень обучения: 1-й класс и выше

20. Опасность

Превратите это знаменитое игровое шоу, чтобы сосредоточиться на своем последнем навыке или модуле, готовя учеников к викторине или тесту. Установка включает в себя прикрепление карманов к бристольской доске, разделение их на столбцы и ряды. Каждый столбец должен быть посвящен определенной теме, а каждая строка должна иметь значение в баллах — 200, 400, 600, 800 и 1000.

Команда может задать вопрос из любого кармана, но другие команды могут ответить первыми, решив задачу и подняв руки. Как только класс ответит на все вопросы, команда, набравшая наибольшее количество баллов, получит приз, который вы предоставите. Но каждый ученик выигрывает с точки зрения участия и практики поддержки сверстников. Это отличная игра для конкурентоспособных студентов, которые могут не работать с традиционными рабочими листами.

Уровень: 3-8 классы

21. Dice Wars

Игры в кости — это простой и доступный способ сделать уроки математики более увлекательными. В этой игре в кости учащиеся могут работать парами или небольшими группами. Каждый из них по очереди бросает два кубика и выполняет математическую операцию на основе выпавших чисел.

Вы можете легко повышать сложность в зависимости от уровня обучения. Например, первоклассников можно попросить бросить два кубика и сложить оба результата вместе. Для более высоких уровней вы можете попросить их умножить или бросить до 4 кубиков.

Уровень класса: 1–8 классы

22. Бросьте и разместите

Это еще одна игра в кости, которая помогает сделать изучение математических понятий более увлекательным, в данном случае — оценочным. В этой игре ученики бросают два кубика. Затем они должны сложить все полученные числа и записать полученные числа в таблице разрядов. Вот распечатанная диаграмма стоимости места, чтобы помочь!

Чтобы усложнить задачу, вы можете попросить учеников бросить дополнительный кубик или округлить число до ближайших десяти.

Уровень обучения: 1-3 классы

23. Стройтесь!

Если ваши ученики привыкают работать с числовыми линиями, эта активная и увлекательная игра — отличный способ поставить их на ноги. Попробуйте это в качестве математического обзора или разминки!

Дайте каждому учащемуся карточку или лист бумаги с разными номерами. У группы есть 5 минут, чтобы выстроиться в очередь. Если вашему классу нужна дополнительная помощь, вы можете установить двух учеников в качестве самого высокого и самого низкого номера в наборе. Эта игра побуждает учащихся четко общаться, объяснять свои рассуждения и развивать чувство числа.

Вы можете усложнить это математическое задание, введя отрицательные числа, выбрав более широкий диапазон чисел или дав им математическую операцию, которую учащиеся должны решить, чтобы узнать свое число.

Уровень класса: 1-3 классы

Последние мысли об этих 23 бесплатных математических играх для детей при дополнении уроков.

Хотя рекомендуемые возрастные диапазоны находятся между 1 и 8 классами, вы, безусловно, можете изменить контент для разных уровней навыков и использовать его для учащихся старших классов, испытывающих затруднения. И, если вы не уверены в преимуществах, попробуйте несколько игр, чтобы увидеть результаты самостоятельно.

Начните работу с Prodigy Math сегодня — математической игрой, ориентированной на учебную программу, которая адаптирует контент в зависимости от индивидуальных потребностей и скорости обучения игроков.

Создайте бесплатную учетную запись учителя

Учебное пособие: Пример задачи производительности CSP

Часть 1: Полный код

Часть 2: Видео

Часть 3: Письменный ответ

900 03

3А.

Предоставьте письменный ответ, который выполняет все три из следующих действий:

i. Описывает общую цель программы

ii. Описывает, какой функционал программы демонстрируется в видеоролике

iii. Описывает ввод и вывод программы, показанной в видео. Видео демонстрирует как викторины на умножение, так и на деление, в которых пользователя просят указать тип задачи, а затем дается 5 задач, на каждую из которых предоставляется возможность ответить, а результаты сообщаются.

Видео демонстрирует 2 разных входа и 3 разных выхода. Демонстрируемые входные данные просят пользователей выбрать тип проблемы, а затем дают предположение о проблемах. Три продемонстрированных вывода: вывод задачи, вывод результатов каждого предположения и вывод окончательной оценки в конце.

3Б.

Захватите и вставьте два сегмента кода программы, разработанные вами во время администрирования этой задачи, которые содержат список (или другой тип коллекции), используемый для управления сложностью вашей программы.

и. Первый сегмент программного кода должен показывать, как данные были сохранены в списке.

ii. Второй сегмент программного кода должен отображать данные в том же используемом списке, например создание новых данных из существующих данных или доступ к нескольким элементам в списке, как часть выполнения цели программы.

Затем предоставьте письменный ответ, содержащий все три пункта:

iii. Идентифицирует имя списка, используемого в этом ответе

iv. Описывает, что данные, содержащиеся в списке, представляют в вашей программе

v. Объясняет, как выбранный список управляет сложностью вашего программного кода, объясняя, почему ваш программный код не может быть написан или как он будет написан по-другому, если вы не использовал список

Первый сегмент кода:

 first_number = [8, 12, 6, 20, 10]
второе_число = [2, 3, 3, 4, 5]

Второй сегмент кода:

 print(first_number[i], end = " "),
если (тип == "М"):
    распечатать("*", конец=" "),
    правильно = первое_число[i] * второе_число[i]
еще:
    распечатать("/", конец = ""),
    правильно = первое_число[i] / второе_число[i]
печать (второе_число [я])

Программа использует два списка: first_number и second_number. В каждом списке хранятся значения, используемые в математических задачах. first_number хранит первое число в задаче, а second_number хранит второе число, которое является делителем для задач на деление.

Списки управляют сложностью двумя разными способами. Во-первых, используя списки вместо отдельных переменных, список может хранить все значения в одной переменной и использовать цикл для создания проблемы. Это также позволяет программе легко расширяться, устанавливая длину цикла в соответствии с длиной списков. Без списка программа должна была бы использовать отдельные переменные и записываться последовательно, а не в цикле.

Кроме того, сохраняя определенные значения для задачи, программа может создавать задачи на деление, которые дают целочисленные ответы. Если бы программа генерировала случайные числа, было бы намного сложнее создавать задачи, которые приводили бы к целочисленным ответам.

3С.

Захватите и вставьте два сегмента кода программы, разработанные вами во время администрирования этой задачи, которые содержат разработанную учащимся процедуру, реализующую алгоритм, используемый в вашей программе, и вызов этой процедуры.

и. Первый сегмент программного кода должен быть разработанной студентом процедурой, которая:

• определяет имя процедуры и тип возвращаемого значения (при необходимости)

• содержит и использует один или несколько параметров, влияющих на функциональность процедура

• Реализует алгоритм, включающий определение последовательности, выборку и итерацию

ii. Второй сегмент программного кода должен показывать, где в вашей программе вызывается процедура, разработанная учащимся.

Затем предоставьте письменный ответ, который выполняет оба следующих действия:

iii. Описывает в целом, что делает указанная процедура и как она влияет на общую функциональность программы

iv. Подробно объясняет, как работает алгоритм, реализованный в указанной процедуре. Ваше объяснение должно быть достаточно подробным, чтобы кто-то другой мог его воссоздать.

Первый сегмент кода:

 по умолчанию вычислить(тип):
оценка = 0
для i в диапазоне (num_problems):
печать (первый_номер [i], конец = " "),
если (тип == "М"):
распечатать("*", конец=" "),
правильно = первое_число[i] * второе_число[i]
еще:
распечатать("/", конец = ""),
правильно = первое_число[i] / второе_число[i]
печать (второе_число [я])
answer = int(input("Введите ответ:"))
если ответ == правильный:
печатать("Верно!")
оценка += 1
еще:
print("Хорошая попытка!")
Распечатать()
обратный счет

Второй сегмент кода:

 оценка = вычислить (тип) * 100 / количество_проблем

Выбранная функция способствует общему выполнению программы, выполняя вопросы викторины и возвращая количество правильных вопросов.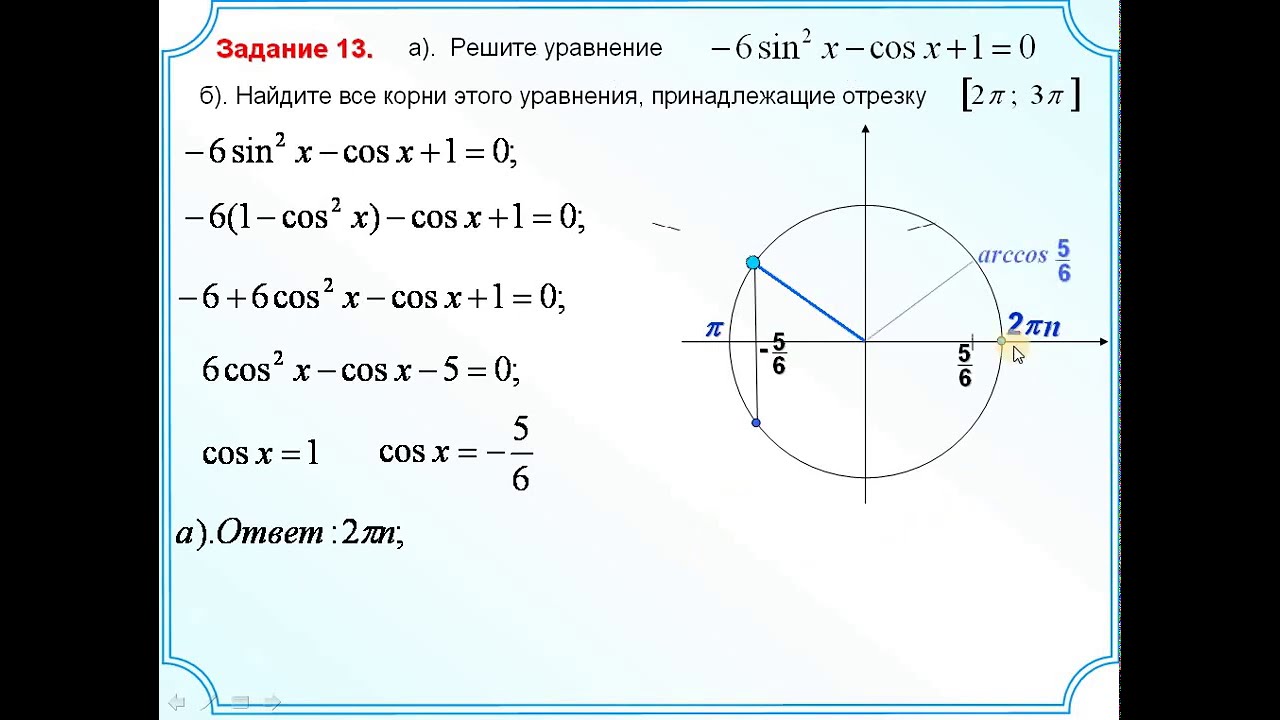 Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов в основную программу.

Функция делает это, перебирая все значения в списке, чтобы создать проблему. Внутри цикла функция начинает с вывода первого числа задачи из списка first_number. Затем он использует оператор выбора, чтобы распечатать оператор и вычислить правильный ответ для задачи на деление или умножение на основе параметра проходов. Затем он выводит второе число из списка second_number и запрашивает у пользователя его предположение. Используя оператор выбора, он сравнивает правильный ответ с вводом пользователя и выводит результаты. Если ответ правильный, он также добавляется к переменной трекера, которая отслеживает количество правильных ответов. В конце цикла функция завершается, возвращая количество правильных ответов.

3D.

Предоставьте письменный ответ, который выполняет все три из следующих действий:

i. Описывает два вызова процедуры, указанной в письменном ответе 3c. Каждый вызов должен передавать разные аргументы, которые вызывают выполнение другого сегмента кода в алгоритме.

ii. Описывает, какие условия проверяются при каждом вызове процедуры

iii. Определяет результат каждого вызова

Два тестовых примера основаны на передаче разных входных данных для создания различных типов задач в функции (умножение или деление). Первый вызов будет передавать букву М. На основе этого вызова программа должна выбрать задачи на умножение для печати. Внутри цикла оператор выбора выполнит первую часть оператора выбора и напечатает задачу с помощью оператора *. Он также рассчитает ответ путем умножения значений из списков first_number и second_number. Результатом вызова будет вывод 5 задач на умножение и возврат количества правильных ответов.

Второй вызов пройдет букву D. На основе этого вызова программа должна выбрать задачу деления. Внутри цикла оператор выбора выполнит предложение else, поскольку D не равно M. В результате код напечатает оператор / и вычислит ответ, разделив значение first_number на значение second_number. Результатом вызова будет вывод 5 задач на деление и возврат количества правильных ответов.

6/6

Ряд 1:

Ответ заработал балл для этой строки, отвечая всем шести критериям:

• Видео демонстрирует, как программа получает пользовательский ввод как для типа задачи, так и для ответов на задачу

• Целью программы является создание математической викторины и видео демонстрирует создание викторины на умножение и деление.

• Программа демонстрирует выходные данные, создавая задачи и отображая результаты каждой задачи и теста.

• Ввод и вывод описываются в ответе следующим образом: предположение для задач. Три продемонстрированных вывода: вывод задачи, вывод результатов каждого предположения и вывод окончательного результата в конце».

Строка 2:

Ответ заработал баллы для этой строки, отвечая всем трем критериям:

• Показаны два отдельных сегмента кода

• Имя списка описывается как first_number

• Состояние ответа какие значения хранятся в списке: «first_number хранит первое число в задаче»

Строка 3:

Ответ заработал балл за эту строку, отвечающую обоим критериям:

• Ответ включает два списка first_number и second_number и используются в цикле для создания нескольких задач

• Ответ объясняет, как он управляет сложностью, заявляя, что «список может хранить все значения в одной переменной и использовать цикл для создания проблемы». Он также объясняет, как программа должна быть написана без списка, заявляя: «Без списка программа должна была бы использовать отдельные переменные и писать последовательно, а не в цикле».

Строка 4:

Ответ заработал баллы для этой строки, отвечая обоим критериям:

• Ответ включает два отдельных сегмента кода, один из которых определяет функцию, вычисляемую с параметром типа, а другой вызывает эту функцию

• Ответ описывает, что делает процедура, заявляя: «Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов обратно в основную программу», и описывает, как она относится к общей функции, заявляя: «Функция выбранная функция способствует общему выполнению программы, выполняя вопросы викторины и возвращая количество правильных вопросов».

Строка 5: