Решение №2664 Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
а) Пусть М – отличная от А1точка пересечения окружностей (двух), описанных около треугольников ΔА1ВС1и ΔA1CB1.
Четырёхугольник А1ВС1М вписан в окружность, поэтому сумма его противолежащих углов равна 180°, выразим ∠А1МС1:
∠А1МС1 = 180° – ∠В
Аналогично для четырёхугольника А1СВ1М:
∠А1МВ1 = 180° – ∠С
Найдём ∠В1МС1:
∠В1МС1 = 360° – (∠А1МС1 + ∠А1МВ1) = 360° – ( 180° – ∠В + 180° – ∠С) = 360° – 360° + ∠В + ∠С = ∠В + ∠С
Сумма углов любого треугольника равна 180° (ΔАВС), тогда:
∠В1МС1 = ∠В + ∠С = 180° – ∠А
Т.к. у четырёхугольника В1АС1М сумма противоположных углов равна 180° (∠А+ ∠В1МС1 = 180°, а значит и ∠АС1М + ∠АВ1М = 180°), значит он тоже вписанный в окружность.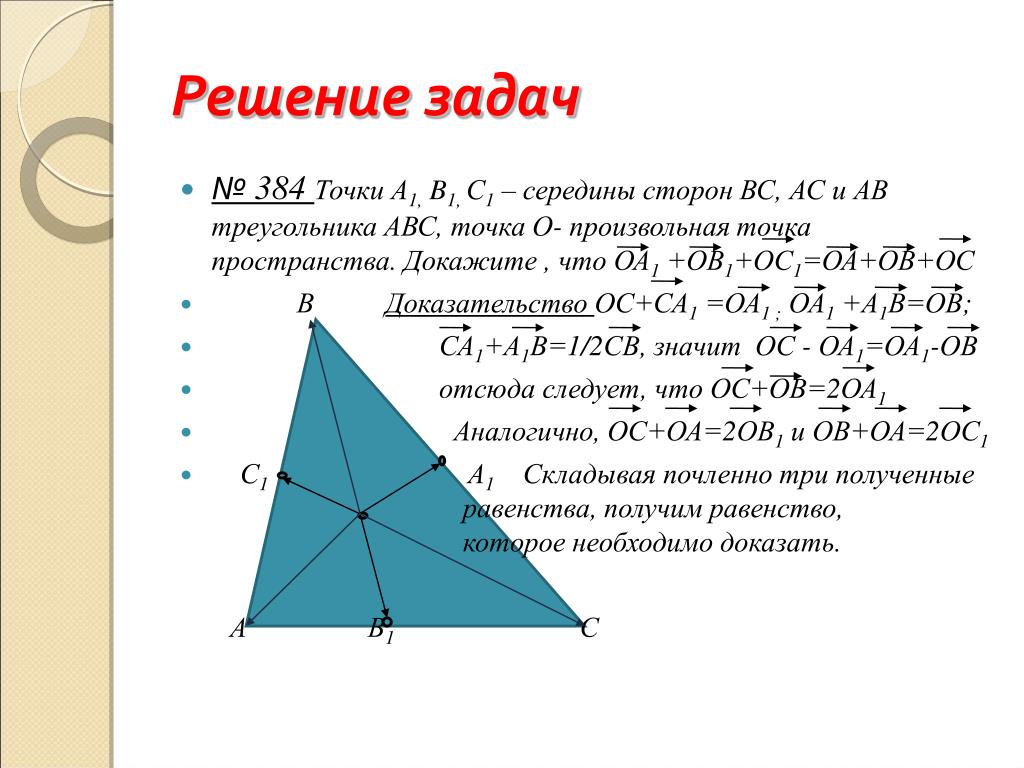
Следовательно, точка М лежит и на описанной окружности (третьей) треугольника ΔB1AC1. Значит все три окружности пересекаются в одной точке М.
Что и требовалось доказать.
б) АВ = АС = 17, ВС = 16, найти r окружности вписанной в ΔО1О2О3, где О1, О2, О3 центры окружностей описанных около А1ВС1, А1СВ1 и В1АС1 соответственно:
Радиус окружности вписанной в ΔО1О2О3 можно найди по формуле:
r=\frac{2\cdot S_{\Delta O_{1}O_{2}O_{3}}}{P_{\Delta O_{1}O_{2}O_{3}}}
По условию АВ = АС, тогда и АС1 = АВ1, значит ΔАС1В1 равнобедренный ⇒ АМ диаметр окружности описанной около равнобедренного треугольника.
Поэтому отрезок МВ1⊥АС (т.к. ΔАМВ1 вписанный опирающийся на диаметр, а значит прямоугольный), значит СМ тоже диаметр (т.к. ∠МВ1С = 90°) описанный около треугольника СВ1А1.
ΔАМВ1 = ΔСМВ1 (МВ1 – общая, АВ1 = СВ1, ∠АВ1М = ∠СВ1М = 90°), тогда и соответствующие стороны равны, они же диаметры окружностей:
АМ = СМ
Аналогично для диаметров АМ и ВМ, тогда:
АМ = СМ = ВМ
Получаем три равнобедренных треугольника ΔАМВ, ΔАМС, ВМС, у которых точки О1, О2, О3 середины сторон (как центры окружностей на диаметрах), тогда О1О3, О1О2, О2О3 средние линии, они равны половине соответствующих оснований, найдём их:
O_{1}O_{3}=\frac{АВ}{2}=\frac{17}{2}=8,5\\O_{2}O_{3}=\frac{АС}{2}=\frac{17}{2}=8,5\\O_{1}O_{2}=\frac{ВС}{2}=\frac{16}{2}=8
Найдём периметр ΔО1О2О3:
РΔ = О1О3 + О2О3 + О1О2 = 8,5 + 8,5 + 8 = 25
По формуле Герона найдём площадь ΔО1О2О3. Полупериметр равен:
Полупериметр равен:
p=\frac{P_{\Delta}}{2}=\frac{25}{2}=12,5
Площадь равна:
S_{\Delta O_{1}O_{2}O_{3}}=\sqrt{p(p-O_{1}O_{3})(p-O_{2}O_{3})(p-O_{1}O_{2})}=\sqrt{12,5(12,5-8,5)(12,5-8,5)(12,5-8)}=\sqrt{12,5\cdot 4\cdot 4\cdot 4,5}=\sqrt{900}=30
Найдём искомый радиус r:
r=\frac{2\cdot S_{\Delta O_{1}O_{2}O_{3}}}{P_{\Delta O_{1}O_{2}O_{3}}}=\frac{2\cdot 30}{25}=\frac{2\cdot 6}{5}=\frac{12}{5}=2,4
Ответ: б) 2,4.
Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС
Задача. Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1, пересекаются в одной точке.
б) Известно, что АВ=АС=17 и ВС=16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Решение.
Так как точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС, то отрезки А1В1, В1С1 и А1С1 являются средними линиями треугольника АВС (рис. 1).
Средняя линия треугольника параллельна третьей стороне и равна её половине.
Вследствие этого мы получаем 4 треугольника, равных между собой по трём сторонам. Нас будут интересовать 3 из них (окрашены).
Около каждого из этих треугольников описана окружность.
Центр окружности, описанной около любого треугольника – это точка пересечения серединных перпендикуляров к сторонам треугольника.
Пусть точка О1 – центр окружности (рис. 2), описанной около ΔА1СВ1 – пересечение серединных перпендикуляров О1Х и О1Х1 к сторонам А1С и В1С;
2), описанной около ΔА1СВ1 – пересечение серединных перпендикуляров О1Х и О1Х1 к сторонам А1С и В1С;
точка О2 – центр окружности, описанной около ΔА1ВС1 – пересечение серединных перпендикуляров О2Y и О2Y1 к сторонам А1B и ВС1. Заметим также, что точки Х, А1 и Y делят ВС на 4 равных отрезка.
точка О3 – центр окружности, описанной около ΔB1AC1 – пересечение серединных перпендикуляров О3Z и О3Z1 к сторонам АB1 и AC1; Заметим также, что точки Х1, В1 и Z делят AС на 4 равных отрезка, a точки Y1, C1 и Z1 делят AB на 4 равных отрезка.
а) Около равных треугольников А1СВ1 и A1BC1 будут описаны равные окружности, которые пересекаются в точках А1 и М (рис.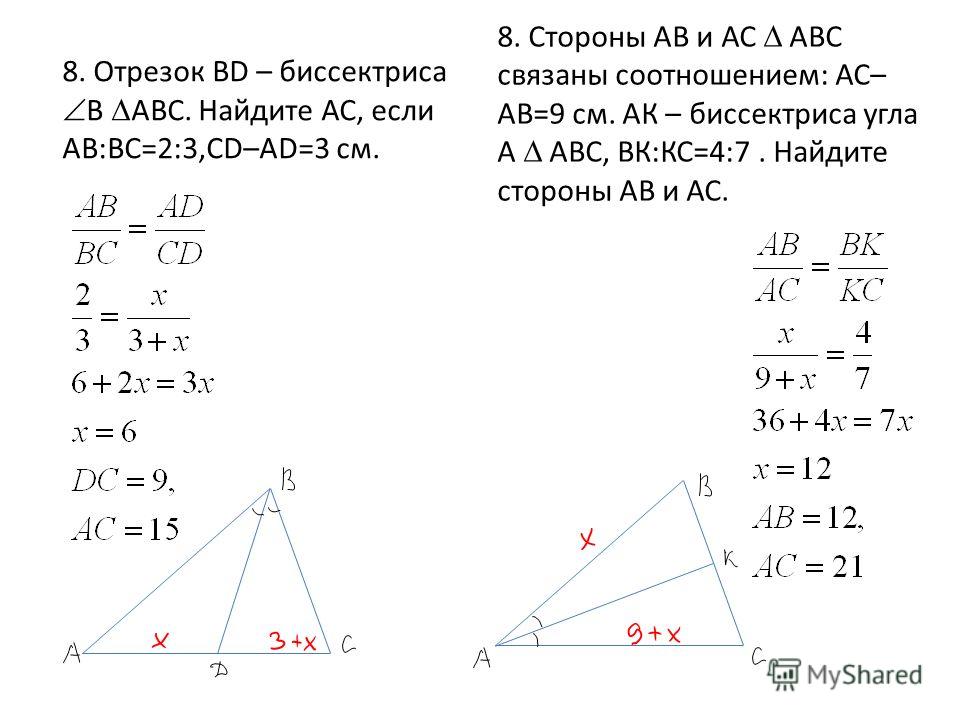 3).
3).
Общая хорда А1М перпендикулярна линии центров О1О2 и проходит через точку К – середину отрезка О1О2. Следовательно, А1М будет осью симметрии для этих окружностей и является серединным перпендикуляром к отрезку ВС.
Итак, А1М Ʇ О1О2 и А1М Ʇ ВС, значит, О1О2 || BC.
В прямоугольнике ХО1О2Y О1О2 = XY, поэтому, очевидно, что О1О2 = ½ ВС.
Аналогично, прямая, проходящая через точки пересечения окружностей с центрами О1 и О3 (рис. 4), будет являться серединным перпендикуляром к стороне АС треугольника АВС, и О1О3 || AC и О1О3 = ½ АС.
Точно так же прямая, проходящая через точки пересечения окружностей с центрами О2 и О3 будет являться серединным перпендикуляром к стороне АВ треугольника АВС, и О2О3 || AВ и О2О3 = ½АВ.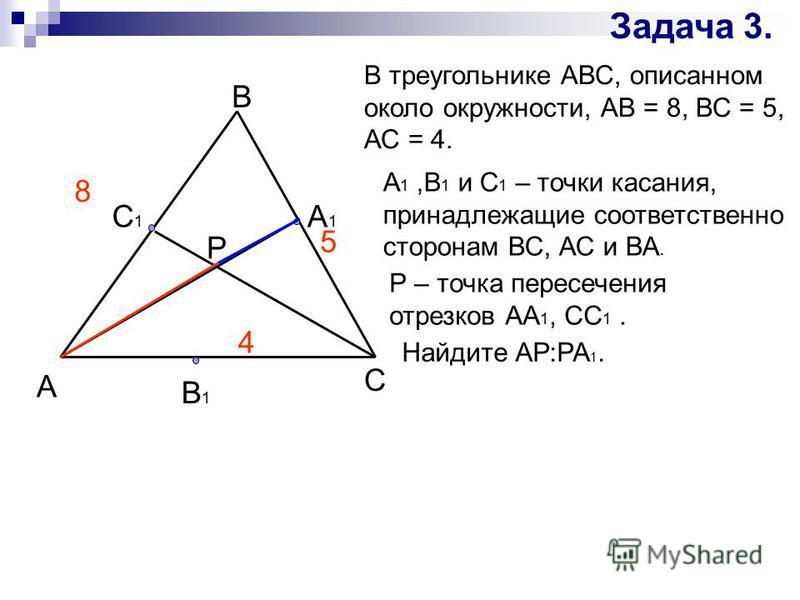
Как известно, серединные перпендикуляры к сторонам любого треугольника пересекаются в одной точке, поэтому все три окружности пересекаются в точке М, ч.т.д. Точка М – центр окружности, описанной около треугольника АВС.
б) Так как длины сторон треугольника О1О2О3 равны соответственно половинам сторон треугольника АВС, то Δ О1О2О3 подобен ΔАВС по трём пропорциональным сторонам с коэффициентом подобия 1/2. Следовательно, радиус окружности, вписанной в треугольник О1О2О3 будет равен половине радиуса окружности, вписанной в треугольник АВС.
Радиус окружности, вписанной в ΔАВС найдём по формуле:
По условию АВ=АС=17 и ВС=16 (рис. 5). Проведём высоту AA1.
В равнобедренном ΔАВС высота AA1 – медиана, поэтому, в прямоугольном ΔAА1B гипотенуза АВ=17, катет ВA1=8, тогда второй катет AA1=15 (пифагорова «тройка» 8, 15, 17 или примените теорему Пифагора).
Тогда 2S = ВС ∙ AA1 = 16 ∙ 15 = 240.
Периметр ΔАВС равен 17+17+16 = 50.
Тогда r = 240 : 50 = 4,8.
Искомый радиус вписанной окружности для Δ О1О2О3 равен половине найденного радиуса вписанной окружности для ΔАВС, делим 4,8 пополам и получаем 2,4.
Ответ: 2,4. Смотреть видео решение.
Запись имеет метки: вписана окружность, егэ геометрия, описана окружность, планиметрия егэ
Навигация
Помогите решить задачу по геометрии | Wyzant Спросите эксперта
Геометрические полиномы Комплексные числа
Спрдало М.
спросил 29.10.19 Пусть $ABC$ — треугольник. Точки $A_1, B_1, C_1$ лежат соответственно на сторонах $BC, AC, AB$ и:
$\frac{AC_1}{C_1B} = \frac{BA_1}{A_1C} = \frac{CB_1 }{B_1A} \neq 1$
Если $\frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = \frac{CA}{C_1A_1}$, докажите, что треугольник $ABC$ равносторонний.
Я нашел эту проблему в разделе, где задачи основаны на комплексных числах, сложной геометрии, многочленах,. .. Тем не менее, любое решение будет приветствоваться (особенно сложное :)). Заранее спасибо.
.. Тем не менее, любое решение будет приветствоваться (особенно сложное :)). Заранее спасибо.
Если Latex не работает:
Пусть ABC — треугольник. Точки A1, B1, C1 лежат соответственно на сторонах BC, AC, AB и:
AC1/C1B} = BA1/A1C = CB1/B1A, что не равно 1
Если AB/A1B1 = BC/B1C1} = CA/C1A1 докажите, что треугольник ABC равносторонний.
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Пол М. ответил 30.10.19
Репетитор
5,0 (26)
Бакалавр математики, MD
Об этом репетиторе ›
Об этом репетиторе ›
Я тоже работал над этой проблемой до того, как Sam Z ответил на нее.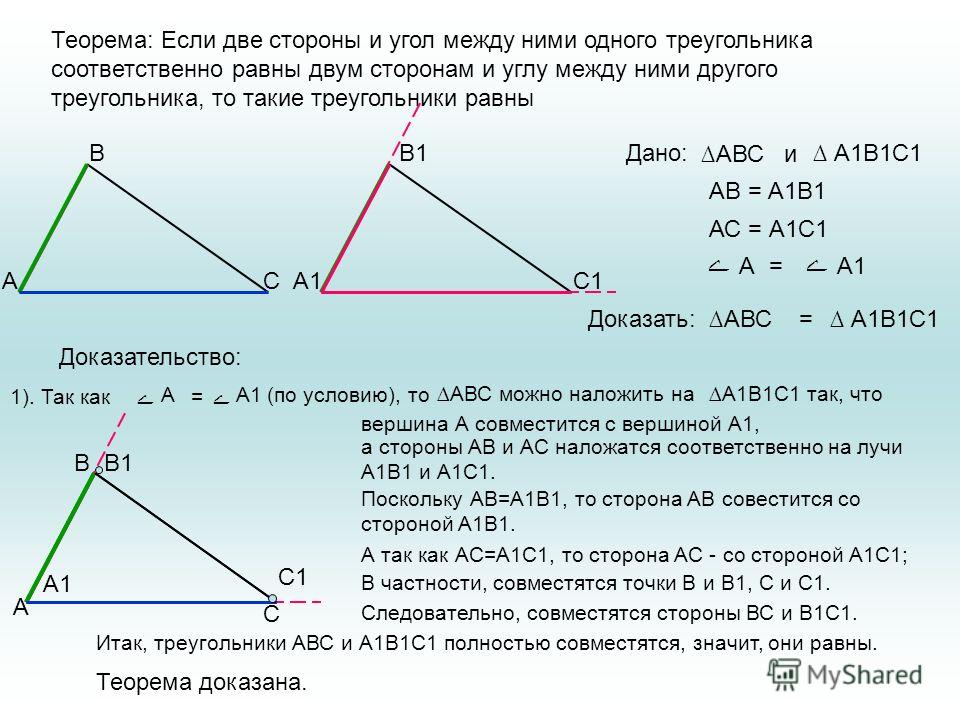
Я еще не все решил, но знаю достаточно, чтобы не согласиться с Сэмом З.
Первое неравенство говорит вам о том, что A1, B1 и C1 НЕ являются серединами сторон.
Равенство говорит вам о том, что ΔABC подобен ΔA1B1C1, потому что стороны пропорциональны.
Хорошо, я понял.
Три треугольника AB1C1, BC1A1 и CA1B1 также подобны, потому что стороны пропорциональны.
Это означает, что ∠A = ∠B = ∠C, потому что они являются соответственными углами подобных треугольников! КЭД
Голосовать за
Подробнее
Отчет
Сэм З. ответил 10/29/19
Репетитор
4.3 (12)
Репетитор по математике/естествознанию
Смотрите таких репетиторов
Смотрите таких репетиторов
Без дисплея; Я полагаю, что 1 = средние точки. Этот равносторонний разделен на четверти. 3 угла и треугольники в центре.
Этот равносторонний разделен на четверти. 3 угла и треугольники в центре.
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Математическая задача: Луны Гиппократа
Вычислите сумму площадей так называемых гиппократовых лунок, которые были вырезаны над катетами прямоугольного треугольника (а = 6 см, b = 8 см). Инструкции: Сначала вычислите площадь полукруга над всеми сторонами треугольника ABC. Сравните сумму площадей полулуний с площадью треугольника ABC.
Инструкции: Сначала вычислите площадь полукруга над всеми сторонами треугольника ABC. Сравните сумму площадей полулуний с площадью треугольника ABC.
Правильный ответ:
S = 24 см 2Пошаговое объяснение:
a=6 см b=8 см c=a2+b2
=62+82 100406 9003
см R=c/2=10/2=5 см S1=2a⋅ b=26⋅ 8=24 см2 Sa=π⋅ (a/2)2/2=3,1416⋅ (6/2)2/ 2≐14,1372 см2 Sb=π⋅ (b/2)2/2=3,1416⋅ (8/2)2/2≐25,1327 см2 Sc=π⋅ R2/2=3,1416⋅ 52/2≐39,2699 см2 S2=Sc −S1=39,2699−24≐15,2699 см2 S=Sa+Sb−S2=14,1372+25,1327−15,2699=24 см2 S=S1 = 2a⋅ b=24 см2
Вы нашли ошибку или неточность? Не стесняйтесь
напишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Для решения этой задачи по математике вам необходимо знать следующие знания:
- геометрия
- теорема Фалеса
- арифметика 915
- сравнение
- 27 планиметрика
- теорема Пифагора
- прямоугольный треугольник
- круг
- площадь фигуры
- круговой сектор
Единицы физических величин:
- площадь
Уровень решения задачи:
- практика для 14-летних 65 15 старшая школа 9056
Мы рекомендуем Вы можете посмотреть это обучающее видео по этой математической задаче: видео1 видео2
- Бесконечная сумма площадей
Равносторонний треугольник A1B1C1 построен выше высоты равностороннего треугольника ABC, построенного как. Над высотой равностороннего треугольника A1B1C1 строится треугольник A2B2C2 и так далее. Процедура повторяется непрерывно. Что такое
Над высотой равностороннего треугольника A1B1C1 строится треугольник A2B2C2 и так далее. Процедура повторяется непрерывно. Что такое - Прямоугольные треугольники
Длины соответствующих сторон двух прямоугольных треугольников относятся как 2:5. При каком отношении медианы относятся к гипотенузе этих прямоугольных треугольников? В каком отношении находятся площади этих треугольников? Меньший прямоугольный треугольник имеет катеты 6 и 8 c - Сконструированный 8161
Периметр прямоугольного треугольника равен 18 см. Сумма площадей квадратов, построенных над тремя его сторонами, равна 128 см². Чему равна площадь треугольника? - Прямоугольный треугольник ABC
Вычислите периметр и площадь прямоугольного треугольника ABC. Если известны длины катетов, то гипотенузой будут 4 см, 5,5 см и 6,8 см. - Квадраты рекурсии
В квадрат ABCD вписал квадрат так, что его вершины лежат в центрах сторон квадрата ABCD. Процедура вписывания квадрата повторяется таким образом.
- Прямоугольный треугольник
Прямоугольный треугольник ABC со стороной a = 19а площадь S = 95. Вычислите длины остальных сторон. - Медианы и стороны
Треугольник ABC в плоскости Oxy; координаты точек: A = 2,7 B = -4,3 C-6-1 Попробуйте вычислить длины всех медиан и всех сторон. - Прямоугольный 40961
Прямоугольный треугольник ABC имеет стороны a = 5 см, b = 8 см. Подобный треугольник A’B’C’ в 2,5 раза меньше. Вычислите, какой процент от площади треугольника ABC составляет площадь треугольника A’B’C’. - Сумма квадратов
Сумма квадратов сторон прямоугольного треугольника равна 900 см². Вычислите площадь квадрата над гипотенузой треугольника. - Построить 1
Построить треугольник ABC, a = 7 см, b = 9 см с прямым углом C, и провести оси всех трех сторон. Измерьте длину стороны c (и напишите). - Треугольная призма
Вычислите поверхность треугольной призмы высотой 10 см, основание которой представляет собой треугольник со сторонами 6 см, 8 см и 8 см - Площадь RT 2
Вычислите площадь прямоугольного треугольника, катеты которого равны 6,2 см и 9,8 см.

 Над высотой равностороннего треугольника A1B1C1 строится треугольник A2B2C2 и так далее. Процедура повторяется непрерывно. Что такое
Над высотой равностороннего треугольника A1B1C1 строится треугольник A2B2C2 и так далее. Процедура повторяется непрерывно. Что такое
Leave A Comment