Функция y = корень квадратный из x, ее свойства и график
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и письменных вычислений, возведение в квадрат, извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе
(перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x2, y = — x2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.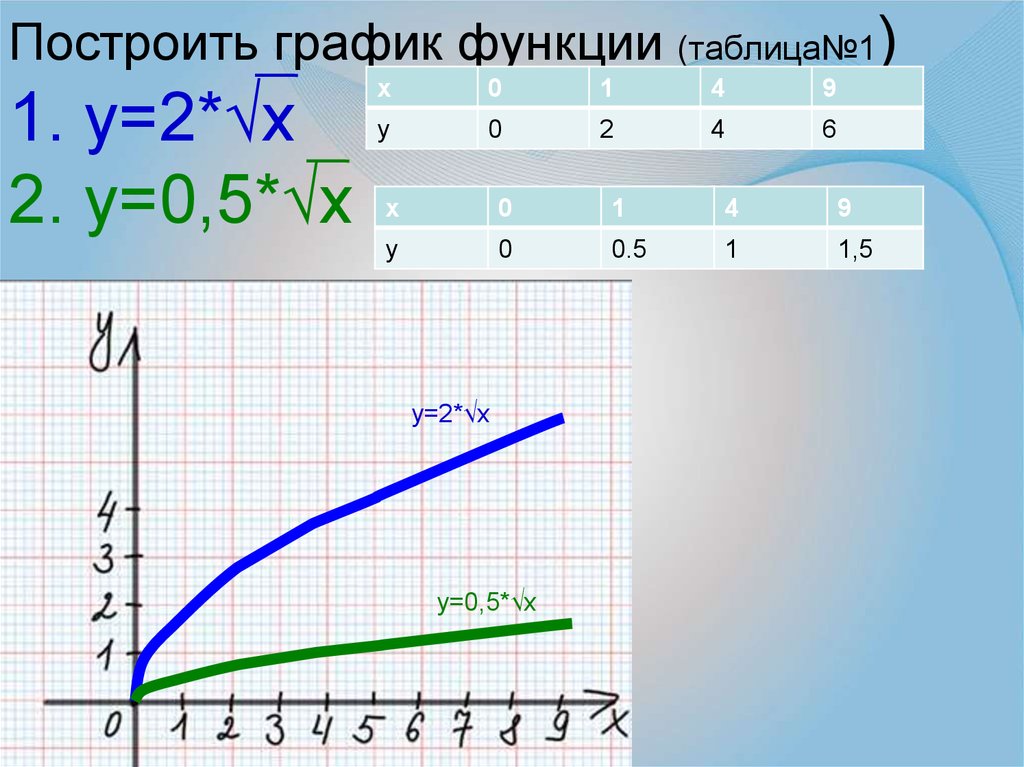
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между двумя величинами, где каждому значению одной переменной соответствует единственное значение другой переменной y = f(x)).
Как называется х? (Независимая переменная - аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c,
y =x
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x2, y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.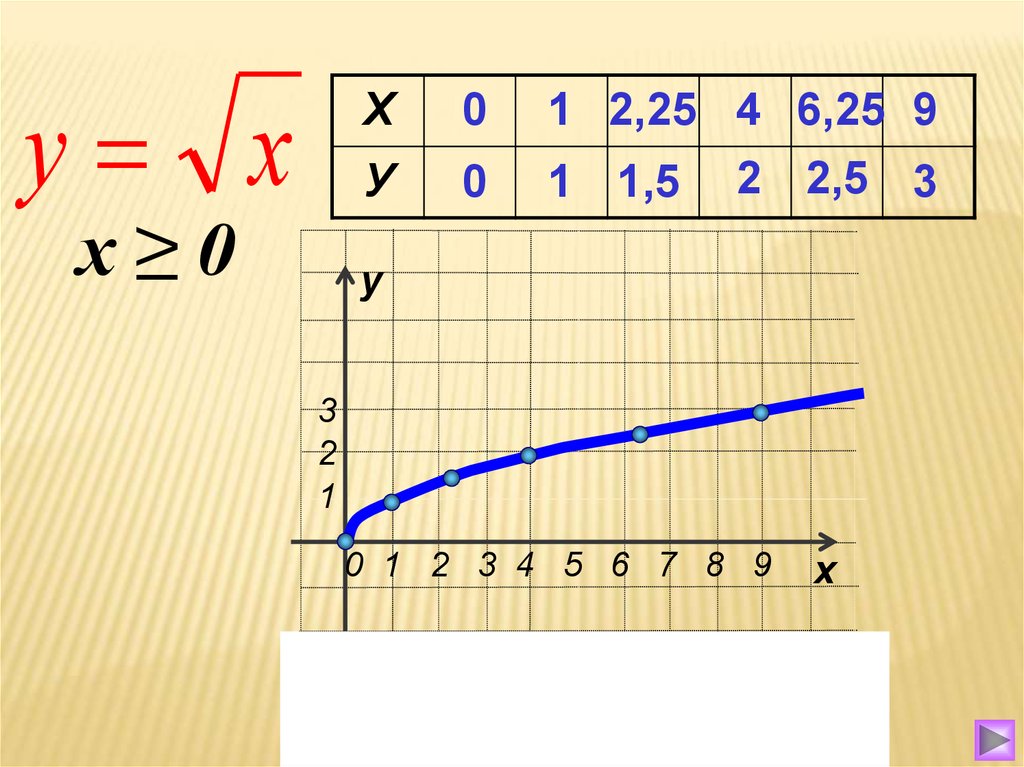
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам,
предложив группам построить график y = , затем
проанализировать получившиеся результаты.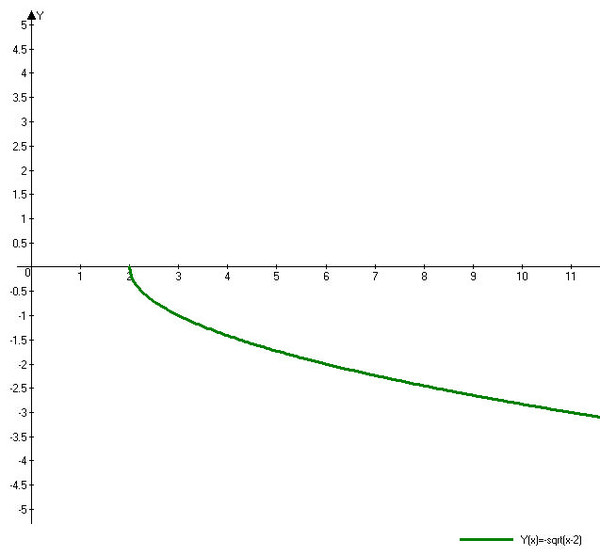
Также
группам можно предложить по алгоритму описать
свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= — и опишите его свойства.
Свойства у= — .
1.Область определения функции.
D(y) =
2.Область значений функции.
E(y) =
3. y = 0, y> 0, y<0.
y =0, если x = 0.
y<0, если х(0;+)
4.Возрастания, убывания функции.
Функция убывает при х [0;+ )
5. Ограниченность функции.
Функция ограничена сверху, и не ограничена снизу.
6.Наибольшее, наименьшее значения функции.
у наиб. = нет у наим. = 0.
7.Непрерывность функции.
Функция непрерывна на все области определения.
№13.2(в)
Используя график функции у=, найдите наименьшее и
наибольшее значения функции на отрезке [1; 9].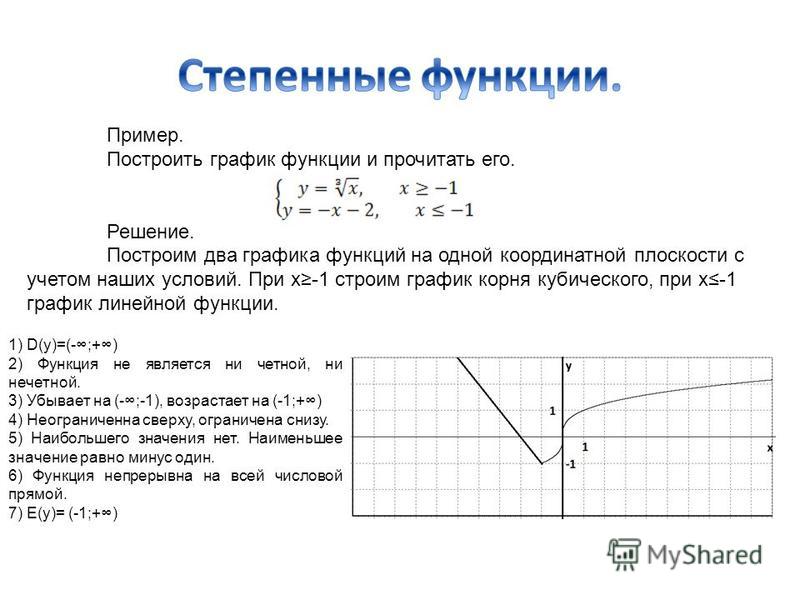
Построим график у=.
Выделим его часть на отрезке [1;9]. Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
№ 13.1(в)
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке [0; 4].
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.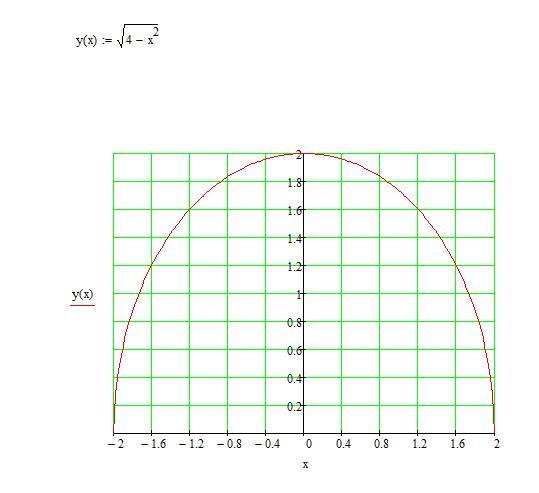
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.
Ответ: 9.
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п.
2
Почему $f(x)=\sqrt x $ не является функцией?
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 15 тысяч раз
$\begingroup$
Почему $f(x)=\sqrt x$ не является функцией? Я понимаю, что определение функции гласит, что каждый «вход» должен быть связан ровно с одним «выходом», но мне любопытно, ПОЧЕМУ.
- функции
$\endgroup$
5
$\begingroup$
$$f(x)=\sqrt{x}$$
действительно является функцией, если ваш домен представляет собой (подмножество) неотрицательных действительных чисел.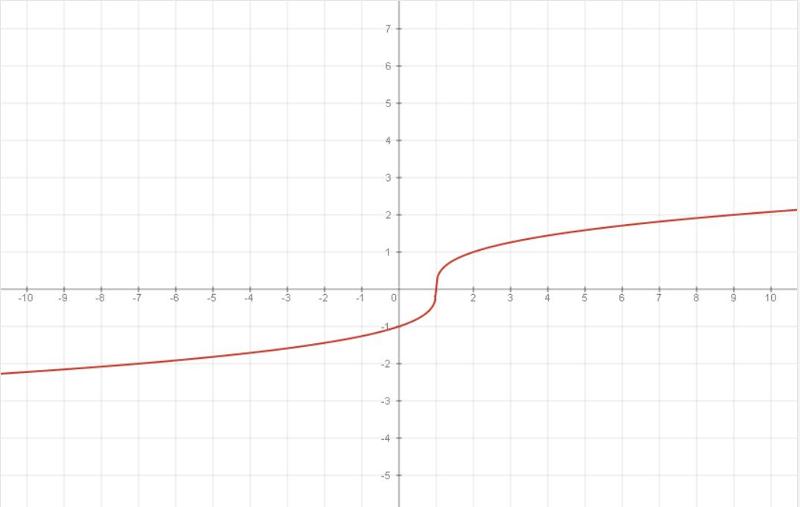
Обратите внимание, что если мы допускаем комплексные числа, то есть более сложный ответ, в котором $f(x)$ может быть функцией, но нам нужно указать больше информации.
$\endgroup$
$\begingroup$
Чтобы правильно определить функцию, необходимо указать:
- Домен, то есть набор всех входов.
- Кодовый домен, то есть набор, в котором лежат выходы.
- Набор отношений, который часто задается уравнением, например $f(x)=\sqrt x$.
Поэтому, если вы не укажете домен и кодовый домен, невозможно сказать, является ли это уравнение функцией.
Например, $f:[0,\infty)\to\Bbb R$, $f(x)=\sqrt x$ — это функция. Но $f:\Bbb R\to\Bbb R$, $f(x)=\sqrt x$ это не так.
Примечание : Обратите внимание, что домен кода не обязательно должен быть набором выходов, так как он может иметь элементы, которые не являются выходом для любого входа.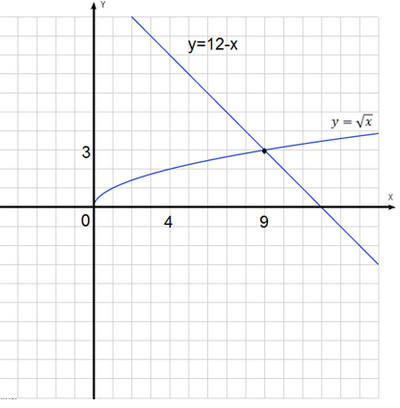
Но кодовый домен должен содержать все выходные данные.
$\endgroup$
1
$\begingroup$
В этом контексте интересно прочитать, например, Великий текст Г. Х. Харди Курс чистой математики . Приведя простые примеры, где $y$ является функцией $x$, он добавляет
…мы должны отметить, что упомянутые простые примеры функций выше, обладают тремя характеристиками, которые никоим образом не связаны с общее представление о функции, а именно:
- $y$ определяется для каждого значения $x$;
- каждому значению $x$, для которого задано значение $y$, соответствует одно и только одно значение $y$;
- связь между $x$ и $y$ выражается с помощью аналитической формулы, из которой можно вычислить значение $y$, соответствующее заданному значению $x$, прямой подстановкой последнего.
2 = x$ или, в одном случае, $f(x) = \sqrt x$, как совершенно хорошую функцию, которая двузначный на $x > 0$.
Современная практика требования, чтобы функции были однозначными, конечно, очень хороша: она позволяет некоторым (многим?) вещам работать более аккуратно. Но Харди, возможно, прав в том, что это не является частью «общей идеи функции».
$\endgroup$
1
$\begingroup$
Это вопрос обозначений, как объясняет Грегори Дж. Пулео в комментариях. Если $x$ — неотрицательное действительное число, то запись $\sqrt{x}$ по соглашению означает уникальный неотрицательный квадратный корень из $x$. Таким образом устраняется неоднозначность положительного действительного числа, обладающего как положительным, так и отрицательным квадратным корнем. Без соглашения такого типа обозначение $\sqrt{x}$ для $x$ положительного действительного числа по своей сути неоднозначно.
$\endgroup$
$\begingroup$
Во многих случаях рассматривается как функция, но теоретически слово «функция» означает разные вещи.
В строгом смысле функция представляет собой отношение между множеством всех возможных входов, называемых областью $X$, и множеством всех возможных выходов, называемых диапазоном , $f(X)$. $f(X)$ является подмножеством кодового домена $Y$. Итак, мы пишем $f: X \to Y$. Например, все возможные входы и выходы в вашем уравнении — действительные числа (давайте просто примем это для удобства), поэтому мы пишем $f: \mathbb R_{> 0} \to \mathbb R$. 92 : y = \sqrt{x} \right\}. $$
Видите? Функция $f$ — это множество, которое содержит не только все $y$, но и все возможные $x$.
Таким образом, $f(x)$ или $\sqrt{x}$ — это не функция, а значение $f$ в точке $x$.
Прежде всего, я думаю, что кратко ответил на ваш вопрос. Если вы хотите узнать больше о функциях, проверьте бинарных отношений , которые, я думаю, написаны в начале большей части математического анализа или реального анализа.
$\endgroup$ 92=х$.
$\endgroup$
алгебраическое предварительное исчисление — График $\sqrt { x } $
спросил
Изменено 3 года, 11 месяцев назад
Просмотрено 572 раза
$\begingroup$
Почему график идет только вправо и вверх? Не будут ли также отрицательные значения y? Так как, например, $\sqrt{4}$ равно $2$ и $-2$
- алгебра-предварительное исчисление
$\endgroup$
2
$\begingroup$
График $y=\sqrt{x}$ идет только вверх, так как:
- отрицательные значения $x$ не допускаются
- отрицательные значения $y$ не допускаются (поскольку $\sqrt{x}$ никогда не может быть отрицательным)
Далее: $\sqrt{4}=2$, но $\sqrt{4}\ne-2$.
2 = x$ или, в одном случае, $f(x) = \sqrt x$, как совершенно хорошую функцию, которая двузначный на $x > 0$.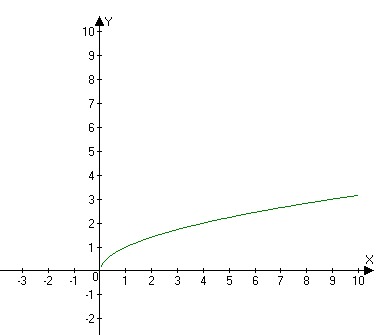
Но когда мы фиксируем выбор неотрицательного корня, мы получаем вполне определенную (непрерывную и т. д.) функцию из $[0,\infty)$ в $\mathbf{R}$.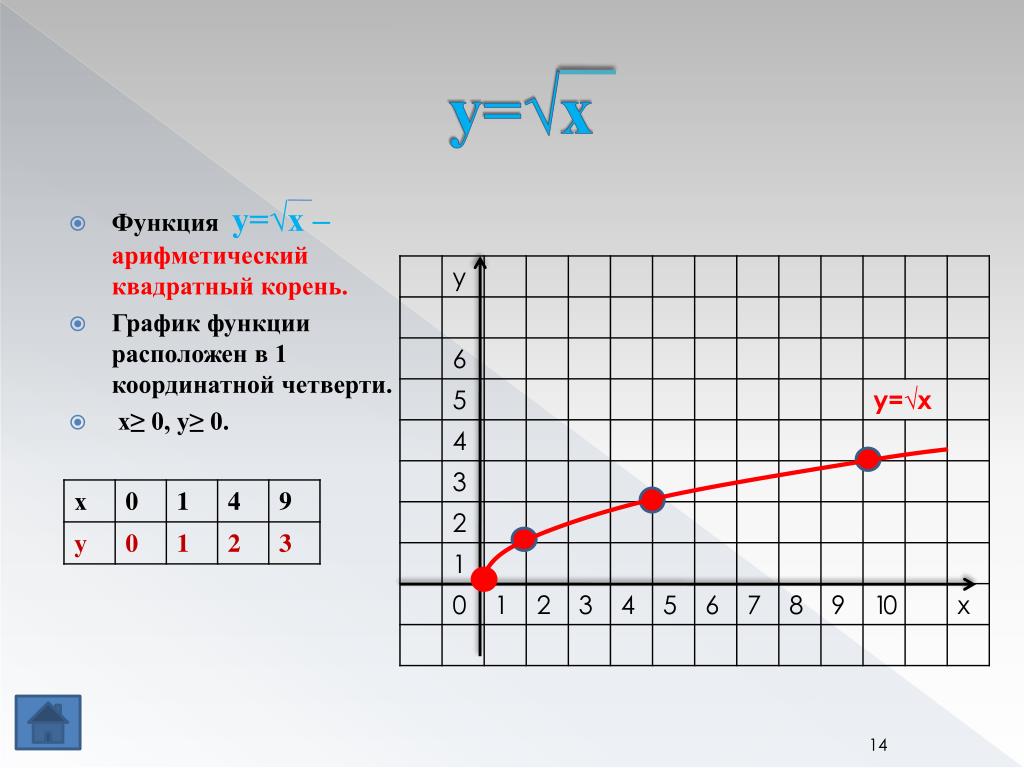
Leave A Comment