Задание 7 ЕГЭ по математике базового уровня 2023

Если задание выполнено на отлично, то сможешь получить 1 первичный балл.

На решение отводится примерно 8 минут.

Чтобы решить задание 7 по математике базового уровня нужно знать:

  • Линейное уравнение: ax + b =0
  • Квадратное уравнение: ax2 + bx + c = 0.
  • Алгоритм решения квадратного уравнения:
  1. Найти дискриминат по формуле D = b2 — 4ac
  2. Корни вычисляются по формулам:
    a) D b) D = 0, x = -\frac{b}{2a}
    c) D > 0, x = \frac{-b \pm\sqrt{D}}{2a}
  3. Свойства корней
  4. Свойства логарифмов

 

Таблица кубов натуральных чисел от 10 до 99 и степеней чисел 2 и 3
n12345678910
n31827641252163435127291000
2n2481632641282565121024
3n3927812437292187656119 68359 049

Could not load xLike class!

Найдите корень уравнения log2(x — 3) = 6

Обсуждение

Решите уравнение \frac{1}{2x-11}=\frac{-5}{x}. {3-4x}=\frac{1}{49}.

Обсуждение

Найдите корень уравнения \log_{0,2}(8x+5)= \log_{0,2}21.

Обсуждение

Начать

Задание 7 из ЕГЭ по математике (профиль)

Все для самостоятельной подготовки к ЕГЭ

Зарегистрироваться

Русский язык Математика (профильная) Обществознание Физика История Биология Химия Английский язык Информатика Литература

Задания Варианты Теория

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18

За это задание вы можете получить 1 балл на ЕГЭ в 2023 году

Разбор сложных заданий в тг-канале:

Посмотреть

Задача 1

На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-5;8)$. Найдите точку экстремума функции $f(x)$, принадлежащую отрезку $[-3;7]$.

Задача 2

На рисунке изображён график функции $y=F(x)$, которая является первообразной для функции $y=f(x)$. Найдите площадь под графиком функции $y=f(x)$ на отрезке $[2; 6]$.

Задача 3

На рисунке изображён график $y=f'(x)$ производной функции $f(x)$. Найдите абсциссу точки, в которой касательная к графику $y=f(x)$ параллельна оси абсцисс или совпадает с ней.

Задача 4

На рисунке изображён график $y=f'(x)$ производной функции $f(x)$. Найдите абсциссу точки, в которой касательная к графику $y=f(x)$ параллельна прямой $y=2x+2$ или совпадает с ней.

Задача 5

На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Задача 6

На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;6)$. 2+53t+161$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите её с…

1 2 3 4 5 … 7

Задание 7 ЕГЭ по математике проверяет способность решать задачи с прикладным содержанием. Этот блок охватывает огромное количество тем, оценивает степень усвоения материала нескольких лет обучения и дисциплин, среди которых арифметика, алгебра и другие.

Под номером 7 экзаменуемому может попасться решение линейного уравнения. Представлено оно будет, например, в виде формулы, по которой рассчитывается скорость транспортного средства, исходя из времени, проведённого в пути, и пройденного расстояния. Экзаменуемому будет нужно найти расстояние при заданных значениях скорости и времени. Ещё одна часто встречаемая подтема «Квадратные и степенные уравнения и неравенства» имеет в своей основе физические мини-задачи. В этом блоке будут примеры формул скорости падения тела с высоты, уменьшения столпа воды в резервуаре в то время, как включен кран на дне сосуда. Многие примеры посвящены ускорению и торможению автомобилей. Ещё есть версии, нацеленные на решение экономических вопросов. Экзаменуемым предлагается высчитать единицы купленного товара при увеличении спроса в геометрической прогрессии.

Упражнения про траекторию движения мячей и шаров, а также о движении по плоскости под углом проверяют знания по тригонометрии. Траектория тел, дистанция от наблюдателя до тела, удаляющегося за горизонт по выпуклой орбите нацелены на прикладное применение иррациональных выражений. Есть в 7 задании и подпункт «Разные задачи». В него составители тестов могут поместить любые мини-задачи на решение всех типов заданий из школьной программы. Выпускники прошлых лет чаще всего сталкивались с упражнениями для вычислений читаемости различных изданий. Цель могла формироваться как прямо («Рассчитайте рейтинг интернет-СМИ»), так и от противного («Вычислите одну из переменных, при которой рейтинг СМИ будет равен 1»).

Теория к заданию 7 по математике (профиль): Производная. Дифференцирование, физический смысл производной

<< Задание 6

Задание 8 >>

Популярные материалы

Составим твой персональный план подготовки к ЕГЭ

Дизайн тестов по математике — New Meridian

Суммативное оценивание по математике доступно в 3–8 классах и старшей школе. Учащиеся решают многошаговые математические задачи, требующие рассуждений и решения реальных ситуаций. Это требует от учащихся математических рассуждений, понимания величин и их взаимосвязей для решения реальных проблем и демонстрации своего понимания.

Многие предыдущие оценки были сосредоточены в основном только на механических процедурах.

Существуют документы со спецификациями тестов, в том числе схемы оценивания высокого уровня и таблицы с доказательствами, чтобы помочь преподавателям и широкой общественности лучше понять структуру итоговых оценок штата. Оценки включают как полную форму New Meridian, так и краткие формы.

Дескрипторы уровня успеваемости описывают, что должен уметь продемонстрировать типичный учащийся на каждом уровне, исходя из его/ее владения стандартами для своего класса.

Схема высокого уровня математики определяет общее количество заданий и/или предметов для оценки любого заданного класса/курса, типы заданий и количество баллов по каждому из них.

  • Схема высокого уровня по математике — полная форма
  • Схема высокого уровня математики – краткая форма

Структура экзамена по математике определяет структуру экзамена по математике, включая количество разделов, время и назначение калькулятора для каждого модуля.

  • Структура отдела оценки математики – Полная форма
  • Структура отдела оценки математики – краткая форма

Документ структуры утверждений определяет основное утверждение оценок по математике, а также четыре дополнительных утверждения, в которых будет измеряться успеваемость учащихся.

  • Структура требований по математике

Заявление о доказательствах Таблицы и Заявления о доказательствах описывают знания и навыки, которые элемент оценивания или задание выявляет у учащихся. Они напрямую связаны с Common Core State Standards и подчеркивают их достижения, особенно в отношении последовательного характера стандартов.

Заявления о доказательствах включают информацию о «Пояснениях, ограничениях и акцентах», связанных с «Математическими практиками» и «Обозначениями калькуляторов».

Заявление о доказательствах Документы

  • Математика 3 класс Заявление о доказательствах
  • Математика 4 класс Заявления о доказательствах
  • Математика 5 класс Заявления о доказательствах
  • Математика 6 класс Заявления о доказательствах
  • Математика 7 класс Заявления о доказательствах
  • Математика 8 класс Доказательства
  • Математическая алгебра I Заявления о доказательствах
  • Математическая алгебра II Заявления о доказательствах
  • Заявления о доказательствах математики и геометрии
  • Математика I Доказательства
  • Математика II Доказательства
  • Математика III Доказательства Заявления

Дескрипторы уровня успеваемости по математике – классы 3–11

Результаты представлены в соответствии с пятью уровнями успеваемости, которые определяют знания, навыки и практические навыки, которые учащиеся могут продемонстрировать:

  • Уровень 1: еще не оправдал ожиданий
  • Уровень 2: частичное соответствие ожиданиям
  • Уровень 3: приблизились к ожиданиям
  • Уровень 4: Оправдал ожидания
  • Уровень 5: Превзошел ожидания

Дескрипторы уровня успеваемости (PLD) показывают, что должен уметь продемонстрировать типичный учащийся на каждом уровне, исходя из его/ее владения стандартами для своего класса.

В математике уровни успеваемости на каждом уровне обучения записываются для каждого из четырех подпунктов оценки:

  • Основной контент
  • Дополнительный и вспомогательный контент
  • Рассуждение
  • Моделирование

Уровни производительности в каждой области требований различаются по ряду факторов, согласующихся с включением в Common Core стандартов как для математического содержания, так и для математических практик, а также для концепции когнитивной сложности для математики.

Дескрипторы уровня успеваемости по группам классов

  • Дескрипторы уровня успеваемости по математике: 3-5 классы
  • Дескрипторы уровня успеваемости по математике: 6-8 классы
  • Дескрипторы уровня успеваемости по математике: средняя школа
  • Дескрипторы уровня успеваемости по математике – краткая форма: 3–5 классы
  • Дескрипторы уровня успеваемости по математике – краткая форма: 6–8 классы
  • Дескрипторы уровня успеваемости по математике — краткая форма: средняя школа

Практический тест TExES Math 7-12 и руководство

Практический тест TExES Math 7-12

Добро пожаловать на нашу страницу практического теста и подготовки TExES Mathematics 7-12. На этой странице мы описываем предметные области и ключевые концепции экзамена TExES Math 7-12. Это бесплатный ресурс, который мы предоставляем, чтобы вы могли увидеть, насколько вы готовы к официальному экзамену.

В то время как в этом бесплатном руководстве описываются компетенции и предметные области, полученные на экзамене, наше платное учебное пособие TExES Math 7-12 охватывает ВСЕ концепции, которые вам нужно знать, и создано для обеспечения вашего успеха! Наше онлайн-руководство по TExES Math 7-12 содержит учебные материалы, ориентированные на тесты, с использованием интерактивных пособий, видео, карточек, викторин и практических тестов.

Пройду ли я, используя эту бесплатную статью? Смогу ли я пройти, используя ваше платное учебное пособие?

Если вы воспользуетесь этим руководством и самостоятельно изучите ключевые понятия экзамена TExES Math 7-12, возможно, вы его сдадите, но зачем рисковать? С нашим платным учебным пособием мы гарантируем, что вы пройдете.

Еще не готовы начать учиться? Это нормально. Продолжайте читать, а когда будете готовы, пройдите наши тренировочные тесты TExES Math 7-12.

В этой статье мы рассмотрим:

  • Texes Math 7-12 Информация о тесте
  • Texes Math 7-12 Ключевые концепции, чтобы узнать

Texes Matematics 7-12 Информация о тестировании

The Texes Mathematics 7-12. Экзамен 7-12 предназначен для оценки того, обладает ли начинающий учитель в штате Техас необходимыми знаниями и способностями для преподавания математики в седьмом-двенадцатом классах.

Стоимость:

$116

Подсчет очков:

Диапазон очков: от 100 до 300. Для прохождения необходимо набрать 240 очков.

Проходной балл:

Согласно отчету TEA за 2016–2021 гг., в 2019–2020 гг. процент сдавших экзамены составил 65%.

Время обучения:

Чтобы пройти тест, вы должны разбить темы теста на свои сильные и слабые стороны. Дайте себе достаточно времени для работы над каждой темой, пока не почувствуете себя уверенно в большинстве тем. Составьте учебный план с подробным описанием времени, необходимого для изучения каждой темы, и дней, в которые вы планируете это делать.


Что испытуемые хотели бы знать:

  • Предоставляется экранный лист с определениями и формулами.
  • Администратор теста предоставит лист бумаги для заметок.
  • Вы должны принести свой собственный графический калькулятор. Утвержденные калькуляторы можно найти здесь.
  • Вы должны угадать, если не знаете ответ, вы не наказаны за неправильные ответы.
  • Используйте учебные материалы для подготовки к экзамену.
  • Принесите два оригинала действительных документов, удостоверяющих личность. Вы можете просмотреть дополнительную информацию о политиках тестирования здесь.

Информация и снимки экрана получены с веб-сайта National Evaluation Series:

https://www. tx.nesinc.com/PageView.aspx?f=GEN_Tests.html

Попробуйте бесплатную предварительную версию TExES (235) Учебное пособие сегодня!

Попробуй перед покупкой

TExES Math 7-12 Ключевые понятия, которые необходимо знать

Экзамен состоит из шести областей:

  • Понятия чисел (14%)
  • Закономерности и алгебра (33%)
  • Геометрия и измерения (19%)
  • Вероятность и статистика (14%)
  • Математические процессы и перспективы (10%)
  • Обучение математике, обучение и Оценка (10%)

Понятия числа


Домен понятия числа содержит около 14 вопросов. Эти вопросы составляют 14% всего экзамена.

Эту область можно четко разделить на 3 компетенции:

  • Действительная система счисления
  • Комплексная система счисления
  • Понятия и принципы теории чисел

Давайте поговорим о концепции, которую вы, скорее всего, встретите на тесте.

Подмножества системы счисления

Образцы и алгебра


В области Образцы и алгебра содержится около 3 вопросов. Эти вопросы составляют 33% всего экзамена.

Эту область можно четко разделить на 7 компетенций:

  • Образцы
  • Функции, отношения и их графики
  • Линейные и квадратичные функции
  • Полиномиальные, рациональные, радикальные, абсолютные значения и логарифмические функции
  • 2 9 Функции
  • Тригонометрические и круговые функции
  • Исчисление

Вот некоторые концепции, которые вы увидите на тесте.

Сложные проценты

Для расчета непрерывных сложных процентов используйте следующую формулу: После t лет остаток A на счете с основной суммой P и годовой процентной ставкой r определяется уравнением:


основная сумма P – сумма на счете на начало периода. Ставка r должна быть записана в виде десятичной дроби. Например, найдите накопленную стоимость инвестиции в размере 4000 долларов США в течение 8 лет при процентной ставке 3,4%, непрерывно начисляемой на сложные проценты.


Нахождение обратных функций


Решение квадратных уравнений

Квадратные уравнения — это уравнения, в которых переменная имеет степень 2.

Давайте решим квадратное уравнение по факторингу; однако это уравнение можно решить только алгебраически, используя квадратичную формулу или построив график. Будем решать по квадратной формуле.

Чтобы использовать этот метод, сначала поместите уравнение в формат

x²+ bx + c = 0. Для этого вычтите 2 из обеих частей уравнения:

5x²+ x – 2 = 0

Теперь мы можем видеть, что a = 5, b = 1 , и с = -2.

Подставим эти коэффициенты в квадратную формулу:

Геометрия и измерения


В области геометрии и измерений около 19 вопросов. Эти вопросы составляют 19% всего экзамена.

Эту область можно четко разделить на 4 компетенции:

  • Измерение
  • Евклидова геометрия как аксиоматическая система
  • Результаты, использование и приложения евклидовой геометрии
  • Координатная, трансформационная и векторная геометрия
    • .

    Нахождение длины дуги

    Чтобы найти длину дуги окружности, нам нужно определить отношение всей окружности, которую она охватывает. Формула длины окружности 2???? r , где r — длина окружности; следовательно, длина дуги пропорциональна этому. Длина дуги = 2???? r C360°, где C — мера центрального угла в градусах.

    Посмотрите на круг внизу. Какова длина дуги дуги до н.э. ?


    Соотношения углов

    Соотношения углов помогают нам найти недостающие углы, когда нам дают диаграмму, часто включающую параллельные и пересекающиеся линии.

    Некоторыми важными отношениями углов являются дополнительные, дополнительные, вертикальные углы, альтернативные внутренние углы и альтернативные внешние углы. Дополнительные углы — это углы, сумма мер которых равна 180 градусам. Если углы расположены рядом друг с другом, они образуют прямую линию. Дополнительные углы — это углы, сумма мер которых равна 90 градусам. Если углы расположены рядом друг с другом, они образуют прямой угол. Например, если ∡a=48° и ∡b=42°, то угол a и угол b дополняют друг друга, так как в сумме они составляют 90°. Вертикальные углы противоположны друг другу по разные стороны от двух пересекающихся прямых. Вертикальные углы всегда конгруэнтны (имеют одинаковую меру).

    Кроме того, угол a и уголок d являются дополнительными, как и угол a и уголок b . Другими дополнительными парами являются: Угол b и угол c Угол c и угол d Секущая — это прямая, пересекающая по крайней мере две другие прямые. образуют альтернативные углы. Альтернативные внутренние углы находятся на противоположных сторонах секущей, но внутри двух линий, пересекаемых секущей.


    *ПРИМЕЧАНИЕ: Если две линии, пересекаемые секущей, параллельны друг другу, то внутренние углы всегда равны.

    *Аналогичным образом параллельные внешние углы конгруэнтны, если две прямые, пересекаемые секущей, параллельны. Это углы на внешней стороне двух линий, но противоположные друг другу. Следовательно,

    Угол e и угол h равны, так как они являются альтернативными внешними углами. Уголок г и угол f также являются альтернативными внешними углами и, следовательно, равны.

    Теорема Пифагора

    Теорема Пифагора используется для нахождения недостающей стороны прямоугольного треугольника.


    For the right triangle, where a and b are the shorter sides of the triangle, and c is the hypotenuse, then a²  +  b ² =  c ² . Пример 1: Предположим, мы знаем, что одна сторона прямоугольного треугольника равна 10 см, а гипотенуза треугольника равна 26 см. Найдите оставшуюся сторону.

    Пусть a = 10 см и c = 26 см. Then we will use the Pythagorean Theorem to find b : a²  +  b ² =  c ² 10²  +  b ²  =  26 ²  b²  =  26 ²  –  10 ²  =   576 ​​ b = √ 576  =  24

    Therefore, the remaining side of the треугольник 24 см.

    Пример 2: Предположим, что два человека начинают идти из одной и той же точки. Через 1 час человек А прошел 4,8 мили строго на север. Человек Б прошел 3,2 мили строго на восток. Найдите расстояние между ними в этот момент.

    Поскольку два человека идут под прямым углом друг к другу, мы можем применить теорему Пифагора. В этом случае расстояние между человеком А и человеком Б равно гипотенузе прямоугольного треугольника.


    Пусть a = 2,8 и b = 3,2. Then a²  +  b²  =  c ² gives:2.8 ²  +3.2 ²  =c ² 18.08 =c ² c  ≈4.25

    Следовательно, человек А и человек Б находятся на расстоянии примерно 4,25 мили друг от друга через 1 час.

    Вероятность и статистика


    Область вероятности и статистики содержит около 14 вопросов. Эти вопросы составляют 14% всего экзамена.

    Эту область можно четко разделить на 3 компетенции:

    • Анализ и представление данных
    • Вероятность
    • Вероятность, выборка и статистика

    Давайте поговорим о некоторых концепциях, которые вы, скорее всего, встретите на тесте.

    Показатели центральной тенденции

    Показатели центральной тенденции помогают нам определить, как распределяются данные. Ниже мы рассмотрим несколько показателей центральной тенденции.

    Среднее значение набора данных — это среднее значение набора данных. Это можно найти, сложив все значения и разделив их на общее количество значений.

    Режим набора данных — это значение, которое чаще всего встречается в наборе данных. В наборе данных может быть более одной моды, если несколько значений встречаются чаще всего.

    Медиана набора данных — это среднее значение в наборе. Если имеется четное количество точек данных, точной середины не будет. В этом случае медиана находится путем взятия среднего значения двух точек данных, ближайших к середине. Например, предположим, что возраст группы из десяти учащихся был собран и указан ниже:

    9, 11, 13, 11, 8, 7, 13, 9, 9, 12

    Чтобы найти среднее значение этого набора данных, сложите все значения и разделите на общее количество значений.


    Чтобы найти моду и медиану набора данных, полезно переупорядочить набор от меньшего к большему.

    7, 8, 9, 9, 9, 11, 11, 12, 13, 13

    Теперь мы можем видеть, что мода набора данных равна 9, так как 9 встречается 3 раза, что больше любых других данных точка.

    Поскольку набор данных содержит четное количество значений, в середине находятся два значения: 9 и 11. Чтобы найти медиану, необходимо усреднить 9 и 11; следовательно, медиана набора данных равна 10.

    Выброс — это точка данных, которая находится далеко за пределами нормального диапазона набора данных. Это далеко от остальных точек данных. Например, предположим, что некоторые дневные высокие температуры в мае месяце для определенной области приведены ниже в градусах Фаренгейта:

    66, 56, 61, 45, 48, 52, 23, 66, 53, 58, 59

    Переупорядочение дает 23, 45, 48, 52, 53, 56, 58, 59, 61, 66, 66

    Среднее значение этих данных равно (66 + 56 + 61 + 45 + 48 + 52 + 23 + 66 + 53 + 58 + 59) /11=53,364

    Режим данных 66, так как это значение встречается дважды.

    Медиана равна 56, так как это среднее значение.

    Однако температура 23 градуса является исключением, потому что разница между ней и любой другой температурой составляет 22 градуса. Следовательно, мы можем удалить этот выброс из данных и снова вычислить среднее значение, моду и медиану, чтобы получить лучшее описание основных тенденций этого набора данных.

    45, 48, 52, 53, 56, 58, 59, 61, 66, 66

    После того, как температура 23 отброшена, новое среднее значение равно 56,4. Режим данных в этом случае все тот же, поскольку 66 — единственная температура, которая встречалась более одного раза. Медиана теперь представляет собой среднее значение 56 и 58, что составляет 57 градусов, поскольку теперь имеется только десять точек данных.

    Точечная диаграмма

    Точечная диаграмма представляет собой график, составленный из точек на плоскости x – y , который показывает взаимосвязь между двумя переменными x и и .

    Если количество точек увеличивается по мере увеличения x , то существует положительная корреляция между двумя переменными. Например, существует положительная корреляция между температурой на улице и продажами мороженого, поскольку чем жарче, тем выше продажи мороженого. Если при увеличении x точки уменьшаются, то между двумя переменными существует отрицательная корреляция. Например, обычно существует отрицательная корреляция между количеством пропусков занятий учащегося и его оценкой, поскольку по мере увеличения количества пропусков его оценка обычно снижается.0278 x увеличивается, то корреляция между переменными отсутствует. Ниже приведены некоторые примеры диаграмм рассеивания:


    Найдя линию наилучшего соответствия на диаграмме рассеивания, можно сделать прогноз относительно будущих точек данных.

    Например, линия наилучшего соответствия показана для диаграммы рассеяния ниже:


    Используя эту линию, мы можем оценить, что при температуре 21 градус Цельсия продажи мороженого составляют около 460 долларов.

    Математические процессы и перспективы


    В области математических процессов и перспектив около 10 вопросов. Эти вопросы составляют 10% всего экзамена.

    Эту область можно четко разделить на 2 компетенции:

    • Математическое мышление и решение проблем
    • Связи и общение

    Взгляните на эти концепции, которые, скорее всего, появятся в тесте.

    Процесс решения проблем

    Процесс решения проблем можно разбить на этапы по-разному, но основная идея одна и та же, как бы вы ее ни формулировали.

    1. Перечитайте задачу. Определите, о чем идет речь.
    2. Определите, какую информацию вы уже знаете, найдя ключевые детали проблемы.
    3. Выберите стратегию решения проблемы.
    4. Решить проблему.
    5. Проверьте свой ответ и убедитесь, что он имеет смысл в контексте.

    Некоторые стратегии решения задач по математике включают работу в обратном направлении, поиск закономерности, оценку, предположение и проверку, а также рисование картинки.

    Давайте вместе решим проблему.

    Пенни купила печенье на распродаже выпечки. Она съела 3 из них и дала 2 из них своей сестре. После того, как она разделила остаток поровну с братом, у нее осталось 8 печений. Со сколькими печеньками она начала?

    Эту проблему можно решить, действуя в обратном направлении от конечного количества файлов cookie, которые у нее есть в конце этого процесса. Она заканчивает с 8 печеньками, что составляет половину того, что у нее было до того, как она поделилась со своим братом. На тот момент у нее было 16 печенек. Она дала 2 печенья своей сестре. Итак, до этого у нее было 18 печенек. Сначала она съела 3 печенья; следовательно, она начала с 21 печенья.

    Угадай и проверь хорошо работает с поиском корней полиномиальных функций. Чтобы определить, является ли значение корнем функции, вы должны сделать разумное предположение, а затем применить синтетическое деление, чтобы определить, равен ли остаток от деления 0. Если да, то вы нашли корень.

    Формальное и неформальное рассуждение

    Формальное рассуждение, также называемое дедуктивным рассуждением, начинается с предпосылок, истинность которых известна, и продолжается до логического завершения.

    Например, люди дышат воздухом. Дэвид — человек; следовательно, Давид дышит воздухом.

    Неформальное рассуждение, также называемое индуктивным рассуждением, начинается с конкретных наблюдений и объединяет их для получения широких обобщений.

    Например, вы заметили, что Джулия опаздывает на работу. Джулия — подросток; следовательно, вы заключаете, что подростки безответственны.

    Выводы, сделанные с помощью индуктивных рассуждений, иногда могут быть ошибочными, но этот тип рассуждений по-прежнему важен. Индуктивное рассуждение чаще всего используется для формирования гипотез, которые затем можно проверить с помощью научного метода.

    Математическое обучение, обучение и оценка


    Математическое обучение, обучение и оценка содержит около 10 вопросов.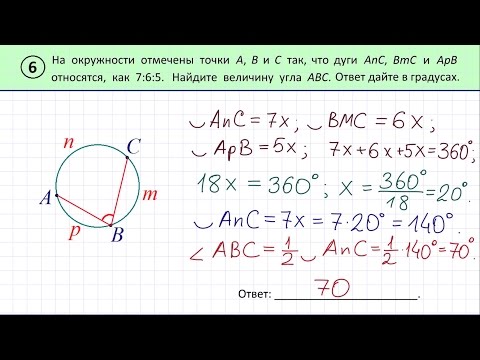 Эти вопросы составляют 10% всего экзамена.

    Эту область можно четко разделить на 2 компетенции:

    • Изучение и преподавание математики
    • Оценка математики

    Давайте поговорим о некоторых понятиях.

    Обучение, основанное на запросах

    Обучение, основанное на запросах, заключается в том, чтобы пробудить любопытство учащегося посредством исследований и открытий. Этот вид обучения не проводится под руководством инструктора; вместо этого учитель помогает облегчить обучение, тщательно выстраивая леса. В математике это может выглядеть как работа в небольших группах для изучения проблемы и обмена идеями друг с другом, или это может включать в себя постановку проблемы учителем и проведение мозгового штурма всем классом. с решением. Например, учитель может представить приведенную ниже диаграмму и попросить учащихся сделать свои собственные наблюдения и задать свои вопросы о рисунках.


    Учащиеся могут задавать такие вопросы, как: «Какая часть каждой фигуры закрашена?» «Как найти площадь каждой из заштрихованных областей?» «Треугольник равносторонний?» Учитель может использовать стратегии построения лесов и давать учащимся подсказки (при необходимости), чтобы помочь ответить на эти и другие вопросы.