Углы авс четырехугольника авсд относятся как 1 2 3 найдите угол д: Углы A, B и C четырехугольника ABCD относятся как 1 : 2 : 3. Найдите… — Задание 6 ЕГЭ по математике (Планиметрия)

параллелограмм, прямоугольник, ромб, квадрат, трапеция – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Вопросы

1. В выпуклом многоугольнике три угла по 80 градусов, а остальные – 150 градусов. Сколько углов в выпуклом многоугольнике?

2. В выпуклом четырехугольнике ABCD диагонали АС = 12 и BD = 10. Найти периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

    

3. Дан выпуклый четырехугольник АВСД. \circ\). Найдите градусную меру угла \(∠Д \)?

4. Какие из наборов углов могут быть углами четырёхугольника?

5. Найдите большую сторону четырехугольника, если его периметр равен 66 см, а одна из сторон больше второй на 8 см и на столько же меньше третьей, а четвертая — в три раза больше второй.

6. Найдите наибольший угол выпуклого четырехугольника, если его углы пропорциональны числам 1, 2, 4, 5.

7. Найдите периметр четырехугольника ABCD, если АВ = 12 см, ВС = 17 см, CD = 5 см и AD = 14 см.

8. Найдите периметр четырехугольника, если АВ = 16 см, ВС = 12 см, СД = 8 см и АД = 18 см.

9. Расстояния от середины стороны АD выпуклого четырехугольника ABCD до середин сторон АВ и CD равны соответственно 6 и 12. Найти длину большей диагонали четырехугольника ABCD.

    

10. Укажите пары противоположных сторон четырёхугольника.

     

11. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.

12. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?

13. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найти периметр прямоугольника, если его меньшая сторона равна 10.

14. В параллелограмме \(ABCD, \ AB=7, AD=3,sinA=\frac67\). Найдите большую высоту параллелограмма.

15. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.

16. Диагональ квадрата \(2\sqrt{8}\) см. Найдите сторону квадрата.

17. Диагональ ромба равна его стороне. Найдите меньший угол ромба.

18. Сторона прямоугольника относится к его диагонали, как 4: 5, а другая сторона равна 6.

    Числовое значение площади прямоугольника принадлежит промежутку

19. В прямоугольном треугольнике один из катетов равен 3, а котангенс прилежащего угла равен 0,75. Найдите гипотенузу.

20. Угол между диагональю и стороной ромба равен 30°. Найдите все углы ромба.

21. В окружность диаметром 10 см вписан квадрат АВСD. Найдите сторону квадрата.

22. АВСD – ромб. Угол А равен 36°. Найдите угол между ВD и DС.

23. Средняя линия трапеции равна 7 м, а одно из оснований больше другого на 4 м. 2\)

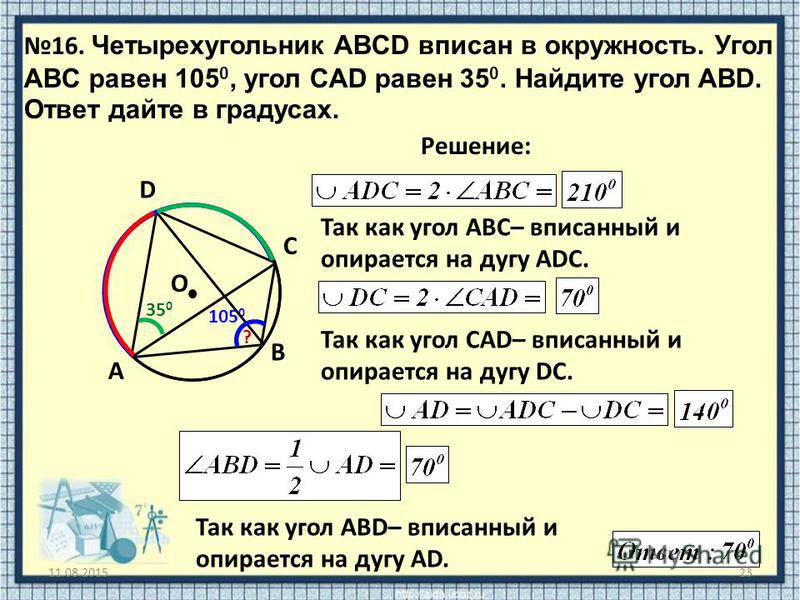
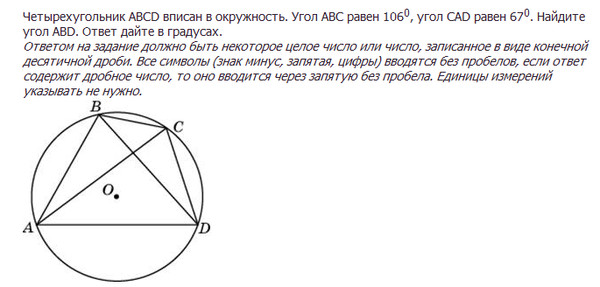
24. Около четырехугольника ABCD описана окружность. Его углы A, B, C относятся как 1 : 2 : 3. Найдите угол D. 

25. Диагональ параллелограмма образует с двумя его сторонами углы 24° и 46°. Найдите углы параллелограмма.
     

26. Периметр прямоугольной трапеции, описанной около окружности, равен 20 см, ее большая боковая сторона равна 6 см. Найдите радиус окружности.

             1) 2 см

             2) 4 см

             3) 10 см

             4) 14 см

27. Дан прямоугольник АВСD. Его диагонали пересекаются в точке О. АЕ и СF перпендикулярны ВD, угол СОD равен 30°, СF = 2 см. Найдите ВD.

28. В параллелограмме АВСD точка Е принадлежит АD, причем АВ = АЕ, угол ВЕА равен 70°. Найдите углы параллелограмма.

29. В четырехугольник ABCD вписана окружность, AB = 11 см, CD = 17 см. Найдите периметр четырехугольника.      

30. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 1: 2, считая от вершины тупого угла. Найдите смежные стороны параллелограмма, если его периметр равен 90 см.

31. Найдите периметр прямоугольника, вписанного в окружность с радиусом 13, если одна из его сторон равна 10.

32. Меньшая сторона прямоугольника равна 3,6 см. Угол между диагоналями равен 120°. Найдите диаметр описанной окружности.

33. В прямоугольнике перпендикуляры, проведенные из точки пересечения диагоналей к его сторонам, равны соответственно 3 см и 5 см. Найдите периметр прямоугольника.

34. Средняя линия трапеции, описанной около окружности, равна 5. Боковая сторона равна 6. Найдите вторую боковую сторону. 1) 3;     2) 4;     3) 5;      4) 6;      5) 7.

35. Найдите радиус окружности, вписанной в ромб со стороной 12 см и углом 30°.

36. Дан треугольник ABC. \(\angle\)C = 90°,  AC = BC = 12 см. Из точки M, взятой на AB, проведены прямые, параллельные катетам. Найдите периметр образовавшегося четырехугольника.

37. Четырехугольник ABCD вписан в окружность. Определите возможный вид четырехугольника ABCD.

Сообщить об ошибке

Измерение углов, связанных с окружностью

1. Углы, связанные с окружностью

Угол с вершиной в центре окружности называется
центральным.
Угол, вершина которого принадлежит окружности,
а стороны пересекают окружность, называется
вписанным.
Каждый центральный угол данной окружности
определяют дугу окружности, которая состоит из
точек окружности, принадлежащих этому углу.

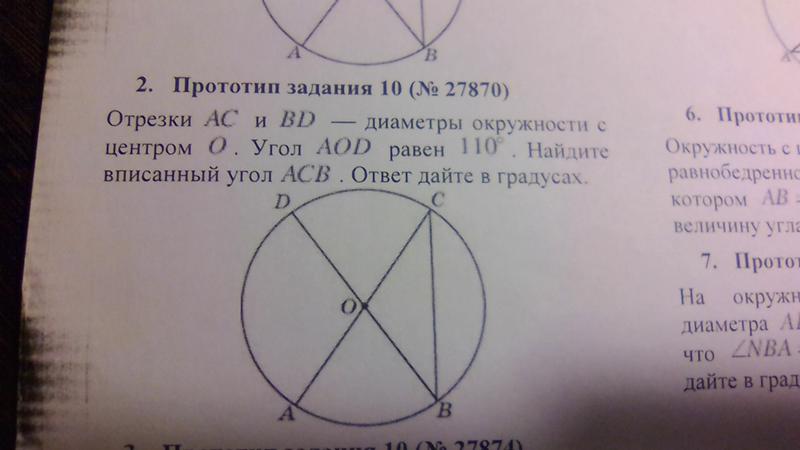
2. Вписанный угол

Теорема. Вписанный угол равен половине центрального
угла, опирающегося на ту же дугу окружности.
Вписанные углы, опирающиеся на одну и ту же дугу
окружности, равны.
Вписанный угол измеряется половиной дуги окружности.

3. Угол между касательной и хордой

Теорема. Угол, с вершиной на окружности, одна сторона
которого лежит на касательной, а вторая – пересекает
окружность, измеряется половиной дуги окружности,
лежащей внутри этого угла.

4. Угол с вершиной внутри окружности

Теорема. Угол, с вершиной внутри окружности,
измеряется полусуммой дуг, на которые опираются
данный угол и вертикальный с ним угол.

5. Угол с вершиной вне окружности

Теорема. Угол, с вершиной вне окружности, стороны
которого
пересекают
окружность,
измеряется
полуразностью дуг окружности, заключенных внутри
этого угла.

6. Угол с вершиной вне окружности

Теорема. Угол, с вершиной вне окружности, одна
сторона которого лежит на касательной к окружности, а
вторая сторона пересекает окружность, измеряется
полуразностью дуг окружности, заключенных внутри
этого угла.

7. Угол с вершиной вне окружности

Теорема. Угол, с вершиной вне окружности, стороны
которого лежат на касательных к окружности, измеряется
полуразностью дуг окружности, заключенных внутри
этого угла.

8. Упражнение 1

Чему равен вписанный угол, опирающийся на
диаметр окружности?
Ответ: 90о.

9. Упражнение 2

Найдите центральный угол AOB, опирающийся
на хорду AB, равную радиусу.
Ответ: 60о.

10. Упражнение 3

Угол ACB вписан в окружность. Градусные
величины дуг AC и BC равны 98о и 48о
соответственно. Найдите угол ACB.
Ответ: 107о.

11. Упражнение 4

Найдите вписанный угол, опирающийся на
1
дугу, которая составляет окружности.
6
Ответ: 30о.

12. Упражнение 5

Найдите вписанный угол, опирающийся на
дугу, которая составляет 10 % окружности.
Ответ: 18о.

13. Упражнение 6

Вписанный угол на 35 меньше центрального
угла, опирающегося на ту же дугу. Найдите
вписанный угол.
Ответ: 35о.

14. Упражнение 7

Центральный угол на 51о больше вписанного
угла, опирающегося на ту же дугу. Найдите
вписанный угол.
Ответ: 51о.

15. Упражнение 8

Под каким углом из точки C дуги окружности
видна стягивающая ее хорда, если дуга содержит
100о?
Ответ: 130о.

16. Упражнение 9

Под каким углом из точки дуги окружности
видна стягивающая ее хорда, если дуга
составляет одну треть окружности?
Ответ: 120о.

17. Упражнение 10

Угол ACB, величиной 50о, вписан в окружность.
Найдите градусную величину дуги ACB.
Ответ: 260о.

18. Упражнение 11

Вершины треугольника ABC, вписанного в
окружность, делят окружность на части,
градусные величины которых равны 100о, 120о и
140о. Найдите наименьший угол треугольника
ABC.
Ответ: 50о.

19. Упражнение 12

Сторона AB треугольника ABC равна 2 , радиус
описанной окружности равен 1. Найдите угол C.
Ответ: 45о.

20.

Упражнение 13Одна сторона треугольника равна радиусу
описанной
окружности.
Найдите
угол
треугольника, противолежащий этой стороне.
Ответ: 30о.

21. Упражнение 14

На рисунке угол ACB равен 30о, угол AEF равен
40о. Найдите угол BDF.
Ответ: 70о.

22. Упражнение 15

Углы ABC и BCD вписаны в окружность и равны
45о и 30о соответственно, S – точка пересечения
AD и BC. Найдите угол ASC.
Ответ: 75о.

23. Упражнение 16

Хорда CD пересекает диаметр AB окружности под
углом 60о. Градусная величина дуги AD равна 80о.
Найдите градусную величину дуги BC.
Ответ: 40о.

24. Упражнение 17

На рисунке угол A равен 40о, угол B равен 30о,
угол D равен 45о. Найдите угол EFC.
Ответ: 115о.

25. Упражнение 18

Стороны угла с вершиной C вне окружности
отсекают от окружности дуги A1B1, A2B2,
градусные величины которых равны 30о и 100о.
Найдите угол C.
Ответ: 35о.

26. Упражнение 19

Углы ABC и BCD вписаны в окружность и равны
20о и 50о соответственно, S – точка пересечения
прямых AB и CD. 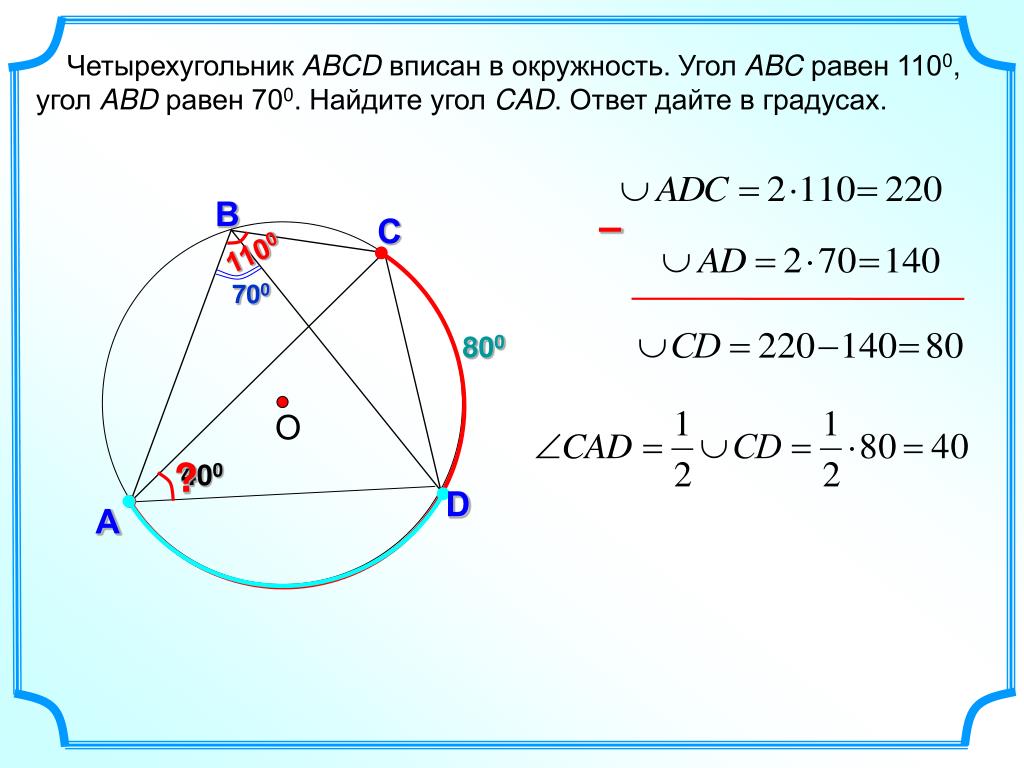Найдите угол ASC.
Ответ: 30о.

27. Упражнение 20

Стороны угла с вершиной C вне окружности отсекают от
окружности дуги AB1, AB2, градусные величины которых
равны 60о и 140о соответственно, CA – касательная.
Найдите угол C.
Ответ: 40о.

28. Упражнение 21

Через концы дуги в 60о проведены касательные,
пересекающиеся в точке C. Найдите угол ACB.
Ответ: 120о.

29. Упражнение 22

Хорда АВ стягивает дугу окружности в 44о.
Найдите углы, которые образует эта хорда с
касательными к окружности, проведенными
через ее концы.
Ответ: 22о.

30. Упражнение 23

Две равные окружности расположены таким
образом, что каждая из них проходит через центр
другой. Найдите угол, под которым видна их
общая хорда AB из центра O1 одной из
окружностей.
Ответ: 120о.

31. Упражнение 24

Острый вписанный угол опирается на хорду,
которая делит окружность на две части,
градусные величины которых относятся как 4 : 5.
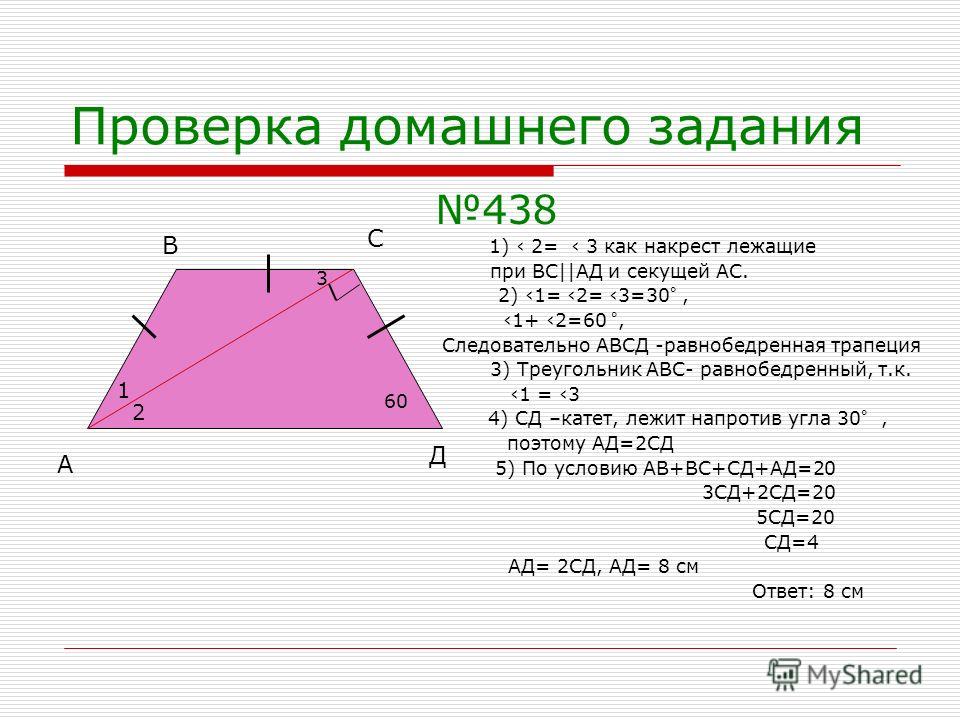
Найдите этот угол.
Ответ: 80о.

32. Упражнение 25

Точки А, В, С, расположенные на окружности c с
центром в точке O, делят эту окружность на три
дуги, градусные величины которых относятся
как 3 : 4 : 5. Найдите угол AOB.
Ответ: 90о.

33. Упражнение 26

Точки А, В, С, расположенные на окружности,
делят эту окружность на три дуги, градусные
величины которых относятся как 2 : 3 : 7.
Найдите больший угол треугольника АВС.
Ответ: 105о.

34. Упражнение 27

Окружность разделена точками A, B, C, D на
четыре части, градусные величины которых
относятся как 3:7:5:3. Найдите меньший угол
четырехугольника ABCD.
Ответ: 60о.

35. Упражнение 28

В четырехугольнике ABCD, вписанном в
окружность, угол A равен 75о, угол B равен 90о.
Найдите разность двух других углов.
Ответ: 15о.

36. Упражнение 29

Углы A и C вписанного в окружность пятиугольника
ABCDE равны 120о и 100о соответственно. 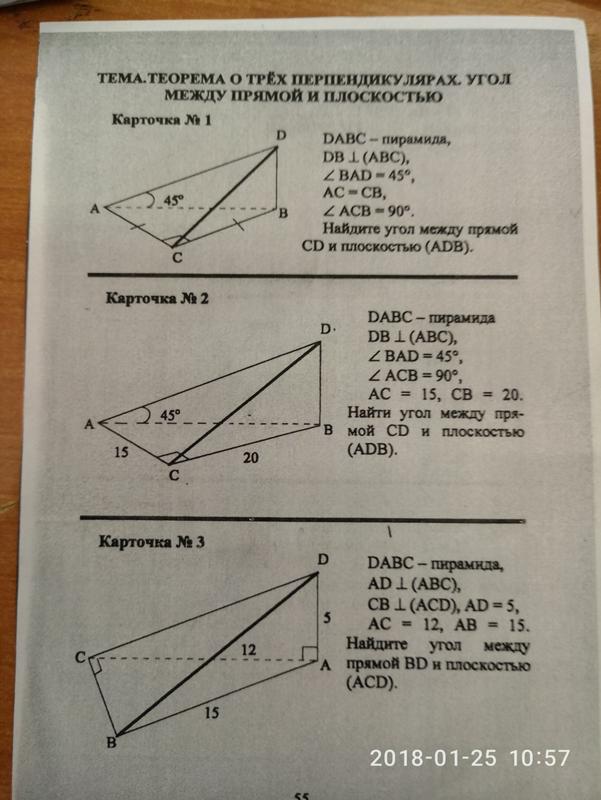Найдите угол
DBE.
Ответ: 40о.

37. Упражнение 30

На рисунке угол A равен 120о, угол C равен 110о.
Найдите угол E.
Ответ: 130о.

38. Упражнение 31

Хорда CD перпендикулярна радиусу OB
окружности и пересекает его в середине E.
Найдите градусную величину дуги BC.
Ответ: 60о.

39. Упражнение 32

Окружность разделена точками A, B, C, D на
четыре части, градусные величины которых
относятся как 3:7:5:3. Найдите угол между
диагоналями AC и BD четырехугольника ABCD.
Ответ: 80о.

40. Упражнение 33

Окружность разделена точками A, B, C, D на
четыре части, градусные величины которых
относятся как 1:2:3:4. Найдите угол между
прямыми AD и BC.
Ответ: 36о.

41. Упражнение 34

Из точки вне окружности проведены к ней две
касательные. Кратчайшее расстояние от этой
точки до окружности равно радиусу окружности.
Найдите угол между касательными.
Ответ: 60о.

42. Упражнение 35

В угол АСB вписана окружность.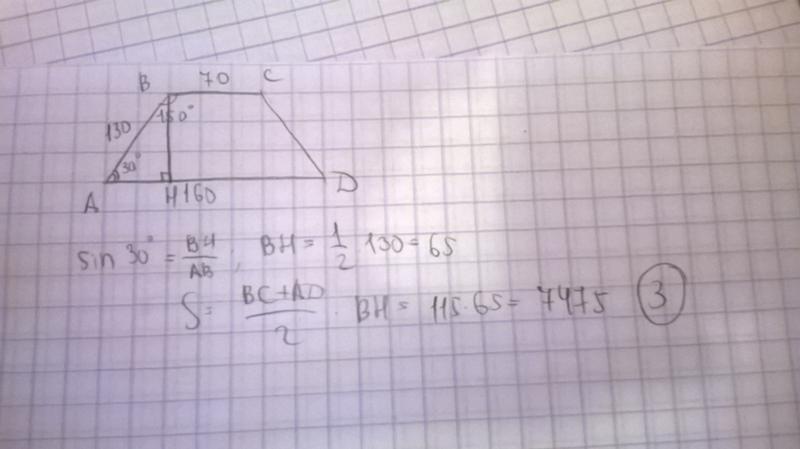 Точки касания
делят окружность на дуги, градусные величины
которых относятся как 3:2. Найдите величину
угла АCB.
Ответ: 36о.

43. Упражнение 36

В угол АСB, величиной 50о, вписана окружность.
Точки касания делят окружность на две дуги.
Найдите градусную величину наибольшей дуги
окружности, заключенной внутри угла ACB.
Ответ: 230о.

44. Упражнение 37

В угол АСB, величиной 45о, вписана окружность.
Точки касания делят окружность на две дуги.
Найдите
число,
выражающее
отношение
градусных величин меньшей и большей дуг
окружности, заключенных внутри угла ACB.
Ответ: 3:5.

45. Упражнение 38

Окружность разделена точками А, В, С на дуги,
градусные величины которых относятся как 11 :
3 : 4. Через точки А, В, С проведены касательные
до их взаимного пересечения. Найдите
наибольший угол образовавшегося треугольника
DEF.
Ответ: 80о.

46. Упражнение 39

Треугольник ABC вписан в окружность. Угол A
равен 40о, угол B равен 60о. Найдите угол между
касательной к окружности, проведенной через
вершину C и прямой AB.
Ответ: 20о.

47. Упражнение 40

Треугольник ABC вписан в окружность. Угол A
равен 40о, угол B равен 60о. Найдите угол между
касательными к окружности, проведенной через
вершины A и B.
Ответ: 20о.

48. Упражнение 41

Стороны четырехугольника ABCD касаются
окружности в точках, делящих эту окружность на
четыре части, градусные величины которых
относятся как 8:7:11:10. Найдите наименьший
угол четырехугольника ABCD.
Ответ: 70о.

49. Упражнение 42

Две окружности касаются внешним образом в
точке C, AB – их общая внешняя касательная, A и
B – точки касания. Найдите угол ACB.
Ответ: 90о.

50. Выполните задание в тетради и пришлите на проверку через электронный журнал

Все задачи должны быть с решением

Если углы ABC и D четырехугольника ABCD, взятые по порядку, относятся как 3764, то ABCD равен .

..

Перейти к

• Четырехугольники — упражнение 8.1
• Четырехугольники — упражнение 8.2
• Четырехугольники — упражнение 8.3
• Четырехугольники — упражнение 8.4

• Системы счисления
• Полиномы
• Координатная геометрия
• Линейные уравнения с двумя переменными
• Введение в геометрию Евклида
• Линии и углы
• Треугольники
• Четырехугольники
• Площади параллелограммов и треугольников
• Круги
• Конструкции
• Формула Герона
• Площади поверхности и объемы
• Статистика и вероятность

Главная > Образцовые решения NCERT Класс 9 Математика > Глава 8 — Четырехугольники > Четырехугольники — упражнение 8. 1 > Вопрос 6

Вопрос 6 Четырехугольники — Упражнение 8.1

Если углы A, B, C и D четырехугольника ABCD, взятые по порядку, относятся как 3:7:6:4, то ABCD является

(A) ромбом

(B) параллелограмм

(C) трапеция

(D) воздушный змей

Ответ:

(C) трапеция

Пояснение:

взятые по порядку, находятся в соотношении 3:7:6:4,

Имеем углы А, В, С и D = 3х, 7х, 6х и 4х.

Итак, сумма углов четырехугольника = 360o.

3x + 7x + 6x + 4x = 360o

⇒ 20x = 360o

⇒ x = 360 ÷ 20 =18o

Итак, углы A, B, C и D четырехугольника ABCD равны

2 3×18° = 54°,

∠B = 7×18° = 126°

∠C = 6×18° = 108°

∠D = 4×18° = 72°

AD и BC — две прямые, пересекаемые поперечной

CD

Сумма углов ∠C и ∠D по одну сторону от поперечной,

∠C +∠D =108o + 72o =180

Следовательно, AD|| BC

Итак, ABCD — четырехугольник, у которого одна пара противоположных сторон параллельна.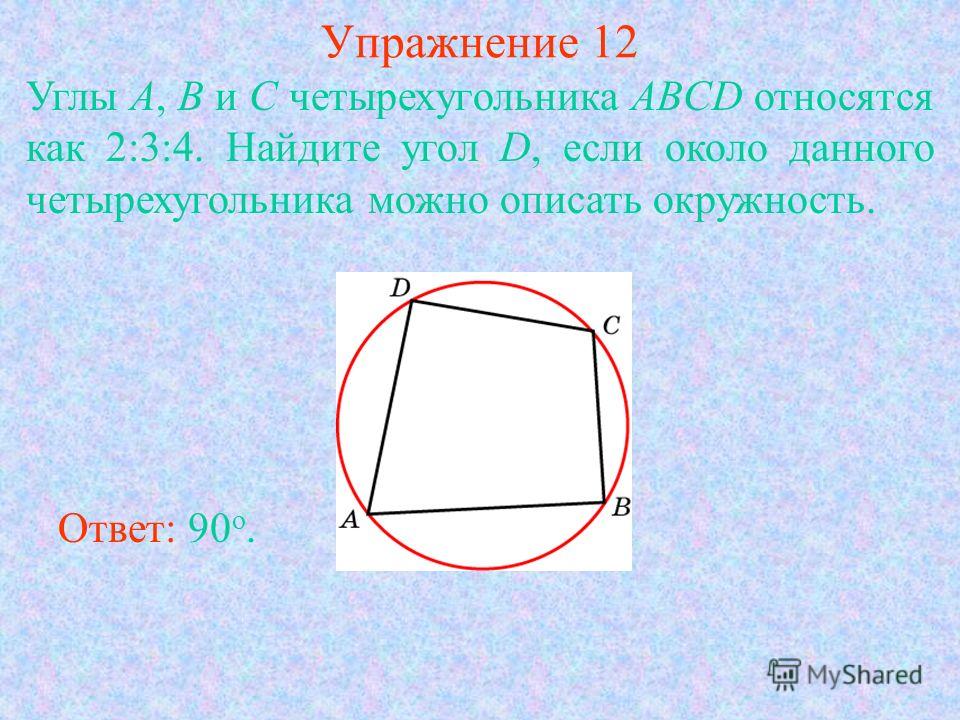

Значит, ABCD — трапеция.

Следовательно, вариант (С) является правильным ответом.

Связанные вопросы

Три угла четырехугольника равны 75°, 90° и 75°. Четвертый угол: (А) 90º (В) 95º (С) 105º (Г) 1…

Диагональ прямоугольника наклонена к одной из сторон прямоугольника под углом 25°. Острый угол между т…

ABCD — такой ромб, что ∠ACB = 40º. Тогда ∠ADB равно (A) 40º(B) 45º(C) 50º(D) 60º

Четырехугольник, образованный соединением середины сторон четырехугольника PQRS, взятого или…

Четырехугольник, образованный соединением середины сторон четырехугольника PQRS, взятого или. ..

Если биссектрисы ∠A и ∠B четырехугольника ABCD пересекаются друг с другом в точке P, ∠B и ∠C в точке Q, ∠…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Четырехестерные — упражнение 8.1

Четырехугородные. к геометрии Евклида

Прямые и углы

Треугольники

Четырехугольники

Площади параллелограммов и треугольников

Окружности

Построения

Формула Герона

Площади поверхностей и объемы

Статистика и вероятность

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Что такое четырехугольник? Определение, свойства, типы, примеры

Что такое четырехугольник?

Четырехугольник — это многоугольник, имеющий четыре стороны, четыре угла и четыре вершины. Слово «четырехугольник» происходит от латинских слов «quadri», что означает четыре, и «latus», что означает сторона.

Изображение выше является примером четырехугольника.

Родственные игры

Части четырехугольника

1. ∠A, ∠B, ∠C и ∠D — четыре угла четырехугольника ABCD
2. AB, BC, CD и DA — четыре стороны четырехугольника ABCD.
3. A, B, C и D — четыре вершины четырехугольника ABCD.
4. AC и BD — две диагонали четырехугольника ABCD.

Непримеры четырехугольников

Фигуры, не имеющие четырех сторон или четырех углов, изогнутые стороны или незамкнутые формы, не являются примерами четырехугольников.

Приведенные выше изображения не являются примерами четырехугольников.

Примеры четырехугольников из жизни

Примеров четырехугольников из жизни много: карты, шахматные доски, дорожные знаки и т. д.

Свойства четырехугольников

Некоторые свойства являются общими для всех четырехугольников. Вот эти свойства:

• У них четыре вершины.
• У них четыре стороны.
• Сумма всех внутренних углов равна 360°.
• У них две диагонали.
• Четырехугольник может быть правильным и неправильным. Правильный четырехугольник должен иметь 4 равные стороны и 4 равных угла, а его диагонали должны пересекаться пополам. Квадрат — единственный четырехугольник, удовлетворяющий всем этим условиям.

Типы Четырехугольников

Четырехугольники можно разделить на параллелограммы, квадраты, прямоугольники и ромбы. Квадрат, прямоугольник и ромб также являются параллелограммами.

Вот список типов четырехугольников с их названиями, изображениями и свойствами: 

Вогнутые и выпуклые четырехугольники

Вогнутые четырехугольники: В вогнутых четырехугольниках один внутренний угол больше 180°.

Четырехугольник называется вогнутым четырехугольником, если хотя бы одна диагональ, т. е. отрезок, соединяющий вершины, не является частью одной и той же области четырехугольника.

Выпуклые четырехугольники:  В выпуклых четырехугольниках каждый внутренний угол меньше 180°. Четырехугольник выпуклый, если отрезок, соединяющий любую из его двух вершин, лежит в одной области.

Периметр четырехугольника

Периметр четырехугольника — это длина его границы. Это означает, что периметр четырехугольника равен сумме всех сторон. Если ABCD — четырехугольник, то его периметр будет равен: AB + BC + CD + DA

Perimeter of quadrilateral ABCD = AB + BC + CD + DA

The formula for the perimeter of some of the common quadrilaterals is given below:

88

Quadrilateral Name	Perimeter
Rectangle	2 (длина + ширина)
квадрат	4 x Сторона
Rhombus	4 x Side
4 x
4 x
4 x
4. 0268
Воздушный змей	2 x сумма смежных сторон

Площадь четырехугольника

Площадь четырехугольника – это область, ограниченная всеми его сторонами. Формулы для нахождения площадей различных типов четырехугольников приведены ниже:

Решенные примеры на четырехугольнике

Пример 1. Найдите недостающий угол в данном четырехугольнике.

Решение:

Мы знаем, что сумма всех углов четырехугольника равна 360°.

Отсюда можно записать так:

х + 77° + 101° + 67 = 360°

х + 245° = 360°

х = 360° – 245°

Следовательно, х = 115 °

Пример 2: Каков будет периметр четырехугольника со сторонами 6 см, 8 см, 10 см и 12 см?

Решение:

Даны стороны четырехугольника равны 6 см, 8 см, 10 см и 12 см.

Следовательно, периметр четырехугольника равен:

P = 6 см + 8 см + 10 см + 12 см = 36 см

Пример 3: Если площадь ромба 60 квадратных единиц, а его высота 6 единиц, какова будет величина его основания?

Решение:

В приведенном выше примере дано, что –

Площадь ромба = 60 квадратных единиц

Высота ромба = 6 единиц

Площадь ромба = основание 60002 3

2 высота

2 = Основание x 6

Основание = 60/6 = 10 единиц

Заключение

Из этой статьи мы узнали, что четырехугольник — это замкнутый многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вертикалями. В SplashLearn ваш ребенок может узнать о четырехугольниках в веселой и игровой форме. Этот простой и уникальный метод обучения быстро привлекает внимание юных учеников. Поэтому родители и учителя могут без особых усилий обучать своих детей четырехугольникам.

Если вы являетесь родителем ребенка, который учится в младших классах и ищете надежные образовательные онлайн-платформы, вы можете зарегистрировать их в SplashLearn. Позвольте вашему ребенку бесстрашно заниматься математикой и зарегистрируйтесь в SplashLearn бесплатно.

Практические задачи на четырехугольник

1

В каком четырехугольнике все углы равны 90°, а противоположные стороны равны?

Прямоугольник

Параллелограмм

Квадрат

Ничего из вышеперечисленного

Правильный ответ: Прямоугольник
Прямоугольник — это четырехсторонний многоугольник, все углы которого равны 90° каждый, а две противоположные стороны равны.

2

Сколько сторон в четырехугольнике?

3

2

4

1

Правильный ответ: 4
Четырехугольник — это многоугольник с четырьмя сторонами.

3

Чему равна сумма всех внутренних углов четырехугольника?

120°

360°

520°

Ничего из перечисленного

Правильный ответ: 360°
Из этой статьи мы узнали, что четырехугольник — это замкнутый многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вертикалями. В SplashLearn ваш ребенок может узнать о четырехугольниках в веселой и игровой форме. Этот простой и уникальный метод обучения быстро привлекает внимание юных учеников. Поэтому родители и учителя могут без особых усилий обучать своих детей четырехугольникам.

Часто задаваемые вопросы о четырехугольнике

Сколько вершин у четырехугольника?

Четырехугольник имеет четыре вершины.

Можем ли мы сказать, что параллелограмм является четырехугольником?

Да, параллелограмм — это замкнутая фигура с четырьмя углами. Следовательно, его можно назвать четырехугольником.