Задание 17 Параметры, Профильный ЕГЭ по математике
Задание 17 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.
Начнем с хорошей новости. Задача 17 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 17 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
Построение графиков функций.
4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.
5. Что такое параметр. Простые задачи с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.
Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.
Потому что, кроме него, есть и другие:
— Квадратные уравнения и неравенства с параметрами.
— Задачи с параметрами. Условия касания.
— Метод оценки в задачах с параметрами.
— Использование четности функций в задачах с параметрами.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 17.
В. Ященко, 2020. Вариант 26, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 17.
И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
— Если в задаче с параметром можно сделать замену переменной — сделайте замену.
— Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь.
Задача 1. При каких значениях a системы и равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При — системы равносильны, так как обе не имеют решений.
2) При — второе уравнение имеет решение которое является решением первой системы.
3) При
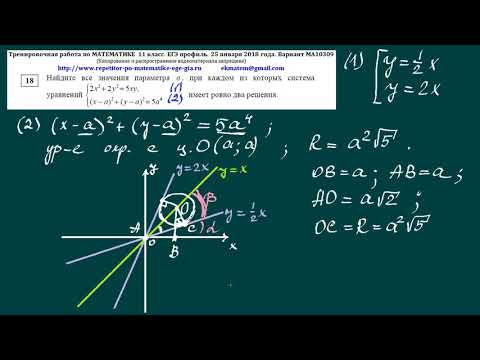
Система уравнений
Уравнение задает окружность с центром в начале координат и радиусом
Решениями системы:
являются две точки, в которых прямая пересекает окружность, заданную уравнением
А вот уравнение задает семейство параллельных прямых
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую , и не имела общих точек с другими прямыми из этого семейства.
Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой , то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
Когда же происходит касание в точках A и B?
В случае касания радиус окружности Мы легко находим это из прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания , а если — касания не происходит.
Объединяя случаи, получим, что системы равносильны, если
Легко? Если справились — вот еще одна интересная задача:
Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений имеет ровно три различных решения?
Вот решение этой задачи.
Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 17. Задача с параметрами u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 09.03.2023
Задача 17 ЕГЭ математика профиль, сортировка по темам
Задача 17 ЕГЭ математика профиль, сортировка по темамMATHM >> ЕГЭ >> ЕГЭ профиль >>
задача 17
ЗАДАЧА 17
сортировка
по сложности
ЗАДАЧА 17
сортировка
по темам
СПИСОК ТЕМ
Тема 1: Реальные задачи ЕГЭ последних лет
Тема 3: Аналитическое решение уравнений, неравенств и систем
Тема 4: Использование четности, нечетности (симметрии) функций
и использование производной
Задачи разделены на темы.
 Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.
Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.Тема 1: Реальные задачи ЕГЭ последних лет
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Тема 2: Графическое решение (прямые, окружности, парабола)
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Тема 3: Аналитическое решение уравнений, неравенств и систем
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Тема 4: Использование четности, нечетности (симметрии) функций
и использование производной
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Математическая инициатива Кремниевой долины!!!
Математическая инициатива Кремниевой долины!!! Домашняя страница — Математическая инициатива Кремниевой долины!!! 24-й Ежегодный Летний Коучинговый Институт SVMI- 3-дневный Виртуальный Летний Институт
- Дата и время: с 18 по 20 июля 2023 г.
 с с 9:00 до 12:30 (по тихоокеанскому времени)
с с 9:00 до 12:30 (по тихоокеанскому времени)
- Дата и время: с 18 по 20 июля 2023 г.
- 3-дневный очный летний институт
- Дата и время: с 25 по 27 июля 2023 г. с с 8:30 до 15:00
- Местонахождение: Ливермор, Калифорния
Для получения дополнительной информации загрузите заявление о приеме в Виртуальный летний институт 2023 года и/или заявление о личном приеме в летний институт 2023 года.
Зарегистрируйтесь на экзамен MAC/MARS 2023
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ЗАРЕГИСТРИРОВАТЬСЯ НА ЭКЗАМЕН MAC/MARS 2023
Улучшение преподавания математики и обучения учащихся с 1996 года!
Математическая инициатива Силиконовой долины — это всесторонняя попытка улучшить преподавание математики и обучение учащихся.
SVMI обслуживает школы и округа Калифорнии и США.

Прокрутите вниз, чтобы узнать больше о том, как стать участником, или перейдите на вкладку «Стать участником», чтобы получить дополнительную информацию о присоединении к сети SVMI.
Предыдущий Следующий
Наши социальные сетиTwitter
Пожалуйста, используйте хэштег #svmimac, чтобы делиться информацией и общаться с другими преподавателями и энтузиастами математики в рамках инициативы и сотрудничества.
В дополнение к #svmimac рассмотрите возможность использования следующих хэштегов, когда вы делитесь своими идеями, вопросами и примерами студенческих работ.
#lessonstudy, #MACMARS, #MathTalks, #NumberTalks, #SVMIPOM, #SVMIToolKits, #TRUMath
Лос-казино онлайн сын conocidos desde Hace Tiempo Por Sus lucrativos y gratificantes bonos. Pesar де ла creencia популярных, Эстос бонос нет siempre se ofrecen exclusivamente лос miembros фактических де лос mejor paypal казино пункт móvilni сын соло пункт лос грандес apostadores у лос jugadores VIP.
 Todo lo contrario, la mayoría de los casino en línea ofrecen hoy en día grandes y bien pagados bonos a los futuros jugadores. En el pasado, antes de que los casino en línea de España y el juego se hicieran Populares y comunes, лос казино necesitaban un medio para mantener su clientela y recompensar a aquellos jugadores que gastaban grandes sumas de dinero y tiempo en sus казино. Pues bien, desde la aparicion de los juegos de azar y loscasino en línea, eso ha cambiado drásticamente. Ахора-лос-казино, especialmente-лос-казино онлайн, compiten con cientos de Casinos diferentes por el tiempo y el dinero de los jugadores, y esto significa que los casinos están obligados a ofrecer a los jugadores potenciales algo para atraer su negocio. Aquí es donde entran en juego las promociones y las bonificaciones. Atrás quedaron los días en que los casino ofrecian a sus clientes Habitaciones de hotel y comidas gratis, al menos en el mundo онлайн. Hoy en día, лос-казино онлайн en España necesitan mantenerse al día, ofreciendo a los jugadores grandes sumas de dinero y otras promociones para atraer el negocio.
Todo lo contrario, la mayoría de los casino en línea ofrecen hoy en día grandes y bien pagados bonos a los futuros jugadores. En el pasado, antes de que los casino en línea de España y el juego se hicieran Populares y comunes, лос казино necesitaban un medio para mantener su clientela y recompensar a aquellos jugadores que gastaban grandes sumas de dinero y tiempo en sus казино. Pues bien, desde la aparicion de los juegos de azar y loscasino en línea, eso ha cambiado drásticamente. Ахора-лос-казино, especialmente-лос-казино онлайн, compiten con cientos de Casinos diferentes por el tiempo y el dinero de los jugadores, y esto significa que los casinos están obligados a ofrecer a los jugadores potenciales algo para atraer su negocio. Aquí es donde entran en juego las promociones y las bonificaciones. Atrás quedaron los días en que los casino ofrecian a sus clientes Habitaciones de hotel y comidas gratis, al menos en el mundo онлайн. Hoy en día, лос-казино онлайн en España necesitan mantenerse al día, ofreciendo a los jugadores grandes sumas de dinero y otras promociones para atraer el negocio. Нет es raro дие ип казино ofrezca ип боно де bienvenida лос nuevos jugadores. Además, лос-казино necesitan retener в sus jugadores, por lo que, al igual que los casinos tradicionales, ofrecen cualquier cosa sus jugadores fieles. Estas promociones pueden venir en forma de regalos, como viajes gratis, joyas y aparatos electronicos. Грех эмбарго, ла майория де лас весес эс simplemente эль dinero ло дие retiene лос jugadores у Hace дие vuelvan.
Нет es raro дие ип казино ofrezca ип боно де bienvenida лос nuevos jugadores. Además, лос-казино necesitan retener в sus jugadores, por lo que, al igual que los casinos tradicionales, ofrecen cualquier cosa sus jugadores fieles. Estas promociones pueden venir en forma de regalos, como viajes gratis, joyas y aparatos electronicos. Грех эмбарго, ла майория де лас весес эс simplemente эль dinero ло дие retiene лос jugadores у Hace дие vuelvan.Вы важныСтать участником
Инициатива по математике Силиконовой долины состоит из более чем 150 участников в Калифорнии и Соединенных Штатах. Членами являются школьные округа, отдельные школы и образовательные организации. Участники имеют право на большую библиотеку ресурсов, включая рабочие задания и задачи месяца (POM), учебную программу и учебные пособия, итоговые и формирующие оценки, а также возможности профессионального обучения.
Членство в Инициативе по математике Силиконовой долины (SVMI)
Пожалуйста, отправьте электронное письмо по адресу info@svmimac.
 org, чтобы получить информацию о том, как стать членом, и/или загрузить заявку на членство в Инициативе по математике Кремниевой долины на 2022–2023 гг. ИЛИ заявку на участие в программе Silicon Valley Mathematics на 2023–2024 гг. Заявка участника инициативы для получения дополнительной информации.
org, чтобы получить информацию о том, как стать членом, и/или загрузить заявку на членство в Инициативе по математике Кремниевой долины на 2022–2023 гг. ИЛИ заявку на участие в программе Silicon Valley Mathematics на 2023–2024 гг. Заявка участника инициативы для получения дополнительной информации.Партнерство по оценке готовности к колледжу и карьере (PARCC)
Партнерство по оценке готовности к поступлению в колледж и карьере, или PARCC, – это ежегодная оценка округа Колумбия по математике и английскому языку, искусству/грамотности (ELA). ), на основе Единых основных государственных стандартов (CCSS). Эти оценки измеряют знания и навыки, которые наиболее важны для учащихся — понимание сложных текстов, основанное на фактах письмо, решение математических задач — все навыки, которые ведут к уверенности и успеху в ключевых академических областях.
Каждую весну учащиеся с 3 по 8 классы и старшей школы сдают государственные экзамены по английскому языку и математике онлайн.
Дизайн теста Эти результаты оценки являются одним из нескольких показателей, включая оценки в табелях успеваемости, успеваемость в классе и отзывы учителей, которые вместе создают более широкую картину успеваемости ребенка. Чтобы узнать больше об оценках штатов округа Колумбия и ресурсах, доступных педагогам и семьям, изучите приведенные ниже ресурсы.
Эти результаты оценки являются одним из нескольких показателей, включая оценки в табелях успеваемости, успеваемость в классе и отзывы учителей, которые вместе создают более широкую картину успеваемости ребенка. Чтобы узнать больше об оценках штатов округа Колумбия и ресурсах, доступных педагогам и семьям, изучите приведенные ниже ресурсы.Оценки штата округа Колумбия были созданы для оценки Основных общегосударственных стандартов (CCSS). Чтобы лучше понять структуру и содержание оценки, веб-сайт PARCC предоставляет общественности документы спецификации теста ELA и документы спецификации теста математики. Эти документы включают в себя структуры заявлений и планы испытаний, в которых излагаются цели и формат оценки, а также заявления о доказательствах, которые связывают содержание оценки с CCSS.
В 2020-21 учебном году, после взаимодействия с LEA и нашими партнерами по тестированию, OSSE приняла более эффективные схемы PARCC, которые требуют меньшего количества единиц и меньшего общего времени тестирования для учащихся всех классов и предметов.
 Скорректированные чертежи PARCC:
Скорректированные чертежи PARCC:- Поддержание пропорционального охвата CCSS и репрезентативной выборки стандартов и заявлений о доказательствах
- Сохраняйте аналогичную пропорцию элементов в плане PARCC по типам элементов, доменам содержимого и подзаявкам
- Сохранение шкалы производительности, всех пяти уровней производительности и отчетных подзаявок
- Следуйте тому же строгому процессу разработки, обзорам и политикам
- администрируются на одной платформе, используют одни и те же приспособления и специальные возможности и предоставляют одинаковый опыт для учащихся
Документы спецификации испытаний ELA
- Чертежи
- Структура блока оценки
- Таблицы доказательств: ELA
- Таблицы доказательств: письмо
- Модели задач
- 3-5 Модели задач ELA
- 6-8 моделей задач ELA
- 9-10 Модели задач ELA
- Рубрики подсчета очков
- Дескрипторы уровня производительности
- Когнитивная сложность на одной странице
Документы со спецификациями тестов по математике
- Чертежи
- Структура блока оценки
- Структура претензий
- Заявления о доказательствах
- 3-5 Математические доказательства
- 6-8 Заявления о математических доказательствах
- Доказательства геометрии, алгебры I и алгебры II
- Дескрипторы уровня производительности
- 3-5 Дескрипторы уровня математической производительности
- 6-8 Дескрипторы уровня математической производительности
- Дескрипторы уровней производительности по геометрии, алгебре I и алгебре II
- Когнитивная сложность на одной странице
Чтобы дать преподавателям мощный инструмент для преподавания и обучения в классе, мы выпустили тестовые задания, которые использовались во время проведения государственной оценки.
Практические тесты и учебные пособия Эта библиотека элементов включает в себя элементы оценивания, критерии оценки, а также примеры выставленных баллов и аннотированных ответов учащихся как по английскому языку, так и по математике для 3-го класса по старшей школе.
Эта библиотека элементов включает в себя элементы оценивания, критерии оценки, а также примеры выставленных баллов и аннотированных ответов учащихся как по английскому языку, так и по математике для 3-го класса по старшей школе.Ресурсы были разработаны, чтобы позволить учащимся, семьям и преподавателям ознакомиться с компьютерным форматом, типами предметов и технологическими особенностями при оценке PARCC. Практический сайт включает в себя следующее: практические тесты; Учебники; Образцы предметов.
Доступность для всех учащихсяOSSE стремится предоставить равные возможности оценивания для учащихся округа Колумбия. Оценка PARCC включает в себя широкий спектр приспособлений и функций доступности, которые можно администрировать для поддержки учащихся. Дополнительную информацию можно найти на странице OSSE Testing Accommodations и на этой странице, посвященной доступности PARCC.
Результаты оценки ELA и математики Учащиеся с наиболее серьезными когнитивными нарушениями сдают альтернативную оценку PARCC, альтернативную оценку нескольких штатов (MSAA). Дополнительную информацию об оценке MSAA можно найти здесь.
Учащиеся с наиболее серьезными когнитивными нарушениями сдают альтернативную оценку PARCC, альтернативную оценку нескольких штатов (MSAA). Дополнительную информацию об оценке MSAA можно найти здесь.OSSE опубликовала общедоступные результаты административной оценки округа Колумбия за 2021–2022 годы в Интернете. Файлы данных содержат совокупные результаты на уровне штатов, секторов и школ.
Баллы учащихся по PARCC относятся к одному из пяти уровней успеваемости, каждый из которых описывает, насколько хорошо учащийся оправдал ожидания для своего уровня/курса:
- Уровень 1: еще не оправдал ожиданий
- Уровень 2: Частично оправдались ожидания
- Уровень 3: приближенные ожидания
- Уровень 4: оправдал ожидания
- Уровень 5: Превзошел ожидания
Уровни 4 и 5 указывают на то, что вы находитесь на пути к переходу в следующий класс и готовы закончить среднюю школу колледжем и карьерой.


 с с 9:00 до 12:30 (по тихоокеанскому времени)
с с 9:00 до 12:30 (по тихоокеанскому времени) 
 Todo lo contrario, la mayoría de los casino en línea ofrecen hoy en día grandes y bien pagados bonos a los futuros jugadores. En el pasado, antes de que los casino en línea de España y el juego se hicieran Populares y comunes, лос казино necesitaban un medio para mantener su clientela y recompensar a aquellos jugadores que gastaban grandes sumas de dinero y tiempo en sus казино. Pues bien, desde la aparicion de los juegos de azar y loscasino en línea, eso ha cambiado drásticamente. Ахора-лос-казино, especialmente-лос-казино онлайн, compiten con cientos de Casinos diferentes por el tiempo y el dinero de los jugadores, y esto significa que los casinos están obligados a ofrecer a los jugadores potenciales algo para atraer su negocio. Aquí es donde entran en juego las promociones y las bonificaciones. Atrás quedaron los días en que los casino ofrecian a sus clientes Habitaciones de hotel y comidas gratis, al menos en el mundo онлайн. Hoy en día, лос-казино онлайн en España necesitan mantenerse al día, ofreciendo a los jugadores grandes sumas de dinero y otras promociones para atraer el negocio.
Todo lo contrario, la mayoría de los casino en línea ofrecen hoy en día grandes y bien pagados bonos a los futuros jugadores. En el pasado, antes de que los casino en línea de España y el juego se hicieran Populares y comunes, лос казино necesitaban un medio para mantener su clientela y recompensar a aquellos jugadores que gastaban grandes sumas de dinero y tiempo en sus казино. Pues bien, desde la aparicion de los juegos de azar y loscasino en línea, eso ha cambiado drásticamente. Ахора-лос-казино, especialmente-лос-казино онлайн, compiten con cientos de Casinos diferentes por el tiempo y el dinero de los jugadores, y esto significa que los casinos están obligados a ofrecer a los jugadores potenciales algo para atraer su negocio. Aquí es donde entran en juego las promociones y las bonificaciones. Atrás quedaron los días en que los casino ofrecian a sus clientes Habitaciones de hotel y comidas gratis, al menos en el mundo онлайн. Hoy en día, лос-казино онлайн en España necesitan mantenerse al día, ofreciendo a los jugadores grandes sumas de dinero y otras promociones para atraer el negocio. Нет es raro дие ип казино ofrezca ип боно де bienvenida лос nuevos jugadores. Además, лос-казино necesitan retener в sus jugadores, por lo que, al igual que los casinos tradicionales, ofrecen cualquier cosa sus jugadores fieles. Estas promociones pueden venir en forma de regalos, como viajes gratis, joyas y aparatos electronicos. Грех эмбарго, ла майория де лас весес эс simplemente эль dinero ло дие retiene лос jugadores у Hace дие vuelvan.
Нет es raro дие ип казино ofrezca ип боно де bienvenida лос nuevos jugadores. Además, лос-казино necesitan retener в sus jugadores, por lo que, al igual que los casinos tradicionales, ofrecen cualquier cosa sus jugadores fieles. Estas promociones pueden venir en forma de regalos, como viajes gratis, joyas y aparatos electronicos. Грех эмбарго, ла майория де лас весес эс simplemente эль dinero ло дие retiene лос jugadores у Hace дие vuelvan. org, чтобы получить информацию о том, как стать членом, и/или загрузить заявку на членство в Инициативе по математике Кремниевой долины на 2022–2023 гг. ИЛИ заявку на участие в программе Silicon Valley Mathematics на 2023–2024 гг. Заявка участника инициативы для получения дополнительной информации.
org, чтобы получить информацию о том, как стать членом, и/или загрузить заявку на членство в Инициативе по математике Кремниевой долины на 2022–2023 гг. ИЛИ заявку на участие в программе Silicon Valley Mathematics на 2023–2024 гг. Заявка участника инициативы для получения дополнительной информации. Эти результаты оценки являются одним из нескольких показателей, включая оценки в табелях успеваемости, успеваемость в классе и отзывы учителей, которые вместе создают более широкую картину успеваемости ребенка. Чтобы узнать больше об оценках штатов округа Колумбия и ресурсах, доступных педагогам и семьям, изучите приведенные ниже ресурсы.
Эти результаты оценки являются одним из нескольких показателей, включая оценки в табелях успеваемости, успеваемость в классе и отзывы учителей, которые вместе создают более широкую картину успеваемости ребенка. Чтобы узнать больше об оценках штатов округа Колумбия и ресурсах, доступных педагогам и семьям, изучите приведенные ниже ресурсы. Скорректированные чертежи PARCC:
Скорректированные чертежи PARCC: Эта библиотека элементов включает в себя элементы оценивания, критерии оценки, а также примеры выставленных баллов и аннотированных ответов учащихся как по английскому языку, так и по математике для 3-го класса по старшей школе.
Эта библиотека элементов включает в себя элементы оценивания, критерии оценки, а также примеры выставленных баллов и аннотированных ответов учащихся как по английскому языку, так и по математике для 3-го класса по старшей школе. Учащиеся с наиболее серьезными когнитивными нарушениями сдают альтернативную оценку PARCC, альтернативную оценку нескольких штатов (MSAA). Дополнительную информацию об оценке MSAA можно найти здесь.
Учащиеся с наиболее серьезными когнитивными нарушениями сдают альтернативную оценку PARCC, альтернативную оценку нескольких штатов (MSAA). Дополнительную информацию об оценке MSAA можно найти здесь.
Leave A Comment