Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Понятия диафрагмы и глубины резкости в фотографии
ОСНОВНЫЕ СВЕДЕНИЯ ПО ОБЪЕКТИВАМ
Диафрагма и экспозиция
Диафрагма объектива (иногда ее еще называют «апертурой») — плод хитроумной инженерной мысли. Это отверстие с переменным диаметром, которое позволяет контролировать количество света, проходящего через объектив. Диафрагма и выдержка — два основных способа управления экспозицией. При одной и той же выдержке чем меньше света, тем больше должна быть открыта диафрагма, чтобы через нее на поверхность матрицы попало больше света. Соответственно, чем больше света, тем меньше должна быть открыта диафрагма, чтобы экспозиция была оптимальной. Как вариант, чтобы добиться аналогичных результатов, можно диафрагму не менять, а менять выдержку. При этом следует помнить, что величина отверстия диафрагмы влияет также на то, насколько «направленным» является свет, проходящий через объектив, а это напрямую влияет на глубину резкости. Поэтому нужно контролировать и диафрагму, и выдержку, чтобы результат съемки всегда соответствовал ожиданиям.
Диафрагма и выдержка — два основных способа управления экспозицией. При одной и той же выдержке чем меньше света, тем больше должна быть открыта диафрагма, чтобы через нее на поверхность матрицы попало больше света. Соответственно, чем больше света, тем меньше должна быть открыта диафрагма, чтобы экспозиция была оптимальной. Как вариант, чтобы добиться аналогичных результатов, можно диафрагму не менять, а менять выдержку. При этом следует помнить, что величина отверстия диафрагмы влияет также на то, насколько «направленным» является свет, проходящий через объектив, а это напрямую влияет на глубину резкости. Поэтому нужно контролировать и диафрагму, и выдержку, чтобы результат съемки всегда соответствовал ожиданиям.
F число и математические расчеты
Небольшой технический экскурс и немного математики
Что такое f число? Диафрагменное или f число — это результат деления фокусного расстояния объектива на диаметр действующего отверстия диафрагмы. Например, если взять объектив 35 мм F1. 4 G, у которого максимальное значение диафрагмы равно f/1.4, диаметр действующего отверстия диафрагмы можно вычислить так: 35 ÷ 1,4 = 25 мм. Обратите внимание, что при изменении фокусного расстояния объектива также изменяется диаметр отверстия диафрагмы и, соответственно, f‑число. Например для телеобъектива с фокусным расстоянием 300 мм и диафрагмой f/1.4 диаметр действующего отверстия диафрагмы можно узнать, решив пример 300 ÷ 1,4 ≈ 214 мм. Такой объектив будет громоздким, неудобным и очень дорогим. Вот почему так редко можно встретить светосильную длиннофокусную оптику, т.е. оптику с большим отверстием диафрагмы. Фотографам необязательно знать фактический диаметр отверстия диафрагмы в миллиметрах, но полезно понимать сам принцип расчетов.
4 G, у которого максимальное значение диафрагмы равно f/1.4, диаметр действующего отверстия диафрагмы можно вычислить так: 35 ÷ 1,4 = 25 мм. Обратите внимание, что при изменении фокусного расстояния объектива также изменяется диаметр отверстия диафрагмы и, соответственно, f‑число. Например для телеобъектива с фокусным расстоянием 300 мм и диафрагмой f/1.4 диаметр действующего отверстия диафрагмы можно узнать, решив пример 300 ÷ 1,4 ≈ 214 мм. Такой объектив будет громоздким, неудобным и очень дорогим. Вот почему так редко можно встретить светосильную длиннофокусную оптику, т.е. оптику с большим отверстием диафрагмы. Фотографам необязательно знать фактический диаметр отверстия диафрагмы в миллиметрах, но полезно понимать сам принцип расчетов.
«F-числа» или «f-ступени» диафрагмы
У всех объективов есть максимальное и минимальное значения диафрагмы (выражаются в «f-числах»), но в технических характеристиках объективов, как правило, приводится именно максимальное значение. Возьмем, к примеру, объектив Sony 35 мм F1. 4 G. Здесь фокусное расстояние объектива — 35 мм (об этом чуть позже), максимальное значение диафрагмы — F1.4. Что конкретно значит обозначение «F1.4»? Подробно об этом можно почитать в статье «F число и математические расчеты» выше. Однако на практике достаточно понимать, что чем меньше f-число, тем больше отверстие диафрагмы, и помнить, что значение f/1.4 считается одним из максимальных в случае с универсальными объективами. Объективы с максимальным значением диафрагмы f/1.4, f/2 или f/2.8 обычно называются «светосильными».
4 G. Здесь фокусное расстояние объектива — 35 мм (об этом чуть позже), максимальное значение диафрагмы — F1.4. Что конкретно значит обозначение «F1.4»? Подробно об этом можно почитать в статье «F число и математические расчеты» выше. Однако на практике достаточно понимать, что чем меньше f-число, тем больше отверстие диафрагмы, и помнить, что значение f/1.4 считается одним из максимальных в случае с универсальными объективами. Объективы с максимальным значением диафрагмы f/1.4, f/2 или f/2.8 обычно называются «светосильными».
Стандартные f-числа, которые вам могут встретиться в маркировке объективов (в порядке убывания): 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, иногда 32. Специально для математиков: это всё степени квадратного корня от числа 2. Эти цифры соответствуют целым значениям (ступеням) диафрагмы. Бывают еще промежуточные значения, соответствующие половине или трети целого значения. Увеличение отверстия диафрагмы на одну ступень вдвое увеличивает количество света, попадающего через объектив на матрицу. Уменьшение отверстия диафрагмы на одну ступень наполовину уменьшает количество света, попадающего через объектив на матрицу.
Уменьшение отверстия диафрагмы на одну ступень наполовину уменьшает количество света, попадающего через объектив на матрицу.
При съемке на коротких фокусных расстояниях диафрагма может быть умеренно открыта, и этого будет достаточно для правильного экспонирования.
Более длинные фокусные расстояния требуют пропорционально более открытой диафрагмы при одинаковых значениях f‑числа и при одинаковой яркости.
F-число = Фокусное расстояние ÷ Эффективная диафрагма
[1] Эффективная диафрагма (размер входного отверстия диафрагмы) [2] Диафрагма [3] Фокусное расстояние Примечание: значения диафрагмы и фокусного расстояния на рисунке указаны приблизительно.
Диафрагма и глубина резкости
С помощью термина «глубина резкости» обозначается диапазон расстояний от объектива камеры, при которых можно достичь приемлемой резкости изображения.
Если рассматривать в качестве примера крайние случаи, то при малой глубине резкости в фокусе оказывается очень узкая область всего в несколько миллиметров, а при большой глубине резкости можно снимать пейзажи, на которых каждый миллиметр снимка получится рассмотреть в мельчайших деталях.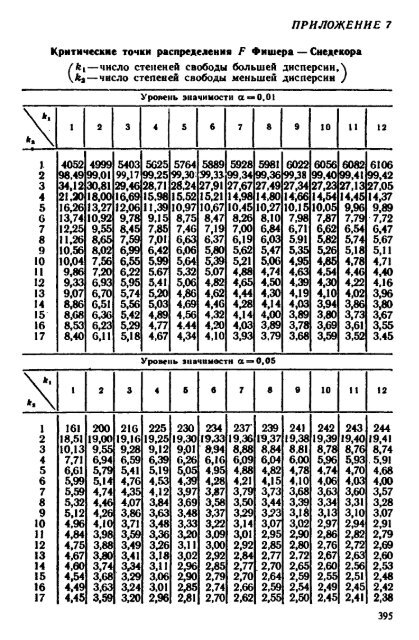 Умение работать с глубиной резкости является одним из базовых приемов в художественной фотографии.
Умение работать с глубиной резкости является одним из базовых приемов в художественной фотографии.
Основной принцип такой: чем больше отверстие диафрагмы, тем меньше фокусное расстояние. Поэтому если вы хотите сделать портрет, на котором фон будет художественно размыт, необходимо открыть диафрагму максимально широко. Однако, здесь важно помнить и о других факторах. Чем длиннее фокусное расстояние объектива, тем больше шанс получить минимальную область резкости. Отчасти об этом уже шла речь выше: диаметр отверстия диафрагмы для объектива с фокусным расстоянием 85 мм при значении f/1.4 будет намного больше, чем для широкоугольного объектива с фокусным расстоянием 24 мм при том же значении f/1.4. Более того, фактическое расстояние между объектами в кадре также может повлиять на восприятие зрителем глубины и объема изображения.
Диафрагма (слева направо): открытая (большое отверстие) — закрытая (маленькое отверстие) Глубина резкости (слева направо): малая — большая
Три фактора, влияющие на рисунок размытия фона
Советы по съемке
Чтобы добиться художественного размытия фона, недостаточно просто выбрать светосильный объектив и снимать на полностью открытой диафрагме. Это первый важный фактор, конечно, но иногда одной лишь полностью открытой диафрагмой желаемого результата не получить. Второй важный фактор — расстояние между объектом съемки и задним планом. Если задний план расположен очень близко за объектом, он может попасть в зону резкости или оказаться настолько близко к ней, что «размыт» не будет. По возможности оставляйте максимальное расстояние между фотографируемым объектом и планом, который вы хотите «размыть». Третий важный фактор — фокусное расстояние объектива, который вы используете. Как мы уже говорили, чем больше фокусное расстояние, тем проще получить небольшую глубину резкости, так что это тоже следует учитывать. Многие фотографы считают, что идеальные фокусные расстояния для портретов с художественным размытием фона — от 75 до 100 мм.
Это первый важный фактор, конечно, но иногда одной лишь полностью открытой диафрагмой желаемого результата не получить. Второй важный фактор — расстояние между объектом съемки и задним планом. Если задний план расположен очень близко за объектом, он может попасть в зону резкости или оказаться настолько близко к ней, что «размыт» не будет. По возможности оставляйте максимальное расстояние между фотографируемым объектом и планом, который вы хотите «размыть». Третий важный фактор — фокусное расстояние объектива, который вы используете. Как мы уже говорили, чем больше фокусное расстояние, тем проще получить небольшую глубину резкости, так что это тоже следует учитывать. Многие фотографы считают, что идеальные фокусные расстояния для портретов с художественным размытием фона — от 75 до 100 мм.
Вы недавно просматривали
Понимание дисперсионного анализа (ANOVA) и F-критерия
Дисперсионный анализ (ANOVA) может определить, различаются ли средние значения трех или более групп. ANOVA использует F-тесты для статистической проверки равенства средних. В этом посте я покажу вам, как работают ANOVA и F-тесты, на примере однофакторного ANOVA.
ANOVA использует F-тесты для статистической проверки равенства средних. В этом посте я покажу вам, как работают ANOVA и F-тесты, на примере однофакторного ANOVA.
Но подождите минутку… вы когда-нибудь задумывались, почему вы используете анализ дисперсии , чтобы определить, означает ли , что отличаются? Я также покажу, как дисперсии предоставляют информацию о средних значениях.
Как и в моих сообщениях о понимании t-тестов, я сосредоточусь на концепциях и графиках, а не на уравнениях, чтобы объяснить F-тесты ANOVA.
Что такое F-статистика и F-тест?
F-тесты названы в честь их тестовой статистики F, названной в честь сэра Рональда Фишера. F-статистика — это просто отношение двух дисперсий. Дисперсия является мерой дисперсии или того, насколько далеко данные разбросаны от среднего значения. Большие значения представляют большую дисперсию.
Дисперсия равна квадрату стандартного отклонения. Нам, людям, легче понять стандартные отклонения, чем дисперсии, потому что они выражены в тех же единицах, что и данные, а не в квадратах. Однако во многих анализах фактически используются дисперсии в расчетах.
Однако во многих анализах фактически используются дисперсии в расчетах.
F-статистика основана на отношении средних квадратов. Термин «средние квадраты» может показаться запутанным, но это просто оценка дисперсии генеральной совокупности, учитывающая степени свободы (DF), используемые для расчета этой оценки.
Несмотря на отношение дисперсий, F-тесты можно использовать в самых разных ситуациях. Неудивительно, что F-тест может оценить равенство дисперсий. Однако, изменяя дисперсии, включенные в соотношение, F-тест становится очень гибким тестом. Например, вы можете использовать F-статистику и F-тесты для проверки общей значимости регрессионной модели, для сравнения соответствия различных моделей, для проверки конкретных условий регрессии и для проверки равенства средних.
Использование F-критерия в однофакторном дисперсионном анализе
Чтобы использовать F-критерий для определения равенства групповых средних, нужно просто включить правильные отклонения в отношение. В однофакторном дисперсионном анализе F-статистика представляет собой следующее соотношение:
В однофакторном дисперсионном анализе F-статистика представляет собой следующее соотношение:
F = вариация между средними значениями выборки / вариация внутри выборки
Лучший способ понять это соотношение — пройтись по примеру однофакторного дисперсионного анализа.
Мы проанализируем четыре образца пластика, чтобы определить, имеют ли они разную среднюю прочность. Вы можете скачать образцы данных, если хотите следовать им. (Если у вас нет Minitab, вы можете загрузить бесплатную 30-дневную пробную версию.) Я вернусь к однофакторному результату дисперсионного анализа при объяснении концепций.
В Minitab выберите Stat > ANOVA > One-Way ANOVA… В диалоговом окне выберите «Сила» в качестве ответа и «Выборка» в качестве фактора. Нажмите OK, и окно сеанса Minitab отобразит следующий вывод:
Числитель: разница между средними значениями образцов
Однофакторный дисперсионный анализ вычислил среднее значение для каждого из четырех образцов пластика. Групповые средние: 11,203, 8,938, 10,683 и 8,838. Эти групповые средние значения распределяются вокруг общего среднего значения для всех 40 наблюдений, что составляет 9.915. Если групповые средние сгруппированы близко к общему среднему, их дисперсия невелика. Однако, если групповые средние разбросаны дальше от общего среднего, их дисперсия выше.
Групповые средние: 11,203, 8,938, 10,683 и 8,838. Эти групповые средние значения распределяются вокруг общего среднего значения для всех 40 наблюдений, что составляет 9.915. Если групповые средние сгруппированы близко к общему среднему, их дисперсия невелика. Однако, если групповые средние разбросаны дальше от общего среднего, их дисперсия выше.
Ясно, что если мы хотим показать, что групповые средние различны, полезно, если они находятся дальше друг от друга. Другими словами, нам нужна большая вариативность средств.
Представьте, что мы выполняем два разных однофакторных ANOVA, где каждый анализ имеет четыре группы. На графике ниже показано распределение средств. Каждая точка представляет собой среднее значение всей группы. Чем дальше разбросаны точки, тем выше значение изменчивости числителя F-статистики.
Какое значение мы используем для измерения дисперсии между средними значениями выборки для примера пластической прочности? В выходных данных одностороннего ANOVA мы будем использовать скорректированное среднеквадратичное значение (Adj MS) для фактора, равное 14,540. Не пытайтесь интерпретировать это число, потому что оно не будет иметь смысла. Это сумма квадратов отклонений, деленная на коэффициент DF. Просто имейте в виду, что чем дальше друг от друга находятся средние значения группы, тем больше становится это число.
Не пытайтесь интерпретировать это число, потому что оно не будет иметь смысла. Это сумма квадратов отклонений, деленная на коэффициент DF. Просто имейте в виду, что чем дальше друг от друга находятся средние значения группы, тем больше становится это число.
Знаменатель: Вариация в выборках
Нам также нужна оценка изменчивости в каждой выборке. Чтобы вычислить эту дисперсию, нам нужно рассчитать, насколько далеко каждое наблюдение от среднего значения группы для всех 40 наблюдений. Технически это сумма квадратов отклонений каждого наблюдения от его среднего группового значения, деленная на ошибку DF.
Если наблюдения для каждой группы близки к среднему по группе, дисперсия в выборках низкая. Однако, если наблюдения для каждой группы дальше от среднего значения группы, дисперсия внутри выборок выше.
На графике панель слева показывает низкую вариацию образцов, а панель справа показывает высокую вариацию. Чем более разбросаны наблюдения от их среднего группового значения, тем выше значение в знаменателе F-статистики.
Если мы хотим показать, что средства различаются, хорошо, когда внутригрупповая дисперсия невелика. Вы можете думать о внутригрупповой дисперсии как о фоновом шуме, который может скрыть разницу между средними значениями.
Для этого примера однофакторного дисперсионного анализа значение, которое мы будем использовать для дисперсии в выборках, — это Adj MS для ошибки, равное 4,402. Это считается «ошибкой», потому что это изменчивость, не объясняемая фактором.
Готовы к демонстрации программного обеспечения Minitab Statistical? Просто спроси!
F-статистика: вариации между средними выборками / вариации внутри выборок
F-статистика — это тестовая статистика для F-тестов. В общем, F-статистика представляет собой отношение двух величин, которые, как ожидается, будут примерно равны при нулевой гипотезе, что дает F-статистику приблизительно 1,9.0003
 Посмотрите на графики ниже и сравните ширину спреда групповых средних с шириной спреда внутри каждой группы.
Посмотрите на графики ниже и сравните ширину спреда групповых средних с шириной спреда внутри каждой группы.На графике низкого значения F показан случай, когда средние групповые значения близки друг к другу (низкая изменчивость) относительно изменчивости внутри каждой группы. График высокого F-значения показывает случай, когда изменчивость групповых средних велика по сравнению с внутригрупповой изменчивостью. Чтобы отвергнуть нулевую гипотезу о том, что средние группы равны, нам нужно высокое F-значение.
В нашем примере с пластической прочностью мы будем использовать множитель Adj MS для числителя (14,540) и Error Adj MS для знаменателя (4,402), что дает нам F-значение 3,30.
Достаточно ли велико наше значение F? Одно F-значение трудно интерпретировать само по себе. Нам нужно поместить наше F-значение в более широкий контекст, прежде чем мы сможем его интерпретировать. Для этого мы будем использовать F-распределение для расчета вероятностей.
F-распределения и проверка гипотез
Для однофакторного дисперсионного анализа отношение межгрупповой изменчивости к внутригрупповой изменчивости соответствует F-распределению, когда нулевая гипотеза верна.
Когда вы выполняете однофакторный дисперсионный анализ для одного исследования, вы получаете одно значение F. Однако если бы мы взяли несколько случайных выборок одинакового размера из одной и той же совокупности и выполнили бы один и тот же однофакторный дисперсионный анализ, мы бы получили много F-значений и могли бы построить распределение для всех из них. Этот тип распределения известен как выборочное распределение.
Поскольку F-распределение предполагает, что нулевая гипотеза верна, мы можем поместить F-значение из нашего исследования в F-распределение, чтобы определить, насколько наши результаты согласуются с нулевой гипотезой, и рассчитать вероятности.
Вероятность, которую мы хотим вычислить, — это вероятность наблюдения F-статистики, которая по крайней мере равна значению, полученному в нашем исследовании. Эта вероятность позволяет нам определить, насколько распространено или редко встречается наше F-значение в предположении, что нулевая гипотеза верна. Если вероятность достаточно мала, мы можем сделать вывод, что наши данные не согласуются с нулевой гипотезой. Доказательства выборочных данных достаточно убедительны, чтобы отвергнуть нулевую гипотезу для всего населения.
Эта вероятность позволяет нам определить, насколько распространено или редко встречается наше F-значение в предположении, что нулевая гипотеза верна. Если вероятность достаточно мала, мы можем сделать вывод, что наши данные не согласуются с нулевой гипотезой. Доказательства выборочных данных достаточно убедительны, чтобы отвергнуть нулевую гипотезу для всего населения.
Вероятность, которую мы рассчитываем, также известна как p-значение!
Чтобы построить F-распределение для нашего примера пластической прочности, я буду использовать графики распределения вероятностей Minitab. Чтобы построить график F-распределения, подходящего для нашего конкретного дизайна и размера выборки, нам нужно указать правильное количество DF. Глядя на наш односторонний результат ANOVA, мы видим, что у нас есть 3 DF для числителя и 36 DF для знаменателя.
На графике показано распределение F-значений, которые мы получили бы, если бы нулевая гипотеза верна и мы повторили наше исследование много раз. Заштрихованная область представляет собой вероятность наблюдения F-значения, которое, по крайней мере, такое же большое, как F-значение, полученное в нашем исследовании. F-значения попадают в эту заштрихованную область примерно в 3,1% случаев, когда нулевая гипотеза верна. Эта вероятность достаточно низка, чтобы отвергнуть нулевую гипотезу, используя общий уровень значимости 0,05. Можно сделать вывод, что не все групповые средние равны.
Заштрихованная область представляет собой вероятность наблюдения F-значения, которое, по крайней мере, такое же большое, как F-значение, полученное в нашем исследовании. F-значения попадают в эту заштрихованную область примерно в 3,1% случаев, когда нулевая гипотеза верна. Эта вероятность достаточно низка, чтобы отвергнуть нулевую гипотезу, используя общий уровень значимости 0,05. Можно сделать вывод, что не все групповые средние равны.
Узнайте, как правильно интерпретировать p-значение.
Оценка средних значений путем анализа вариации
Дисперсионный анализ использует F-критерий, чтобы определить, превышает ли изменчивость между средними группами изменчивость наблюдений внутри групп. Если это отношение достаточно велико, можно сделать вывод, что не все средства равны.
Это возвращает нас к тому, почему мы анализируем вариации, чтобы судить о средних значениях. Подумайте над вопросом: «Являются ли группы средствами разными?» Вы неявно спрашиваете об изменчивости средств. Ведь если группа значит не различаются или не отличаются больше, чем позволяет случайность, тогда вы не можете сказать, что средства различны. Вот почему вы используете дисперсионный анализ для проверки средств.
Ведь если группа значит не различаются или не отличаются больше, чем позволяет случайность, тогда вы не можете сказать, что средства различны. Вот почему вы используете дисперсионный анализ для проверки средств.
Формула F-теста | Как выполнить F-тест? (Шаг за шагом)
[wbcr_snippet id=”77105″]
Формула F-критерия, которую можно использовать для выполнения статистического теста, помогающего лицу, проводящему тест, определить, имеют ли два множества населения нормальное распределение точки данных имеют одинаковое стандартное отклонение.
F-тест — это любой тест, использующий F-распределение. F-значение — это значение F-распределения. Различные статистические тесты генерируют значение F. Значение может определить, является ли тест статистически значимым. Например, чтобы сравнить две дисперсии, нужно рассчитать отношение двух дисперсий, которое выглядит следующим образом:
Значение F = Большая выборочная дисперсия / Меньшая выборочная дисперсия = σ 1 2 / σ 2 2
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство?
д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство?
Хотя F-тест в ExcelF-тест в ExcelF-тест в Excel — это статистический инструмент, который помогает нам решить, равны ли дисперсии двух совокупностей, имеющих нормальное распределение, или нет. F-тест является неотъемлемой частью модели дисперсионного анализа (ANOVA). Более того, нам нужно сформулировать нулевую и альтернативную гипотезы. Затем нам нужно определить уровень значимости, при котором должен проводиться тест. Впоследствии мы должны определить степени свободы. Степени свободы. Степени свободы (df) относятся к числу независимых значений (переменных) в выборке данных, используемой для поиска недостающей части информации (фиксированной) без нарушения каких-либо ограничений, наложенных в динамической системе. . Эти номинальные значения могут свободно изменяться, что облегчает пользователям поиск неизвестного или отсутствующего значения в наборе данных. Подробнее о числителе и знаменателе. Это поможет определить значение F-таблицы.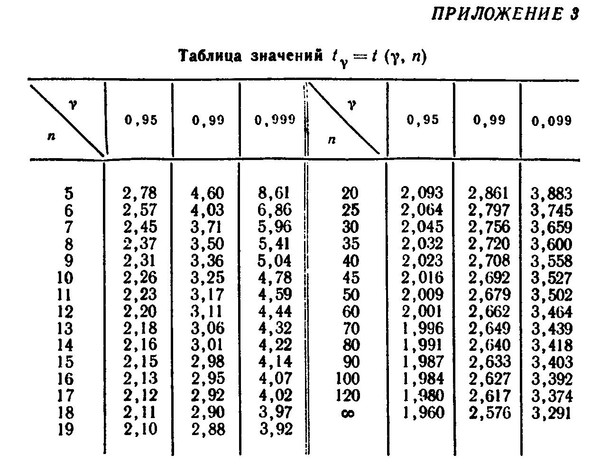 F-значение, показанное в таблице, затем сравнивается с рассчитанным F-значением, чтобы определить, следует ли отвергать нулевую гипотезу.
F-значение, показанное в таблице, затем сравнивается с рассчитанным F-значением, чтобы определить, следует ли отвергать нулевую гипотезу.
СОДЕРЖАНИЕ
- ОПРЕДЕЛЕНИЕ Формулы F-теста
- Шаг за шагом расчеты F-теста
- Пример
- Пример № 1
- Пример #2
- Пример № 1
- #2
- Пример № 1
- #2
- . Пример № 1
- #2
- .
- Формула F-теста в Excel (с шаблоном Excel)
- Рекомендуемые статьи
Пошаговое вычисление F-теста
Ниже приведены шаги, на которых формула F-теста используется для нулевой гипотезы о том, что дисперсии двух популяций равны:
- Во-первых, сформулируйте нулевую и альтернативную гипотезы.
Нулевая гипотеза предполагает, что дисперсии равны. H 0 : σ 1 2 = σ 2 2 . Альтернативная гипотеза утверждает, что дисперсии неравны.
 H 1 : σ 1 2 ≠ σ 2 2 . Здесь σ 1 2 и σ 2 2 являются символами дисперсий.
H 1 : σ 1 2 ≠ σ 2 2 . Здесь σ 1 2 и σ 2 2 являются символами дисперсий. - Рассчитать статистику теста.
(распределение F). т.е., = σ 1 2 / σ 2 2 , где σ 1 2 IS APS APS APS AP AP AP AP AP AP APS AP APS AP APS AP APS AP APS APS APS APS APS APS AP APS AP APS APS APS APS APS APS APS APS APS APS APS APS APS APS APS APS AB – меньшая выборочная дисперсия
- Вычислите степени свободы.
Степень свободы (df1) = n1 – 1 и Степень свободы (df2) = n2 – 1, где n1 и n2 — размеры выборки.
- Посмотрите значение F в таблице F.
Для двусторонних тестов разделите альфа на 2, чтобы найти правильное критическое значение. Таким образом, F-значение находится путем просмотра степеней свободы в числителе и знаменателе в F-таблице.
 Df1 читается в верхнем ряду. Df2 читается в первой колонке.
Df1 читается в верхнем ряду. Df2 читается в первой колонке.Примечание: Существуют разные F-таблицы для разных уровней значимости. Выше приведена таблица F для альфа = 0,050.
- Сравните F-статистику, полученную на шаге 2, с критическим значением, полученным на шаге 4. Мы отвергаем нулевую гипотезу, если F-статистика превышает критическое значение на требуемом уровне значимости. Если F-статистика, полученная на шаге 2, меньше критического значения на требуемом уровне значимости, мы не можем отклонить нулевую гипотезу. Пример №1 Он получил статистику F как 2,38. Полученные им степени свободы составили 8 и 3. Узнать значение F из таблицы F и определить, можем ли мы отвергнуть нулевую гипотезу при уровне значимости 5% (односторонний критерий).
Решение:
Мы должны искать 8 и 3 степени свободы в таблице F. Критическое значение F, полученное из таблицы, равно 8,845 .
 Поскольку F-статистика (2.38) меньше значения таблицы F (8.845), мы не можем отвергнуть нулевую гипотезу.
Поскольку F-статистика (2.38) меньше значения таблицы F (8.845), мы не можем отвергнуть нулевую гипотезу.Пример #2
Страховая компания продает полисы медицинского страхования и автострахования. Клиенты платят премии за эти политики. Генеральный директор страховой компании задается вопросом, являются ли премии, уплачиваемые одним из страховых сегментов (медицинское страхование и автострахование), более изменчивыми, чем другие. Он находит следующие данные о выплаченных премиях:
Провести двусторонний F-тест с уровнем значимости 10%.
Solution:
- Step 1: Null Hypothesis H 0 : σ 1 2 = σ 2 2
Alternate Hypothesis H a : σ 1 2 ≠ σ 2 2
- Шаг 2: F статистика = F значение = σ 1 2 / σ 2 2 = 200/50 = 4
- Шаг 3: DF 1 = N 1 —6 16 =6 =6 =6 =6 =6 =6 =6 =6 =6 =6 =6.
 = n 2 – 1 = 51-1 = 50
= n 2 – 1 = 51-1 = 50- Шаг 4: Поскольку это двусторонний тест, альфа-уровень = 0,10/2 = 0,050. Значение F из таблицы F со степенями свободы 10 и 50 равно 2,026.
- Шаг 5: Поскольку F-статистика (4) больше полученного табличного значения (2,026), мы отклоняем нулевую гипотезу.
Пример №3
Банк имеет головной офис в Дели и филиал в Мумбаи. В одном офисе большие очереди клиентов, а в другом короткие. Операционный менеджер банка задается вопросом, являются ли клиенты в одном отделении более изменчивыми, чем количество клиентов в другом. Он проводит исследование клиентов.
Дисперсия клиентов головного офиса в Дели составляет 31, а для филиала в Мумбаи — 20. Размер выборки для головного офиса в Дели — 11, а для филиала в Мумбаи — 21. хвостатый F-критерий с уровнем значимости 10%.
Solution:
- Step 1: Null Hypothesis H 0 : σ 1 2 = σ 2 2
Alternate Hypothesis H a : σ 1 2 ≠ σ 2 2
- Step 2: F statistic = F Value = σ 1 2 / σ 2 2 = 31/20 = 1.
 55
55 - Шаг 3: DF 1 = N 1 -1 = 11-1 = 10
DF 2 = N 2 -1 = 21-1 = 20
- Шаг 4: , так как A-. двусторонний тест, альфа-уровень = 0,10/2 = 0,05. Значение F из таблицы F со степенями свободы 10 и 20 равно 2,348.
- Шаг 5: Поскольку F-статистика (1,55) меньше полученного табличного значения (2,348), мы не можем отвергнуть нулевую гипотезу.
Актуальность и использование
Формулу F-теста можно использовать в самых разных условиях:
- F-тест используется для проверки гипотезы о равенстве дисперсий двух совокупностей.
- Используется для проверки гипотезы о том, что означает, что заданных нормально распределенных совокупностей с тем же стандартным отклонением равны.
- Используется для проверки гипотезы о том, что предлагаемый регрессионно-регрессионный анализ представляет собой статистический подход для оценки взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными.
 Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее модель хорошо соответствует данным.
Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее модель хорошо соответствует данным.
Формула F-теста в Excel (с шаблоном Excel)
Рабочие в организации выплачивают дневную заработную плату. Однако генеральный директор организации обеспокоен разницей в оплате труда мужчин и женщин в организации. Ниже приведены данные, взятые из выборки мужчин и женщин.
Проведите односторонний F-тест с уровнем значимости 5%.
Решение:
- Шаг 1: H 0 : σ 1 2 = σ 2 2 , H 1 : σ 1 2 ≠ σ 2 2
- Step 2: Click on Data Tab > Data Analysis in Excel .
- Шаг 3: Появится указанное ниже окно. Выберите «F-Test Two-Sample for Variances», а затем нажмите «ОК».

- Шаг 4: Щелкните поле «Диапазон переменной 1» и выберите диапазон A2:A8. Нажмите на поле «Диапазон переменной 2» и выберите диапазон B2: B7. Нажмите A10 в «Диапазоне вывода». Выберите 0,05 в качестве «Альфа», так как уровень значимости составляет 5%. Затем нажмите «ОК».
Он будет отображать значения F-статистики и F-таблицы вместе с другими данными.
- Шаг 4: Из приведенной выше таблицы видно, что F-статистика (8,296) больше, чем F критическая односторонняя (4,95), поэтому мы отвергаем нулевую гипотезу.
Примечание 1: Дисперсия «Переменной 1» должна быть выше, чем у «Переменной 2». В противном случае расчеты, сделанные в Excel, будут неверными. Если нет, то поменять местами данные.
Примечание 2: Если кнопка «Анализ данных» недоступна в Excel, выберите «Файл» > «Параметры». В разделе «Надстройки» выберите «Пакет анализа» и нажмите кнопку «Перейти».
 Затем отметьте «Пакет инструментов анализа» и нажмите «ОК».
Затем отметьте «Пакет инструментов анализа» и нажмите «ОК».Примечание 3: В Excel используется формула для расчета значения F-таблицы. Его синтаксис:
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле F-теста. Здесь мы узнаем, как выполнить F-тест, чтобы определить, следует ли отклонить нулевую гипотезу, а также примеры и загружаемый шаблон Excel. Вы можете узнать больше о статистическом моделировании из следующих статей: –
- Формула размера выборкиФормула размера выборкиФормула размера выборки отражает соответствующий диапазон генеральной совокупности, на которой проводится эксперимент или опрос. Он измеряется с использованием размера популяции, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности.Подробнее гипотеза верна. Кроме того, это помогает определить значимость результатов. Нулевая гипотеза — это позиция по умолчанию, согласно которой между двумя измеряемыми явлениями нет никакой связи.


 H 1 : σ 1 2 ≠ σ 2 2 . Здесь σ 1 2 и σ 2 2 являются символами дисперсий.
H 1 : σ 1 2 ≠ σ 2 2 . Здесь σ 1 2 и σ 2 2 являются символами дисперсий. Df1 читается в верхнем ряду. Df2 читается в первой колонке.
Df1 читается в верхнем ряду. Df2 читается в первой колонке. Поскольку F-статистика (2.38) меньше значения таблицы F (8.845), мы не можем отвергнуть нулевую гипотезу.
Поскольку F-статистика (2.38) меньше значения таблицы F (8.845), мы не можем отвергнуть нулевую гипотезу. = n 2 – 1 = 51-1 = 50
= n 2 – 1 = 51-1 = 50 55
55 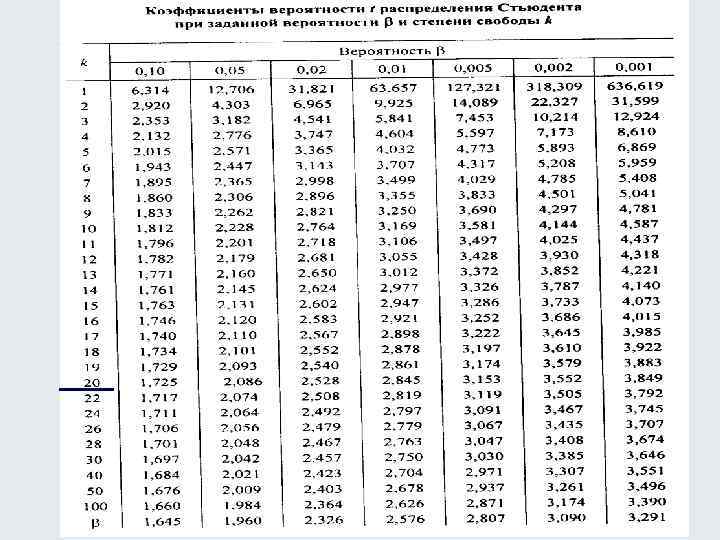 Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее модель хорошо соответствует данным.
Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее модель хорошо соответствует данным.
 Затем отметьте «Пакет инструментов анализа» и нажмите «ОК».
Затем отметьте «Пакет инструментов анализа» и нажмите «ОК».
Leave A Comment