Физика — 10
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой ω являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:
x = xmcos(ωt + φ0).
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь ωt + φ0 = φ фаза колебания, φ0 — начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах: π (рад) = 180°.
Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрать так, чтобы φ0 = 0. В этом случае формулу гармонических колебаний пружинного маятника можно записать так:
x = xm cosωt или x = xm sinωt. (4.13)
(4.13)
Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Исследование-2. Применение. Как изменятся период и частота колебания?
Задача. Как изменятся частота и период колебаний пружинного маятника, если амплитуду его
колебаний увеличить в 2 раза, а массу груза, подвешенного к пружине, уменьшить в 2 раза?
- Как период и частота колебаний пружинного маятника зависят от амплитуды колебаний и массы груза?
Применение в повседневной жизни: Какие параметры упругих рессор, связанные с осью вращения колес автомобиля, вагона и самолета, необходимо принять во внимание при их создании?
- Какие понятия повторили на уроке? Что из этого вы хорошо поняли, а что осталось вам не ясным?
- От каких величин зависит период колебания пружинного маятника? Представьте графики этих зависимостей.

- От каких величин зависит частота колебания пружинного маятника? Представьте графики этих зависимостей.
- От каких величин зависит циклическая частота пружинного маятника? Представьте графики этих зависимостей.
Лабораторная работа. ИЗУЧЕНИЕ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
ИЗУЧЕНИЕ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Повторите: «физика-11».
Груз, подвешенный на стальной пружине и выведенный из положения равновесия, совершает под действием сил тяжести и упругости пружины гармонические колебания. Собственная частота колебаний такого пружинного маятника определяется выражением
где k — жесткость пружины; m — масса тела.
Задача данной работы заключается в том, чтобы экспериментально проверить полученную теоретически закономерность. Для решения этой задачи сначала необходимо определить жесткость k пружины, применяемой в лабораторной установке, массу m груза и вычислить собственную частоту и период колебаний маятника. Затем, подвесив груз массой m на пружину, экспериментально проверить полученный теоретически результат.
Выполнение работы
Оборудование: 1) набор грузов по механике; 2) держатель со спиральной пружиной; 3) штатив для фронтальных работ; 4) метр демонстрационный; 5) секундомер карманный или часы с секундной стрелкой.
1. Подготовьте таблицу для записи результатов измерений и вычислений.
№ опыта | F. Н
| x. м | k, Н/м | m,. | t, с | |||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2. Укрепите пружину с держателем в лапке штатива и подвесьте к ней груз массой 100 г. Рядом с грузом укрепите вертикально измерительную линейку и отметьте начальное положение груза (рис. 1).
3. Подвесьте к пружине груза массой по 100 г и измерьте ее удлинение x, вызванное действием силы . По измеренному удлинению x и известной силе F вычислите жесткость пружины:
4. Зная жесткость пружины, вычислите собственную частоту колебаний и период пружинного маятника массой 200 и 400 г.
5. Подвесьте к пружине 2 груза массой по 100 г, выведите пружинный маятник из положения равновесия, сместив его на 5–7 см, и экспериментально определите частоту колебаний маятника. Для этого измерьте интервал времени t, закоторый маятник совершает 20 полных колебаний, и произведите расчет по формуле
где n — число колебаний.
6. Такие же измерения и вычисления выполните с маятником массой 400 г.
7. Вычислите отклонение расчетного значения собственной частоты колебаний пружинного маятника от частоты , полученной экспериментально. Результаты измерений и вычислений занесите в таблицу.
Рис. 1
Контрольные вопросы
1. По какому закону происходит колебание тела, подвешенного на пружине?
2. Зависит ли частота колебаний пружинного маятника от амплитуды колебаний?
3. Каким был бы результат опыта в условиях невесомости?
5.5 Простое гармоническое движение — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать закон Гука и простое гармоническое движение
- Описать периодическое движение, колебания, амплитуду, частоту и период
- Решение задач простого гармонического движения с участием пружин и маятников
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные концепции.
 Учащийся знает характеристики и поведение волн. Ожидается, что студент:
Учащийся знает характеристики и поведение волн. Ожидается, что студент:- (A) исследуют и описывают колебательное движение и распространение волн в различных типах сред.
Кроме того, руководство по физике для средней школы обращается к содержанию этого раздела лабораторной работы под названием «Движение в двух измерениях», а также к следующим стандартам:
- (7) Научные понятия. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
- (А) изучить и описать колебательное движение и распространение волн в различных типах сред.
Основные термины раздела
| амплитуда | деформация | положение равновесия | частота |
| Закон Гука | период | периодическое движение | |
| восстанавливающая сила | простое гармоническое движение | простой маятник |
Закон Гука и простое гармоническое движение
Представьте себе машину, припаркованную у стены. Если бульдозер втолкнет машину в стену, машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы является деформацией. Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях могут произойти две важные вещи. Во-первых, в отличие от примера с автомобилем и бульдозером, объект возвращается к своей первоначальной форме после прекращения действия силы. Во-вторых, размер деформации пропорционален силе. Это второе свойство известно как закон Гука. В форме уравнения закон Гука равен
Если бульдозер втолкнет машину в стену, машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы является деформацией. Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях могут произойти две важные вещи. Во-первых, в отличие от примера с автомобилем и бульдозером, объект возвращается к своей первоначальной форме после прекращения действия силы. Во-вторых, размер деформации пропорционален силе. Это второе свойство известно как закон Гука. В форме уравнения закон Гука равен
F=−kx,F=−kx,
, где x – величина деформации (например, изменение длины), вызванная восстанавливающей силой F , а k – константа, зависящая от форму и состав предмета. Возвращающая сила — это сила, возвращающая объект в положение равновесия; знак минус стоит потому, что восстанавливающая сила действует в направлении, противоположном перемещению. Обратите внимание, что восстанавливающая сила пропорциональна деформации х . Деформацию также можно рассматривать как отклонение от равновесия. Это изменение положения под действием силы. В отсутствие силы объект находился бы в положении равновесия. Силовая постоянная k связана с жесткостью системы. Чем больше силовая постоянная, тем жестче система. Более жесткую систему труднее деформировать, и она требует большей восстанавливающей силы. Единицы k — ньютоны на метр (Н/м). Одним из наиболее распространенных применений закона Гука является решение задач, связанных с пружинами и маятниками, которые мы рассмотрим в конце этого раздела.
Деформацию также можно рассматривать как отклонение от равновесия. Это изменение положения под действием силы. В отсутствие силы объект находился бы в положении равновесия. Силовая постоянная k связана с жесткостью системы. Чем больше силовая постоянная, тем жестче система. Более жесткую систему труднее деформировать, и она требует большей восстанавливающей силы. Единицы k — ньютоны на метр (Н/м). Одним из наиболее распространенных применений закона Гука является решение задач, связанных с пружинами и маятниками, которые мы рассмотрим в конце этого раздела.
Поддержка учителей
Поддержка учителей
[BL] Повторить концепцию силы.
[BL][OL][AL] Ввести закон Гука и силовую постоянную пружины.
Колебания и периодическое движение
Что общего у океанского буя, ребенка на качелях, гитары и биения сердец? Все они колеблются. То есть они перемещаются туда и обратно между двумя точками, как линейка, показанная на рис. 5.37. Все колебания связаны с силой. Например, вы толкаете ребенка на качелях, чтобы он начал движение.
5.37. Все колебания связаны с силой. Например, вы толкаете ребенка на качелях, чтобы он начал движение.
Рисунок 5,37 Линейка смещена из положения равновесия.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Найдите пружины или резиновые ленты с различной степенью жесткости. Попросите учащихся прикрепить к ним грузы, чтобы построить осцилляторы. Познакомить с терминами «частота» и «период времени». Попросите учащихся понаблюдать, как жесткость пружины влияет на них. Как на них влияет масса системы? Как влияет на них начальная сила?
Первый закон Ньютона подразумевает, что объект, колеблющийся вперед и назад, испытывает силы. Без силы объект двигался бы по прямой линии с постоянной скоростью, а не колебался бы. Рассмотрим, например, выдергивание пластиковой линейки влево, как показано на рис. 5.38. Деформация линейки создает силу в противоположном направлении, известную как восстанавливающая сила. После освобождения восстанавливающая сила заставляет линейку вернуться к своему устойчивому положению равновесия, где результирующая сила, действующая на нее, равна нулю. Однако к тому времени, когда линейка туда попадает, она набирает обороты и продолжает двигаться вправо, вызывая противоположную деформацию. Затем его толкают влево, обратно через равновесие, и процесс повторяется до тех пор, пока он постепенно не потеряет всю свою энергию. Простейшие колебания возникают, когда возвращающая сила прямо пропорциональна смещению. Напомним, что закон Гука описывает эту ситуацию уравнением F = − кх . Следовательно, закон Гука описывает и применяется к простейшему случаю колебаний, известному как простое гармоническое движение.
После освобождения восстанавливающая сила заставляет линейку вернуться к своему устойчивому положению равновесия, где результирующая сила, действующая на нее, равна нулю. Однако к тому времени, когда линейка туда попадает, она набирает обороты и продолжает двигаться вправо, вызывая противоположную деформацию. Затем его толкают влево, обратно через равновесие, и процесс повторяется до тех пор, пока он постепенно не потеряет всю свою энергию. Простейшие колебания возникают, когда возвращающая сила прямо пропорциональна смещению. Напомним, что закон Гука описывает эту ситуацию уравнением F = − кх . Следовательно, закон Гука описывает и применяется к простейшему случаю колебаний, известному как простое гармоническое движение.
Рисунок
5,38
(а) Пластиковая линейка отпущена, и возвращающая сила возвращает линейку в положение равновесия. (b) Суммарная сила равна нулю в положении равновесия, но линейка имеет импульс и продолжает двигаться вправо. в) Возвращающая сила направлена в противоположную сторону. Он останавливает линейку и снова возвращает ее к равновесию. (d) Теперь импульс линейки направлен влево. д) При отсутствии демпфирования (вызванного силами трения) линейка достигает исходного положения. Оттуда движение будет повторяться.
в) Возвращающая сила направлена в противоположную сторону. Он останавливает линейку и снова возвращает ее к равновесию. (d) Теперь импульс линейки направлен влево. д) При отсутствии демпфирования (вызванного силами трения) линейка достигает исходного положения. Оттуда движение будет повторяться.
Когда вы дергаете гитарную струну, в результате получается устойчивый звук, который длится долгое время. Каждое колебание струны занимает столько же времени, сколько и предыдущее. Периодическое движение — это движение, которое повторяется через равные промежутки времени, например, когда объект подпрыгивает вверх и вниз на пружине или маятник качается вперед и назад. Время совершения одного колебания (полного цикла движения) остается постоянным и называется периодом T . Его единицами обычно являются секунды.
Частота f — количество колебаний в единицу времени. Единицей частоты в системе СИ является герц (Гц), определяемый как количество колебаний в секунду. Соотношение между частотой и периодом составляет
Соотношение между частотой и периодом составляет
f= 1/T.f= 1/T.
Как видно из уравнения, частота и период — это разные способы выражения одного и того же понятия. Например, если вы получаете зарплату два раза в месяц, вы можете сказать, что частота выплат — две в месяц, или что период между чеками — полмесяца.
Если нет трения, замедляющего его, то объект в простом движении будет вечно колебаться с одинаковым смещением по обе стороны от положения равновесия. Положение равновесия — это положение, в котором объект естественным образом находился бы в отсутствие силы. Максимальное отклонение от равновесия называется амплитудой X . Единицы амплитуды и смещения одинаковы, но зависят от типа колебаний. Для объекта на пружине, показанного на рис. 5.39, единицами измерения амплитуды и перемещения являются метры.
Рисунок
5,39
Объект, прикрепленный к пружине, скользящей по поверхности без трения, представляет собой простой гармонический осциллятор. При выходе из равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T . Максимальная скорость объекта возникает, когда он проходит через точку равновесия. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .
При выходе из равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T . Максимальная скорость объекта возникает, когда он проходит через точку равновесия. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .
Масса m и силовая постоянная k являются единственными факторами, влияющими на период и частоту простого гармонического движения. Период простого гармонического осциллятора равен
T=2πmkT=2πmk
и, поскольку f = 1/ T , частота простого гармонического осциллятора равна
f=12πкм.f=12πкм.
Смотреть физику
Введение в гармоническое движение
В этом видеоролике показано, как построить график смещения пружины в направлении x с течением времени на основе периода.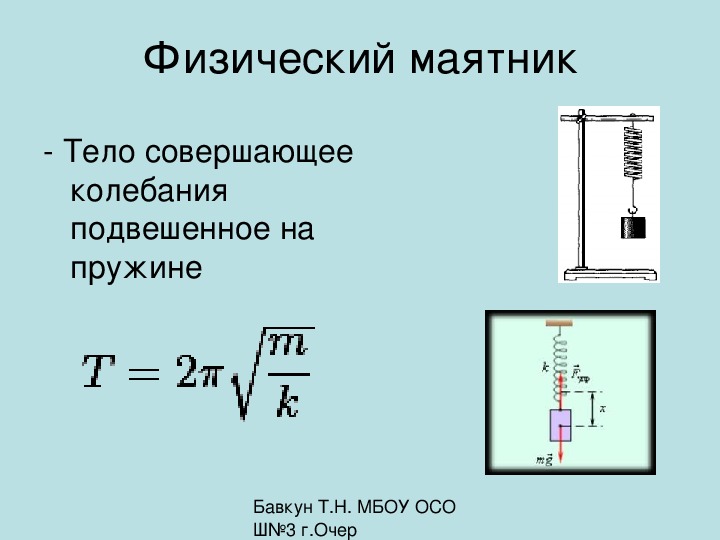 Посмотрите первые 10 минут видео (вы можете остановиться, когда рассказчик начнет освещать исчисление).
Посмотрите первые 10 минут видео (вы можете остановиться, когда рассказчик начнет освещать исчисление).
Если бы амплитуда смещения пружины была больше, как бы это повлияло на график смещения во времени? Что произошло бы с графиком, если бы период был больше?
Большая амплитуда привела бы к более высоким пикам и впадинам, а более длинный период привел бы к большему разделению во времени между пиками.
Большая амплитуда приведет к меньшим пикам и впадинам, а более длинный период приведет к большему расстоянию между пиками.
Большая амплитуда приведет к более высоким пикам и впадинам, а более длинный период приведет к более короткому расстоянию между пиками.

Большая амплитуда приведет к меньшим пикам и впадинам, а более длинный период приведет к более короткому расстоянию между пиками.
Решение задач о пружине и маятнике с помощью простого гармонического движения
Прежде чем решать задачи с пружинами и маятниками, важно сначала понять, как работает маятник. На рис. 5.40 представлена полезная иллюстрация простого маятника.
Рисунок
5.40
Простой маятник имеет груз небольшого диаметра и нить, которая имеет очень маленькую массу, но достаточно прочна, чтобы не растягиваться. Линейное смещение от равновесия равно s, длине дуги. Также показаны силы, воздействующие на груз, в результате чего результирующая сила равна − мг 9 .0126 sin θ к положению равновесия, т.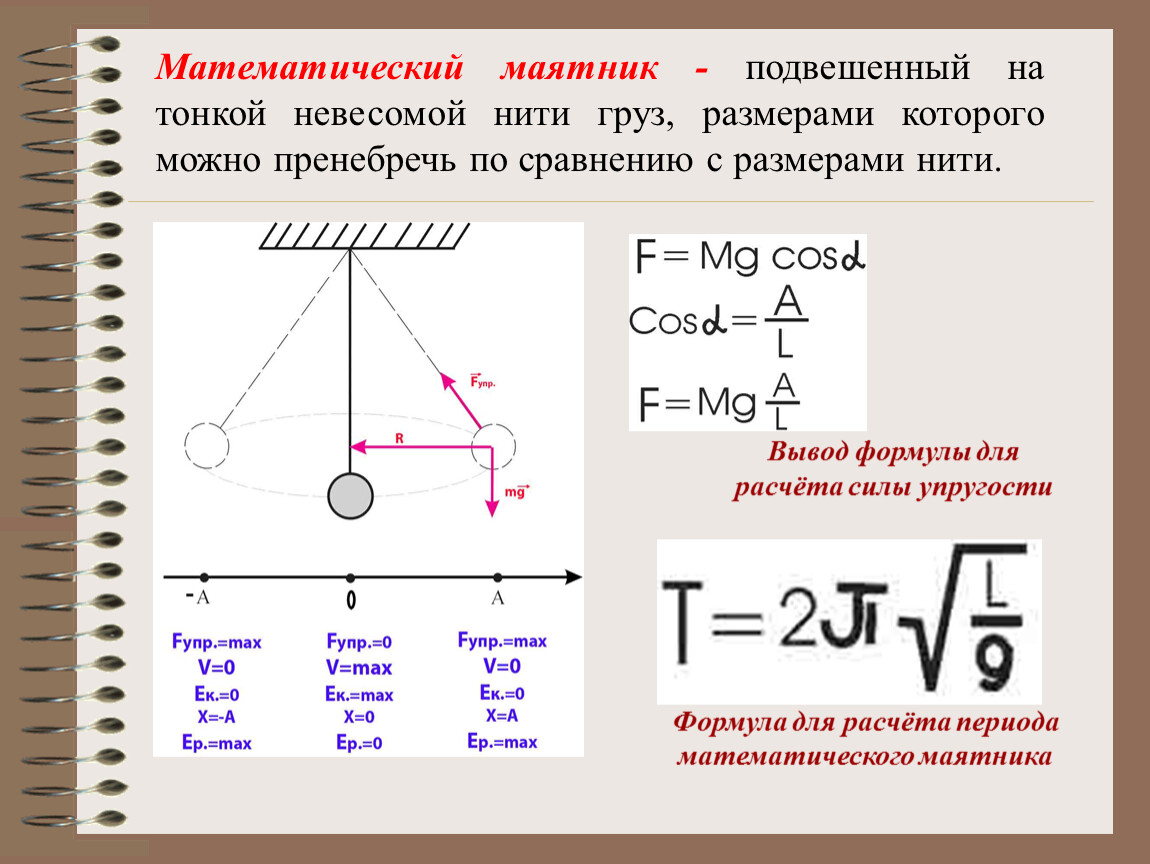 е. восстанавливающая сила.
е. восстанавливающая сила.
Поддержка учителей
Поддержка учителей
[BL] Обзор простого гармонического движения.
К повседневным маятникам относятся старомодные часы, детские качели или грузило на леске. При небольших смещениях менее 15 градусов маятник испытывает простые гармонические колебания, а это означает, что его возвращающая сила прямо пропорциональна его смещению. Маятник в простом гармоническом движении называется простым маятником. Маятник имеет объект с небольшой массой, также известный как маятник, который висит на тонкой проволоке или веревке. Положение равновесия маятника — это когда угол θθ равен нулю (то есть когда маятник висит прямо вниз). Вполне логично, что без приложения силы именно здесь будет лежать маятниковый груз.
Поддержка учителей
Поддержка учителей
[BL][OL][AL]Построить простые маятники разной длины. Попросите студентов измерить их периоды времени или частоты. Постоянны ли они для данного маятника? Как масса влияет на частоту? Как на это влияет начальное смещение? Что произойдет, если слегка подтолкнуть маятник, чтобы он запустился? Это меняет частоту? Как длина влияет на частоту?
Попросите студентов измерить их периоды времени или частоты. Постоянны ли они для данного маятника? Как масса влияет на частоту? Как на это влияет начальное смещение? Что произойдет, если слегка подтолкнуть маятник, чтобы он запустился? Это меняет частоту? Как длина влияет на частоту?
Перемещение маятника на длину дуги с . Вес м г имеет составляющие м г cos θθ вдоль струны и м г sin θθ по касательной к дуге. Натяжение струны точно компенсирует составляющую м г cos θθ, параллельную струне. Это оставляет чистую восстанавливающую силу обратно к положению равновесия, которая проходит по касательной к дуге и равна — м г sin θθ .
Для малоугловых колебаний простого маятника период равен T=2πLg. T=2πLg.
T=2πLg.
На период простого маятника влияют только его длина и ускорение свободного падения. Период совершенно не зависит от других факторов, таких как масса или амплитуда. Однако обратите внимание, что T зависит от g . Это означает, что если мы знаем длину маятника, мы можем использовать его для измерения гравитации! Это пригодится в книге «Измерение ускорения под действием силы тяжести: период маятника».
Советы для успеха
Напряжение представлено переменной T , а период представлен переменной T . Важно не путать их, поскольку напряжение — это сила, а период — это продолжительность времени.
Рабочий пример
Измерение ускорения свободного падения: период маятника
Каково ускорение свободного падения в области, где простой маятник длиной 75 000 см имеет период 1,7357 с?
Стратегия
Нас просят найти g , зная период T и длину L маятника. Мы можем решить T=2πLgT=2πLg для g , предполагая, что угол отклонения меньше 15 градусов. Напомним, что когда угол отклонения меньше 15 градусов, считается, что маятник находится в простом гармоническом движении, что позволяет нам использовать это уравнение.
Мы можем решить T=2πLgT=2πLg для g , предполагая, что угол отклонения меньше 15 градусов. Напомним, что когда угол отклонения меньше 15 градусов, считается, что маятник находится в простом гармоническом движении, что позволяет нам использовать это уравнение.
Решение
- Возведите в квадрат T=2πLgT=2πLg и найдите г .
г=4π2LT2g=4π2LT2
- Подставить известные значения в новое уравнение.
г=4π20,75000 м(1,7357 с)2g=4π20,75000 м(1,7357 с)2
- Вычислите, чтобы найти г .
г = 9,8281 м/с2g = 9,8281 м/с2
Обсуждение
Этот метод определения г может быть очень точным. Вот почему в этом примере длина и период даны пятизначным числам.
Рабочий пример
Закон Гука: насколько жестки автомобильные пружины?
Чему равна постоянная силы системы подвески автомобиля, показанной на рис. 5.41, которая оседает на 1,20 см, когда в нее садится человек массой 80,0 кг?
5.41, которая оседает на 1,20 см, когда в нее садится человек массой 80,0 кг?
Рисунок 5.41 Автомобиль на стоянке. (exfordy, Flickr)
Стратегия
Считайте, что автомобиль находится в положении равновесия x = 0 до того, как человек сядет в него. Затем автомобиль опускается на 1,20 см, что означает, что он смещается в положение x = −1,20×10 −2 м.
В этой точке пружины создают восстанавливающую силу F , равную весу человека
w = м г = (80,0 кг)(9,80 м/с 2 24) Мы принимаем эту силу равной F по закону Гука. Зная F и x , мы можем найти силовую постоянную k . Решение Решить закон Гука, F = − kx , для k . k=Fxk=Fx Подставьте известные значения и найдите k . k=-784 Н-1,20×10-2 м=6,53×104 Н/мк=-784 Н-1,20×10-2 м=6,53×104 Н/м Обсуждение Обратите внимание, что F и x имеют противоположные знаки, потому что они в противоположных направлениях — восстанавливающая сила вверх, а смещение вниз. Также обратите внимание, что автомобиль будет раскачиваться вверх и вниз, когда человек садится в него, если бы не амортизаторы. Подпрыгивающие автомобили — верный признак плохих амортизаторов. 20. Сила 70\,\text{Н}, приложенная к пружине, заставляет ее сместиться на 0,3\,\text{м}. Чему равна постоянная силы пружины? {-233}\,\text{Н/м} {-21}\,\text{Н/м} 21\,\text{Н/м}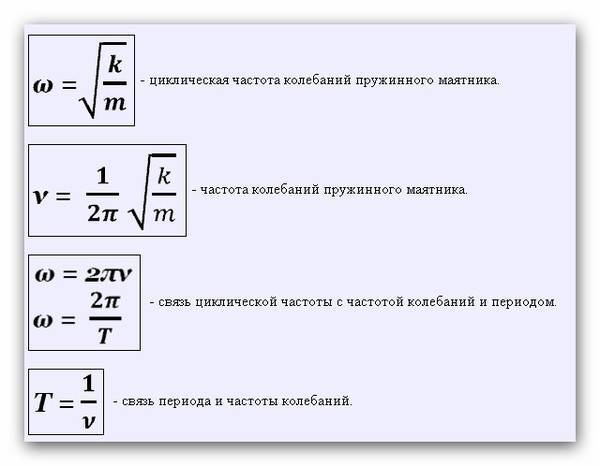
Практические задачи
Снап Лаборатория
Нахождение гравитации с помощью простого маятника
Используйте простой маятник, чтобы найти ускорение свободного падения g в вашем доме или классе.
- 1 строка
- 1 секундомер
- 1 маленький плотный предмет
- Отрежьте кусок нити или зубной нити длиной около 1 м.
- Прикрепите к концу шнура небольшой предмет высокой плотности (например, металлическую гайку или ключ от машины).
- Начиная с угла менее 10 градусов, дайте маятнику раскачиваться и измерьте период маятника для 10 колебаний с помощью секундомера.
- Вычислить г .
Проверка захвата
Насколько точно это измерение для г ? Как это можно улучшить?
- Точность для значения г будет увеличиваться с увеличением массы плотного объекта.
- Точность для значения г будет увеличиваться с увеличением длины маятника.
- Значение г будет более точным, если угол отклонения больше 15°.

- Значение г будет более точным, если оно поддерживает простое гармоническое движение.
Проверьте свое понимание
22.
Что такое деформация?
Деформация – это величина восстанавливающей силы.
Деформация – это изменение формы из-за приложения силы.
Деформация — это максимальное усилие, которое можно приложить к пружине.
Деформация восстанавливает первоначальную форму после устранения внешней силы.

23.
Чему по закону Гука пропорциональна деформация?
- Сила
- Скорость
- Рабочий объем
- Постоянная силы
24.
Что такое колебания?
- Движение, приводящее к небольшим перемещениям
- Движение, которое периодически повторяется
- Периодическое повторяющееся движение между двумя точками
- движение, противоположное направлению возвращающей силы
25.
Верно или неверно — Колебания могут происходить без приложения силы.
- Правда
- Ложь
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, достигают ли учащиеся целей обучения в этом разделе. Если учащиеся не могут справиться с определенной задачей, функция «Проверить понимание» поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Если учащиеся не могут справиться с определенной задачей, функция «Проверить понимание» поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Факторы, которые могут повлиять на период колебаний
Обновлено 13 декабря 2020 г.
Автор: Мэтью Пердью на пружине или электронной схеме. За один цикл система перемещается из начального положения через точки максимума и минимума, затем возвращается в начало перед началом нового, идентичного цикла. Вы можете определить факторы, влияющие на период колебаний, изучив уравнения, определяющие период колебательной системы.
Качающийся маятник
Уравнение для периода (T) качающегося маятника:
T=2\pi \sqrt{\frac{L}{g}}
где π (pi) математическая константа, L — длина плеча маятника, а g — ускорение свободного падения, действующее на маятник. Изучение уравнения показывает, что период колебаний прямо пропорционален длине руки и обратно пропорционален силе тяжести; таким образом, увеличение длины плеча маятника приводит к последующему увеличению периода колебаний при постоянном ускорении силы тяжести. Тогда уменьшение длины приведет к уменьшению периода. Для гравитации обратная зависимость показывает, что чем сильнее гравитационное ускорение, тем меньше период колебаний. Например, период маятника на Земле будет меньше, чем у маятника такой же длины на Луне.
Тогда уменьшение длины приведет к уменьшению периода. Для гравитации обратная зависимость показывает, что чем сильнее гравитационное ускорение, тем меньше период колебаний. Например, период маятника на Земле будет меньше, чем у маятника такой же длины на Луне.
Масса на пружине
Расчет периода (T) колебаний пружины с массой (m) описывается как:
T=2\pi \sqrt{\frac{m}{k} }
где pi — математическая константа, m — масса, прикрепленная к пружине, а k — константа пружины, связанная с «жесткостью» пружины. Таким образом, период колебаний прямо пропорционален массе и обратно пропорционален жесткости пружины. Более жесткая пружина с постоянной массой уменьшает период колебаний. Увеличение массы увеличивает период колебаний. Например, тяжелая машина с пружинами в подвеске медленнее подпрыгивает при наезде на неровность, чем легкая машина с такими же пружинами.
Волна
Волны, такие как рябь на озере или звуковые волны, распространяющиеся по воздуху, имеют период, равный обратной частоте; формула:
T=\frac{1}{f}
, где T — период колебаний, а f — частота волны, обычно измеряемая в герцах (Гц).

 кг
кг Учащийся знает характеристики и поведение волн. Ожидается, что студент:
Учащийся знает характеристики и поведение волн. Ожидается, что студент:


Leave A Comment