Движение — что это, определение и ответ
Движением тела называется изменение его положения в пространстве относительно других.
Координата — величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.
Траектория — это линия, вдоль которой движется тело.
Путь — это длина траектории, вдоль которой движется тело.
Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела \(\overrightarrow{S}\) к времени t, за которое это перемещение произошло:
\(\overrightarrow{v} = \frac{\overrightarrow{S}}{t}\)
Скорость ― это векторная величина!
В заданиях, где дана зависимость скорости тела от времени. {2}}{2}\)
{2}}{2}\)
Где x0 ― начальная координата тела;
v0 ― проекция начальная скорость на ось x;
a ― проекция ускорения на ось x;
t ― время движения.
Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получив взяв производную по времени от этой зависимости.
Скорость ― это производная координаты тела по времени vx(t) = x‘(t). Например, если зависимость координаты тела при равноускоренном движении имеет вид x(t) = 6 – 2t + 12t2, то, взяв первую производную от координаты мы получим зависимость скорости тела от времени vx(t) = –2 + 12 ∙ 2t = –2 + 24t.
Точно так же, ускорение ― это производная от скорости тела. ax(t) = vx‘(t).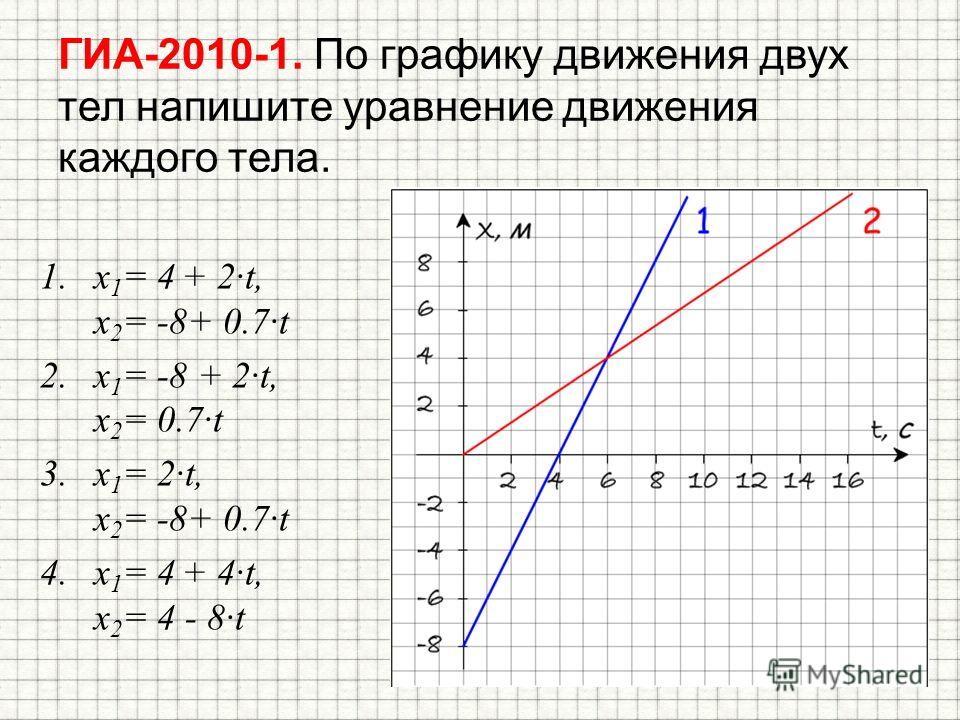 {2}}{2}\),
{2}}{2}\),
Где:
H(t) — высота тела над нулевым уровнем в момент времени t [м],
h — начальная высота тела над нулевым уровнем [м],
v0 — начальная скорость тела [м/с]
α — угол, под которым бросили тело [°],
t — время движения тела [c],
g — ускорении свободного падения [м/с2].
Зависимость горизонтальной координаты от времени при движении под углом к горизонту:
S(t) = v0 ‧ cos a ‧ t, где:
S(t) — путь, пройденный телом за время t [м]
Угол между вектором скорости тела и горизонтом в любой момент времени может быть выражен из геометрических соображений как:
\(\alpha\left( t \right) = arctg(\frac{v_{y}}{v_{x}})\),
Где:
α(t) — угол между скоростью и горизонтом в момент времени t [°],
vy = v0 ∙ sin α – gt — вертикальная проекция скорости тела в момент времени t [м/с],
vх = v0 ∙ cos α — горизонтальная проекция скорости тела [м/с].
Работа силы тяжести при падении тела на тот же уровень, с которого тело взлетело (с Земли на Землю, с балкона на балкон и т.д.) равна нулю.
В этом случае выполняется симметрия полета:
угол, под которым тело упадет, равен углу, под которым тело бросили;
скорость, с которой тело упадет, равна скорости, с которой тело бросили;
время взлета тела до максимальной высоты равно времени падания с неё обратно.
Если работа силы тяжести не равна нулю (бросок с Земли на балкон, с балкона на Землю и так далее), симметрия полета не выполняется.
Время взлета на максимальную высоту:
\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\).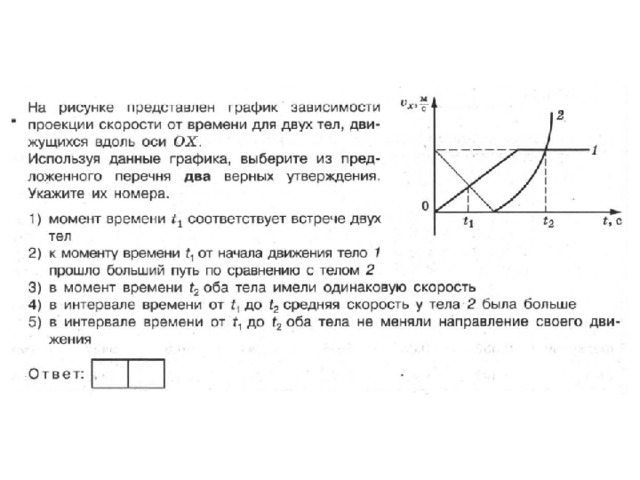 {2}\sin{2\alpha}}{g}\).
{2}\sin{2\alpha}}{g}\).
Выводится с помощью подставления прошлой формулы в уравнения равномерного движения вдоль горизонтальной оси:
S = v0 ‧ cos a ‧ t полета
Здесь используются формула синуса двойного угла и свойство симметрии полета: время взлета равно времени падения, или полное время движения равно удвоенному времени взлета: tполета = 2tвзлета
Очевидно, что формула применима только при падении тела на тот же уровень, с которого оно взлетело.
Время падения тела с балкона (без начальной скорости) или при броске горизонтально:
\(t_{падения} = \sqrt{\frac{2H}{g}}\)
Формула выводится при проецировании уравнения координаты при равноускоренном движении на ось OY:
\(H\left( t \right) = h + v_{0}\sin a \cdot t — \frac{gt^{2}}{2}\)
с учетом, что проекция начальной скорости на эту ось равна нулю, а конечная координата — тоже ноль:
\(0 = h — \frac{gt_{падения}^{2}}{2}\)
Максимальная высота подъема тела над Землей:
\(\ h = \frac{v_{0}^{2}\sin^{2}\alpha}{2g}\)
Формулу легко получить объединением уравнения координаты при равноускоренном движении на ось OY с поверхности Земли:
\(\left( t \right) = h + v_{0} \cdot \sin a \cdot t — \frac{gt^{2}}{2}\)
с формулой времени подъема тела на максимальную высоту:
\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\)
Все представленные выше формулы могут быть использованы без вывода в задачах первой части, но в задачах второй части за это будут снимать баллы.
При движении по окружности часто удобно использовать не обычную скорость, а угловую скорость.
Угловая скорость численно равна углу поворота радиуса за единицу времени.
Угловая скорость для тела, двигающегося из точки 1 в точку 2, будет равна:
\(\omega = \frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t}\), где
∆φ ― угол поворота [рад],
∆t ― промежуток времени [с],
ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).
Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как: v = ωR.
Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.
Период — время, за которое тело делает полный оборот по окружности.
\(T = \frac{2\pi R}{v}\), где
T ― период [с],
R ― радиус окружности [м],
v ― скорость [м/с].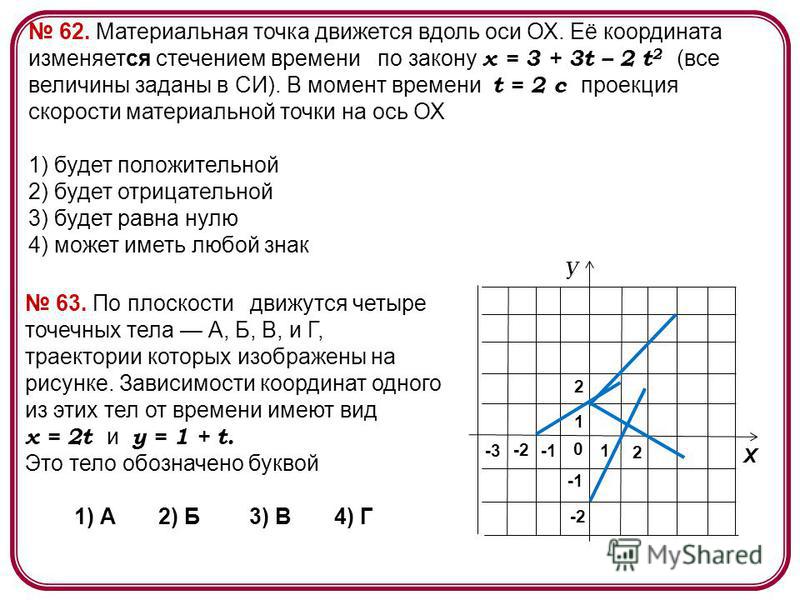 {2}R\), где
{2}R\), где
R ― радиус окружности [м],
an ― нормальное ускорение [м/с2],
v ― скорость [м/с],
ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).
Уравнение координаты при равноускоренном прямолинейном движении
Определение и формулыУравнение координаты — зависимость координаты тела от времени:
x = x(t)
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x
В момент времени t = 10 c координата автомобиля равна:
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).

- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Отсюда t1 = 0 с, а t2 = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение телСуществует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает вид:
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с
Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два корня: t1 = 0,6 с, а t2 = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
 Уравнение координаты при равноускоренном прямолинейном движении имеет вид: Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно,
Уравнение координаты при равноускоренном прямолинейном движении имеет вид: Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, pазбирался: Алиса Никитина | обсудить разбор | оценить
 Чему равна скорость грузовика?
Чему равна скорость грузовика?Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
Исходные данные:
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с2.
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет вид:
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
Ответ: 10pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 14k
Система отсчета
Система отсчетаДалее: Рабочий пример 4.
 1: В Up: Законы движения Ньютона
1: В Up: Законы движения Ньютона Рассмотрим векторное уравнение
| (116) |
что схематически представлено на рис.
 12. Предположим, что мы сместили начало координат
нашей системы координат, или повернуть оси координат. Понятно, в общем, комплектующие векторов , и будут изменены этим изменением
в нашей схеме координат.
Однако рис. 12 по-прежнему остается в силе. Отсюда делаем вывод, что вектор
уравнение (116) также остается в силе. Другими словами, хотя индивидуум
компоненты векторов , и модифицируются изменением
координатная схема, взаимосвязь между этими компонентами, выраженная в уравнении. (116) остается
инвариант.
Это наблюдение позволяет предположить, что независимость законов
физика от произвольного выбора местоположения начала базовой системы координат,
или столь же произвольный выбор ориентации различных осей координат, может быть сделан
проявить, просто записав эти законы как взаимосвязи между векторами.
В частности, второй закон движения Ньютона,
12. Предположим, что мы сместили начало координат
нашей системы координат, или повернуть оси координат. Понятно, в общем, комплектующие векторов , и будут изменены этим изменением
в нашей схеме координат.
Однако рис. 12 по-прежнему остается в силе. Отсюда делаем вывод, что вектор
уравнение (116) также остается в силе. Другими словами, хотя индивидуум
компоненты векторов , и модифицируются изменением
координатная схема, взаимосвязь между этими компонентами, выраженная в уравнении. (116) остается
инвариант.
Это наблюдение позволяет предположить, что независимость законов
физика от произвольного выбора местоположения начала базовой системы координат,
или столь же произвольный выбор ориентации различных осей координат, может быть сделан
проявить, просто записав эти законы как взаимосвязи между векторами.
В частности, второй закон движения Ньютона, | (117) |
явно инвариантен относительно сдвигов начала нашей системы координат или изменений в ориентации различных осей координат.
 Обратите внимание, что количество
( т.е. , масса тела, движение которого исследуется),
фигурирующее в приведенном выше уравнении, инвариантно относительно любых изменений координаты
система, так как измерения
массы совершенно не зависят от измерения расстояния. Мы ссылаемся на
такое количество как скаляр (это улучшенное определение).
Делаем вывод, что действующие законы
физики должны состоять из комбинаций скаляров и векторов, иначе
они сохранят нефизическую зависимость от деталей выбранной системы координат.
Обратите внимание, что количество
( т.е. , масса тела, движение которого исследуется),
фигурирующее в приведенном выше уравнении, инвариантно относительно любых изменений координаты
система, так как измерения
массы совершенно не зависят от измерения расстояния. Мы ссылаемся на
такое количество как скаляр (это улучшенное определение).
Делаем вывод, что действующие законы
физики должны состоять из комбинаций скаляров и векторов, иначе
они сохранят нефизическую зависимость от деталей выбранной системы координат. До сих пор мы неявно предполагали, что все наши наблюдатели неподвижны ( т.е. , все они неподвижно стоят на поверхности Земли). Давайте, теперь,
ослабить это предположение. Рассмотрим двух наблюдателей и , системы координат которых
моментально совпадают в . Предположим, что наблюдатель неподвижен (на поверхности
Земля), тогда как наблюдатель движется (относительно наблюдателя) с равномерная скорость . Как показано на рис. 34, если представляет
перемещение некоторого тела в системе отсчета неподвижного наблюдателя за время , тогда
соответствующее смещение в системе отсчета движущегося наблюдателя просто
34, если представляет
перемещение некоторого тела в системе отсчета неподвижного наблюдателя за время , тогда
соответствующее смещение в системе отсчета движущегося наблюдателя просто
| (118) |
Скорость тела в системе отсчета неподвижного наблюдателя определяется как
| (119) |
Следовательно, соответствующая скорость в системе отсчета движущегося наблюдателя принимает вид
| (120) |
Наконец, ускорение тела в неподвижной системе отсчета наблюдателя равно определяется как
| (121) |
тогда как соответствующее ускорение в системе отсчета движущегося наблюдателя принимает вид
| (122) |
Следовательно, ускорение тела равно в обеих системах отсчета.

Ясно, что если наблюдатель сделает вывод, что тело движется с постоянной
скорости и, следовательно, при нулевой результирующей силе, то наблюдатель согласится
с этим выводом. Более того, если наблюдатель сделает вывод, что тело
ускоряется, а значит, на него действует сила , то наблюдатель
останется в согласии. Отсюда следует, что законы движения Ньютона
одинаково справедливы в системах отсчета движущегося и неподвижного наблюдателя.
Такие кадры называются инерциальная система отсчета . Есть бесконечно много
инерциальные системы отсчета, в которых законы движения Ньютона в равной степени действительны, все
движутся с постоянной скоростью по отношению друг к другу. Следовательно, не существует универсального
стандарт покоя в физике. Наблюдатель может утверждать, что он покоится по сравнению с наблюдателем,
и наоборот : однако обе точки зрения одинаково верны. Более того, есть
абсолютно никакого физического
эксперимент, который наблюдатель мог бы провести, чтобы продемонстрировать, что он
отдых, пока наблюдатель движется. Это, по сути, принцип специальный
относительность , впервые сформулированная Альбертом Эйнштейном в 1905 году.
Более того, есть
абсолютно никакого физического
эксперимент, который наблюдатель мог бы провести, чтобы продемонстрировать, что он
отдых, пока наблюдатель движется. Это, по сути, принцип специальный
относительность , впервые сформулированная Альбертом Эйнштейном в 1905 году.
Далее: Рабочий пример 4.1: В Up: Законы движения Ньютона Предыдущий: Трение Ричард Фицпатрик 2006-02-02
Учебник по физике: движение маятника
Простой маятник состоит из относительно массивного объекта, подвешенного на веревке к неподвижной опоре. Обычно он висит вертикально в положении равновесия. Массивный объект ласково называют маятник . Когда груз выводят из равновесия, а затем отпускают, он начинает совершать возвратно-поступательные колебания вокруг фиксированного положения равновесия. Движение регулярное и повторяющееся, пример периодического движения. Маятниковое движение было представлено ранее в этом уроке, когда мы попытались понять природу вибрирующих объектов. Движение маятника снова обсуждалось, когда мы рассматривали математические свойства объектов, находящихся в периодическом движении. Здесь мы исследуем движение маятника еще более подробно, сосредоточившись на том, как различные величины изменяются с течением времени. Такие величины будут включать в себя силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Маятниковое движение было представлено ранее в этом уроке, когда мы попытались понять природу вибрирующих объектов. Движение маятника снова обсуждалось, когда мы рассматривали математические свойства объектов, находящихся в периодическом движении. Здесь мы исследуем движение маятника еще более подробно, сосредоточившись на том, как различные величины изменяются с течением времени. Такие величины будут включать в себя силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Силовой анализ маятника
Ранее в этом уроке мы узнали, что на вибрирующий объект действует восстанавливающая сила. Возвращающая сила заставляет вибрирующий объект замедляться по мере удаления от положения равновесия и ускоряться по мере приближения к положению равновесия. Именно эта возвращающая сила и отвечает за вибрацию. Итак, какие силы действуют на маятник? А какова возвращающая сила маятника? На маятник действуют две доминирующие силы 9. 0010 боб в течение всего времени своего движения. Существует сила тяжести, которая действует вниз на груз. Это происходит из-за того, что масса Земли притягивает массу боба. И есть сила натяжения, действующая вверх и к оси вращения маятника. Сила натяжения возникает из-за того, что струна натягивается на боб маятника. В нашем обсуждении мы будем игнорировать влияние сопротивления воздуха — третьей силы, которая всегда противодействует движению поплавка, когда он качается туда-сюда. Сила сопротивления воздуха относительно слаба по сравнению с двумя доминирующими силами.
0010 боб в течение всего времени своего движения. Существует сила тяжести, которая действует вниз на груз. Это происходит из-за того, что масса Земли притягивает массу боба. И есть сила натяжения, действующая вверх и к оси вращения маятника. Сила натяжения возникает из-за того, что струна натягивается на боб маятника. В нашем обсуждении мы будем игнорировать влияние сопротивления воздуха — третьей силы, которая всегда противодействует движению поплавка, когда он качается туда-сюда. Сила сопротивления воздуха относительно слаба по сравнению с двумя доминирующими силами.
Сила гравитации очень предсказуема; она всегда в одном и том же направлении (вниз) и всегда имеет одну и ту же величину — масса * 9,8 Н/кг. Сила натяжения значительно менее предсказуема. Как его направление, так и его величина меняются, когда поплавок качается туда-сюда. Направление силы натяжения всегда направлено к точке поворота. Так как груз качается влево от своего положения равновесия, сила натяжения находится под углом — направлена вверх и вправо. И по мере того, как боб качается вправо от своего положения равновесия, напряжение направлено вверх и влево. На приведенной ниже диаграмме показано направление этих двух сил в пяти различных положениях на пути маятника.
И по мере того, как боб качается вправо от своего положения равновесия, напряжение направлено вверх и влево. На приведенной ниже диаграмме показано направление этих двух сил в пяти различных положениях на пути маятника.
В физических ситуациях, когда силы, действующие на объект, не имеют одинакового, противоположного или перпендикулярного направления, принято разлагать одну или несколько сил на составляющие. Это была практика, используемая при анализе проблем с подвеской вывесок и задач с наклонной плоскостью. Обычно одна или несколько сил разлагаются на перпендикулярные составляющие, лежащие вдоль координатных осей, направленных в направлении ускорения или перпендикулярно ему. Таким образом, в случае маятника решается сила тяжести, поскольку сила натяжения уже направлена перпендикулярно движению. На диаграмме справа показан маятник в положении справа от его положения равновесия и на полпути к точке максимального смещения. На схеме изображена система координатных осей, а сила тяжести разложена на две составляющие, лежащие вдоль этих осей. Одна из составляющих направлена по касательной к дуге окружности, по которой движется маятниковый груз; этот компонент обозначен как Fgrav-тангенс. Другая компонента направлена перпендикулярно дуге; он помечен как Fgrav-perp. Вы заметите, что перпендикулярная составляющая силы тяжести находится в направлении, противоположном силе натяжения. Вы также можете заметить, что сила натяжения немного больше этой составляющей силы тяжести. Тот факт, что сила натяжения (Ftens) больше, чем перпендикулярная составляющая силы тяжести (Fgrav-perp), означает, что результирующая сила будет перпендикулярна дуге движения грузика. Это должно быть так, поскольку мы ожидаем, что объекты, движущиеся по круговым траекториям, будут испытывать внутреннюю или центростремительную силу. Тангенциальная составляющая силы тяжести (Fgrav-тангенс) не уравновешивается любой другой силой. Таким образом, существует результирующая сила, направленная по другим осям координат. Именно эта тангенциальная составляющая силы тяжести действует как восстанавливающая сила.
Одна из составляющих направлена по касательной к дуге окружности, по которой движется маятниковый груз; этот компонент обозначен как Fgrav-тангенс. Другая компонента направлена перпендикулярно дуге; он помечен как Fgrav-perp. Вы заметите, что перпендикулярная составляющая силы тяжести находится в направлении, противоположном силе натяжения. Вы также можете заметить, что сила натяжения немного больше этой составляющей силы тяжести. Тот факт, что сила натяжения (Ftens) больше, чем перпендикулярная составляющая силы тяжести (Fgrav-perp), означает, что результирующая сила будет перпендикулярна дуге движения грузика. Это должно быть так, поскольку мы ожидаем, что объекты, движущиеся по круговым траекториям, будут испытывать внутреннюю или центростремительную силу. Тангенциальная составляющая силы тяжести (Fgrav-тангенс) не уравновешивается любой другой силой. Таким образом, существует результирующая сила, направленная по другим осям координат. Именно эта тангенциальная составляющая силы тяжести действует как восстанавливающая сила. При движении маятника вправо от положения равновесия эта составляющая силы направлена против его движения обратно к положению равновесия.
При движении маятника вправо от положения равновесия эта составляющая силы направлена против его движения обратно к положению равновесия.
Приведенный выше анализ относится к одному месту на дуге маятника. В других местах вдоль дуги сила натяжения будет разной. Тем не менее, процесс разделения гравитации на две составляющие вдоль осей, перпендикулярных и касательной к дуге, остается прежним. На приведенной ниже диаграмме показаны результаты силового анализа для нескольких других положений.
Необходимо сделать пару замечаний. Во-первых, обратите внимание на диаграмму, когда груз смещается до своего максимального смещения вправо от положения равновесия. Это положение, в котором маятниковый груз на мгновение имеет скорость 0 м/с и меняет свое направление. Сила натяжения (Ftens) и перпендикулярная составляющая силы тяжести (Fgrav-perp) уравновешивают друг друга. В этот момент времени результирующая сила, направленная вдоль оси, перпендикулярной движению, отсутствует. Поскольку движение объекта равно на мгновение остановился , нет необходимости в центростремительной силе.
Поскольку движение объекта равно на мгновение остановился , нет необходимости в центростремительной силе.
Во-вторых, обратите внимание на диаграмму, когда груз находится в положении равновесия (струна полностью вертикальна). В этом положении нет составляющей силы вдоль касательного направления. При движении через положение равновесия восстанавливающая сила моментально отсутствует. После того, как вернули в положение равновесия, возвращающей силы нет. Возвращающая сила необходима только тогда, когда груз маятника смещен от положения равновесия. Вы также можете заметить, что сила натяжения (Ftens) больше, чем перпендикулярная составляющая силы тяжести (Fgrav-perp), когда груз проходит это положение равновесия. Поскольку груз движется по дуге окружности, в этом положении должна действовать центростремительная сила.
Синусоидальный характер движения маятника В предыдущей части этого урока мы исследовали синусоидальный характер движения массы на пружине. Аналогичное исследование мы проведем здесь для движения маятникового груза. Давайте предположим, что мы можем измерить величину, на которую груз маятника смещается влево или вправо от его положения равновесия или покоя с течением времени. Смещение вправо от положения равновесия будет рассматриваться как положительное смещение; а смещение влево будет рассматриваться как отрицательное смещение. Используя эту систему отсчета, положение равновесия будет рассматриваться как нулевое положение. И предположим, что мы построили график, показывающий изменение положения во времени. Результирующий график зависимости положения от времени показан ниже. Подобно тому, что наблюдалось для массы пружины, положение маятникового груза (измеренное вдоль дуги относительно его положения покоя) является функцией синуса времени.
Аналогичное исследование мы проведем здесь для движения маятникового груза. Давайте предположим, что мы можем измерить величину, на которую груз маятника смещается влево или вправо от его положения равновесия или покоя с течением времени. Смещение вправо от положения равновесия будет рассматриваться как положительное смещение; а смещение влево будет рассматриваться как отрицательное смещение. Используя эту систему отсчета, положение равновесия будет рассматриваться как нулевое положение. И предположим, что мы построили график, показывающий изменение положения во времени. Результирующий график зависимости положения от времени показан ниже. Подобно тому, что наблюдалось для массы пружины, положение маятникового груза (измеренное вдоль дуги относительно его положения покоя) является функцией синуса времени.
Теперь предположим, что мы используем наш детектор движения, чтобы исследовать, как скорость маятника изменяется во времени. Когда маятник совершает движений вперед и назад , скорость постоянно меняется. Будут времена, когда скорость имеет отрицательное значение (для движения влево), и другие моменты времени, когда она будет положительной (для движения вправо). И, конечно, будут моменты времени, когда скорость равна 0 м/с. Если построить график изменения скорости с течением времени, результирующий график будет похож на показанный ниже.
Будут времена, когда скорость имеет отрицательное значение (для движения влево), и другие моменты времени, когда она будет положительной (для движения вправо). И, конечно, будут моменты времени, когда скорость равна 0 м/с. Если построить график изменения скорости с течением времени, результирующий график будет похож на показанный ниже.
Теперь попробуем понять взаимосвязь между положением боба по дуге его движения и скоростью, с которой он движется. Предположим, мы идентифицируем несколько мест вдоль дуги, а затем связываем эти положения со скоростью маятникового груза. На приведенном ниже рисунке показана попытка установить такую связь между положением и скоростью.
Как часто говорят, картинка стоит тысячи слов. А теперь слова. График выше основан на положении равновесия (D), обозначенном как нулевое положение. Смещение влево от положения равновесия рассматривается как отрицательное положение. Смещение вправо считается положительным положением. Анализ графиков показывает, что скорость наименьшая при наибольшем смещении. И скорость наибольшая, когда смещение боба наименьшее. Чем дальше груз отошел от положения равновесия, тем медленнее он движется; и чем ближе грузик к положению равновесия, тем быстрее он движется. Это можно объяснить тем, что при удалении груза от положения равновесия действует восстанавливающая сила, противодействующая его движению. Эта сила замедляет движение боба. Так как груз перемещается влево из положения D в E в F в G, сила и ускорение направлены вправо, а скорость уменьшается по мере его движения по дуге из D в G. В точке G — максимальное смещение влево — маятник груз имеет скорость 0 м/с. Вы можете думать о бобе как о на мгновение остановился и готов изменить свое направление. Затем груз движется вправо по дуге от G к F, затем к E и D. При этом восстанавливающая сила направлена вправо в том же направлении, что и груз. Эта сила будет ускорять груз, придавая ему максимальную скорость в положении D — положении равновесия.
Анализ графиков показывает, что скорость наименьшая при наибольшем смещении. И скорость наибольшая, когда смещение боба наименьшее. Чем дальше груз отошел от положения равновесия, тем медленнее он движется; и чем ближе грузик к положению равновесия, тем быстрее он движется. Это можно объяснить тем, что при удалении груза от положения равновесия действует восстанавливающая сила, противодействующая его движению. Эта сила замедляет движение боба. Так как груз перемещается влево из положения D в E в F в G, сила и ускорение направлены вправо, а скорость уменьшается по мере его движения по дуге из D в G. В точке G — максимальное смещение влево — маятник груз имеет скорость 0 м/с. Вы можете думать о бобе как о на мгновение остановился и готов изменить свое направление. Затем груз движется вправо по дуге от G к F, затем к E и D. При этом восстанавливающая сила направлена вправо в том же направлении, что и груз. Эта сила будет ускорять груз, придавая ему максимальную скорость в положении D — положении равновесия. По мере того, как груз проходит положение D, он движется вправо по дуге к С, затем к В и затем к А. При этом действует направленная влево восстанавливающая сила, противодействующая его движению и заставляющая его замедляться. Таким образом, по мере увеличения смещения от D до A скорость уменьшается из-за противодействующей силы. Как только груз достигает положения А — максимального смещения вправо — он достигает скорости 0 м/с. Опять же, скорость боба наименьшая, когда смещение наибольшее. Боб завершает свой цикл, двигаясь влево от A до B, затем от C до D. По этой дуге от A до D восстанавливающая сила направлена в направлении движения, таким образом ускоряя груз. Так что логично было бы заключить, что при уменьшении положения (по дуге от А до D) скорость увеличивается. Оказавшись в положении D, груз будет иметь нулевое смещение и максимальную скорость. Скорость наибольшая, когда смещение наименьшее. Анимация справа (используется с разрешения Викисклада; особая благодарность Хьюберту Кристиану) обеспечивает наглядное изображение этих принципов.
По мере того, как груз проходит положение D, он движется вправо по дуге к С, затем к В и затем к А. При этом действует направленная влево восстанавливающая сила, противодействующая его движению и заставляющая его замедляться. Таким образом, по мере увеличения смещения от D до A скорость уменьшается из-за противодействующей силы. Как только груз достигает положения А — максимального смещения вправо — он достигает скорости 0 м/с. Опять же, скорость боба наименьшая, когда смещение наибольшее. Боб завершает свой цикл, двигаясь влево от A до B, затем от C до D. По этой дуге от A до D восстанавливающая сила направлена в направлении движения, таким образом ускоряя груз. Так что логично было бы заключить, что при уменьшении положения (по дуге от А до D) скорость увеличивается. Оказавшись в положении D, груз будет иметь нулевое смещение и максимальную скорость. Скорость наибольшая, когда смещение наименьшее. Анимация справа (используется с разрешения Викисклада; особая благодарность Хьюберту Кристиану) обеспечивает наглядное изображение этих принципов.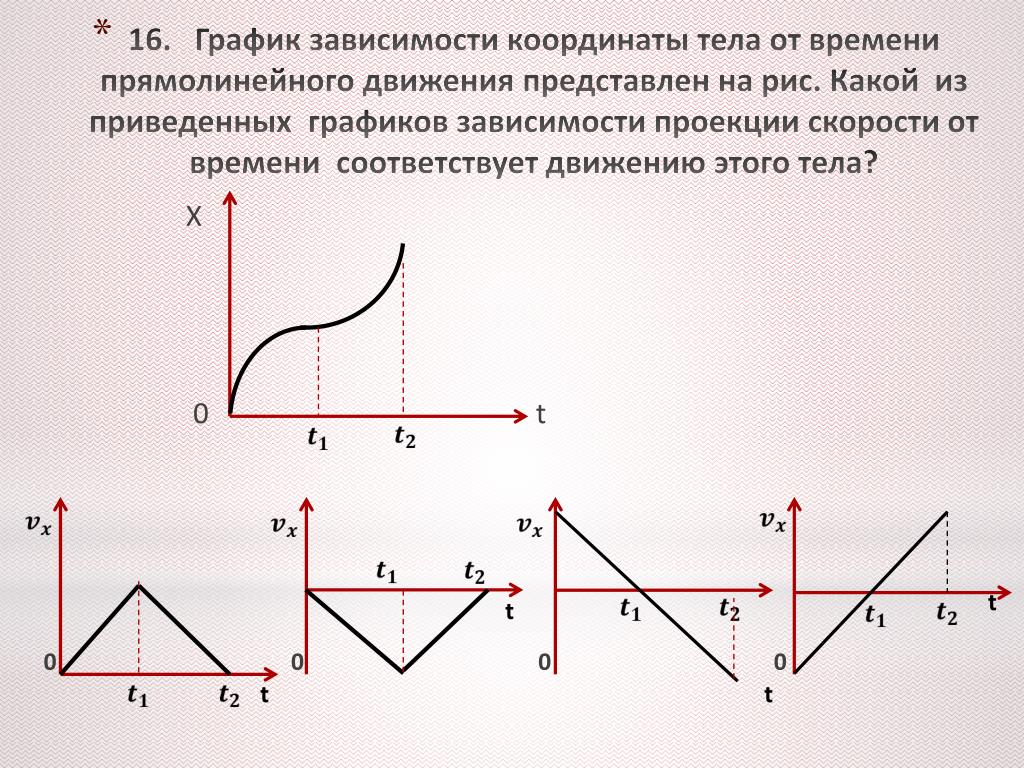 Показанный вектор ускорения объединяет как перпендикулярное, так и тангенциальное ускорения в один вектор. Вы заметите, что этот вектор полностью касается дуги при максимальном смещении; это согласуется с анализом силы, рассмотренным выше. И вектор вертикальный (по направлению к центру дуги), когда находится в положении равновесия. Это также согласуется с приведенным выше силовым анализом.
Показанный вектор ускорения объединяет как перпендикулярное, так и тангенциальное ускорения в один вектор. Вы заметите, что этот вектор полностью касается дуги при максимальном смещении; это согласуется с анализом силы, рассмотренным выше. И вектор вертикальный (по направлению к центру дуги), когда находится в положении равновесия. Это также согласуется с приведенным выше силовым анализом.
В предыдущей главе учебника физики обсуждалась энергия, которой обладает маятник. Мы расширим это обсуждение здесь, поскольку попытаемся связать описанные выше характеристики движения с понятиями кинетической энергии, потенциальной энергии и полной механической энергии.
Кинетическая энергия, которой обладает объект, — это энергия, которой он обладает благодаря своему движению. Это величина, которая зависит как от массы, так и от скорости. Уравнение, связывающее кинетическую энергию (KE) с массой (m) и скоростью (v), имеет вид 9.0023
KE = ½•m•v 2
Чем быстрее движется объект, тем большей кинетической энергией он обладает. Мы можем объединить эту концепцию с приведенным выше обсуждением того, как скорость изменяется в ходе движения. Это смешение концепций привело бы нас к выводу, что кинетическая энергия маятникового груза увеличивается по мере того, как груз приближается к положению равновесия. И кинетическая энергия уменьшается по мере того, как груз удаляется от положения равновесия.
Мы можем объединить эту концепцию с приведенным выше обсуждением того, как скорость изменяется в ходе движения. Это смешение концепций привело бы нас к выводу, что кинетическая энергия маятникового груза увеличивается по мере того, как груз приближается к положению равновесия. И кинетическая энергия уменьшается по мере того, как груз удаляется от положения равновесия.
Потенциальная энергия, которой обладает объект, представляет собой накопленную энергию положения. В учебнике по физике обсуждаются два типа потенциальной энергии — гравитационная потенциальная энергия и упругая потенциальная энергия. Упругая потенциальная энергия присутствует только тогда, когда пружина (или другая упругая среда) сжимается или растягивается. Простой маятник не состоит из пружины. Форма потенциальной энергии, которой обладает маятниковый груз, — это гравитационная потенциальная энергия. Количество гравитационной потенциальной энергии зависит от массы (m) объекта и высоты (h) объекта. Уравнение для гравитационной потенциальной энергии (PE) равно
Уравнение для гравитационной потенциальной энергии (PE) равно
PE = m•g•h
, где g представляет собой силу гравитационного поля (иногда называемую ускорением, вызванным силой тяжести) и имеет значение 9,8 Н/кг.
Высота объекта выражается относительно некоторого произвольно назначенного нулевого уровня . Другими словами, высота должна измеряться как расстояние по вертикали над некоторой опорной точкой. Для маятникового боба самое нижнее положение принято называть исходным положением или нулевым уровнем. Таким образом, когда груз находится в положении равновесия (самом низком положении), его высота равна нулю, а его потенциальная энергия равна 0 Дж. Как и маятниковый груз назад и вперед , есть моменты, в течение которых груз удаляется от положения равновесия. При этом его высота увеличивается по мере того, как он удаляется все дальше и дальше. Он достигает максимальной высоты, когда достигает положения максимального смещения от положения равновесия. По мере того, как груз движется к своему положению равновесия, он уменьшает свою высоту и уменьшает свою потенциальную энергию.
По мере того, как груз движется к своему положению равновесия, он уменьшает свою высоту и уменьшает свою потенциальную энергию.
Теперь давайте соединим эти два понятия кинетической энергии и потенциальной энергии, рассматривая движение маятника, движущегося по дуге, показанной на диаграмме справа. Мы будем использовать гистограмму энергии, чтобы представить изменения в двух формах энергии. Количество каждой формы энергии представлено полосой. Высота полосы пропорциональна количеству этой формы энергии. В дополнение к полосе потенциальной энергии (PE) и полосе кинетической энергии (KE) есть третья полоса, обозначенная как TME. Полоса TME представляет собой общее количество механической энергии, которой обладает маятниковый груз. Полная механическая энергия – это просто сумма двух форм энергии – кинетической плюс потенциальной энергии. Потратьте некоторое время, чтобы изучить гистограммы, показанные ниже, для позиций A, B, D, F и G. Что вы заметили?
Когда вы смотрите на гистограммы, становится очевидным, что по мере того, как груз перемещается из точки A в D, кинетическая энергия увеличивается, а потенциальная энергия уменьшается. Однако общее количество этих двух форм энергии остается постоянным. Любая потеря потенциальной энергии при переходе из положения А в положение D проявляется в виде кинетической энергии. Существует преобразование потенциальной энергии в кинетическую энергию, когда груз перемещается из положения A в положение D. Однако полная механическая энергия остается постоянной. Мы бы сказали, что механическая энергия сохраняется. Когда боб перемещается от положения D к положению G, наблюдается обратное. Кинетическая энергия уменьшается по мере того, как груз движется вправо и (что более важно) вверх к положению G. Этому уменьшению кинетической энергии сопутствует увеличение потенциальной энергии. Энергия переходит из кинетической формы в потенциальную. Тем не менее, как показано на полосе TME, общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в главе «Энергия» учебника «Физический класс».
Однако общее количество этих двух форм энергии остается постоянным. Любая потеря потенциальной энергии при переходе из положения А в положение D проявляется в виде кинетической энергии. Существует преобразование потенциальной энергии в кинетическую энергию, когда груз перемещается из положения A в положение D. Однако полная механическая энергия остается постоянной. Мы бы сказали, что механическая энергия сохраняется. Когда боб перемещается от положения D к положению G, наблюдается обратное. Кинетическая энергия уменьшается по мере того, как груз движется вправо и (что более важно) вверх к положению G. Этому уменьшению кинетической энергии сопутствует увеличение потенциальной энергии. Энергия переходит из кинетической формы в потенциальную. Тем не менее, как показано на полосе TME, общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в главе «Энергия» учебника «Физический класс».
Период маятника
Наше последнее обсуждение будет относиться к периоду маятника. Как обсуждалось ранее в этом уроке, период — это время, за которое вибрирующий объект завершает свой цикл. В случае с маятником это время, когда маятник начинает движение с одного крайнего , перемещается к противоположному крайнему , а затем возвращается в исходное положение. Здесь нас будет интересовать вопрос Какие переменные влияют на период маятника? Мы займемся возможными переменными. Переменными являются масса маятникового груза, длина нити, на которой он висит, и угловое смещение . Угловое смещение или угол дуги — это угол, который струна образует с вертикалью при выходе из состояния покоя. Эти три переменные и их влияние на период легко изучаются и часто находятся в центре внимания физической лаборатории на вводном уроке физики. В приведенной ниже таблице данных представлены репрезентативные данные для такого исследования.
Как обсуждалось ранее в этом уроке, период — это время, за которое вибрирующий объект завершает свой цикл. В случае с маятником это время, когда маятник начинает движение с одного крайнего , перемещается к противоположному крайнему , а затем возвращается в исходное положение. Здесь нас будет интересовать вопрос Какие переменные влияют на период маятника? Мы займемся возможными переменными. Переменными являются масса маятникового груза, длина нити, на которой он висит, и угловое смещение . Угловое смещение или угол дуги — это угол, который струна образует с вертикалью при выходе из состояния покоя. Эти три переменные и их влияние на период легко изучаются и часто находятся в центре внимания физической лаборатории на вводном уроке физики. В приведенной ниже таблице данных представлены репрезентативные данные для такого исследования.
Пробная версия | Масса (кг) | Длина (м) | Угол дуги (°) | Период(ы) |
1 | 0,02- | 0,40 | 15,0 | 1,25 |
2 | 0,050 | 0,40 | 15,0 | 1,29 |
3 | 0,100 | 0,40 | 15,0 | 1,28 |
4 | 0,200 | 0,40 | 15,0 | 1,24 |
5 | 0,500 | 0,40 | 15,0 | 1,26 |
6 | 0,200 | 0,60 | 15,0 | 1,56 |
7 | 0,200 | 0,80 | 15,0 | 1,79 |
8 | 0,200 | 1,00 | 15,0 | 2. |
9 | 0,200 | 1,20 | 15,0 | 2,19 |
10 | 0,200 | 0,40 | 10,0 | 1,27 |
11 | 0,200 | 0,40 | 20,0 | 1,29 |
12 | 0,200 | 0,40 | 25,0 | 1,25 |
13 | 0,200 | 0,40 | 30,0 | 1,26 |
В испытаниях с 1 по 5 масса боба систематически изменялась, в то время как другие величины оставались постоянными. Таким образом, экспериментаторы смогли исследовать возможное влияние массы на период. Как видно из этих пяти испытаний, изменения массы мало влияют на период маятника.
Как видно из этих пяти испытаний, изменения массы мало влияют на период маятника.
В испытаниях 4 и 6-9 масса поддерживается постоянной на уровне 0,200 кг, а угол дуги поддерживается постоянным на уровне 15°. Однако длина маятника различна. Таким образом, экспериментаторы смогли исследовать возможное влияние длины струны на период. Как видно из этих пяти испытаний, изменения длины определенно влияют на период маятника. По мере удлинения нити период маятника увеличивается. Существует прямая зависимость между периодом и продолжительностью.
Наконец, экспериментаторы исследовали возможное влияние угла дуги на период в испытаниях 4 и 10-13. Масса поддерживается постоянной на уровне 0,200 кг, а длина струны остается постоянной на уровне 0,400 м. Как видно из этих пяти испытаний, изменения угла дуги практически не влияют на период маятника.
Таким образом, вывод из такого эксперимента состоит в том, что единственная переменная, влияющая на период маятника, — это длина струны. Увеличение длины приводит к увеличению периода. Но расследование не должно останавливаться на достигнутом. Количественное уравнение, связывающее эти переменные, может быть определено, если данные нанесены на график и проведен линейный регрессионный анализ. Два графика ниже представляют такой анализ. На каждом графике значения периода (зависимой переменной) размещены на вертикальной оси. На графике слева длина маятника отложена по горизонтальной оси. Форма кривой указывает на своего рода степенную зависимость между периодом и длиной. На графике справа изображен квадратный корень из длины маятника (длина в степени ½). Показаны результаты регрессионного анализа.
Увеличение длины приводит к увеличению периода. Но расследование не должно останавливаться на достигнутом. Количественное уравнение, связывающее эти переменные, может быть определено, если данные нанесены на график и проведен линейный регрессионный анализ. Два графика ниже представляют такой анализ. На каждом графике значения периода (зависимой переменной) размещены на вертикальной оси. На графике слева длина маятника отложена по горизонтальной оси. Форма кривой указывает на своего рода степенную зависимость между периодом и длиной. На графике справа изображен квадратный корень из длины маятника (длина в степени ½). Показаны результаты регрессионного анализа.
Уклон: 1,7536 | Уклон: 2,0045 |
Анализ показывает, что данные и линия регрессии лучше подходят для графика справа. Таким образом, график справа является основой для уравнения, связывающего период и длину. Для этих данных уравнение
Таким образом, график справа является основой для уравнения, связывающего период и длину. Для этих данных уравнение
Период = 2,0045•Длина 0,5 + 0,0077
Используя T как символ периода и L как символ длины, уравнение можно переписать как
T = 2,0045•L 0,5 + 0,007 обычно сообщаемое уравнение, основанное на теоретическом развитии, имеет вид
T = 2•Π•(л/г) 0,5
, где g — постоянная, известная как сила гравитационного поля или ускорение свободного падения (9,8 Н/кг). Значение 2,0045, полученное в результате экспериментального исследования, хорошо согласуется с тем, что можно было бы ожидать от этого теоретически представленного уравнения. Подстановка значения g в это уравнение дает константу пропорциональности 2Π/g 0,5 , что равно 2,0071, очень похоже на константу пропорциональности 2,0045, полученную в ходе эксперимента.
Используйте виджет «Исследование маятника » ниже, чтобы исследовать влияние длины маятника на его период. Просто введите значение длины в поле ввода и нажмите кнопку Submit 9.кнопка 0004. Поэкспериментируйте с различными значениями длины маятника.
Просто введите значение длины в поле ввода и нажмите кнопку Submit 9.кнопка 0004. Поэкспериментируйте с различными значениями длины маятника.
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Pendulum Motion Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте.
Посетите: Pendulum Motion Interactive
Проверьте свое понимание
1. Маятниковый груз отводят обратно в положение A и отпускают из состояния покоя. Боб совершает обычную дугу окружности и ловится в положении С. Определить положение (А, В, С или все равно), где …
а. … сила тяжести наибольшая?
б.… восстанавливающая сила наибольшая?
в. … скорость самая большая?
д. … потенциальная энергия наибольшая?
е. … кинетическая энергия самая большая
ф. … полная механическая энергия наибольшая?
2. Используйте энергосбережение, чтобы заполнить пропуски на следующей диаграмме.
3. Пара воздушных гимнастов в цирке качается на канатах, прикрепленных к большой возвышенной платформе. Предположим, что исполнителей можно рассматривать как простой маятник длиной 16 м. Определить период одного полного возвратно-поступательного цикла.
4. Какая частота вибрации будет самой высокой?
Маятник A: груз массой 200 г, прикрепленный к нити длиной 1,0 м
Маятник B: груз массой 400 г, прикрепленный к нити длиной 0,5 м
5. Анна Литикал хочет сделать простой маятник, служащий таймером. Она планирует сделать его таким, чтобы его период составлял 1,00 секунды.


 01
01 … восстанавливающая сила наибольшая?
… восстанавливающая сила наибольшая?
Leave A Comment