Решение задачи:
Под действием силы Лоренца заряженная частица в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если частица движется по окружности радиуса \(R\) со скоростью \(\upsilon\), то период обращения \(T\), то есть время, за которое частица сделает один оборот (или пройдет одну длину окружности, равную \(2\pi R\)), можно найти так:
\[T = \frac{{2\pi R}}{\upsilon }\]
Частоту вращения частицы \(\nu\) можно найти как величину, обратную периоду обращения \(T\):
\[\nu = \frac{1}{T}\]
\[\nu = \frac{\upsilon }{{2\pi R}}\;\;\;\;(1)\]
Силу Лоренца \(F_Л\) определяют по следующей формуле:
\[{F_Л} = B\upsilon q\sin \alpha \;\;\;\;(2)\]
Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость заряженной частицы, \(q\) – модуль заряда частицы, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. 2}}}{R}\]
2}}}{R}\]
Имеем:
\[Bq\sin \alpha = \frac{{m\upsilon }}{R}\]
Откуда отношение \(\frac{\upsilon}{R}\), которое нам будет нужно в ходе дальнейшего решения, равно:
\[\frac{\upsilon }{R} = \frac{{Bq\sin \alpha }}{m}\]
Полученное выражение подставим в (1):
\[\nu = \frac{{Bq\sin \alpha }}{{2\pi m}}\]
Запишем полученную формулу дважды для двух случаев, описанных в условии задачи:
\[\left\{ \begin{gathered}
{\nu _1} = \frac{{{B_1}q\sin \alpha }}{{2\pi m}} \hfill \\
{\nu _2} = \frac{{{B_2}q\sin \alpha }}{{2\pi m}} \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда искомое отношение \(\frac{\nu_2}{\nu_1}\) равно:
\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{{B_2}}}{{{B_1}}}\]
По условию величину индукции магнитного поля увеличивают в два раза, то есть \(B_2=2B_1\), поэтому:
\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{2{B_1}}}{{{B_1}}} = 2\]
Ответ: увеличится в 2 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.23 Электрон движется в магнитном поле с индукцией 2 мТл по винтовой линии радиусом
8.2.25 Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают
8.2.26 Протон и дейтрон (ядро изотопа водорода 2h2), имеющие одинаковые скорости, влетают
2.1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле
Основные формулы
Сила, действующая на электрический заряд , движущийся со скоростью в магнитном поле
, (18)
где – вектор магнитной индукции поля.
Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
, (19)
где
–
модуль заряда частицы; –
модуль вектора скорости;
–
модуль вектора индукции магнитного
поля,
–
угол между векторами
и
.
Направление силы определяется по правилу левой руки:
если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции
Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила
, (20)
формула (20) называется формулой Лоренца.
Методические рекомендации
1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.
Эту
силу разделяют на электрическую и
магнитную составляющие. Если заряженная
частица находится только в магнитном
поле, то силу, определяемую выражением
(18), обычно и называют силой Лоренца.
Если заряженная
частица находится только в магнитном
поле, то силу, определяемую выражением
(18), обычно и называют силой Лоренца.
Важная особенность силы Лоренца – она всегда перпендикулярна вектору скорости заряда и поэтому не совершает над зарядом работы. Следовательно, в постоянном магнитном поле энергия движущейся заряженной частицы всегда постоянна.
Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.
2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.
Если
скорость частицы перпендикулярна линиям
магнитной индуции, то частица движется
по круговой траектории (рис.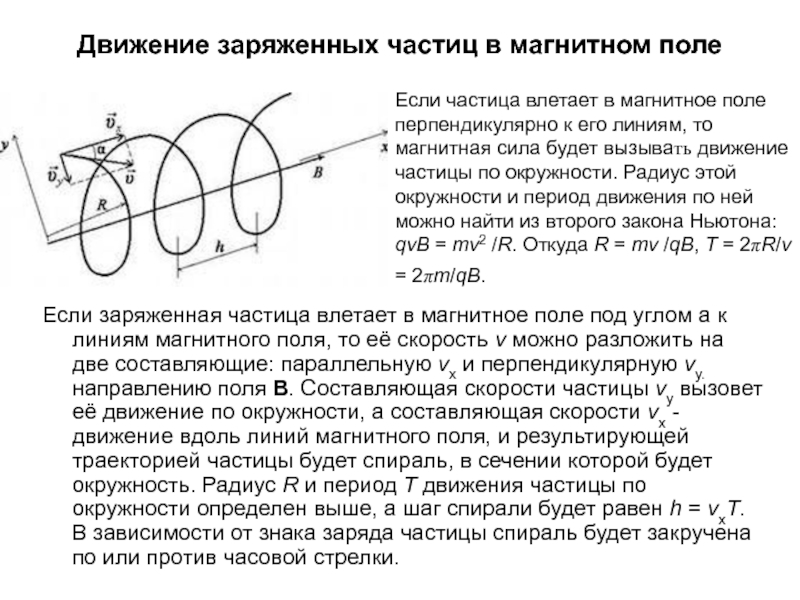
Радиус окружности траектории
;
Рис. 23
период вращения частицы по окружности:
,
где – масса частицы; – модуль скорости частицы; – модуль вектора индукции магнитного поля; – модуль электрического заряда.
Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.
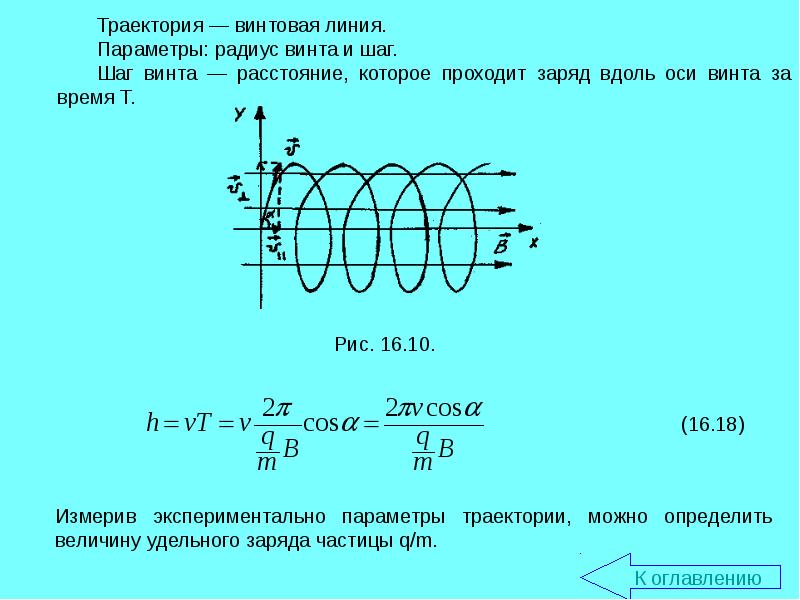
Если угол между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).
Рис. 24
– тангенциальная составляющая скорости ; ;
– нормальная составляющая скорости; ;
–
шаг
винтовой линии; .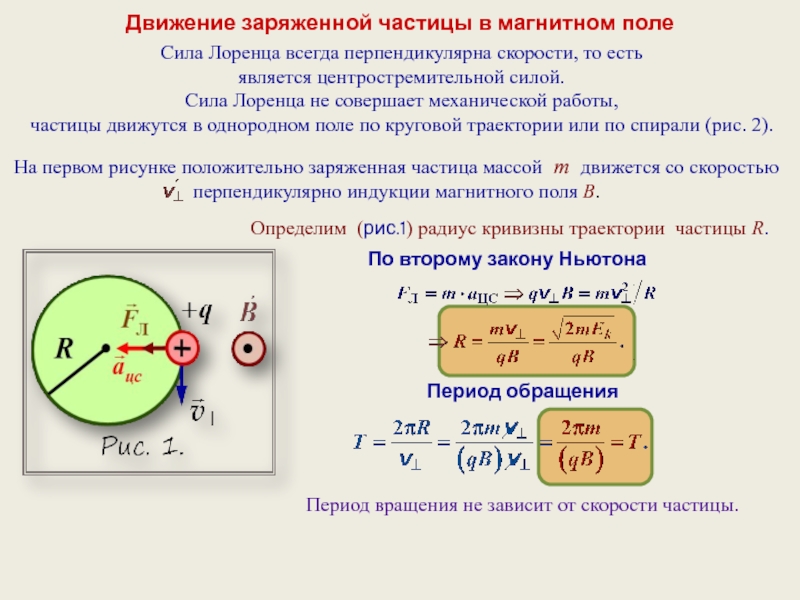
► Векторы и взаимно-перпендикулярны и скорость положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическая и магнитная , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю ( ), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.
Если
силы, действующие на движущуюся заряженную
частицу сонаправлены, то движение
частицы также будет представлять
суперпозицию двух движений: прямолинейного
с ускорением вдоль линий вектора
и
вращательного вокруг линий вектора
.
► Частица влетает в область пространства параллельно векторам и . В этом случае на нее действует только электрическая сила (сила Лоренца , так как и ). Под действием этой силы частица движется прямолинейно с ускорением .
Примеры решения задач
Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля. Сколько оборотов в секунду будет делать протон в магнитном поле?
Решение
На заряженную частицу в магнитном поле действует сила
, (а)
где – заряд частицы, – индукция магнитного поля, – скорость частицы, – угол между векторами и .
В данной задаче , значит протон будет двигаться в магнитном поле по окружности радиуса с центростремительным (нормальным) ускорением
(б)
По второму закону Ньютона
, (в)
где
–
масса частицы.
Приравнивая правые части выражений (б) и (в), с учетом формулы (а), получаем
, (г)
так как , то после небольшого преобразования получаем
. (д)
С другой стороны,
, (е)
где – угловая скорость.
Получаем
. (ж)
Приравняем правые части уравнений (д) и (л), получим
,
откуда выразим – частоту вращения, т. е. число оборотов в секунду,
. (и)
Размерность: .
Подставляем числовые значения в формулу (и):
.
Вычисления дают .
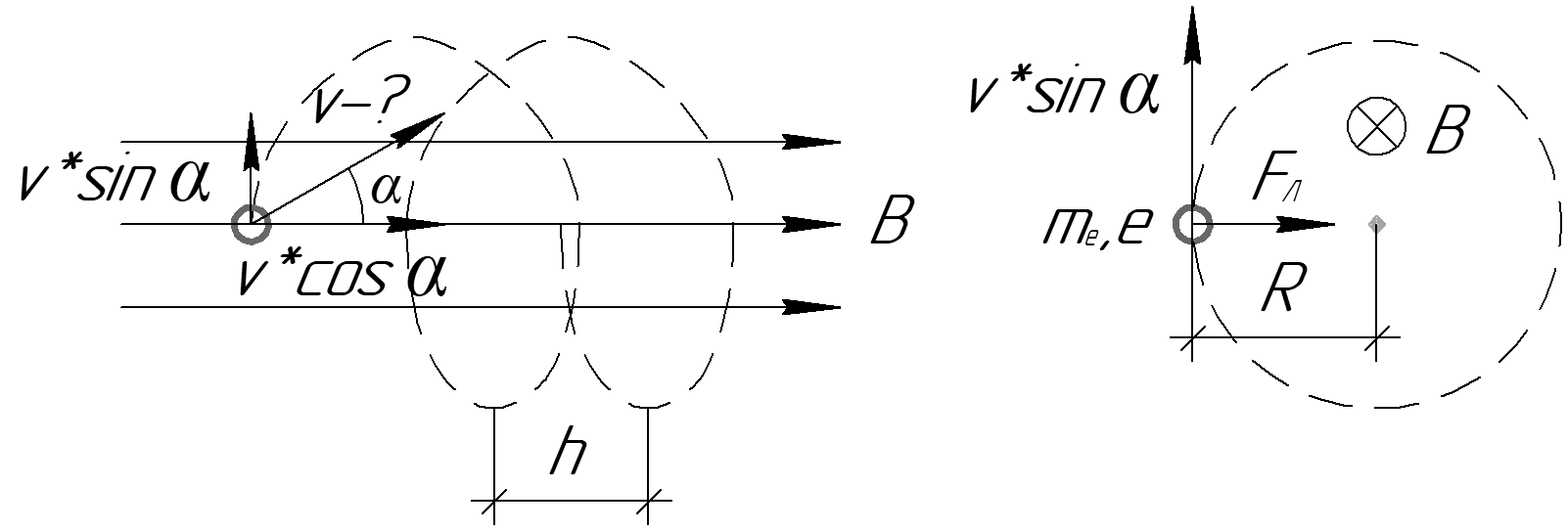
Пример 2. Электрон, имеющий скорость 8·106 м/с, влетает в однородное магнитное поле с индукцией 31,4 мТл под углом 30° к его направлению. Определите радиус и шаг винтовой линии, по которой будет двигаться электрон (рис. 24).
Решение
Скорость разложим на две составляющие: тангенциальную , параллельную линиям индукции магнитного поля и нормальную , перпендикулярную им,
; (а)
. (б)
На электрон действует магнитная сила (благодаря нормальной составляющей скорости)
. (в)
Под действием этой силы электрон будет двигаться по окружности радиуса , который можно найти из условия:
, (г)
так
как сила Лоренца является центростремительной
силой.
Из формулы (г) получаем
, (д)
где – модуль заряда электрона; – масса электрона; – индукция магнитного поля.
Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью .
В результате суперпозиции двух движений электрон будет двигаться по винтовой линии радиусом и шагом винта :
, (е)
где – период движения по окружности,
. (ж)
С учетом формул (б), (д) и (ж), уравнение (е) принимает вид:
. (и)
Размерность: .
Подставляем числовые данные в выражение (и):
.
Вычисления дают:
.
Пример 3. Перпендикулярно магнитному полю с индукцией 0,1 Тл возбуждено электрическое поле напряженностью 1·105 В/м. Перпендикулярно обоим полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Найти скорость этой частицы (рис. 25). Решение Согласно условию задачи, частица движется равномерно и прямолинейно ( ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца , где – электрическая составляющая силы Лоренца, – её магнитная составляющая (рис. 25). |
|
Следовательно, ,
т. е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
откуда скорость частицы равна:
Согласно условию ( ), поэтому
.
Размерность:
.
Подставляем числовые данные: .
Получаем при вычислении: .
Пример 4. Электрон влетает со скоростью 600 м/с в область пространства, где имеются сонаправленные однородные электрическое и магнитное поля, под углом 60° к силовым линиям полей. Напряженность электрического поля 0,2 кВ/м, индукция магнитного поля 20 мТл. С каким ускорением станет двигаться электрон в этой области пространства? (рис. 26). Решение Согласно второму закону Ньютона, ускорение электрона имеет вид: , где
–
сила Лоренца, действующая на электрон
со стороны электрического и магнитного
полей;
–
масса электрона. Сила Лоренца определяется по формуле |
|
,
где – электрическая составляющая силы Лоренца; – её магнитная составляющая (рис. 26).
Вектор направлен противоположно вектору , так как заряд электрона отрицательный. Вектор магнитной силы перпендикулярен вектору магнитной индукции. Следовательно, векторы и взаимно-перпендикулярны.
Модуль силы находится по теореме Пифагора:
,
где – модуль заряда электрона (элементарный заряд).
Ускорение
.
Направление совпадает с направлением вектора , определяемом по правилу сложения векторов.
Подставим числовые значения:
=
600 м/с;
=
60°; =
0,2 кВ/м = 200 В/м;
=
20 мТл = 2·10-2 Тл;
=
1,6 ·10-19 Кл;
=
9,11·10-31 кг.
Вычисления дают: = 3,5 ·1013 м/с2.
Пример 5. Шарик массой , заряженный положительным зарядом и подвешенный на нити длиной , движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол с вертикалью.
Решение
Выберем систему отсчета x0y, начало которой поместим в ту точку пространства, где находится шарик в начальный момент времени. Предположим, что нить – невесома, нерастяжима и неэлектропроводна. Заряженный шарик примем за материальную точку. Заряд шарика будем считать точечным.
На шарик действуют сила тяжести , сила натяжения нити и сила со стороны магнитного поля (рис. 27).
|
|
По второму закону Ньютона
. (а)
(а)
Направление всех сил указано на рис. 27 в предположении, что вектор магнитной индукции направлен вверх, а шарик движется по часовой стрелке.
Запишем уравнение (а) в проекциях на выбранные оси координат
; (б)
. (в)
После преобразования, получаем
; (г)
. (д)
Разделим (г) на (д), получим
. (и)
Шарик движется с нормальным ускорением , (к)
где – линейная скорость шарика по окружности, – радиус окружности.
Из чертежа следует:
. (л)
(л)
Сила Лоренца определяется выражением
, (м)
где = 90° (по условию задачи),
С учетом выражений (к)–(м) уравнение (и) принимает вид:
,
или
.
Решаем квадратное уравнение относительно переменной :
,
получаем
.
Так как модуль скорости > 0, то из последнего выражения следует:
.
Кинетическая энергия определяется соотношением:
.
Задачи для самостоятельного решения
1.
Пучок
электронов движется в вакууме в магнитном
поле с напряженностью 5,56·103 А/м по окружности радиусом 3 см.
Определите скорость и энергию электронов,
период обращения и момент импульса.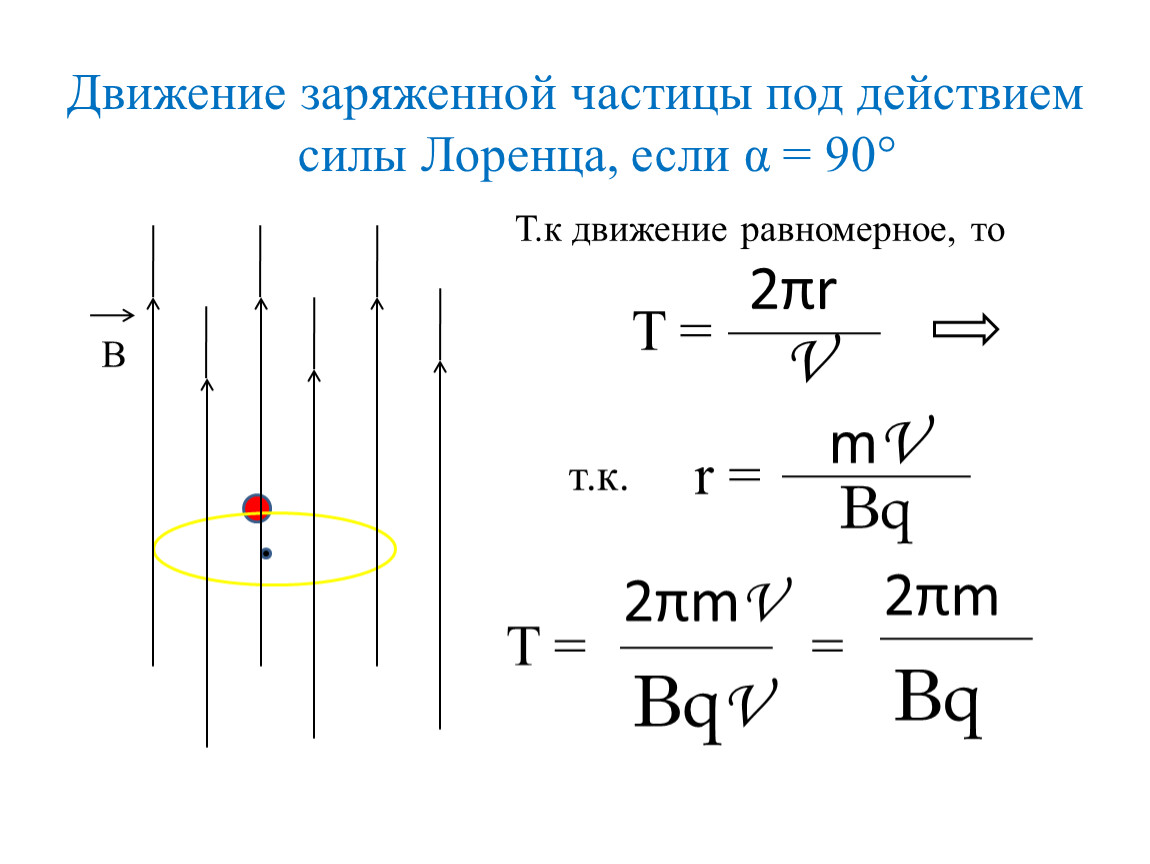
(Ответ: = 36,3·106 м/с; = 33·10-23 Дж; = 5·10-9 с; = 99·10-26 (кг·м2)/с).
2. В однородном магнитном поле с индукцией 0,1 Тл по окружности движется электрон. Найти величину эквивалентного кругового тока, созданного движением электрона.
(Ответ: = 4,5·10-10 А).
3. Однозарядный ион натрия прошел ускоряющую разность потенциалов 1 кВ и влетел в однородное магнитное поле с индукцией 0,5 Тл перпендикулярно силовым линиям поля. Определите относительную массу иона, если он описал окружность радиусом 4,37 см.
(Ответ: 23 а.е.м.).
4.
Протон,
прошедший ускоряющую разность потенциалов
600 В, влетел в однородное магнитное поле
с напряженностью 2,4·104 А/м перпендикулярно линиям магнитной
индукции. Найти радиус описанной протоном
окружности, его импульс и частоту
вращения протона в магнитном поле.
(Ответ: = 0,33 м; = 18·10-21 Н·с; = 3·103с-1).
5. Два иона, имеющие одинаковый заряд и прошедшие одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле. Первый ион движется по дуге окружности радиусом 5 см, второй – по дуге окружности радиусом 2,5 см. Определите отношение масс ионов.
(Ответ: ).
6. Электрон влетает в область магнитного поля ширины . Скорость электрона перпендикулярна как индукции поля, так и границам области. Под каким углом к границам области электрон вылетит из магнитного поля?
(Ответ: , если ; рад, если ).
7. Предполагая, что электрон в атоме водорода движется по круговой орбите радиусом 53 пм, определите период обращения электрона вокруг ядра и индукцию магнитного поля, создаваемого движущимся электроном в центре его орбиты.
(Ответ:
=
1,5·10-16 с;
=
12,45 Тл).
8. Частица, имеющая элементарный заряд, влетает в однородное магнитное поле под углом 45° к линиям индукции и движется по винтовой линии с шагом 2 см. Определите импульс частицы, если индукция поля равна 10-2 Тл.
(Ответ: = 7,2·10-24 кг·м/с).
9. Электрон, кинетическая энергия которого 1,5 МэВ, движется по окружности в однородном магнитном поле с индукцией 20 мТл. Определите период обращения электрона.
(Ответ: = 7 нс).
10. Электрон в однородном магнитном поле движется по винтовой линии радиусом 5 см и шагом 20 см. Определить скорость электрона, если индукция магнитного поля 0,1 Тл.
(Ответ: = 1,04 Мм/с).
11.
Протон,
находящийся в магнитном поле с индукцией
20 мТл описывает окружность радиусом 40
см. Найти импульс протона и его кинетическую
энергию.
Найти импульс протона и его кинетическую
энергию.
(Ответ: = 1,3·10-21 кг·м/с; = 5·10-16 Дж).
12. Протон и альфа-частица влетают в однородное магнитное поле перпендикулярно его силовым линиям. Во сколько раз различаются радиусы окружностей, по которым движутся эти частицы, если у них одинаковы: а) скорость; б) кинетическая энергия? Заряд альфа-частицы в два раза больше заряда протона, а масса альфа-частицы в четыре раза больше массы протона.
(Ответ: (а) ; б) ).
13. В масс-спектрографе заряженная частица, пролетев без начальной скорости ускоряющую разность потенциалов , влетает в однородное магнитное поле индукцией перпендикулярно магнитным линиям. Удельный заряд частицы . Определить диаметр окружности , по которой стала двигаться частица.
(Ответ: ).
14. В вертикальном направлении создано однородное магнитное поле индукцией . Шарик массой и зарядом , подвешенный на нити длиной , движется по окружности так, что нить составляет угол с вертикалью. Найти угловую скорость движения шарика.
(Ответ: ).
15. Однозарядные ионы гелия и водорода, ускоренные из состояния покоя в электрическом поле напряжением 2 кВ, влетают вместе в магнитное поле индукцией 100 мТл перпендикулярно магнитным линиям. Описав полуокружность, они попадают на фотопластинку. Найти расстояние между следами этих ионов на фотопластинке.
(Ответ: = 1,3 см).
16. Электрон с кинетической энергией 1 кэВ попал в однородное магнитное поле с индукцией 21 мТл и стал двигаться по окружности. Определить магнитный момент эквивалентного кругового тока.
(Ответ: = 7,6·10-15 А·м2).
17.
Электрон,
ускоренный разностью потенциалов 300 В,
движется параллельно прямолинейному
длинному проводу на расстоянии 4 мм от
него. Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
(Ответ: = 4·10-16 Н).
18. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона 4·107 м/с. Индукция магнитного поля 1 мТл. Найти тангенциальное и нормальное ускорения электрона в магнитном поле. (Ответ: = 0; = 7·1015 м/с2). 19.
Пучок
электронов, ускоренных разностью
потенциалов 300 В, влетает в однородное
магнитное поле, направленное от чертежа
«к нам»
(рис. 28). Ширина
поля
=
2,5 см. В отсутствие магнитного поля
пучок электронов дает пятно в точке
А флуоресцирующего экрана, расположенного
на расстоянии
=
5 см от края полюсов магнита. |
|
(Ответ: x = 4,9 см).
20. В
установке для разделения изотопов
U235 и U238 пучок однократно ионизованных
ускоренных ионов с энергией 5 кэВ
попадает от источника через щель S
(рис. 29) в однородное магнитное поле,
перпендикулярное к плоскости рисунка.
В магнитном поле ионы разных масс
движутся по различным окружностям и,
совершив полуоборот, попадают в
приемники. Конструкция последних
должна быть такова, чтобы расстояние
между пучками изотопов на выходе было
не меньше
=
5 мм. (Ответ: 4000 Гс). |
|
21. В конденсаторе, электроды которого составляют часть коаксиальных цилиндрических поверхностей радиусами 5 и 6 см, вдоль оси цилиндров действует однородное магнитное поле с индукцией 0,2 Тл (рис. 30). Через узкую щель в диафрагме АА в конденсатор влетает α-частица с энергией 1 кэВ. Какую разность потенциалов следует создать между электродами конденсатора, чтобы α-частица прошла посередине между электродами? (Внешний электрод имеет отрицательный потенциал).
(Ответ: = 38,5 В).
22.
В
магнетроне анод представляет металлический
цилиндр радиусом
=1
см, а катод – металлическую нить радиусом ,
расположенную по оси цилиндра (рис. 31).
Постепенно увеличивая индукцию магнитного
поля, направленного вдоль оси цилиндра,
добились того, что при анодном напряжении
100 В и индукции 6,7·10-3 Тл анодный ток стал равен нулю. Какое
значение удельного заряда получается
по результатам этого опыта?
Какое
значение удельного заряда получается
по результатам этого опыта?
(Ответ: = 1,76·1011 Кл/кг).
Рис. 30 Рис. 31
23. Магнитное поле напряженностью 8 кА/м и электрическое поле напряженностью 1 кВ/м направлены одинаково. Электрон влетает в электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное и полное ускорение электрона. Задачу решить для случая, когда скорость электрона направлена параллельно силовым линиям полей.
(Ответ: = 0; = 1,76·1014 м/с2).
24.
Магнитное
поле напряженностью 8 кА/м и электрическое
поле напряженностью 1 кВ/м направлены
одинаково. Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
(Ответ: = 0; = 2,5·1014 м/с2).
25. Магнитное поле с индукцией 0,5 мТл направлено перпендикулярно электрическому полю напряженностью 1 кВ/м. Электрон влетает в электромагнитное поле перпендикулярно к плоскости, в которой лежат векторы и . Найти скорость электронов, если при одновременном действии обоих полей пучок не испытывает отклонения. Каким будет радиус траектории движения электронов при условии включения одного магнитного поля?
(Ответ: = 2·106 м/с; = 2,3 см)
26.
Электрон
влетает в плоский горизонтальный
конденсатор параллельно его пластинам
со скоростью 107 м/с. Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
(Ответ: = 5 мм; = 3,6 см).
27. Протон влетел в скрещенные под углом 120° магнитное и электрическое поля. Определить ускорение протона, если его скорость 4·105 м/с перпендикулярна векторам и , напряженность электрического поля 20 кВ/м, индукция магнитного поля 50 мТл.
(Ответ: = 3,3·1012 м/с2)
28.
Через
сечение алюминиевой
пластинки (
– толщина,
–
высота) пропускается ток
=
5 А. Пластинка помещена в магнитное поле,
перпендикулярное к ребру
и
направлению тока. Найти возникающую
при этом поперечную разность потенциалов.
Индукция магнитного поля
=
0,5 Тл. Толщина пластинки
=
0,1 мм. Концентрацию электронов проводимости
считать равной концентрации атомов.
Концентрацию электронов проводимости
считать равной концентрации атомов.
(Ответ: = 2,7 мкВ).
29. Через сечение медной пластинки ( – толщина, – высота) пропускается ток = 20 А. При помещении пластинки в магнитное поле, перпендикулярное к ребру и направлению тока, возникает поперечная разность потенциалов = 3,1 мкВ. Индукция магнитного поля = 1 Тл. Найти концентрацию электронов проводимости в меди и их скорость при этих условиях.
(Ответ: = 8,1 ·1028 м-3; = 0,31 мм/с).
30.
Заряженная
частица, двигаясь перпендикулярно
скрещенным под прямым углом электрическому
(
= 400 кВ/м) и магнитному (
= 0,25 Тл) полям,
не испытывает отклонений от своей
траектории при определенной скорости.
Определить эту скорость и возможные
отклонения от нее, если значения индукции
магнитного и напряженности электрического
полей могут быть обеспечены с точностью,
не превышающей 0,2 %.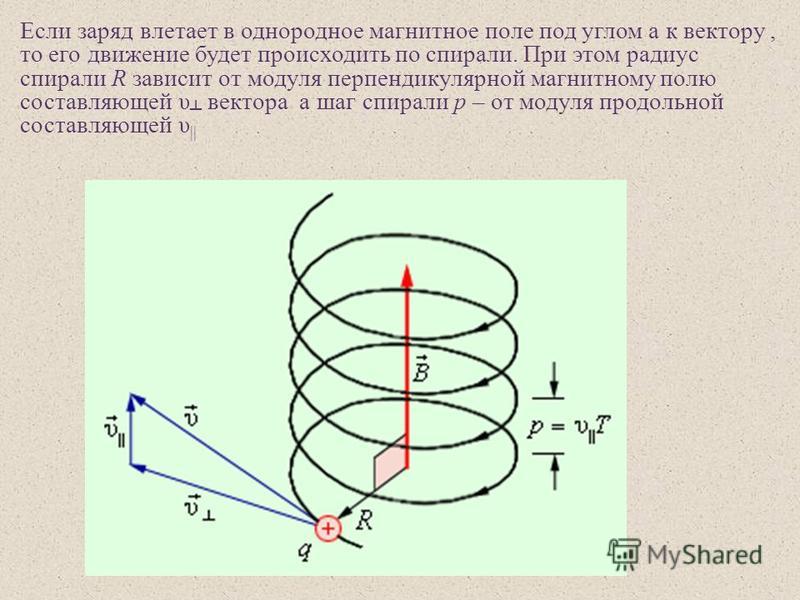
(Ответ: = 1,6·106 м/с; = 6,4 ·103 м/с).
Заряженная частица входит в магнитное поле H со своей начальной скоростью
Вопрос
Обновлено: 26.04.2023БЕЗОШИБОЧНЫЙ-МАГНИТНЫЙ ЭФФЕКТ ТОКА-Упражнение
20 видеоРЕКЛАМА
9 0002 Текст РешениеА
Прямая линия
B
Окружность
C
Эллипс
D
Спираль
Ответ
Правильный ответ D 90 003
Ответ
Пошаговое решение от экспертов, которое поможет вам в сомнениях оформление и отличные оценки на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Видео по теме
Заряженная частица входит в однородное магнитное поле с вектором скорости под углом 45∘ к магнитному полю. Шаг винтовой траектории, по которой движется частица, равен p. радиус спирали будет
11313921
Заряженный заряд попадает в однородное магнитное поле с вектором скорости под углом 45∘ к магнитному полю. Шаг винтовой траектории, по которой следуют частицы, равен ρ. Радиус спирали будет 9@ с линиями поля. Путь частицы:
Шаг винтовой траектории, по которой следуют частицы, равен ρ. Радиус спирали будет 9@ с линиями поля. Путь частицы:
344756639
Text Solution
क चुम्बकीय क्षेत्र B में प्रवेश करता है चुम्बकी य क्षेत्र B के साथ का 45∘ कोण बनाते हुए प्रविष्ट आव ेशित कण का पथ होगा|
358842894
ेत्र में बल रेखाओं से 850 का कोण बनाता हुआ प्रवेश करता है। कण का पथ वृत्ताकार है।
364564701
Заряженная частица входит в магнитное поле с вектором скорости, составляющим угол 30∘ по отношению к направлению магнитного поля. Путь частицы равен
481099448
चुम्बकीय क्षेत्र की दिशा के लम्बवत् है तो उसका पथ होगा
565112904
Заряженная частица входит в магнитное поле B с начальной скоростью v, составляющей угол π4 и B. путь частицы будет
571107736
Текст Решение
Заряженная частица входит в магнитное поле B с начальной скоростью, составляющей угол 45° с B. Путь частицы будет
9@ входит в однородное магнитное поле с вектором скорости под углом . Шаг спирального пути, по которому движется частица, равен p. Радиус Кундалини будет:
Шаг спирального пути, по которому движется частица, равен p. Радиус Кундалини будет:647720268
Заряженная частица движется в магнитном поле vec(b)=1 vec(b) wi-Turito
Вы уверены, что хотите выйти?
Вопрос
- прямая
- круг
- спиральный
- нет
Правильный ответ: спиральный
Вопросы по теме
Общие
Физика-
круговая орбита радиуса R, перпендикулярная однородной магнитной индукции Если кинетическая энергия удвоится, а магнитная индукция утроится, радиус станет равен
. Электрон с кинетической энергией T движется по круговой орбите радиусом R, перпендикулярной однородной магнитной индукции. Если кинетическая энергия удвоится, а магнитная индукция утроится, радиус будет стать
Общая физика
Общая
Физика-
Два длинных проводника расположены, как показано выше, в виде перекрывающихся цилиндров, каждый из которых имеет радиус r, центры которых разделены расстоянием d.
 Ток плотностью J течет в плоскость страницы по заштрихованной части одного проводника, и такой же ток вытекает из плоскости страницы по заштрихованной части другого проводника, как показано на рисунке. Каковы величина и направление магнитного поля в точке А?
Ток плотностью J течет в плоскость страницы по заштрихованной части одного проводника, и такой же ток вытекает из плоскости страницы по заштрихованной части другого проводника, как показано на рисунке. Каковы величина и направление магнитного поля в точке А? Два длинных проводника расположены, как показано выше, в виде перекрывающихся цилиндров, каждый из которых имеет радиус r, центры которых разнесены на расстояние d. Ток плотностью J течет в плоскость страницы по заштрихованной части одного проводника, и такой же ток вытекает из плоскости страницы по заштрихованной части другого проводника, как показано на рисунке. Каковы величина и направление магнитного поля в точке А?
физика общая
общая
физика-
Длинный прямой металлический стержень имеет очень длинное отверстие радиуса «а», просверленное параллельно оси стержня, как показано на рисунке. Если по стержню течет ток «i», найдите значение магнитной индукции на оси отверстия, где OC = c
Длинный прямой металлический стержень имеет очень длинное отверстие радиуса «a», просверленное параллельно оси стержня.
 как показано на рисунке. Если по стержню течет ток i, найдите значение магнитной индукции на оси отверстия, где OC = c
как показано на рисунке. Если по стержню течет ток i, найдите значение магнитной индукции на оси отверстия, где OC = c Общая физика
Общие сведения
Физика-
Полый цилиндр бесконечной длины, по которому по окружности течет постоянный ток на единицу длины, как показано на рисунке. Магнитное поле внутри цилиндра равно
Полый цилиндр бесконечной длины, по окружности которого течет постоянный ток на единицу длины, как показано на рисунке. Магнитное поле внутри цилиндра равно
Общая физика
Общая
Общая физика
Длинный прямой провод, по которому течет ток I, согнут в средней точке под углом 45°. Индукция магнитного поля в точке P, удаленной R от точки изгиба, равна:
Длинный прямой провод, по которому течет ток I, изогнут в средней точке под углом 45°. Индукция магнитного поля в точке P, удаленной от точки изгиба R, равна:
Общая физика
Общая
Общая физика
По длинной тонкостенной трубе радиусом R протекает ток I по ее длине.
 Плотность тока одинакова по окружности трубы. Магнитное поле в центре трубы из-за показанной четверти части трубы составляет
Плотность тока одинакова по окружности трубы. Магнитное поле в центре трубы из-за показанной четверти части трубы составляет По длинной тонкостенной трубе радиуса R течет ток I по всей ее длине. Плотность тока одинакова по окружности трубы. Магнитное поле в центре трубы из-за четверти показанной части трубы составляет
Общая физика
Общая
Физика-
Найдите магнитное поле в точке P из-за показанного расположения
Найдите магнитное поле в точке P из-за показанного расположения
Общая физика
Общая
Физика-
Два взаимно перпендикулярных проводника с токами I
1 и I 2 лежат в одной плоскости. Геометрическое место точки, в которой магнитная индукция равна нулю, представляет собой. Два взаимно перпендикулярных проводника с токами I
1 и I 2 лежат в одной плоскости. Геометрическое место точки, в которой магнитная индукция равна нулю, представляет собойОбщая физика
Общая физика
0134 Бесконечное количество прямых проводов, каждый из которых несет ток I, расположены одинаково, как показано на рисунке. Соседние провода имеют ток в противоположном направлении. Суммарное магнитное поле в точке P равно
Соседние провода имеют ток в противоположном направлении. Суммарное магнитное поле в точке P равно
Бесконечное число прямых проводов, по каждому из которых течет ток I, расположены одинаково, как показано на рисунке. Соседние провода имеют ток в противоположном направлении. Чистое магнитное поле в точке P равно
Общая физика
Общая
Общая физика
Ток I течет по замкнутому пути в горизонтальной плоскости круга, как показано на рисунке. Путь состоит из восьми дуг с чередующимися радиусами r и 2r. Каждый сегмент дуги образует одинаковый угол в общем центре P. Магнитное поле, создаваемое путем тока в точке P, равно
Ток I течет по замкнутому пути в горизонтальной плоскости круга, как показано на рисунке. Путь состоит из восьми дуг с чередующимися радиусами r и 2r. Каждый сегмент дуги образует равный угол в общем центре P. Магнитное поле, создаваемое путем прохождения тока в точке P, равно взаимно перпендикулярны друг другу и каждый имеет свой центр в начале системы координат.
 Если через каждое кольцо протекает ток I, то величина магнитного поля в общем центре равна
Если через каждое кольцо протекает ток I, то величина магнитного поля в общем центре равна Три кольца, каждое из которых имеет одинаковый радиус R, расположены взаимно перпендикулярно друг другу и каждое имеет центр в начале системы координат. Если через каждое кольцо протекает ток I, то величина магнитного поля в общем центре равна
Общая физика
Общая
Общая физика
Заряженная частица A с зарядом q = 2 C имеет скорость v = 100 РС. Когда он проходит через точку А и имеет скорость в указанном направлении. Напряженность магнитного поля в точке B из-за этого движущегося заряда равна (r = 2 м).
Заряженная частица A с зарядом q = 2 Кл имеет скорость v = 100 м/с. Когда он проходит через точку А и имеет скорость в указанном направлении. Напряженность магнитного поля в точке B из-за этого движущегося заряда равна (r = 2 м).
Общая физика
Общая
Физика-
Магнитное поле, создаваемое токопроводящей прямоугольной петлей стороны a в точке, расположенной симметрично на расстоянии a/2 от ее центра (как показано)
Магнитное поле, создаваемое токопроводящей прямоугольной петлей со стороной а в точке, расположенной симметрично на расстоянии а/2 от ее центра (как показано)
общая физика
общая
физика-
Суммарное магнитное поле в центре круга O из-за контура с током, как показано на рисунке (q
< 180°)Суммарное магнитное поле в центр окружности O из-за контура с током, как показано на рисунке (q
< 180°)Общая физика
Общая
Физика-
Через каждый из изогнутых проводов протекает ток силой 1 ампер.


 При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл.
При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл.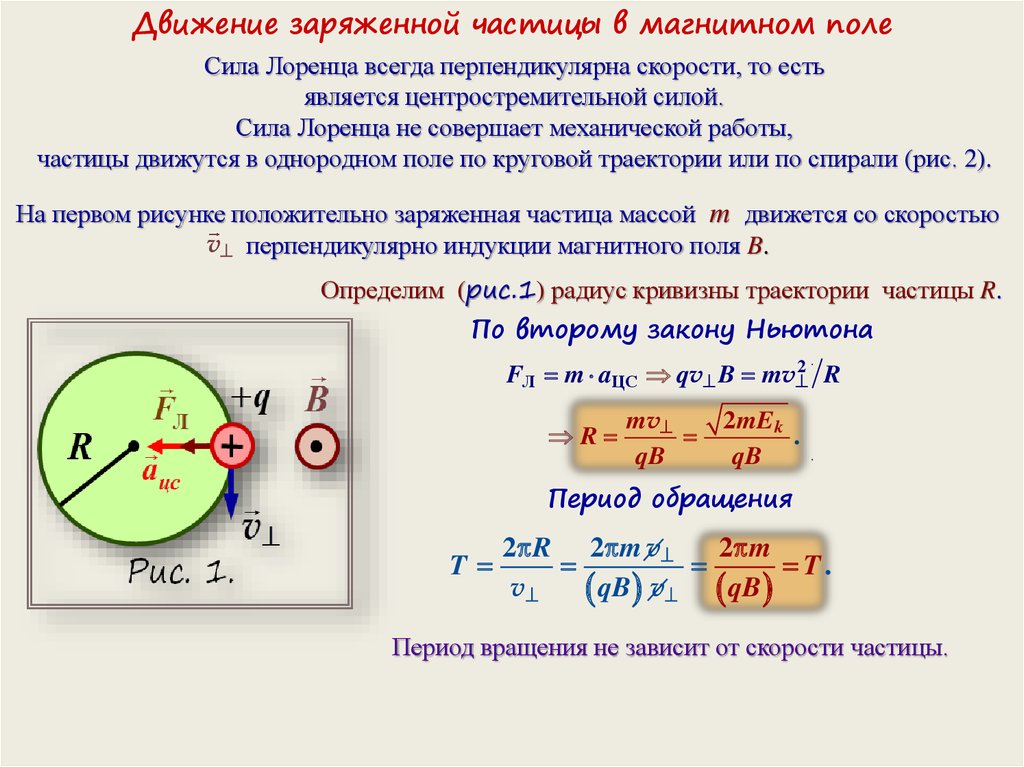 Каково должно быть магнитное
поле, удовлетворяющее этому
условию?
Каково должно быть магнитное
поле, удовлетворяющее этому
условию?
Leave A Comment