Задачи. Равномерное движение по окружности — PhysBook
Уровень А
1. Колесо совершает за одну минуту:
а) 30 оборотов;
б) 1500 оборотов.
Определите его период.
Решение
2. Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
Решение
3. Определите частоту движения:
а) секундной;
б) минутной, – стрелок механических часов.
Секундная стрелка часов совершает один оборот за 1 мин, минутная стрелка – один оборот за 1 ч.
Решение
4. Частота вращения воздушного винта самолета 25 Гц. За какое время винт совершает 3000 оборотов.
Решение
5. Период вращения Земли вокруг своей оси равен 1 сут. Определите частоту ее вращения.
Решение
6. Колесо совершило 15 полных оборотов. Определите его угловое перемещение.
Решение
7. Колесо радиуса 0,5 м прокатилось 100 м. Определите угловое перемещение колеса.
Решение
Решение
9. Угловая скорость барабана сепаратора 900 рад/с. Определите угловое перемещение барабана за 15 с.
Решение
10. Определите угловую скорость вала, вращающегося:
а) с периодом 10 с;
б) с частотой 30 Гц.
Решение
11. Маховик вращается с постоянной угловой скоростью 9 рад/с. Определите:
а) частоту его вращения;
б) период его вращения.
Решение
12. Укажите направление скорости в точках А, В, С, D (рис. 1), если круг вращается:
а) по часовой стрелке;
б) против часовой стрелки.
Рис. 1
Решение
13. Колесо велосипеда имеет радиус 25 см. Определите линейную скорость точек обода колеса, если оно вращается с частотой 4 Гц.
Решение
14. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
Решение
15. Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2,0 км/с. Найдите период вращения Солнца вокруг своей оси, если радиус Солнца 6,96∙108 м.
Решение
16. Тело движется по окружности радиусом 3 м со скоростью 12π м/с. Чему равна частота обращения?
Решение
17. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость тела, если известно, что его угловая скорость равна
Решение
18. Спортсмен бежит равномерно по окружности радиусом 100 м со скоростью 10 м/с. Определите его угловую скорость.
Решение
19. Укажите направление ускорения в точках A, B, C, D при движении по окружности (рис. 2).
Рис. 2
Решение
20. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
Решение
21. Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 1 м/с
Решение
22. С какой скоростью велосипедист проходит закругление велотрека радиусом 50 м, если он имеет центростремительное ускорение 2 м/с2?
Решение
23. Шкив вращается с угловой скоростью 50 рад/с. Определите центростремительное ускорение точек находящихся на расстоянии 20 мм от оси вращения.
Решение
24. Земля вращается вокруг своей оси с центростремительным ускорением 0,034 м/с2. Определите угловую скорость вращения, если радиус Земли 6400 км.
Решение
Уровень B
1. Может ли тело двигаться по окружности без ускорения?
Решение
2. Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей «Союз-4» и «Союз-5» 16 января 1969 г., имела период вращения 88,85 мин и среднюю высоту над поверхностью Земли 230 км (считайте орбиту круговой). Найдите среднюю скорость движения станции. Радиус Земли принять равным 6400 км.
Решение
3. Искусственный спутник Земли (ИСЗ) движется по круговой орбите со скоростью 8,0 км/с с периодом вращения 96 мин. Определите высоту полета спутника над поверхностью Земли. Радиус Земли принять равным 6400 км.
Решение
4. Какова линейная скорость точек Земной поверхности на широте Санкт-Петербурга (60°) при суточном вращении Земли? Радиус Земли принять равным 6400 км.
Решение
5. Допустимо ли насадить точильный круг на вал двигателя, делающего 2850 оборотов в минуту, если на круге имеется штамп завода «35 м/с, Ø 250 мм»?
Решение
6. Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?
Решение
7. Какова угловая скорость вращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов?
Решение
8. За какое время колесо, имеющее угловую скорость 4π рад/с, сделает 100 оборотов?
Решение
9. Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за 4 с. Какова угловая скорость вращения диска?
Решение
10. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость движения тела и пройденный им путь, если известно, что его угловое перемещение за 10 с равно 1,57 рад.
Решение
11. Как изменится линейная скорость вращения материальной точки по окружности, если угловую скорость точки увеличить в 2 раза, а расстояние от точки до оси вращения уменьшить в 4 раза?
Решение
12. Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?
Решение
Решение
14. Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль, если его средняя высота над Землей 320 км? Радиус Земли принять равным 6400 км.
Решение
15. Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.
Решение
16. Две материальные точки движутся по окружностям радиусами R
Решение
17. Две материальные точки движутся по окружностям радиусами R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.
Решение
www.physbook.ru
ФИЗИКА: Задачи на Движение тела по окружности
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2. С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3. Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4. Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5. Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6. Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7. Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8. Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9. Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10. ОГЭ Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11. ЕГЭ Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
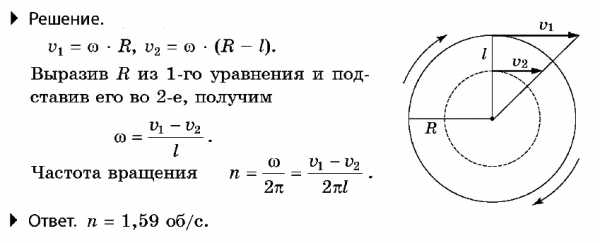
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
ЗАДАЧИ на Движение тела по окружности
5 (100%) 2 votesuchitel.pro
Движение по окружности. Примеры решения задач по физике. 9-10 класс
Движение по окружности. Примеры решения задач по физике. 9-10 класс
Задачи по физике — это просто!
Вспомним
Формулы центростремительного ускорения и центростремительной силы:
Формулы скорости движения тела по окружности и частоты вращения:
Единица измерения частоты вращения — 1/с или оборот/с.
А теперь к задачам!
Элементарные задачи из курса школьной физики на движение по окружности с постоянной по модулю скоростью.
Задача 1
C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?
Задача 2
Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.
Задача 3
Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?
Задача 4
С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?
Задача 5
Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?
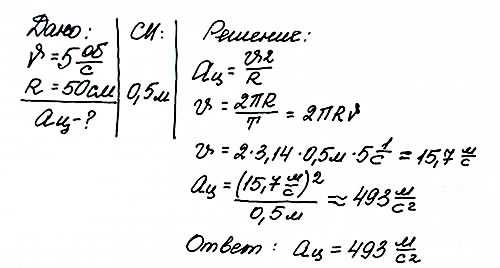
Задача 6
Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.
Задача 7
Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?
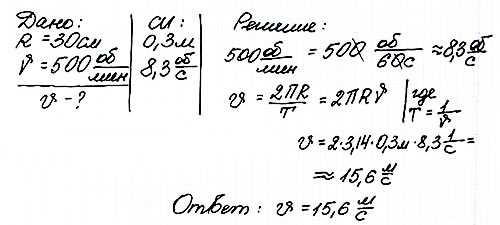
Задача 8
Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?
Задача 9
Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.
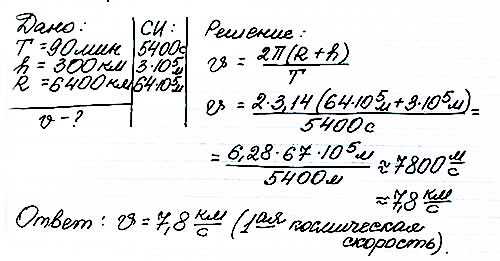
class-fizika.ru
Движение по окружности — задачи
Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость и модуль средней скорости .
Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.
Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с
Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол .
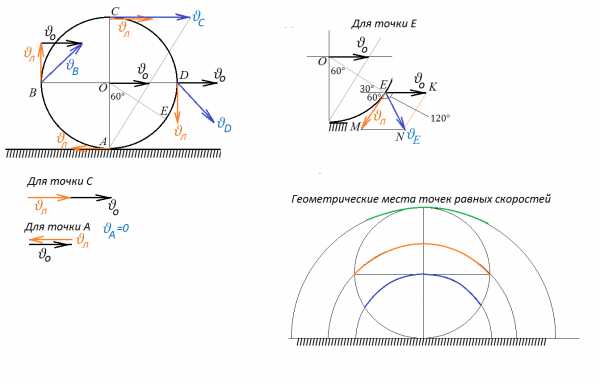
Скорость точек окружности
Решение:
Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с. Линейные скорости показаны для точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: . В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.
Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.
Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол . Тогда в параллелограмме угол , а так как
, то все углы в треугольнике равны и он равносторонний, то есть м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.
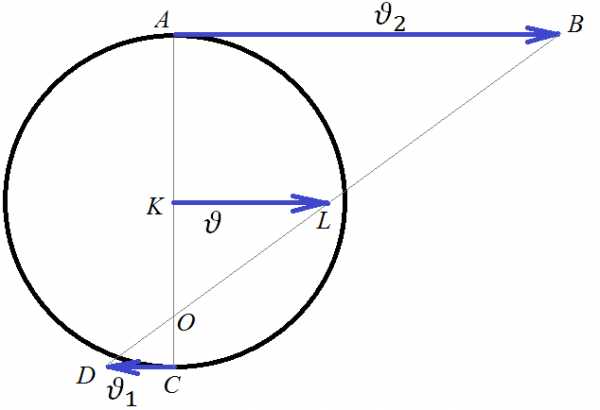
Пробуксовывание
Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки м/c, а верхней – м/c.
Решение:
Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и запишем отношения сходственных сторон:
Тогда
Тогда
Теперь обратимся к подобным треугольникам и . Для них отношение сходственных сторон равно:
Откуда м/с.
Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и , при этом не забываем о векторном сложении скоростей, берем скорость со знаком «минус»:
м/с.
Ответ: 4 м/с.
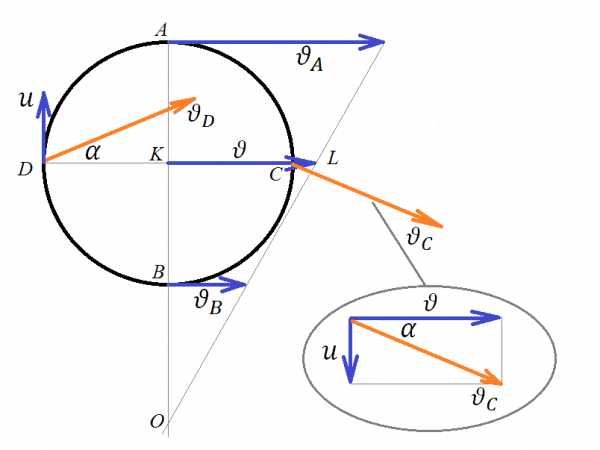
Проскальзывание
Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки B м/с. Определить скорость концов диаметра , перпендикулярного к , для того же момента времени. Под какими углами они направлены к горизонту?
Решение:
Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:
м/с.
Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра колеса , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек и равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:
Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как
Ответ: ,
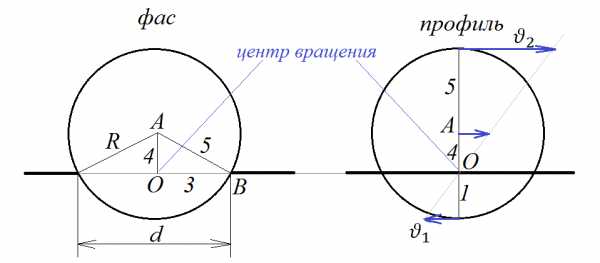
Шарик катится по двум линейкам
Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?
На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки будет
Таким же способом определяем скорость верхней точки :
Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.
Задача 6. Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное , нормальное и полное ускорения в момент времени с.
Решение.
Путь:
Производная пути – линейная скорость:
Вторая производная – тангенциальное ускорение:
Нормальное ускорение:
Полное ускорение:
Задача7. Угол поворота диска радиусом см изменяется со временем по закону . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.
Решение: угловая скорость – производная угла:
Угловое ускорение – производная угловой скорости:
Линейная скорость:
Задача 8. Точка движется по окружности с постоянным угловым ускорением рад/. Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.
Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.
Известно, что нормальное ускорение , тангенциальное ускорение . При этом , или . Тогда
Искомый угол:
Ответ:
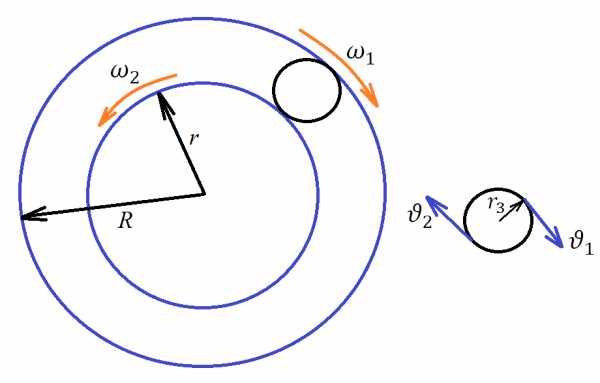
Два концентрических колеса
Задача 9. Два концентрических колеса радиусами см и см вращаются с угловыми скоростями рад/c и рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.
Решение: определим радиус маленького (третьего) колеса, м:
Определим линейную скорость точек первого колеса:
Определим линейную скорость точек второго колеса:
Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:
Ответ: 20 рад/с
Задача 10. Гайку закручивают на болт за время . Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .
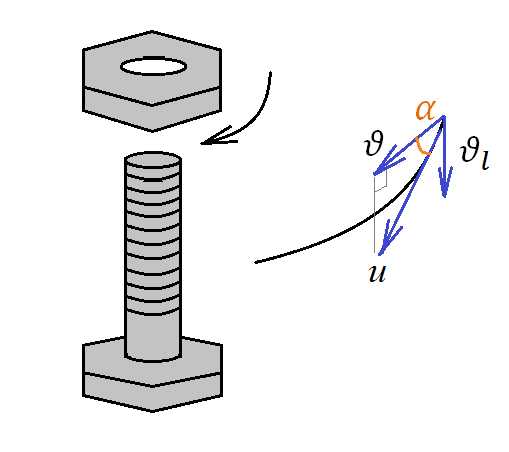
Скорость вращения гайки по ходу завинчивания на болт
Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (). Тогда .
Из рисунка видно, что
С другой стороны, так как длина болта , а гайка спускается по нему за время , то
Тогда
И можно определить :
Тогда
Ответ:
easy-physic.ru
Задачи на движение по кругу
Вашему вниманию представляются задачи на движение по кругу, в том числе задачи со стрелками часов, которые часто вызывают трудности.
Задача 1. Двигаясь по окружности в одном направлении, две точки встречаются каждые 12 минут. Так же известно, что первая точка обходит всю окружность на 10 секунд быстрее, чем вторая. Определить, сколько времени потребуется второй точке, чтобы обойти всю окружность.
Составим первое уравнение по первому предложению задачи: раз точки, двигаясь с разными скоростями, встречаются, следовательно, одна обгоняет другую ровно на 1 круг. Тогда
Здесь – скорость «догоняющей» точки, длина круга принята за 1, минуты переведены в секунды.
Время, за которое первая точка обходит 1 круг, равно , а время, за которое вторая точка обходит круг, равно . Между этими значениями разница в 10 с (по условию), откуда получим второе уравнение: .
Можем выразить скорость из второго уравнения: , или
Подставим полученное значение в первое уравнение:
Решение квадратного уравнения, которое получится, приводить не буду, один из корней отрицательный, то есть не подходит по условию задачи, а положительный равен . Иными словами, перая точка двигается с такой скоростью, что обходит 1 круг за 80 секунд. Так как вторая обходит круг на 10 секунд дольше, то время ее движения равно 90 с.
Ответ: 90 с.
Задача 2. На окружности взята некоторая точка А. Из этой точки одновременно выходят два тела, которые движутся по данной окружности равномерно в противоположных направлениях. В момент их встречи оказалось, что первое тело прошло на 10 метров больше второго. Кроме того, первое тело пришло в точку А через 9 секунд, а второе – через 16 секунд после встречи. Определить длину окружности в метрах.
Да, представьте себе, иногда в задачах на движение объекты двигаются в разные стороны!
Пусть – скорость одной точки, движущейся по часовой стрелке, а – скорость второй. Тогда до встречи первая точка пройдет расстояние , а вторая пройдет расстояние .
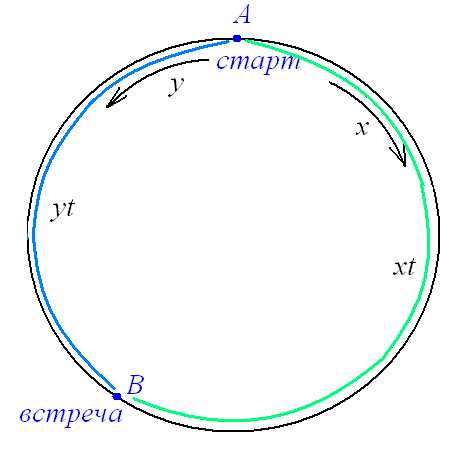
Тела на круговой дистанции
После встречи первой точке до места старта нужно пройти такое расстояние, какое вторая прошла до встречи, и тратит первая точка на это время, равное 10 с, а второй наоборот, нужно пройти то расстояние, которое прошла до встречи первая, и тратит она на это 16 с. Получим такие равенства:
Выразим время движения точек до встречи :
откуда имеем
По условию, первое тело прошло на 10 м больше второго, то есть
Заменяем в этом уравнении одну из неизвестных:
И находим : , откуда .
Полная длина круга равна:
Ответ: длина окружности 70 м.
Задача 3. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 8 км до окончания первого круга, ему сообщили, что второй бегун прошел первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 9 км/час меньше скорости второго.
Обозначим скорости бегунов и . Тогда сразу можно записать их разность, которая составляет 9 км/час:
Теперь поразмыслим над первым условием задачи. Если спустя час стало известно, что второй бегун прошел круг, значит, он прошел его за 57 минут. Обозначим длину круга . Тогда скорость второго бегуна равна . Первый же бегун преодолел расстояние за 60 минут, значит, его скорость . Подставляем эти выражения в первое уравнение. Так как в задаче присутствует неудобное число минут – 57, то представим все скорости, в том числе разность скоростей, в км/мин. Получим:
Рассчитаем скорости обоих бегунов: – это 11 км/час, – а это 20 км/час.
Задача 4. Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
Такие задачи часто решаются очень-очень просто: если стрелки в n-ный раз встречаются в полдень или полночь, то есть в 12 часов. Только в этом случае стрелки не только совмещаются сами, но и встреча их происходит строго на риске деления. Все остальные встречи стрелок (не в полночь) происходят между часовыми делениями, и точно сказать, где, навскидку не получится.
Итак, рассуждаем: на данный момент часовая стрелка находится между 6-часовой отметкой и 7-часовой – где-то посередине, так как из 60 минут данного часа прошло 35 – приблизительно половина. А минутная указывает ровно на 7-часовую отметку. То есть, встреча стрелок недавно состоялась, и в течение данного часа они уже не встретятся. (Вот этот момент – самый важный: понять, состоится встреча стрелок в течение этого часа или нет. Некоторые репетиторы даже советуют надеть на руку на экзамен механические часы.) Первая их встреча произойдет где-то между 7 и 8 часами, и пока нам неважно, где точно. Вторая встреча будет между 8-ми и 9-тичасовой отметками, третья – между 9-ти и 10-тичасовой, далее между 10 и 11 – четвертая и между 11 и 12 – пятая. Но встреча между 11 и 12 не может произойти «между» часовыми делениями, она произойдет ровно в 12 часов! Осталось вычесть из 12.00 часов 6.35, не забыв, что в часе не 100 минут, а 60: минут.
Задача 5. Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?
Решение этой задачи может быть проведено совершенно аналогичным способом: в текущем часе стрелки уже не повстречаются. Они встретятся впервые лишь между 5-ю и 6-ю часами. Второй раз – между 6-ю и 7-ю, потом между 7-ю и 8-ю, и далее между 8 и 9, 9 и 10, 10 и 11, и, наконец, между 11 и 12, а именно, в 12 часов, потому что, как мы помним, стрелки совмещаются ровно в полночь (или полдень). Сколько же пройдет времени от 4.45 до 12.00? Пятнадцать минут до пяти часов и еще 7 часов, или минут.
Попробуем решить задачу иначе.
Скорость минутной стрелки 12 делений в час, а часовой – одно деление в час. Так как они в конце концов совместятся – и даже неважно, в который раз – значит, время их движения одинаково. Попробуем записать время движения каждой стрелки, применим для этого стандартную формулу для равномерного движения: . То есть .
Время движения часовой стрелки равно , время минутной . Со скоростями мы разобрались, а теперь поймем, какой путь каждая проделает. Часовая пройдет неизвестное нам количество делений, пусть это будет делений. Минутная пройдет столько, сколько разделяет на данный момент стрелки – а это семь целых делений и, за счет того, что прошло уже 45 минут от начала текущего часа, то есть часа – еще деления. Затем минутная обгонит часовую еще 6 раз – а это полных шесть кругов, или делений, да еще делений, на которые уйдет часовая стрелка – всего . Тогда запишем уравнение:
Или , то есть
То есть до седьмой встречи часовая стрелка пройдет 7 целых и одну четверть часа – или 435 минут.
Все-таки второй способ немного сложнее первого, «жизненного», не находите?
easy-physic.ru
Задачи на тему Равномерное движение тела по окружности
Частота обращения ветроколеса ветродвигателя 30 об/мин, якоря электродвигателя 1500 об/мин, барабана сепаратора 8400 об/мин, шпинделя шлифовального станка 96 000 об/мин. Вычислить их периодыРЕШЕНИЕ
Найти частоту обращения Луны вокруг Земли (см. табл. 14).
РЕШЕНИЕ
Скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 м/с. Допустима ли посадка круга на вал электродвигателя, совершающего 1400 об/мин; 2800 об/мин
РЕШЕНИЕ
Частота обращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч
РЕШЕНИЕ
Период обращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м
РЕШЕНИЕ
Диаметр передних колес трактора в 2 раза меньше, чем задних. Сравнить частоты обращения колес при движении трактора
РЕШЕНИЕ
Радиус рукоятки колодезного ворота в 3 раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки при поднятии ведра с глубины 10 м за 20 с
РЕШЕНИЕ
С какой скоростью и в каком направлении должен лететь самолет по шестидесятой параллели, чтобы прибыть в пункт назначения раньше (по местному времени), чем он вылетел из пункта отправления? Возможно ли это для современных пассажирских самолетов
РЕШЕНИЕ
Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей Союз-4 и Союз-5 16 января 1969 г., имела период обращения 88,85 мин и среднюю высоту над поверхностью Земли 230 км (считая орбиту круговой). Найти среднюю скорость движения станции
РЕШЕНИЕ
При увеличении в 4 раза радиуса круговой орбиты искусственного спутника Земли период его обращения увеличивается в 8 раз. Во сколько раз изменяется скорость движения спутника по орбите
РЕШЕНИЕ
Минутная стрелка часов в 3 раза длиннее секундной. Найти отношение скоростей концов стрелок
РЕШЕНИЕ
Движение от шкива I (рис. 21) к шкиву IV передается при помощи двух ременных передач. Найти частоту обращения (в об/мин) шкива IV, если шкив I делает 1200 об/мин, а радиусы шкивов r1 = 8 см, r2 = 32 см, r3 = 11 см,r4 = 55 см. Шкивы II и III жестко укреплены на одном валу
РЕШЕНИЕ
Циркулярная пила имеет диаметр 600 мм. На ось пилы насажен шкив диаметром 300 мм, который приводится во вращение посредством ременной передачи от шкива диаметром 120 мм, насаженного на вал электродвигателя. Какова скорость зубьев пилы, если вал двигателя совершает 1200 об/мин
РЕШЕНИЕ
Диаметр колеса велосипеда Пенза d 70 см, ведущая зубчатка имеет z1 = 48 зубцов, а ведомая z2 = 18 зубцов. С какой скоростью движется велосипедист на этом велосипеде при частоте вращения педалей n= 1 об/с? С какой скоростью движется велосипедист на складном велосипеде Кама при той же частоте вращения педалей, если у этого велосипеда соответственно d = 50 см,z1 = 48 зубцов, z2 = 15 зубцов
РЕШЕНИЕ
Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 20 м/с
РЕШЕНИЕ
Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2 км/с. Найти период обращения Солнца вокруг своей оси и центростремительное ускорение точек экватора
РЕШЕНИЕ
Период обращения молотильного барабана комбайна Нива диаметром 600 мм равен 0,046 с. Найти скорость точек, лежащих на ободе барабана, и их центростремительное ускорение
РЕШЕНИЕ
С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение было равно ускорению свободного падения
РЕШЕНИЕ
Рабочее колесо турбины Красноярской ГЭС имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины
РЕШЕНИЕ
Найти центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 72 км/ч и при этом частота обращения колеса 8 с-1
РЕШЕНИЕ
Две материальные точки движутся по окружности радиусами R1 и R2, причем R1 = 2R2. Сравнить их центростремительные ускорения в случаях: равенства их скоростей; равенства их периодов обращения
РЕШЕНИЕ
Радиус рабочего колеса гидротурбины в 8 раз больше, а частота обращения в 40 раз меньше, чем у паровой турбины. Сравнить скорости и центростремительные ускорения точек обода колес турбин
РЕШЕНИЕ
Детский заводной автомобиль, двигаясь равномерно, прошел расстояние s за время *. Найти частоту обращения и центростремительное ускорение точек на ободе колеса, если диаметр колеса равен d. По возможности конкретные данные задачи получите опытным путем
РЕШЕНИЕ
famiredo.ru
Презентация . Задачи на движение по окружности
ЕГЭ-2014 Решение задач
Движение по окружности (замкнутой трассе)
Школа
ЕГЭ
Фабер Галина Николаевна –
учитель математики высшей категории
КМОУ «Гимназия имени Горького А.М.»
Москаленского муниципального района Омской области
v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 . В момент, когда 1-й велосипедист в первый раз догоняет 2-го, он проходит расстояние на один круг больше. Показать В момент, когда 1-й велосипедист во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д. Продолжить»
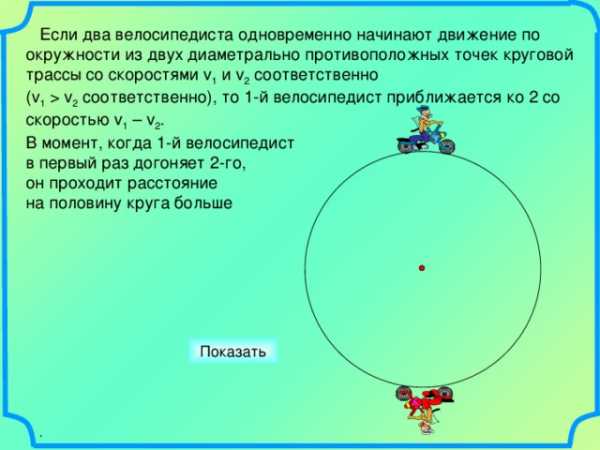
Если два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v 1 и v 2 соответственно
(v 1 v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 .
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д.
Продолжить
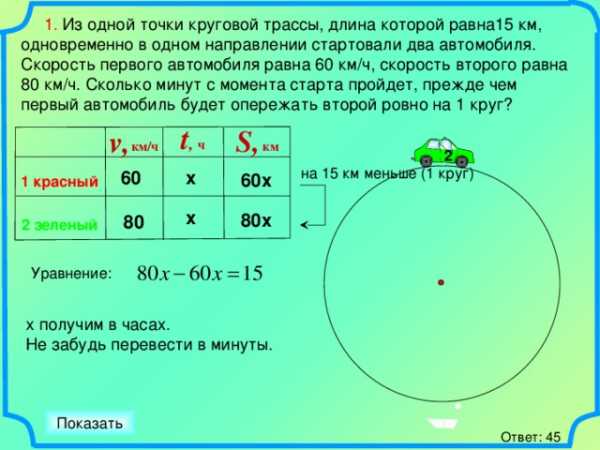
1. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
t ,
S,
v,
ч
км
км/ч
1
2
на 15 км меньше (1 круг)
60
х
60х
1 красный
х
80х
80
2 зеленый
Уравнение:
На слайде приводится алгебраический способ решения. Хотя можно решить задачу и арифметическим способом.
1) 80 – 60 = 20 (км/ч) скорость вдогонку. С этой скоростью 2-й автомобиль должен преодолеть расстояние в 1 круг (15 км).
2) 15:20 = 3/4(ч) = 45 (мин).
х получим в часах.
Не забудь перевести в минуты.
Показать
Ответ: 45
3
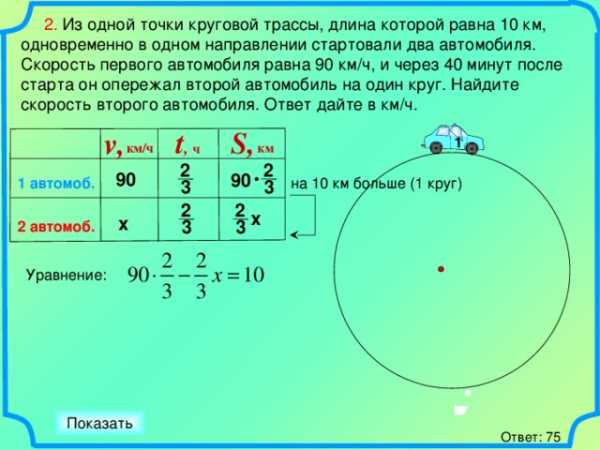
2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
t ,
S,
v,
1
2
км
км/ч
ч
2
2
90
90
1 автомоб.
на 10 км больше (1 круг)
3
3
2
2
х
х
3
3
2 автомоб.
Уравнение:
Задачу можно решить другим способом.
1) 90*(2/3) = 60 (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль.
2) 60 – 10 = 50 (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 50 : (2/3) = 75 (км/ч)
Ответ: 75 км/ч скорость второго автомобиля.
Показать
Ответ: 75
4
v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 . В момент, когда 1-й велосипедист в первый раз догоняет 2-го, он проходит расстояние на половину круга больше Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч. Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – пол круга от 14 км всей трассы). 7 : 21 = 1/3 (ч) Осталось перевести 1/3 ч в минуты – это 20 мин. Надо понимать, что за эти 20 минут мотоциклист проедет не 7 км(!), а может больше круга. Показать . 4″
Если два велосипедиста одновременно начинают движение по окружности из двух диаметрально противоположных точек круговой трассы со скоростями v 1 и v 2 соответственно
(v 1 v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 .
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние
на половину круга больше
Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч.
Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – пол круга от 14 км всей трассы).
7 : 21 = 1/3 (ч)
Осталось перевести 1/3 ч в минуты – это 20 мин.
Надо понимать, что за эти 20 минут мотоциклист проедет не 7 км(!), а может больше круга.
Показать
.
4
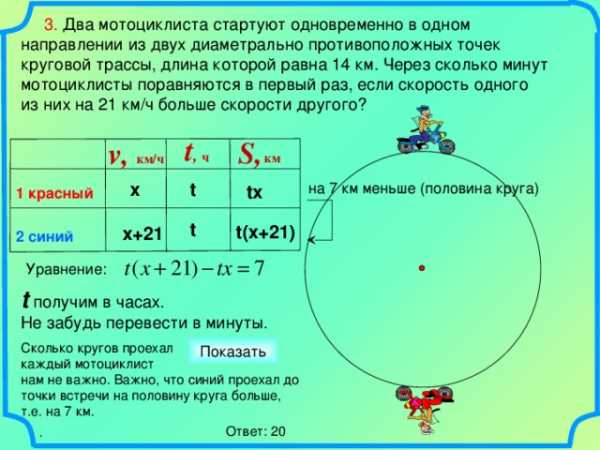
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
t ,
S,
v,
ч
км
км/ч
х
t
на 7 км меньше (половина круга)
tх
1 красный
t
t(х+21)
х+21
2 синий
Уравнение:
t получим в часах.
Не забудь перевести в минуты.
Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч.
Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – пол круга от 14 км всей трассы).
7 : 21 = 1/3 (ч)
Осталось перевести 1/3 ч в минуты – это 20 мин.
Надо понимать, что за эти 20 минут мотоциклист проедет не 7 км(!), а может больше круга.
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Показать
Ответ: 20
.
6
старт
финиш
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать
Пусть полный круг – 1 часть.
1
2
1
2
1
2
1
2
2
1
7
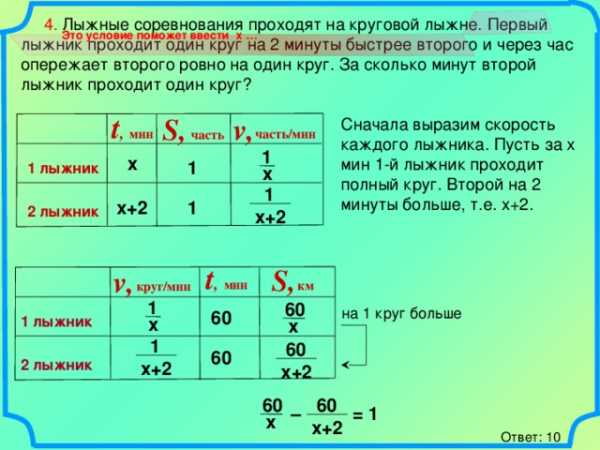
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Это условие поможет ввести х …
t ,
v,
S,
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
мин
часть/мин
часть
1
х
1
1 лыжник
х
1
х+2
1
2 лыжник
х+2
t ,
S,
v,
мин
км
круг/мин
1
60
на 1 круг больше
60
1 лыжник
х
х
1
60
60
2 лыжник
х+2
х+2
60
60
– = 1
х
х+2
Ответ: 10
8
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1
2
S,
t ,
v,
км/ч
км
ч
2
2
на 14 км больше (1 круг)
80
80
1 желтый
3
3
2
2
х
х
3
3
2 синий
Уравнение:
1) 80 *(2/3)= 160/3=53(1/3) (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль, т.е. на 14 км.
2) 53(1/3) – 14 = 39(1/3) (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 39(1/3) : (2/3) = 59 (км/ч)
Ответ: 59 км/ч скорость второго автомобиля.
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
t
=
v
S
Показать
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Ответ: 59
9
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1
2
S,
t ,
v,
км/ч
км
ч
2
2
на 14 км больше (1 круг)
80
80
1 желтый
3
3
2
2
х
х
3
3
2 синий
Уравнение:
1) 80 *(2/3)= 160/3=53(1/3) (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль, т.е. на 14 км.
2) 53(1/3) – 14 = 39(1/3) (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 39(1/3) : (2/3) = 59 (км/ч)
Ответ: 59 км/ч скорость второго автомобиля.
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
t
=
v
S
Показать
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Ответ: 59
10
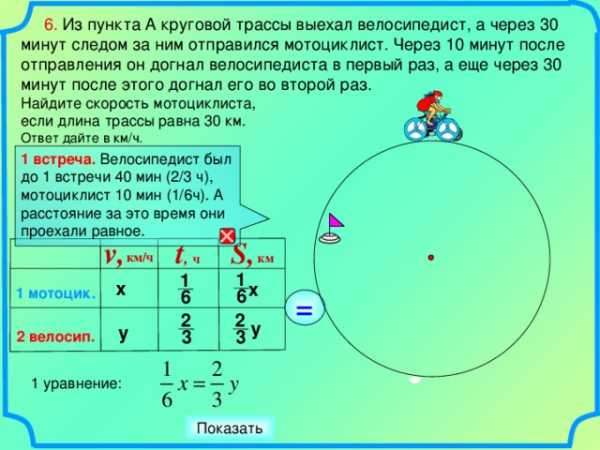
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
v,
t ,
S,
км/ч
км
ч
1
1
х
х
1 мотоцик.
6
6
=
Можно составить уравнение и иначе.
2
2
у
у
3
3
2 велосип.
1 уравнение:
Показать
11
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.
2 встреча. Велосипедист и мотоциклист были в пути
до 2-й встречи 30 мин (1/2 ч).
А расстояние за это время мотоциклист проехал на 1 круг больше.
v,
S,
t ,
км/ч
км
ч
1
1
х
х
на 30 км больше (1 круг)
1 мотоцик.
2
2
Можно составить уравнение и иначе.
1
1
у
у
2
2
2 велосип.
2 уравнение:
Искомая величина – х
Показать (2)
Ответ 80
12
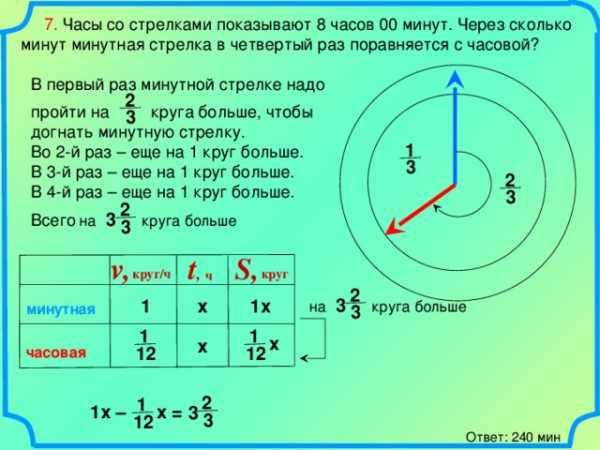
7. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
В первый раз минутной стрелке надо
пройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.
Всего
2
3
1
3
2
3
2
3
на круга больше
3
t ,
S,
v,
круг/ч
круг
ч
2
Минутная стрелка догоняет часовую один раз в час. Последний, четвертый раз догонит в 12:00, т.е. через 4 часа, или 240 минут.
3
1х
х
1
на круга больше
минутная
3
1
1
х
х
12
12
часовая
2
1
1х – =
х
3
3
12
Ответ: 240 мин
13
Проверка
В первый раз минутной стрелке надо
пройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.
Всего
2
3
12
11
1
2
10
2
3
на круга больше
3
3
9
Минутная стрелка догоняет часовую один раз в час. Последний, четвертый раз догонит в 12:00, т.е. через 4 часа, или 240 минут.
4
8
5
7
6
Показать (4)
Другой способ – в комментариях.
14
№ 99599.
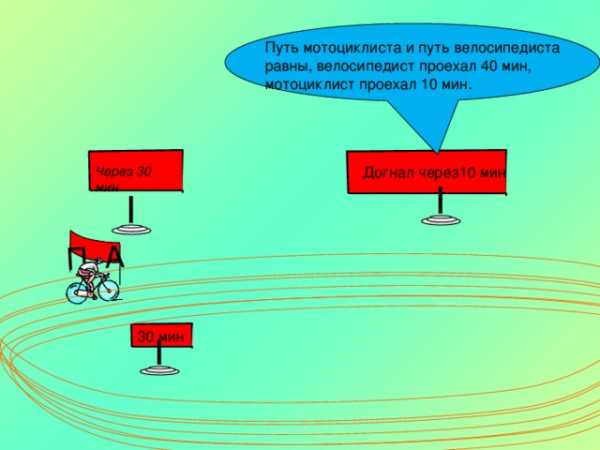
Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
П. А
Путь мотоциклиста и путь велосипедиста
равны, велосипедист проехал 40 мин,
мотоциклист проехал 10 мин.
Догнал через10 мин
Через 30 мин
30 мин
Решение.
Так как мотоциклист догнал велосипедиста через 10 минут, то их пути равны.
x км/ч – скорость вел., y км/ч – скорость мот.
Длина трассы 30 км, т.к. мотоциклист догнал второй раз велосипедиста , то они за 30 мин прошли S км, тогда путь мотоциклиста за 0,5 ч –( S+30), а у велосипедиста S км.
Значит путь мотоциклиста равен 30+10=40 км .
v(мот)= 40:0,5=80 км/ч
Ответ: 80 км/ч
№ 99596.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Один из них проехал на половину круга
больше, то есть на 7 км больше.
Через сколько минут они
Поравняются в первый раз?
Решение.
Один из них проехал на половину круга больше, то есть
Ответ: 20 минут
kopilkaurokov.ru
Leave A Comment