За что отвечает коэффициент b: Основные элементарные функции — Умскул Учебник

Коэффициенты k и b | 7 класс | Алгебра

Содержание

На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.

Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.

Например,

• $y = \textcolor{blue}{5}x + \color{green}{10}$ – линейная функция
• $\color{blue} k = 5$
• $\color{green} b = 10$.

График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.

Коэффициент k

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

При $k > 0$ угол между графиком и осью $Ox$ меньше $90 \degree$ (острый)

При $k < 0$ угол между графиком и осью $Ox$ больше $90 \degree$ (тупой)

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат. 

Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.

• Если $b > 0$, график сдвинут вверх,
• если $b < 0$, то график сдвинут вниз.

На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

График функции $y=50x + 500$

Частные случаи. b = 0

Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.

Подставим в формулу $x = 0$, получим: $$y = k \times 0$$

Значит, график будет проходить через начало координат $O(0;0)$.

Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.

{
    "questions": [{
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 2,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=2x$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 1,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=x$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0.  5,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=0.5x$[[graph]]"
    }]
}

k = 0

Если коэффициент $k = 0$, угол наклона также будет равен $0$.

Функция при этом принимает вид $y = 0 \times x + b$, то есть $y = b$.

Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.

Пример. График функции $y = 2$

{
    "questions": [{
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 2
                }
            }
        },
        "content": "Постройте график функции $y=2$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 1.  5
                }
            }
        },
        "content": "Постройте график функции $y=1.5$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=0$[[graph]]"
    }]
}

Таблица

5

Оценить урок

Поделиться уроком →

Что можно улучшить?

Изложение материала

Непонятное объяснение

Урок неполный, не хватает информации

Урок перегружен, слишком много информации

Тесты плохого качества

Тестов недостаточно

Тестов слишком много

Тесты слишком легкие

Тесты слишком сложные

Изображения

Изображения плохого качества

Изображений недостаточно

Изображений слишком много

Другое




Войдите, чтобы оценивать уроки

Что нужно исправить?




Спасибо, что помогаете нам стать лучше!

Проверим знания по теме?

Построение графиков функции y = kx

Комментарии

3.

Линейная функция вида y = kx + b

Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная. В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b). Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью. Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат. Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки. Свойства линейной функции: 1) Область определения линейной функции есть вся вещественная ось; 2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b; 3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b. a) b ≠ 0, k = 0, следовательно, y = b – четная; b) b = 0, k ≠ 0, следовательно y = kx – нечетная; c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида; d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция. 4) Свойством периодичности линейная функция не обладает; 5) Точки пересечения с осями координат: Ox:  y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс. Oy:  y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат. Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной 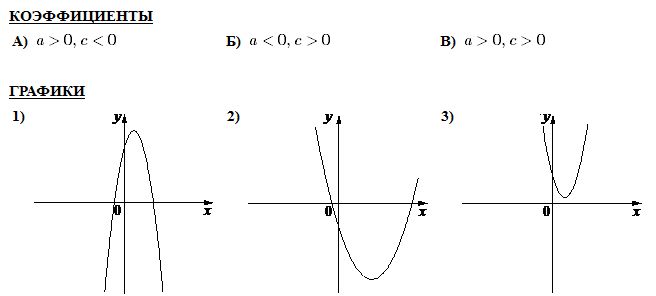х. 6) Промежутки знакопостоянства зависят от коэффициента k. a) k > 0;  kx + b > 0, kx > -b, x > -b/k. y = kx + b – положительна при x  из (-b/k; +∞), y = kx + b – отрицательна при x  из (-∞; -b/k). b) k < 0; kx + b < 0, kx < -b, x < -b/k. y = kx + b – положительна при x  из (-∞; -b/k), y = kx + b – отрицательна при x  из (-b/k; +∞). c) k = 0, b > 0; y = kx + b положительна на всей области определения, k = 0, b < 0; y = kx + b отрицательна на всей области определения. 7) Промежутки монотонности линейной функции зависят от коэффициента k. k > 0, следовательно y = kx + b возрастает на всей области определения, k < 0, следовательно y = kx + b убывает на всей области определения. 8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.

рисков | Бесплатный полнотекстовый | Статистический вывод для бета-коэффициента

1. Введение

Метод выбора портфеля, представленный Марковицем (1952), стал очень популярным среди практиков и ученых финансового рынка из-за его простоты и хорошей обработки результатов. Этот подход можно представить двумя эквивалентными способами: (i) максимизировать ожидаемую доходность портфеля при условии, что его дисперсия равна заранее определенному уровню, или (ii) минимизировать дисперсию портфеля при условии, что его ожидаемая доходность равна заданный уровень. Решения этих двух задач оптимизации составляют набор оптимальных портфелей средней дисперсии, который представляет собой параболу в пространстве средней дисперсии и известен как эффективная граница (см. , например, Мертона 19).72; Боднар и Шмид, 2009 г.; Баудер и др. 2019). Несколько оптимальных портфелей, полученных как решения других задач оптимизации, также относятся к эффективной границе, например портфель глобальной минимальной дисперсии (Фрам и Меммель, 2010; Боднар и др., 2018), минимальная стоимость риска (VaR) и минимальный условный портфель. оптимальные портфели с учетом риска (CVaR) (см., например, Александр и Баптиста, 2002, 2004; Боднар и др., 2012) и портфель с максимальным коэффициентом Шарпа (Шарп, 1994; Шмид и Заболоцкий, 2008).

Еще одно важное направление исследований портфельной теории посвящено объяснению динамики стохастического поведения доходности активов, при этом ключевую роль играет модель ценообразования капитальных активов (CAPM). Модель САРМ была предложена в основополагающих работах Шарпа (1964), Линтнера (1965) и Моссина (1966), где предполагалось, что доходность активов следует однофакторной модели с доходностью рыночного портфеля в качестве фактора. Берк (1997) доказал, что одним из необходимых условий САРМ является допущение, что доходность активов следует эллиптическому распределению, в то время как Чжоу (19)93) расширил выводы Gibbons et al. (1989), применив свой тест достоверности САРМ к эллиптически распределенным доходам. Еще один тест на достоверность этой модели был предложен Hodgson et al. (2002).

Коэффициент бета определяет соотношение между доходностью активов или доходностью холдингового портфеля и доходностью рыночного портфеля и играет центральную роль в теории САРМ. Чтобы рассчитать бета-коэффициент для отдельного актива, необходимо подобрать линейную регрессию доходности актива по сравнению с доходностью рыночного портфеля. Напротив, бета портфеля может быть рассчитана одним из следующих двух методов (см., например, Damodaran (2012, стр. 120)): каждого актива, включенного в портфель, или путем регрессии доходности портфеля по отношению к доходности рыночного портфеля. Александер (2001, стр. 231) указал, что эти два метода эквивалентны при использовании обычной оценки методом наименьших квадратов (МНК) для параметров модели линейной регрессии.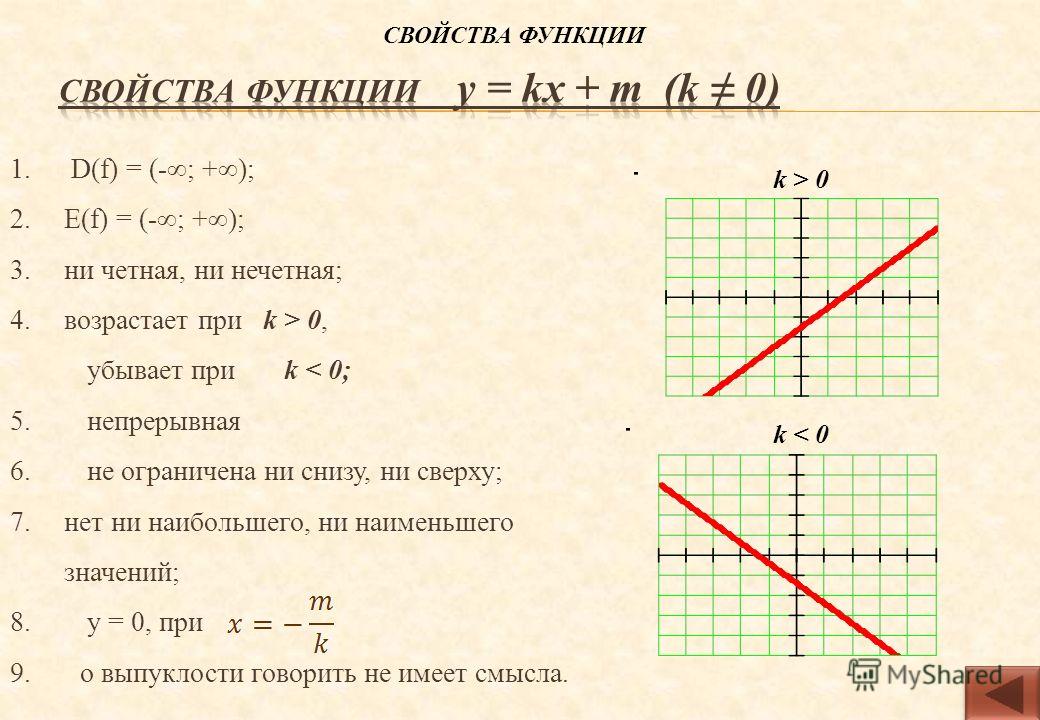

Похоже, что бета портфеля полностью определяется ковариационной матрицей доходности активов, которая на практике является ненаблюдаемой величиной. В результате он оценивается с использованием исторических данных доходности активов. Из-за случайности в поведении доходности активов оценочная ковариационная матрица оказывается случайной, и, следовательно, оценочная бета портфеля также является случайной. Мы вносим свой вклад в эту статью, получая точное распределение конечной выборки бета-версии портфеля. Мы показываем, что расчетный бета-коэффициент следует t-распределению. Этот вывод позволяет нам количественно оценить ошибку оценки, представленную в коэффициенте бета, на практике, а также провести статистический тест для бета портфеля.

Остальная часть статьи организована следующим образом. В следующем разделе представлены теоретические выводы статьи. Здесь мы получаем как конечную выборку, так и асимптотические распределения оценочной бета-версии портфеля, а также обеспечиваем ее интервальную оценку.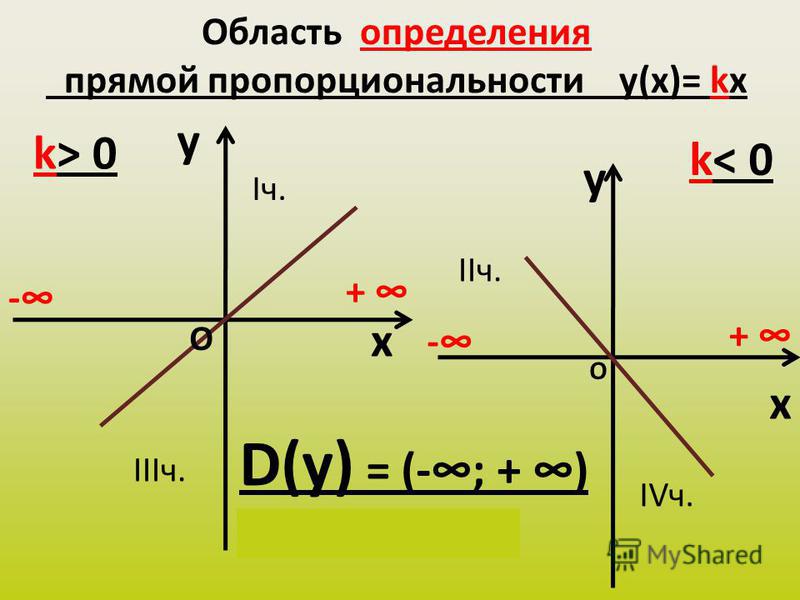 Эти результаты применяются к реальным данным, основанным на доходности 30 акций, включенных в индекс DAX (Deutscher Aktienindex (немецкий фондовый индекс)) в разделе 3. В разделе 4 обсуждается устойчивость полученных результатов к нарушению предположения о нормальности, использованного в вывод теоретических выводов. Заключительные замечания представлены в разделе 5.

2. Расчетный бета-коэффициент и его распределительные свойства

Пусть веса портфеля инвестора заданы как вес эталонного (рыночного) портфеля. Вектор доходности активов в момент времени t обозначим через Xt=(X1t,X2t,…,Xkt)′. После CAPM коэффициент бета определяется как:

где:

означает доходность эталонного портфеля в момент времени t и:

обозначает доходность портфеля инвестора с весами w в момент времени t.

Предположим, что вектор доходности активов Xt следует слабо стационарному процессу, и обозначим через µ=E(Xt) и Var(Xt)=Σ его средний вектор и ковариационную матрицу соответственно.

Тогда (1) можно переписать так:

которая оказывается независимой от t.

Хотя (2) обеспечивает простой способ вычисления бета-коэффициента портфеля с весами w на практике, к сожалению, эта формула не может быть непосредственно применена на практике, поскольку параметры распределения доходности активов, участвующие в (2), а именно , μ и Σ, являются неизвестными величинами и должны быть оценены с использованием исторических данных доходности активов. Учитывая выборку X1,…,Xn, их оценки становятся: 9β, они не предоставляют полной информации, необходимой для построения доверительного интервала, интервальной оценки β или для разработки теории проверки. Необходимы дальнейшие исследования по этой теме, и они обсуждаются в текущем разделе.

С точки зрения асимптотической статистики непротиворечивая оценка σ2/σb2−β2 дала бы нам возможность получить асимптотический доверительный интервал для β, который можно использовать при относительно большом размере выборки. Ситуация усложняется, когда необходимо получить точный доверительный интервал конечной выборки. В качестве отправной точки вывода мы используем двойственность между теорией тестов и интервальной оценкой, рассматривая тест на бета-коэффициент (см., например, Aitchison 19).64). А именно, мы проверили гипотезы:

для некоторого целевого значения β0.

Результаты теоремы 1 мотивируют применение следующей тестовой статистики:

Конечное нулевое распределение T получено в теореме 2. −γ) доверительный интервал для бета-коэффициента β портфеля с весами w, выраженный как:

где t1−γ/2,n−2 обозначает квантиль (1−γ/2) t-распределения с n−2 степенями свободы. Аналогичным образом были получены односторонние доверительные интервалы. Нижний односторонний (1−γ) доверительный интервал определяется как:

а верхний односторонний (1−γ) доверительный интервал следующий:

Более того, поскольку одномерное t-распределение сходится к стандартному нормальному распределению при стремлении степеней свободы к бесконечности, мы также можем использовать асимптотическую достоверность интервал для β. Например, двусторонний асимптотический (1−γ) доверительный интервал определяется как:

где z1−γ/2 обозначает (1−γ/2) квантиль стандартного нормального распределения.

Наконец, мы представляем распределение T при альтернативной гипотезе в (11) в теореме 3.

Результаты теоремы 3 значительно упрощают исследование мощности предложенного критерия для коэффициента бета. В частности, эти данные приводят к выражению функции мощности в виде:

где третья линия следует из симметрии t-распределения (см., например, Гупта и др., 2013), а символ Ftn−2(δy)(.) обозначает кумулятивную функцию распределения нецентрального t-распределения с ( n−2) степеней свободы и параметр нецентральности δy. Более того, оказывается, что степенная функция зависит от Σ только через δ. В результате он позволяет оценить функцию мощности как функцию δ только для заданного значения n.

На рисунке 1 мы отобразили мощность предложенного теста как функцию δ для n∈{60,120,250,500}. Мы наблюдаем, что даже для небольшого размера выборки, такого как n=60, тест способен отклонить нулевую гипотезу уже при небольших отклонениях от целевого значения β0. Например, мощность теста больше 60%, когда δ составляет всего около 0,3, и она приблизительно равна 1, если δ = 0,6. Кроме того, мощность теста увеличивается по мере увеличения размера выборки. Например, мощность около 1 уже для δ, близкого к 0,3, когда n=250, и для δ около 0,2, когда n=500.

3. Эмпирическая иллюстрация

В этом разделе мы применяем теоретические выводы раздела 2 к реальным данным, основанным на ежедневной доходности активов, включенных в индекс DAX, за период с 1 января 2018 года по 31 декабря 2018 года (251 наблюдение). ). В качестве эталонного портфеля wb выбран индекс DAX, веса которого представлены на официальном сайте немецкого рынка капитала, а именно на сайте www.boerse.de. В качестве целевого портфеля, для которого мы стремимся вывести бета-коэффициент, мы берем равновзвешенный портфель шести измерений, а именно, k∈{5,10,15,20,25,30}, который состоит из соответствующих первых k активы, включенные в индекс DAX, в алфавитном порядке. принадлежат интервалу [0,96,1] при k=30. Наконец, бета-коэффициенты равновзвешенных портфелей падают во второй половине октября 2018 г., что согласуется с мнением о том, что октябрь 2018 г. был худшим месяцем за более чем шесть лет (с мая 2012 г.) для мировых рынков капитала с глобальный финансовый кризис 2008 года. Некоторые события, такие как разочаровывающие доходы крупных технологических компаний и бюджетный спор между Италией и Европейским союзом, по-видимому, оказали большое влияние на общие показатели немецкого рынка капитала.

Наконец, доверительные интервалы, построенные для бета-коэффициентов рассматриваемых равновзвешенных портфелей, покрывают единицу почти во всех рассмотренных случаях за исключением, присутствующим в течение нескольких недель в октябре 2018 г. – декабре 2018 г. для k=5, для k= 25, и для размерного равновзвешенного портфеля k=30. В конце 2018 года оценочные бета-коэффициенты увеличиваются, и только доверительные интервалы, построенные для 5-мерного портфеля, не включают значение единицы.

4. Устойчивость к нарушению предположения о нормальности

Теоретические выводы раздела 3 были получены в предположении, что доходность активов распределяется нормально. В этом разделе мы исследуем, насколько важно предположение о нормальности для производительности бета-оценщика и свойств распределения тестовой статистики T, представленной в разделе 2.2. Результаты были получены методом Монте-Карло путем взятия случайной выборки размера n из k-мерного многомерного t-распределения с d∈{5,10} степенями свободы. Рассматриваются несколько значений k и n, а именно k∈{5,10,15,20,25,30} и n∈{60,120,250,500,1000,2000}. Для каждого возможного выбора (k,n) мы брали выборку из t-распределения с 5 и 10 степенями свободы, с вектором местоположения и ковариационной матрицей, равными выборочному среднему вектору, и к выборочной ковариационной матрице, вычисленной из ежедневная доходность активов, включенных в индекс DAX, за период с 1 января 2018 г. по 31 декабря 2018 г. (251 наблюдение). На основе смоделированных данных была рассчитана стандартизированная реализация оценочного бета-коэффициента, а также значение тестовой статистики T, приведенное в разделе 2.2. Наконец, вся процедура была повторена B = 50 000 раз для каждого возможного значения d, k и n. Полученные выборки стандартизированных оценок бета-коэффициента и значений тестовой статистики T использовались для оценки их выборочного распределения с использованием ядерной оценки плотности с ядром Епанечникова.

На рисунках 3 и 4 показаны результаты для t-распределения с 5 и 10 степенями свободы. На обоих рисунках мы представляем оценки ядерной плотности и асимптотическую плотность стандартизированной оценки для коэффициента бета, определяемого как:

с:

и обратите внимание, что аналогичные результаты также присутствуют для значений тестовой статистики T. Графики в случае T не включены в статью и доступны у соответствующего автора по запросу. Независимо от размера выборки плотность ядра стандартизированной оценки коэффициента бета примерно симметрична относительно нуля. Небольшие отклонения от асимптотического распределения, которое является стандартным нормальным распределением, присутствуют в случае ядерных плотностей, рассчитанных, когда размер выборки относительно мал, а доходность активов генерируется из t-распределения с 5 степенями свободы. Если данные генерируются из t-распределения с 10 степенями свободы, то сходимость ядерных плотностей наблюдается уже для небольшого размера выборки, равного 120, и по этой причине ядерные плотности, вычисленные для большого размера выборки, отсутствуют. на рис. 4.

5. Резюме

Модель ценообразования капитальных активов является одним из наиболее популярных в финансовой литературе подходов к моделированию компромисса между доходностью портфеля (актива) и риском, который был независимо введен Шарпом (1964), Линтнером (1965). ) и Мосин (1966). Уравнение модели связывает доходность активов с доходностью рынка с помощью линейной функции, наклон которой известен как бета-коэффициент. В результате бета-коэффициент обладает несколькими интересными и важными свойствами в финансах, одним из которых является способность учитывать риск портфеля/ценной бумаги.

С эконометрической точки зрения САРМ также можно рассматривать как однофакторную модель или как модель линейной регрессии, параметры которой можно оценить с помощью обычного метода наименьших квадратов (см. Greene 2003; Dhrymes 2017). Такой подход, в частности, позволяет получить точечную оценку коэффициента бета портфеля. С другой стороны, доходность рыночного портфеля не является детерминированной переменной, как это обычно предполагается при построении регрессионной модели, а представляет собой случайную величину, случайность которой следует учитывать при установлении доверительного интервала для коэффициента бета генеральной совокупности. построена или разработана соответствующая теория тестов. Мы рассматриваем этот вопрос в настоящей статье, используя методы многомерного статистического анализа. Эта процедура позволяет изучить свойства распределения оцененного бета-коэффициента путем получения его функции плотности конечной выборки и путем введения точного критерия для бета-коэффициента генеральной совокупности. Кроме того, распределение предлагаемой тестовой статистики получено как при нулевой гипотезе, так и при альтернативной гипотезе. В то время как результаты, полученные в соответствии с нулевой гипотезой, могут быть использованы для построения области отклонения теста, результаты в соответствии с альтернативной гипотезой предоставляют информацию о мощности предлагаемого теста.

Полученные теоретические результаты не только ограничиваются изучением стохастических свойств оцениваемого бета-коэффициента, но также применимы в общей теории линейных моделей со стохастическими регрессорами. Таким образом, они открывают статистический подход, основанный на распределительных свойствах распределения Уишарта, который может быть применим в различных задачах, связанных с моделями, в которых независимые переменные являются стохастическими. Хотя мы имеем дело только с одним стохастическим фактором, расширение на общий случай с произвольным фиксированным числом стохастических независимых переменных может быть рассмотрено аналогичным образом. Таким образом, развитая теория CAPM может быть расширена на другую популярную в финансовой литературе линейную модель, а именно на теорию арбитражного ценообразования (см., например, Ross 19).76).

Участие авторов

Расследование: Т.Б., А.К.Г., В.В. и Т.З.; Написание чернового варианта, Т.Б., А.К.Г., В.В. и Т.З.

Финансирование

Это исследование не получило внешнего финансирования.

Благодарности

Авторы благодарны Ивану Вангу и четырем анонимным рецензентам за внимательное прочтение статьи и за их предложения, которые улучшили предыдущую версию этой статьи.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. Эйчисон, Джон. 1964. Тесты доверительной области. Журнал Королевского статистического общества: серия B (методологическая) 26: 462–76. [Google Scholar] [CrossRef]
2. Александр, Кэрол. 2001. Рыночные модели: Руководство по анализу финансовых данных. Хобокен: Джон Уайли и сыновья. [Google Scholar]
3. Александр, Гордон Дж. и Александр М. Баптиста. 2002. Экономические последствия использования модели среднего отклонения для выбора портфеля: сравнение с анализом среднего отклонения. Журнал экономической динамики и управления 26: 1159–93. [Google Scholar] [CrossRef]
4. Александр, Гордон Дж. и Александр М. Баптиста. 2004. Сравнение ограничений var и cvar на выбор портфеля с моделью средней дисперсии. Наука управления 50: 1261–73. [Google Scholar] [CrossRef]
5. Баудер, Давид, Ростислав Боднар, Тарас Боднар и Вольфганг Шмид. 2019. Байесовская оценка границы эффективности. Скандинавский статистический журнал. предстоящий. [Google Scholar] [CrossRef]
6. Берк, Джонатан Б. 1997. Необходимые условия для капм. Журнал экономической теории 73: 245–57. [Академия Google] [CrossRef]
7. Боднар, Тарас, Вольфганг Шмид и Тара Заболоцкие. 2012. Минимальный var и минимальный cvar оптимальные портфели: Оценщики, доверительные области и тесты. Статистика и моделирование рисков с приложениями в области финансов и страхования 29: 281–314. [Google Scholar]
8. Боднар, Тарас и Вольфганг Шмид. 2009. Эконометрический анализ границы эффективности выборки. Европейский финансовый журнал 15: 317–35. [Google Scholar] [CrossRef]
9. Боднар, Тарас, Нестор Пароля и Вольфганг Шмид. 2018. Оценка глобального портфеля минимальной дисперсии в больших размерах. Европейский журнал операционных исследований 266: 371–9.0. [Google Scholar] [CrossRef]
10. Дамодаран, Асват. 2012. Оценка инвестиций: инструменты и методы определения стоимости любого актива. Хобокен: Джон Уайли и сыновья. [Google Scholar]
11. Драймес, Феб. 2017. Введение в эконометрику. Берлин: Спрингер. [Google Scholar]
12. Фрам, Габриэль и Кристоф Меммель. 2010. Доминирующие оценщики портфелей с минимальной дисперсией. Журнал эконометрики 159: 289–302. [Google Scholar] [CrossRef]
13. Гиббонс, Майкл Р., Стивен А. Росс и Джей Шанкен. 1989. Проверка эффективности данного портфеля. Эконометрика 57: 1121–1152. [Google Scholar] [CrossRef]
14. Грин, Уильям Х. 2003. Эконометрический анализ. Ченнаи: Pearson Education India. [Google Scholar]
15. Гупта, Арджун К., Тамас Варга и Тарас Боднар. 2013. Эллиптически очерченные модели в статистике и теории портфеля. Нью-Йорк: Спрингер. [Google Scholar]
16. Ходжсон, Дуглас Дж., Оливер Линтон и Кит Воркинк. 2002. Эффективное тестирование модели ценообразования капитальных активов в условиях эллиптической симметрии: полупараметрический подход. Журнал прикладной эконометрики 17: 617–39.. [Google Scholar] [CrossRef]
17. Линтнер, Джон. 1965. Оценка рисковых активов и выбор рискованных вложений в портфели акций и бюджеты капиталовложений. Обзор экономики и статистики 47: 13–37. [Google Scholar] [CrossRef]
18. Марковиц, Гарри. 1952. Выбор портфолио. Финансовый журнал 7: 77–91. [Google Scholar]
19. Мертон, Роберт С. 1972. Аналитический вывод границы эффективного портфеля. Журнал финансового и количественного анализа 7: 1851–1872. [Академия Google] [CrossRef]
20. Моссин, январь 1966 г. Равновесие на рынке капитальных активов. Эконометрика: Журнал Эконометрического общества 34: 768–83. [Google Scholar] [CrossRef]
21. Мюрхед, Робб Дж. 1982. Аспекты многомерной статистической теории. Нью-Йорк: Уайли. [Google Scholar]
22. Росс, Стивен А. 1976. Арбитражная теория ценообразования капитальных активов. Журнал экономической теории 13: 341–60. [Google Scholar] [CrossRef]
23. Шмид, Вольфганг и Тарас Заболоцкий. 2008. О существовании несмещенных оценок весов портфелей, полученных путем максимизации коэффициента шарпа. Достижения AStA в статистическом анализе 92: 29–34. [Google Scholar] [CrossRef]
24. Шарп, Уильям Ф. 1964. Цены на капитальные активы: теория рыночного равновесия в условиях риска. Финансовый журнал 19: 425–42. [Google Scholar]
25. Шарп, Уильям Ф. 1994. Коэффициент Шарпа. Журнал управления портфелем 21: 49–58. [Google Scholar] [CrossRef]
26. Чжоу, Гофу. 1993. Тесты оценки активов при альтернативном распределении. Финансовый журнал 48: 1927–42. [Академия Google] [CrossRef]

Рисунок 1. Степенная функция для n∈{60 120 250 500} и γ = 0,05.

Рисунок 1. Степенная функция для n∈{60 120 250 500} и γ = 0,05.

Рисунок 2. Выборочные оценки и доверительные интервалы для коэффициента бета равновзвешенного портфеля, построенного для первого k=5 (вверху слева ), k=10 ( вверху справа ), k=15 ( в середине слева ), k =20 ( в середине справа ), k=25 ( внизу слева ) и k=30 ( внизу справа ) активы, включенные в индекс DAX, в алфавитном порядке.

Рисунок 2. Выборочные оценки и доверительные интервалы для коэффициента бета равновзвешенного портфеля, построенного для первого k=5 (вверху слева ), k=10 ( вверху справа ), k=15 ( в середине слева ), k =20 ( в середине справа ), k=25 ( внизу слева ) и k=30 ( внизу справа ) активов, включенных в индекс DAX, в алфавитном порядке.

Рисунок 3. Оценки плотности ядра для n∈{60,120,250,500,1000,2000} и асимптотическая плотность стандартизированной оценки для коэффициента бета в случае k=5 ( вверху слева ), k=10 ( вверху справа ), k=15 ( средний левый ), k=20 ( средний правый ), k=25 ( нижний левый ) и k=30 ( нижний правый ) размерный равновзвешенный портфель. Доходы от активов взяты из многомерного t-распределения с 5 степенями свободы.

Рис. 3. Оценки плотности ядра для n∈{60,120,250,500,1000,2000} и асимптотическая плотность стандартизированной оценки для коэффициента бета в случае k=5 ( вверху слева ), k=10 ( вверху справа ), k=15 ( средний левый ), k=20 ( средний правый ), k=25 ( нижний левый ) и k=30 ( нижний правый ) размерный равновзвешенный портфель. Доходы от активов взяты из многомерного t-распределения с 5 степенями свободы.

Рисунок 4. Оценки плотности ядра для n∈{60,120} и асимптотическая плотность стандартизированной оценки коэффициента бета в случае k=5 ( вверху слева ), k=10 ( вверху справа ), k=15 ( средний левый ), k=20 ( средний правый ), k=25 ( нижний левый ), abd k=30 ( нижний правый ) размерный равновзвешенный портфель. Доходы от активов взяты из многомерного t-распределения с 10 степенями свободы.

Рис. 4. Оценки плотности ядра для n∈{60,120} и асимптотическая плотность стандартизированной оценки коэффициента бета в случае k=5 ( вверху слева ), k=10 ( вверху справа ), k=15 ( средний левый ), k=20 ( средний правый ), k=25 ( нижний левый ), abd k=30 ( нижний правый ) размерный равновзвешенный портфель. Доходы от активов взяты из многомерного t-распределения с 10 степенями свободы.


© 2019 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/).

Применение стандартизированного коэффициента регрессии в мета-анализе

Коэффициент β представляет собой оценку, полученную в результате анализа переменных, которые были стандартизированы таким образом, что их стандартные отклонения (и дисперсии) равны единице. Таким образом, стандартизированный коэффициент относится к тому, на сколько стандартных отклонений изменится переменная ответа или результата при увеличении стандартного отклонения в объясняющей или предикторной переменной. Таким образом, стандартизированный коэффициент β можно рассматривать как попытку сделать коэффициенты регрессии более сопоставимыми и использовать в качестве оценки размера эффекта, когда уровни воздействия в оригинальных исследованиях измеряются в разных единицах измерения.

1.

Стандартизированный коэффициент регрессии как показатель величины эффекта в мета-анализе

Многопараметрические модели линейной регрессии используются для анализа связей между одной количественной зависимой переменной и несколькими независимыми переменными. Нестандартизированный коэффициент регрессии (b), рассчитанный по модели линейной регрессии, представляет собой легко интерпретируемую статистику, описывающую, как независимая переменная влияет на значения переменной результата. Эти коэффициенты обычно снабжаются их стандартными ошибками (SE) или доверительными интервалами (CI) в статьях, сообщающих о результатах регрессионных моделей ^{[1] [2]} . Нестандартизированный коэффициент регрессии b описывает эффект изменения независимой переменной на одну единицу, и, следовательно, его размер зависит от масштаба, используемого для измерения независимой переменной. Однако в рассмотренных исследованиях основная объяснительная характеристика часто измеряется с использованием различных методов и показателей. Таким образом, прямое объединение нестандартизированных коэффициентов регрессии не имеет смысла в разных исследованиях. Чтобы объединить эффекты независимых переменных, измеренных с помощью разных шкал, они должны быть выражены сопоставимым образом. В таком случае стандартизированный коэффициент регрессии β может предложить возможность синтезировать результаты ^{[3] [4]} .

Статистическую значимость стандартизированного коэффициента регрессии можно проверить с помощью t-критерия нулевой гипотезы H ₀ : β = 0 или, говоря по существу, отсутствия систематической связи между предиктором и результатом. Значение p выше 0,05 подтверждает нулевую гипотезу об отсутствии связи. Доверительный интервал для коэффициента β предоставляет информацию о диапазоне β. Положительное (отрицательное) значение β подтверждает гипотезу о том, что высокий уровень воздействия увеличивает (уменьшает) реакцию. Если доверительный интервал не включает 0, то связь между объясняющей переменной и переменной результата считается статистически значимой в соответствии с p-значением t-критерия <0,05.

При рассмотрении размера эффекта возникает естественный вопрос: что представляет собой большой, средний и малый размер эффекта. Руководство Коэна ^[5] по классификации величины эффекта широко цитируется в научных отчетах. Для коэффициента β размеры эффекта от 0,10 до 0,29 считаются лишь небольшими, размеры эффекта от 0,30 до 0,49 — средними, а размеры эффекта 0,50 и выше — большими ^{[5] [6]} .

Важной особенностью количественного метаанализа является его способность сравнивать величину эффектов в разных исследованиях, что требует использования единого показателя размера эффекта для измерения этих эффектов. Использование стандартизированного коэффициента регрессии β в качестве общей меры размера эффекта включает в себя извлечение результатов рассмотренных исследований, выраженных в виде нестандартизированных коэффициентов регрессии, коэффициентов корреляции или средних различий. Затем эти статистические данные повторно выражаются в виде стандартизированных коэффициентов регрессии и их стандартных ошибок. Этот процесс включает в себя несколько преобразований, вычислений и приближений.

В мета-анализе результаты (и размеры эффекта) объединены из рассмотренных исследований. Однако размер каждого наблюдаемого эффекта неодинаков в отношении надежности информации, которую он несет ^[7] . Следовательно, каждое значение размера эффекта должно быть взвешено с помощью термина, который представляет его точность. Оптимальный подход заключается в использовании в качестве веса значения, обратного квадрату стандартной ошибки значения размера эффекта. Таким образом, более крупные исследования с меньшими стандартными ошибками получают больший вес, чем более мелкие исследования с большими стандартными ошибками. Также должна быть указана формула для расчета соответствующей стандартной ошибки. Чтобы получить суммарный эффект всех рассмотренных исследований, средневзвешенный размер эффекта можно рассчитать по следующей формуле:

где k = количество исследований, β _i  – стандартный коэффициент регрессии из исследования I, SE(β _i ) – стандартная ошибка βi, а w _i  – величина, обратная (SE(β _i ) ) ² . Дисперсия (SE(β _i )) ² может быть рассчитана с использованием модели фиксированных или случайных эффектов ^{[7] [8]} . Эта версия процедуры метаанализа обычно называется общим обратным подходом 90-290 [9].] . Подход реализован во всех стандартных пакетах программ для метаанализа.

Мета-анализы обычно сообщают об общей величине эффекта M с мерой точности (SE или CI) и p-значением на рисунке. Этот рисунок, график леса, отображает оценки эффекта и доверительные интервалы для отдельных исследований, а также суммарный эффект. На рисунке 1 представлены два примера лесных участков. Следуя рекомендациям Коэна ^[5] и существенным эмпирическим обзорам ^{[6] [10]} , для абсолютного (неотрицательного) значения объединенного размера эффекта |M|»>|M| значение 0,10–0,19 представляет собой небольшой размер эффекта, объединенное значение 0,20–0,29 классифицируется как средняя величина эффекта, а объединенное значение 0,30 или более — как большая величина эффекта

2.

Применение

В следующих подразделах я привожу примеры метааналитических исследований, в которых стандартизированного коэффициента регрессии послужили полезным инструментом для обобщения результатов многочисленных исследований по той или иной теме.К сожалению, я также нашел метаанализы, где коэффициенты r, b и β были перепутаны ^{[11] [12] [13]} .

2.1. Общественное здравоохранение

В исследованиях окружающей среды и общественного здравоохранения несколько результатов и объясняющих факторов часто измеряются с помощью различных методов и единиц измерения. Джамбов и соавт. ^[14] изучали, связаны ли зеленые насаждения и общая зелень в среде обитания беременных женщин с массой тела при рождении их младенцев и какова направленность этого влияния. Они провели метаанализ восьми опубликованных исследований, изучающих связь между зеленым цветом жилья и массой тела при рождении. В большинстве исследований использовалась линейная регрессия с несколькими переменными для определения влияния зеленых насаждений на корректировку массы тела при рождении для личных ковариат. В первоначальных исследованиях в качестве показателя озеленения жилых помещений были выбраны разные показатели. Таким образом, стандартизированный коэффициент регрессии предлагает одно решение для объединения результатов. Сообщаемый объединенный β составлял 0,001 (95% ДИ = от -0,001 до 0,003), демонстрируя незначительную связь между зеленым цветом и массой тела при рождении. Авторы отметили, что результаты были сходными, когда коэффициент корреляции использовался в качестве показателя размера эффекта.

Keenan A. Ramsay и ее соавторы ^[15] представили в своем мета-анализе, что более высокая физическая активность (PA) и более низкий малоподвижный образ жизни (SB) связаны с большей силой скелетных мышц и мышечной мощностью у пожилых людей. Статьи включались в метаанализ, если связь между показателями PA или SB и силой хвата кисти или тестом в положении стоя на стуле выражалась в виде скорректированных стандартизированных коэффициентов регрессии (β) и их 95% ДИ или SE, или когда их можно рассчитать. Они выявили значительную неоднородность в дизайне исследования, определениях показателей результатов и объясняющих переменных, а также в статистическом анализе, используемом для представления ассоциаций. Это создало методологические проблемы для сравнения и синтеза результатов.

У здоровых людей и людей с хронической болью сообщалось об обратной связи между уровнем физической активности и болью (например, больше активности и меньше боли). Джонс и др. ^[16] изучали взаимосвязь между аэробной способностью и болью у здоровых людей и людей с фибромиалгией. Они сопоставили свои новые данные с данными предыдущих оригинальных исследований на здоровых людях. Для объединения результатов, полученных в результате поиска литературы, были рассчитаны стандартизированные коэффициенты регрессии и их стандартные ошибки. Это включало преобразование результатов анализа с использованием корреляции, линейной регрессии или размеров эффекта различий между группами и преобразование их в стандартизированные коэффициенты β с их стандартными ошибками. Затем 9Для представления данных о лесных участках были рассчитаны 5% доверительные интервалы βs. Интересно, что авторы отметили, что объединенная величина эффекта для этих исследований не рассчитывалась, потому что они представили несколько величин эффекта между различными показателями боли и независимыми переменными, оцененными в тех же исследованиях. Таким образом, результаты не дают независимых оценок эффекта. Представленные лесные диаграммы (стандартизированные коэффициенты β с их доверительными интервалами 95 %) результатов исследований ясно показывают, что связи между физической подготовкой и болью, как правило, невелики и сильно различаются в рамках исследований и между ними 9.0290 [16] .

В 2020 году Wang et al. ^[17] опубликовал хорошо составленный количественный обзор пренатального воздействия свинца (Pb) на массу тела при рождении. Поскольку количественные переменные из каждой рецензируемой статьи сообщались с использованием разных метрик и разных мер связи, они использовали стандартизированные коэффициенты регрессии, чтобы можно было объединить результаты рецензируемых исследований. Объединение результатов проводилось отдельно для материнской крови и пуповинной крови в качестве показателей воздействия. Кроме того, анализы ограничивались нескорректированными результатами и исследованиями, в которых учитывались потенциальные искажающие факторы. Между пренатальным воздействием свинца и массой тела при рождении была выявлена ​​значительная отрицательная связь. В нескорректированных исследованиях снижение массы тела при рождении было слабо связано с повышенным уровнем свинца в материнской крови (объединенный β = -0,094, 95% ДИ = от -0,157 до -0,030) и пуповинной крови (объединенные β = -0,120, 95% ДИ = от -0,239 до -0,001). При ограничении скорректированными исследованиями эти ассоциации были слабее.

В исследовании Николаса Берроуза и его соавторов ^[18] сообщается о мета-анализе исследований, в которых изучалась взаимосвязь между болью от остеоартрита коленного сустава и физической активностью или фитнесом. Величины эффекта из оцененных исходных исследований были преобразованы в стандартизированные коэффициенты регрессии, чтобы их можно было включить в лесные участки и оценить объединенный стандартизированный коэффициент. Данные их собственного нового исследования также были включены в метаанализ. Из 33 включенных исследований 13 предоставили данные для анализа связи между болью и физической активностью, а 21 предоставили данные для связи между болью и физической активностью. Извлеченные переменные физической активности представляли собой либо показатели активности на основе анкеты, либо объективно измеренную активность с использованием шагомеров или акселерометров. Отдельные мета-анализы были выполнены для мышечной силы, мышечной силы и аэробной способности. Между объективно измеренной физической активностью и интенсивностью боли были обнаружены статистически значимые объединенные βs. Более физически активные люди сообщали о меньшей боли при исходном измерении и в течение семидневного периода измерения физической активности.

Маклафлин и др. ^[19] проанализировали исследования, связанные с связью между участием в цифровом вмешательстве в области физической активности и результатами физической активности. Во включенных исследованиях использовались различные методы ассоциации. Для отчетливого метаанализа авторам потребовалось преобразовать несколько оценок в один согласованный индекс эффекта. В качестве индекса эффекта был выбран стандартизированный коэффициент регрессии. Во многих включенных исследованиях сообщалось о более чем одной ассоциации. Для метаанализа они использовали иерархические критерии отбора, чтобы выбрать одну ассоциацию из каждого исследования для включения в объединенный синтез. Когда исследование не предоставило достаточных данных, необходимых для метаанализа (т. е. информации для расчета оценки эффекта и измерения вариабельности оценки эффекта), авторы исключили это исследование из метаанализа. Метаанализ 11 включенных исследований показал очень небольшую, но статистически значимую положительную связь между вовлеченностью в цифровое здравоохранение и физической активностью (объединенный β = 0,08, 95% ДИ = от 0,01 до 0,14).

2.2. Психология

Чарли Риу и соавторы ^[20] опубликовали интересное исследование, в котором βs использовались для представления размера эффекта взаимодействия между темпераментом и семейными переменными на употребление психоактивных веществ или экстернализирующее поведение при контроле других переменных, включенных в проверенная модель различными исследованиями. Авторы искали исследования, изучающие взаимодействие между темпераментом и семейной средой на переменные результата. Анализ взаимодействий между двумя независимыми переменными можно проводить с использованием методов ANOVA или моделей множественной регрессии. Интерпретация взаимодействий сложна, потому что разные модели взаимодействия между темпераментом и семейными переменными могут иметь разные последствия. Из-за проблем с условиями взаимодействия и различиями в измерениях исследователи были осторожны и не сообщали об объединенных размерах эффекта. Тем не менее, сообщаемые величины отдельных эффектов и их интерпретация в тексте по-прежнему предоставляют полезную информацию о возможном взаимодействии между проанализированными независимыми переменными.

Кейтлин Вулли и Айелет Фишбах ^[21] исследовали взаимосвязь между немедленным и отсроченным вознаграждением и настойчивостью в достижении долгосрочных целей (например, здоровое питание, физические упражнения). Авторы провели пять различных интервенционных исследований для изучения ассоциаций. В каждом исследовании они проводили регрессионный анализ для оценки взаимосвязей и сообщали о βs. Наконец, они объединили β, используя метааналитический подход, чтобы оценить общую закономерность в пяти исследованиях. Таким образом, в то время как отсроченное вознаграждение может мотивировать постановку целей и намерения преследовать долгосрочные цели, метаанализ их исследований показал, что немедленное вознаграждение более тесно связано с фактической настойчивостью в достижении долгосрочной цели. Влияние немедленного вознаграждения на настойчивость с учетом отсроченного вознаграждения считалось средним и статистически значимым (объединенный β = 0,35, 95% ДИ = от 0,28 до 0,42, p < 0,001).

Чой и др. ^[22] использовали подход, аналогичный подходу Вули и Фишбаха ^[21] , и объединили результаты пяти различных исследований, используя β в качестве величины эффекта. В каждом дополнительном исследовании они изучали предикторы успеха в различных областях достижений с использованием регрессионных моделей. Проведя метаанализ, они изучили общую закономерность исследований. Их результаты показывают, что самоконтроль предсказывает успех в областях, связанных с достижениями (β = 0,27, 95% ДИ = от 0,21 до 0,32), в то время как эмоциональное благополучие предсказывает успех в областях, связанных с отношениями (β = 0,36, 95% ДИ = 0,29 до 0,43).

Два метаанализа изучали связанные с болью факторы у лиц с хронической скелетно-мышечной болью ^{[23] [24]} . В обоих исследованиях для объединенных результатов были рассчитаны стандартизированные коэффициенты регрессии и их 95% доверительные интервалы. Рассмотренные исследования исключались из этого анализа, если они не предоставляли достаточно информации для расчета SE коэффициента регрессии. Более высокие уровни страха боли, тревоги, связанной с болью, и убеждений об избегании страха были значительно связаны с большей интенсивностью боли и инвалидностью ^[23] . Кроме того, более высокие уровни чрезмерно негативных мыслей в ответ на боль или связанные с ней сигналы были связаны с большей интенсивностью боли и уровнями инвалидности 90–290 [24] 90–291 . Авторы отмечают, что важным наблюдением в их обзорах было то, что, несмотря на очень большое количество исследований, проведенных для оценки связи между факторами, связанными с болью, и болью, и инвалидностью, качество исследований, как правило, было очень низким. К ним относятся вопросы статистического анализа и отчетности. Эти недостатки затрудняли проведение метаанализа.

2.3. Другие подполя

Статья Yong Jei Lee и сотрудников ^[25] является примером из криминологии. Цель их работы состояла в том, чтобы показать, на сколько стандартных отклонений числа преступлений изменится при увеличении (или уменьшении) стандартного отклонения переменной численности полиции в США. Они объединили стандартизированные коэффициенты регрессии из 62 исследований, чтобы оценить общую величину эффекта. Предполагаемый объединенный размер эффекта составил -0,030 (95% ДИ = от -0,078 до 0,019).). Незначительный и крошечный средний размер эффекта между численностью полиции и преступностью предполагает, что простое увеличение численности полиции может не помочь снизить преступность, а если и поможет, то ненамного уменьшит преступность.

Мета-регрессию можно использовать в мета-анализе для оценки взаимосвязи между ковариатами уровня исследования и величиной эффекта ^[7] . Sanghee Park ^[26] применил метарегрессию для изучения влияния различных характеристик исследования на наблюдаемую связь между гендерным представительством в рабочей силе и эффективностью общественной организации с использованием объединенного β в качестве индекса размера эффекта в 72 исследованиях, опубликованных между 1999 и 2017. Несколько ковариантов объяснили вариации в сообщаемых βs. К сожалению, посылу статьи Парка препятствует неадекватная связь между теорией метарегрессии и описанием прикладной области метаанализа.

Yahui Tian и Jijun Yao ^[27] применили метаанализ для анализа в общей сложности 20 величин эффекта из 11 статей о влиянии инвестиций китайских школ на успеваемость учащихся. Они обнаружили, что общее влияние школьных ресурсов на успеваемость учащихся является значительным (объединенный β = 0,09). 3, 95% ДИ = от 0,039 до 0,147). Поскольку в этом исследовании в качестве величины эффекта использовался стандартный коэффициент регрессии, увеличение на одно стандартное отклонение инвестиций в школьные ресурсы повысит успеваемость учащихся на 0,093 стандартных балла. Следует отметить, что для объединения результатов человеческих, материальных и финансовых ресурсов с общей суммой вложенных ресурсов в каждом исследовании требовалось несколько вычислительных шагов.

Стандартизированные коэффициенты регрессии также применялись в экономических исследованиях. В статье, опубликованной Araujo et al. в 2020 г. обеспечивает всесторонний синтез фактических данных о макропруденциальной политике ^[28] . Опираясь на 58 эмпирических исследований, авторы обобщили влияние макропруденциальной политики на несколько результатов (например, кредит, кредит домохозяйствам и цены на жилье). В экономической литературе нет стандартного определения переменных, используемых для измерения результатов макропруденциальной политики.