3.Линейная функция вида y = kx + b
Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).
Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.
Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при
b) k < 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b < 0; y = kx + b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k < 0, следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскос
Графики функций — ГИА В3
Здравствуйте, уважаемый посетитель! В этой статье будут разобраны задания В3 из ГИА, те, что связаны с графиками функций. Мы научимся определять все коэффициенты параболы по графику, находить точки пересечения прямой с осями координат и ее коэффициент наклона, а также ближе познакомимся с гиперболой.
Давайте начнем разбор этих заданий со знакомства с прямой и ее уравнением.
Прямая задается уравнением: 

Уравнение прямой и его коэффициенты
И тот, и другой коэффициенты могут быть как положительными, так и отрицательными. В случае с коэффициентом b все понятно: [stextbox id=”alert” bwidth=”1″ bcolor=”5e56a9″ bgcolor=”0cb2f2″]если он положительный, то прямая пересекает ось y выше оси х, а если отрицательный – то ниже[/stextbox]. На рисунке этот коэффициент равен 2 для красной прямой (
 , для розовой –
, для розовой – 

Прямые с различными значениями коэффициентов
А как быть с k? Давайте разберемся. Как узнать по графику, положительный ли коэффициент k или он меньше 0? Посмотрим на графики на рисунке выше: они наклонены в разные стороны. Вот за наклон-то как раз и отвечает коэффициент k, и по наклону прямой мы “вычислим” его знак.
Признак такой: если прямая образует острый угол с положительным направлением оси х, то коэффициент k – положительный. Если прямая образует тупой угол с положительным направлением оси х, то коэффициент k – отрицательный
Посмотрим на наш рисунок:

Коэффициенты уравнения прямой и их значение
У красной и розовой прямых – положительный коэффициент наклона, у зеленой – отрицательный.
Чтобы определить оба коэффициента (а не только их знаки), нужно взять 2 точки на прямой (любые) и подставить их координаты в уравнение прямой. Тогда мы получим систему уравнений, которая позволит определить оба коэффициента. В отдельных случаях можно обойтись и одним уравнением: если прямая проходит через начало координат, или если можно определить коэффициент b по рисунку. Примеры:
Определим коэффициент k для прямой, изображенной на рисунке:

Определение коэффициента наклона прямой
Так как прямая проходит через начало координат, то  . Тогда, чтобы определить k, потребуется всего одно уравнение. Возьмем любую точку, принадлежащую прямой, например, точку (1;3) – точки удобно брать с целыми координатами. Подставляем координаты точки в уравнение прямой вместо x и y:
. Тогда, чтобы определить k, потребуется всего одно уравнение. Возьмем любую точку, принадлежащую прямой, например, точку (1;3) – точки удобно брать с целыми координатами. Подставляем координаты точки в уравнение прямой вместо x и y:

Еще пример:

Определение обоих коэффициентов уравнения прямой
Определим уравнение прямой, для этого найдем коэффициенты b и k ее уравнения. Возьмем две точки на прямой, хорошо, если координаты точек целые. У нас это точки (5;0) и (-3;-2). В общее уравнение прямой подставим координаты этих точек:

Вычтем второе уравнение из первого, это позволит определить коэффициент k:

Чтобы найти b, подставим найденный коэффициент наклона в любое из двух уравнений:

Тогда уравнение этой прямой будет таким:

Иногда коэффициент наклона помогает определить знание следующего факта: если прямая лежит под углом 45 или 135 градусов к оси х (то есть проходит по диагоналям клеточек – как красные прямые на рисунке) – то модуль ее коэффициента наклона равен 1. Если прямая “прижимается” к оси y – желтая область на рисунке – то модуль ее коэффициента наклона больше 1. Если же она “жмется” к оси х (зеленая область) – модуль ее коэффициента k меньше 1. Данный факт помогает при решении таких задач, где необходимо сопоставить графики нескольких прямых и данные уравнения. Тем не менее, чтобы не ошибиться, лучше все же определить коэффициент аналитически: подставив координаты выбранной точки в уравнение.

Коэффициенты прямой, которые превосходят 1 по модулю, и меньше 1 по модулю
Пример такого задания:
Один из графиков на рисунке – график функции y=3x. Каким цветом он изображен?

Определение коэффициента наклона по графику
Рассуждаем так: коэффициент наклона положительный – угол наклона прямой к оси х будет острым – ни зеленый, ни желтый графики не подходят. Модуль коэффициента наклона больше 1 (равен 3) – прямая будет располагаться ближе к оси у, чем к оси х: значит, это график голубого цвета. После этих рассуждений надо обязательно (!) проверить их правильность: просто теперь нам придется проверять не все графики, а только один: голубому графику принадлежит точка (1;3). Подставим ее в уравнение:

Получилось тождество, значит, мы правы. Посмотрите видео-исследование прямой:
Переходим теперь к параболе. Парабола задается квадратичной функцией: . Коэффициент а определяет форму параболы, а также направление ее ветвей: если он положителен – то ветви параболы смотрят вверх, если отрицателен – вниз. От коэффициента b зависит расположение вершины параболы, то есть, в конечном счете, сдвиг по оси х вправо-влево. Наконец, коэффициент с показывает, какова ордината точки, в которой парабола пересечет ось y.
. Коэффициент а определяет форму параболы, а также направление ее ветвей: если он положителен – то ветви параболы смотрят вверх, если отрицателен – вниз. От коэффициента b зависит расположение вершины параболы, то есть, в конечном счете, сдвиг по оси х вправо-влево. Наконец, коэффициент с показывает, какова ордината точки, в которой парабола пересечет ось y.
Рассмотрим несколько графиков, чтобы отработать определение последнего коэффициента – с, как наиболее простого.

Общий вид парабол с разными коэффициентами
Итак, с – точка пересечения параболой оси y. Для первой параболы на рисунке это 8, для второй – 3, для третьей – 6, для четвертой – (-5). А вот точка пересечения пятого графика с осью y только угадывается. Можно сказать с определенностью, что коэффициент с для нее меньше ноля. Однако его точное значение зависит также и от формы параболы, которая определяется величиной коэффициента a. Если этот коэффициент задан и равен (-1), то можно догадаться, что с для нее равен (-19). Однако. чтобы точно определить все коэффициенты, необходимо взять несколько точек, принадлежащих этому графику функции, и, подставив их координаты в уравнение квадратичной функции, решить систему уравнений, которая и позволит точно найти a,b и с.
Разберем такое задание: график какой из приведенных ниже функций изображен на рисунке?

Подбор формулы, задающей график функции

Посмотрим на график. Ветви параболы направлены вверх, значит, коэффициент a – положительный. Тогда нам не подойдут ни первая, ни последняя функция. Две оставшиеся отличаются одним лишь знаком коэффициента b, поэтому найдем абсциссу вершины параболы. Для второй:

Для третьей:

Тогда, значит, подходит вторая функция, так как видно, что вершина лежит в области отрицательных значений х.
Следующая задача такая: найдите значение а по графику функции  , изображенному на рисунке.
, изображенному на рисунке.

Парабола, у которой коэффициент а=1
Есть два пути для решения данной задачи. Первый – рациональный. Находим точки, принадлежащие графику, подставляем их координаты в уравнение, получаем систему (как минимум, понадобится три точки, чтобы определить три коэффициента, и система будет из трех уравнений), решаем систему.
Есть и второй путь – эмпирический. Этот метод “тыка” иногда упрощает задачу очень существенно, тем более что “тык” будет у нас вполне обоснованным, а не случайным.
Давайте рассуждать:ветви направлены вверх? – коэффициент а – положительный. Где находится вершина параболы? Правильно, в точке (2;0). Значит, ее ось симметрии –

Парабола, у которой коэффициент а=1
прямая х=2. Тогда все ее точки должны располагаться симметрично по обе стороны от этой прямой.
Возьмем две точки на оси х, отстоящие на единицу от оси симметрии параболы – точки х=1, х=3. Какие им соответствуют ординаты? y=1 в обоих случаях. Теперь возьмем точки, отстоящие на 2 единицы от оси симметрии – х=0 и х=4. Какие ординаты будут им соответствовать? y=4! Иными словами, ординаты точек этого графика получаются, если просто возводить в квадрат разность абсцисс точки и вершины параболы:  и т.д. Тогда коэффициент a этой параболы равен 1!
и т.д. Тогда коэффициент a этой параболы равен 1!
Наши рассуждения можно пояснить рисунком:
Теперь рассмотрим задачи более сложные, связанные как раз с необходимостью составлять систему уравнений.
Иногда вершина предлагаемого графика располагается не в пересечении клеточек, то есть координаты вершины – дробные числа. Кроме того, форма параболы отличается от “классической”, которую мы получаем, если а=1. Тогда “метод научного тыка” не годится, “на глазок” коэффициенты уже не определить. Вот здесь необходимо найти принадлежащие графику точки, лучше, если они будут находиться на пересечении клеток, то есть их координаты будут целыми. Сколько же потребуется таких точек? Если возможно определить коэффициент с по графику, то две, а если нельзя – три.
Рассмотрим задачу: необходимо найти все коэффициенты уравнения, задающего график:

Найти все коэффициенты по графику функции
Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:
координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

Последние два уравнения вычтем:

Данное выражение подставим в первое и второе уравнения:

Вычтем два получившихся уравнения:
 Зная а, можем найти и остальные коэффициенты:
Зная а, можем найти и остальные коэффициенты:

Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

Найти все коэффициенты по графику функции
Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:


Найти все коэффициенты по графику функции
Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:
Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.
Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:

Из первого уравнения вычитаем второе:

Полученное подставим в первое и третье:

Полученные уравнения вычтем вновь, и найдем искомое:

Посмотрите видео-исследование параболы:
Наконец, нужно познакомиться с гиперболой. График ее задается функцией:  . Он интересен тем, что располагается всегда в двух квадрантах: в первом и третьем, либо во втором и четвертом. От знака коэффициента k зависит вид функции: если знак положителен, то ветви гиперболы расположатся в первом и третьем квадрантах, если отрицателен – во втором и четвертом. Кроме того, от этого коэффициента зависит и форма гиперболы. Если
. Он интересен тем, что располагается всегда в двух квадрантах: в первом и третьем, либо во втором и четвертом. От знака коэффициента k зависит вид функции: если знак положителен, то ветви гиперболы расположатся в первом и третьем квадрантах, если отрицателен – во втором и четвертом. Кроме того, от этого коэффициента зависит и форма гиперболы. Если  , то гипербола непременно пройдет через точки (1;1), (-1;-1). Если
, то гипербола непременно пройдет через точки (1;1), (-1;-1). Если  , то гипербола будет “прижиматься” к осям координат, а если , то наоборот, точки графика будут лежать дальше от начала координат. Это иллюстрирует рисунок (одна клеточка – единичный отрезок):
, то гипербола будет “прижиматься” к осям координат, а если , то наоборот, точки графика будут лежать дальше от начала координат. Это иллюстрирует рисунок (одна клеточка – единичный отрезок):

Коэффициент гиперболы
Здесь зеленая область – область, где лежат точки гипербол с положительным коэффициентом k, меньшим 1. Желтая область – область точек гипербол с положительным коэффициентом k, большим 1. Черным цветом изображена “классическая” гипербола, k=1.
Для отрицательных k (одна клеточка – единичный отрезок):

Коэффициент гиперболы
Разберем задачу: нужно определить, график какой из приведенных ниже функций изображен на рисунке.

Коэффициент гиперболы

Рассмотрим график. Все его точки лежат во второй и четвертой четвертях, это означает, что положительным х соответствуют отрицательные y, а отрицательным – положительные, то есть коэффициент у функции, задающей этот график, должен быть отрицательным. Тогда ни первая, ни третья функции не подходят. Значит, надо выбирать из второй и четвертой, причем у второй  , а у четвертой
, а у четвертой  . Значит, график второй функции должен быть расположен ближе к осям координат, чем точка (1;-1) – голубая область на предыдущем рисунке. У нас график расположен не так, если бы мы перенесли его на предыдущий рисунок, он бы попал в серую область, значит, предположительно, изображен график четвертой функции, однако, в этом надо быть уверенным наверняка. Поэтому возьмем точку на графике и подставим ее координаты в уравнение, например, точку (3;-1):
. Значит, график второй функции должен быть расположен ближе к осям координат, чем точка (1;-1) – голубая область на предыдущем рисунке. У нас график расположен не так, если бы мы перенесли его на предыдущий рисунок, он бы попал в серую область, значит, предположительно, изображен график четвертой функции, однако, в этом надо быть уверенным наверняка. Поэтому возьмем точку на графике и подставим ее координаты в уравнение, например, точку (3;-1):

Получилось тождество, значит, уравнение выбрано верно.
Еще задача:
На одном из графиков изображен график функции  . Какой это рисунок?
. Какой это рисунок?

Определение графика по заданной функции
Во-первых, не все изображенные графики – гиперболы. Сразу отбросим “лишние” – это розовый график функции  – номер 2, и фиолетовый – номер 1, который расположен “не в тех” квадрантах. Остаются два графика – 3 и 4 – которые очень похожи друг на друга. Поскольку коэффициент перед х в заданной функции отрицательный, нам нужен 4 график – тот, что изображен черным цветом.
– номер 2, и фиолетовый – номер 1, который расположен “не в тех” квадрантах. Остаются два графика – 3 и 4 – которые очень похожи друг на друга. Поскольку коэффициент перед х в заданной функции отрицательный, нам нужен 4 график – тот, что изображен черным цветом.
Последняя задача: найдите коэффициент k по графику функции  , изображенному на рисунке:
, изображенному на рисунке:

Определение коэффициента функции по графику
Здесь достаточно взять только одну точку, принадлежащую графику, и подставить ее координаты в уравнение:

Посмотрите короткое видео с исследованием гиперболы:
Надеюсь, эта статья поможет вам в подготовке к экзамену! Всего вам хорошего, вопросы можно задать в комментариях, я постараюсь ответить.
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида  , где
, где 
 называется квадратичной функцией.
называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:
имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции  , составим таблицу:
, составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент  , то график квадратичной функции имеет ровно такую же форму, как график функции
, то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.
при любых значениях остальных коэффициентов.
График функции  имеет вид:
имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции  симметричен графику функции
симметричен графику функции  относительно оси ОХ.
относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции
— это точки пересечения графика функции  с осью ОХ.
с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции  с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение  .
.
В случае квадратичной функции  нужно решить квадратное уравнение
нужно решить квадратное уравнение  .
.
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант:  , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если 
 ,то уравнение
,то уравнение  не имеет решений, и, следовательно, квадратичная парабола
не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если
не имеет точек пересечения с осью ОХ. Если 
 ,то график функции выглядит как-то так:
,то график функции выглядит как-то так:

2. Если 
 ,то уравнение
,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола
имеет одно решение, и, следовательно, квадратичная парабола  имеет одну точку пересечения с осью ОХ. Если
имеет одну точку пересечения с осью ОХ. Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

3. Если 
 ,то уравнение
,то уравнение  имеет два решения, и, следовательно, квадратичная парабола
имеет два решения, и, следовательно, квадратичная парабола  имеет две точки пересечения с осью ОХ:
имеет две точки пересечения с осью ОХ:
 ,
, 
Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:



Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.
с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль:
с осью OY, нужно в уравнение параболы вместо х подставить ноль:  .
.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой  .
.
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 
1. Направление ветвей параболы.
Так как 
 ,ветви параболы направлены вверх.
,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 



Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение: 
 ,
, 
3. Координаты вершины параболы:


4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы


Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид  — в этом уравнении
— в этом уравнении  — координаты вершины параболы
— координаты вершины параболы
или в уравнении квадратичной функции 
 , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Построим для примера график функции  .
.
Вспомним линейные преобразования графиков функций. Чтобы построить график функции  , нужно
, нужно
- сначала построить график функции
 ,
, - затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции  . В уравнении этой функции
. В уравнении этой функции  , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат: 
Следовательно, координаты вершины параболы:  . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда 
2. Координаты вершины параболы: 

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.
Перед вами график квадратичной функции вида  .
.
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции  от значения коэффициента
от значения коэффициента  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения 
— направления ветвей параболы от знака коэффициента 
— координат вершины параболы  от значений
от значений  и
и  :
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Муниципальное бюджетное образовательное учреждение
Глуховская школа-интернат №2
г. Ногинск Московской обл.
Конспект открытого урока по теме:
«ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b И с НА РАСПОЛОЖЕНИЕ
ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ»
Урок составлен и проведён:
учителем математики
МБОУ ГШИ №2 Потапова С.А.
дата проведения: 18. 10. 2018 уч.г.
г. Ногинск
Обобщающий урок по алгебре 9-А класс
по теме: «Влияние коэффициентов а, b и с на расположение графика квадратичной функции»
Цель урока: повторить тему «Квадратичная функция и её график», использовать её для решения задач, входящих в раздел «Алгебра » ОГЭ.
Задачи:
-образовательные: Повторить определение и свойства квадратичной функции, что могут показывать коэффициенты квадратного трёхчлена; рассмотреть задачи, входящие в ОГЭ по данной теме.
-развивающие: Развивать умения анализировать, сопоставлять, логически мыслить, обобщать, развивать память, активность и самостоятельность, способность к самоорганизации.
-воспитательные: Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата.
Тип урока: Урок систематизации знаний и умений.
Формы работы учащихся: Фронтальная, самостоятельная.
Необходимое техническое оборудование: интерактивная доска, компьютер.
Ход урока:
1.Организационный момент. (2-3 минуты)
2. Постановка целей урока. (1 мин.) (Формулировка цели урока)
3. Актуализация знаний. (10 мин)
4. ( тренинг) Фронтальная работа с использованием интерактивной доски. (12 мин)
3. Повторим определение квадратичной функции. (определение на интерактивной доске.)
3.1 Квадратичной функцией называется функция, которую можно задать формулой у=ах2 + bх + с, где а, b, с — некоторые числа, причём а не равно нулю.
3.2 Обобщение и уточнение материала: (беседа после постановки проблемного вопроса).
Проблемный вопрос: какую информацию можно получить о графике квадратичной функции, зная коэффициенты квадратного трёхчлена.
(На интерактивной доске установить соответствие между знаками коэффициентов а и с и дискриминанта с расположением графика функции на координатной плоскости).
3.3 Как зависит расположение параболы в системе координат от коэффициентов a, b и c?
Коэффициент а влияет на направление ветвей параболы (как?)
Коэффициент b влияет на расположение вершины параболы (как?)
Если b = 0, то где расположена вершина параболы? (лежит на оси ОУ).
Коэффициент с влияет на пересечение параболы с осью ОУ и расположением вершины графика относительно оси ОХ – ниже, если с меньше нуля и выше, если с больше нуля.
Помним, что если с < 0, то график расположен ниже оси х, если с > 0, то выше. То же самое должно быть и с b, только относительно оси y
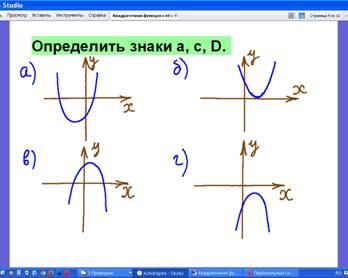
4.1 Задание: (фронтально) Расположение параболы в системе координат в зависимости от коэффициентов:
Найдите правильный ответ:
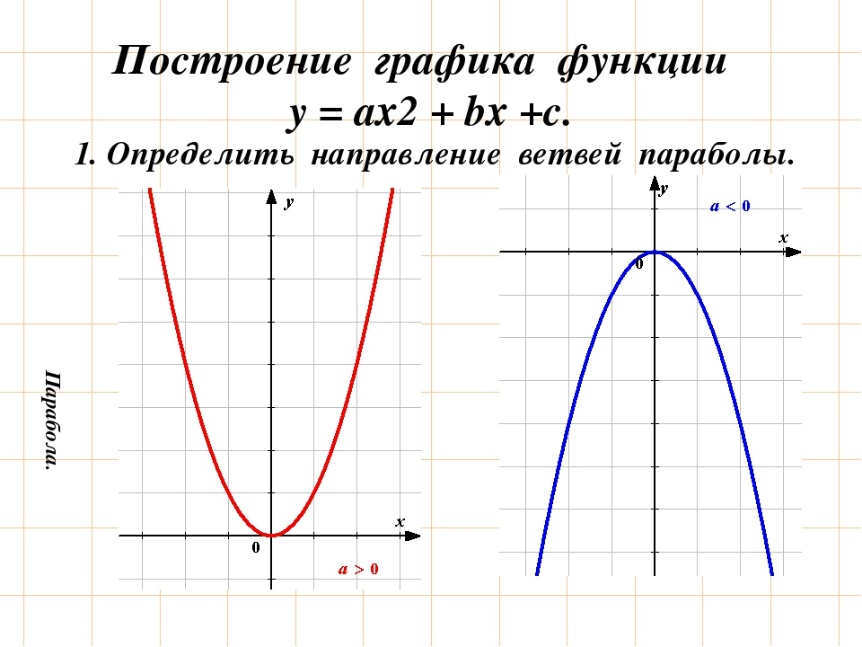
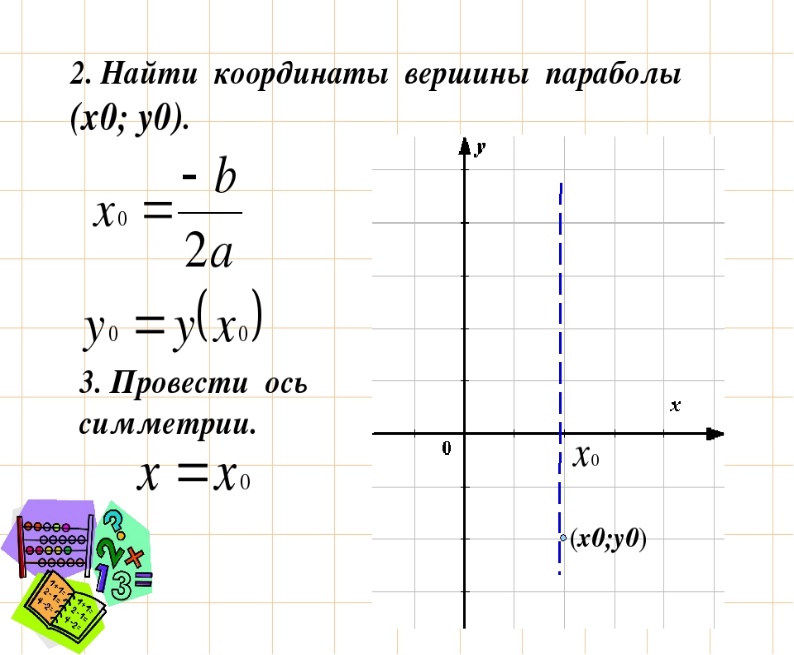
1) Если коэффициент а > 0, то…. (ветви – вверх)
2) Если коэффициент а < 0, то…. (ветви – вниз)
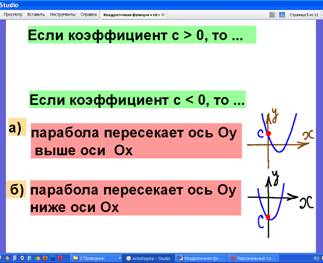
3) Если коэффициент с > 0, то… (парабола пересекается с осью ОУ выше оси ОХ)
4) Если коэффициент с < 0, то … (парабола пересекается с осью ОУ ниже оси ОХ)
5) Коэффициент b влияет на смещение вершины параболы вдоль оси ОХ
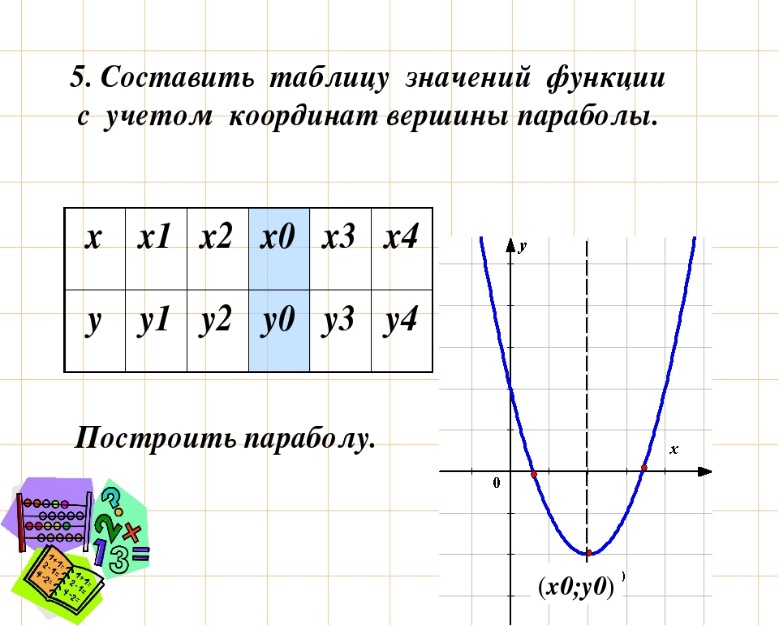
4.2 (Слайды из презентации, или рисунки на доске):

Физкультминутка: (показать на материале 4.3. Движение рук, туловища, глаз)
4.3 Провести повторение вышеизложенного материала по слайдам:
«Зависимость расположения графиков квадратичной функции от
кооффициентов»
Урок алгебры в 9 классе
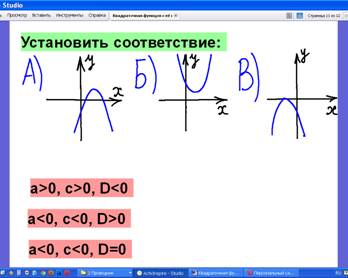
4.4 Фронтальная работа на интерактивной доске на установление соответствия с пояснениями – повторение зависимости пересечений графика с осями координат от дискриминанта квадратного трёхчлена.
Разработала учитель математики
Мезрина Марина Владимировна
Повторить алгоритм построения графика квадратичной функции и построить график функций. Работа в парах с объяснением и взаимопроверкой:
у = х2 + 2х — 8;
1. Постройте график функции (указанной функции) и найдите, используя график:
а) нули функции;
б) промежутки, в которых у > 0 и y < 0;
в) промежутки возрастания и убывания функции;
г) наименьшее значение функции;
д) область значения функции.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Опишите алгоритм построения квадратичной функции.
– Перечислите свойства функции у= ах2 + bх+ с при а > 0 и при а < 0.
–Как влияют коэффициенты а, b и с на расположение графика квадратичной функции?
Рефлексия. Выбери утверждение, которое соответствует тому, как тебе работалось на уроке. Выведены на интерактивную доску.
1) Мне было всё понятно, я смог повторить теоретический материал и могу решать задачи без посторонней помощи.
2) Я вспомнил теоретический материал, решил задачи, но некоторые задачи требуют посторонней помощи.
3) Я плохо знаю теоретический материал, не смог его вспомнить и не могу решать задачи по данной теме.
Домашнее задание:
№ 127 (б), № 128.
Д о п о л н и т е л ь н о выполнить задания по вариантам:
(Раздаточный материал: 8 карточек с заданиями по 2-4 вариантам)
В а р и а н т 1 (четыре карточки)
1.Найдите координаты вершины параболы: а) у = -х2— 4х + 1 б) у = 3х2 — 12х + 22.
Постройте график функции у = х2 — 6х + 4 и найдите, используя график:
а) нули функции;
б) промежутки, в которых у > 0 и y < 0;
в) промежутки возрастания и убывания функции;
г) наименьшее значение функции;
д) область значения функции.
В а р и а н т 2 (четыре карточки)
1.Найдите координаты вершины параболы: а) у= -х2 + 6х + 3 б) у = 4х2 — 8х — 1
2.Постройтеграфик функции у = х2 + 4х + 2 и найдите, используя график:
а) нули функции;
б) промежутки, в которых у > 0 и y < 0;
в) промежутки возрастания и убывания функции;
г) наибольшее значение функции;
д) область значения функции.
Использована литература:
1. Учебник для общеобразовательных организаций:
Алгебра 9 класс, под редакцией С.А. Теляковского, 4-е издание, Москва
«Просвещение» 2017 г.
2. Тесты: «Алгебра 9 класс» (М.: Мнемозина), издательство «ЭКЗАМЕН»
Москва 2016 г.
3. Интернет-ресурсы: videouroki.net
Квадратичная функция
Квадратичная функция — функция вида:
f(x)=ax2+bx+c
или
y(x)=ax2+bx+c
Где a≠0.
В уравнении квадратичной функции:
a –старший коэффициент
b – второй коэффициент
с свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции
y(x)=x2
или
f(x)=x2
.
Имеет вид и строится по «базовым точкам»:
a>0
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
Парабола состоит из 2 частей: одна находится в I четверти, где значения X и Y положительные, а вторая часть – во II четверти, где значения X отрицательные, а значения Y положительные.
y(x)>0, при x∈(-∞;0)∪(0;+∞)
Если двигаться по одной ветви параболы от -∞ к 0, то мы замечаем, что функция убывает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы замечаем, что функция возрастает.
Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как y(x)=x2 при любых значениях остальных коэффициентов.
График функции
y(x)=-x2
Имеет вид и строится по «базовым точкам»:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-4 |
-1 |
0 |
-1 |
-4 |
-9 |
Парабола состоит из 2 частей: одна находится в III четверти, где значения X и Y отрицательные, а вторая часть – в IV четверти, где значения X положительные, а значения Y отрицательные.
y(x)<0, при x∈(-∞;0)∪(0;+∞)
Если двигаться по одной ветви параболы от -∞ к 0, то мы замечаем, что функция возрастает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы замечаем, что функция убывает.
Свойства функции y(x)=x2:
1) Область определения функции:
D(f)=(-∞;0)∪(0;+∞).
2)Область значения функции:
Если a<0
E(f)=(-∞;0].
Если a>0
E(f)=[0;+∞).
3)Наибольшее и наименьшее значение функции:
Если a<0, то Yнаиб=0,Yнаим нет.
Если a>0, тоYнаим=0, Yнаиб нет.
4)Y(x)=x2— четная функция(т.к.f(-x)=x2=(-x)2=f(x) ).
График симметричен относительно оси oY .
5) Ограниченность функции:
Если a>0, функция ограничена снизу.
Если a<0, функция ограничена сверху.
6) Функция пересекает оси oX и oY в точке (0;0)
Перемещение параболы y(x)=x2
Если добавить константу d (где d любое число), в качестве слагаемого к X, то произойдет перемещение параболыпо оси (вместе с вертикальной асимптотой).
В таком случае уравнением функции станет:
y(x)=(x±d)2
Если d>0 (y(x)=(x+d)2), то график функции передвигается по оси oX влево.
Для примера возьмем уравнение y=(x+2)2
Если d<0 (y(x)=(x-d)2), то график функции передвигается по оси oX вправо.
Для примера возьмем уравнение y=(x-2)2
Если добавить константу c(где cлюбое число) к X2 в качестве слагаемого, то произойдет перемещение параболы по оси oY (вместе с горизонтальной асимптотой)
В таком случае уравнением функции станет:
y(x)=(x)2±c
Если c>0 (y(x)=(x)2+c), то график функции передвигается по оси oY вверх.
Для примера возьмем уравнение y=(x)2+2
Если c<0 (y(x)=(x)2-c), то график функции передвигается по оси oY вниз.
Для примера возьмем уравнение y=(x)2-3
Дискриминант и нахождение корней
y=ax2+bx+c
ax2+bx+c=0
D=(b)2-4ac
1) 1) Если D>0 то уравнение ax2+bx+c=0 имеет 2 решения, уравнение y=ax2+bx+c имеет 2 точки пересечения с осью oX:
Если a>0, график функции будет иметь примерный вид:
2) Если D=0, то уравнение ax2+bx+c=0 имеет 1 решение,=> уравнениеy=ax2+bx+c имеет 1 точку пересечения с осью oX.
Если a>0, график функции будет иметь примерный вид:
3) Если D<0, то уравнение ax2+bx+c=0 не имеет решения, => уравнениеy=ax2+bx+c не имеет общих точек пересечения с осью oX.
Если a>0, график функции будет иметь примерный вид:
Координаты вершины параболы
Координаты вершины параболы находятся через данные формулы:
Прямая, проходящая через вершину параболы является осью симметрии параболы.
Точка пересечения с осью oY
Так как абсцисса любой точки, лежащей на оси oY равна нулю, чтобы найти точку пересечения параболы y=ax2+bx+c с осью oY, нужно в уравнение параболы вместо Xподставить 0, тогда y(0)=c.
Алгоритм построения квадратичной параболы
1) Направление ветвей.
2) Координаты вершины параболы.
3) Корни дискриминанта.
4) Дополнительные точки.
5) Построение графика.
Разложениеквадратного трехчлена
Пример №1
Построим функцию y=x2-6x+15
В квадратичном трехчлене x2-6x+15, чтобы выразить квадрат разности, используем формулу сокращенного умножения.
Базовая формула: (a±b)2=x2±2ab+b2,
Выразим квадрат разности: x2-6x+15=(x2-6x+9)+6,
Соберем формулу: (x2-6x+9)+6=(x-3)2+6,
У нас получилась функция y=(x-3)2+6,
Мы замечаем, что график функции смещен на 3 по оси oX вправо и на 6 по оси oY вверх.
Следовательно, график функции y=(x-3)2+6 будет выглядеть таким образом:
Пример №2
Построим функцию y=x2+8x+17
В квадратичном трехчлене x2+8x+17,чтобы выразить квадрат разности, используем формулу сокращенного умножения.
Базовая формула: (a±b)2=x2±2ab+b2,
Выразим квадрат разности: x2+8x+17=(x2+8x+16)+1,
Соберем формулу: (x2+8x+16)+1=(x+4)2+1,
У нас получилась функция y=(x+4)2+1,
Мы замечаем, что график функции смещен на 4 oX влево и на 1 по оси oY вверх.
Следовательно, график функции y=(x+4)2+1 будет выглядеть таким образом:
Итог:
Чтобы разложить квадратный трехчлен, использую такой алгоритм:
1) Выразим квадрат разности из данного трехчлена, с помощью формул сокращенного умножения;
2) Соберем, получившуюся формулу;
3) «Прочитаем» график, на смещение, относительно осей координат;
4) Построим график.
Автор статьи: Мажаров Данила Михайлович
Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна
Все знают, как выглядит парабола y = x2. В седьмом классе мы рисовали таблицу:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
После этого по точкам строили график:
Параболу y = ax2 + bx + c мы не станем строить каждый раз «по точкам» — для выпускника школы это просто несолидно. Ведь нам надо знать закономерности поведения данной функции. А эти закономерности таковы.
1. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.
На рисунке приведены две параболы y = ax2 с равными по модулю, но противоположными по знаку значениями a.

2. Абсолютная величина коэффициента a отвечает за «раскрыв» параболы. Чем больше |a|, тем у́же парабола (больше прижата к оси Y). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X).
На рисунке приведены две параболы y = a1x2 и y = a2x2, у которых a2 > a1 > 0

3. Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить x0 в уравнение параболы. Но вообще, полезно помнить, что
где D = b2 − 4ac — дискриминант.
4. Точки пересечения параболы y = ax2 + bx + c с осью X находятся с помощью решения квадратного уравнения ax2 + bx + c = 0. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
5. Точка пересечения с осью Y находится легко: мы просто подставляем x = 0 в уравнение параболы. Получается точка (0, c).
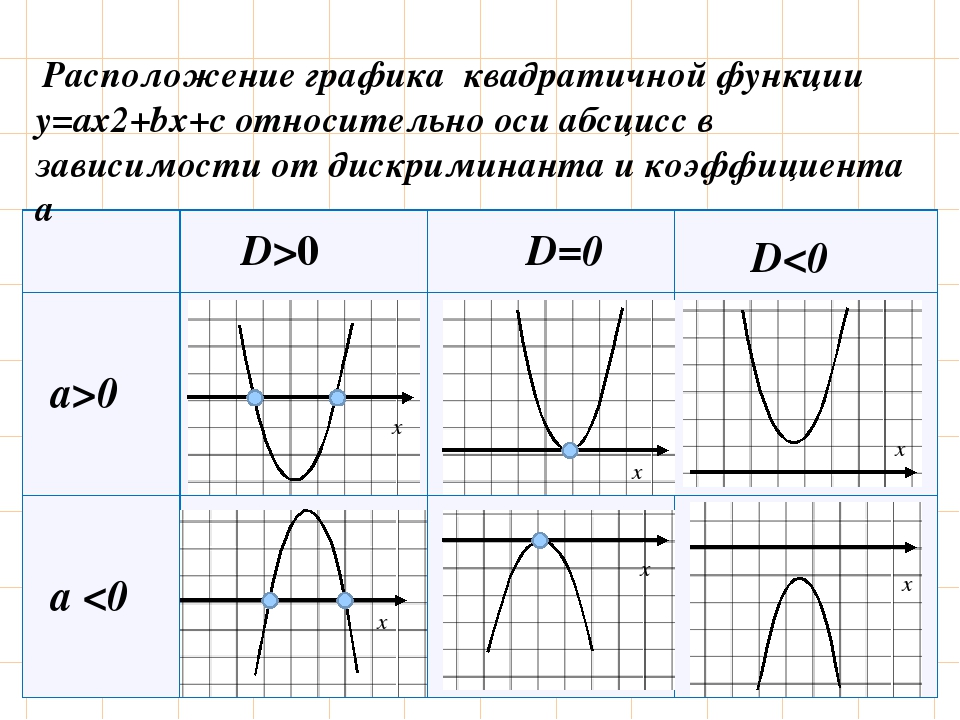
Посмотрим, как расположена квадратичная функция (парабола) в зависимости от знака коэффициента а и дискриминанта D.

Где же в реальной жизни можно увидеть параболу (квадратичную функцию)?
Мяч, брошенный под углом к горизонту, летит по параболе. Зависимость его высоты от времени — квадратичная функция. Струя воды из фонтана или шланга, направленная под углом к горизонту, рисует в пространстве именно параболу. Но это не всё. Разберите карманный фонарик. Вы увидите, что за лампочкой расположено зеркальце, имеющее параболическую форму. Спутниковая антенна или антенна телескопа имеют форму параболы. Случайно ли это?
Оказывается, параболическое зеркало обладает интереснейшим свойством — весь поток света, падающий на его поверхность, оно собирает в одной точке, называемой фокусом параболы. Вот почему форма антенн — параболическая. И наоборот, если в фокусе параболы расположен источник света, то отражённые от зеркала лучи света будут параллельны. Поэтому карманный фонарик дает направленный луч света, хорошо видимый в темноте.

Решая задачи ЕГЭ с физическим или экономическим содержанием, мы часто будем замечать в них квадратичные зависимости одной переменной от другой. И конечно, будем пользоваться свойствами квадратичной функции.
Знаки коэффициентов квадратного трехчлена
Знаки коэффициентов квадратного трехчлена.
В этой статье я расскажу, как по графику квадратичной функции найти знаки коэффициентов квадратного трехчлена.
Чтобы определить знаки коэффициентов квадратного трехчлена по графику квадратичной функции  , нужно вспомнить теорему Виета.
, нужно вспомнить теорему Виета.
Согласно теореме Виета, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.
Квадратное уравнение называется приведенным, если его старший коэффициент равен единице.
Чтобы уравнение  стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение
стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение  . Для него справедливы соотношения:
. Для него справедливы соотношения:

И эти же соотношения справедливы для уравнения 
По графику квадратичной функции мы легко можем определить знак коэффициента  — если ветви параболы направлены вверх, то
— если ветви параболы направлены вверх, то 
 , а если вниз, то
, а если вниз, то 
 .
.
Также по графику легко определяются знаки корней (корни квадратного трехчлена  — это абсциссы точек пересечения графика функции
— это абсциссы точек пересечения графика функции  с осью абсцисс), а также знак корня с большим модулем.
с осью абсцисс), а также знак корня с большим модулем.
Если оба корня положительны, то 
 .
.
Если оба корня отрицательны, то 
 .
.
Если корень с большим модулем положителен, то 
 .
.
Если корень с большим модулем отрицателен, то 
 .
.
Если корни имеют одинаковые знаки, то 
 .
.
Если корни имеют разные знаки, то 
 .
.
Во всех случаях, определив знак коэффициента  по направлению ветвей параболы, мы легко найдем знаки коэффициентов
по направлению ветвей параболы, мы легко найдем знаки коэффициентов  и
и 
Рассмотрим примеры.
1. Определить знаки коэффициентов квадратного трехчлена  , если график функции
, если график функции  имеет вид:
имеет вид:

1. Ветви параболы направлены вниз, следовательно, 
 .
.
2. Корни имеют одинаковые знаки, следовательно, их произведение положительно: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
3. Оба корня отрицательны, следовательно, их сумма отрицательна: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
Ответ: 
 ,
, 
 ,
, 
 .
.
2. Определить знаки коэффициентов квадратного трехчлена  , если график функции
, если график функции  имеет вид:
имеет вид:

1. Ветви параболы направлены вверх, следовательно, 
 .
.
2. Корни имеют разные знаки, следовательно, их произведение отрицательно: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
3. Корень с большим модулем положителен, следовательно, сумма корней положительна: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
Ответ: 
 ,
, 
 ,
, 
 .
.
Замечание:  — ордината точки пересечения параболы с осью
— ордината точки пересечения параболы с осью  , поэтому знак
, поэтому знак  можно определить сразу.
можно определить сразу.

Факторинг в алгебре
Факторы
Номера имеют факторы:
И выражения (например, x 2 + 4x + 3 ) также имеют факторы:
Факторинг
Факторинг(в Великобритании называемый «Факторинг ») — это процесс , нахождение факторов :
Факторинг: Найти, что умножить вместе, чтобы получить выражение.
Это похоже на «разбиение» выражения на умножение более простых выражений.
Пример: фактор 2y + 6
2y и 6 имеют общий множитель 2:
Таким образом, мы можем разделить все выражение на:
2y + 6 = 2 (y + 3)
Итак, 2y + 6 «учтено» в 2 и y + 3
Факторинг также является противоположностью Расширения:
Общий Фактор
В предыдущем примере мы видели, что 2y и 6 имели общий множитель 2
Но для правильной работы нам необходим наивысший общий коэффициент , включая любые переменные
Пример: коэффициент 3y 2 + 12y
Во-первых, 3 и 12 имеют общий коэффициент 3.
Итак, мы могли бы иметь:
3y 2 + 12y = 3 (y 2 + 4y)
Но мы можем сделать лучше!
3y 2 и 12y также делят переменную y.
Вместе, что делает 3y:
- 3y 2 — 3y × y
- 12y 3y × 4
Таким образом, мы можем разделить все выражение на:
3y 2 + 12y = 3y (y + 4)
Чек: 3y (y + 4) = 3y × y + 3y × 4 = 3y 2 + 12y
Более сложный факторинг
Факторинг может быть трудным!
Примеры пока просты, но факторинг может быть очень сложным.
Потому что мы должны изобразить , на которое умножили , чтобы получить выражение, которое нам дано!
Это все равно что пытаться найти, какие ингредиенты
пошли в торт, чтобы сделать его таким вкусным.
Это может быть трудно понять!
опыта помогает
С большим опытом факторинг становится проще.
Пример: коэффициент 4x 2 — 9
Хммм … кажется, нет общих факторов.
Но знание специальных биномиальных продуктов дает нам ключ, называемый «разницей квадратов» в :
Потому что 4x 2 — это (2x) 2 , а 9 — это (3) 2 ,
Итак, у нас есть:
4x 2 — 9 = (2x) 2 — (3) 2
И это можно получить по формуле разности квадратов:
(a + b) (a-b) = 2 — b 2
, где a — 2x, а b — 3.
Итак, давайте попробуем сделать это:
(2x + 3) (2x − 3) = (2x) 2 — (3) 2 = 4x 2 — 9
Да!
Итак, коэффициенты 4x 2 — 9 равны (2x + 3) и (2x − 3) :
Ответ: 4x 2 — 9 = (2x + 3) (2x − 3)
Как вы можете научиться делать это? Получая много практики и зная «идентичности»!
Помните эти идентичности
Ниже приведен список распространенных «идентичностей» (включая использованную выше «разницу квадратов» ).
Стоит помнить об этом, поскольку они могут упростить факторинг.
| a 2 — b 2 | = | (a + b) (a − b) |
| a 2 + 2ab + b 2 | = | (a + b) (a + b) |
| a 2 — 2ab + b 2 | = | (a-b) (a-b) |
| a 3 + b 3 | = | (a + b) ( 2 −ab + b 2 ) |
| a 3 — b 3 | = | (a-b) ( 2 + ab + b 2 ) |
| a 3 + 3a 2 b + 3ab 2 + b 3 | = | (a + b) 3 |
| a 3 −3a 2 b + 3ab 2 −b 3 | = | (a-b) 3 |
Есть еще много подобных, но это самые полезные.
Советы
Факторизованная форма обычно лучшая.
При попытке факторинга выполните следующие действия:
- «Фактор» любые общие термины
- Посмотрите, подходит ли оно какой-либо личности, плюс еще вы можете знать
- Продолжайте, пока вы не можете больше не учитывать
Существуют также системы компьютерной алгебры (называемые «CAS»), такие как Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce и многие другие, которые хороши в факторинге.
Дополнительные примеры
Опыт помогает, поэтому вот еще несколько примеров, которые помогут вам в пути:
Пример: ш 4 — 16
Показатель 4? Может быть, мы могли бы попробовать показатель степени 2:
Вт 4 — 16 = (Вт 2 ) 2 — 4 2
Да, это разница квадратов
w 4 — 16 = (w 2 + 4) (w 2 — 4)
А «(ш 2 — 4)» — это еще одно отличие квадратов
w 4 — 16 = (w 2 + 4) (w + 2) (w — 2)
Это насколько я могу (если я не использую мнимые числа)
Пример: 3u 4 — 24uv 3
Удалить общий множитель «3u»:
3u 4 — 24uv 3 = 3u (u 3 — 8v 3 )
Тогда разница в кубах:
3u 4 — 24uv 3 = 3u (u 3 — (2v) 3 )
= 3u (u − 2v) (u 2 + 2uv + 4v 2 )
Это так далеко, как я могу пойти.
Пример: z 3 — z 2 — 9z + 9
Попробуйте разложить первые два и вторые два отдельно:
z 2 (z − 1) — 9 (z − 1)
Wow, (z-1) на обоих, так что давайте использовать это:
(z 2 −9) (z − 1)
А z 2 −9 это разность квадратов
(z-3) (z + 3) (z-1)
Это так далеко, как я могу пойти.
Теперь получите больше опыта:
,2?Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra
- тригонометрия и алгебра
- Статистика
- тригонометрия
Все о факторах числа
Факторы числа — важная подтема из систем счисления. В этой статье мы обсудим основы факторов ряда. Почти каждый конкурсный экзамен имеет 2-3 средних и сложных вопросов на основе ряда факторов. Принимая это во внимание, мы обсудим расширенное применение этой темы, чтобы дать вам преимущество перед другими кандидатами.
Каковы факторы числа?
Факторы числа N относятся ко всем числам, которые делят N полностью.Их также называют делителями числа.
Основная формула, связанная с множителями числа:
Это некоторые основные формулы, относящиеся к факторам числа N, таким, что
N = p a q b r c
Где p, q и r — простые множители числа n.
a, b и c — неотрицательные степени / показатели степени
- Количество факторов N = (a + 1) (b + 1) (c + 1)
- Произведение факторов N = N Нет.факторов / 2
- Сумма факторов: (p 0 + p 1 + … + p a ) (q 0 + q 1 + …. + q b ) (r 0 + r 1 + … + r c ) / (p a -1) (q b -1) (r c -1)
Решенные вопросы о факторах числа:
Пример 1: Рассмотрим число 120. Найдите следующее для n- Сумма факторов
- Количество факторов
- Продукт факторов
- Сумма факторов = [(2 0 +2 1 +2 2 +2 3 ) (3 0 +3 1 ) (5 0 +5 1 )] / [(2-1) (3-1) (5-1)] = 45
- Количество факторов = (3 + 1) (1 + 1) (1 + 1) = 16
- Продукт факторов = 120 (16/2) = 120 8
- Количество нечетных факторов
- Количество четных факторов
Решение: Путем простой факторизации 84, 84 = 2 2 × 3 1 × 7 1
Общее количество факторов = (2 + 1) (1 + 1) (1 + 1) = 12
- Количество нечетных факторов будет всеми возможными комбинациями степеней 3 и 5 (исключая любую степень 2).Следовательно, число нечетных факторов = (1 + 1) (1 + 1) = 4
. При ручной проверке эти факторы равны 1, 3, 7 и 21. - Количество четных факторов = всего нет. факторов — нет. четных факторов
= 12 — 4 = 8
Знай, где ты стоишь в Факторах. Пройди этот тест сейчас.
Расширенные концепции факторов числа
Пример 3: Пусть N = 3 15 × 7 43 . Сколько факторов N 2 меньше, чем N, но не делят N полностью?
Решение: Пусть N = 6, тогда N 2 = 36.
При первичной факторизации N = 2 × 3 и N 2 = 2 2 × 3 2 . Число факторов N 2 = 9, которые составляют 1, 2, 3, 4, 6, 9, 12, 18, 36. Теперь из них первые пять меньше, чем N, то есть 1, 2,3,4 и 6. Но из них 1, 2, 3 и 6 полностью делятся 6. Это оставляет нас с 4. Следовательно, нет. из факторов, которые меньше чем N, но не делят N полностью, составляет 1 .
Чтобы прийти к этому по формуле,
- Добавить 1 к числу факторов N 2 Нет.из факторов = (2 + 1) (2 + 1) = 9; добавив 1, 9 + 1 = 10
- Разделите это на 2, чтобы получить количество пар Количество пар = 10/2 = 5
- Из этого полученного числа вычтите количество факторов из N. Число факторов из N = (1 + 1) (1 + 1) = 4; 5-4 = 1, , который является ответом.
Давайте перейдем к проблеме, выполнив шаги,
- N 2 = 330 x 786; Количество факторов = (30 + 1) (86 + 1) = 31x 87 = 2697; добавление 1 дает 2698
- Количество пар = 2698/2 = 1349 №
- из факторов N = (15 + 1) (43 + 1) = 704; Ответ 1349-704 = 645
Обучение
- Этот вопрос появляется на конкурсных экзаменах каждый год. Следовательно, мы разработали ярлык для данной проблемы. Согласно ей, ответ на такую проблему дает произведение степеней простых чисел Н.
- Для вышеупомянутой проблемы ответ может быть получен непосредственно: 15 × 43 = 645!
Пример 4: Найти число положительных интегральных решений уравнения, x 2 -y 2 = 840?
Решение: Алгебраическое выражение может быть записано как x 2 -y 2 = (x + y) (x-y)- Следовательно, чтобы получить решение x и y, нам нужно найти пары, произведение которых равно 840.
- Первичная факторизация 840 = 2 3 × 3 × 5 × 7. Итак, число факторов 840 = (3 + 1) (1 + 1) (1 + 1) (1 + 1) = 32.
- Количество пар, которые дадут уникальные положительные интегральные решения для этого уравнения = нет. факторов / 2 = 32/2 = 16. Поскольку для каждой пары, скажем, 4 x 210, мы получаем уникальные решения для x и y.
Обучение
- x и y будут давать только различные интегральные значения, при условии, что правая часть уравнения является нечетным числом или кратным 4.
Готовы ли вы ответить на наши вопросы продвинутого уровня? Пройди этот тест и узнай.
Практический вопрос: Сколько натуральных чисел ниже 100 можно записать как разность двух натуральных чисел?
(Подсказка: применить вышеупомянутое обучение для решения этого вопроса)
Ответ: 75
Факторы числа: Key Learning
- Некоторые однотипные вопросы среднего и сложного уровня задаются год за годом на нескольких конкурсных экзаменах.Тщательная практика примеров вопросов (как показано в видео) может дать вам большое конкурентное преимущество для управления временем.
Учитесь напрямую у эксперта! Посмотрите это видео, чтобы понять все концепции факта о факторах из числа
Смотри ,| Существительное | 1. |  фактор — все, что причинно приводит к результату; «ряд факторов определил результат» причина — события, которые обеспечивают порождающую силу, которая является источником чего-либо; «они пытаются определить причину краха» фундаментально — любой фактор, который можно считать важным для понимания конкретного бизнеса; параметр «фундаментальные параметры включают рост компании, доходы, прибыль, управление и структуру капитала» — любой фактор, который определяет систему и определяет (или ограничивает) ее производительность, неизвестное количество — фактор в данной ситуации, значение и важность которого не очевидны; «Я не знаю, что будет делать новый человек; он все еще неизвестное количество» — непредсказуемый фактор; «погода была дикой картой», высвобождающий фактор, высвобождающий гормон, RF — вещество, вырабатываемое гипоталамусом, способное ускорять секрецию данного гормона фактором передней доли гипофиза, — вещество, вырабатываемое слизистой оболочкой желудка и кишечник, необходимый для усвоения витамина В12; «Недостаток внутреннего фактора может привести к пагубной анемии» фактор — все, что причинно приводит к результату; «ряд факторов определил результат» причина — события, которые обеспечивают порождающую силу, которая является источником чего-либо; «они пытаются определить причину краха» фундаментально — любой фактор, который можно считать важным для понимания конкретного бизнеса; параметр «фундаментальные параметры включают рост компании, доходы, прибыль, управление и структуру капитала» — любой фактор, который определяет систему и определяет (или ограничивает) ее производительность, неизвестное количество — фактор в данной ситуации, значение и важность которого не очевидны; «Я не знаю, что будет делать новый человек; он все еще неизвестное количество» — непредсказуемый фактор; «погода была дикой картой», высвобождающий фактор, высвобождающий гормон, RF — вещество, вырабатываемое гипоталамусом, способное ускорять секрецию данного гормона фактором передней доли гипофиза, — вещество, вырабатываемое слизистой оболочкой желудка и кишечник, необходимый для усвоения витамина В12; «Недостаток внутреннего фактора может привести к пагубной анемии» |
| 2. |  фактор — абстрактная часть чего-либо; «ревность была составной частью его характера»; «две составляющие музыкальной композиции — мелодия и гармония»; «грамматические элементы предложения»; «ключевой фактор ее успеха»; элемент сюжета «юмор: эффективный ингредиент речи» — компонент или элемент сюжета сюжетной точки — геометрический элемент, который имеет положение, но не имеет расширения; «точка определяется своими координатами» деление, сечение, часть — одна из частей, на которые что-то расценивается как разделенная и которые вместе составляют единое целое; «письменная часть экзамена»; «финансовый отдел компании»; «Инженерное подразделение Би-би-си» фактор — абстрактная часть чего-либо; «ревность была составной частью его характера»; «две составляющие музыкальной композиции — мелодия и гармония»; «грамматические элементы предложения»; «ключевой фактор ее успеха»; элемент сюжета «юмор: эффективный ингредиент речи» — компонент или элемент сюжета сюжетной точки — геометрический элемент, который имеет положение, но не имеет расширения; «точка определяется своими координатами» деление, сечение, часть — одна из частей, на которые что-то расценивается как разделенная и которые вместе составляют единое целое; «письменная часть экзамена»; «финансовый отдел компании»; «Инженерное подразделение Би-би-си» | |
| 3. | множитель — одно из двух или более целых чисел, которое может быть точно разделено на другое целое число; «каковы 4 фактора из 6?» — главный фактор — главные факторы величины — это все простые величины, которые будут точно делить данное целое число, целое число — любое натуральное число (положительное или отрицательное) или ноль; «целое число — это число, которое не является дробью» коэффициент эквивалентных двоичных цифр — среднее количество двоичных цифр, необходимое для выражения одной радикальной цифры в системе счисления, которая не является двоичной; в среднем число, которое может быть выражено в N десятичных цифрах, занимает 3.3N двоичных цифр | |
| 4. |  фактор — бизнесмен, который покупает или продает за другого в обмен на брокера по заказу — агент для владельца судна; получает груз и может организовать его погрузку или разгрузку. Брокерский агент — агент по купле-продаже акций и облигаций — агент, назначенный представлять город или университет или корпорацию в качестве агента по бизнес-операциям — кто-то, кто продает или организует поездки или туры для клиентов фактор — бизнесмен, который покупает или продает за другого в обмен на брокера по заказу — агент для владельца судна; получает груз и может организовать его погрузку или разгрузку. Брокерский агент — агент по купле-продаже акций и облигаций — агент, назначенный представлять город или университет или корпорацию в качестве агента по бизнес-операциям — кто-то, кто продает или организует поездки или туры для клиентов | |
| 5. | фактор — любое из чисел (или символов), которые образуют произведение при умножении на вместе, дефлятор — статистический фактор, предназначенный для устранения влияния инфляции; Переменные с поправкой на инфляцию находятся в постоянном долларовом количестве — понятие количества, включающее ноль и единицы; «у каждого числа есть уникальная позиция в последовательности» коэффициент преобразования — коэффициент, на который необходимо умножить количество, выраженное в одном наборе единиц, чтобы преобразовать его в другой набор единиц | |
| 6. | фактор — независимая переменная в статистике | |
| 7. |  фактор — (генетика) сегмент ДНК, который участвует в производстве полипептидной цепи; он может включать области, предшествующие и следующие за кодирующей ДНК, а также интроны между экзонами; считается единицей наследственности; «гены раньше назывались факторами» — доминантный ген — ген, который продуцирует один и тот же фенотип в организме независимо от того, идентичен ли его аллель; аллель «доминантный ген для карие глаза», аллеломорф — (генетика) любая из пары (или серии) альтернативных форм гена, которые могут занимать один и тот же локус в конкретной хромосоме и которые контролируют один и тот же характер; «некоторые аллели доминируют над другими» генетический маркер — специфический ген, который продуцирует узнаваемый признак и может использоваться в семейном или популяционном исследовании гомеотического гена — один из генов, участвующих в эмбриологическом развитии летального гена — любой ген, обладающий эффектом, вызывающим гибель организма на любой стадии жизненно важной группы, связанные гены — любая пара генов, которые имеют тенденцию передаваться вместе; «Мутантный ген« дрозофилы »делится на четыре группы сцепления» — ген, который изменился таким образом, что на нормальную передачу и экспрессию данного признака влияют ноналлели — гены, которые не являются конкурентами в одном и том же гене локус-оператора — ген, который активирует продукцию РНК-мессенджер со смежным структурным геном-полигиленом — геном, который сам по себе мало влияет на фенотип, но который может действовать вместе с другими, вызывая наблюдаемые вариации протоонкогена — нормального гена, который потенциально может стать онкогенно-рецессивным геном — гена, который производит свою характеристику фенотип только тогда, когда его аллель идентичен; репрессорный ген «рецессивный ген для голубых глаз» — ген, который препятствует транскрибированию структурного гена неаллеля — гена, который контролирует выработку определенного белка или пептидтрансгена — экзогенного гена, внедренного в геном другого организма — хромосомы — нитевидной цепи ДНК в клеточном ядре, которое несет гены в линейном порядке; «у людей есть 22 пары хромосом плюс две половые хромосомы» молекулярная биология — раздел биологии, который изучает структуру и активность макромолекул, необходимых для жизненной (и особенно их генетической роли) последовательности — последовательное расположение, в котором вещи следуют в логическом порядке или рецидивирующая картина; «последовательность имен была алфавитной»; «он изобрел метод определения последовательности пар оснований в ДНК» дезоксирибонуклеиновая кислота, дезоксирибонуклеиновая кислота, ДНК — (биохимия) длинный линейный полимер, найденный в ядре клетки и образованный из нуклеотидов и имеющий форму двойной спирали; связанные с передачей генетической информации; «ДНК — король молекул» фактор — (генетика) сегмент ДНК, который участвует в производстве полипептидной цепи; он может включать области, предшествующие и следующие за кодирующей ДНК, а также интроны между экзонами; считается единицей наследственности; «гены раньше назывались факторами» — доминантный ген — ген, который продуцирует один и тот же фенотип в организме независимо от того, идентичен ли его аллель; аллель «доминантный ген для карие глаза», аллеломорф — (генетика) любая из пары (или серии) альтернативных форм гена, которые могут занимать один и тот же локус в конкретной хромосоме и которые контролируют один и тот же характер; «некоторые аллели доминируют над другими» генетический маркер — специфический ген, который продуцирует узнаваемый признак и может использоваться в семейном или популяционном исследовании гомеотического гена — один из генов, участвующих в эмбриологическом развитии летального гена — любой ген, обладающий эффектом, вызывающим гибель организма на любой стадии жизненно важной группы, связанные гены — любая пара генов, которые имеют тенденцию передаваться вместе; «Мутантный ген« дрозофилы »делится на четыре группы сцепления» — ген, который изменился таким образом, что на нормальную передачу и экспрессию данного признака влияют ноналлели — гены, которые не являются конкурентами в одном и том же гене локус-оператора — ген, который активирует продукцию РНК-мессенджер со смежным структурным геном-полигиленом — геном, который сам по себе мало влияет на фенотип, но который может действовать вместе с другими, вызывая наблюдаемые вариации протоонкогена — нормального гена, который потенциально может стать онкогенно-рецессивным геном — гена, который производит свою характеристику фенотип только тогда, когда его аллель идентичен; репрессорный ген «рецессивный ген для голубых глаз» — ген, который препятствует транскрибированию структурного гена неаллеля — гена, который контролирует выработку определенного белка или пептидтрансгена — экзогенного гена, внедренного в геном другого организма — хромосомы — нитевидной цепи ДНК в клеточном ядре, которое несет гены в линейном порядке; «у людей есть 22 пары хромосом плюс две половые хромосомы» молекулярная биология — раздел биологии, который изучает структуру и активность макромолекул, необходимых для жизненной (и особенно их генетической роли) последовательности — последовательное расположение, в котором вещи следуют в логическом порядке или рецидивирующая картина; «последовательность имен была алфавитной»; «он изобрел метод определения последовательности пар оснований в ДНК» дезоксирибонуклеиновая кислота, дезоксирибонуклеиновая кислота, ДНК — (биохимия) длинный линейный полимер, найденный в ядре клетки и образованный из нуклеотидов и имеющий форму двойной спирали; связанные с передачей генетической информации; «ДНК — король молекул» | |
| Глагол | 1. | фактор — разделить на факторы; «квантовый компьютер может вычислять число 15», арифметика — раздел чистой математики, занимающийся теорией численных расчетов |
| 2. | фактор — быть способствующим фактором; «превращать вещи в прибыльность компании» вносить, одалживать, придавать, добавлять, дарить, приносить — дарить качество; «Ее присутствие придает компании определенный смысл»; «Музыка многое добавила к пьесе»; «Она привносит особую атмосферу в наши встречи»; «Это добавляет легкую заметку к программе» | |
| 3. | Фактор — считают актуальным при принятии решения; «Вы должны учитывать последние события», подумайте, изучите — тщательно продумайте; «рассмотреть возможность переезда» |

Leave A Comment