2

Построение и решение графиков Функций

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:

  • Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

  • Графический способ — наглядно.

  • Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

  • Словесный способ.

Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Например, для функции вида область определения выглядит так

Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Запоминаем!

Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Исследование функции

Важные точки графика функции y = f(x):

Стационарные точки — точки, в которых производная функции f(x) равна нулю.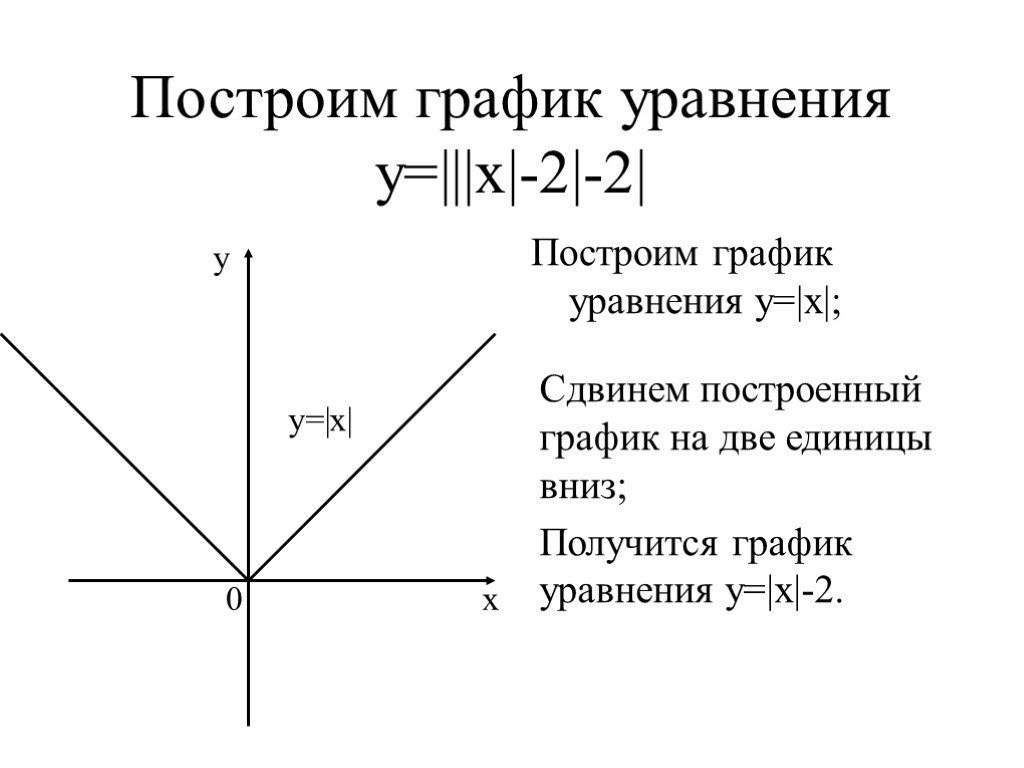

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых значение функции равно нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.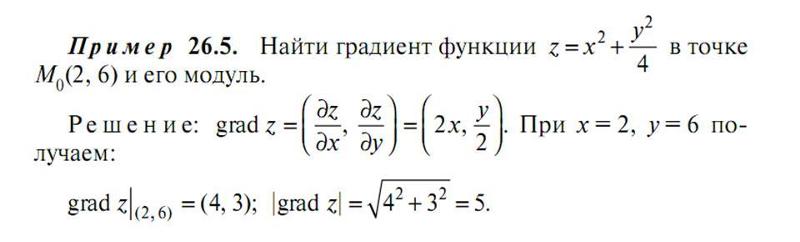

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

 

  1. Найти область определения функции.

  2. Найти область допустимых значений функции.

  3. Проверить не является ли функция четной или нечетной.

  4. Проверить не является ли функция периодической.

  5. Найти точку пересечения с осью OY (если она есть).

  6. Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.

  7. Промежутки знакопостоянства.

  8. Асимптоты.

  9. На основании проведенного исследования построить график функции.

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2.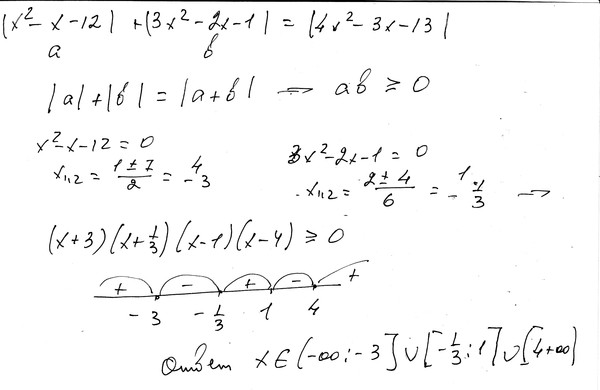 Построим график функции

Как решаем:

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y

и растянутая в 10 раз по сравнению с графиком функции

Задача 3. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

xy
0-1
12

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.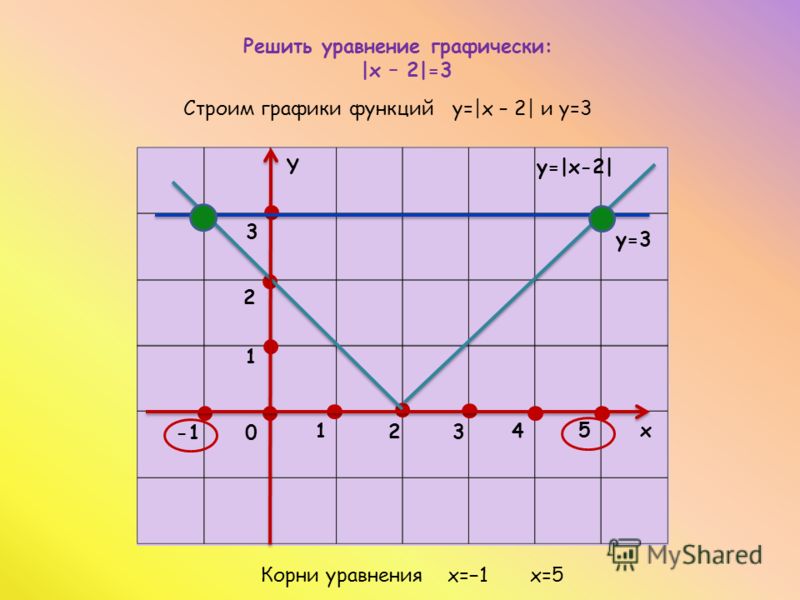

б) y = -x + 2

xy
02
11

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

xy
00
0		2

k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.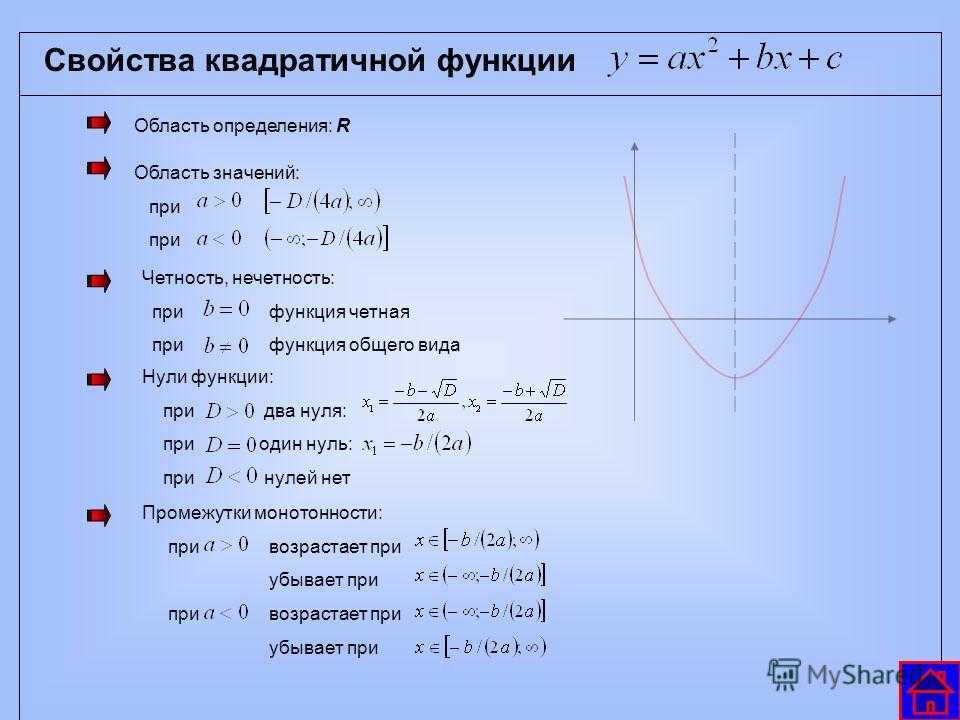

 

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

  1. Ветви вниз, следовательно, a < 0.

    Точка пересечения с осью Oy — c = 0.

    Координата вершины

  2. Ветви вверх, следовательно, a > 0.

    Точка пересечения с осью Oy — c > 0.

    Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

  3. Ветви вниз, следовательно, a < 0.

    Точка пересечения с осью Oy — c > 0.

    Координата вершины , т. к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 5. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Построить графики можно при помощи элементарных преобразований.

Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).

  • y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;

  • y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;

  • y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;

  • y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.

Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.

  • Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.

  • Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.

а)

Преобразование в одно действие типа f(x) + a.

y = x²


Сдвигаем график вверх на 1:

y = x² + 1


б)

Преобразование в одно действие типа f(x — a).


Сдвигаем график вправо на 1:


в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.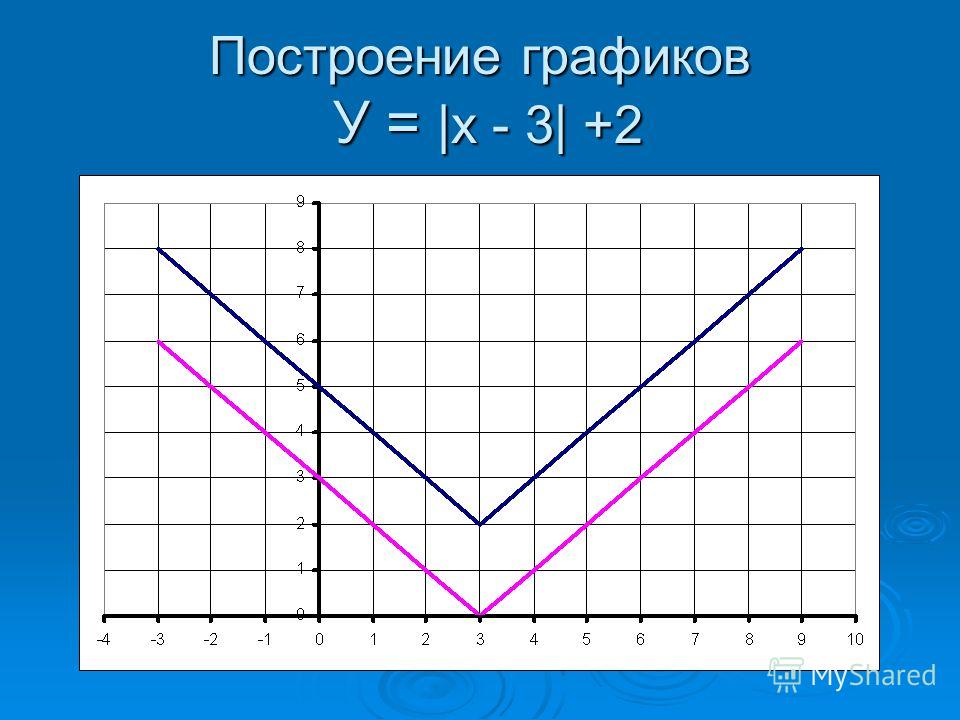

y = x²


Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2


г)

Преобразование в одно действие типа

y = cos(x)


Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:


д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.




Сжимаем график в два раза вдоль оси абсцисс:



Сдвигаем график влево на 1/2 вдоль оси абсцисс:



Отражаем график симметрично относительно оси абсцисс:



3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Что такое обозначение функций и почему меня это должно волновать?

Вычисление четных и нечетных функций в выражениях

Purplemath

Вы уже некоторое время играете с » y =» типами уравнений.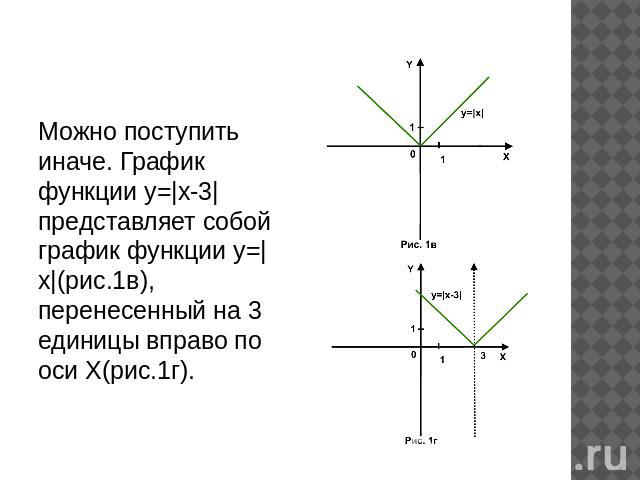 И вы видели, что «хорошие» уравнения (скажем, прямые линии, а не эллипсы) — это те, которые вы можете решить для « y =» и затем вставить в свой графический калькулятор. Эти « у =» уравнения — это функции. Но вопрос, с которым вы сталкиваетесь в данный момент, заключается в следующем: «Зачем мне нужна эта запись функций, особенно когда у меня есть прекрасное ‘ y =’, и как эта запись работает?»

Вспомните, когда вы учились в начальной школе. Ваш учитель давал вам рабочие листы, содержащие такие утверждения, как «[  ] + 2 = 4», и велел вам заполнить поле. Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4″ и сказал вам «решить для x «.

Содержимое продолжается ниже

MathHelp.com

Обозначение функций

Почему ваши учителя перешли от блоков к переменным? Подумайте об этом: сколько форм вам пришлось бы использовать для формул, подобных этой для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? )( a + b )

Если вы попытаетесь выразить вышесказанное или что-то более сложное, используя коробки различной формы, у вас быстро закончатся формы. Кроме того, вы знаете из опыта, что « А » означает «площадь», « h » означает «высота», а « а » и « b » обозначают длины параллельных вершин и нижние стороны. Одному небу известно, что может означать квадратная коробка или треугольная коробка!

Другими словами, они перешли от блоков к переменным, потому что хотя блоки и буквы означают одно и то же (а именно, слот, ожидающий заполнения значением), переменные лучше. Переменные более гибкие, их легче читать, и они могут дать вам больше информации.

То же самое верно для « y » и « f ( x )» (произносится как «эфф-оф-экс»). Для функций эти два обозначения означают одно и то же, но « f  ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « х = 2 х + 3; найдите х , когда х = −1». Теперь вы говорите: « f ( x ) = 2 x + 3; найдите f (−1)» (произносится как « f -из- x равно 2 x плюс три; найти f -отрицательной-единицы»).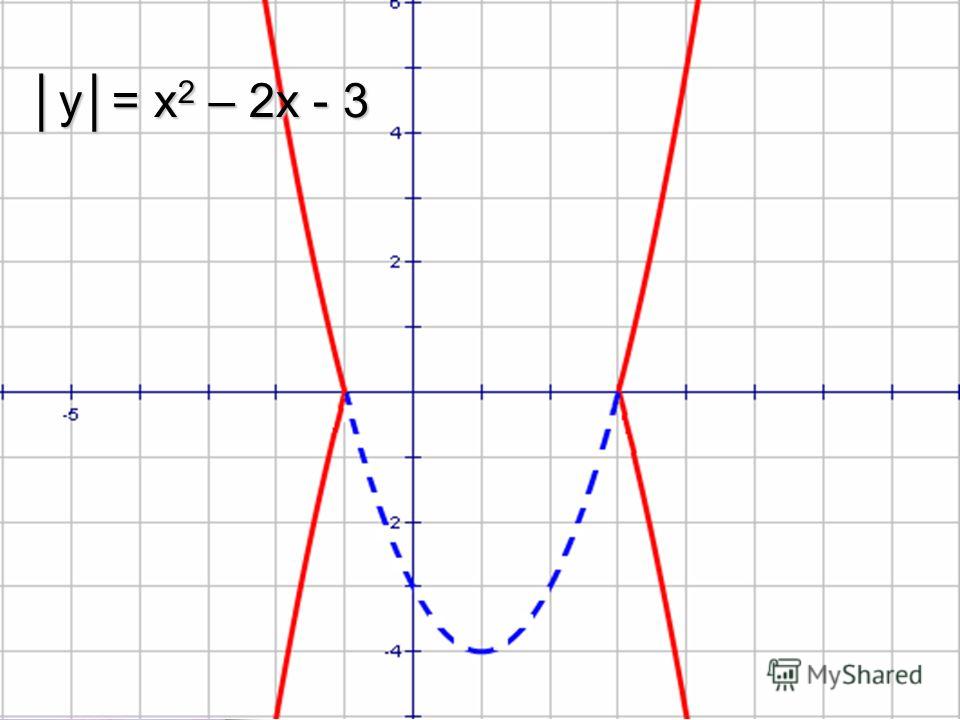 В любом случае вы делаете одно и то же: подставляете -1 вместо x , умножаете на 2, а затем прибавляете 3, упрощая, чтобы получить конечное значение +1.

Но обозначение функций дает вам большую гибкость, чем использование только » y » для каждой формулы. Например, ваш графический калькулятор будет перечислять различные функции как y1, y2 и т. д., так что вы можете сказать уравнения друг от друга, когда, скажем, вы просматриваете их значения в «ТАБЛИЦЕ».0907

Точно так же в учебниках и при записи мы используем разные имена функций, такие как f ( x ), g ( x ), h ( x ), ( t ) и т. д., чтобы отслеживать и работать с более чем одной формулой в любом отдельном контексте. Благодаря нотации функций мы теперь можем использовать более одной функции одновременно, не запутываясь и не путая формулы, заставляя себя задаваться вопросом: «Хорошо, а что y ‘является ли этим ?» И обозначения могут быть полезными пояснениями.

Из геометрии вы знаете, что « A ( r ) = π r 2 » указывает площадь окружности, заданной в терминах значения радиуса r , в то время как « C ( r ) = 2π r » указывает на длину окружности, заданную в терминах радиуса r . Обе функции имеют один и тот же плагин- в переменной (« r «), но « A » напоминает вам, что первая функция — это формула «площади», а « C » напоминает вам, что вторая функция — это формула «длины окружности». )» — это то же самое, что и « y «. Вы даже можете пометить ось y на ваших графиках как « f  ( x )», если хотите.

Пусть Я поясню еще один момент. В то время как круглые скобки до сих пор всегда обозначали умножение, это не относится к обозначению функций. Вопреки всему предыдущему опыту, скобки для обозначения функций делают , а не указывают на умножение.

Выражение « f  ( x )» означает «формула с именем f имеет x в качестве входной переменной». , а не означает «умножить на и на »!

Не смущайтесь, произнося (или думая) « f  ( x )» как « f умножить на x », и никогда не пытайтесь «умножить» имя функции на ее ввод в скобках.

В обозначениях функций « x » в « f  ( x )» называется «аргументом функции» или просто «аргументом». Так что, если вам дадут выражение « ф (2)» и спросят «аргумент», ответ будет просто «2».

Почему ввод функции называется «аргументом»?

Термин «аргумент» имеет долгую историю. Первоначально это был логический термин, относящийся к заявлению, которое выдвигало доказательство или, в менее формальном смысле, к утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить. В конце концов, в раннем научном контексте этот термин стал обозначать любое математическое значение, которое было необходимо в качестве исходных данных для других вычислений, или любое значение, от которого зависели более поздние результаты.

В двадцатом веке, когда компьютерное кодирование стало популярным, кодировщики приняли математический смысл для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» — это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а выход функции — это зависимая переменная (та, значение которой зависит от того, что было подключено). in, обычно это значение y ).

Сначала сделаю вторую часть. Аргументом является то, что находится внутри круглых скобок, поэтому аргумент здесь равен 9.0911 с .

Имя функции — это переменная, которая стоит перед круглыми скобками. В этом случае имя функции h .

имя функции: h

аргумент: s

Аргументом является то, что подключено. В этом конкретном (необычном) случае подключаемая переменная — « y «. (В конце концов, нет правила, согласно которому y не может быть независимой переменной.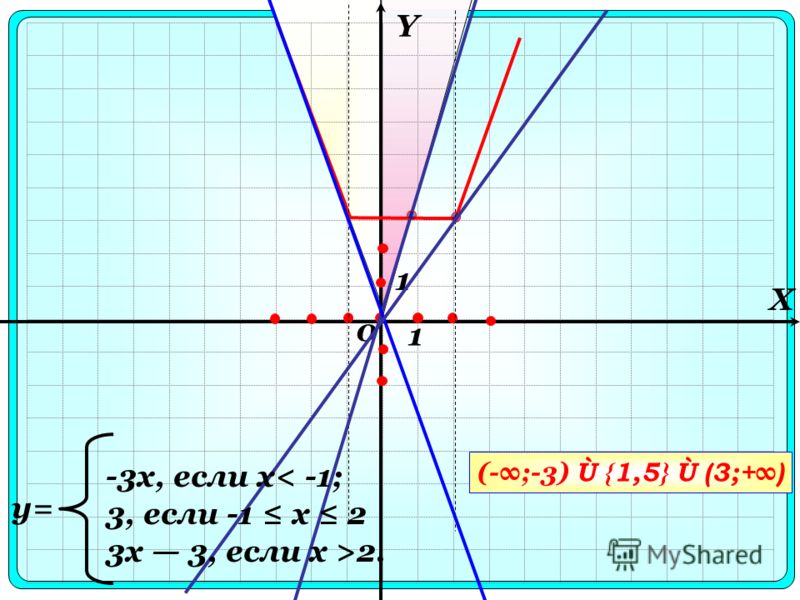 ) Итак:

аргумент равен 9.0911 y

Имя функции стоит перед круглыми скобками, поэтому имя функции здесь g .

Во второй части вопроса от меня требуют аргумент. В первой части, где мне дали имя функции и аргумент (часть « g ( t )») и формулу (часть « t  2 + t »), аргумент был т . Но во второй части они подставили конкретное значение для 9.0911 т . Итак, во второй части аргументом является число −1.

имя функции: g

аргумент g (-1): -1

Как функция вычисляется по числу?

Вы оцениваете « f  ( x )» точно так же, как вы всегда оценивали « y »; а именно, вы берете число, которое они вам дают, в качестве входной переменной, подставляете его в качестве переменной и упрощаете, чтобы получить ответ. Например:

Чтобы вычислить f ( x ) при x = 2, я подставлю 2 для каждого экземпляра x в правиле функции:

f (2) = 947 2 +2(2) − 1

Чтобы все было ясно в голове (и ясно в моей работе), я заключил в скобки каждый экземпляр аргумента 2 в формуле для f .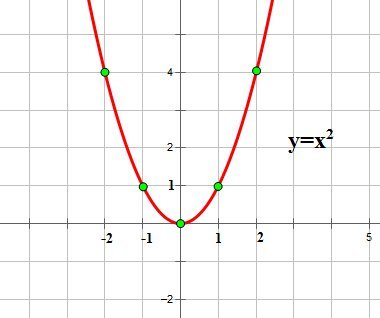 Теперь я могу упростить:

(2) 2 + 2(2) — 1

= 4 + 4 — 1

= 7

Тогда мой ответ:

f  (2) = 7

Чтобы оценить, я делаю то, что делал всегда. Я подставлю заданное значение (−3) для указанной переменной ( x ) в данную формулу:

f (−3) = (−3) 2 + 2(−3) − 1

Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу. В этом случае скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:

(−3) 2 + 2(−3) − 1

= 9 − 6 − 1

= 2

Тогда мой ответ:

f (−3) = 7 909 2 9 вы испытываете трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как, например, находится ли показатель степени на знаке «минус». И вообще это хорошая привычка, которую нужно развивать.

Важный тип функции называется «кусочной» функцией, потому что она состоит из частей. Например, следующая функция является кусочной:

Как видите, эта функция разделена на две половины: половина, предшествующая x = 1, и половина, идущая от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:

  • Учитывая функцию
    f  ( x ), определенную выше, оцените функцию при следующих значениях: x  = −1, x  = 3 и x  = 1,

Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожен, чтобы вставить аргумент в правильную часть функции.

Сначала они хотят, чтобы я оценил x  = −1. Так как это меньше 1, то этот аргумент входит в первую часть функции. Для обновления функция такова:

Затем я подставлю −1 в правило ) − 1

= 2 − 1 = 1

Далее они хотят, чтобы я нашел значение f (3). Поскольку 3 больше 1, мне нужно будет подключить вторую часть функции, так что:

f (3) = (3) + 4 = 7

Наконец, они хотят, чтобы я вычислил f ( x ) на x = 1. Это единственное значение x , которое немного сложно. Какую половину я использую?

Внимательно изучив правила для функций, я вижу, что первая часть — это правило для x — значений, которые строго меньше 1; правило не применяется, когда x равно 1. С другой стороны, вторая часть применяется, когда x больше или равно 1. Поскольку я имею дело с x = 1, то применяется правило второй части.

е (1) = (1) + 4 = 5

Тогда мой ответ:

е (−1) = 1

е ( 9 97 9 1) = 5

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций с заданным числовым значением. Попробуйте введенное упражнение или введите свое собственное упражнение.