Формулы сокращенного умножения
У нас есть сумма (разница) двух чисел и нам необходимо избавиться от скобок, используя формулы для сокращенного умножения: (x + y)2 = x2 + 2xy + y2
(x — y)2 = x2 — 2xy + y2
Пример: если x = 10, y = 5a
(10 + 5a)2 = 102 + 2.10.5a + (5a)2 = 100 + 100a + 25a2
(10 — 4)2 = 102 — 2.10.4 + 42 = 100 — 80 + 16 = 36
Конечно, если мы имеем следующую ситуацию:
25 + 20a + 4a2 = 52 + 2.2.5 + (2a)2 = (5 + 2a)2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x — y)3 = x3 — 3x2y + 3xy2 — y3
Пример: (1 + a2)3 = 13 + 3.12.a2 +
3.1.(a2)2 + (a2)3 = 1 + 3a
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2xz + 2yz
(x — y — z)2 = x2 + y2 + z2 — 2xy — 2xz + 2yz
x2 — y2 = (x — y)(x + y)
x2 + y2 = (x + y)2 — 2xy
или
x2 + y2 = (x — y)2 + 2xy
Пример: 9a2 — 25b2 = (3a)2 — (5b)2 = (3a — 5b)(3a + 5b)
x3 — y3 = (x — y)(x2 + xy + y2)
x3 + y3 = (x + y)(x2 — xy + y2)
x
Если n есть чётное (n = 2k)
xn + yn = (x + y)(xn-1 — xn-2y +. 2 + 20$
2 + 20$
3) Решите уравнение: x2 — 25 = 0
Решение: x2 — 25 = (x — 5)(x + 5)
=> чтобы решить это уравнение мы должны решить 2 следующих выражения:
x — 5 = 0 или x + 5 = 0
и поэтому уравнение имеет два решения: x = 5 и x = -5
Больше
Тест — формулы сокращенного умножения
Действия с многочленами — задачи с решениями
Разложиние на множители — задачи с решениями
Формулы сокращенного умножения в математическом форуме
11.3.1. Показательная функция, ее свойства и график.
Автор Татьяна Андрющенко На чтение 5 мин. Просмотров 426 Опубликовано
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»8834522701″
data-ad-format=»auto»>
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=
- Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
- Показательная функция y=ax возрастает при a>1.
- Показательная функция y=ax убывает при 0<a<1.
Справедливы все свойства степенной функции:
- а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
- а1=а Любое число в первой степени равно самому себе.
- ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

- ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
- (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
- (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
- (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
- а-х=1/ax
- (a/b)-x=(b/a)x.
Примеры.
1) Построить график функции y=2x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=20=1; Точка А.
x=1, y=21=2; Точка В.
x=2, y=22
x=3, y=23=8; Точка D.
x=-1, y=2-1=1/2=0,5; Точка K.
x=-2, y=2-2=1/4=0,25; Точка M.
x=-3, y=2-3=1/8=0,125; Точка N.
Большему значению аргумента х соответствует и большее значение функции
2) Построить график функции y=(1/2)x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=(½)0=1; Точка A.
x=1, y=(½)1=½=0,5; Точка B.
x=2, y=(½)2=¼=0,25; Точка C.
x=3, y=(½)3=1/8=0,125; Точка D.
x=-1, y=(½)-1=21=2; Точка
x=-2, y=(½)-2=22=4; Точка M.
x=-3, y=(½)-3=23=8; Точка N.
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции 0<(1/2)<1.
3) В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
4) В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы.
Смотрите построение графика функции y=(1/2)x
Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0<a<1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3x=4-x.
В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3).
Ответ: 1.
2) 0,5х=х+3.
В одной координатной плоскости строим графики функций: у=0,5х
(y=(1/2)x )
и у=х+3.
Графики пересеклись в точке В(-1; 2).
Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0<2x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:
— ∞<-2x<0.
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
0<(1/3)x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0+1<(1/3)x+1<+∞+1;
1<(1/3)x+1<+∞.
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0<3x<+∞; умножаем все части двойного неравенства на 3:
0∙3<3x∙3<(+∞)∙3;
0<3x∙3<+∞; из всех частей двойного неравенства вычитаем 5:
0-5<3x∙3-5<+∞-5;
— 5<3x∙3-5<+∞.
Ответ: Е(у)=(-5; +∞).
Смотрите Карту сайта, и Вы найдете нужные Вам темы!
Угол между прямыми
Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентомy = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
tg γ = k1 — k21 + k1·k2
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + bто вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; -k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k1 — k21 + k1·k2 = 2 — (-3)1 + 2·(-3) = 5-5 = 1Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ = |1 · 2 + 2 · 1|12 + 22 · 22 + 12 = 45 · 5 = 0. 8
8Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ = k1 — k21 + k1·k2 = -23 — 431 + (-23)·43 = -631 — 89 = 18Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + cто направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02 = 06 · 5 = 0Ответ. φ = 90°
Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
-x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
Ответ. φ ≈ 74.63°
Координаты точки пересечения двух прямых
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.
Точка пересечения двух прямых – определение
Необходимо дать определение точкам пересечения двух прямых.
Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.
Определение точки пересечения прямых звучит так:
Определение 1Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.
Рассмотрим на рисунке, приведенном ниже.
Нахождение координат точки пересечения двух прямых на плоскости
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.
Если на плоскости имеется система координат Оху, то задаются две прямые a и b. Прямой a соответствует общее уравнение вида A1x+B1y+C1=0, для прямой b — A2x+B2y+C2=0. Тогда M0(x0, y0) является некоторой точкой плоскости необходимо выявить , будет ли точка М0 являться точкой пересечения этих прямых.
Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A1x+B1y+C1=0 и A2x+B2y+C2=0. Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M0(x0, y0) считается их точкой пересечения.
Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A1x+B1y+C1=0 и A2x+B2y+C2=0. Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M0(x0, y0) считается их точкой пересечения.
Даны две пересекающиеся прямые 5x-2y-16=0 и 2x-5y-19=0. Будет ли точка М0 с координатами (2,-3) являться точкой пересечения.
Решение
Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что
5·2-2·(-3)-16=0⇔0=02·2-5·(-3)-19=0⇔0=0
Оба равенства верные, значит М0 (2, -3) является точкой пересечения заданных прямых.
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.
Ответ: заданная точка с координатами (2,-3) будет являться точкой пересечения заданных прямых.
Пример 2Пересекутся ли прямые 5x+3y-1=0 и 7x-2y+11=0 в точке M0 (2, -3)?
Решение
Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что
5·2+3·(-3)-1=0⇔0=07·2-2·(-3)+11=0⇔31=0
Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7x-2y+11=0. Отсюда имеем, что точка М0 не точка пересечения прямых.
Чертеж наглядно показывает, что М0— это не точка пересечения прямых. Они имеют общую точку с координатами (-1,2).
Ответ: точка с координатами (2,-3) не является точкой пересечения заданных прямых.
Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.
Задаются две пересекающиеся прямые a и b уравнениями вида A1x+B1y+C1=0 и A2x+B2y+C2=0, расположенных в Оху. При обозначении точки пересечения М0 получим, что следует продолжить поиск координат по уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0.
Из определения очевидно, что М0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0. Иными словами это и есть решение полученной системы A1x+B1y+C1=0A2x+B2y+C2=0.
Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.
Пример 3Заданы две прямые x-9y+14=0 и 5x-2y-16=0 на плоскости. необходимо найти их пересечение.
Решение
Данные по условию уравнения необходимо собрать в систему, после чего получим x-9y+14=05x-2y-16=0. Чтобы решить его, разрешается первое уравнение относительно x, подставляется выражение во второе:
x-9y+14=05x-2y-16=0⇔x=9y-145x-2y-16=0⇔⇔x=9y-145·9y-14-2y-16=0⇔x=9y-1443y-86=0⇔⇔x=9y-14y=2⇔x=9·2-14y=2⇔x=4y=2
Получившиеся числа являются координатами, которые необходимо было найти.
Ответ: M0 (4, 2) является точкой пересечения прямых x-9y+14=0 и 5x-2y-16=0.
Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.
Пример 4Определить координаты точек пересечения прямых x-5=y-4-3 и x=4+9·λy=2+λ, λ∈R.
Решение
Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x=4+9·λy=2+λ, λ∈R преобразуется таким образом:
x=4+9·λy=2+λ⇔λ=x-49λ=y-21⇔x-49=y-21⇔⇔1·(x-4)=9·(y-2)⇔x-9y+14=0
После чего беремся за уравнение канонического вида x-5=y-4-3 и преобразуем. Получаем, что
x-5=y-4-3⇔-3·x=-5·y-4⇔3x-5y+20=0
Отсюда имеем, что координаты – это точка пересечения
x-9y+14=03x-5y+20=0⇔x-9y=-143x-5y=-20
Применим метод Крамера для нахождения координат:
∆=1-93-5=1·(-5)-(-9)·3=22∆x=-14-9-20-5=-14·(-5)-(-9)·(-20)=-110⇒x=∆x∆=-11022=-5∆y=1-143-20=1·(-20)-(-14)·3=22⇒y=∆y∆=2222=1
Ответ: M0 (-5, 1).
Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λ, λ∈R. Тогда вместо значения x подставляется x=x1+ax·λ и y=y1+ay·λ, где получим λ=λ0, соответствующее точке пересечения, имеющей координаты x1+ax·λ0, y1+ay·λ0.
Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λ, λ∈R. Тогда вместо значения x подставляется x=x1+ax·λ и y=y1+ay·λ, где получим λ=λ0, соответствующее точке пересечения, имеющей координаты x1+ax·λ0, y1+ay·λ0.
Определить координаты точки пересечения прямой x=4+9·λy=2+λ, λ∈R и x-5=y-4-3.
Решение
Необходимо выполнить подстановку в x-5=y-4-3 выражением x=4+9·λ, y=2+λ, тогда получим:
4+9·λ-5=2+λ-4-3
При решении получаем, что λ=-1. Отсюда следует, что имеется точка пересечения между прямыми x=4+9·λy=2+λ, λ∈R и x-5=y-4-3. Для вычисления координат необходимо подставить выражение λ=-1 в параметрическое уравнение. Тогда получаем, что x=4+9·(-1)y=2+(-1)⇔x=-5y=1.
Ответ: M0 (-5, 1).
Для полного понимания темы, необходимо знать некоторые нюансы.
Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A1x+B1y+ C1=0A2x+B2+C2=0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Даны прямые x3+y-4=1 и y=43x-4. Определить, имеют ли они общую точку.
Решение
Упрощая заданные уравнения, получаем 13x-14y-1=0 и 43x-y-4=0.
Следует собрать уравнения в систему для последующего решения:
13x-14y-1=013x-y-4=0⇔13x-14y=143x-y=4
Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x3+y-4=1 и y=43x-4 определяют одну и ту же прямую. Поэтому нет точек пересечения.
Ответ: заданные уравнения определяют одну и ту же прямую.
Найти координаты точки пересекающихся прямых 2x+(2-3)y+7=0 и 23+2x-7y-1=0.
Решение
По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:
2x+(2-3)y+7=02(3+2)x-7y-1=0⇔2x+(2-3)y=-72(3+2)x-7y=1⇔⇔2x+2-3y=-72(3+2)x-7y+(2x+(2-3)y)·(-(3+2))=1+-7·(-(3+2))⇔⇔2x+(2-3)y=-70=22-72
Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.
Второй способ решения.
Для начала нужно определить наличие пересечения прямых.
n1→=(2, 2-3) является нормальным вектором прямой 2x+(2-3)y+7=0, тогда вектор n2→=(2(3+2), -7 — нормальный вектор для прямой 23+2x-7y-1=0.
Необходимо выполнить проверку коллинеарности векторов n1→=(2, 2-3) и n2→=(2(3+2), -7). Получим равенство вида 22(3+2)=2-3-7. Оно верное, потому как 223+2-2-3-7=7+2-3(3+2)7(3+2)=7-77(3+2)=0. Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.
Ответ: точек пересечения нет, прямые параллельны.
Пример 8Найти координаты пересечения заданных прямых 2x-1=0 и y=54x-2.
Решение
Для решения составляем систему уравнений. Получаем
2x-1=054x-y-2=0⇔2x=154x-y=2
Найдем определитель основной матрицы. Для этого 2054-1=2·(-1)-0·54=-2. Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:
2x=154x-y=2⇔x=1245x-y=2⇔x=1254·12-y=2⇔x=12y=-118
Получили, что точка пересечения заданных прямых имеет координаты M0(12, -118).
Ответ: M0(12, -118).
Нахождения координат точки пересечения двух прямых в пространстве
Таким же образом находятся точки пересечения прямых пространства.
Когда заданы прямые a и b в координатной плоскости Охуz уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D1=0 а прямая b — A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0.
Когда точка М0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0
Рассмотрим подобные задания на примерах.
Пример 9Найти координаты точки пересечения заданных прямых x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0
Решение
Составляем систему x-1=0y+2z+3=03x+2y+3=04x-2z-4=0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A=10001232040-2 и расширенную T=1001012-340-24. Определяем ранг матрицы по Гауссу.
Получаем, что
1=1≠0, 1001=1≠0, 100012320=-4≠0, 1001012-3320-340-24=0
Отсюда следует, что ранг расширенной матрицы имеет значение 3. Тогда система уравнений x-1=0y+2z+3=03x+2y+3=04x-27-4=0 в результате дает только одно решение.
Базисный минор имеет определитель 100012320=-4≠0, тогда последнее уравнение не подходит. Получим, что x-1=0y+2z+3=03x+2y+3=04x-2z-4=0⇔x=1y+2z=-33x+2y-3 . Решение системы x=1y+2z=-33x+2y=-3⇔x=1y+2z=-33·1+2y=-3⇔x=1y+2z=-3y=-3⇔⇔x=1-3+2z=-3y=-3⇔x=1z=0y=-3.
Значит, имеем, что точка пересечения x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0 имеет координаты (1, -3, 0).
Ответ: (1, -3, 0).
Система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 имеет только одно решение. Значит, прямые a и b пересекаются.
В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.
Поэтому система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.
Если решений бесконечное множество, то они совпадают.
Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.
Пример 10Заданы уравнения прямых x+2y-3z-4=02x-y+5=0 и x-3z=03x-2y+2z-1=0. Найти точку пересечения.
Решение
Для начала составим систему уравнений. Получим, что x+2y-3z-4=02x-y+5=0x-3z=03x-2y+2z-1=0 . решаем ее методом Гаусса:
12-342-10-510-303-221~12-340-56-130-20-40-811-11~~12-340-56-1300-125650075-1595~12-340-56-1300-1256500031110
Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.
Ответ: нет точки пересечения.
Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.
Пример 11Заданы две прямые x=-3-λy=-3·λz=-2+3·λ, λ∈R и x2=y-30=z5 в Охуz. Найти точку пересечения.
Решение
Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что
x=-3-λy=-3·λz=-2+3·λ⇔λ=x+3-1λ=y-3λ=z+23⇔x+3-1=y-3=z+23⇔⇔x+3-1=y-3x+3-1=z+23⇔3x-y+9=03x+z+11=0x2=y-30=z5⇔y-3=0x2=z5⇔y-3=05x-2z=0
Находим координаты 3x-y+9=03x+z+11=0y-3=05x-2z=0, для этого посчитаем ранги матрицы. Ранг матрицы равен 3, а базисный минор 3-10301010=-3≠0, значит, что из системы необходимо исключить последнее уравнение. Получаем, что
3x-y+9=03x+z+11=0y-3=05x-2z=0⇔3x-y+9=03x+z+11=0y-3=0
Решим систему методом Крамер. Получаем, что x=-2y=3z=-5. Отсюда получаем, что пересечение заданных прямых дает точку с координатами (-2, 3, -5).
Ответ: (-2, 3, -5).
Аналитическая геометрия в пространстве (Лекция №19)
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α1
и α2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то
Очевидно, что угол между нормальными векторами и плоскостей α1
и α2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то
.
Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.
Условие параллельности двух плоскостей.
Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .
Таким образом, .
Примеры.
- Составить уравнение плоскости, проходящей через точку
M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.
Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.
Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.
Итак, искомое уравнение 3x+2y-7z+32=0.
- Составить уравнение
плоскости, проходящей через точки M1(1;
1; 1), M2(0;
1; –1) перпендикулярно плоскости x+y+z=0.
Так как M1Î α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.
Далее, так как M2Î α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.

Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.
Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.
Окончательно получаем -2x+y+z=0.
- Составить уравнение
плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно
плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.
Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.
По условию задачи , поэтому
Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.
ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М1 и вектора , параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М1(x1, y1, z1), лежащую на прямой параллельно вектору .
Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .
Векторы и коллинеарны, поэтому найдётся такое число t, что ,
где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М1 и
М соответственно через и ,
получаем .
Это уравнение называется векторным уравнением прямой. Оно
показывает, что каждому значению параметра t соответствует радиус-вектор
некоторой точки М, лежащей на прямой.
Запишем это уравнение в координатной форме. Заметим, что , и отсюда
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Пусть М1(x1, y1, z1) – точка, лежащая на прямой l, и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .
Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,
– канонические уравнения прямой.
Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем или .
Пример. Записать уравнение прямой в параметрическом виде.
Обозначим , отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox. Тогда направляющий вектор прямой перпендикулярен Ox, следовательно, m=0. Следовательно, параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.
Примеры.
- Составить канонические и параметрические уравнения прямой,
проходящей через точку М1(1;0;-2) параллельно вектору .

Канонические уравнения: .
Параметрические уравнения:
- Составить уравнения прямой,
проходящей через две точки М1(-2;1;3), М2(-1;3;0).
Составим канонические уравнения прямой. Для этого найдем направляющий вектор . Тогда l: .
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить прямую, заданную уравнениями
Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z= 0:
Решив эту систему, найдем точку M1(1;2;0).
Аналогично, полагая y= 0, получим точку пересечения прямой с плоскостью xOz:
От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М1 на прямой и направляющий вектор прямой.
Координаты точки М1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:
.
Пример. Привести общие уравнения прямой к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y= 0 и решим систему уравнений:
Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет
. Следовательно, l: .
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен .
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .
Примеры.
- Найти угол между прямыми и .
- Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:
Поскольку искомая прямая l параллельна l1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1.
- Составить уравнения прямой,
проходящей через точку М1(-4;0;2) и перпендикулярной прямым: и .
Направляющий вектор прямой l можно найти как векторное произведение векторов и :
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и плоскостью
будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Пусть прямаяи плоскость заданы уравнениями
Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .
Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
Примеры.
- Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым и .
Так как M1Î α, то уравнение плоскости будем искать в виде
.
Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений
Отсюда
Итак, или .
- Найти угол между прямой и плоскостью .
Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,
- Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .
Составим уравнение плоскости α перпендикулярной l. MÎ α, . Следовательно, или .
Найдём точку пересечения прямой l и α:
Итак, N(0.5;-0.5;0.5). Пусть искомая точка М1 имеет координаты М1(x,y,z). Тогда очевидно равенство векторов , т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2, z=3 или М1(1;2;3).
 .
.
Вычисление двойных интегралов: теория и примеры
Записывается двойной интеграл так:
.
Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x, а сверху и снизу – равенствами, в которых слева переменная y. Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D.
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D.
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D, которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
Случай прямоугольной области:
Случай криволинейной области:
А это
уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы
интегрирования. Выражения, задающие линии, которые ограничивают фигуру D, будут пределами
интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Выражения, задающие линии, которые ограничивают фигуру D, будут пределами
интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Случай прямоугольной области
Пусть дана функция двух переменных f(x, y) и ограничения для D: D = {(x; y) | a ≤ x ≤ b; c ≤ y ≤ d}, означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b, а снизу и сверху — прямые y = c и y = d. Здесь a, b, c, d — числа.
Пусть для такой функции существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 1. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.
Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области
Пусть снова дана функция двух переменных f(x, y), а ограничения для D: уже несколько другого вида:
.
Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b, но снизу и сверху — кривые, которые заданы уравнениями и . Иными словами, и — функции.
Пусть для такой функции также существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a и b — числа, а и — функции. В случае треугольной области одна из функций или — это уравнение прямой линии. Такой случай будет разобран в примере 3.
Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый
определённый интеграл.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 3. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:
.
Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:
.
Пример 4. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О’Генри:
«Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки —
человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же:
«Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая
по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)
Результат, так же по О’Генри один и тот же:
«Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая
по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)
Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 8. Сменить порядок интегрирования для повторного интеграла
.
Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:
(нижний) и (верхний).
Таким образом, после смены порядка интегрирования повторный интеграл запишется так:
.
После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые
трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а
разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1, y = 3, x = 0, x = 2y.
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC, которые заданы уравнениями y = 1 и y = x/2, что видно на рисунке ниже.
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ. Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0, x = 2 и кривыми и .
Как видно на рисунке ниже, прямая, параллельная оси 0x, будет пересекать нижнюю границу области интегрирования более чем в двух точках.
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для :
Для :
Для :
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к
повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
y — 2x ≤ 0;
2y — x ≥ 0;
xy ≤ 2.
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2. Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x).
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:
.
В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1.
Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1, а справа прямой y = 1 — x. (рисунок ниже).
Решая как систему уравнения этих линий, получаем точки их пересечения: . Ординаты этих точек — — 2 и 1 будут соответственно нижним и верхним пределами интегрирования по игреку. Итак, площадь фигуры найдём как двойной интеграл, сведённый к повторному:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.
Объём криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси 0z, а направляющей служит контур области, вычисляется также по формуле двойного интеграла. То есть, с помощью двойного интеграла можно вычислять объёмы тел.
Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0, y = 0, z = 0 и x + y + z = 1 (рисунок ниже).
Расставляя пределы интегрирования, получаем следующий повторный интеграл:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.
Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями . В каждой из этих частей выберем произвольную точку и составим сумму
,
которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. 2 + n-72) = 1 / (n + 9)
Системы линейных уравнений — Бесплатная математическая справка
Системы линейных уравнений имеют место, когда существует более одного связанного математического выражения.Например, в \ (y = 3x + 7 \) есть только одна линия со всеми точками на этой линии, представляющая набор решений для приведенного выше уравнения.
Когда вам задают 2 уравнения в одном и том же вопросе и просят решить для единственного ответа, вы можете визуализировать проблему как две линии на одной плоскости xy. Следующие два уравнения изображены на одной плоскости xy:
$$ y = 3x + 5 $$ $$ y = — x $$Решение любого уравнения — это место пересечения ОБЕИХ уравнений на плоскости xy.Это место встречи называется Точкой пересечения. Если у вас есть линейное уравнение и квадратное уравнение в одной плоскости xy, могут быть ДВЕ ТОЧКИ, где график каждого уравнения будет встречаться или пересекаться. Вот геометрический вид:
Вот пример двух уравнений с двумя неизвестными переменными:
Пример
$$ x + y = 10 $$ $$ 3x + 2y = 20 $$Есть три метода решить наш примерный вопрос.
- 1) Решаем графически
- 2) Мы можем решить это алгебраически
- 3) Мы также можем решить это с помощью алгебраического исключения
Решу вопрос всеми 3-мя способами.Метод 1. Решить графически:
Для графического решения лучше всего написать ОБЕИХ уравнения в форме пересечения наклона или в форме: \ (y = mx + b \), где m = наклон, а b = точка пересечения y в качестве первого шага. Таким образом, \ (x + y = 10 \) становится \ (y = — x + 10 \) (форма пересечения наклона). Затем \ (3x + 2y = 20 \) становится \ (y = — \ frac {3x} {2} + 10 \) при записи в форме пересечения наклона.
Затем нарисуйте две линии, ведущие к точке пересечения. Построив эти линии, вы обнаружите, что ОБА уравнения пересекаются в точке (0,10).Точка (0,10) означает, что если вы подставите x = 0 и y = 10 в ОБЕИ исходные уравнения, вы обнаружите, что это решает оба уравнения. Вот как эти два уравнения выглядят на плоскости xy:
Метод 2. Решить алгебраически
Шагов:
1) Решите относительно x или y в первом уравнении (\ (x + y = 10 \)). Решу за у. Итак, \ (x + y = 10 \) становится \ (y = -x + 10 \).
2) Подставьте значение y (то есть -x + 10) во второе уравнение, чтобы найти x. Наше второе уравнение было \ (3x + 2y = 20 \) и после подстановки становится \ (3x + 2 (-x + 10) = 20 \)
Далее: Решите относительно x.
$$ 3x -2x + 20 = 20 $$ $$ x + 20 = 20 $$ $$ x = 0 $$3) Подставьте x = 0 в ЛЮБОЕ исходное уравнение, чтобы найти значение y. Я буду использовать наше второе уравнение.
$$ 3x + 2y = 20 $$ $$ 3 (0) + 2y = 20 $$ $$ 0 + 2y = 20 $$ $$ y = 10 $$Итак, наша точка пересечения снова (0,10).
Метод 3: Алгебраическое исключение
Этот метод имеет дело с сопоставлением переменных для ELIMINATE или устранением одной. Имейте в виду, что какую переменную удалить в первую очередь — это ваш выбор.
ЦЕЛЬ: исключить x и решить вместо y или наоборот. Вернемся к нашим исходным уравнениям.В нашем втором 3x + 2y = 20, вы можете исключить 3x, умножив -3 на КАЖДЫЙ член в нашем первом уравнении (x + y = 10).
x + y = 10
3x + 2y = 20
-3 (x) + -3 (y) = -3 (10)
3x + 2y = 20
-3x + -3y = -30
3x + 2y = 20
ВНИМАНИЕ, что -3x и 3x исключаются. Видеть это? Понять, почему? И вот почему: отрицательный плюс положительный = ноль.
Теперь у нас есть это:
-3y = -30
2y = 20
-3y + 2y = -30 + 20
-y = -10
y = 10.
Далее: чтобы найти x, мы подставляем y = 10 в ЛЮБОЕ из исходных уравнений. К настоящему времени вы должны увидеть, что наш ответ для x будет НУЛЬ.
Вот он:
Я буду использовать x + y = 10
x + 10 = 10
x = 0.
Вы видите то, что вижу я? Да, я снова нашел ту же самую точку пересечения, которая составляет (0,10).
Г-н Фелиз
(c) 2005
Поиск линейных уравнений
Для любой точки на прямой и ее наклона мы можем найти уравнение для этой прямой.Начните с применения формулы наклона к заданной точке (x1, y1) и переменной точке (x, y).
Уравнение y − y1 = m (x − x1) называется формой точечного уклона линии Любая невертикальная прямая может быть записана в форме y − y1 = m (x − x1), где m — наклон. и (x1, y1) — любая точка на прямой. Любое невертикальное линейное уравнение может быть записано в этой форме. Это полезно для нахождения уравнения прямой с учетом наклона и любого упорядоченного парного решения.
Пример 7: Найдите уравнение прямой с наклоном m = 12, проходящей через (4, −1).
Решение: Используйте форму «точка-наклон», где m = 12 и (x1, y1) = (4, −1).
На этом этапе мы должны выбрать представление уравнения нашей прямой либо в стандартной форме, либо в форме пересечения наклона.
В этом учебнике мы представим наши линии в форме пересечения наклона. Это облегчает построение графиков в будущем.
Пример 8: Найдите уравнение прямой, проходящей через (−5, 3) с наклоном m = −25.
Решение: Подставьте (−5, 3) и m = −25 в форму точечного уклона.
Всегда важно понимать, что происходит геометрически. Сравните ответ для последнего примера с соответствующим графиком ниже.
Понимание геометрии важно, потому что вам часто будут предлагать графики, по которым вам нужно будет определить точку на линии и наклон.
Решение: Между точками (1, 1) и (3, 0) мы можем видеть, что подъем равен -1 единице, а пробег равен 2 единицам. Наклон линии равен m = riserun = −12 = −12.Используйте это и точку (3, 0), чтобы найти следующее уравнение:
Пример 10: Найдите уравнение прямой, проходящей через (-1, 1) и (7, -1).
Решение: Начните с вычисления наклона по формуле наклона.
Затем подставьте в форму «точка-уклон», используя одну из заданных точек; не имеет значения, какая точка используется. Используйте m = −14 и точку (−1, 1).
Попробуй! Найдите уравнение прямой, проходящей через (4, −5) и (−4, 1).
Тематические упражнения
Часть A: Форма пересечения откоса
Определите наклон и y -пересечение.
1. 5x − 3y = 18
2. −6x + 2y = 12
3. x − y = 5
4. −x + y = 0
5. 4x − 5y = 15
6. −7x + 2y = 3
7. y = 3
8. y = −34
9.15x − 13y = −1
10. 516x + 38y = 9
11. −23x + 52y = 54
12. 12x − 34y = −12
Часть B: Поиск уравнений в форме пересечения наклона
Учитывая наклон и y -пересечение, определите уравнение прямой.
13. м = 1/2; (0, 5)
14. м = 4; (0, -1)
15. м = −2/3; (0, −4)
16. м = −3; (0, 9)
17. m = 0; (0, -1)
18. м = 5; (0, 0)
Учитывая график, найдите уравнение в форме углового пересечения.
19.
20.
21.
22.
23.
24.
Найдите уравнение с учетом наклона и точки.
25. м = 2/3; (−9, 2)
26. м = -1/5; (5, −5)
27. м = 0; (−4, 3)
28. м = 3; (−2, 1)
29. м = −5; (−2, 8)
30. м = −4; (1/2, −3/2)
31. м = -1/2; (3, 2)
32. м = 3/4; (1/3, 5/4)
33. м = 0; (3, 0)
34. m undefined; (3, 0)
Дайте две точки, найдите уравнение прямой.
35. (−6, 6), (2, 2)
36. (−10, −3), (5, 0)
37. (0, 1/2), (1/2, -1)
38.(1/3, 1/3), (2/3, 1)
39. (3, −4), (−6, −7)
40. (-5, 2), (3, 2)
41. (−6, 4), (−6, −3)
42. (−4, −4), (−1, −1)
43. (3, −3), (−5, 5)
44. (0, 8), (−4, 0)
Часть C: Уравнения с использованием формы точечного уклона
Найдите уравнение с учетом наклона и точки.
45. м = 1/2; (4, 3)
46. м = -1/3; (9, −2)
47. м = 6; (1, −5)
48. м = −10; (1, −20)
49. м = −3; (2, 3)
50. м = 2/3; (−3, −5)
51. м = −3/4; (−8, 3)
52. м = 5; (1/5, −3)
53. м = −3; (-1/9, 2)
54. м = 0; (4, −6)
55. м = 0; (−5, 10)
56. м = 5/8; (4, 3)
57. м = −3/5; (-2, -1)
58. м = 1/4; (12, −2)
59. м = 1; (0, 0)
60. м = −3/4; (0, 0)
Учитывая график, используйте формулу угла наклона точки, чтобы найти уравнение.
61.
62.
63.
64.
65.
66.
Используйте формулу угла наклона точки, чтобы найти уравнение прямой, проходящей через две точки.
67.(−4, 0), (0, 5)
68. (-1, 2), (0, 3)
69. (−3, −2), (3, 2)
70. (3, −1), (2, −3)
71. (-2, 4), (2, -4)
72. (−5, −2), (5, 2)
73. (−3, −1), (3, 3)
74. (1, 5), (0, 5)
75. (1, 2), (2, 4)
76. (6, 3), (2, −3)
77. (10, −3), (5, −4)
78.(−3, 3), (−1, 12)
79. (4/5, -1/3), (-1/5, 2/3)
80. (5/3, 1/3), (−10/3, −5/3)
81. (3, -1/4), (4, -1/2)
82. (0, 0), (−5, 1)
83. (2, −4), (0, 0)
84. (3, 5), (3, −2)
85. (-4, 7), (-1, 7)
86. (-8, 0), (6, 0)
Часть D: Приложения
87. Джо следил за своими счетами за сотовый телефон в течение последних двух месяцев.Счет за первый месяц составил 38 долларов США за 100 минут использования. Счет за второй месяц составил 45,50 долларов за 150 минут использования. Найдите линейное уравнение, которое дает общий ежемесячный счет, основанный на минутах использования.
88. Компания за первый год своей деятельности выпустила 150 учебных пособий на общую сумму 2 350 долларов США. В следующем году компания выпустила еще 50 руководств по цене 1450 долларов. Используйте эту информацию, чтобы найти линейное уравнение, которое дает общую стоимость производства учебных пособий из количества выпущенных руководств.
89. Фермер кукурузы в Калифорнии смог произвести 154 бушеля кукурузы с акра через 2 года после начала своей работы. В настоящее время после 7 лет работы он увеличил урожайность до 164 бушелей с акра. Используйте эту информацию, чтобы написать линейное уравнение, которое дает общую урожайность с акра на основе количества лет эксплуатации, и используйте его для прогнозирования урожайности на следующий год.
90. Веб-мастер заметил, что количество зарегистрированных пользователей неуклонно растет с начала рекламной кампании.До того, как начать рекламировать, у него было 1200 зарегистрированных пользователей, а после 3 месяцев рекламы у него теперь есть 1590 зарегистрированных пользователей. Используйте эти данные, чтобы написать линейное уравнение, которое дает общее количество зарегистрированных пользователей с учетом количества месяцев после начала рекламы. Используйте уравнение, чтобы спрогнозировать количество пользователей за 7 месяцев рекламной кампании.
91. Автомобиль, купленный новым, стоил 22 000 долларов и был продан 10 лет спустя за 7 000 долларов. Напишите линейное уравнение, определяющее стоимость автомобиля с учетом его возраста в годах.
92. Старинные часы были куплены в 1985 году за 1 500 долларов и проданы на аукционе в 1997 году за 5 700 долларов. Составьте линейное уравнение, моделирующее значение часов в годах с 1985 года.
Часть E: Темы дискуссионной доски
93. Обсудите достоинства и недостатки формы «точка-наклон» и формы « y «.
94. Изучите и обсудите линейную амортизацию. Что представляют собой наклон и пересечение y в линейной модели амортизации?
Wolfram | Примеры альфа: пошаговые дифференциальные уравнения
Разделимые уравнения
Посмотрите, как решаются разделяемые уравнения:
Другие примеры
Линейные уравнения первого порядка
Решите линейные уравнения первого порядка:
См. Шаги, которые используют преобразования Лапласа для решения ОДУ:
Другие примеры
Точные уравнения первого порядка
Превратите в точное уравнение:
Другие примеры
Уравнения Бернулли
Научитесь решать уравнения Бернулли:
Другие примеры
Замены первого порядка
Примените линейную замену:
Решите однородное уравнение первого порядка с помощью замены:
Сделайте общие замены:
Другие примеры
Уравнения типа Чини
Решите уравнение Риккати:
Решите уравнение Абеля первого рода с постоянным инвариантом:
Решите уравнение Чини с постоянным инвариантом:
Другие примеры
Общие уравнения первого порядка.
См. Шаги для решения уравнения Клеро:
Решите уравнение Даламбера:
Посмотрите, как решаются обыкновенные дифференциальные уравнения первого порядка:
Другие примеры
Линейные уравнения второго порядка с постоянными коэффициентами
Решите линейное однородное уравнение с постоянными коэффициентами:
Решите линейное уравнение с постоянными коэффициентами несколькими методами:
См. Шаги, которые используют преобразования Лапласа для решения ОДУ:
Другие примеры
Снижение порядка
Сведите к уравнению первого порядка:
Выведите уравнение цепной линии:
Другие примеры
Уравнения Эйлера – Коши.
Решите уравнения Эйлера – Коши:
Другие примеры
Общие уравнения второго порядка
Посмотрите, как решаются обыкновенные дифференциальные уравнения второго порядка:
Другие примеры
Уравнения высшего порядка
См. Шаги для уравнений высшего порядка:
Другие примеры
Уравнение прямой
Уравнение прямой обычно записывают так:
(или «y = mx + c» в Великобритании см. ниже)
Что это означает?
y = насколько далеко вверх
x = расстояние до
м = Наклон или градиент (насколько крутая линия)
b = значение y , когда x = 0
Как найти «м» и «б»?
- b легко: просто посмотрите, где линия пересекает ось Y.
- м (Уклон) требует расчета:
| м = Изменение в Y Изменение X |
Зная это, мы можем составить уравнение прямой:
Пример 1
м = 2 1 = 2
b = 1 (значение y при x = 0)
Итак: y = 2x + 1
С этим уравнением теперь вы можете…
… выберите любое значение для x и найдите соответствующее значение для y
Например, когда x равно 1:
y = 2 × 1 + 1 = 3
Убедитесь сами, что x = 1 и y = 3 действительно на линии.
Или мы могли бы выбрать другое значение для x, например 7:
y = 2 × 7 + 1 = 15
Итак, когда x = 7, у вас будет y = 15
Положительный или отрицательный наклон?
Двигаясь слева направо, велосипедист должен проехать P на выезде P , наклонный наклон:
Пример 2
м = −3 1 = −3
b = 0
Это дает нам y = −3x + 0
Ноль нам не нужен!
Итак: y = −3x
Пример 3: Вертикальная линия
Какое уравнение представляет собой вертикальная линия?
Наклон undefined … а где он пересекает ось Y?
Фактически, это особый случай , и вы используете другое уравнение, а не « y = …», а вместо этого используете « x = …».
Как это:
x = 1.5
Каждая точка на линии имеет координату x 1,5 ,
, поэтому ее уравнение x = 1,5
Взлетай и беги
Иногда используются слова «взлетать» и «бегать».
- Рост — насколько далеко вверх
- Run — это расстояние до
Итак, уклон «м» равен:
м = подъем пробег
Возможно, вам будет легче запомнить.
Другие формы
Мы смотрели на форму «наклон-пересечение». Уравнение прямой можно записать многими другими способами .
Еще одна популярная форма — это уравнение прямой и наклонной линии.
Сноска
Страна Примечание:
В разных странах учат разным «обозначениям» (прислал мне добрые читатели):
| В США, Австралии, Канаде, Эритрее, Иране, Мексике, Португалии, Филиппинах и Саудовской Аравии обозначение: | у = mx + b |
| В Великобритания, Австралия (также), Багамы, Бангладеш, Бельгия, Бруней, Болгария, Кипр, Египет, Германия, Гана, Индия, Индонезия, Ирландия, Ямайка, Кения, Кувейт, Малайзия, Малави, Мальта, Непал , Новая Зеландия, Нигерия, Оман, Пакистан, Перу, Сингапур, Соломоновы Острова, Южная Африка, Шри-Ланка, Турция, ОАЭ, Замбия и Зимбабве | y = mx + c |
| В Афганистан, Албания, Алжир, Бразилия, Китай, Чешская Республика, Дания, Эфиопия, Франция, Ливан, Нидерланды, Косово, Кыргызстан, Норвегия, Польша, Румыния, Южная Корея, Суринам, Испания, Тунис и Вьетнам Нам: | у = ах + Ь |
| В Азербайджане, Китае, Финляндии, России и Украине : | у = kx + b |
| В Греция : | ψ = αχ + β |
| В Италия : | у = mx + q |
| В Япония : | y = mx + d |
| В Куба и Израиль : | y = mx + n |
| В Румыния : | у = gA + C |
| В Латвии и Швеции : | y = kx + m |
| В Сербии и Словении : | y = kx + n |
| В вашей стране: | сообщите нам! |
… но все это означает одно и то же, только разные буквы.
Введение в линейные функции | Безграничная алгебра
Что такое линейная функция?
Линейные функции — это алгебраические уравнения, графики которых представляют собой прямые линии с уникальными значениями наклона и пересечения по оси Y.
Цели обучения
Опишите части и характеристики линейной функции
Основные выводы
Ключевые моменты
- Линейная функция — это алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- Функция — это отношение со свойством, согласно которому каждый вход связан ровно с одним выходом.
- Отношение — это набор упорядоченных пар.
- График линейной функции — это прямая линия, но вертикальная линия не является графиком функции.
- Все линейные функции записываются в виде уравнений и характеризуются своим наклоном и интервалом [латекс] y [/ латекс].
Ключевые термины
- отношение : набор упорядоченных пар.
- переменная : символ, представляющий величину в математическом выражении, используемом во многих науках.
- линейная функция : алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- функция : отношение между набором входов и набором допустимых выходов со свойством, что каждый вход связан ровно с одним выходом.
Что такое линейная функция?
Линейная функция — это алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.Например, обычное уравнение [латекс] y = mx + b [/ latex] (а именно форма пересечения наклона, о которой мы узнаем больше позже) является линейной функцией, потому что оно удовлетворяет обоим критериям с [латекс] x [/ latex] и [latex] y [/ latex] в качестве переменных и [latex] m [/ latex] и [latex] b [/ latex] в качестве констант. Он линейный: показатель степени члена [latex] x [/ latex] равен единице (первая степень), и он следует определению функции: для каждого входа ([latex] x [/ latex]) существует ровно один выход ([latex] y [/ latex]). Также его график представляет собой прямую линию.
Графики линейных функций
Название «линейный» происходит от того факта, что множество решений такого уравнения образует прямую линию на плоскости. На графиках линейной функции ниже константа [latex] m [/ latex] определяет наклон или градиент этой линии, а постоянный член [latex] b [/ latex] определяет точку, в которой линия пересекает ось [latex] y [/ latex], иначе известная как перехватчик [latex] y [/ latex].
Графики линейных функций: Синяя линия, [latex] y = \ frac {1} {2} x-3 [/ latex] и красная линия, [latex] y = -x + 5 [/ latex] обе являются линейными функциями.Синяя линия имеет положительный наклон [latex] \ frac {1} {2} [/ latex] и [latex] y [/ latex] -пересечение [latex] -3 [/ latex]; красная линия имеет отрицательный наклон [латекс] -1 [/ латекс] и пересечение [латекс] y [/ латекс] [латекс] 5 [/ латекс].
Вертикальные и горизонтальные линии
Вертикальные линии имеют неопределенный наклон и не могут быть представлены в форме [latex] y = mx + b [/ latex], а могут быть представлены в виде уравнения формы [latex] x = c [/ latex] для константы [ latex] c [/ latex], потому что вертикальная линия пересекает значение на оси [latex] x [/ latex], [latex] c [/ latex].Например, график уравнения [latex] x = 4 [/ latex] включает в себя одно и то же входное значение [latex] 4 [/ latex] для всех точек на линии, но будет иметь разные выходные значения, такие как [latex ] (4, -2), (4,0), (4,1), (4,5), [/ latex] и так далее. Однако вертикальные линии НЕ являются функциями, поскольку каждый вход связан с более чем одним выходом.
Горизонтальные линии имеют нулевой наклон и представлены в виде [latex] y = b [/ latex], где [latex] b [/ latex] — пересечение [latex] y [/ latex]. График уравнения [latex] y = 6 [/ latex] включает в себя одно и то же выходное значение 6 для всех входных значений в строке, например [latex] (- 2,6), (0,6), (2 , 6), (6,6) [/ латекс] и т. Д.Горизонтальные линии ЯВЛЯЮТСЯ функцией, потому что отношение (набор точек) имеет свойство, состоящее в том, что каждый вход связан ровно с одним выходом.
Склон
Уклон описывает направление и крутизну линии и может быть рассчитан по двум точкам на линии.
Цели обучения
Рассчитайте наклон линии с помощью «превышения пробега» и определите роль наклона в линейном уравнении
Основные выводы
Ключевые моменты
- Наклон линии — это число, которое описывает как направление, так и крутизну линии; его знак указывает направление, а величина указывает крутизну.
- Отношение подъема к разбегу — это наклон линии, [латекс] m = \ frac {rise} {run} [/ latex].
- Наклон линии можно рассчитать по формуле [латекс] m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex], где [латекс] (x_1, y_1) [/ latex] и [latex] (x_2, y_2) [/ latex] — это точки на линии.
Ключевые термины
- крутизна : скорость, с которой функция отклоняется от задания.
- направление : увеличение, уменьшение, горизонтальное или вертикальное.
Наклон
В математике наклон линии — это число, которое описывает как направление , так и крутизну линии. Наклон часто обозначают буквой [латекс] м [/ латекс]. Вспомните форму отрезка-пересечения линии, [латекс] y = mx + b [/ latex]. Ввод уравнения линии в эту форму дает вам наклон ([латекс] м [/ латекс]) линии и его [латекс] y [/ латекс] -пересечение ([латекс] b [/ латекс]). Теперь мы обсудим интерпретацию [latex] m [/ latex] и то, как рассчитать [latex] m [/ latex] для данной линии.
Направление линии: увеличение, уменьшение, горизонтальное или вертикальное. Линия увеличивается, если она идет вверх слева направо, что означает положительный наклон ([latex] m> 0 [/ latex]). Линия уменьшается, если она идет вниз слева направо и наклон отрицательный ([латекс] m <0 [/ latex]). Если линия горизонтальна, наклон равен нулю и является постоянной функцией ([latex] y = c [/ latex]). Если линия вертикальная, наклон не определен.
Наклоны линий: наклон линии может быть положительным, отрицательным, нулевым или неопределенным.
Крутизна или уклон линии измеряется абсолютным значением уклона. Уклон с большим абсолютным значением указывает на более крутую линию. Другими словами, линия с наклоном [латекс] -9 [/ латекс] круче, чем линия с наклоном [латекс] 7 [/ латекс].
Расчет уклона
Наклон рассчитывается путем нахождения отношения «вертикального изменения» к «горизонтальному изменению» между любыми двумя отдельными точками на линии. Это соотношение представлено частным («подъем за пробегом») и дает одно и то же число для любых двух различных точек на одной линии.Он представлен как [латекс] m = \ frac {rise} {run} [/ latex]. [Latex] [/ latex]
Визуализация уклона: уклон линии рассчитывается как «подъем за пробегом».
Математически уклон м линии составляет:
[латекс] \ displaystyle m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex]
Две точки на линии необходимы, чтобы найти [латекс] м [/ латекс]. Учитывая две точки [латекс] (x_1, y_1) [/ latex] и [latex] (x_2, y_2) [/ latex], взгляните на график ниже и обратите внимание, как «подъем» наклона определяется разницей в значениях [latex] y [/ latex] двух точек, а «пробег» определяется разницей в значениях [latex] x [/ latex].
Наклон, представленный графически: Наклон [латекс] m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex] рассчитывается по двум точкам [латекс ] \ left (x_1, y_1 \ right) [/ latex] и [latex] \ left (x_2, y_2 \ right) [/ latex].
Теперь мы посмотрим на некоторые графики на координатной сетке, чтобы найти их наклоны. Во многих случаях мы можем найти уклон, просто посчитав подъем и разбег. Начнем с определения двух точек на линии. Если возможно, мы стараемся выбирать точки с координатами, которые являются целыми числами, чтобы упростить наши вычисления.
Пример
Найдите наклон линии, показанной на координатной плоскости ниже.
Найдите наклон линии: Обратите внимание, что линия увеличивается, поэтому обязательно ищите положительный наклон.
Найдите две точки на графике, выбирая точки, координаты которых являются целыми числами. Мы будем использовать [latex] (0, -3) [/ latex] и [latex] (5, 1) [/ latex]. Начиная с точки слева, [latex] (0, -3) [/ latex], нарисуйте прямоугольный треугольник, идущий от первой точки ко второй точке, [latex] (5, 1) [/ latex].
Обозначьте точки на линии: нарисуйте треугольник, чтобы обозначить подъем и бег.
Посчитайте подъем на вертикальной ножке треугольника: [латекс] 4 [/ латекс] единицы.
Посчитайте пробег по горизонтальной стороне треугольника: [латекс] 5 [/ латекс] единиц.
Используйте формулу наклона, чтобы получить отношение подъема к пробегу:
[латекс] \ displaystyle \ begin {align} m & = \ frac {rise} {run} \\ & = \ frac {4} {5} \ end {align} [/ latex]
Наклон линии [латекс] \ frac {4} {5} [/ latex].Обратите внимание, что наклон положительный, поскольку линия наклонена вверх слева направо.
Пример
Найдите наклон линии, показанной на координатной плоскости ниже.
Найдите наклон линии: мы видим, что наклон уменьшается, поэтому обязательно ищите отрицательный наклон.
Найдите две точки на графике. Ищите точки с целыми координатами. Мы можем выбрать любые точки, но мы будем использовать [latex] (0, 5) [/ latex] и [latex] (3, 3) [/ latex].
Определите две точки на линии: Точки [латекс] (0, 5) [/ латекс] и [латекс] (3, 3) [/ латекс] находятся на линии.
[латекс] \ displaystyle m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex]
Пусть [latex] (x_1, y_1) [/ latex] будет точкой [latex] (0, 5) [/ latex], а [latex] (x_2, y_2) [/ latex] будет точкой [latex] ( 3, 3) [/ латекс].
Подставляя соответствующие значения в формулу наклона, получаем:
[латекс] \ displaystyle \ begin {align} m & = \ frac {3-5} {3-0} \\ & = \ frac {-2} {3} \ end {align} [/ latex]
Наклон линии [латекс] — \ frac {2} {3} [/ latex]. Обратите внимание, что наклон отрицательный, так как линия наклоняется вниз слева направо.
Прямая и обратная вариация
Две переменные в прямой вариации имеют линейную зависимость, а переменные в обратной вариации — нет.
Цели обучения
Распознайте примеры функций, которые изменяются прямо и обратно
Основные выводы
Ключевые моменты
- Говорят, что две переменные, которые изменяются пропорционально друг другу, находятся в прямом изменении.
- Связь между двумя прямо пропорциональными переменными может быть представлена линейным уравнением в форме пересечения наклона и легко моделируется с помощью линейного графика.
- Обратное изменение противоположно прямому изменению; две переменные считаются обратно пропорциональными, когда изменение выполняется для одной переменной, а противоположное — для другой
. - Связь между двумя обратно пропорциональными переменными не может быть представлена линейным уравнением, и его графическое представление представляет собой не линию, а гиперболу.
Ключевые термины
- гипербола : Коническое сечение, образованное пересечением конуса с плоскостью, которая пересекает основание конуса и не касается конуса.
- пропорциональный : с постоянным соотношением. Две величины (числа) называются пропорциональными, если вторая арифметически изменяется в прямой зависимости от первой.
Прямая вариация
Проще говоря, две переменные находятся в прямом изменении, когда то же самое, что происходит с одной переменной, происходит с другой. Если [latex] x [/ latex] и [latex] y [/ latex] находятся в прямой вариации, а [latex] x [/ latex] удваивается, то [latex] y [/ latex] также удваивается.Эти две переменные можно считать прямо пропорциональными.
Например, зубная щетка стоит [латекс] 2 [/ латекс] доллара. Покупка зубных щеток [латекс] 5 [/ латекс] будет стоить [латекс] 10 [/ латекс] долларов, а покупка зубных щеток [латекс] 10 [/ латекс] будет стоить [латекс] 20 [/ латекс] долларов. Таким образом, мы можем сказать, что стоимость напрямую зависит от стоимости зубных щеток.
Прямое изменение представлено линейным уравнением и может быть смоделировано путем построения линии. Поскольку мы знаем, что отношения между двумя значениями постоянны, мы можем определить их отношение с помощью:
[латекс] \ displaystyle \ frac {y} {x} = k [/ latex]
Где [латекс] k [/ латекс] — постоянная величина.
Переписав это уравнение, умножив обе части на [latex] x [/ latex], получим:
[латекс] \ displaystyle y = kx [/ latex]
Обратите внимание, что это линейное уравнение в форме пересечения наклона, где [latex] y [/ latex] -intercept [latex] b [/ latex] равно [latex] 0 [/ latex].
Таким образом, любая линия, проходящая через начало координат, представляет собой прямую вариацию между [latex] x [/ latex] и [latex] y [/ latex]:
Прямо пропорциональные переменные: График [latex] y = kx [/ latex] демонстрирует пример прямого изменения между двумя переменными.
Возвращаясь к примеру с зубными щетками и долларами, мы можем определить ось [latex] x [/ latex] как количество зубных щеток и ось [latex] y [/ latex] как количество долларов. При этом переменные будут подчиняться соотношению:
[латекс] \ displaystyle \ frac {y} {x} = 2 [/ latex]
Любое увеличение одной переменной приведет к равному увеличению другой. Например, удвоение [latex] y [/ latex] приведет к удвоению [latex] x [/ latex].
Обратная вариация
Обратное изменение противоположно прямому изменению.В случае обратного изменения увеличение одной переменной приводит к уменьшению другой. Фактически, две переменные считаются обратно пропорциональными, когда операция изменения выполняется с одной переменной, а противоположное происходит с другой. Например, если [latex] x [/ latex] и [latex] y [/ latex] обратно пропорциональны, если [latex] x [/ latex] удваивается, то [latex] y [/ latex] уменьшается вдвое.
Например, время, затрачиваемое на поездку, обратно пропорционально скорости движения.Если ваш автомобиль движется с большей скоростью, путь к месту назначения будет короче.
Зная, что взаимосвязь между двумя переменными постоянна, мы можем показать, что их взаимосвязь:
[латекс] \ displaystyle yx = k [/ latex]
Где [латекс] k [/ латекс] — это константа, известная как константа пропорциональности. Обратите внимание, что пока [latex] k [/ latex] не равно [latex] 0 [/ latex], ни [latex] x [/ latex], ни [latex] y [/ latex] не могут равняться [latex] 0 [/ latex] тоже.Мы можем изменить приведенное выше уравнение так, чтобы переменные располагались по разные стороны:
[латекс] \ displaystyle y = \ frac {k} {x} [/ latex]
Обратите внимание, что это не линейное уравнение. Невозможно представить это в виде перехвата склона. Таким образом, обратная зависимость не может быть представлена линией с постоянным наклоном. Обратное изменение можно проиллюстрировать графом в форме гиперболы, изображенным ниже.
Обратно пропорциональная функция: Обратно пропорциональная связь между двумя переменными графически представлена гиперболой.
Нули линейных функций
Ноль или перехват [латекс] x [/ latex] — это точка, в которой значение линейной функции будет равно нулю.
Цели обучения
Практика нахождения нулей линейных функций
Основные выводы
Ключевые моменты
- Ноль — это точка, в которой значение функции будет равно нулю. Его координаты [latex] (x, 0) [/ latex], где [latex] x [/ latex] равно нулю графика.
- Нули можно наблюдать графически или решать алгебраически.
- Линейная функция не может иметь нуля, одного или бесконечного числа нулей. Если функция является горизонтальной линией (slope = [latex] 0 [/ latex]), она не будет иметь нулей, если только ее уравнение не будет [latex] y = 0 [/ latex], и в этом случае их будет бесконечно много. Если линия не горизонтальная, у нее будет один ноль.
Ключевые термины
- ноль : также известен как корень; значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].
- линейная функция : алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- y-intercept : точка, в которой линия пересекает ось [latex] y [/ latex] декартовой сетки.
График линейной функции представляет собой прямую линию. Графически то место, где линия пересекает ось [latex] x [/ latex], называется нулем или корнем. Алгебраически ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].Линейные функции могут не иметь нуля, одного или бесконечного числа нулей. Если через любую точку оси [latex] y [/ latex], кроме нуля, проходит горизонтальная линия, нулей нет, так как линия никогда не пересечет ось [latex] x [/ latex]. Если горизонтальная линия перекрывает ось [latex] x [/ latex] (проходит через ось [latex] y [/ latex] в нуле), то имеется бесконечно много нулей, поскольку линия пересекает [latex] x [/ latex] — ось несколько раз. Наконец, если линия вертикальная или имеет наклон, то будет только один ноль.
Нахождение нулей линейных функций графическим способом
Нули можно наблюдать графически. [Latex] x [/ latex] -перехват, или ноль, является свойством многих функций. Поскольку [latex] x [/ latex] -intercept (ноль) является точкой, в которой функция пересекает ось [latex] x [/ latex], она будет иметь значение [latex] (x, 0) [/ латекс], где [латекс] х [/ латекс] — ноль.
Все линии со значением наклона будут иметь один ноль. Чтобы найти нуль линейной функции, просто найдите точку, в которой линия пересекает ось [latex] x [/ latex].
Нули линейных функций: синяя линия, [latex] y = \ frac {1} {2} x + 2 [/ latex], имеет ноль в [latex] (- 4,0) [/ latex]; красная линия, [latex] y = -x + 5 [/ latex], имеет ноль в [latex] (5,0) [/ latex]. Поскольку каждая линия имеет значение для наклона, каждая линия имеет ровно один ноль.
Алгебраическое нахождение нулей линейных функций
Чтобы найти нуль линейной функции алгебраически, установите [latex] y = 0 [/ latex] и решите относительно [latex] x [/ latex].
Нуль от решения линейной функции выше графически должен соответствовать алгебраическому решению той же функции.
Пример: найти ноль [latex] y = \ frac {1} {2} x + 2 [/ latex] алгебраически
Сначала замените [latex] 0 [/ latex] на [latex] y [/ latex]:
[латекс] \ displaystyle 0 = \ frac {1} {2} x + 2 [/ latex]
Затем решите [латекс] x [/ латекс]. Вычтите [латекс] 2 [/ латекс], а затем умножьте на [латекс] 2 [/ латекс], чтобы получить:
[латекс] \ displaystyle \ begin {align} \ frac {1} {2} x & = — 2 \\ x & = — 4 \ end {align} [/ latex]
Ноль [латекс] (- 4,0) [/ латекс]. Это тот самый ноль, который был найден с помощью графического метода.
Уравнения пересечения наклона
Форма линии с пересечением наклона резюмирует информацию, необходимую для быстрого построения ее графика.
Цели обучения
Преобразуйте линейные уравнения в форму с пересечением наклона и объясните, почему это полезно
Основные выводы
Ключевые моменты
- Угловая форма линии определяется выражением [latex] y = mx + b [/ latex], где [latex] m [/ latex] — наклон линии, а [latex] b [/ latex] — [latex] y [/ latex] -перехват.
- Константа [latex] b [/ latex] известна как перехват [latex] y [/ latex]. Из формы пересечения наклона, когда [латекс] x = 0 [/ latex], [latex] y = b [/ latex], а точка [latex] (0, b) [/ latex] является уникальной точкой на линия также на оси [latex] y [/ latex].
- Чтобы построить линию в форме пересечения наклона, сначала постройте точку пересечения [latex] y [/ latex], затем используйте значение наклона, чтобы найти вторую точку на линии. Если значение наклона является целым числом, используйте [латекс] 1 [/ латекс] в качестве знаменателя.
- Используйте алгебру, чтобы найти [latex] y [/ latex], если уравнение не записано в форме пересечения наклона. Только тогда можно точно определить значение наклона и точки пересечения [латекс] y [/ латекс] из уравнения.
Ключевые термины
- наклон : отношение вертикального и горизонтального расстояний между двумя точками на линии; ноль, если линия горизонтальная, неопределенная, если линия вертикальная.
- y-intercept : точка, в которой линия пересекает ось [latex] y [/ latex] декартовой сетки.
Форма пересечения откоса
Одно из наиболее распространенных представлений линии — это форма пересечения наклона. Такое уравнение задается формулой [latex] y = mx + b [/ latex], где [latex] x [/ latex] и [latex] y [/ latex] — переменные, а [latex] m [/ latex] и [ latex] b [/ latex] — константы. При записи в этой форме константа [latex] m [/ latex] является значением наклона, а [latex] b [/ latex] является перехватом [latex] y [/ latex]. Обратите внимание, что если [latex] m [/ latex] равно [latex] 0 [/ latex], то [latex] y = b [/ latex] представляет собой горизонтальную линию.Обратите внимание, что это уравнение не допускает вертикальных линий, поскольку для этого потребуется, чтобы [latex] m [/ latex] было бесконечным (неопределенным). Однако вертикальная линия определяется уравнением [латекс] x = c [/ latex] для некоторого постоянного [latex] c [/ latex].
Преобразование уравнения в форму пересечения наклона
Написание уравнения в форме пересечения наклона полезно, поскольку по форме легко определить наклон и точку пересечения [латекс] y [/ латекс]. Это помогает находить решения различных проблем, таких как построение графиков, сравнение двух линий, чтобы определить, параллельны они или перпендикулярны, и решение системы уравнений.
Пример
Давайте запишем уравнение в форме пересечения наклона с [latex] m = — \ frac {2} {3} [/ latex] и [latex] b = 3 [/ latex]. Просто подставьте значения в форму пересечения наклона, чтобы получить:
[латекс] \ displaystyle y = — \ frac {2} {3} x + 3 [/ latex]
Если уравнение не в форме пересечения наклона, решите для [латекс] y [/ латекс] и перепишите уравнение.
Пример
Давайте запишем уравнение [латекс] 3x + 2y = -4 [/ latex] в форме пересечения наклона и определим наклон и точку пересечения [латекс] y [/ латекс].Чтобы решить уравнение для [latex] y [/ latex], сначала вычтите [latex] 3x [/ latex] из обеих частей уравнения, чтобы получить:
[латекс] \ displaystyle 2y = -3x-4 [/ латекс]
Затем разделите обе части уравнения на [латекс] 2 [/ латекс], чтобы получить:
[латекс] \ displaystyle y = \ frac {1} {2} (- 3x-4) [/ latex]
Что упрощается до [латекс] y = — \ frac {3} {2} x-2 [/ latex]. Теперь, когда уравнение имеет форму пересечения наклона, мы видим, что наклон [латекс] m = — \ frac {3} {2} [/ latex] и [латекс] y [/ latex] -перерез [латекс] б = -2 [/ латекс].
Построение уравнения в форме пересечения наклона
Начнем с построения графика уравнения из предыдущего примера.
Пример
Мы строим график линии [latex] y = — \ frac {3} {2} x-2 [/ latex], используя метод пересечения наклона. Начнем с построения [latex] y [/ latex] -intercept [latex] b = -2 [/ latex], координаты которого равны [latex] (0, -2) [/ latex]. Значение наклона диктует, где разместить следующую точку.
Поскольку значение наклона равно [latex] \ frac {-3} {2} [/ latex], подъем составляет [latex] -3 [/ latex], а пробег равен [latex] 2 [/ latex].Это означает, что от интервала [latex] y [/ latex], [latex] (0, -2) [/ latex] переместите [latex] 3 [/ latex] единицы вниз и переместите [latex] 2 [/ латекс] единицы правая. Таким образом, мы приходим к точке [латекс] (2, -5) [/ латекс] на линии. Если поставить знак минус вместе со знаменателем вместо того, чтобы наклон был записан как [latex] \ frac {3} {- 2} [/ latex], мы можем вместо этого переместить [latex] 3 [/ latex] единицы и влево [ latex] 2 [/ latex] единицы из [latex] y [/ latex] -перехвата, чтобы прибыть в точку [latex] (- 2,1) [/ latex], также на линии.
График угла наклона: график линии [латекс] y = — \ frac {3} {2} x-2 [/ latex].
Пример
Изобразим уравнение [латекс] 12x-6y-6 = 0 [/ latex]. Сначала мы решаем уравнение для [latex] y [/ latex], вычитая [latex] 12x [/ latex], чтобы получить:
[латекс] \ displaystyle -6y-6 = -12x [/ латекс]
Затем добавьте [latex] 6 [/ latex], чтобы получить:
[латекс] \ displaystyle -6y = -12x + 6 [/ latex]
Наконец, разделите все члены на [latex] -6 [/ latex], чтобы получить форму пересечения наклона:
[латекс] \ displaystyle y = 2x-1 [/ латекс]
Наклон составляет [латекс] 2 [/ латекс], а интервал [латекс] y [/ латекс] равен [латекс] -1 [/ латекс].Используя эту информацию, легко построить графики. Начните с построения [latex] y [/ latex] -intercept [latex] (0, -1) [/ latex], затем используйте значение наклона, [latex] \ frac {2} {1} [/ latex ], чтобы переместить [латекс] на 2 [/ латекс] единицы и вправо [латекс] на 1 [/ латекс] единицу.
График угла наклона: График линии [латекс] y = 2x-1 [/ latex].
Уравнения точечного уклона
Уравнение «точка-наклон» — это еще один способ представления линии; нужен только наклон и единичная точка.
Цели обучения
Используйте форму «точка-наклон», чтобы найти уравнение прямой, проходящей через две точки, и убедитесь, что она эквивалентна форме «наклон-пересечение» уравнения
Основные выводы
Ключевые моменты
- Уравнение точки и наклона задается следующим образом: [латекс] y-y_ {1} = m (x-x_ {1}) [/ latex], где [латекс] (x_ {1}, y_ {1}) [ / latex] — это любая точка на линии, а [latex] m [/ latex] — это наклон линии.
- Уравнение «точка-уклон» требует наличия хотя бы одной точки и уклона. Если есть две точки и нет наклона, наклон можно сначала рассчитать по двум точкам, а затем выбрать одну из двух точек для написания уравнения.
- Уравнение точки-наклона и уравнения откоса-пересечения эквивалентны. Можно показать, что с учетом точки [латекс] (x_ {1}, y_ {1}) [/ latex] и наклона [латекс] m [/ latex], [латекс] y [/ latex] -перехват ([ latex] b [/ latex]) в уравнении угла наклона есть [latex] y_ {1} -mx_ {1} [/ latex].
Ключевые термины
- Уравнение угла наклона точки : Уравнение линии, заданной точкой [латекс] (x_ {1}, y_ {1}) [/ латекс] и наклоном [латекс] м [/ латекс]: [латекс] y-y_ {1} = m (x-x_ {1}) [/ латекс].
Уравнение точечного уклона
Уравнение точки-наклона — это способ описания уравнения прямой. Форма «точка-наклон» идеальна, если вам даны наклон и только одна точка, или если вам даны две точки и вы не знаете, что такое [latex] y [/ latex] -перехват.Учитывая наклон, [латекс] м [/ латекс] и точку [латекс] (x_ {1}, y_ {1}) [/ latex], уравнение угла наклона точки:
[латекс] \ displaystyle y-y_ {1} = m (x-x_ {1}) [/ latex]
Убедитесь, что форма «точка-уклон» эквивалентна форме
Чтобы показать, что эти два уравнения эквивалентны, выберите общую точку [latex] (x_ {1}, y_ {1}) [/ latex]. Подставьте общую точку в уравнение [латекс] y = mx + b [/ latex]. Уравнение теперь [латекс] y_ {1} = mx_ {1} + b [/ latex], что дает нам упорядоченную пару, [латекс] (x_ {1}, mx_ {1} + b) [/ latex] .Затем подставьте эту точку в уравнение угла наклона точки и решите для [latex] y [/ latex], чтобы получить:
[латекс] \ displaystyle y- (mx_ {1} + b) = m (x-x_ {1}) [/ latex]
Распределите отрицательный знак и распределите [latex] m [/ latex] через [latex] (x-x_ {1}) [/ latex]:
[латекс] \ displaystyle y-mx_ {1} -b = mx-mx_ {1} [/ latex]
Добавьте [латекс] mx_ {1} [/ latex] с обеих сторон:
[латекс] \ displaystyle y-mx_ {1} + mx_ {1} -b = mx-mx_ {1} + mx_ {1} [/ latex]
Объедините похожие термины:
[латекс] \ displaystyle y-b = mx [/ латекс]
Добавьте [латекс] b [/ латекс] с обеих сторон:
[латекс] \ displaystyle y-b + b = mx + b [/ latex]
Объедините похожие термины:
[латекс] \ displaystyle y = mx + b [/ латекс]
Следовательно, два уравнения эквивалентны, и любое из них может выразить уравнение линии в зависимости от того, какая информация дается в задаче, или какой тип уравнения запрашивается в задаче.
Пример: напишите уравнение линии в форме точки-наклона, учитывая точку [латекс] (2,1) [/ latex] и наклон [латекс] -4 [/ latex], и преобразуйте ее в форму пересечения наклона
Запишите уравнение прямой в виде точки с уклоном:
[латекс] \ displaystyle y-1 = -4 (x-2) [/ latex]
Чтобы преобразовать это уравнение в форму пересечения наклона, решите уравнение для [латекс] y [/ латекс]:
[латекс] \ displaystyle y-1 = -4 (x-2) [/ latex]
Раздать [латекс] -4 [/ латекс]:
[латекс] \ displaystyle y-1 = -4x + 8 [/ латекс]
Добавьте [латекс] 1 [/ латекс] с обеих сторон:
[латекс] \ displaystyle y = -4x + 9 [/ латекс]
Уравнение имеет то же значение, в какой бы форме оно ни было, и дает один и тот же график.
Линейный график: График линии [латекс] y-1 = -4 (x-2) [/ latex] через точку [latex] (2,1) [/ latex] с наклоном [латекс] -4 [/ latex], а также наклонно-перехватывающая форма [latex] y = -4x + 9 [/ latex].
Пример: напишите уравнение линии в форме «точка-уклон», учитывая точку [латекс] (- 3,6) [/ latex] и точку [латекс] (1,2) [/ latex], и преобразуйте ее в наклон- форма перехвата
Поскольку у нас есть две точки, но нет наклона, мы должны сначала найти наклон:
[латекс] \ displaystyle m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} [/ latex]
Подставляем значения баллов:
[латекс] \ displaystyle \ begin {align} m & = \ frac {-2-6} {1 — (- 3)} \\ & = \ frac {-8} {4} \\ & = — 2 \ end {align} [/ латекс]
Теперь выберите любую из двух точек, например [латекс] (- 3,6) [/ латекс].Подставьте эту точку и рассчитанный наклон в уравнение угла наклона точки, чтобы получить:
[латекс] \ displaystyle y-6 = -2 [x — (- 3)] [/ latex]
Будьте осторожны, если одна из координат отрицательная. Распределяя отрицательный знак через круглые скобки, окончательное уравнение будет:
[латекс] \ displaystyle y-6 = -2 (x + 3) [/ latex]
Если вы выберете другой пункт, уравнение будет выглядеть следующим образом: [латекс] y + 2 = -2 (x-1) [/ latex], и любой ответ правильный.
Далее раздаем [латекс] -2 [/ латекс]:
[латекс] \ displaystyle y-6 = -2x-6 [/ латекс]
Добавьте [латекс] 6 [/ латекс] с обеих сторон:
[латекс] \ displaystyle y = -2x [/ латекс]
Опять же, две формы уравнений эквивалентны друг другу и образуют одну и ту же линию.Единственное отличие — это форма, в которой они написаны.
Линейные уравнения в стандартной форме
Линейное уравнение, записанное в стандартной форме, позволяет легко вычислить нулевой или [латексный] х [/ латексный] интервал уравнения.
Цели обучения
Объясните процесс и полезность преобразования линейных уравнений в стандартную форму
Основные выводы
Ключевые моменты
- Стандартная форма линейного уравнения записывается как: [латекс] Ax + By = C [/ latex].
- Стандартная форма полезна при вычислении нуля уравнения. Для линейного уравнения в стандартной форме, если [latex] A [/ latex] не равно нулю, то перехват [latex] x [/ latex] происходит в [latex] x = \ frac {C} {A} [/ latex ].
Ключевые термины
- ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна 0.
- форма пересечения наклона : Линейное уравнение, записанное в форме [латекс] y = mx + b [/ latex].
- y-intercept : точка, в которой линия пересекает ось y декартовой сетки.
Стандартная форма
Стандартная форма — это еще один способ составить линейное уравнение. В стандартной форме линейное уравнение записывается как:
[латекс] \ displaystyle Ax + By = C [/ latex]
, где [latex] A [/ latex] и [latex] B [/ latex] не равны нулю. Уравнение обычно записывается так, что [latex] A \ geq 0 [/ latex], по соглашению. График уравнения представляет собой прямую линию, и каждая прямая линия может быть представлена уравнением в стандартной форме.
Например, рассмотрим уравнение в форме перехвата наклона: [латекс] y = -12x +5 [/ latex]. Чтобы записать это в стандартной форме, обратите внимание, что мы должны переместить член, содержащий [latex] x [/ latex], в левую часть уравнения. Добавляем [latex] 12x [/ latex] с обеих сторон:
[латекс] \ displaystyle y + 12x = 5 [/ латекс]
Уравнение теперь в стандартной форме.
Использование стандартной формы для поиска нулей
Напомним, что ноль — это точка, в которой значение функции будет равно нулю ([latex] y = 0 [/ latex]), и это перехват функции [latex] x [/ latex].Мы знаем, что точку пересечения y линейного уравнения можно легко найти, поместив уравнение в форму углового пересечения. Однако, когда линейное уравнение находится в такой форме, нуль уравнения не сразу очевиден. Однако нулевой или [latex] x [/ latex] -перехват линейного уравнения может быть легко найден путем преобразования его в стандартную форму.
Для линейного уравнения в стандартной форме, если [latex] A [/ latex] не равно нулю, то перехват [latex] x [/ latex] происходит в [latex] x = \ frac {C} {A} [/ латекс].
Например, рассмотрим уравнение [латекс] y + 12x = 5 [/ latex].
В этом уравнении значение [latex] A [/ latex] равно 1, а значение [latex] C [/ latex] равно 5. Следовательно, ноль уравнения находится в [latex] x = \ frac {5} {1} = 5 [/ латекс]. Ноль — это точка [латекс] (5, 0) [/ латекс].
Обратите внимание, что пересечение и наклон [latex] y [/ latex] также могут быть рассчитаны с использованием коэффициентов и константы уравнения стандартной формы. Если [latex] B [/ latex] не равно нулю, то пересечение y , то есть y -координата точки, в которой график пересекает ось y (где [latex] x [ / latex] равно нулю), это [latex] \ frac {C} {B} [/ latex], а наклон линии равен [latex] — \ frac {A} {B} [/ latex].
Пример. Найдите ноль уравнения [latex] 3 (y — 2) = \ frac {1} {4} x +3 [/ latex]
Мы должны записать уравнение в стандартной форме, [latex] Ax + By = C [/ latex], что означает получение членов [latex] x [/ latex] и [latex] y [/ latex] с левой стороны, и константы в правой части уравнения.
Распределите 3 на левой стороне:
[латекс] \ displaystyle 3y — 6 = \ frac {1} {4} x +3 [/ latex]
Добавьте 6 к обеим сторонам:
[латекс] \ displaystyle 3y = \ frac {1} {4} x + 9 [/ latex]
Вычтите [латекс] \ frac {1} {4} x [/ latex] с обеих сторон:
[латекс] \ displaystyle 3y — \ frac {1} {4} x = 9 [/ latex]
Переставить в [латекс] Ax + By = C [/ latex]:
[латекс] \ displaystyle — \ frac {1} {4} x + 3y = 9 [/ latex]
Уравнение имеет стандартную форму, и мы можем подставить значения для [латекс] A [/ латекс] и [латекс] C [/ латекс] в формулу для нуля:
[латекс] \ displaystyle \ begin {align} x & = \ frac {C} {A} \\ & = \ frac {9} {- \ frac {1} {4}} \\ & = -36 \ end {align} [/ латекс]
Ноль — [латекс] (- 36, 0) [/ латекс].
Решенные проблемы | PDF | Совместно непрерывные случайные переменные
5.2.5 Решенные проблемы
ПроблемаПусть $ X $ и $ Y $ — совместно непрерывные случайные величины с совместной PDF \ begin {уравнение} \ nonumber f_ {X, Y} (x, y) = \ left \ { \ begin {array} {l l} cx + 1 & \ quad x, y \ geq 0, x + y
- Показать диапазон $ (X, Y) $, $ R_ {XY} $ в плоскости $ x-y $.
- Найдите постоянную $ c $.
- Найдите PDF-файлы на полях $ f_X (x) $ и $ f_Y (y) $.{1-y} 3x + 1 \ hspace {5pt} dx \\ \ nonumber & = \ frac {1} {2} (1-y) (5–3y), \ hspace {10pt} \ textrm {for} y \ in [0,1]. \ end {align} Таким образом, мы имеем \ begin {уравнение} \ nonumber f_Y (y) = \ left \ { \ begin {array} {l l} \ frac {1} {2} (1-год) (5–3 года) & \ quad 0 \ leq y \ leq 1 \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right. \ end {уравнение}
- Чтобы найти $ P (Y
Проблема
Пусть $ X $ и $ Y $ — совместно непрерывные случайные величины с совместной PDF \ begin {уравнение} \ nonumber f_ {X, Y} (x, y) = \ left \ { \ begin {array} {l l} 6e ^ {- (2x + 3y)} & \ quad x, y \ geq 0 \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right.{-5y} dy \\ \ nonumber & = \ frac {3} {5}. \ end {align}
Проблема
Пусть $ X $ — непрерывная случайная величина с PDF \ begin {уравнение} \ nonumber f_X (x) = \ left \ { \ begin {array} {l l} 2x & \ quad 0 \ leq x \ leq 1 \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right. \ end {уравнение} Мы знаем, что при $ X = x $ случайная величина $ Y $ равномерно распределена на $ [- x, x] $.
- Найдите совместный PDF-файл $ f_ {XY} (x, y) $.3) $.
- Решение
- Прежде всего отметим, что по предположению \ begin {уравнение} \ nonumber f_ {Y | X} (y | x) = \ left \ { \ begin {array} {l l} \ frac {1} {2x} & \ quad -x \ leq y \ leq x \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right. \ end {уравнение} Таким образом, мы имеем \ begin {уравнение} \ nonumber f_ {XY} (x, y) = f_ {Y | X} (y | x) f_X (x) = \ left \ { \ begin {array} {l l} 1 & \ quad 0 \ leq x \ leq 1, -x \ leq y \ leq x \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right.3} {2x} \ right) 2x dx \ hspace {20pt} \ textrm {поскольку} Y | X = x \ hspace {5pt} \ sim \ hspace {5pt} Uniform (-x, x) \\ \ nonumber & = \ frac {1} {2}. \ end {align}
Проблема
Пусть $ X $ и $ Y $ — две совместно непрерывные случайные величины с совместной PDF \ begin {уравнение} \ nonumber f_ {X, Y} (x, y) = \ left \ { \ begin {array} {l l} 6xy & \ quad 0 \ leq x \ leq 1, 0 \ leq y \ leq \ sqrt {x} \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right.\ end {уравнение}
- Показать $ R_ {XY} $ в плоскости $ x-y $.
- Найдите $ f_X (x) $ и $ f_Y (y) $.
- Независимы ли $ X $ и $ Y $?
- Найдите условную PDF $ X $ при $ Y = y $, $ f_ {X | Y} (x | y) $.
- Найдите $ E [X | Y = y] $ для $ 0 \ leq y \ leq 1 $.
- Найдите $ \ textrm {Var} (X | Y = y) $ для $ 0 \ leq y \ leq 1 $.
- Решение
- Рисунок 5.9 показывает $ R_ {XY} $ в плоскости $ x-y $.
Рисунок 5.2 \ leq 1 \}. \ end {align} Предположим, что мы выбираем точку $ (X, Y) $ равномерно случайным образом в $ D $. То есть совместная PDF $ X $ и $ Y $ задается формулой \ begin {уравнение} \ nonumber f_ {XY} (x, y) = \ left \ { \ begin {array} {l l} \ frac {1} {\ pi} & \ quad (x, y) \ in D \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right. \ end {уравнение} Пусть $ (R, \ Theta) $ — соответствующие полярные координаты, как показано на рисунке 5.10. Обратное преобразование дается формулой \ begin {уравнение} \ nonumber \ left \ { \ begin {array} {l} X = R \ cos \ Theta \\ Y = R \ sin \ Theta \ end {array} \ right.\ end {уравнение} где $ R \ geq 0 $ и $ — \ pi
Рисунок 5.10: Полярные координаты
- Решение
- Здесь $ (X, Y) $ совместно непрерывны и связаны с $ (R, \ Theta) $ взаимно однозначным соотношением. Воспользуемся методом преобразований (теорема 5.1). Функция $ h (r, \ theta) $ задается формулой \ begin {уравнение} \ nonumber \ left \ { \ begin {array} {l} х = h_1 (г, \ тета) = г \ соз \ тета \\ у = ч_2 (г, \ тета) = г \ грех \ тета \ end {array} \ right. \ end {уравнение} Таким образом, мы имеем \ begin {align} \ nonumber f_ {R \ Theta} (r, \ theta) & = f_ {XY} (h_1 (r, \ theta), h_2 (r, \ theta)) | J | \\ \ nonumber & = f_ {XY} (r \ cos \ theta, r \ sin \ theta) | J |.\ end {align} куда \ begin {align} \ nonumber J = \ det \ begin {bmatrix} \ frac {\ partial h_1} {\ partial r} & \ frac {\ partial h_1} {\ partial \ theta} \\ & \\ \ frac {\ partial h_2} {\ partial r} & \ frac {\ partial h_2} {\ partial \ theta} \\ \ end {bmatrix} = \ det \ begin {bmatrix} \ cos \ theta & -r \ sin \ theta \\ & \\ \ sin \ theta & r \ cos \ theta \\ \ end {bmatrix} = г \ соз ^ 2 \ тета + г \ грех ^ 2 \ тета = г.
- Решение
- Рисунок 5.9 показывает $ R_ {XY} $ в плоскости $ x-y $.

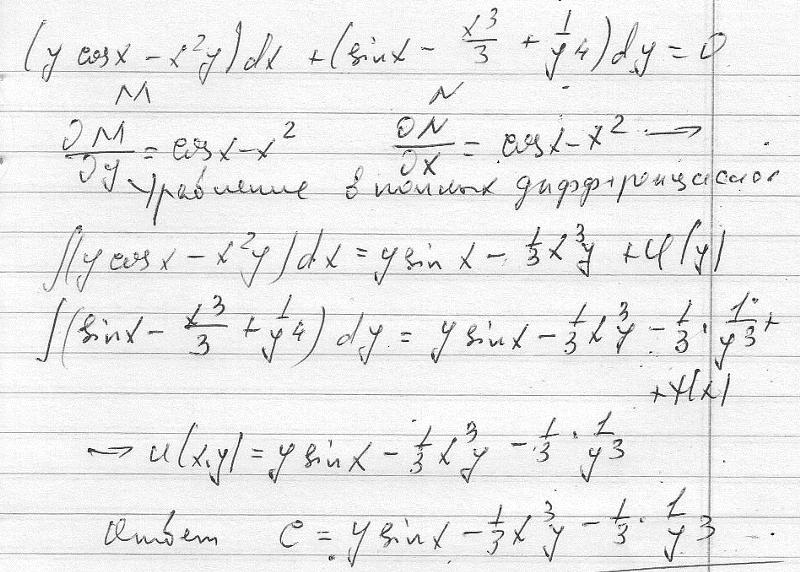
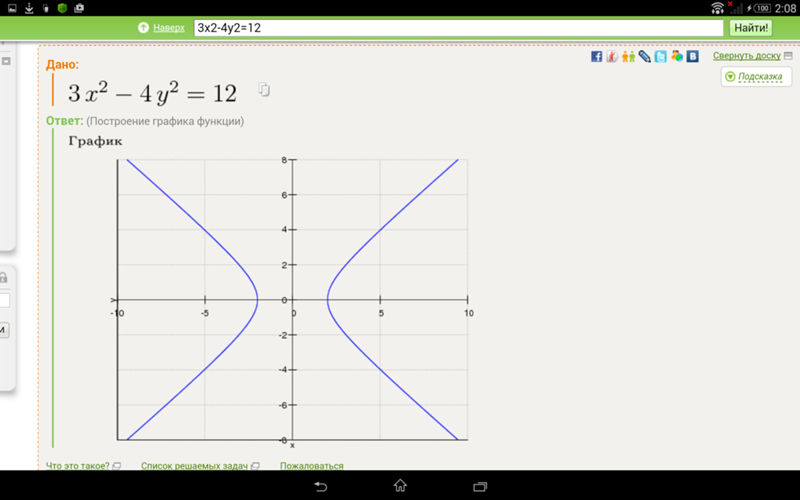

 .
.
Leave A Comment