Взаимосвязь между силой и деформацией кто открыл: Закон Гука • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Закон Гука • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Сила противодействия упругого вещества линейному растяжению или сжатию прямо пропорциональна относительному увеличению или сокращению длины.

Представьте, что вы взялись за один конец упругой пружины, другой конец которой закреплен неподвижно, и принялись ее растягивать или сжимать. Чем больше вы сдавливаете пружину или растягиваете ее, тем сильнее она этому сопротивляется. Именно по такому принципу устроены любые пружинные весы — будь то безмен (в нем пружина растягивается) или платформенные пружинные весы (пружина сжимается). В любом случае пружина противодействует деформации под воздействием веса груза, и сила гравитационного притяжения взвешиваемой массы к Земле уравновешивается силой упругости пружины. Благодаря этому мы можем измерять массу взвешиваемого объекта по отклонению конца пружины от ее нормального положения.

Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Первоначально в своем опыте он использовал даже не пружину, а струну, измеряя, насколько она удлиняется под воздействием различных сил, приложенных к одному ее концу, в то время как другой конец жестко закреплен. Ему удалось выяснить, что до определенного предела струна растягивается строго пропорционально величине приложенной силы, пока не достигает предела упругого растяжения (эластичности) и не начинает подвергаться необратимой нелинейной деформации (см. ниже). В виде уравнения закон Гука записывается в следующей форме:

    F = –kx

где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействует деформации: при растяжении стремится укоротиться, а при сжатии — распрямиться.

Закон Гука лег в основу раздела механики, который называется теорией упругости. Выяснилось, что он имеет гораздо более широкие применения, поскольку атомы в твердом теле ведут себя так, будто соединены между собой струнами, то есть упруго закреплены в объемной кристаллической решетке. Таким образом, при незначительной упругой деформации эластичного материала действующие силы также описываются законом Гука, но в несколько более сложной форме. В теории упругости закон Гука принимает следующий вид:

    σ/η = E

где σ — механическое напряжение (удельная сила, приложенная к поперечной площади сечения тела), η — относительное удлинение или сжатие струны, а Е — так называемый модуль Юнга, или модуль упругости, играющий ту же роль, что коэффициент упругости k. Он зависит от свойств материала и определяет, насколько растянется или сожмется тело при упругой деформации под воздействием единичного механического напряжения.

Вообще-то, Томас Юнг гораздо более известен в науке как один из сторонников теории волновой природы света, разработавший убедительный опыт с расщеплением светового луча на два пучка для ее подтверждения (см. Принцип дополнительности и Интерференция), после чего сомнений в верности волновой теории света ни у кого не осталось (хотя до конца облечь свои идеи в строгую математическую форму Юнг так и не сумел). Вообще говоря, модуль Юнга представляет собой одну из трех величин, позволяющих описать реакцию твердого материала на приложенную к нему внешнюю силу. Вторая — это модуль смещения (описывает, насколько вещество смещается под воздействием силы, приложенной по касательной к поверхности), а третья — соотношение Пуассона (описывает, насколько твердое тело истончается при растяжении). Последнее названо в честь французского математика Симеона Дени Пуассона (Siméon-Denis Poisson, 1781–1840)^.

Конечно, закон Гука даже в усовершенствованной Юнгом форме не описывает всего, что происходит с твердым веществом под воздействием внешних сил. Представьте себе резиновую ленту. Если растянуть ее не слишком сильно, со стороны резиновой ленты возникнет возвратная сила упругого натяжения, и как только вы ее отпустите, она тут же соберется и примет прежнюю форму. Если растягивать резиновую ленту и дальше, то рано или поздно она утратит свою эластичность, и вы почувствуете, что сила сопротивления растяжению ослабла. Значит, вы перешли так называемый предел эластичности материала. Если тянуть резину и дальше, через какое-то время она вообще порвется, и сопротивление исчезнет полностью — это вы перешли через так называемую точку разрыва.

Иными словами, закон Гука действует только при относительно небольших сжатиях или растяжениях. Пока вещество сохраняет свои упругие свойства, силы деформации прямо пропорциональны ее величине, и вы имеете дело с линейной системой — каждому равному приращению приложенной силы соответствует равное приращение деформации. Стоит перетянуть резину за предел эластичности, и межатомные связи-пружины внутри вещества сначала ослабевают, а затем рвутся — и простое линейное уравнение Гука перестает описывать происходящее. В таком случае принято говорить, что система стала нелинейной. Сегодня исследование нелинейных систем и процессов является одним из основных направлений развития физики.

Сила упругости и закон Гука

☰

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

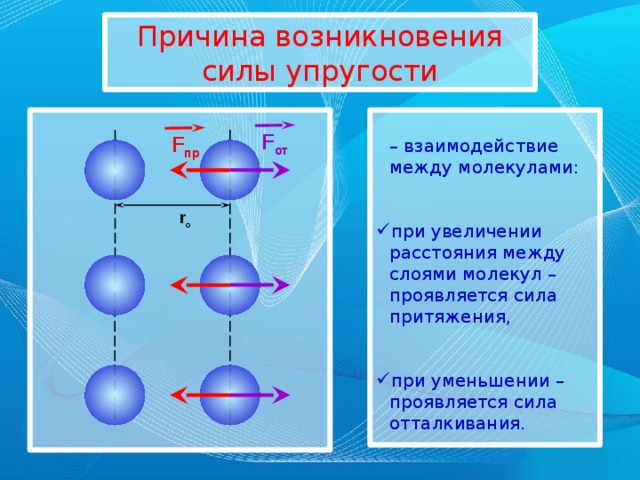
Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆l (l₁ – l₀, где l

0 — начальная длина, l₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

F_упр = kx или F_упр = k∆l, (∆l = l₁ – l₀ = x)

В формуле используется коэффициент k. Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F

упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние — в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения F_упр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F

упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры.

Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Закон Гука | Описание и уравнение

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Викторины

• Физика и естественное право

Закон Гука и эластичность.

Откройте для себя их 5 магических достоинств

Последнее обновление: 15 ноября 2022 г., Сара Ассем

Истинное чудо творческого разума и инженерии человечества — это весна! Благодаря множеству различных форм и специфических функций — спиральной пружине, пружине сжатия, пружине растяжения, пружине кручения и т. д. — нашему человечеству была предоставлена ​​возможность изготовить и изобрести множество других полезных предметов.

Эта рукотворная революция инструментов и приложений стала следствием научной революции, имевшей место в 17-м и 18-м веках. Пружины подчиняются определенному закону физики, научно известному как: закон напряжения-деформации Гука, закон упругости Гука или просто закон Гука .

Что такое закон Гука? Применяется ли это к эластичным материалам или к неэластичным материалам? Как работает закон Гука? И почему закон Гука важен в физике и в нашей жизни вообще? Это все вопросы, которые могли прийти вам на ум в тот момент, когда вы прочитали слово «закон Гука».

В этом плодотворном блоге закон Гука будет подробно объяснен, и вы поймете его природу, узнаете, каковы его примеры и приложения, поймете, какие математические уравнения описывают его, и поймете, как его объяснить… Поехали!

 

Попробуйте провести эксперимент по закону Гука прямо сейчас!

 

Содержание

Какова история пружины закона Гука?

Способность пружины успешно накапливать механическую энергию в дополнение к ее эластичности — свойству, которое заставляет материал/объект восстанавливать свою первоначальную форму после деформации — позволило широко использовать ее в различных приложениях. Эти приложения варьируются от знаменитого Slinky до маятниковых часов, заводных игрушек, ловушек для крыс, цифровых микрозеркальных устройств, автомобильных подвесных систем, ручных ножниц и часов.

Прежде чем какое-либо новое изобретенное устройство будет пригодно для использования во многих приложениях, мы должны по-настоящему понять лежащую в его основе механику, по крайней мере, самые основы. И здесь, говоря о пружинах, эластичность, сила и кручение — свойства, на которые нам нужно обратить внимание. Вместе они составляют то, что называется законом Гука.

В 1676 году английский физик Роберт Гук сформулировал закон, продемонстрировав связь между упругостью пружины и приложенными к ней силами. Хотя закон связан с упругостью и силами, он также связан с расстоянием растяжения или сжатия. Музыкант, дергающий за струны своей гитары, или количество ветра, дующего на высокое здание, заставляющее его сгибаться и раскачиваться, считаются примерами закона Гука, согласно которому эти упругие тела в некоторой степени деформируются.

Роберт Гук, ученый, разработавший закон Гука (Источник: Britain Unlimited)

Обобщенный закон Гука

Прежде чем углубляться в детали и расчеты закона Гука, вы должны знать, что это всего лишь линейная аппроксимация пружин первого порядка. реальный отклик, как и других упругих тел, на приложенные к ним силы. Материалы нельзя растягивать сверх максимального размера, а также нельзя сжимать сверх определенного предела.

Другими словами, этот линейный закон нарушается всякий раз, когда приложенные силы превышают допустимые пределы деформации. Эти пределы известны как пределы упругости , в то время как большинство материалов будут сталкиваться с изменением состояния или постоянной деформацией, когда они достигнут этих пределов. Для большинства твердых тел и малых деформаций закон Гука является точным приближением, достаточно хорошо описывающим процесс. То есть закон активно и широко используется практически во всех отраслях техники и науки.

Этот закон является основополагающим принципом для многих приложений; таких как: баланс механических часов, гальванометр, манометр (он же манометр) и пружинная шкала, а также управляет многими дисциплинами вокруг нас, такими как акустика, молекулярная механика и сейсмология.

Обобщение закона Гука было успешно осуществлено современной теорией упругости . Теория определяет, что напряжение , приложенное к упругому материалу/объекту, и напряжение (деформация) пропорциональны друг другу.

Однако коэффициент пропорциональности может быть выражен не как одно действительное число, а скорее как тензор , поскольку общие напряжения и деформации могут иметь несколько независимых компонентов. Тензор представляет собой форму математических выражений, которая представлена ​​ матрицей действительных чисел.

Используя эту общую форму закона Гука, легко вывести соотношение напряжение-деформация для объектов сложной формы. Это основано на изучении внутренних свойств материалов объекта. Однородный стержень с однородным поперечным сечением будет вести себя так же, как простая пружина, когда ее растягивают. Такое соотношение связывает жесткость (k), которая равна прямо пропорционально площади поперечного сечения стержня, а обратно пропорционально его длине.

 

БЕСПЛАТНО! Создайте учетную запись, чтобы попробовать эксперимент с законом Гука

Эксперимент с законом Гука

Поскольку законы и теории нуждаются в экспериментах, чтобы проверить, верны они или нет, закон Гука был доказан экспериментом, который волшебным образом подтвердился. Эксперимент по закону Гука прост в выполнении, с его удобной настройкой и продуманной концепцией. Именно простота проведения этого эксперимента делает его выбранным для проведения в любой физической лаборатории первого года обучения. Теперь вы можете угадать его концепцию работы и объем поставки?

Эксперимент по закону Гука фокусируется на рассмотрении упругих тел, следовательно, на изучении их эластичности и того, как они прилипают к деформациям и реагируют на них. Установка эксперимента состоит из винтовой пружины и подвешенных к ней сменных грузов. Изменение длины пружины пропорционально силе тяжести, обозначаемой как F , которая воздействует на подвешенный вес.

Демонстрация действия закона Гука (Источник: Science Sparks)

Эксперимент можно проводить с использованием одной винтовой пружины и множества грузов или с использованием разных винтовых пружин и разных грузов. Во всех случаях мы изучаем удлинение катушки — изменение длины — в ответ на используемые веса. Разумный выбор диаметра как проволоки, так и катушки приведет к заметной проверке закона Гука.

Изучение уравнения закона Гука

Чтобы аналитически понять, как будут выглядеть графики и данные эксперимента по закону Гука, нам сначала необходимо получить определенные знания об уравнении, управляющем самим законом Гука.

Удлинение спиральной пружины — это то, что мы измеряем в этом эксперименте, чтобы вывести значение того, что научно известно как константа пружины , обозначается как k .

Формула закона Гука имеет следующий вид:

где

F с : приложенная сила тяжести, вызванная весами (измеряется в 91*, 9171 ньютонов). ),
k: константа пропорциональности упругости, зависящая от материала и размеров пружины (измеряется в ньютонов/метр ), и
x: сжатие или растяжение пружины из положения равновесия (измеряется в м ).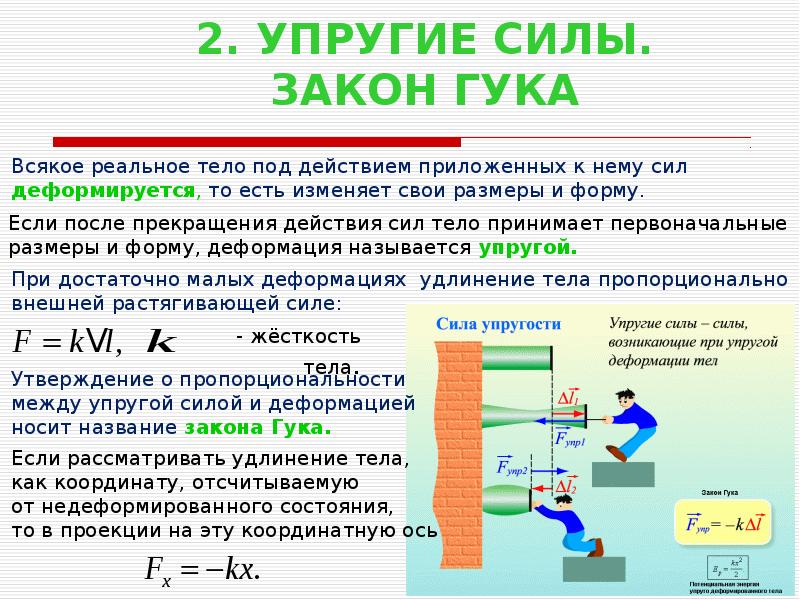

Еще одно важное замечание, которое следует учитывать при записи ваших измерений, — следить за единицами закона Гука, упомянутыми ранее. Уравнение закона Гука имеет жизненно важное значение во многих приложениях и примерах, с которыми мы сталкиваемся на регулярной основе и в повседневной жизни.

Закон применяется, когда прямая бетонная балка (подобная той, что используется в зданиях) или стальной стержень, поддерживаемый с обоих концов, изгибается под действием веса, помещенного в промежуточной точке вдоль него. В этом случае отклонение балки равно смещению (x) , и это рассматривается как пример закона Гука.

График закона Гука

По логике график эксперимента по закону Гука должен быть связан с ранее упомянутыми терминами и характеристиками. Следовательно, мы записываем следующие показания:

1. Масса (в килограммах)
2. Длина пружины (в метрах)
3. Удлинение (в метрах)

Пример таблицы данных показан на рисунке ниже.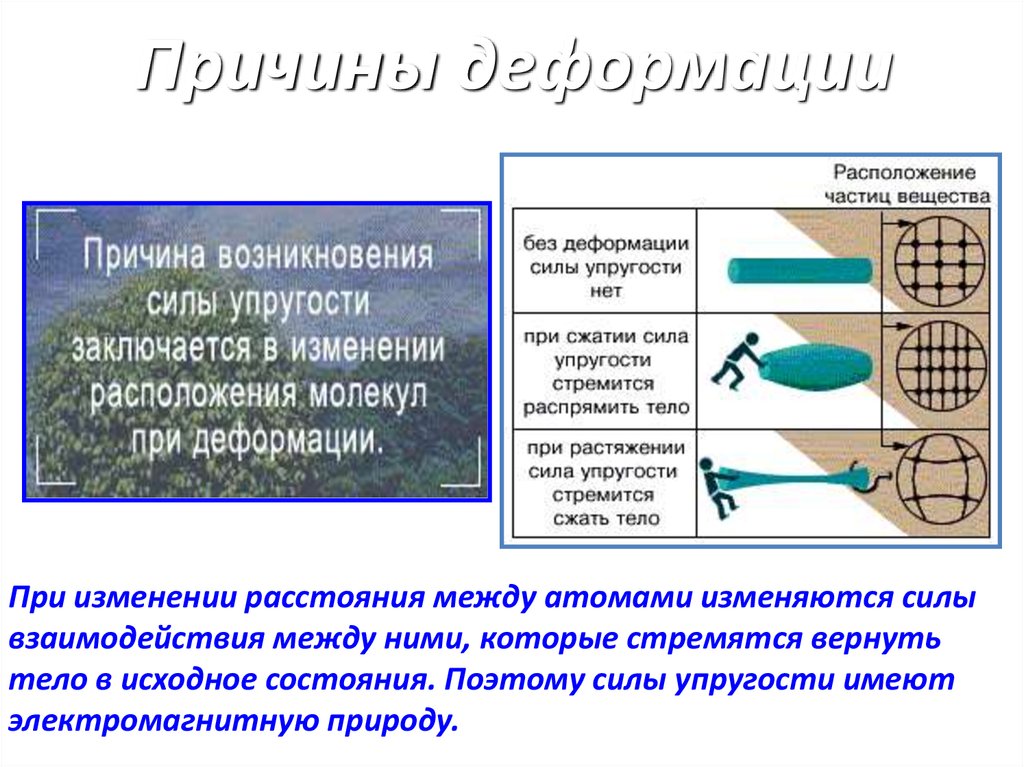

Калькулятор закона Гука включает еще два математических расчета, основанных на этих показаниях. Расчеты следующие:

1. Сила, равная произведению массы на ускорение свободного падения (в ньютонах или кг*м/с ² )
2. Постоянная пружины (в ньютонах/метр)

Желаемое значение постоянной пружины определяется путем построения графика силы по оси Y и отклонения пружины от положения равновесия по оси X. В результате получается прямая, и отваливается только при превышении пластикового лимита. Вычисляя наклон графика, мы легко получаем константу пружины. больше жесткость пружины, k, больше усилие пружины на величину смещения.

График для сжатия или расширения выглядит следующим образом:

Теперь вы можете легко изучить закон Гука самостоятельно для бесплатно и узнать больше о применении закона и правилах только в виртуальных лабораториях PraxiLabs. !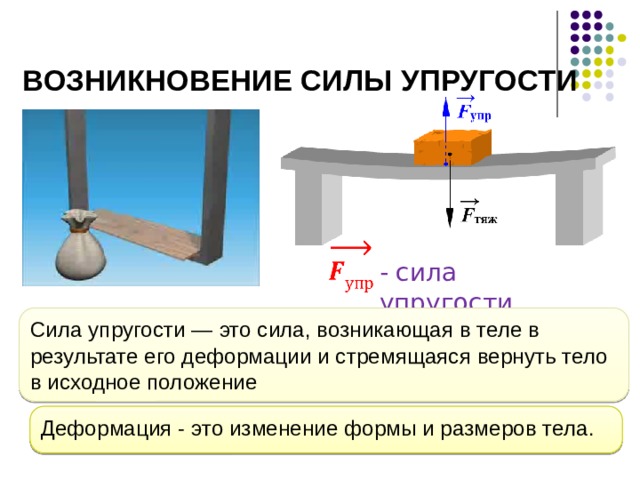

О Шеруке Бадре Шехате

Шерук Бадр Шехата — старший создатель научного контента и студент магистратуры по теоретической физике из Египта. Будучи выпускником факультета физики и астрономии, Шерук начала свою карьеру в 2017 году в качестве научного переводчика и создателя контента, при этом этому также предшествовали два года волонтерской работы в той же области. Опыт Шерука распространился на многие авторитетные иностранные организации и компании как в области научного перевода, так и в области публикации, такие как: Pearson Middle East в ОАЭ, Kitab Sawti в Швеции, I Believe in Science в Ливане, а также многие египетские компании и PraxiLabs в верхней части этого списка. В своих работах Шерук стремится безупречно повысить качество предоставляемого научного контента и стремится создавать богатые и интересные произведения как на арабском, так и на английском языках. Она также стремится поощрять и подталкивать учащихся, родителей и людей в целом к ​​тому, чтобы они больше читали о науке, и особенно о естественных науках, поскольку она считает, что наука и искусство являются главными ключами к прогрессу и процветанию наций.