Вычислите силу лоренца действующую на протон движущийся со скоростью 10: Определить силу Лоренца действующую на движущийся протон в магнитном поле

Самостоятельная работа по теме: Магнитное поле

Самостоятельная работа по теме: Магнитное поле.

Вариант 1.

Задание 1.

Какая сила действует на проводник длиной 0,1 м в однородном магнитном поле с индукцией 2 Тл, если ток в проводнике 5 А, а угол между направлением тока и линиями индукции 30⁰?
Определите величину силы Лоренца действующей на протон (заряд протона 1,6 ·10^-19 Кл), если индукция магнитного поля 80 мТл, а скорость движения протона 200 км/с. Угол между направлением скорости и индукцией равен 90⁰.

Задание 2. Определить как направлены: сила Ампера, сила Лоренца, вектор магнитной индукции в зависимости от варианта задания.

1 ) 2) 3) 5)

Варианты ответов: 4)

а) вверх б) вниз

в) от нас г) к нам

д) по часовой стрелке

е) против часовой стрелки

ж) равна нулю или не действует

и) вправо

к) влево

Самостоятельная работа по теме: Магнитное поле.

Вариант 2.

Задание 1.

Вычислите силу Лоренца, действующую на протон (заряд протона 1,6 ·10^-19 Кл), движущийся со скоростью 10⁶м/с в однородном магнитном поле с индукцией 0,3 Тл перпендикулярно линиям индукции.
В однородном магнитном поле с индукцией 0,8 Тл на проводник с током 30 А, длина активной части которого 10 см, действует сила 1,5 Н. Под каким углом к вектору магнитной индукции расположен проводник?

З адание 2. Определить как направлены: сила Ампера, сила Лоренца, вектор магнитной индукции в зависимости от варианта задания.

2) 3) 5)

Варианты ответов:

а) вверх б) вниз

в) от нас г) к нам

д) по часовой стрелке

е) против часовой стрелки

ж) равна нулю или не действует

и) вправо

к) влево

Самостоятельная работа по теме: Магнитное поле.

Вариант 3.

Задание1 .

Вычислите индукцию магнитного поля, в котором на проводник длиной 0,3 м при токе 0,5 А действует максимальная сила 10 мН.
В однородном магнитном поле с индукцией 1 Тл протон (заряд протона 1,6 ·10^-19 Кл) движется со скоростью 10⁸ м/с перпендикулярно к линиям индукции. Определите силу, действующую на протон.

1 ) 2) 3) 5)

Варианты ответов:

а ) вверх б) вниз

в) от нас г) к нам

д) по часовой стрелке

е) против часовой стрелки

ж) равна нулю или не действует

и) вправо

к) влево

Самостоятельная работа по теме: Магнитное поле.

Вариант 4.

Какую работу выполняет однородное магнитное поле с индукцией 0,015 Тл при перемещении на расстояние 20 см проводника длиной 2 м, по которому течет ток 10 А? перемещение осуществляется в направлении действия сил. Проводник размещен под углом 30⁰ к направлению линий магнитной индукции.
Определите величину вектора магнитной индукции, если действующая на электрон (заряд электрона 1,6 ·10^-19 Кл) сила Лоренца равна 0,5 пН, а скорость движения электрона 10 Мм/с. Электрон движется перпендикулярно линиям магнитной индукции.

З адание 2. Определить как направлены: сила Ампера, сила Лоренца, вектор магнитной индукции в зависимости от варианта задания.

2) 3) 5)

Варианты ответов:

а) вверх б) вниз

в) от нас г) к нам

д) по часовой стрелке

е) против часовой стрелки

ж) равна нулю или не действует

и) вправо

к) влево

Самостоятельная работа по теме: Магнитное поле.

Вариант 5.

Задание 1.

Электрон(заряд электрона 1,6 ·10^-19 Кл) влетает в однородное магнитное поле с индукцией 0,0014 Тл в вакууме со скоростью 500 км/с перпендикулярно линиям магнитной индукции. Определите силу, действующую на электрон.
Определите величину силы Ампера, действующей на проводник в магнитном поле с индукцией0,1 Тл, сила тока в проводнике равна 20 А, а длина 4 см. Проводник расположен перпендикулярно линиям магнитного поля.

З адание 2. Определить как направлены: сила Ампера, сила Лоренца, вектор магнитной индукции в зависимости от варианта задания.

2) 3) 5)

Варианты ответов:

а) вверх б) вниз

в) от нас г) к нам

д) по часовой стрелке

е) против часовой стрелки

ж) равна нулю или не действует

и) вправо

к) влево

Самостоятельная работа по теме: Магнитное поле.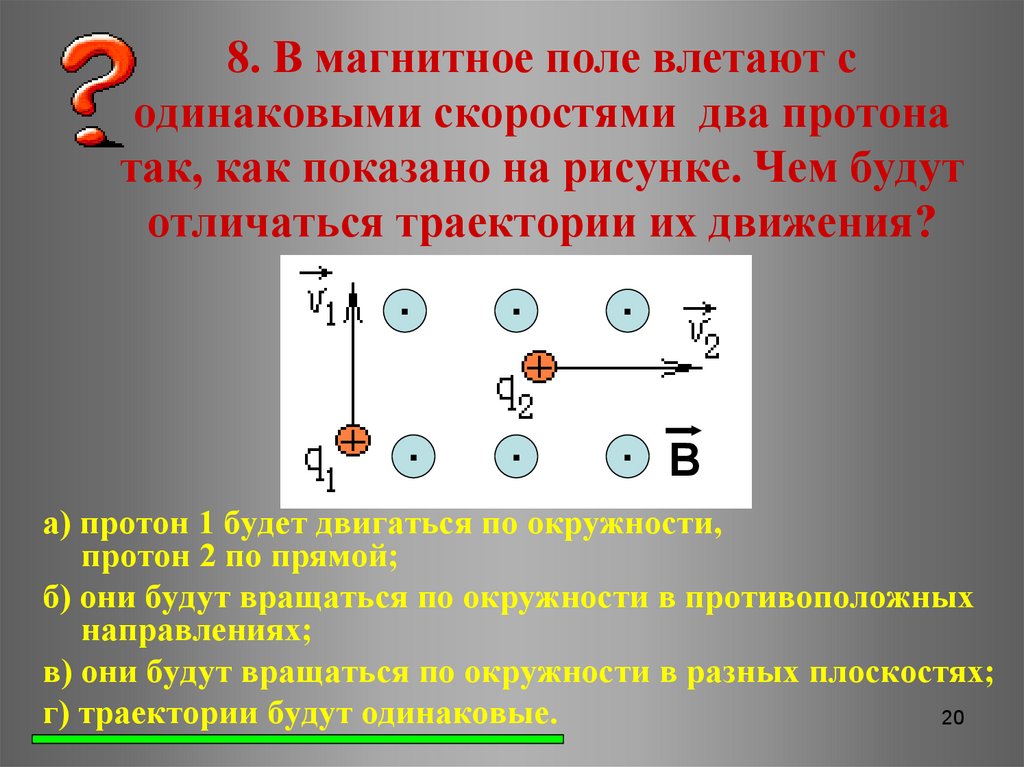 \circ\), \(h-?\)

Решение задачи:

Если электрон влетает в магнитное поле под некоторым углом \(\alpha\) к линиям индукции, то он будет совершать сложное движение, состоящее из:

равномерного прямолинейного движения со скоростью \(\upsilon \cdot \cos \alpha\) вдоль линий индукции магнитного поля;
равномерного движения по окружности со скоростью \(\upsilon \cdot \sin \alpha\) в плоскостях, перпендикулярных линиям индукции магнитного поля.

Два этих движения дают в сумме движение электрона по так называемой винтовой линии.

Искомый шаг винта \(h\) – это расстояние, которое пройдет электрон вдоль линий индукции магнитного поля за время, равное периоду вращения электрона \(T\). Поэтому:

\[h = \upsilon \cos \alpha \cdot T\;\;\;\;(1)\]

Зная скорость движения электрона по окружности, можно найти период вращения электрона \(T\) по формуле:

\[T = \frac{{2\pi R}}{{\upsilon \sin \alpha }}\;\;\;\;(2)\]

На электрон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:

\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(3)\]

Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость электрона, \(e\) – модуль заряда электрона, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции. { – 5}}\;м = 89,3\;мкм\]

Ответ: 89,3 мкм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.19 Протон движется в вакууме в однородном магнитном поле с индукцией 94,2 мкТл
8.2.21 Электрон, прошедший некоторую разность потенциалов, влетает в однородное магнитное
8.2.22 Если конденсатор с расстоянием между пластинами 1 см определенным образом

сила Лоренца

Магнитное поле действует на заряженную частицу с силой, перпендикулярной скорости частицы и направление магнитного поля. Сила Лоренца является векторным произведением и поэтому подчиняется правилу правой руки.

Простой двигатель может проиллюстрировать действие силы Лоренца. Можете ли вы объяснить, что заставляет это работать?
1.
В каком направлении будет действовать сила, действующая на движущийся, как показано, протон со стороны этого магнитного поля?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. из страницы
2. В каком направлении будет действовать сила на протоне, движущемся, как показано, этим магнитным полем?

A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. из страницы
3. В каком направлении будет действовать сила на электрон, движущийся, как показано, под действием этого магнитного поля?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. из страницы
4. В каком направлении будет действовать сила на протоне, движущемся, как показано, этим магнитным полем?
A. вверх
B. вниз
C. вправо
D. влево
E.

на страницу
F. наружу
5. Как будет направлена сила, действующая на протон движется, как показано, под действием этого магнитного поля?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. за пределы страницы
На заряженную частицу, движущуюся в плоскости, перпендикулярной магнитному полю, действует сила Лоренца. Сила Лоренца всегда перпендикулярна скорости, поэтому она постоянно отклоняет частицу в сторону.
Частица движется по окружности с постоянной скоростью. Сила направлена радиально внутрь.
Поскольку сила перпендикулярна скорости, мы можем просто записать силу как qvB и связать ее с центростремительной силой.

Это позволяет нам легко найти радиус кругового пути частицы и ее частоту.
Радиус и частота зависят от отношения q/m, которое является хорошим идентификатором для определенного типа частиц. Измерение радиуса или частоты частицы на циклотроне — мощный инструмент для изучения атомных и субатомных частиц.
Если скорость частицы также имеет составляющую, параллельную магнитному полю, она будет двигаться по спирали.

Посетите этот сайт для интерактивного моделирования трехмерного движения заряженных частиц в магнитном поле.
1. Какова скорость протона, движущегося по окружности радиусом 2,45 см в магнитном поле величиной 125 мТл?
Предположим, что плоскость окружности перпендикулярна магнитному полю.
Масса протона = 1,67 х 10 ^-27 кг, заряд протона = 1,60 х 10 ^-19 Кл.
Формулу для магнитной силы, действующей на длину l провода с током, легко вывести из закона Био-Савара используя скорость дрейфа по длине провода. Вектор длины имеет то же направление, что и положительное течение тока.

1. Каково направление суммарной магнитной силы, действующей на провод В от провода А?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. за пределы страницы
G. результирующая сила равна нулю 9.0 0 0 04 Как направлена результирующая магнитная сила, действующая на провод А от провода В?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. из страницы
G. результирующая сила равна нулю

3. Каково направление чистого крутящего момента на проводе A от провода B?
A. вверх
B. вниз
C. вправо
D. влево
E. на страницу
F. за пределы страницы
G. чистый крутящий момент равен нулю Рассмотрим два длинных параллельных провода, по которым течет ток, как показано на рисунке. В какой точке или точках на оси x магнитное поле равно нулю?
« Предыдущий
1
2
3
4

5
6
» Следующий
Lorentz Force Calculator
, созданный Miłosz Panfil, PhD
, рассмотрено Bogna Szyk и Steven Wooding
приложения
Часто задаваемые вопросы
Вы можете использовать этот Калькулятор силы Лоренца для расчета влияния магнитного поля на заряженные частицы. Читая текст, вы узнаете о законе силы Лоренца, соответствующем уравнении силы Лоренца и о применении силы Лоренца в повседневной жизни.
Закон силы Лоренца
Сила Лоренца является общим эффектом электрических и магнитных полей, действующих на заряженную частицу. Мы сосредоточимся здесь только на магнитной части силы. Для электрической части вы можете проверить наш калькулятор закона Кулона.
Закон силы Лоренца гласит, что магнитное поле действует на движущуюся заряженную частицу . Величина силы зависит от заряда, скорости и напряженности магнитного поля.
Что немного особенного, так это то, что направление силы не совпадает ни с траекторией движения частицы, ни с направлением магнитного поля. Направление силы Лоренца перпендикулярно как направлению частицы, так и магнитному полю. В результате траектория частицы изгибается в магнитном поле .
Также сила Лоренца равна нулю, если частица движется точно вдоль линий магнитного поля. Как мы можем записать эти наблюдения в математической форме? Это уравнение силы Лоренца.
Уравнение силы Лоренца
Уравнение силы Лоренца:
F=qvBsin⁡(α)\small F = qvB\sin(\alpha)F=qvBsin(α)
где:
qqq – заряд частицы;
vvv – скорость частицы;
ВВВ – напряженность магнитного поля;
ααα – Угол между направлением траектории частицы и направлением магнитного поля; и
FFF – Результирующая сила.
В нашем калькуляторе силы Лоренца мы устанавливаем угол α = 90° для простоты. Если вы хотите изменить его, перейдите в расширенный режим
. Вы можете видеть, что сила максимальна для этого угла, и если мы положим α = 0° , она также будет равна 0.
Применение силы Лоренца
Сила Лоренца находит применение во многих областях. В науке он используется для ускорения частиц в циклотронах в поисках фундаментальных законов физики элементарных частиц. Он также используется в масс-спектрометрах, позволяющих идентифицировать атомы и молекулы.
Практическое ежедневное применение включает в себя электродвигатели, громкоговорители и, что менее распространено среди обычных домашних хозяйств, рельсотроны.
Часто задаваемые вопросы
Как рассчитать силу Лоренца?
Чтобы вычислить силу Лоренца, выполните следующие простые шаги:
Измерьте заряд частицы q в кулонах.
Измерьте напряженность магнитного поля B в теслах.
Найти скорость частицы v в метрах в секунду.
Вычислите угол α между траекторией частицы и магнитным полем.
Умножьте эти значения на формулу, чтобы получить силу Лоренца:
F= q × v × B × sin(α) .
Как найти направление отклонения под действием силы Лоренца?
Направление отклонения под действием силы Лоренца зависит от относительного угла между траекторией частицы и направлением магнитного поля, в котором движется частица.
Для положительно заряженной частицы :
Совместите большой палец правой руки со скоростью частицы.
Совместите правый указательный палец с магнитным полем.
Вытягивание правого среднего пальца перпендикулярно плоскости, созданной другим, дает направление силы Лоренца.

При работе с отрицательными частицами измените направление силы.
Какова сила Лоренца, действующая на электрон, движущийся в поле 0,5 Тл при 0,1 c?
Сила 2.402e-12 N . Чтобы найти этот результат, используйте следующие данные:
q = 1×e = 1,602e-19 C .
Б = 0,5 Т .
v = 0,1 c = 2,998e7 м/с
Предположим, что α = 90° . Используйте формулу для силы Лоренца:
F = q × v × B × sin(90°)
F = 1,602e-19 C × 0,5 T × 2,998e7 м/с
F = 2,402e- 12 N .