Площадь многоугольника
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2016-11-10
Площадь многоугольника. Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:
Как выводится эта формула? Просто!
Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:
Используя формулу площади треугольника можем записать:
Вынесем общие множители:
Уверен, сам принцип вам понятен.
*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:
*Дополнительная информация!
Известна формула радиуса окружности вписанной в треугольник
Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):
27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Вычисляем:
Ответ: 30
Ещё пара задач с многоугольниками.
27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 540. Найдите n.
Если угол между радиусом окружности и стороной многоугольника равен 540, то угол между сторонами многоугольника будет равен 1080. Тут необходимо вспомнить формулу угла правильного многоугольника:
Остаётся подставить в формулу значение угла и вычислить n:
Ответ: 5
27595. Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.
Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k2 раз. *Свойство подобия фигур.
*Свойство подобия фигур.
Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)2 раза. Таким образом, площадь большего многоугольника равна:
Ответ: 343
27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Посмотреть решение
27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Посмотреть решение
27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50
Всего доброго! Учитесь с удовольствием!
С уважением, Александр.
Категория: Площади фигур | ЕГЭ-№1Формулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Онлайн калькулятор: Площадь многоугольника
УчебаМатематикаГеометрия
Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники
Пример многоугольникаДанный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры.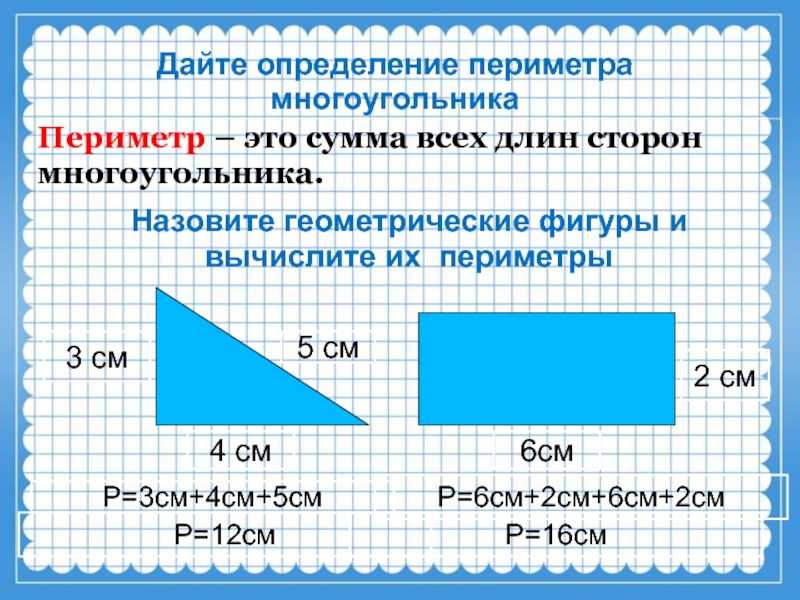 Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площадь многоугольника
Стороны и диагонали
| Название стороны или диагонали | Длина | ||
|---|---|---|---|
51020501001000
Стороны и диагонали
Название стороны или диагонали
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5
Загрузить данные из csv файла
Точность вычисления
Знаков после запятой: 2
Площадь
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ошибка
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Расчет площади треугольника по формуле Герона
- • Площадь треугольника по координатам вершин
- • Площадь правильного многоугольника
- • Длина стороны правильного многоугольника
- • Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
- • Раздел: Геометрия ( 96 калькуляторов )
Геометрия Математика многоугольник площадь треугольник формула Герона
PLANETCALC, Площадь многоугольника
Timur2020-11-03 14:19:28
Площадь и периметр многоугольников
Существуют различные типы многоугольников, для которых нет единой формулы для определения площади и периметра. На самом деле, для каждого типа многоугольника существует своя формула. Именно поэтому в этом ресурсе мы охватим площади и периметры часто используемых полигонов.
Периметр
Часто студенты спрашивают что такое периметр ? Это вычисление длины границы любой формы . Лучший способ научиться легко находить периметр — сложить все внешние стороны фигуры. Полигон не является исключением. Короче говоря, периметр многоугольника равен сумме длины его сторон .
Лучший способ научиться легко находить периметр — сложить все внешние стороны фигуры. Полигон не является исключением. Короче говоря, периметр многоугольника равен сумме длины его сторон .
Лучшие репетиторы по математике
Поехали
Площадь
Найти периметр проще, но найти площадь немного сложнее. Площадь — это область, которую занимает фигура. Нет простого способа найти площадь, вам нужно будет запомнить некоторые формулы для нахождения площади. Но вопрос в том, что такое площадь многоугольника? площадь многоугольника является мерой области, ограниченной сторонами многоугольника.
Периметр треугольника
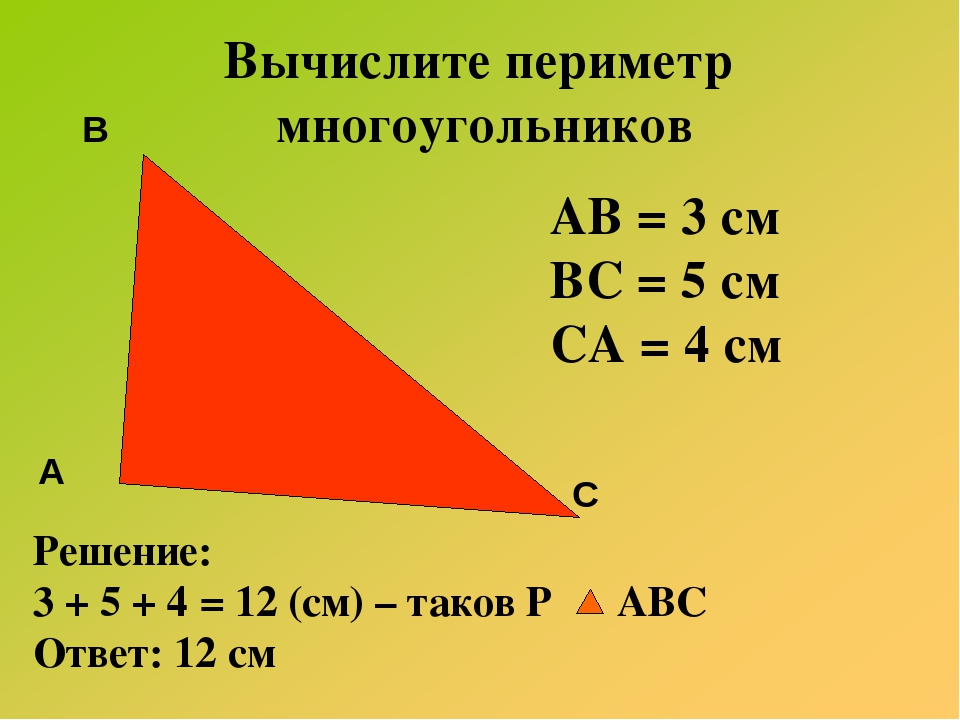
Давайте начнем с чего-то, чего вы будете много раз в жизни, и да, это треугольник. Вычислить периметр треугольника очень просто. Все, что вам нужно сделать, это добавить все длины сторон. В треугольнике три стороны, а это значит, что вам нужно сложить все три стороны, чтобы найти периметр. Это основная концепция периметра треугольника, но треугольник также имеет три типа. Означает ли это, что у каждого треугольника будет свой способ нахождения периметра? Точно нет! Концепция останется той же, что и добавление трех сторон. Давайте посмотрим на это.
Это основная концепция периметра треугольника, но треугольник также имеет три типа. Означает ли это, что у каждого треугольника будет свой способ нахождения периметра? Точно нет! Концепция останется той же, что и добавление трех сторон. Давайте посмотрим на это.
| Equilateral Triangle | Isosceles Triangle | Scalene Triangle |
Above is a comparison of all three triangles с их формулами периметра. У разностороннего треугольника все стороны разные, следовательно, формула остается той же, однако с равносторонними и равнобедренными треугольниками что-то другое? Ничего не изменилось, концепция та же, но с изюминкой. В равнобедренном треугольнике две стороны равны, допустим одна сторона равна «л» . Значит будем иметь, так как основание равнобедренного треугольника всегда разное. Общее уравнение будет таким, потому что добавляются обе длины. Тот же случай с равносторонним треугольником, все три стороны равны и если одна сторона равна «l» , то их сумма будет равна .
Общее уравнение будет таким, потому что добавляются обе длины. Тот же случай с равносторонним треугольником, все три стороны равны и если одна сторона равна «l» , то их сумма будет равна .
Площадь треугольника
Независимо от того, работаете ли вы с равнобедренным или разносторонним треугольником, вам потребуется только одна формула, которая может вычислить площадь треугольника. Короче говоря, эту формулу можно использовать для нахождения площади любого треугольника, с которым вы работаете. Эта формула действительна только для треугольников, вы не можете использовать ее для других многоугольников. Если у многоугольника три стороны, то площадь этого многоугольника будет:
Площадь треугольника равна половине произведения основания и высоты.
Пример
Найдите площадь и периметр следующего треугольника:
Площадь и периметр квадрата является самым простым из многоугольников
5 90.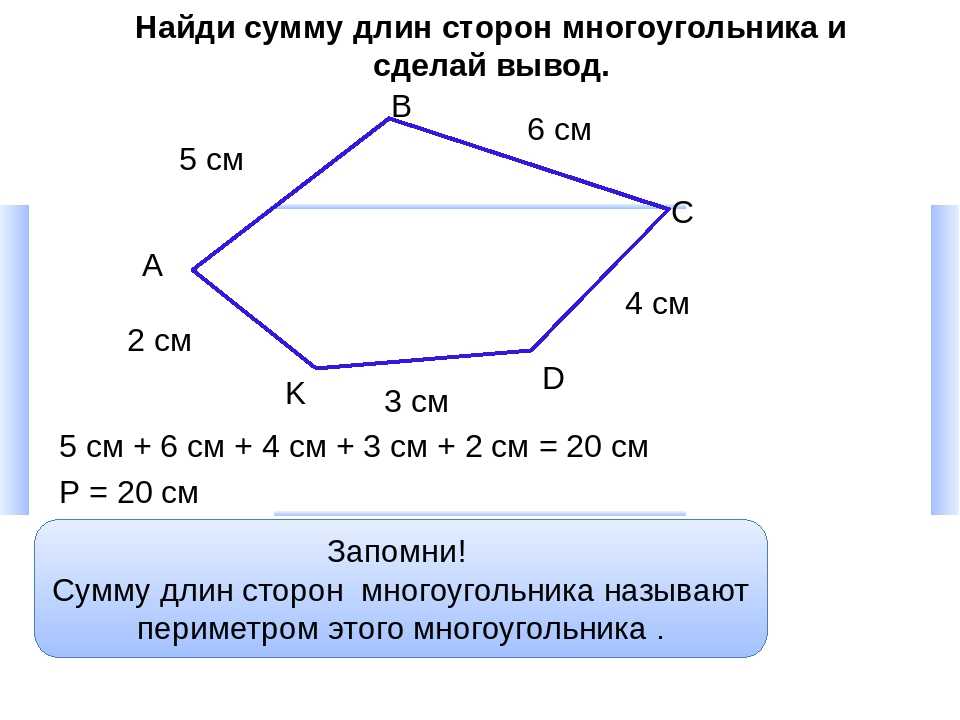 Все стороны равны, и этот многоугольник имеет четыре стороны. Вершины имеют угол . Возможно, вы уже догадались о периметре, да, он равен, потому что все стороны равны, а поскольку у квадрата четыре стороны, поэтому он будет равен . Чтобы найти площадь многоугольника с 4 сторонами, вам нужно умножить длину этого многоугольника на ширину (ширину) многоугольника. Поскольку все стороны равны, длина ( «l» ) умножить на ширину ( «l» ), следовательно:
Все стороны равны, и этот многоугольник имеет четыре стороны. Вершины имеют угол . Возможно, вы уже догадались о периметре, да, он равен, потому что все стороны равны, а поскольку у квадрата четыре стороны, поэтому он будет равен . Чтобы найти площадь многоугольника с 4 сторонами, вам нужно умножить длину этого многоугольника на ширину (ширину) многоугольника. Поскольку все стороны равны, длина ( «l» ) умножить на ширину ( «l» ), следовательно:
Все, что вам нужно, это длина любой стороны квадрата, чтобы найти площадь и периметр квадрата.
Пример
Вычислите площадь и периметр квадрата со сторонами.
Площадь и периметр прямоугольника
Не всегда длина и ширина четырехстороннего многоугольника будут одинаковыми. Если длина и ширина четырехстороннего многоугольника различны, значит, вы имеете дело с прямоугольником. Однако понятие периметра и площади будет одинаковым для четырехстороннего многоугольника.
Пример
Вычислите площадь и периметр прямоугольника с основанием и высотой .
Ромб
Ромб — еще один четырехугольник, но с другими свойствами. Понятие периметра и площади будет одинаковым для ромба. Чтобы найти периметр, нам нужно сложить все четыре стороны ромба. Поскольку все стороны ромба равны, они все складываются, и самый простой способ найти периметр ромба — умножить длину одной из его сторон на четыре. Тем не менее, найти район может быть немного сложно. У ромба две диагонали, одна большая диагональ, а другая короткая. Площадь ромба будет равна половине произведения обеих диагоналей.
Пример
Вычислите площадь и периметр ромба, диагонали которого равны и , а его стороны равны .
Площадь и периметр ромба
Ромб может выглядеть как ромб, но это не так. Возможно, вы не знакомы с названием ромбоид, он также известен как параллелограмм. У ромба две противоположные стороны параллельны друг другу. Периметр будет суммой всех четырех сторон. Поскольку у ромба противоположные стороны равны, вы можете сложить длину и ширину, а затем умножить их на два. Площадь ромбоида равна произведению ширины и высоты ромбоида.
У ромба две противоположные стороны параллельны друг другу. Периметр будет суммой всех четырех сторон. Поскольку у ромба противоположные стороны равны, вы можете сложить длину и ширину, а затем умножить их на два. Площадь ромбоида равна произведению ширины и высоты ромбоида.
Пример
Вычислите площадь и периметр ромбовидной фигуры с 4 сторонами по 4,5 см и высотой 4 см.
Площадь и периметр трапеции
Трапеция (также известная как «Трапеция», состоящая из пяти сторон многоугольника ). Уникальность этого многоугольника в том, что он имеет две параллельные стороны. Это делает трапецию уникальной среди всех других пятисторонних многоугольников. Площадь трапеции равна половине произведения высоты на сумму параллельных сторон. Периметр этой фигуры очень прост, достаточно сложить все граничные длины трапеции.
Пример
Рассчитайте область и периметр следующего трапеции:
и периметр из регулярного полига
.
 его стороны равны по длине. Обычно у многоугольников не все стороны равны, однако в случае правильного многоугольника все стороны должны быть равны. Поскольку все стороны равны, это означает, что все углы также будут равны. Чтобы найти периметр любого правильного многоугольника, достаточно умножить количество сторон на длину одной стороны. Однако найти площадь правильного многоугольника довольно сложно. Площадь будет равна половине произведения периметра и апофемы. Апофема — это расстояние от центра многоугольника до середины любой стороны правильного многоугольника.
его стороны равны по длине. Обычно у многоугольников не все стороны равны, однако в случае правильного многоугольника все стороны должны быть равны. Поскольку все стороны равны, это означает, что все углы также будут равны. Чтобы найти периметр любого правильного многоугольника, достаточно умножить количество сторон на длину одной стороны. Однако найти площадь правильного многоугольника довольно сложно. Площадь будет равна половине произведения периметра и апофемы. Апофема — это расстояние от центра многоугольника до середины любой стороны правильного многоугольника.где n — количество сторон.
Примеры
Вычислите площадь и периметр правильного пятиугольника со сторонами .
. Применив теорему Pythagorean для одной из треугольников, мы получаем:
Рассчитают Расчет области. круг радиуса.
Площадь многоугольника не имеет определенной формы
9000. Если фигура удовлетворяет всем условиям, мы будем называть ее многоугольником. Рассмотрим приведенную выше геометрию. Он выглядит по-другому, но мы можем разбить его на четыре разных треугольника, а поскольку треугольник — это многоугольник, то фигура выше также является многоугольником. Чтобы найти площадь вышеуказанной геометрии, вам нужно разбить фигуру, а затем вычислить площадь сломанных частей. Площадь получается путем триангуляции многоугольника и добавления площади этих треугольников.
Если фигура удовлетворяет всем условиям, мы будем называть ее многоугольником. Рассмотрим приведенную выше геометрию. Он выглядит по-другому, но мы можем разбить его на четыре разных треугольника, а поскольку треугольник — это многоугольник, то фигура выше также является многоугольником. Чтобы найти площадь вышеуказанной геометрии, вам нужно разбить фигуру, а затем вычислить площадь сломанных частей. Площадь получается путем триангуляции многоугольника и добавления площади этих треугольников.
Вычислите площадь следующего многоугольника:
Вышеприведенная геометрия может быть разбита на две фигуры, одна из которых представляет собой треугольник, а другая — ромбоид. Чтобы найти периметр, просто сложите все длины границ.
Площадь многоугольников – Формула, Примеры площади правильных многоугольников
Площадь многоугольника определяется как площадь, заключенная в него. Другими словами, мы говорим, что область, занимаемая любым многоугольником, дает его площадь. В этом уроке мы научимся определять площадь многоугольников и детально находить разницу между периметром и площадью многоугольников.
В этом уроке мы научимся определять площадь многоугольников и детально находить разницу между периметром и площадью многоугольников.
| 1. | Какова площадь многоугольника? |
| 2. | Разница между периметром и площадью полигонов |
| 3. | Формулы площади многоугольника |
| 4. | Площадь полигонов с координатами |
| 5. | Часто задаваемые вопросы о площади полигонов |
Какова площадь многоугольника?
Определение площади многоугольника — это мера площади, заключенной в него. Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.
Разница между периметром и площадью полигонов
Периметр и площадь многоугольников являются измеримыми величинами, которые зависят от длины сторон многоугольника. Чтобы различать их обоих, необходимо понять основную разницу между периметром и площадью. Обратите внимание на приведенную ниже таблицу, чтобы лучше понять эту разницу.
| Критерии отличия | Периметр многоугольника | Площадь полигона |
|---|---|---|
| Определение | Определяется как общая длина границы многоугольника, которую можно получить, сложив длины всех его сторон. | Определяется как область или пространство, окруженное любым многоугольником. |
| Формула | Периметр многоугольника = длина стороны 1 + длина стороны 2 + …+ длина стороны N (для N-стороннего многоугольника) | Площадь многоугольников можно найти по разным формулам в зависимости от того, является ли многоугольник правильным или неправильным. |
| Блок | Единица измерения периметра многоугольника выражается в метрах, сантиметрах, дюймах, футах и т. д. | Единица площади многоугольников выражается в (метрах) 2 , (сантиметрах) 2 , (дюймах) 2 , (футах) 2 и т. д. |
Сходство между вычислением периметра и площади многоугольника заключается в том, что оба они зависят от длины сторон формы, а не от внутренних или внешних углов многоугольника.
Формулы площади многоугольника
Многоугольник может быть классифицирован как правильный или неправильный многоугольник в зависимости от длины его сторон. Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как:
- Площадь треугольника = (1/2) × основание × высота
Мы также можем найти площадь треугольника, если известна длина его сторон, используя формулу Герона, которая выглядит следующим образом: Площадь = \(\sqrt{s(s-a)(s-b)(s-c)}\), где s = периметр/ 2 = (a + b + c)/2, a, b и c — длины его сторон.
- Площадь прямоугольника = длина × ширина
- Площадь параллелограмма = основание × высота
- Площадь трапеции = (1/2) × (сумма длин ее параллельных сторон или оснований) × высота
- Площадь ромба = (1/2) × (произведение диагоналей)
Чтобы вычислить площадь многоугольника, необходимо сначала узнать, является ли данный многоугольник правильным или неправильным многоугольником.
Площадь правильных многоугольников
Правильный многоугольник — это многоугольник с равными сторонами и равными углами. Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников:
| Названия правильных многоугольников | Площадь правильного многоугольника |
|---|---|
| Равносторонний треугольник | |
| Квадрат | Площадь = (длина) 2 |
| Обычный пятиугольник | Площадь = 5/2 × длина стороны × длина апофемы 92\) |
| Правильный шестигранник | Площадь = [3√3 ×(длина стороны) 2 ]/2 |
Для определения площади правильного многоугольника, если известно число его сторон, дается формула:
- Площадь правильного многоугольника = (число сторон × длина одной стороны × апофема)/2 , где длина апофемы задается как \(\dfrac{l}{2\tan(\dfrac{180}{n})}\), где l — длина стороны, а n — количество сторон правильный многоугольник.

⇒ A = 84,3 квадратных дюймаТаким образом, площадь правильного пятиугольника равна 84,3 квадратных дюйма.
Площадь неправильных многоугольников
Неправильный многоугольник представляет собой плоскую замкнутую форму, не имеющую равных сторон и равных углов. Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей. Рассмотрим пример, приведенный ниже.
Многоугольник ABCD является неправильным многоугольником. Таким образом, мы можем разделить многоугольник ABCD на два треугольника ABC и ADC. Площадь треугольника можно получить: 92 }\)
- Шаг 2: Зная размеры многоугольников, определите, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 3: Если многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как (длина одной стороны )/(2 ×(tan(180°/количество сторон))).
 2}\) = 2 единицы 92}\) = 2 единицы
2}\) = 2 единицы 92}\) = 2 единицыТеперь, когда мы знаем, что длина всех сторон данного многоугольника одинакова, это показывает, что это квадрат. Таким образом, площадь многоугольника ABCD определяется как A = (длина)
Следовательно, площадь многоугольника с координатами (0,0), (0, 2), (2, 2) и (2, 0) равна 4 квадратным единицам.
Важные примечания
- Если известна длина одной стороны, можно найти площадь правильного многоугольника, найдя апофему.
- Апофема падает на середину стороны под прямым углом, разделяя ее на две равные части.
- Равносторонний треугольник — это правильный многоугольник с 3 сторонами, а квадрат — правильный многоугольник с 4 сторонами. Следовательно, они не имеют обычного префикса перед именем формы.
Часто задаваемые вопросы о площади полигонов
Что такое определение площади многоугольника?
Пространство, ограниченное любым многоугольником на двумерной плоскости, определяется как площадь многоугольника.
 Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).Как найти площадь многоугольника?
Площадь многоугольника можно рассчитать, поняв, является ли данный многоугольник правильным или неправильным многоугольником. Шаги для вычисления площади многоугольников:
- Шаг 1: Определите, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 2: Если это правильный многоугольник или имеет стандартную формулу расчета, используйте ее для определения значения при всех заданных размерах многоугольника, в противном случае площадь многоугольника можно вычислить, разделив его на множество правильные многоугольники, площадь которых можно сложить, чтобы получить площадь требуемого многоугольника.
Какова площадь многоугольника с n сторонами?
Если задано количество сторон многоугольника, площадь многоугольника можно рассчитать по формуле Площадь = [(L 2 n)/4 tan(180/n)]; где L — длина его стороны, а «n» — количество сторон многоугольника.

В чем разница между периметром и площадью многоугольников?
Периметр многоугольника — это общая длина его границы, тогда как площадь многоугольника — это занимаемая им область. Периметр многоугольника получается путем сложения длин всех его сторон, а площадь многоугольника получается с помощью требуемой формулы в зависимости от того, является ли данный многоугольник правильным многоугольником или нет. Единица периметра многоугольника всегда дается в линейных единицах, поскольку она одномерна, в то время как единица площади многоугольника всегда дается в квадратных единицах, поскольку площадь является двумерным понятием. 92 }\)
- Шаг 2: Как только нам известны размеры многоугольников, мы определяем, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 3: Если вывод из шага 2 показывает, что многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как , Апофема = [(длина одной стороны)/{2 ×(tan(180/количество сторон))}].
 С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
Как найти площадь правильного многоугольника?
Площадь правильного многоугольника можно найти по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2. Соблюдайте следующие шаги для всей процедуры:
- Шаг 1: Найдите количество сторон многоугольника.
- Шаг 2: Если для заданного правильного многоугольника существует стандартная формула, примените ее. Если нет, обратитесь к шагам, приведенным ниже.
- Шаг 3: Проверьте измерение длины одной стороны.
- Шаг 4: Используйте значения, полученные на шагах 1 и 2, для определения значения апофемы по формуле Апофема = [(длина одной стороны)/{2 ×(тангенс(180/количество сторон))}].
- Шаг 5: Теперь найдите площадь правильного многоугольника по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2.




 2}\) = 2 единицы 92}\) = 2 единицы
2}\) = 2 единицы 92}\) = 2 единицы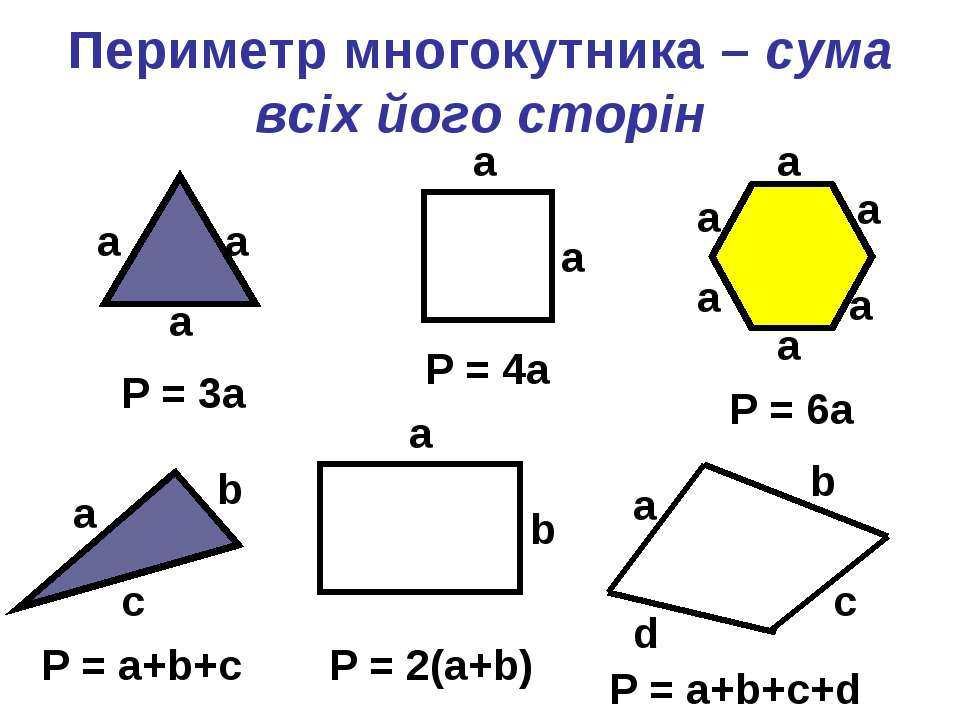 Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
 С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
Leave A Comment