Задание №10 ОГЭ математика 2021

#9 класс #Алгебра #Математика #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование

Задание №10

Задача №1 В фирме такси в данный момент свободно 25 машин: 3 черные, 7 желтых и 15 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

Задача №1 В фирме такси в данный момент свободно 25 машин: 3 черные, 7 желтых и 15 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. Решение: Ответ: 0,28.

Задача №2 В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием.

Найдите вероятность того, что первым будет стартовать спортсмен не из России.

Задача №2 В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России. Решение: 13 + 2 + 5 = 20 ( спортсменов) – всего

Задача №2 В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России. Решение: 13 + 2 + 5 = 20 ( спортсменов) – всего 2 + 5 = 7 ( спортсменов) – не из России

Задача №2 В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России. Решение: 13 + 2 + 5 = 20 ( спортсменов) – всего 2 + 5 = 7 ( спортсменов) – не из России Ответ: 0,35. – вероятность того, что не из России

Задача №3 На экзамене 25 билетов. Арсений не выучил 4 из них. Найдите вероятность того, что Арсению попадется выученный билет.

Задача №3 На экзамене 25 билетов. Арсений не выучил 4 из них. Найдите вероятность того, что Арсению попадется выученный билет. Решение: 25 – 4 = 21 (билет) – выучил Арсений

Задача №3 На экзамене 25 билетов. Арсений не выучил 4 из них. Найдите вероятность того, что Арсению попадется выученный билет. Решение: 25 – 4 = 21 (билет) – выучил Арсений Ответ: 0,84. – вероятность того, что попадется выученный билет

Задача №4 На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 8 с рисом и 25 с повидлом. Сергей наугад берет один пирожок. Найдите вероятность того, что пирожок окажется с повидлом.

Задача №4 На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 8 с рисом и 25 с повидлом. Сергей наугад берет один пирожок. Найдите вероятность того, что пирожок окажется с повидлом. Решение: 7 + 8+ 25 = 40( пирожков) – всего на тарелке

Задача №4 На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 8 с рисом и 25 с повидлом. Сергей наугад берет один пирожок. Найдите вероятность того, что пирожок окажется с повидлом. Решение: Ответ: 0,625. 7 + 8+ 25 = 40( пирожков) – всего на тарелке – вероятность того, что с повидлом

Задача №5 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,08. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

.

Задача №5 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,08. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо. . Решение: Ответ: 0,92. 1 – 0,08 = 0,92 – вероятность того, что ручка пишет хорошо

Задача №6 В среднем из 150 карманных фонариков, поступивших в продажу, девять неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен..

Задача №6 В среднем из 150 карманных фонариков, поступивших в продажу, девять неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.. Решение: 150 – 9 = 141( фонарик) – окажется исправен

Задача №6 В среднем из 150 карманных фонариков, поступивших в продажу, девять неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен. . Решение: Ответ: 0,94. 150 – 9 = 141( фонарик) – окажется исправен – вероятность того, что фонарик окажется исправен

Задача №7 Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что жребий начинать игру Кате не выпадет.

Задача №7 Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что жребий начинать игру Кате не выпадет. Решение: Ответ: 0,8. 5 – 1 = 4 – не выпадет – вероятность того, что Кате жребий начинать игру не выпадет

Задача №8 В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно 3 раза.

Задача №8 В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно 3 раза.

Решение: Ответ: 0,125. – вероятность того, что орел выпадет 3 раза ООО РРР ООР РРО РОО ОРР ОРО РОР

Задача №9 Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 7 или 10.

Задача №9 Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 7 или 10. Решение: Ответ: 0,25. – вероятность того, что сумма 7 или 10 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66

Задача №10 Стрелок 3 раза стреляет по мишеням.

Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что стрелок первый раз попал в мишень, а последние два раза промахнулся.

Задача №10 Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что стрелок первый раз попал в мишень, а последние два раза промахнулся. Решение: Ответ: 0,096. 1 – 0,6 = 0,4 – вероятность промаха при одном выстреле

Задача №11 На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача по теме «Площадь», равна 0,15, а по теме «Окружность» равна 0,3. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.

Задача №11 На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача по теме «Площадь», равна 0,15, а по теме «Окружность» равна 0,3.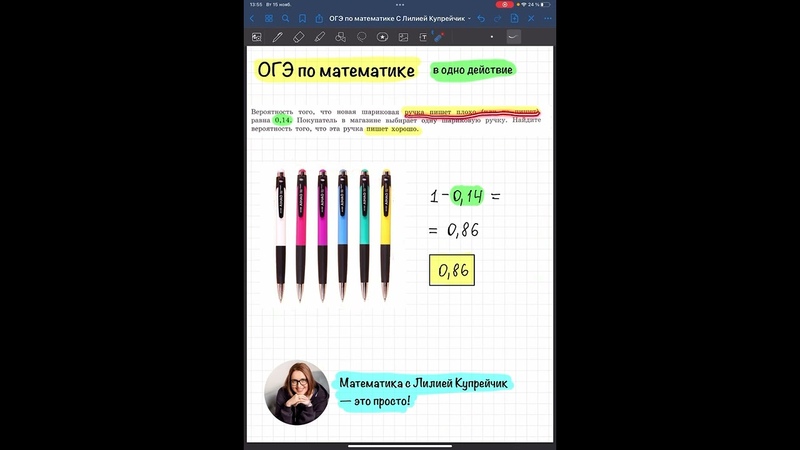 Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем. Решение: Ответ: 0,45. 0,15 + 0,3 = 0,45 – вероятность того, что достанется задача по одной из двух тем

Задача №12 Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.

Задача №12 Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. Решение: Ответ: 0,85. 20 – 3 = 17(каналов) – комедия не идет – вероятность того, что комедия не идет

Задача №13 В магазине канцтоваров продается 144 ручки: 30 красных, 24 зеленых, 18 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или черной.

Задача №13 В магазине канцтоваров продается 144 ручки: 30 красных, 24 зеленых, 18 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или черной. Решение: 144 – ( 30 + 24 + 18) = 144 – 72 = 72 ( ручек) – синие и черные

Задача №13 В магазине канцтоваров продается 144 ручки: 30 красных, 24 зеленых, 18 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или черной. Решение: Ответ: 0,5. 144 – ( 30 + 24 + 18) = 144 – 72 = 72 ( ручек) – синие и черные – вероятность того, что ручка будет синей или черной

Задача №14 На олимпиаде по химии 400 участников рассаживали по трем аудиториям. В первых двух посадили по 110 человек, оставшихся проводили в запасную аудиторию. Найдите вероятность того, что случайно выбранный участник попал в запасную аудиторию.

Задача №14 На олимпиаде по химии 400 участников рассаживали по трем аудиториям. В первых двух посадили по 110 человек, оставшихся проводили в запасную аудиторию. Найдите вероятность того, что случайно выбранный участник попал в запасную аудиторию. Решение: 400 – ( 110 + 110) = 400 – 220 = 180 ( участников) – в запасной аудитории

Задача №14 На олимпиаде по химии 400 участников рассаживали по трем аудиториям. В первых двух посадили по 110 человек, оставшихся проводили в запасную аудиторию. Найдите вероятность того, что случайно выбранный участник попал в запасную аудиторию. Решение: Ответ: 0,45. 400 – ( 110 + 110) = 400 – 220 = 180 ( участников) – в запасной аудитории – вероятность того, что участник попал в запасную аудиторию

Задача №15 На птицеферме есть только куры и гуси, причем кур в 19 раз больше, чем гусей. Найдите вероятность того, что случайно выбранная птица на этой ферме окажется гусем.

Задача №15 На птицеферме есть только куры и гуси, причем кур в 19 раз больше, чем гусей. Найдите вероятность того, что случайно выбранная птица на этой ферме окажется гусем. Решение: Ответ: 0,05. 19 + 1 = 20 ( частей) – всего – вероятность того, что выбранная птица окажется гусем

Задача №16 На семинар приехали 5 ученых из Норвегии, 6 из России и 9 из Испании. Каждый ученый подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад ученого из России.

Задача №16 На семинар приехали 5 ученых из Норвегии, 6 из России и 9 из Испании. Каждый ученый подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад ученого из России. Решение: 5 + 6 + 9 = 20 ( ученых) – всего Ответ: 0,3. – вероятность того, что восьмым окажется доклад ученого из России

Задача №17 Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 71 спортсмен, среди которых 22 спортсмена из России, в том числе Петров. Найдите вероятность того, что в первом туре Петров будет играть с каким-нибудь спортсменом из России.

Задача №17 Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 71 спортсмен, среди которых 22 спортсмена из России, в том числе Петров. Найдите вероятность того, что в первом туре Петров будет играть с каким-нибудь спортсменом из России. Решение: 71 – 1 = 70 ( участников) – всех без Петрова

Задача №17 Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 71 спортсмен, среди которых 22 спортсмена из России, в том числе Петров. Найдите вероятность того, что в первом туре Петров будет играть с каким-нибудь спортсменом из России. Решение: 71 – 1 = 70 ( участников) – всех без Петрова 22 – 1 = 21 ( участник) – из России без Петрова

Задача №17 Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 71 спортсмен, среди которых 22 спортсмена из России, в том числе Петров. Найдите вероятность того, что в первом туре Петров будет играть с каким-нибудь спортсменом из России. Решение: 71 – 1 = 70 ( участников) – всех без Петрова Ответ: 0,3. 22 – 1 = 21 ( участник) – из России без Петрова

Задача №18 Вероятность того, что новый фен прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,86. Найдите вероятность того, что фен прослужит меньше двух лет, но больше года.

Задача №18 Вероятность того, что новый фен прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,86. Найдите вероятность того, что фен прослужит меньше двух лет, но больше года. Решение: 0,98 – 0,86 = 0,12 – вероятность того, что фен прослужит меньше двух лет, но больше года Ответ: 0,12.

Задача №19 В группе туристов 8 человек. С помощью жребия они выбирают трех человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Давыдов, входящий в состав группы, пойдет в магазин?

Задача №19 В группе туристов 8 человек. С помощью жребия они выбирают трех человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Давыдов, входящий в состав группы, пойдет в магазин? Решение: Ответ: 0,375. – вероятность того, что Давыдов пойдет в магазин

Задача №20 В магазине канцтоваров продается 100 ручек: 37 красных, 8 зеленых, 17 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.

Задача №20 В магазине канцтоваров продается 100 ручек: 37 красных, 8 зеленых, 17 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной. Решение: 100 – ( 37 + 8 + 17) = 100 – 62 = 38 ( ручек) – вместе синие и черные

Задача №20 В магазине канцтоваров продается 100 ручек: 37 красных, 8 зеленых, 17 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной. Решение: 100 – ( 37 + 8 + 17) = 100 – 62 = 38 ( ручек) – вместе синие и черные 38 : 2 = 19( ручек) – черного цвета, синего цвета отдельно

Теория вероятностей для сдачи ОГЭ и ЕГЭ

Справится с задачей по теории вероятности можно запросто, если знаешь формулу нахождения вероятности и если повезет с задачей. Пока практика показывает, что на экзамене даются задачи проще, чем на пробнике. 

К таким простым задачам будем относить задачи из разряда «на тарелке лежат столько-то пирожков, найти вероятность, что попадется пирожок с вишней», с кубиками/монетками и задачки на подобие «найти вероятность того, что ручка не пишет, если вероятность того, что она пишет равна 0,6».

Все остальные типы задач будем считать сложными, т.к. не каждый сможет к ним подступиться без определенных знаний.

Начнем разбор задач с формулы нахождения вероятности:

P=m:n, где P – вероятность какого-либо события, m – благоприятные события (то, что нас спрашивают в вопросе), n – всевозможные события.

Разберемся с поиском благоприятных событий на примере.

#1.

Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А=«сумма очков равна 10»?

Задаем себе вопрос: в каких случаях сумма очков будет равна 10?

  1 кубик 2 кубик
1 4 6
2 5 5
3 6 4

Это и есть все благоприятные события. Итого, их 3.

Ответ: 3.

Ну и теперь рассмотрим несколько простейших задач.

Простейшие задачи на нахождение вероятности.

#2.

На тарелке лежат 15 пирожков. Из них 4 с вишней, 5 с яблоком, остальные с абрикосом. Вова наугад берет пирожок. Найдите вероятность того, что ему попадется пирожок с абрикосом.

Благоприятные события – это пирожки с абрикосом. Их в тарелке 15-4-5=6.

Всевозможные события – это все пирожки. Их 15.

Вероятность=Благоприятные : Всевозможные, т.е.

P=6:15=0,4.

!!! Обратите внимание на то, что вероятность не может быть больше 1! Это связано с тем, что 100%-ая вероятность равна 1.

Ответ: 0,4.

#3.

На научной конференции будут выступать 3 докладчика из Германии, 2 из России и 5 из Японии. Найдите вероятность того, что последним будет выступать докладчик из России, если порядок выступления определяется жребием.

Благоприятные события – это российские докладчики. Их 2.

Всевозможные события – это все прибывшие докладчики. Их 3+2+5=10.

P=2:10=0,2

Ответ: 0,2

#4.

Из слова «МАТЕМАТИКА» случайным образом выбирается одна буква. Найдите вероятность того, что эта буква окажется гласной.

Благоприятные события – это гласные буквы. Их 5.

Всевозможные события – это все буквы в слове. Их 10.

Р=5:10=0,5

Ответ: 0,5

#5.

Из класса, в котором учатся 12 мальчиков и 8 девочек, выбирают по жребию одного дежурного. Найдите вероятность того, что дежурным окажется мальчик.

Благоприятные события – это все мальчики. Их 12.

Всевозможные события – все дети в классе. Их 12+8=20.

Р=12:20=0,6

Ответ: 0,6

#6.

В партии из 1000 компьютеров оказалось 5 бракованных. Какова вероятность купить исправный компьютер?

Благоприятные события – это исправные компьютеры. Их 1000-5=995.

Всевозможные события – это все компьютеры. Их 1000.

 Р=995:1000=0,995

Ответ: 0,995

#7.

В урне лежат 3 белых, 2 желтых и 5 красных шаров. Найдите вероятность того, что извлеченный наугад шар будет красного цвета.

Благоприятные события – это красные шарики. Их 5.

Всевозможные события – это все шарики. Их 3+2+5=10.

Р=5:10=0,5

Ответ: 0,5

#8.

В каждой пятой банке кофе есть приз. Призы распределены случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдет приз.

Благоприятные события – это банки, в которых нет приза. Их 4.

Всевозможные события – это все банки. Их 5.

P=4:5=0,8

Ответ: 0,8.

 

Из простых задач остались самые элементарные.

Мы уже знаем, что если какое-либо событие происходит стопроцентно, то его вероятность обозначают за 1. 

Если вероятность выпадения снега 50%, то логично предположить, что вероятность того, что снег не выпадет равна так же 50%. Избавимся от процентов. Вероятность выпадения снега равна 0,5, вероятность невыпадения – 0,5. В сумме эти два числа равны 1.

Если вероятность того, что при письме карандаш сломается равна 0,24, то, чтобы найти вероятность того, что он не сломается, надо из 1 вычесть 0,24. Получится 0,76.

#9.

Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,06. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что ручка пишет хорошо.

Р=1-0,06=0,94

Ответ: 0,94.

Задачи с кубиками.

Следующий тип простых задач – это задачи с кубиками.

У кубика, как известно, 6 сторон. Значит, при подбрасывании одного кубика, всевозможных событий у нас будет 6. А при подбрасывании двух кубиков? Можно, конечно, расписать все варианты, но если кубиков не два, а три/четыре/пять? Всё время экзамена уйдет на это.

Нужно запомнить, что если количество сторон кубика возвести в степень, равную количеству кубиков, то мы получим число всевозможных событий.

6количество кубиков=всевозможные события

Для нахождения благоприятных событий такой формулы нет, поэтому разминаем мозг и ищем все самостоятельно.

#10.

В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.

Найдем благоприятные события. В каких случаях сумма очков будет равна 10? Распишем, главное, ничего не забыть.

  1 кубик 2 кубик 3 кубик
1 1 3 6
2 1 4 5
3 1 5 4
4 1 6 3
5 2 2 6
6 2 3 5
7 2 4 4
8 2 5 3
9 2 6 2
10 3 1 6
11 3 2 5
12 3 3 4
13 3 4 3
14 3 5 2
15 3 6 1
16 4 1 5
17 4 2 4
18 4

3

 3
19 4 4 2
20 4 5 1
21 5 1 4
22 5 2 3
23 5 3 2
24 5 4 1
25 6 1 3
26 6 2 2
27 6 3 1

Итого, благоприятных событий 27, а всевозможных – 63=216.

Р=27:216=0,125. Округляем до сотых – 0,13.

Ответ: 0,13.

#11.

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.

С двумя кубиками совсем просто.

Всевозможных событий — 62=36

Благоприятных событий — 3 (в сумме выйдет 4, если выпадут 1 и 3, или 3 и 1, или 2 и 2)

Р=3:36=0,08333

Ответ: 0,08

Задачи с монетами.

Задачи с монетками похожи на задачки с кубиками, но придется все всевозможные варианты выписать, чтобы найти благоприятные. Не уверены, что выписали всё? По аналогии с кубиками, можно сделать проверку: количество сторон монеты возвести в степень, равную количеству монеток.

2количество монет=всевозможные события

#12.

Одновременно бросают две монеты. Найдите вероятность, что на обеих монетах выпадет орел.

О – орел, Р — решка

О О
Р Р
О Р
Р О

Благоприятных – 1

Всевозможных – 4

Р=1:4=0,25

Ответ: 0,25

#13.

Одновременно бросают три монеты. Найдите вероятность, что на выпадут два орла и одна решка.

Всевозможных событий у нас 23=8. Выпишем их.

О О О
О О Р
О Р О
О Р Р
Р О О
Р О Р
Р Р О
Р Р Р

Благоприятных событий 3.

Р=3:8=0,375

Ответ: 0,375.

На этом приятности заканчиваются, и начинаются неприятности. 

Задачи на нахождение вероятности совместных и несовместных событий.

В предыдущих задачах события были случайными. Но еще есть такие виды событий как совместные и несовместные. Из названий понятно, что совместные события могут происходить одновременно, а несовместные нет. Например, к совместным событиям относятся снег с дождем, т.е. одновременно идет снег И дождь; к несовместным событиям относятся наступление дня и наступление ночи, т.к. в природе может быть ИЛИ день, ИЛИ ночь. Что-то одно. 

Союзы и/или я выделила не просто так. В информатике есть тема «Логические операции». Правда не могу сказать, в каких классах ее изучают. Определенно в старших. В этой теме есть такие понятия как логическое сложение и логическое умножение. Так вот. Союз И отвечает за логическое умножение, а союз ИЛИ – за логическое сложение.  

О чем это говорит? Если в задаче нам даны вероятности совместных событий, то их необходимо умножать. Если даны вероятности несовместных событий, то их будем складывать.

И – умножаем

ИЛИ — складываем

#14.

В уличном фонаре три лампы. Вероятность перегорания лампы в течении года равно 0,8. Найдите вероятность того, что в течении года хотя бы одна лампа не перегорит.

Начинаем рассуждать. Если лампа перегорает с вероятностью 0,8, то она не перегорает с вероятностью 1-0,8=0,2.

Возможны несколько случаев. 

1) 1 лампа остается И 2 лампы перегорают. Вероятность такого расклада равна 0,2*0,8*0,8=0,128. Причем остаться гореть может первая лампа, вторая ИЛИ третья. Т.е. первый случай разбивается еще на три таких же. Учитывая этот факт, вероятность того, что одна лампа не перегорит, равна 0,128*3=0,384.

2) 2 лампы остаются И 1 перегорает. Этот случай так же разбивается на три. Найдем вероятность: (0,2*0,2*0,8)*3=0,096.

3) 3 лампы остаются гореть. И первая, и вторая, и третья. Вероятность данного события равна 0,2*0,2*0,2=0,008.

Что получаем на выходе? Произойти может или первый случай, или второй, или третий. Найдем вероятность:

Р=0,384+0,096+0,008=0,488

И решим задачу вторым способом. Более коротким. 

Вероятность того, что все лампы перегорят (и первая, и вторая, и третья) равна 0,8*0,8*0,8=0,512

Т.к. нас интересует противоположный результат, то вероятность того, что в течении года хотя бы одна лампа не перегорит равна 1-0,512=0,488

Ответ: 0,488

#15.

Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

Вероятность ничьей = 1-0,4-0,4=0,2.

Команду ожидают две игры. За эти игры она должна набрать 4 очка. Это возможно осуществить тремя способами. Либо они одерживают победу в обоих играх, либо одерживают победу в первой игре и играют вничью во второй, либо играют вничью в первой игре и побеждают во второй. Расставим союзы и/или, чтобы составить полноценную формулу:

(победа и победа) или (победа и ничья) или (ничья и победа)

Заменяем союзы на знаки и получим, что вероятность того, что команда попадет в следующий тур равна 0,4*0,4+0,4*0,2+0,2*0,4=0,32.

Ответ: 0,32.

 

Успехов в учебе!

Автор статьи, но не задач: Васильева Анна

Динамика жидкости

— Что заставляет шариковые ручки писать с перерывами?

Через некоторое время шариковая ручка перестает писать очень хорошо. Он будет писать на небольшом расстоянии, затем оставит пробел, затем, возможно, напишет небольшими штрихами, а затем, возможно, снова напишет правильно. Кажется, что со старыми ручками дело обстоит хуже, но я наблюдал это и с новыми ручками прямо из коробки.

Проведенные мной эксперименты:

  • Выньте картридж и посмотрите на количество чернил. Есть еще много.
  • Осмотрите шар с помощью ювелирной лупы, видимых повреждений нет, все гладкое и чистое.
  • Новые неиспользованные ручки хранятся острием вниз, чтобы устранить гравитацию, медленно вытягивая чернила из шарика и оставляя воздушный карман. Некоторые из ручек проявляют этот симптом даже при первом использовании с никогда не снимаемой колпачком и хранении таким образом в течение года.
  • Вставьте проволоку в открытый конец резервуара для чернил, чтобы посмотреть, может ли конец высохнуть до твердой пробки, чтобы новые чернила не могли стекать вниз, когда они удаляются из резервуара при письме. Я никогда не находил ничего твердого, и наблюдал те же симптомы даже после того, как немного «пошевелил» верх бачка проволокой.
  • Когда ручка перестанет писать, сильно встряхните ее, как переустанавливаете термометр лихорадки. Кажется, это помогает ненадолго, но помогает и простое ожидание нескольких секунд, так что я не уверен, что встряхивание уместно.
  • Оставил шариковую ручку в стакане с водой на ночь. Мысль заключалась в том, что если чернила прямо над шаром высохнут, может быть, это восстановит его. Некоторые чернила явно растворялись в воде, так как она была окрашена, но как только ручка снова была запущена, симптомы не изменились.
  • Холод, кажется, усугубляет симптомы, но нагревание до температуры тела их не устраняет.

Это не просто ручка или модель. У меня есть куча разных ручек разных моделей, которые делают это. Мне интересно, чем это вызвано?

Добавлено:

Я провел еще несколько экспериментов, и кажется, что Эмиль Йетцер был прав. Причина, по-видимому, в том, что чернила настолько вязкие, что новые чернила не стекают достаточно быстро, чтобы заменить то, что удаляется шариком. Два эксперимента подтверждают эту гипотезу:

  1. Через некоторое время ручка снова начнет писать, если просто положить ее шариком вниз, но время значительно сокращается, когда вы встряхиваете ее, как если бы вы сбрасывали градусник.
  2. Некоторые ручки-стикеры герметичны, за исключением небольшого отверстия для воздуха в верхней части. Соприкосновение губ с верхней частью пера и приложение давления, как будто вы пытаетесь подуть на него, быстро сбрасывает действие письма. Более того, я могу писать такими ручками гораздо дольше, чем обычно, держа рот сверху и применяя постоянное давление воздуха.

Итак, думаю, загадка раскрыта. Вероятно, чернила в резервуаре со временем медленно высыхают из-за потери водяного пара сверху. Это делает все чернила более вязкими, что объясняет, почему старые, но неиспользованные ручки также проявляют этот симптом.

Следующий эксперимент заключается в том, чтобы взять такую ​​ручку и добавить немного воды в верхнюю часть резервуара для чернил, затем оставить ее на неделю и посмотреть, какая разница.

Добавлено 2:

Я добавил немного воды на конец резервуара для чернил в одной из проблемных ручек. Я сделал это, используя небольшую гибкую трубку (пластиковая изоляция снята с провода № 22), чтобы налить немного воды прямо на конец чернил без пузырьков между чернилами и водой.

Сначала симптом не изменился. Примерно через 2 недели ручка стала работать значительно лучше. В этой ручке было около 1 1/2 дюйма чернил в резервуаре, поэтому, по-видимому, потребовалось столько же времени, чтобы вода распространилась до конца шарика.

Я думаю, что этот и другие тесты убедительно доказывают, что проблема заключается в том, что чернила со временем высыхают, что делает их более вязкими, что не позволяет им стекать на шарик просто под действием силы тяжести так быстро, как шарик способен удалить чернила.

Как шариковая ручка изменила почерк

Технология

Более густые чернила, меньше пятен и более напряженные руки: наглядный урок

Джош Гисбрехт

Наю Ким / Flickr

90 057 28 августа 2015 г.

Сохраненные истории

Недавно Бик запустила кампанию по «сохранению почерка». Названный «Борьба за свое письмо», он включает в себя обязательство «поощрять рукописное письмо» в доме и в сообществе того, кто берет на себя обязательство, и подчеркивает необходимость использования большего количества шариковых ручек компании в классах.

Как учитель, я не мог не задаться вопросом, как кто-то мог подумать, что есть нехватка. Шариковые ручки я нахожу повсюду: на полу в классе, за партами. Десятки потерпевших кораблекрушение собираются в чашках на каждом учительском столе. Они настолько вездесущи, что слово «шариковая» используется редко; они просто «ручки». Но, несмотря на свою популярность, шариковая ручка — относительно новое явление в истории почерка, и ее влияние на популярный почерк гораздо сложнее, чем предполагала кампания Bic.

История создания шариковой ручки имеет тенденцию выделять несколько ключевых личностей, прежде всего венгерского журналиста Ласло Биро, которому приписывают ее изобретение. Но, как и в случае с большинством историй об индивидуальном гении, этот взгляд затемняет гораздо более длинную историю итеративных инженерных и маркетинговых успехов. На самом деле Биро был не первым, кто разработал эту идею: шариковая ручка была первоначально запатентована в 1888 году американским кожевником по имени Джон Лауд, но его идея так и не получила дальнейшего развития. В течение следующих нескольких десятилетий были выданы десятки других патентов на ручки с шариковым наконечником, но ни один из них не вышел на рынок.

Эти первые ручки были неудачными не из-за их механической конструкции, а из-за выбора чернил. Чернила, используемые в перьевой ручке, предшественнице шариковой ручки, тоньше, чтобы облегчить протекание через перо, но поместите эти более тонкие чернила внутрь шариковой ручки, и вы получите негерметичный беспорядок. Именно в чернилах Ласло Биро вместе со своим братом-химиком Дьёрдь внес решающие изменения: они экспериментировали с более густыми и быстросохнущими чернилами, начиная с чернил, используемых в газетных печатных машинах. В конце концов, они усовершенствовали как чернила, так и дизайн шарикового наконечника, чтобы создать ручку, которая не протекает сильно. (Это была эпоха, когда ручка могла иметь огромный успех, потому что из нее вытекали только чернила9.0067 иногда .)

Однако Биро жили в неспокойное время. Венгерский писатель Дьёрдь Молдова пишет в своей книге «Шариковая ручка » о бегстве Ласло из Европы в Аргентину, чтобы избежать преследований нацистов. В то время как его деловые сделки в Европе были в беспорядке, он запатентовал дизайн в Аргентине в 1943 году и начал производство. Его большой прорыв произошел позже в том же году, когда британские ВВС в поисках ручки, которая могла бы работать на больших высотах, закупили 30 000 таких ручек. Вскоре патенты были зарегистрированы и проданы различным компаниям в Европе и Северной Америке, и шариковая ручка начала распространяться по всему миру.

Всеобщий успех шариковой ручки изменил отношение большинства людей к чернилам.

Бизнесмены нажили значительные состояния, купив права на производство шариковых ручек в своей стране, но один из них заслуживает особого внимания: Марсель Бич, человек, купивший патентные права во Франции. Бич не просто заработал на шариковой ручке; он выиграл гонку, чтобы сделать ее дешевой. Когда она впервые появилась на рынке в 1946 году, шариковая ручка продавалась примерно за 10 долларов, что примерно эквивалентно сегодняшним 100 долларам. Конкуренция неуклонно снижала эту цену, но дизайн Биха сбил ее с ног. Когда Bic Cristal появился на американском рынке в 1959 цена упала до 19 центов за ручку. Сегодня Cristal продается примерно по той же цене, несмотря на инфляцию.

Всеобщий успех шариковой ручки изменил отношение большинства людей к чернилам. Его более густые чернила протекали с меньшей вероятностью, чем у его предшественников. В большинстве случаев это была победа — больше не было испачканных чернилами рубашек, не было необходимости в этих стереотипно гиковских карманных протекторах. Однако более густые чернила также меняют физический опыт письма, не обязательно в лучшую сторону.

Я бы не заметил разницы, если бы не моя привязанность к необычным ручкам, которая и привела меня к моей первой хорошей авторучке. Всю жизнь, пишущую шариковой ручкой и с небольшими вариациями концепции (гелевые ручки, шарики-роллеры), я не был готов к тому, насколько совершенно иначе будет ощущаться перьевая ручка. Его тонкие чернила немедленно оставляют след на бумаге даже при малейшем прикосновении к поверхности без давления. В моем письме внезапно появились дополнительные линии, появляющиеся между тем, что раньше было отдельными штрихами пера. Моя рука, натренированная шариковой ручкой, ожидала, что ослабления давления пера будет достаточно, чтобы перестать писать, но я обнаружил, что должен полностью оторвать ее от бумаги. Однако, как только я начал приспосабливаться к этому изменению, это было похоже на находку; менее твердое нажатие на страницу также означало меньшую нагрузку на мою руку.

Моя перьевая ручка современная и, вероятно, не является лучшим представителем типичных ручек 1940-х годов, но у нее все еще есть некоторые проблемы, которые досаждали перьевым ручкам и перьям прошлого. Я должен быть осторожен, когда кладу руку на бумагу, иначе я рискую смазать последнюю еще влажную линию в неразборчивое пятно. А так как жидкие чернила текут быстрее, мне приходится часто заправлять перо. Шариковая ручка решила эти проблемы, предоставив писателям долговечную ручку и бумагу без пятен при небольших затратах на дополнительное давление руки.

Как учитель, чьи дети обычно работают с числами и компьютерами, почерк не так важен для меня, как для многих моих коллег. Но время от времени я сталкиваюсь с другой историей об упадке почерка. Неизбежно, эти статьи сосредоточены на том, как письмо было вытеснено новыми, цифровыми формами общения — набором текста, текстовыми сообщениями, Facebook, Snapchat. Они обсуждают потерю времени в классе для практики письма, которое вместо этого посвящается урокам печати. В прошлом году 9В статье 0067 New York Times , которая с тех пор была отмечена кампанией Bic «Борьба за ваше письмо», было поднято исследование фМРТ, предполагающее, что письмо от руки может быть лучше для обучения детей, чем использование компьютера.

Не могу припомнить, когда в последний раз видел, как ученики передавали в классе настоящие бумажные заметки, но я отчетливо помню, как ученики проверяли свои телефоны (недавно и часто). В своей истории почерка The Missing Ink автор Филип Хеншер вспоминает момент, когда он понял, что понятия не имеет, как выглядит почерк его хорошего друга. «Это никогда раньше не казалось мне странным… Мы могли бы продолжать так вечно, почти не замечая, что нам больше не нужен почерк».

Почерк не нужен? Наверняка должна быть какая-то причина, по которой я продолжаю повсюду находить ручки.

Конечно, значение «почерка» может быть разным. Романтики почерка обычно не имеют в виду какие-либо грубые формы букв, созданные пером и чернилами. Они изображают плавные, соединенные буквы метода Палмера, который доминировал в педагогике первого и второго классов на протяжении большей части 20-го века. (Или, возможно, они тоскуют по прошлому, которого на самом деле никогда не испытывали, представляя остроугольный спенсерианский шрифт 1800-х годов.) Несмотря на распространение рукописных хвалебных речей, кажется, что никто на самом деле не возражает против того факта, что все до сих пор пишет — мы просто склонны использовать несвязанный шрифт, а не плавный стиль Палмера, и используем его реже.

Перьевая ручка Хочу для соединения букв. Шариковую ручку нужно убедить писать.

У меня смешанные чувства по поводу такого положения дел. Мне было больно, когда я столкнулся со студентом, который вообще не мог читать почерк. Но вскоре после поступления в колледж мое собственное письмо превратилось из палмеровского письма в преимущественно печатное. Как и большинство постепенных изменений в привычках, я не могу точно вспомнить, почему это произошло, хотя я помню, что изменение произошло в то время, когда мне регулярно приходилось переписывать стопки конспектов для лекций по математике и инженерии.

В своей книге Научитесь лучшему письму эксперт по почерку и дизайнер шрифтов Розмари Сассун отмечает, что «большинству из нас нужен гибкий способ письма — быстрый, почти как каракули для нас самих, и все более медленный и разборчивый для других». другие цели». Сравнивая несвязанный шрифт с соединенным письмом, она отмечает, что «отдельные буквы редко бывают такими же быстрыми, как соединенные». Итак, если объединенный почерк должен быть быстрее, зачем мне отказываться от него в то время, когда мне больше всего нужно писать быстро? Учитывая то количество времени, которое я провожу за компьютером, самоуверенному наблюдателю было бы легко посчитать мой почерк еще одной жертвой компьютерных технологий. Но я знал сценарий, я использовал его в старшей школе и отошел от него в то время, когда больше всего писал.

Мой опыт работы с перьевыми ручками подсказывает новый ответ. Возможно, моему почерку мешала не цифровая технология, а технология, которую я держал в руках, когда прикладывал перо к бумаге. Перьевые ручки хотят для соединения букв. Шариковые ручки нужно убедить писать, их нужно вонзать в бумагу, а не просто касаться ее. Карандаши № 2, которые я использовал для математических заметок, тоже не сильно ломались, требуя давления, аналогичного шариковой ручке.

Более того, цифровые технологии по-настоящему не взлетели до тех пор, пока перьевая ручка уже не начала свой закат, а шариковая — подъем. Шариковая ручка стала популярной примерно в то же время, что и мейнфреймы. Статьи об упадке почерка относятся как минимум к 1960-е — намного позже появления пишущей машинки, но за целое десятилетие до появления домашних компьютеров.

Проведенный Сассуном анализ того, как нас учат держать ручку, убедительно доказывает роль шариковой ручки в упадке скорописи. Она объясняет, что тип захвата ручки, которому учат в современной начальной школе, — это тот же захват, который использовался на протяжении поколений, задолго до того, как все писали шариковыми ручками. Однако для письма шариковыми ручками и другими современными ручками требуется, чтобы они располагались под большим, более вертикальным углом к ​​бумаге — положение, которое, как правило, неудобно при традиционном держании ручки. Еще до того, как компьютерные клавиатуры превратили так много людей в страдающих запястным каналом, шариковая ручка уже напрягала руки и запястья. Вот Сассун:

Мы должны найти способы держать современные ручки, которые позволят нам писать без боли. …Мы также должны поощрять эффективные письма, подходящие для современных ручек. Если мы не начнем делать что-то разумное как с буквами, так и с ручками, мы будем способствовать исчезновению рукописного ввода больше, чем это сделало появление компьютеров.

Интересно, сколько других приземленных навыков, предназначенных для работы с устаревшими объектами, остаются за пределами их полезности.