Задание № 1. Планиметрия. ЕГЭ. Математика. 2

1.  Планиметрия 

2.  Стереометрия 
3.  Начала теории вероятностей 

4.  Теория вероятностей

5.  Простейшие уравнения
6.  Преобразование выражений 
7.  Производная функции 
8.  Практические задачи 
9.  Текствые задачи 
10.  Графики функций 
11.  Исследование функций
12.  Уравнения 
13.  Стереометрия с доказ-вом
14.  Неравенства 
15.  Финансовая математика 
16.  Планиметрия с доказ-вом 
17.  Задачи с параметром 
18.  Задачи на логику 

      БАЗА ЗАДАНИЙ

Задание № 1. Планиметрия.

47. В треугольнике ABC CH — высота, AD — биссектриса, угол BAD=26°. Найдите угол AOC. Ответ дайте в градусах.

Ответ: 116°

48. В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E— такая точка на AB, что AE=AC. Найдите угол BDE. Ответ дайте в градусах.

Ответ: 40°

49. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E

, что CE=CB. Найдите угол BDE.

Ответ: 56°

50. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF.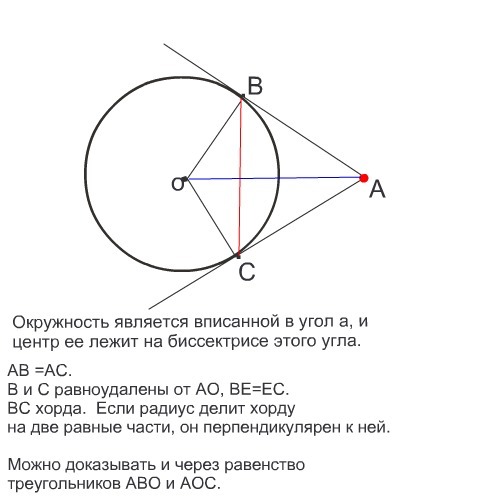 Ответ дайте в градусах.

Ответ: 49°

51. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Ответ: 82°

52. Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Ответ: 20

53. Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

Ответ: 41°

54. Углы треугольника относятся как 2 : 3 : 4. Найдите меньший из них. Ответ дайте в градусах.

Ответ: 40°

55. Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.

Ответ: 72°

56. Один угол равнобедренного треугольника на 90° больше другого.

Найдите меньший угол. Ответ дайте в градусах.

Ответ: 30°

57. Периметр прямоугольной трапеции, описанной около окружности, равен 40, её большая боковая сторона равна 11. Найдите радиус окружности.

Ответ: 4,5

58. Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.

Ответ: 18,5

59. В четырёхугольник ABCD вписана окружность, AB=13, BC=7 и AD=11. Найдите четвёртую сторону четырёхугольника.

Ответ: 5

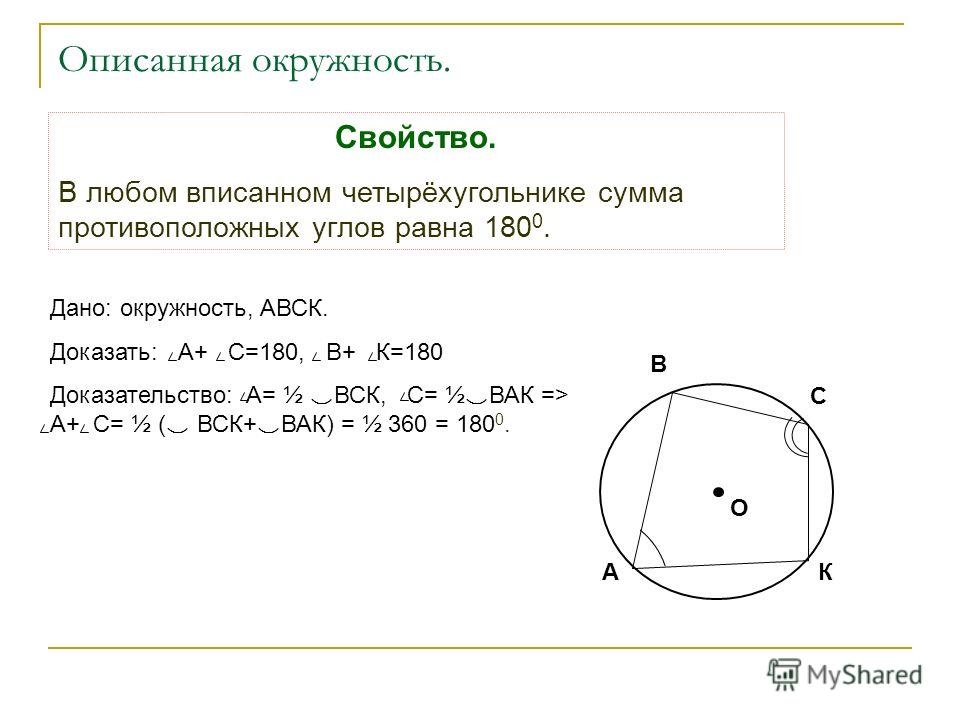
60. Два угла вписанного в окружность четырёхугольника равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.

Ответ: 103°

61. Окружность вписана в равнобедренную трапецию, основания которой равны 18 и 50. Прямая, проходящая через центр окружности и вершину D трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.

Ответ: 0,5

62. Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности. Ответ дайте в градусах.

Ответ: 36°

63. На окружности отмечены точки

A, B и C. Дуга окружности AC, не содержащая точку B, составляет 200°. Дуга окружности BC, не содержащая точку A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Ответ: 40°

64. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 82°, угол ABD равен 47°. Найдите угол CAD. Ответ дайте в градусах.

Ответ: 35°

65. Четырёхугольник ABCD вписан в окружность. Угол CAD равен 32°, угол ABD равен 57°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 89°

66. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Ответ: 30°

67. Найдите хорду, на которую опирается угол равный 30°, вписанный в окружность радиуса 3.

Ответ: 3

68. Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Ответ: 150°

69. Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную √2. Ответ дайте в градусах.

Ответ: 45°

70. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную √2. Ответ дайте в градусах.

Ответ: 135°

71. Найдите хорду, на которую опирается угол 120, вписанный в окружность радиуса √3.

Ответ: 3

72. Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C? Ответ дайте в градусах.

Ответ: 105°

73. Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника ABC.

Ответ дайте в градусах.

Ответ: 100°

74. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95°, 49°, 71°, 145°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Ответ: 108°

75. Сторона правильного треугольника равна √3. Найдите радиус окружности, описанной около этого треугольника.

Ответ: 1

76. Радиус окружности, описанной около правильного треугольника, равен 38√3. Найдите сторону этого треугольника.

Ответ: 114

77. Отрезки AC и BD — диаметры окружности с центром

O. Угол AOD равен 114°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Ответ: 33°

78. Угол ACB равен 54°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 138°. Найдите угол DAE. Ответ дайте в градусах.

Ответ: 15°

79. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна 58°. Найдите угол ACB. Ответ дайте в градусах.

Ответ: 122°

80. Угол ACO равен 28°. Его сторона

CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D. Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Ответ: 118°

81. Найдите периметр прямоугольника, если его площадь равна 270, а отношение соседних сторон равно 2 : 15.

Ответ: 102

82. Периметр прямоугольника равен 76, а площадь 192. Найдите большую сторону прямоугольника.

Ответ: 32

83. Периметр прямоугольника равен 26, а диагональ равна 12. Найдите площадь этого прямоугольника.

Ответ: 12,5

84.

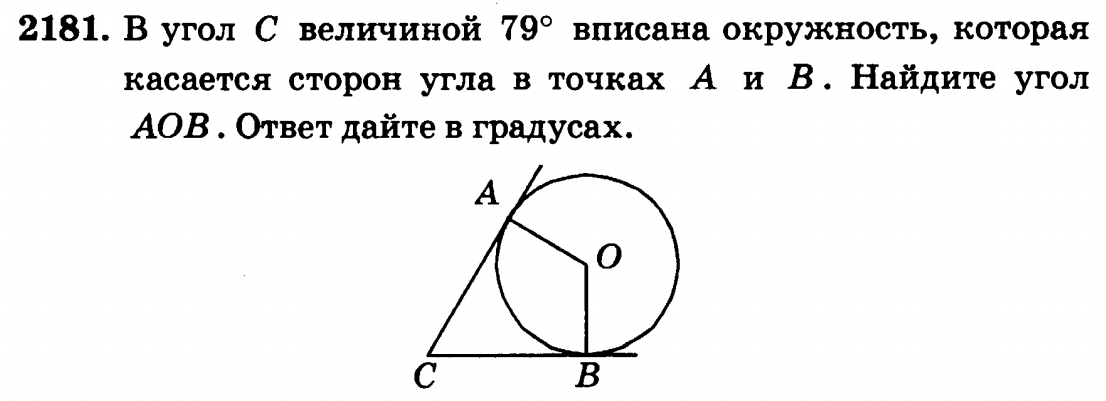
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.

Ответ: 48

85. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.

Ответ: 8

1     2     3

Главная

86. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 8:5, считая от вершины острого угла. Найдите боковую сторону параллелограмма, если его периметр равен 84.

Ответ: 16

87. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Ответ: 30

88. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Ответ: 2

89.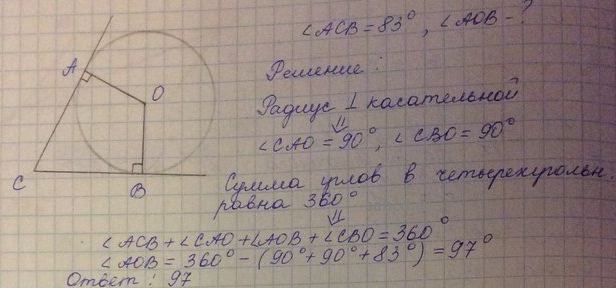  В параллелограмме ABCD AB=21, AD=3, sinA=6/7. Найдите большую высоту параллелограмма.

Ответ: 18

90. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Ответ: 10

91. В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.

Ответ: 6

92. Сумма двух углов параллелограмма равна 100°. Найдите один из оставшихся углов. Ответ дайте в градусах.

Ответ: 130°

93. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Ответ: 90°

94. Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах.

Ответ: 126°

1: Задание 10

1. B 7 № 90. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Ответ: 6

2. B 7 № 116. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.

Ответ: 70

3. B 7 № 142. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

Ответ: 30

4. B 7 № 194. Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.

Ответ: 3

5. B 7 № 311319. Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

Ответ: 144

6. B 7 № 311331. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.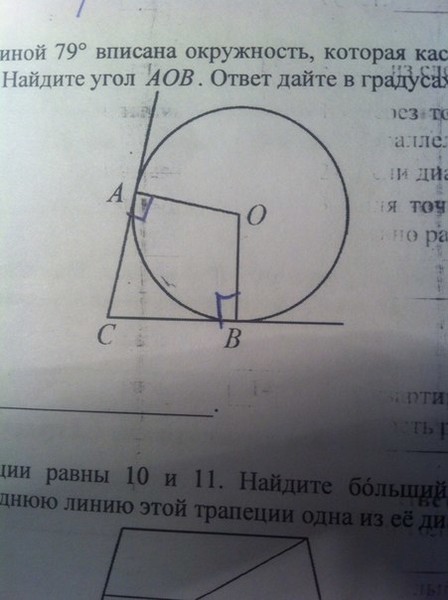

Ответ: 71

7. B 7 № 311342. Найдите  ∠KOM, если градусные меры дуг  KO  и  OM  равны 112° и 170° соответственно.

Ответ: 39

8. B 7 № 311354. Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера ∠AOC равна 96°.

Ответ: 42

9. B 7 № 311374. Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.

Ответ: 56

10. B 7 № 311386. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 112°. Найдите вписанный угол  ACB. Ответ дайте в градусах.

Ответ: 34

11. B 7 № 311398. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.

Ответ: 128

12. B 7 № 311410. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей.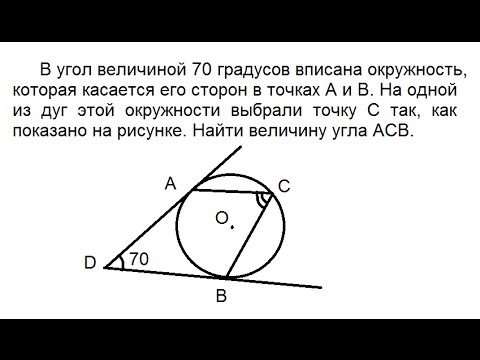 Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

Ответ: 6

13. B 7 № 311464. Радиус OB окружности с центром в точке O пересекает хорду MN в её середине — точке K. Найдите длину хорды MN, если  KB = 1 см, а радиус окружности равен 13 см.

Ответ: 10

14. B 7 № 311479. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

Ответ: 6,5

15. B 7 № 311483. Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

Ответ: 162

16. B 7 № 311487. Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.

Ответ: 5

17. B 7 № 311488. Найдите величину (в градусах) вписанного угла α, опирающегося на хорду  AB, равную радиусу окружности.

Ответ: 30

18. B 7 № 311494. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.

Ответ: 25

19. B 7 № 311497. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.

Ответ: 70

20. B 7 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Ответ: 22,5

21. B 7 № 311507. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Ответ: 90

22. B 7 № 311510. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.

Ответ: 55

23. B 7 № 311517. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.

Ответ: 35

24. B 7 № 311523. Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.

Ответ: 65

25. B 7 № 311681. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Ответ: 5

26. B 7 № 311760. В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.

Ответ: 10

27. B 7 № 311816. В треугольнике ABC угол C равен 90°, BC = 20, = 0,5. Найдите AC.

Ответ: 40

28. B 7 № 311848. В треугольнике ABC угол C равен 90°, BC = 18, tgA = 3. Найдите AC.

Ответ: 6

29. B 7 № 311912.

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.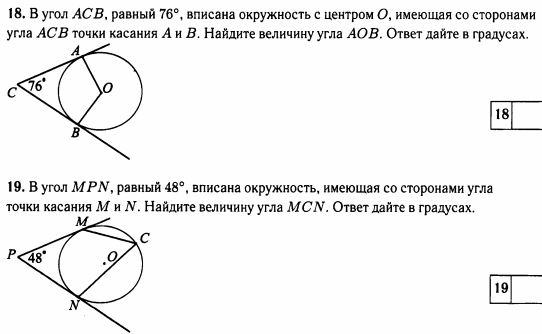

Ответ: 17,5

30. B 7 № 311956.

Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.

Ответ: 24

31. B 7 № 314807. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.

Ответ: 8

32. B 7 № 314811. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

Ответ: 42

33. B 7 № 314850. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70° . Найдите величину угла OCD.

Ответ: 70

34. B 7 № 314873. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах).

Ответ: 48

35. B 7 № 314956. Точка О — центр окружности, ∠BAC = 70° (см.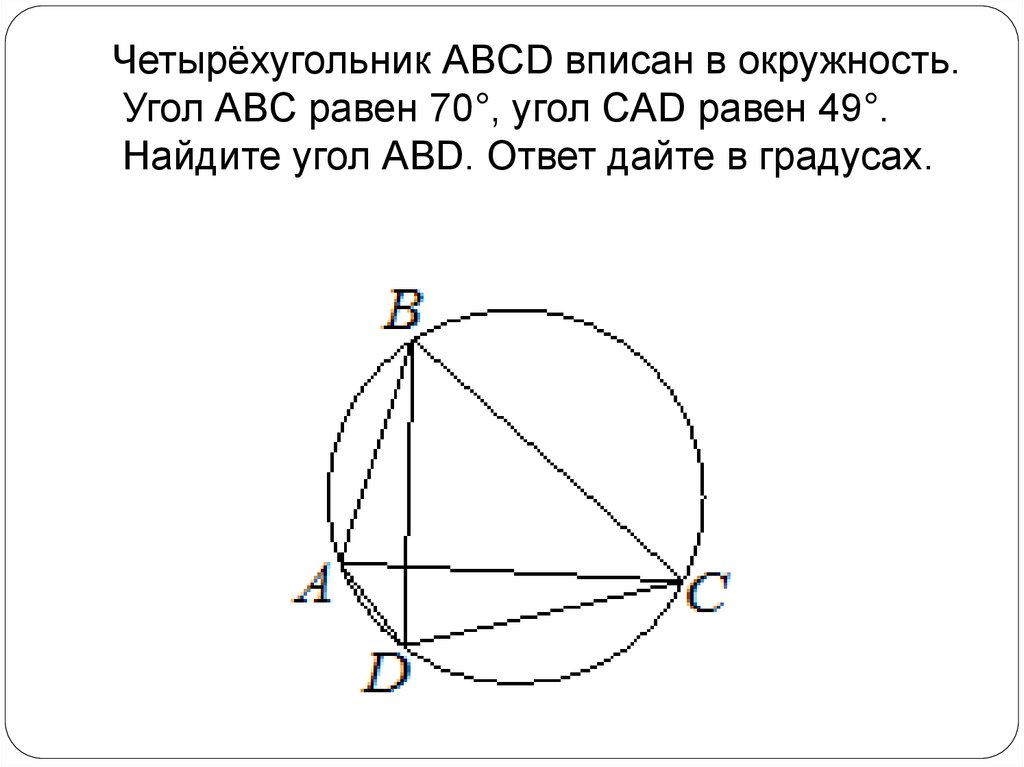 рисунок). Найдите величину угла BOC (в градусах).

36. B 7 № 315006. Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.

Ответ: 4

37. B 7 № 316230. В треугольнике ABC угол C равен 90° , BC = 20, tgA = 0,5. Найдите AC.

Ответ: 40

38. B 7 № 316257. В треугольнике ABC угол C равен 90°, BC = 18, tgA = 3. Найдите AC.

Ответ: 6

39. B 7 № 316320. В треугольнике ABC угол C равен 90°, AC = 12 , tgA = 1,5. Найдите BC.

Ответ: 18

40. B 7 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Ответ: 8

41. B 7 № 316372. Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Ответ: 10


Центральные углы и дуги

Существует несколько различных углов, связанных с окружностями.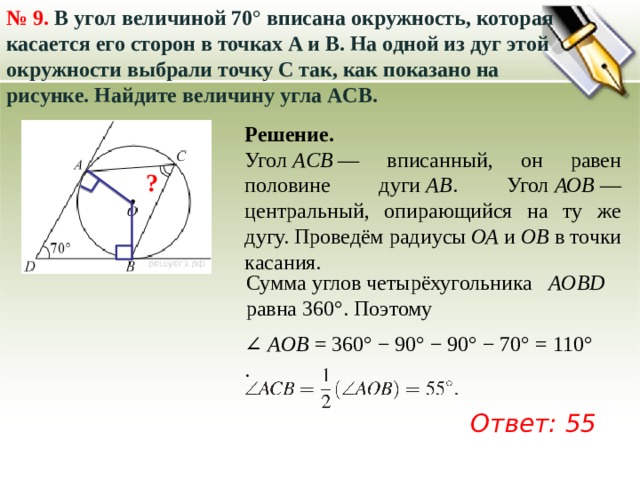 Возможно, первое, что приходит на ум, это центральный угол. Это способность центрального угла проходить по дуге в 360 градусов, которая определяет количество градусов, которое обычно считается заключенным в окружность.

Центральные углы — это углы, образованные любыми двумя радиусами окружности. Вершина является центром окружности. На рисунке 1 ∠  AOB  является центральным углом.

Рисунок 1 Центральный угол окружности.

Дуги

дуга  окружности является непрерывной частью окружности. Он состоит из двух конечных точек и всех точек на окружности между этими конечными точками. Символ используется для обозначения дуги. Этот символ пишется над конечными точками, образующими дугу. Существует три типа дуг:

  • Полуокружность:  дуга, концы которой являются конечными точками диаметра. Он назван с использованием трех точек. Первая и третья точки являются конечными точками диаметра, а средняя точка является любой точкой дуги между конечными точками.
  • Малая дуга:  дуга, которая меньше полукруга. Второстепенная дуга называется с использованием только двух конечных точек дуги.
  • Большая дуга:  дуга, которая больше, чем полукруг. Он назван по трем пунктам. Первая и третья — это конечные точки, а средняя точка — это любая точка на дуге между конечными точками.

На рисунке 2 AC – это диаметр. представляет собой полукруг.

Рисунок 2 Диаметр круга и полукруга.

На рисунке 3  это малая дуга окружности  P .

Рисунок 3 Малая дуга окружности.

На рисунке 4  это большая дуга окружности  Q .

Рисунок 4 Большая дуга окружности.

Дуги измеряются тремя различными способами. Они измеряются в градусах и в единицах длины следующим образом:

  • Градусная мера полукруга:  Это 180°. Его единичная длина равна половине длины окружности.
  • Градусная мера малой дуги:  Определяется так же, как мера соответствующего центрального угла. Единица его длины — это часть окружности. Его длина всегда меньше половины окружности.
  • Градусная мера большой дуги:  Это 360° минус градусная мера малой дуги, которая имеет те же конечные точки, что и большая дуга. Его единичная длина является частью окружности и всегда больше половины окружности.

В этих примерах м  обозначает градусную меру дуги AB , l  обозначает длину дуги AB и  обозначает саму дугу.

Пример 1:  На рисунке 5 окружность O с диаметром AB имеет OB  = 6 дюймов. Найдите (а) м и (б) л .

Рисунок 5 Градусная мера и длина дуги полукруга.

представляет собой полукруг.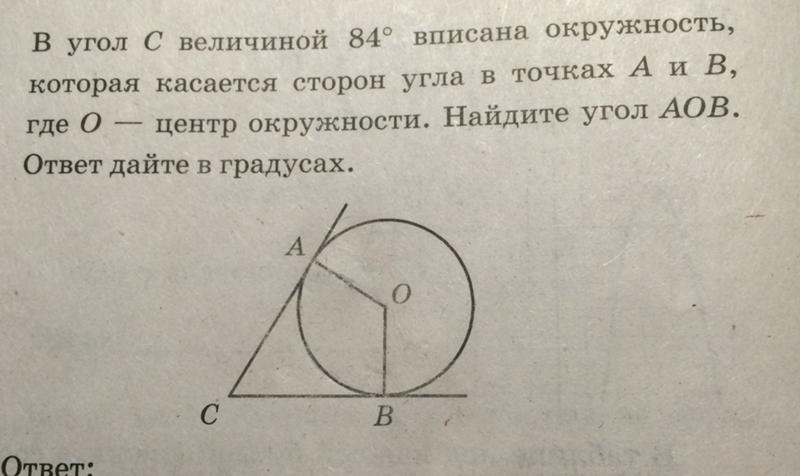 м   = 180°.

Так как это полукруг, его длина составляет половину окружности.

Постулат 18 (Постулат сложения дуги):  Если B  является точкой на , то м   + м   = м  .

Пример 2:  Используйте рисунок 6, чтобы найти  м   ( м   = 60°, м   = 150°).

 

Рисунок 6 Использование постулата сложения дуги .

Пример 3:  Используйте фигуру круга P  с диаметром QS, чтобы ответить на следующие вопросы.

а. Найти м

б. Найти м

в. Найти м

д. Найти м

Рисунок 7 Нахождение градусных мер дуг.

и . m   (Градусная мера малой дуги равна мере ее соответствующего центрального угла.)

б. = 180° (  является полукругом.)

с . м   = 130°

д. м   = 310° (  является большой дугой.) Градусная мера большой дуги равна 360° минус градусная мера малой дуги, которая имеет те же конечные точки, что и большая дуга.

Легко доказываются следующие теоремы об дугах и центральных углах.

Теорема 68:  В окружности, если два центральных угла имеют одинаковую меру, то соответствующие им малые дуги имеют одинаковую меру.

Теорема 69:  В окружности, если две малые дуги имеют одинаковую меру, то их соответствующие центральные углы имеют одинаковую меру.

Пример 4:  На рисунке 8 показана окружность O  с диаметрами AC и BD. Если м ∠1 = 40°, найдите каждое из следующего.

Рисунок 8 Окружность с двумя диаметрами и хордой (не диаметральной).

а. m   = 40° (Мера малой дуги равна мере ее соответствующего центрального угла.)

б. м   = 40° (Поскольку вертикальные углы имеют равные меры, м  ∠1 = м  ∠2.