В цилиндрический сосуд налили 1800 см3 воды уровень жидкости 12 см: В сосуд налили 1800 см3 воды, уровень оказался 12 см

Объём цилиндра в заданиях ЕГЭ

Похожие презентации:

Объём цилиндра

Объемы прямой призмы и цилиндра. (ЕГЭ. Задачи В10, В1)

Геометрическое тело цилиндр

Объемы прямой призмы и цилиндра

Объем. Цилиндр, призма

Объем цилиндра, призмы

Подготовка к ЕГЭ по математике. Решение задач В9

Практикум № 7 по решению стереометрических задач

Задания B6, B9 (геометрия) с решениями. По заданиям ЕГЭ 2010-2012 годов

Объем цилиндра и призмы

2. Цели урока:

1) закрепить у учащихся знания о теле
вращения – цилиндре;
2) совершенствовать умение применять
формулу объёма цилиндра в процессе
решения типовых задач и задач
практического характера;
3) развивать пространственные
представления на примере круглых тел
Содержание
1. Задачи на погружение детали I типа
2. Задачи на погружение детали II типа
3. Задачи на переливание жидкости
4. Задачи про два цилиндра
5.

Задачи про две кружки

4. Основание цилиндра

d
диаметр
r
S r
2
d
S
2
4
r радиус
d диаметр

5. Объём цилиндра

V Sосн h
h
r
о
б
р
а
з
у
ю
щ
а
я
Sосн r
2
V r h
2
r радиус
h высота
Заполнить таблицу
r
2
3
4
5
h
9
8
5
2
Sосн
4
9
16 25
V
36 72
80 50
Sосн r
2
V Sосн h
27045-П. В цилиндрический сосуд налили
2000 см3 воды. Уровень жидкости оказался равным 12 см. В
воду полностью погрузили деталь. При этом уровень
жидкости в сосуде поднялся на 9 см. Чему равен объём
детали. Ответ выразите в см3 .
Vдет V2 V1
S h3 S h2
9
12
S h3 h2
2000
9 1500
12
B9
I 5 0 0
3
10 х
х
Погружение
V
27091-П. В цилиндрический сосуд, в
котором находится 6 куб.см воды, опущена деталь. При
этом уровень жидкости в сосуде поднялся в 1,5 раза.

Чему
равен объём детали. Ответ выразите в куб.см.
Vдет V2 V1
S 1,5h S h
1,5 S h 1 S h
1,5h
h
0,5 S h
0,5 6 3
B12 3
3
10 х
х
Погружение
V
27046-П. В цилиндрическом сосуде

уровень жидкости достигает 16 см. На какой высоте будет
находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в 2 раза больше
диаметра первого? Ответ выразите в сантиметрах.
V1 V2 S1 h2 S2 h3
d
16
2
2d
2
h2
h3
4
4
2
2
d
4d
16
h3
4
4
16 4 h3
B9
4
3
10 х
х
h3 4
V
27053-П. Дано два цилиндра. Объём
первого цилиндра равен 12. У второго цилиндра высота
в 3 раза больше, а радиус основания в 2 раза меньше,
чем у первого. Найдите объём второго цилиндра.
Радиус
Первый
Второй
B9 9
3
10 х
Высота
Объём
4 r h 12
2
2r
h
r
3h 3 r h 9
2
х
V
27118-П.

Одна цилиндрическая кружка
вдвое выше второй, зато вторая в полтора раза шире.
Найдите отношение объёма второй кружки к объёму
первой.
Диаметр
Объём
2 d h
4
2
9 d h
4 4
2
Первая
кружка
Вторая кружка
B9
Высота
I , I 2 5
3
10 х
х
d
2h
3d
2
h
V
4909. В цилиндрический сосуд налили
1800 см3 воды. Уровень жидкости оказался равным 12 см. В
воду полностью погрузили деталь. При этом уровень
жидкости в сосуде поднялся на 2 см. Чему равен объём
детали. Ответ выразите в см3 .
Vдет V2 V1
Sосн h3 Sосн h2
9
12
S h3 h2
1800
3 450
12
B9
4 5 0
3
10 х
х
Погружение
74103. В цилиндрический сосуд, в
котором находится 8 куб.см воды, опущена деталь. При
этом уровень жидкости в сосуде поднялся в 2,3 раза. Чему
равен объём детали. Ответ выразите в куб.см.
Vдет V2 V1
Sосн 2,3h Sосн h
2,3 S h 1 S h
2,3h
h
1,3 Sосн h
1,3 8 10,4
B12 I 0 , 134
0х
х
Погружение
4921.

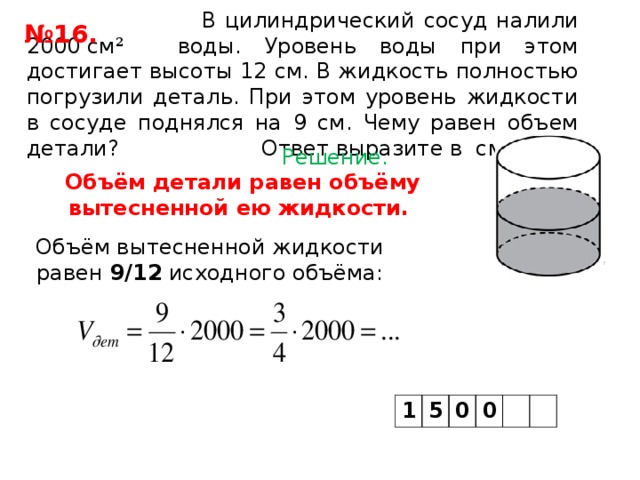В цилиндрическом сосуде
уровень жидкости достигает 8 см. На какой высоте будет
находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в 2 раза больше
диаметра первого? Ответ выразите в сантиметрах.
V1 V2 S1 h2 S2 h3
d
8
2
2d
2
h2
4
4
2
2
d
4d
8
h3
4
4
8 4 h3
B12 2
3
10 х
х
h3
h3 2
72355. Дано два цилиндра. Объём
первого цилиндра равен 81. У второго цилиндра высота в
4 раза больше, а радиус основания в 3 раза меньше, чем у
первого. Найдите объём второго цилиндра.
Радиус
3r
Первый
r
Второй
B9 3 6
3
10 х
х
Высота
Объём
h
9 r h 81
2
4h 4 r h 36
2
13.14. Две кружки имеют форму цилиндра. Первая
кружка вдвое выше второй, а диаметр основания
второй кружки втрое больше диаметра основания
первой. Во сколько раз объём второй кружки
больше объёма первой?
Диаметр
Высота
2 d h
4
2
9 d h
4
2
Первая
кружка
d
2h
3d
h
Вторая кружка
B13 4 , 5 13 0 х
Объём
х

English Русский Правила

Вариант 3 Задание B1

Вариант 3

Задание B1. Теплоход рассчитан на 1000 пассажиров и 30 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

Задание B2. На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат – крутящий момент в Нм. Какое наименьшее число оборотов в минуту должен поддерживать водитель, чтобы крутящий момент был не меньше 100Нм?

Задание B3. Найдите (в см²) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите .

Задание B4. Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 29 секунд. Петя загружает файл размером 28 Мб за 27 секунд, а Миша загружает файл размером 32 Мб за 27 секунд. Сколько секунд будет загружаться файл размером 544 Мб на компьютер с наибольшей скоростью загрузки?

Задание B5.

Решите уравнение

Задание B6. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.

Задание B7. Найдите значение выражения при b = 2.

Задание B8. Прямая является касательной к графику функции . Найдите

b, учитывая, что абсцисса точки касания больше 0.
Задание B9. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S – вершина,
SO = 4, AC = 6. Найдите боковое ребро SC.

Задание B10. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 13 очков. Результат округлите до сотых.

Задание B11. В цилиндрический сосуд налили 1800 см

³ воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объем детали? Ответ выразите в см³.

Задание B12. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью м/с под острым углом к рельсам. От толчка платформа начинает ехать со скоростью (м/с), где

m = 80 кг — масса скейтбордиста со скейтом, а M = 480 кг — масса платформы. Под каким максимальным углом (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,5 м/с?

Задание B13. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 75 км/ч и 55 км/ч. Длина пассажирского поезда равна 300 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 18 секундам. Ответ дайте в метрах.

Задание B14. Найдите наибольшее значение функции .

Объем цилиндра — веб-формулы

Объем цилиндра:
В геометрии цилиндр — это трехмерная фигура с круглым основанием, круглым верхом и прямыми сторонами.

Это сплошная фигура, которую вы получите, если повернете прямоугольник вокруг одной из его сторон. В большинстве случаев, когда мы говорим об объеме баллона, мы имеем в виду, сколько жидкости он может вместить.

Совершенно правильно сказать, что это « том , окруженный цилиндр «- количество жидкости, которое он содержит. Но во многих учебниках просто говорится, что « объем цилиндра » означает то же самое.

Помните, что радиус и высота должны быть в одних и тех же единицах измерения. — преобразовать их при необходимости.
Полученный объем будет в этих кубических единицах. Итак, если высота и радиус указаны в сантиметрах, то

объем будет в кубических сантиметрах.

Объем цилиндра находится путем умножения площади его верха или основания на его высоту и определяется как: V = π · r ² · h

Пример 1: Цилиндрический резервуар для хранения воды имеет внутреннее основание радиус 7м и глубина 11м. Найдите вместимость бака в килолитрах (1кл = 1м ³ ).
Решение :
Базовый радиус: r = 7 м
Высота: h = 11 м
Резервуар для воды имеет форму цилиндра. Таким образом, используя формулу объема цилиндра, мы можем найти его объем.

V = π· r ² · h
V = π· 7 ² · 11
V = 1692.46 m ³ = 1692.46 kl

Example 2: Найдите объем цилиндра, у которого радиус основания 6 см, а высота 4 см.
Раствор :
Радиус основания: r = 6 см
Высота: h = 4 см
V = π· r ²· H
V = 3,14 · 6 ² · 4
V = 452,16 см ³

3: , если пропускная способность A Cylindr, 1848 88 888 88 88 88 888 888 88 88 888 88 88 888 888 88 88 88 88 88 888 88 88 88 88 88 88 88 88 88 88 888

^{. диаметр его основания 14 м, найдите глубину резервуара.
Раствор :
Пусть глубина резервуара h метров. Тогда имеем:
V = π· r ² · h
h = V / π· r ²
h = 12 м
Пример 4: Конический сосуд с внутренним радиусом и высотой 20 см и 50 см соответственно наполнен жидкостью. Найдите высоту жидкости, если ее поместить в цилиндр с радиусом основания 10 см.
Раствор :
Объем сосуда:
V = π ∙ r ²
∙ h / 3
V = π · 20 ² · 50 / 3
V = 90944 см0028 3}
Объем жидкости одинаков независимо от того, находится она в сосуде или в цилиндре, поэтому имеем:
V1 = V2 , где V1 объем сосуда и V2 — объем, определяемый по формуле для цилиндра.
20944 = π · 10 ² · ч
Таким образом:
ч = 20944 / ( π · 10 ² )
h = 66,67 см
Пример 5: Найдите объем прямоугольного цилиндра, площадь кривизны которого равна 2640 см ²
А окружность его основания 66 см.