Помогите пожалуйста!!! не могу решить задачу!! объясните пожалуйста. в треугольнике высота bh делит сторону am пополам и равна 5 см. периметр треугольника abh равен 15 см. найдите периметр треугольника аbm — Школьные Знания.net
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
В треугольнике высота BH делит сторону AM пополам и равна 5 см.
Периметр треугольника ABH равен 15 см. Найдите периметр треугольника АBM
Ответ дан
Пеппер
Ответ:
20 см
Объяснение:
Дано: ΔАВМ, ВН — высота, АН=МН. Р(АВН)=15 см.
Найти Р(АВМ).
ΔАВМ — равнобедренный, т.к. ВН — высота и медиана по условию.
АВ+АН=15-ВН=15-5=10 см
МН+ВМ=АВ+АН=10 см
Р=10+10=20 см.
Ответ дан
takushnir
Из условия следует, что ΔАВМ -равнобедренный, т.к. в нем высота является медианой. Пусть АВ=ВМ=х, АН=МН=у, тогда периметр данного ΔАВН х+у+5=15, откуда х+у=10, периетр ΔАВМ состоит из суммы х+х+у+у=2*(х+у)=2*10=
Геометрия: свойства треугольника — intmag24.ru
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
На рисунке: Треугольник ABC;
A, B, C – вершины треугольника ABC;
AB, AC, BC – стороны треугольника ABC;
∠BAC, ∠ABC, ∠ACB – углы треугольника ABC.
Содержание
- Виды треугольников
- Свойства сторон треугольника
- Свойства углов треугольника
- Свойства высоты треугольника
- Свойства медианы треугольника
- Свойства биссектрисы треугольника
- Средняя линия треугольника
- Равнобедренный треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Треугольник и окружность
- Основные формулы
- Теорема Чевы
- Теорема Менелая
Виды треугольников
- Треугольник называется остроугольным, если все его углы острые.
- Треугольник называется тупоугольным, если один из его углов тупой.
- Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны. Основные признаки равенства треугольников: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам.
Свойства сторон треугольника
- Сумма любых двух сторон треугольника больше его третьей стороны.
На рисунке: b+c>a, a+c>b, a+b>c. - Длина каждой стороны треугольника больше разности длин двух других сторон. На рисунке: |a-b| <c, |a-c|<b, |b-c|<a.
Свойства углов треугольника
- Сумма углов треугольника равна 180°:
- Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.
Свойства высоты треугольника
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны. На рисунке: BD – высота треугольника ABC.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. На рисунке: H – ортоцентр треугольника ABC.
Свойства медианы треугольника
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (AM).
— Она делит треугольник на два равновеликих (с равными площадями) треугольника.
— Три медианы треугольника делят его на шесть равновеликих треугольников. Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины треугольника. На рисунке: AG/GA1=BG/GB1=CG/GC1=2/1.
Формула медианы:
Свойства биссектрисы треугольника
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
На рисунке: AL – биссектриса треугольника ABC.
Свойство биссектрисы треугольника: Отношение отрезков, на которые биссектриса делит сторону треугольника, равно отношению прилежащих к этим отрезкам сторон треугольника. На рисунке: BL/CL=AB/AC.
Биссектрисы треугольника пересекаются в одной точке. Эта точка равноудалена от всех сторон треугольника и является центром окружности, вписанной в треугольник.
Формула нахождения длины биссектрисы:
Средняя линия треугольника
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника.
На рисунке: MN – средняя линия треугольника ABC.
Средняя линия треугольника параллельна третьей стороне треугольника и равна её половине.
На рисунке: MN||AC,MN=AC/2.
Средние линии разбивают треугольник на четыре равных треугольника, подобных исходному с коэффициентом 1/2. Треугольник из средних линий называется срединным треугольником.
На рисунке: MNP – срединный треугольник треугольника ABC.
Равнобедренный треугольник
Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
На рисунке:
△ABC равнобедренный;
AC – основание,
AB, BC – боковые стороны.
Свойства равнобедренного треугольника:
- В равнобедренном треугольнике углы при основании равны.
На рисунке: ∠BAC=∠BCA - В равнобедренном треугольнике медиана, проведённая к основанию, является и
На рисунке: AD=DC, ∠ABD=∠CBD, BD⊥AC.
Признаки равнобедренного треугольника:
- Если два угла треугольника равны, то этот треугольник равнобедренный. На рисунке: ∠BAC=∠CAB⇒AB=BC.
- Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, BD⊥AC ⇒ AB=BC.
- Если в треугольнике медиана и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, ∠ABD=∠CBD ⇒ AB=BC.
- Если в треугольнике высота и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: BD⊥AC, ∠ABD=∠CBD ⇒ AB=BC.
На рисунке: AD=DC, BD⊥AC ⇒ AB=BC.Равносторонний треугольник
- Все стороны равностороннего треугольника равны.
- Все углы равностороннего треугольника равны 60°.
- Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
На рисунке: ∠C=90∘,CM – медиана △ABC⇒AM=BM=CM.
Высота, проведённая к гипотенузе, делит прямоугольный треугольник на два треугольника подобных друг другу и исходному треугольнику. На рисунке: △ACH∽△CBH∽△ABC.
В прямоугольном треугольнике катет, лежащий напротив угла в 30∘, равен половине гипотенузы.
На рисунке: если ∠A=30∘⇔BC=AB/2.
Основные метрические соотношения в прямоугольном треугольнике:
Пусть в треугольнике ABC ∠C=90∘, a=BC, b=AC – катеты, c=AB – гипотенуза, h=CH – высота к гипотенузе, a1=BH, b1=AH – проекции катетов на гипотенузу. Тогда:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы: Радиус r окружности, вписанной в прямоугольный треугольник, может быть вычислен по формуле: r=(a+b−c)/2, где a и b – катеты треугольника, c – его гипотенуза.
Калькулятор для прямоугольного треугольника поможет вычислить все его характеристики: стороны, углы, периметр и площадь, радиус вписанной и описанной окружности.
Треугольник и окружность
Около любого треугольника можно описать окружность, и только одну. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус описанной окружности треугольника ABC может быть вычислен по формулам: где a, b и c – длины сторон треугольника ABC, S – его площадь.
В любой треугольник можно вписать окружность, и только одну. Центром вписанной окружности треугольника является точка пересечения биссектрис треугольника.
Пусть a, b и c – длины сторон треугольника ABC и p=(a+b+c)/2 – его полупериметр. Тогда
— длины отрезков касательных из вершин A, B, C до точек касания вписанной окружности со сторонами треугольника равны p−a, p−b, p−c соответственно.
Радиус r вписанной окружности треугольника может быть вычислен по формуле: где a, b и c – длины сторон треугольника, p=(a+b+c)/2 – его полупериметр, S – площадь треугольника.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: площадь треугольника равна половине произведения стороны треугольника на высоту, проведённую к этой стороне.
Площадь по сторонам и углу между ними: площадь треугольника равна половине произведения двух его сторон на синус угла между ними. или половине произведения катетов:
Площадь по формуле Герона (где p=(a+b+c)/2 – полупериметр, a, b, c – стороны треугольника):
Площадь по трем сторонам и радиусу вписанной окружности (где p=(a+b+c)/2 – полупериметр треугольника, r — радиус вписанной окружности): Площадь по трем сторонам и радиусу описанной окружности:
Стороны прямоугольного треугольника (Теорема Пифагора):
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами и r — радиус вписанной окружности, R — радиус описанной окружности
Для нахождения характеристик простого, равнобедренного или равностороннего треугольника, воспользуйтесь калькулятором для треугольника.
Чтобы вычислить все характеристики прямоугольного треугольника, воспользуйтесь калькулятором для прямоугольного треугольника.
Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие. |
Теорема Чевы
Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Прямые AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда:
Теорема Менелая
Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Точки A1, B1 и C1 лежат на одной прямой тогда и только тогда, когда:
Площадь треугольника Формула и примеры решения
Площадь треугольника — это ограниченная им область на плоской плоскости.
Как мы знаем, треугольник — это фигура с замком, имеющая три стороны и три вершины. Таким образом, площадь треугольника по формуле — это все пространство, занимаемое внутри трех сторон треугольника. Общая процедура нахождения площади треугольника по формуле задается половиной произведения его основания и высоты.
В широком спектре термин «область» описывается как область, занимаемая внутри поля плоского объекта или фигуры. Измерение производится в квадратных единицах со средней единицей измерения в квадратных метрах (м 2 ). Для расчета площади существуют предопределенные формулы для квадратов, прямоугольников, кругов, треугольников и т. д. В этом блоге мы будем изучать формулы площади треугольников для различных типов треугольников, а также некоторые проблемы с иллюстрациями.
Как определить площадь треугольника?
Площадь треугольника по формуле можно описать как общую область, ограниченную тремя сторонами любого определенного треугольника.
Следовательно, чтобы найти площадь трехстороннего многоугольника, мы должны знать основание (b) и высоту (h). Это относится ко всем категориям треугольников, будь то разносторонний, равнобедренный или равносторонний. Обратите внимание на то, что основание и высота треугольника находятся под прямым углом друг к другу. Тогда единица площади рассчитывается в квадратных единицах (м 2 , см 2 ).
Иллюстрация: Можете ли вы найти площадь треугольника с основанием b = 3 см и высотой h = 4 см?
Используя формулу,
Площадь треугольника, A = 1/2 × b × h = 1/2 × 4 см × 3 см = 2 см × 3 см = 6 см²
Помимо формулы накладных расходов, мы есть метод Герона для вычисления площади треугольника, когда мы определяем длину его трех сторон. Точно так же тригонометрические функции используются для определения площади, когда мы знаем две стороны и угол между ними в треугольнике. Мы проанализируем область для всех приведенных здесь ситуаций.
Формула площади треугольника
Формула площади треугольника приведена ниже:
Формула площади треугольника = A = ½ (b × h) квадратных единиц
Где b и h — основание, а высота треугольника соответственно.
Теперь давайте разберемся, как вычислить площадь треугольника по данной формуле. Соответственно, как найти площадь треугольника с 3 сторонами по формуле Герона с примерами.
Площадь прямоугольного треугольника
В девяностоградусном треугольнике, также называемом прямоугольным, один угол равен 90°, а сумма двух дополнительных острых углов составляет 90°. В результате высота треугольника будет равна длине перпендикулярной стороны.
Площадь прямоугольного треугольника = A = ½ × основание × высота (Перпендикулярное пространство)
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, в котором все стороны равны. Стойка болта, проведенная от вершины треугольника к основанию, делит основание на две одинаковые части.
Чтобы оценить площадь равностороннего треугольника, нужно знать размеры его сторон.
• Площадь равностороннего треугольника = A = (√3)/4 × сторона²
Площадь равнобедренного треугольника
У равнобедренного треугольника две стороны равны, а также углы, противоположные равным сторонам, равны.
• Площадь равнобедренного треугольника = 1/4 b√(4a² – b²)
Периметр треугольника
Граница треугольника – это расстояние, заключенное вокруг треугольника, и рассчитывается путем суммирования всех трех стороны треугольника.
• Периметр треугольника = P = (a + b + c) единиц
Где a, b и c — поля треугольника.
Часть треугольника с тремя сторонами измененных мер можно найти по формуле Герона. Формула Герона состоит из двух важных шагов. Первым шагом является нахождение полупериметра треугольника путем суммирования всех трех сторон треугольника и деления его на 2.
Следующим шагом является применение значения полупериметра треугольника в центральной формуле, называемой «Формула Герона», к найти площадь треугольника.
В настоящее время возникает вопрос, когда мы знаем две стороны треугольника и угол между ними, то как найти его площадь.
Итак, если заданы любые два поля и угол между ними, то методы вычисления площади треугольника задаются следующим образом:
Площадь (∆ABC) = ½ bc sin A
Площадь (∆ABC) = ½ ab sin C
Площадь (∆ABC) = ½ ca sin B
Эти формулы очень легко составить, а также проанализировать.
Например, если в ∆ABC A = 30° и b = 2, c = 4 в единицах. Тогда площадь будет;
Площадь (∆ABC) = ½ bc sin A
= ½ (2) (4) sin 30
= 4 x ½ (поскольку sin 30 = ½)
= 2 кв.
Площадь треугольника Решенные примеры
Иллюстрация 1:
Найдите площадь остроугольного треугольника с основанием 13 дюймов и высотой 5 дюймов.
Пояснение:
A = (½) × b × h кв.
Единицы
⇒ A = (½) × (13 дюймов) × (5 дюймов)
⇒ A = (½) × (65 дюймов²) = 32,5 дюйма²
Иллюстрация 2:
Найдите площадь треугольника с углом наклона 90 градусов, основанием 7 см и высотой 8 см.
Пояснение:
A = (½) × b × h квадрат Единицы измерения
⇒ A = (½) × (7 см) × (8 см)
⇒ A = (½) × (56 см²)
⇒ A = 28 см²
Иллюстрация 3:
Найдите площадь тупоугольного треугольника с основанием 4 см и высотой 7 см.
Объяснение:
A = (½) × b × h квадратных единиц
⇒ A == (½) × (4 см) × (7 см)
⇒ A = (½) × (28 см²)
⇒ A = 14 см²
Вы можете узнать о формулах площади треугольника для различных типов треугольников, таких как равносторонний треугольник, прямоугольный треугольник и равнобедренный треугольник ниже.
• Площадь прямоугольного треугольника
В девяностоградусном треугольнике, также называемом прямоугольным, один угол равен 90°, а сумма двух других острых углов составляет 90°.
По этой причине высота треугольника равна длине стороны прямого угла.
Площадь прямоугольного треугольника = A = 1/2 × B × H
• Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, у которого все стороны равны. Перпендикуляр, проведенный из вершины треугольника к основанию, делит основание на две одинаковые части. Чтобы оценить площадь равностороннего треугольника, мы должны знать размеры его сторон.
Площадь равностороннего треугольника = A = (√3)/4 × сторона²
• Площадь равнобедренного треугольника
У равнобедренного треугольника двойные стороны равны, и углы, противоположные равным сторонам, также равны.
Площадь равнобедренного треугольника = A = 1/4 × b√4a 2 −b 2 4a 2 −b 2
Где «b» — основание, а «a» — степень единицы. одинаковых сторон.
Обратите внимание на приведенную ниже таблицу, в которой приведены все формулы площади треугольника.
| Заданные размеры | Формула площади треугольника |
| В то время как основание и высота треугольника указаны. | A = 1/2 (основание × высота) |
| В то время как стороны треугольника указаны как a, b и c. | (формула Герона) Площадь разностороннего треугольника = √s(s−a)(s−b)(s−c)s(s−a)(s−b)(s−c) , где a, b и c — стороны, а «s» — полупериметр; с = (а + b + с)/2 |
| Пока указаны две стороны и прилежащий угол. | A = 1/2 × плоскость 1 × плоскость 2 × sin(θ) , где θ — угол между данными двумя сторонами |
| При известном основании и высоте. | Площадь прямоугольного треугольника = 1/2 × Основание × Высота |
| Хотя это равносторонний треугольник и одна сторона указана. | Площадь равностороннего треугольника = (√3)/4 × плоскость 2 |
Хотя это равнобедренный треугольник, и известны эквивалентная сторона и основание. | Площадь равнобедренного треугольника = 1/4 × b√4a 2 −b 2 4a 2 −b 2 , где «b» — заданное основание, а «a» — указанная длина равной стороны. |
Вы вычисляете площадь треугольника, применяя различные методы. Например, есть основная формула, согласно которой площадь треугольника равна произведению основания на высоту. Этот метод работает, конечно, только пока вы определяете высоту треугольника.
Дополнительным является формула Герона, которая вычисляет площадь по трем сторонам треугольника в явном виде как квадратный корень из произведения s(s – a)(s – b)(s – c), где s – это полу периметр треугольника, то есть s = (a + b + c)/2.
Теперь мы рассмотрим формулу площади треугольника, если вы определите две стороны и угол между ними. Предположим, мы знаем значения двух сторон треугольника a и b и прилежащего угла C.
Опустите под прямым углом AD из вершины A треугольника на сторону BC и обозначьте эту высоту h.
Тогда конкретный треугольник ACD является прямоугольным, поэтому sin C будет равен h/b. Следовательно, h = b sin C. Следовательно, площадь треугольника равна половине произведения основания на высоту h, следовательно, площадь также равна половине ab sin C. Несмотря на то, что фигура представляет собой остроугольный треугольник, вы можете понять из рассуждения в предыдущем разделе, что h = b sin C также выполняется, когда треугольник прямоугольный или тупоугольный. В результате получаем общую формулу
Как определить площадь поверхности треугольников
Треугольник — это многоугольник, три стороны которого могут быть одинаковыми или неравными. Площадь поверхности треугольника – это вся площадь поверхности внутри границ треугольника. Площадь поверхности указывается в квадратных единицах, таких как квадратные сантиметры или квадратные дюймы. Вычисление площади поверхности треугольника — обычная задача геометрии.
Измерьте три стороны треугольника. Самая длинная сторона является основанием треугольника.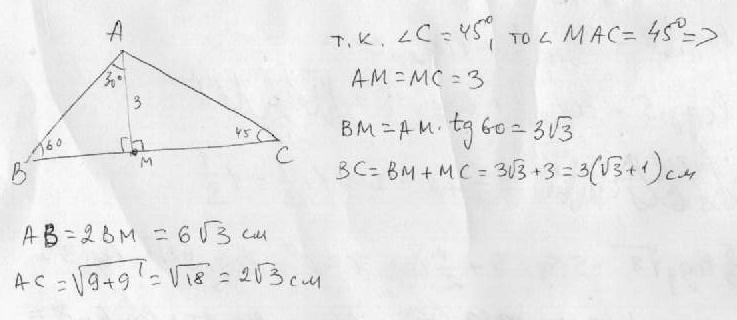
Если треугольник на бумаге, вы можете отмаркировать основание размером; или же, напишите свою базовую длину на блокноте.
Оцените высоту треугольника. Высота — это расстояние от основания до самого высокого угла треугольника. Линия высоты вертикальна к основанию и пересекает противоположный угол треугольника. Нарисуйте эту линию высоты на своем треугольнике, если это возможно, и отметьте измерение. Линия высоты будет проходить от конца до конца внутри треугольника.
Увеличьте базовую длину на высоту. Например, если ваш базовый размер равен 10 см, а высота равна 6 см, основание, увеличенное на высоту, составит 60 квадратных см.
Разделите результат умножения основания на высоту на два, чтобы определить площадь поверхности. На рисунке, когда вы делите 60 квадратных см на два, у вас есть итоговая площадь поверхности 30 квадратных см.
Чтобы найти площадь треугольника, умножьте основание на высоту, а затем разделите на 2. Деление на 2 происходит из-за того, что параллелограмм можно разделить на 2 треугольника.
Поскольку часть параллелограмма равна A = B * H, площадь треугольника должна составлять половину площади параллелограмма. В итоге формула площади треугольника:
A= 1/2.b.h или A= b.h/2
Где b — основание, h — высота, а · означает умножение.
Основание и высота треугольника должны быть под прямым углом друг к другу. На каждой из приведенных ниже иллюстраций основание является стороной треугольника. Тем не менее, в зависимости от треугольника, высота может быть или не быть стороной треугольника. Например, в прямоугольном треугольнике на иллюстрации 2 высота является стороной треугольника, поскольку она перпендикулярна основанию. В треугольниках на рисунках 1 и 3 боковые стороны не расположены под прямым углом к основанию, поэтому для обозначения высоты нарисована пунктирная линия.
Иллюстрация 1: Найдите площадь остроугольного треугольника с основанием 15 дюймов и высотой 4 дюйма.
Ответ:
A= 1/2 .
b.h
A= 1/2· (15 дюймов) · (4 дюйма)
A= 1/2· (60 дюймов²)
A= 30 дюймов²
________________________________________
Иллюстрация 2: Найдите площадь прямоугольного треугольника с основанием 6 см и высотой 9 см.
Ответ:
A= 1/2.b.h
A= 1/2 ·(6 см) · (9 см)
A= 1/2.(54 см²)
A= 27 см²
________________________________________
Рисунок 3: Найдите площадь тупоугольного треугольника с основание 5 дюймов и высота 8 дюймов.
Ответ:
A=1/2.b.h
A= 1/2 (5 дюймов) · (8 дюймов)
A= 1/2 (40 дюймов²)
A= 20 дюймов²
________________________________________
Иллюстрация 4: Коврик треугольной формы имеет площадь 18 квадратных футов и основание 3 фута. Найдите высоту.
Ответ:
На этом рисунке мы указали площадь треугольника и одно измерение, и нам предлагается работать в обратном направлении, чтобы найти другое измерение.
A= 1/2.b.h
18 футов² = 1/2\B7 (3 фута) · h
Умножая по отдельности две части уравнения на 2, мы получаем:
36 футов² = (3 футов) · h
Разделив по отдельности две части уравнения на 3 фута, мы получим:
12 футов = h
Вычислив это уравнение, мы получим:
h = 12 футов
__________________________________________
Краткий обзор: Укажите основание и высоту треугольника, и мы сможем определить площадь. Зная площадь и основание или высоту треугольника, мы можем обнаружить другое измерение. Формула площади треугольника:
A=1/2bh или A=b.h/2, где b — основание, а h — высота.
Какова площадь треугольника?
Все мы знаем, что треугольник — это многоугольник, у которого три стороны. Площадь треугольника – это размер площади, покрытой треугольником. Получаем площадь треугольника в квадратных единицах. Площадь треугольника можно определить, используя следующие две формулы: основание увеличивается на высоту треугольника, деленную на 2, а вторая — методом Герона.
Давайте обсудим формулу площади треугольника по существу.
Формула площади треугольника
Площадь многоугольника — это количество квадратных единиц, покрываемых многоугольником. Площадь треугольника определяется путем умножения основания треугольника и высоты треугольника, а затем деления на 2. Деление на 2 подготовлено по той причине, что треугольник является частью параллелограмма, который можно разделить на 2 треугольника.
Площадь параллелограмма = Основание × Высота
Где,
| В | основание параллелограмма |
| Н | высота параллелограмма |
Точно так же треугольник составляет половину параллелограмма, поэтому площадь треугольник:
A= 12×b×h
Где,
| B | основание треугольника |
| H | 901 69 высота треугольника
Метод Герона для вычисления площади треугольника
Формула Герона — это метод вычисления площади треугольника, когда заданы длины всех трех сторон треугольника.
Пусть a, b и c — длины сторон треугольника.
Площадь треугольника:
Площадь = s(s−a)(s−b)(s−c)− √
Где s — половина периметра,
s= a+b+c2
Мы также можем определить площадь треугольника с помощью следующих процедур:
1. В этом методе две Стороны, одна из которых включает Угол, является точным
Площадь = 12×a×b×sinc
В приведенной выше формуле a, b и c должны рассматриваться как длины сторон треугольника
2. В этом методе мы находим площадь равностороннего треугольника
Площадь = 3√×a24
3. Таким образом, мы находим площадь треугольника на координатной плоскости с помощью Матрицы
12×⎡⎣⎢x1x2x3y1y2y3111⎤⎦⎥
Где, (x1, y1), (x2, y2) , (x3, y3) — прямые трех вершин
4. В этом методе мы находим площадь треугольника, в котором два вектора из одной вершины находятся под рукой.
Площадь треугольника = 12(u→×v→)
Q.1: Предположим, что стороны прямоугольного треугольника ABC имеют следующие размеры; 5 см, 12 см и 13 см.
соответственно
Ответ: В △ABC, в котором основание= 12 см, а высота= 5 см Найдите площадь треугольника, две стороны которого равны 12 см и 11 см, а периметр равен 36 см.
Ответ: Здесь периметр треугольника = 36 см, a = 12 см и b = 11 см.
Третья сторона c = 36 см – (12 + 11) см = 13 см
Следовательно, получаем 2s = 36, т. е. s = 18 см,
с – a = (18 – 12) см = 6 см,
с – b = (18 – 11) см = 7 см,
и, s – c = (18 – 13) см = 5 см.
Площадь треугольника = s(s-a)(s-b)(s-c)——————-√
A= 18×6×7×5 ————-√
A= 6105—√ см 2
Часто задаваемые вопросы
1.
Что вы понимаете под площадью треугольника? Площадь треугольника — это площадь, ограниченная его границей или тремя сторонами треугольника.
2. Какова будет площадь, если известны две стороны треугольника и угол между ними?Площадь будет эквивалентна половине произведения двух заданных сторон и синуса угла между ними.
3. Как узнать площадь треугольника, у которого известны три стороны?Хотя значения трех сторон треугольника известны, мы сможем найти площадь этого треугольника, используя формулу Герона.
4. Как с помощью векторов найти площадь треугольника?Предположим, векторы u и v образуют треугольник в пространстве. Теперь площадь этого треугольника эквивалентна половине произведения этих двух векторов, так что A = ½ |u × v|.
5. Как вычислить площадь треугольника? Для предполагаемого треугольника, где основание треугольника равно b, а высота равна h, площадь треугольника может быть заранее рассчитана по формуле, например; A = ½ (b × h) кв.
Единица измерения
Математическое выражение: площадь треугольника
00:00:03.230
В этом уроке мы узнаем о площади треугольника.
00:00:08.100
Сначала рассмотрим этот параллелограмм с основанием B и высотой H.
00:00:15.060
На предыдущем уроке мы узнали, что площадь параллелограмма A = BH.
00:00:22,220
Заметьте, что если мы разрежем этот параллелограмм пополам и удалим эту часть, мы получим треугольник с основанием B и высотой H.
00:00:33,210
Так как площадь этого треугольника, составляет половину площади параллелограмма, формула площади этого треугольника А = 1/2ВН.
00:00:45.080
Обратите внимание на то, что очень важно включить устройство. Поскольку это формула площади, ее единица измерения будет в виде квадратной единицы.
00:00:55.050
Мы увидим больше пояснений по этому поводу в следующем примере.
00:01:00.140
Теперь давайте рассмотрим несколько примеров использования этой формулы.
00:01:05.070
Найдите площадь этого треугольника, если его основание равно 5 см, а высота 4 см.
00:01:13.020
Сначала мы начнем с формулы площади треугольника, A = 1/2BH.
00:01:20.040
Поскольку основание равно 5 см, мы можем заменить B на 5.
00:01:26.240
Точно так же, поскольку высота равна 4 см, мы можем заменить H на 4.
00:01:34,120
Далее мы можем упростить, умножив 5 на 4. Это даст 20.
00:01:42,070
Обратите внимание, что одна половина скобки 20 может быть переписана как 1 скобка над 2.
00:01:49.220
Продолжим. 1 умножает 20, возвращает 20.
00:01:55.140
20 делит на 2, дает 10.
00:01:59.140
Обратите внимание, что это число не имеет смысла, если мы не включим для него единицу измерения.
00:02:04.170
Поскольку единицы измерения даны в сантиметрах, единицей измерения площади будет квадратный сантиметр.
00:02:11.140
Следовательно, площадь этого треугольника равна 10 квадратных сантиметров.
00:02:17.200
Следующий пример, учитывая, что площадь этого треугольника составляет 24 квадратных фута, а его основание равно 6 футам. Найдите его высоту.
00:02:27.070
Снова начнем с формулы площади треугольника, A = 1/2BH.
00:02:34.030
Теперь, поскольку площадь и основание известны, мы можем найти высоту, решив это уравнение относительно h. Вот как.
00:02:43.110
Легче работать с этим уравнением, если мы перепишем этот термин, половина BH как, 1 BH больше 3. 1BH равно BH.
00:02:55,020
Далее, обратите внимание, что мы можем удалить эту дробь, умножив обе части уравнения на 2.
00:03:02,050
Таким образом, мы имеем 2A = BH.
00:03:07.080
Далее, поскольку площадь равна 24, мы можем заменить «A» на 24.
00:03:14.050
2 умножить на 24, получится 48.
00:03:19.000
Точно так же, поскольку основание равно 6 футам, мы можем заменить B на 6.
00:03:26.020
Теперь у нас есть 6h равно 48.
Leave A Comment