В треугольнике угол равен в 90 высота найдите: В треугольнике ABC угол C равен 90`, CH — высота, АВ = 27, sin A…

Задание 15 — разбор задания ЕГЭ по предмету Математика (базовый)

• Newtonew
• ProTeachers
• MOOC 2016
• Большая переменная

Мы в соц.сетях:

• Статьи
• ·
• Разборы
• ·
• Новости

Написать статью

Решение №1

1. Давайте вспомним определение косинуса в прямоугольном треугольнике.
2. Косинус в прямоугольником треугольнике — это отношение прилежащего катета (маленькой стороны рядом с углом) к гипотенузе (самой длинной стороне прямоугольного треугольника).
3. Рассмотрим треугольник AHC. 
4. Известно, что \(\cos \mathrm{A} = 0.8\)
5. Но что такое «косинус угла А» по определению? Это отношение прилежащей стороны к гипотенузе. 
6. То есть:
    \(\cos \mathrm{A} = \cfrac{AH}{AC} \\ 0.8 = = \cfrac{AH}{AC} \\ AH = 0.8\cdot AC = 0.8\cdot 4 = 3.2\)

Ответ: длина отрезка AH равна 3,2 см.

Evgeny Smirnov

Сообщение:

Запрос успешно отправлен. В ближайшее время расширенный доступ будет предоставлен.

– Oбразование как Стиль Жизни

Присылайте свои колонки

и предложения

У вас есть интересная новость или материал из сферы образования или популярной науки?

Расскажите нам!

[email protected]

© 2014-2023 Newtonew. 12+

Просветительский медиа-проект об образовании, посвящённый самым актуальным и полезным концепциям, теориям и методикам, технологиям и исследованиям, продуктам и сервисам. Мы говорим о том, как развиваются и изменяются образование и наука.
Копирование материалов возможно только с разрешения редакции Newtonew.

ЕГЭ спецпроект ProTeachers

MOOC 2016 Большая переменная

Физика: игра света

Маршрут в будущее

Считаные годы

Образование XXI века

Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.

App Store Google Play

Подписаться на рассылку

Подписаться на рассылку

Авторизация на сайте

Вход через соц.сети:

ВКонтакте Facebook Google

---

Новый пользователь

Введите ваш email:

Введите пароль:

Повторите пароль:

---

  назад

Напомнить пароль

Введите email, на который вы зарегистрированы:

---

  назад

Пароль выслан

Мы выслали ваш пароль для входа в систему на указанный email.

---

Не забывайте о том, что вы можете авторизоваться в системе через социальные сети. Если при регистрации в соц.сетях вы указывали тот же email что и на нашем сайте, то после авторизации вы попадете в свой профиль.

Вход через соц.сети:

ВКонтакте Facebook Google

Подтвердите регистрацию

На указанный e-mail было отправлено письмо со ссылкой. Пожалуйста, перейдите по ссылке для подтверждения.

Вход через соц.сети:

ВКонтакте Facebook Google

Регистрация подтверждена

Вы успешно зарегистрировались

3. В треугольнике АВС угол С равен 90°, угол В равен 35°, СD — высота. Найдите углы… 7 класс А.П. Ершова Геометрия. КП-4 Вариант А 1 – Рамблер/класс

3. В треугольнике АВС угол С равен 90°, угол В равен 35°, СD — высота. Найдите углы… 7 класс А.П. Ершова Геометрия. КП-4 Вариант А 1 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

3.
В треугольнике АВС угол С
равен 90°, угол В равен 35°,
СD — высота. Найдите углы
треугольника АСD.

ответы

ответ

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

1. Доказать: ∆АВС — равнобедренный. Геометрия 7 класс А.П. Ершова. СП-6 Вариант В-1

(Подробнее…)

ГДЗЕршова А.П.7 классГеометрия

Геометрия. 10 Класс

1. Через середину М сторони АВ трикутника АВС проведено площину, яка паралельна, прямій АС і перетинає сторону ВС у точці N. Довести NM (Подробнее…)

ГеометрияУчителяДосугОГЭЭкзаменыЕГЭГИАВыпускнойГДЗУчебники

Какие два числа надо поменять местами, чтобы квадрат стал магическим? ГДЗ по математике 3 класс Моро Часть 1 стр 30 задание 15

Всем привет) А как вы думаете?)
Какие два числа надо поменять местами, чтобы квадрат стал магическим?
 6  9  2 (Подробнее. ..)

ГДЗ3 классМатематикаМоро М.И.

№ 569. ГДЗ Математика 5 класс Никольский. Помогите доказать!

Докажите, что длина ломаной ABС больше длины ломаной АDС (рис. 118).
  (Подробнее…)

ГДЗМатематика5 классНикольский С.М.

2. Один из внутренних углов треугольника в 3 раза больше другого, а внешний угол, смежный… А.П. Ершова Геометрия 7 класс. СП-9 Вариант Б-2

2.
Один из внутренних углов
треугольника в 3 раза больше другого, а внешний угол, (Подробнее…)

ГДЗГеометрияЕршова А.П.7 класс

Калькулятор высоты треугольника

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Адена Бенн

Последнее обновление: 01 марта 2023 г.

Содержание:

• Какова высота треугольника?
• Как найти высоту треугольника – формулы
• Как найти высоту равностороннего треугольника
• Как найти высоту равнобедренного треугольника
• Как найти высоту прямоугольного треугольника
• Как найти высоту треугольника с помощью этого калькулятора высоты треугольника?
• Часто задаваемые вопросы

Если вы ищете простой инструмент для расчета высоты в любом треугольнике , вы находитесь в правильном месте — этот калькулятор высоты треугольника является инструментом для вас. Если вы ищете формулы высоты треугольника для специальных треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник или любой разносторонний треугольник, этот калькулятор является безопасной ставкой — он может вычислить высоты треугольника, а также стороны треугольника, углы, периметр, площадь. Пожалуйста, не ждите больше; Попробуй!

Если вас все еще интересует формула высоты равностороннего треугольника или как найти высоту без площади, продолжайте прокручивать, и вы найдете ответ.

Какова высота треугольника?

Каждая сторона треугольника может быть основанием, и из каждой вершины можно провести линию, перпендикулярную линии, содержащей основание – это высота треугольника. Каждый треугольник имеет три высоты, которые также называются высотами . Рисование высоты известно как падение высоты в этой вершине.

Как найти высоту треугольника – формулы

Существует много способов найти высоту треугольника. Наиболее популярная формула использует площадь треугольника, но существует множество других формул:

1. Заданная площадь треугольника

   Известное уравнение площади треугольника можно преобразовать в формулу высоты прямоугольного треугольника:

   • площадь=b×h/2\mathrm{площадь} = b \times h / 2площадь=b×h/2, где bbb — основание, hhh — высота; и

   • Итак, h=2×площадь/bh = 2 \times \mathrm{площадь} / bh=2×площадь/b.

   Но как найти высоту треугольника без площади? Самые популярные формулы:

2. Данные стороны треугольника

   Использование уравнения, называемого формулой Герона, позволяет вычислить площадь по сторонам треугольника. Затем, когда вы знаете площадь, вы можете использовать основное уравнение, чтобы узнать, какова высота треугольника:

   Формула Герона :

площадь = 0,25 × (a+b+c)×(−a+b+c)×(a−b+c)×(a+b−c)\qquad \маленький \начать{разделить} \mathrm{площадь}=\ &0,25 \times \sqrt{(a + b + c)}\\[0,5em] & \times\sqrt{(-a + b + c)} \\[.5em] &\times\sqrt{ (a — b + c)}\\[.5em] &\times\sqrt{ (а + б — в)} \конец{разделить} площадь = ​0,25×(a+b+c)

​×(−a+b+c)

​×(a−b+c)

​×(a+b−c)

​

Следовательно, :

h=0,5b×(a+b+c)×(−a+b+c)×(a−b+c)×(a+b−c)\qquad \маленький \начать{разделить} h = \frac{0.

5}{b}&\times\sqrt{(a + b + c)}\\[0,5em] &\times\sqrt{(-a + b + c)}\\[.5em] &\times\sqrt{(a — b + c)}\\[.5em] &\times\sqrt{(a + b — c)} \end{split}h=b0,5​​×(a+b+c)

​×(−a+b+c)

​×(a−b+c)

​×(a+b−c)

Более подробно об этом уравнении вы можете узнать в нашем специальном Калькулятор формулы Герона.

3. Даны две стороны и угол между ними

   Используйте тригонометрию или другую формулу площади треугольника:

площадь=0,5×a×b×sin⁡(γ)\qquad \маленький \mathrm{площадь} = 0,5 \times a \times b \times \sin(\gamma)площадь=0,5×a×b×sin(γ)

(или площадь=0,5×a×c×sin⁡(β) \mathrm{площадь} = 0,5 \times a \times c \times \sin(\beta)площадь=0,5×a×c×sin(β) или площадь=0,5×b×c×sin⁡(α)\mathrm{ площадь} = 0,5 \times b \times c \times \sin(\alpha)area=0,5×b×c×sin(α), если даны разные стороны):

ч=2×0,5×а×b×sin⁡(γ)b=a×sin⁡(γ)\qquad \маленький \начать{разделить} h &= \frac{2 \times 0,5 \times a \times b \times \sin(\gamma)}{b} \\ &= а\раз\грех(\гамма) \end{split}h​=b2×0. 5×a×b×sin(γ)​=a×sin(γ)​

Если ваша фигура относится к особому типу треугольника, прокрутите вниз, чтобы найти формулы высоты треугольника. Упрощенные версии общих уравнений легче запомнить и вычислить.

Как найти высоту равностороннего треугольника

Равносторонний треугольник — это треугольник, у которого все три стороны равны и все три угла равны 60°60\градус60°. Все три высоты имеют одинаковую длину, которая может быть рассчитана из:

• hΔ=a×3/2hΔ = a \times \sqrt{3} / 2hΔ=a×3​/2, где aaa — сторона треугольника.

В равностороннем треугольнике высоты, биссектрисы, биссектрисы и медианы совпадают.

Если вас интересуют формулы площади и периметра, посетите наш специальный калькулятор равностороннего треугольника.

Как найти высоту равнобедренного треугольника

Равнобедренный треугольник — это треугольник, две стороны которого имеют одинаковую длину. Есть две разные высоты равнобедренного треугольника; формула для вершины: 92}\раз б/у \end{split}ha​=2×площадь/a=a2−(0,5×b)2

​×b/a​

Тригонометрия :

ha=b×sin⁡(β)\qquad \маленький h_{\rm a} = b \times \sin(\beta)ha​=b×sin(β)

Формулы площади и периметра треугольника этого типа можно найти на нашем специальном калькуляторе равнобедренного треугольника.

Как найти высоту прямоугольного треугольника

Прямоугольным треугольником называется треугольник, один угол которого равен 90°90\градус90°. Две высоты найти несложно, так как катеты перпендикулярны: если более короткий катет — основание, то более длинный катет — высота (и наоборот). Третью высоту треугольника можно вычислить по формуле:

hc=площадь×2/c=a×b/ch_c=\mathrm{площадь}\times 2/c = a\times b/chc​=площадь×2/c=a×b/c

Если вы Вас интересуют уравнения площади и периметра этого треугольника, посмотрите на наш калькулятор прямоугольного треугольника.

Как найти высоту треугольника с помощью этого калькулятора высоты треугольника?

Прочитав наше объяснение, мы почти уверены, что теперь вы понимаете, как найти высоту треугольника без заданной площади или какова высота треугольника. Но давайте рассмотрим простой пример, чтобы показать вам гибкость нашего инструмента:

1. Выберите тип треугольника . Предположим, мы хотим вычислить высоты разностороннего треугольника, поэтому мы не меняем параметр по умолчанию.
2. Введите указанные значения . Это может быть три стороны или две стороны и угол. Остановимся на первом варианте: a=6 ina = 6\ \mathrm{in}a=6 in, b=14 inb = 14\ \mathrm{in}b=14 in, c=17 inc = 17\ \mathrm {дюйм}c=17 дюймов 90 010
3. Калькулятор высоты треугольника отобразил все три высоты — они равны 13,17 дюйма, 13,17\ \mathrm{дюйма}13,17 дюйма, 5,644 дюйма, 5,644\ \mathrm{дюйма}, 5,644 дюйма и 4,648 дюйма, 4,648\ \mathrm {in}4,648 дюйма. Более того, калькулятор показал нам все углы треугольника, площадь и периметр.

Разве это не прекрасно?

Часто задаваемые вопросы

Как найти высоту треугольника, если все стороны равны?

Чтобы определить высоту равностороннего треугольника:

1. Запишите длину стороны вашего треугольника.
2. Умножьте на √3 ≈ 1,73 .
3. Разделить результат на 2 .
4. Вот оно! В результате получится высота вашего треугольника!

Все ли высоты треугольника равны?

Обычно нет , каждая высота треугольника может иметь разную длину. Однако если все три высоты имеют равные длины , то этот треугольник равносторонний , то есть все его стороны тоже равны (но не равны высотам!).

Как найти высоту треугольника по углам?

Вы не можете определить высоту треугольника, зная только углы треугольника. Это потому, что треугольников с такими углами бесконечно много, и длины высот в каждом из этих треугольников разные!

Как найти высоту прямоугольного треугольника?

Каждая из перпендикулярных сторон (катетов) прямоугольного треугольника является его высотой. Чтобы вычислить третью высоту h ₃ , воспользуемся формулой площади:

½ × катет ₁ × катет ₂ = площадь = ½ × гипотенуза × h ₃ В следствии:

h ₃ = катет ₁ × катет ₂ / гипотенуза

Какова наименьшая высота треугольника 3 4 5?

Ответ: 2. 4 . Чтобы получить этот результат, обратите внимание, что площадь равна Площадь = ½ × 3 × 4 = 6 .

С другой стороны, Площадь = ½ × Гипотенуза × Наименьшая высота .

Так как Гипотенуза = 5 и Площадь = 6 , мы получаем Кратчайшая высота = 2 × Площадь / Гипотенуза = 2 × 6 / 5 = 2,4 .

Ханна Памула, доктор философии

Особый треугольник?

Высоты (высоты)

Углы

Прочие

Периметр

Посмотреть 18 подобных калькуляторов треугольников 🔺

30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… еще 15

Как найти высоту равнобедренного прямоугольного треугольника 45/45/90 909002 901 Вся основная геометрия Ресурсы

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Справка по базовой геометрии » Плоская геометрия » Треугольники » 45/45/90 прямоугольных равнобедренных треугольников » Как найти высоту прямоугольного равнобедренного треугольника

Возможные ответы:

Правильный ответ:

2

2

5 Объяснение:

Сообщить об ошибке

Найдите высоту прямоугольного треугольника 45-45-90 с гипотенузой .

Возможные ответы:

Правильный ответ:

Объяснение:

Если гипотенуза прямоугольного треугольника 45-45-90 тогда:

Высота и основание треугольника будут одинаковой длины, так как это равнобедренный треугольник 45-45-90.

Поскольку как A, так и B будут равы треугольник, если его гипотенуза равна  см.

Возможные ответы:

Правильный ответ:

Пояснение:

Учитывая, что это треугольник 45/45/90, это означает, что он также равнобедренный. Поскольку гипотенуза равна 2√7 см, это означает, что основание и высота (две оставшиеся стороны) будут равны.

Длину одной из ножек можно определить одним из двух способов.

1. Теорема Пифагора

2. Использование

 

Используя теорему Пифагора, мы уже определили, что «a» и «b» — одно и то же число. Скажем. Это позволяет переписать уравнение в виде , что может быть упрощено до 

. Поскольку s – это наше неизвестное, мы будем решать для s.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника, то какова его высота?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова. Мы можем переписать приведенное выше уравнение следующим образом:

Упрощение.

Умножить дробь на единицу в виде:

Подставить.

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты треугольника?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова. Мы можем переписать приведенное выше уравнение следующим образом:

Упростить.

Умножить дробь на единицу в виде:

Подставить.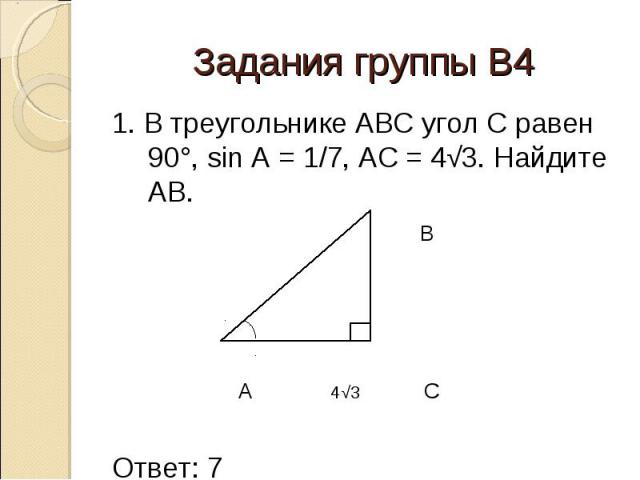

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова. Мы можем переписать приведенное выше уравнение следующим образом:

Упростить.

Умножьте дробь на единицу в виде:

Заместитель.

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Упрощение.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты треугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова. Мы можем переписать приведенное выше уравнение следующим образом:

Упростить.

Умножьте дробь на единицу в виде:

Замена.

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Упрощение.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомните теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова. Мы можем переписать приведенное выше уравнение следующим образом:

Упростить.

Умножить дробь на единицу в виде:

Подставить.

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Упрощение.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, основание и высота имеют одинаковую длину. Мы можем переписать приведенное выше уравнение следующим образом:

Упростить.

Умножить дробь на единицу в виде:

Подставить.

Решить.

Теперь подставьте значение гипотенузы, чтобы найти высоту данного треугольника.

Упрощение.

Сообщить об ошибке

Если гипотенуза равнобедренного прямоугольного треугольника равна , какова длина высоты?

Возможные ответы:

Правильный ответ:

Пояснение:

Равнобедренный прямоугольный треугольник — это еще один способ сказать, что треугольник является треугольником.

Теперь вспомним теорему Пифагора:

Поскольку мы работаем с треугольником, длина основания и высоты одинакова.