Задание № 6. Планиметрия. ЕГЭ. Математика.
БАЗА ЗАДАНИЙ
Задание № 6. Планиметрия.
1. У треугольника со сторонами 12 и 15 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 10. Найдите длину высоты, проведенной ко второй стороне.
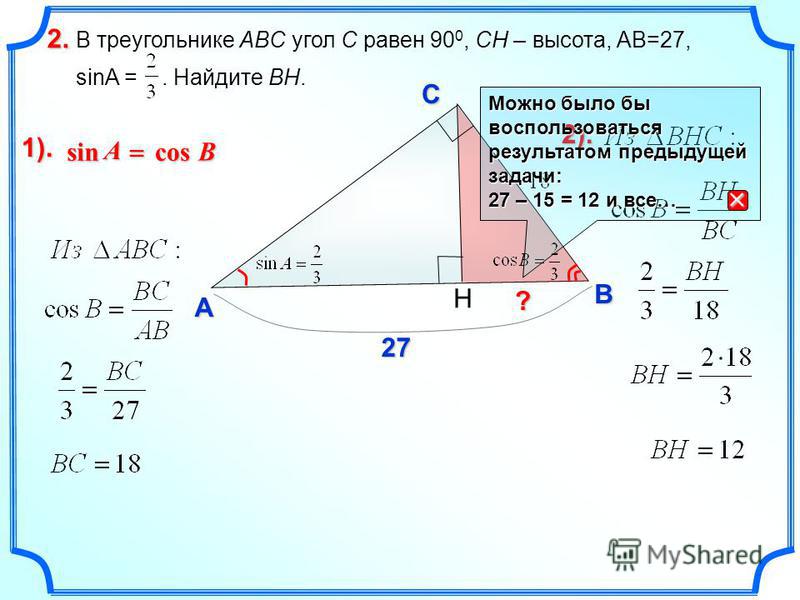
2. В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
3. В треугольнике ABC угол C равен 66°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.
4. Угол A прямоугольного треугольника равен 64°. Найдите угол AOE, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
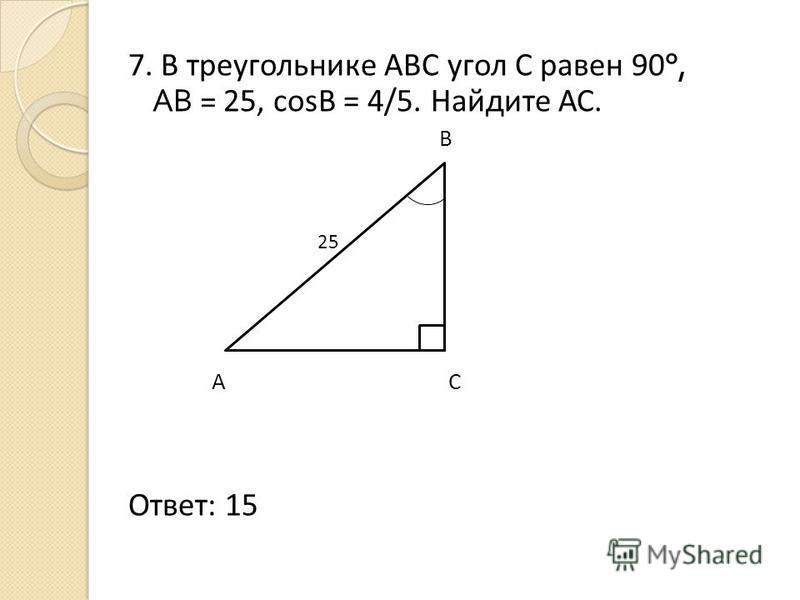
5. В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла
6. В треугольнике ABC AC = BC, AB = 8, sin∠BAC = 0,5. Найдите высоту AH.
7. В треугольнике ABC известно, что AC = BC, AH – высота, sin∠BAC=7/25. Найдите sin∠BAH.
8. В треугольнике ABC известно, что AC = BC, AH – высота, tg∠BAC=7/24. Найдите cos∠BAH.
9. В треугольнике ABC известно, что AC = BC=4√15, cos∠BAC=0,25. Найдите высоту AH.
10. В треугольнике ABC угол C равен 90°, AB=10, AC=√51. Найдите sin∠A.
11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.
12. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°.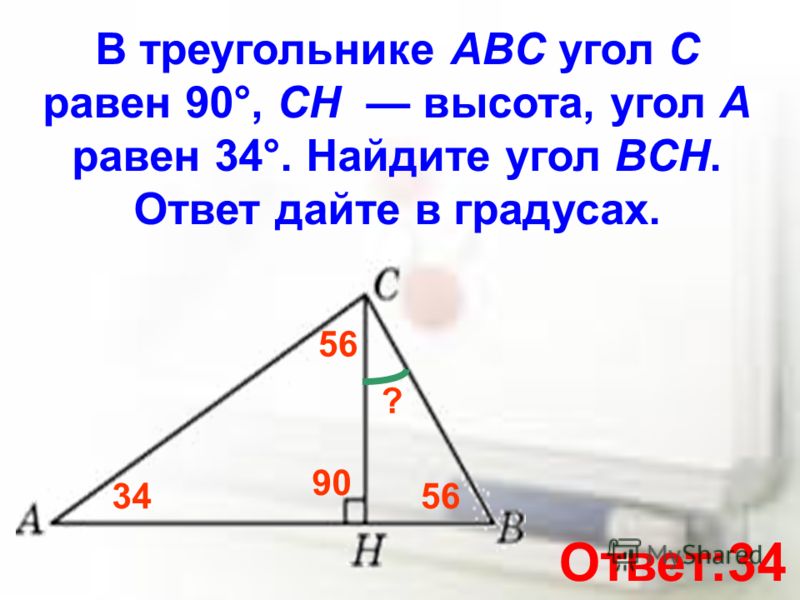 Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
13. Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
14. Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.
15. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.
16. В треугольнике ABC AC=BC=20, AB=28. Найдите косинус угла A.
17. В треугольнике ABC известно, что AC=BC=7, tg∠A= √33/4 . Найдите AB.
18. В треугольнике ABC AC = BC = 5, sin∠A =0,8. Найдите АВ.
19. В равностороннем треугольнике ABC высота CH равна 45√3. Найдите AB.
20. В треугольнике ABC известно, что AC = BC, AB = 1, cos∠A= √17/17. Найдите высоту
21. В треугольнике ABC известно, что AC = BC, AB = 16, tg∠A=0,5. Найдите высоту CH.
22. В треугольнике ABC известно, что AC = BC, AB = 4, высота CH=2√3. Найдите угол С.
23. В треугольнике ABC угол C равен 90°, AC=6, tg∠A=√5/2. Найдите AB.
24. В треугольнике ABC стороны AC и BC равны, угол C равен 156°, угол CBD – внешний. Найдите угол CBD. Ответ дайте в градусах.
25. В прямоугольном треугольнике АВС из вершины прямого угла проведена медиана CD
26. Высота AD треугольника АВС делит противоположную сторону на части: CD = 4, BD =1,5. Найдите длину стороны АC, если tg∠B = 2.
Найдите длину стороны АC, если tg∠B = 2.
27. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin∠A=0,5. Найдите BH.
28. В треугольнике ABC угол C равен 90°, AB = 5, cos∠A = 0,6. Найдите высоту CH.
29. В треугольнике ABC угол C равен 90°, угол A
30. В треугольнике ABC угол C равен 90°, CH — высота, BC = 3, cos∠A= √35/6. Найдите AH.
31. В треугольнике ABC угол C равен 90°, CH — высота, AB = 13, tg∠A = 1/5. Найдите AH.
32. В треугольнике ABC угол C равен 90°, AB = 13, tg∠A = 1/5. Найдите высоту CH.
33. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cos∠A.
34. В тупоугольном треугольнике ABC AC = BC=8, высота AH равна 4. Найдите sin∠
35. В тупоугольном треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите sin∠BAC.
36. В тупоугольном треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos∠BAC.
37. В треугольнике ABC угол C равен 90°, синус ∠В=7/25. Найдите синус внешнего угла при вершине А.
38. В треугольнике ABC угол C равен 90°, косинус угла В=0,6. Найдите косинус внешнего угла при вершине А.
39. В треугольнике ABC угол C равен 90°, косинус внешнего угла при вершине A равен -0,1. Найдите синус ∠B
40. В треугольнике ABC угол C равен 90°, тангенс внешнего угла при вершине A равен -2. Найдите тангенс ∠B.
Найдите тангенс ∠B.
41. В треугольнике ABC AC=BC=√17, AB=8. Найдите тангенс внешнего угла при вершине В.
42. В треугольнике ABC AC=BC=8, косинус внешнего угла при вершине В равен -0,5. Найдите AB.
43. Один из внешних углов треугольника равен 85°. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
44. В треугольнике
45. В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.
46. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Под редакцией А. Л. Семенова и И. В. Ященко — Реферат
4.1. Первое решение. Рассмотрим прямоугольный треугольник OBC. Его катет BC равен 3, гипотенуза OB
Второе решение. Угол AOB равен 45о. Следовательно, sin A = .
Ответ. 2.
4.2. Рассмотрим прямоугольный треугольник OBC. Его катеты BC и OC равны соответственно 4 и 2. Следовательно, тангенс угла BOC равен 2. Учитывая, что тангенс смежного угла равен тангенсу данного угла, взятому с противоположным знаком, получаем, что тангенс угла AOB равен – 2.
Ответ. – 2.
4.3. Рассмотрим треугольник OBС. OC =
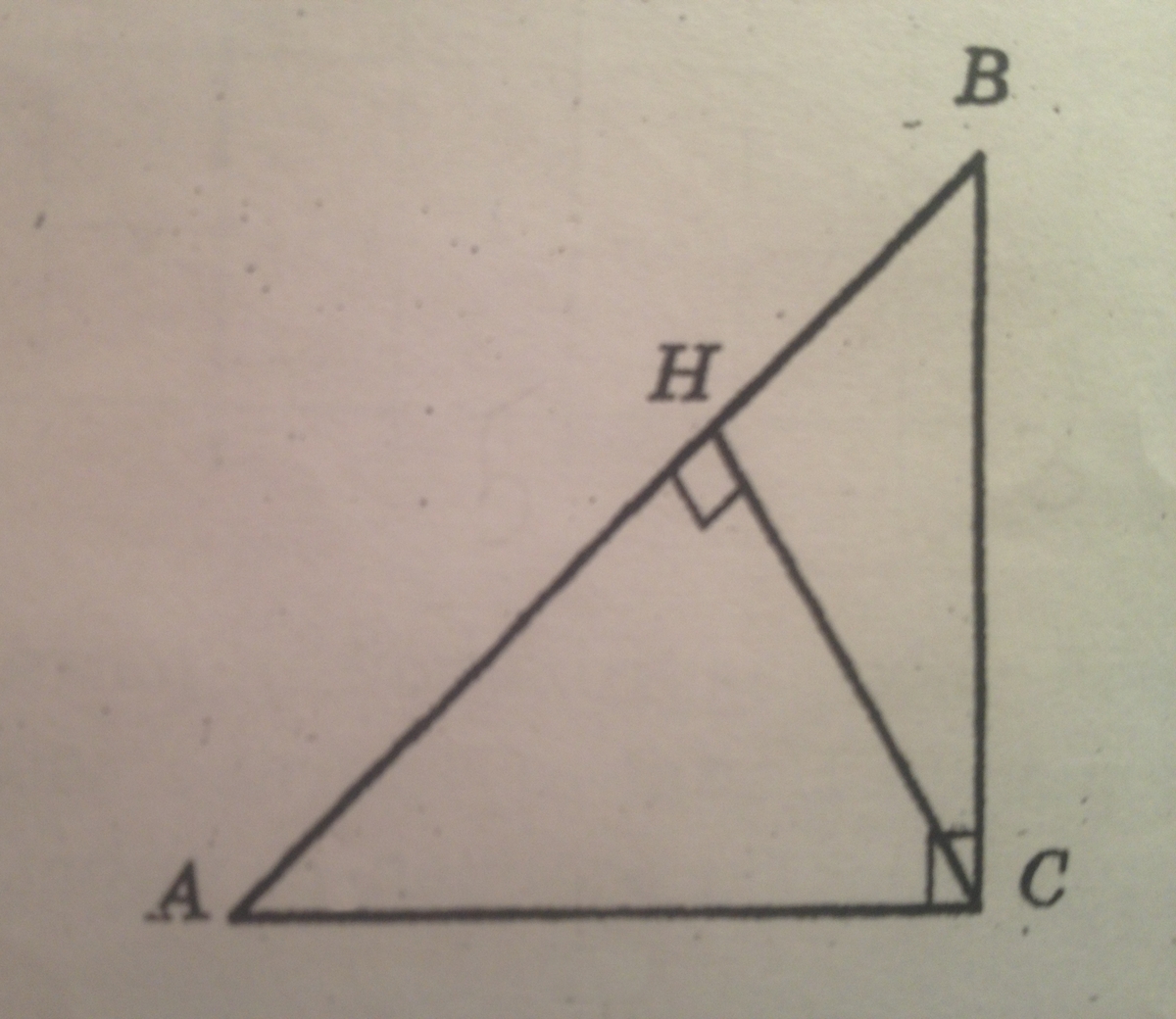 Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен .
Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен .Ответ. 2.
5.1. Подставляя в формулу BC = ABsin A данные значения BC и sin A, находим AB = 5.
Ответ. 5.
5.2. Имеем BC = ACtg A = 80,75
= 6. По теореме Пифагора находим AB =
Ответ. 10.
5.3. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cosBCH = 0,8. CH = BCcosBCH = 4,8.
Ответ. 4,8.
6.1. Первое решение. Проведем высоту CH. Имеем CH = ACsin A = 8. По теореме Пифагора находим AH = и, следовательно, AB = 12.
Второе решение. Проведем высоту CH. Воспользуемся формулой , выражающей косинус острого угла через его синус. Тогда cos
Ответ. 12.
6.2. Первое решение. В равнобедренном треугольнике ABC угол A равен углу B, BH = ABcos B = 6. По теореме Пифагора находим AH = .
Второе решение. Воспользуемся
формулой ,
выражающей синус острого угла через
его косинус. Тогда sin A = = 0,8. Следовательно, поскольку в
равнобедренном треугольнике A = B,
получаем AH = ABsin B = 8.
Ответ. 8.
6.3. Первое решение. В равнобедренном треугольнике ABC угол A равен углу C, значит, tg A = tg C и AH = . По теореме Пифагора находим AC = = 10.
Второе решение. Так как tg C = , то угол C равен 30о. Угол A равен углу C. Так как катет прямоугольного треугольника, лежащий против угла в 30о, равен половине гипотенузы, то AC = 10.
Ответ. 10.
Тренировочные работы
1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника
1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите cos A.
2. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите tg A.
3. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите sin A.
4. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите tg A.
5. В треугольнике ABC угол C равен 90о, tg A = 0,75. Найдите sin A.
6. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите cos B.
7.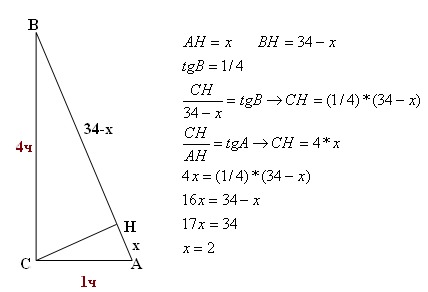 В треугольнике ABC угол C равен
90о, cos A = 0,8. Найдите sin B.
В треугольнике ABC угол C равен
90о, cos A = 0,8. Найдите sin B.
8. В треугольнике ABC угол C равен 90о, CH – высота, AC = 10, AH = 8. Найдите cos B.
9. В треугольнике ABC угол C равен 90о, CH – высота, BC = 10, BH = 6. Найдите cos A.
2. Нахождение значений тригонометрических функций острых углов равнобедренного треугольника
1. В треугольнике ABC AC = BC = 10, AB = 12. Найдите cos A.
2. В треугольнике ABC AC = BC = 10, AB = 16. Найдите tg A.
3. В треугольнике ABC AC = BC = 10, AB = 16. Найдите sin A.
4. В треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите sin A.
5. В треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите cos A.
6. В треугольнике ABC AC = BC, AB = 10, AH – высота, BH = 6. Найдите cos A.
7. В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите косинус угла BAH.
8. В треугольнике ABC AB = BC, AC = 16, высота CH равна 8. Найдите синус угла ACB.
Найдите синус угла ACB.
9. В треугольнике ABC AB = BC, AC = 5, CH – высота, AH = 4. Найдите синус угла ACB.
3. Нахождение значений тригонометрических функций тупых углов
1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите косинус внешнего угла при вершине A.
2. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите тангенс внешнего угла при вершине A.
3. В треугольнике ABC угол C равен 90о, cos B = 0,8. Найдите косинус внешнего угла при вершине A.
4. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите синус внешнего угла при вершине A.
5. В треугольнике ABC угол C равен 90о, tg A = 0,75. Найдите косинус внешнего угла при вершине A.
6. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите косинус внешнего угла при вершине B.
7. В треугольнике ABC AC = BC = 10, AB = 12. Найдите синус внешнего угла при вершине B.
8. В треугольнике ABC AB = BC, AB = 10, высота CH равна 8. Найдите косинус угла ABC.
Найдите косинус угла ABC.
9. В треугольнике ABC AB = BC, CH – высота, AB = 10, BH = 6. Найдите синус угла ABC.
4. Нахождение тригонометрических функций углов, изображенных на клетчатой бумаге
1. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
2. Найдите тангенс угла AOB.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
4. Найдите тангенс угла AOB.
5. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
6. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
7. Найдите тангенс угла AOB.
8. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
9. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
5. Нахождение элементов прямоугольных треугольников
1. В треугольнике ABC угол C равен 90о, , AC = 8. Найдите AB.
2. В треугольнике ABC угол C равен 90о, tg A = 0,75, BC = 9. Найдите AC.
3. В
треугольнике ABC угол C равен 90о,
sin A = 0,6, BC = 6. Найдите AB.
В
треугольнике ABC угол C равен 90о,
sin A = 0,6, BC = 6. Найдите AB.
4. В треугольнике ABC угол C равен 90о, cos A = 0,8, BC = 3. Найдите AB.
5. В треугольнике ABC угол C равен 90о, sin A = 0,6, AC = 4. Найдите AB.
6. В треугольнике ABC угол C равен 90о, tg A = , BC = 6. Найдите AB.
7. В треугольнике ABC угол C равен 90о, CH – высота, AB = 25, cos A = 0,8. Найдите AH.
8. В треугольнике ABC угол C равен 90о, CH – высота, AB = 25, sin A = 0,6. Найдите BH.
9. В треугольнике ABC угол C равен 90о, CH – высота, AH = 16, tg A = 0,75. Найдите BH.
6. Нахождение элементов равнобедренных треугольников
1. В треугольнике ABC AC = BC, AB = 18, cos A = 0,6. Найдите AC.
2. В треугольнике ABC AC = BC = 10, sin B = 0,8.
 Найдите AB.
Найдите AB.
3. В треугольнике ABC AC = BC, AB = 18, sin A = 0,8. Найдите AC.
4. В треугольнике ABC AC = BC, AB = 4, tg A = 0,75. Найдите высоту CH.
5. В треугольнике ABC AC = BC, AB = 30, sin A = 0,8. Найдите высоту AH.
6. В треугольнике ABC AC = BC, AB = 30, cos A = 0,6. Найдите высоту AH.
7. В треугольнике ABC AC = BC, AB = 30, sin A = 0,8, AH — высота. Найдите BH.
8. В треугольнике ABC AC = BC, AB = 30, cos A = 0,6, AH — высота. Найдите BH.
9. В треугольнике ABC AB = BC, AC = 10, sin C = 0,6. Найдите высоту CH.
Самостоятельные работы
Самостоятельная работа 1
1. В треугольнике ABC угол C равен 90о, tg A = . Найдите sin B.
2. В треугольнике ABC угол C равен 90о, CH – высота, AC = 10, AH = 8. Найдите sin B.
3. В треугольнике ABC AC = BC = 5, AB = 6. Найдите cos B.
4. В треугольнике ABC AC = BC, AB = 5, высота BH равна 4. Найдите sin B.
Найдите sin B.
5. В треугольнике ABC AB = BC, AC = 5, CH – высота, AH = 4. Найдите синус угла ACB.
6. В треугольнике ABC угол C равен 90о, AB = 5, BC = 3. Найдите косинус внешнего угла при вершине A.
7. В треугольнике ABC AB = BC, AB = 5, высота CH равна 4. Найдите косинус угла ABC.
8. Найдите тангенс угла AOB.
9. В треугольнике ABC AC = BC, AB = 15, sin B = 0,8. Найдите высоту BH.
10. В треугольнике ABC AB = BC, AC = 10, cos C = 0,8, CH — высота. Найдите AH.
Самостоятельная работа 2
1. В треугольнике ABC угол C равен 90о, sin B = 0,8. Найдите tg A.
2. В треугольнике ABC угол C равен 90о, AC = 5, высота CH равна 3. Найдите cos B.
3. В треугольнике ABC AC = BC = 5, AB = 8. Найдите tg B.
4. В треугольнике ABC AC = BC, AB = 5, высота BH равна 4. Найдите cos B.
5.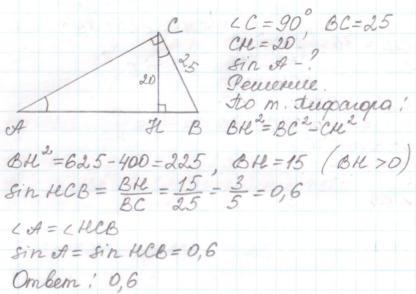 В треугольнике ABC AB = BC, AC = 8, высота CH равна 4. Найдите синус угла ACB.
В треугольнике ABC AB = BC, AC = 8, высота CH равна 4. Найдите синус угла ACB.
6. В треугольнике ABC угол C равен 90о, AB = 5, BC = 3. Найдите тангенс внешнего угла при вершине A.
7. В треугольнике ABC AB = BC, CH – высота, AB = 5, BH = 3. Найдите синус угла ABC.
8. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
9. В треугольнике ABC AC = BC, AB = 15, cos B = 0,6. Найдите высоту BH.
10. В треугольнике ABC AB = BC, AC = 10, cos С = 0,8. Найдите высоту CH.
Самостоятельная работа 3
1. В треугольнике ABC угол C равен 90о, cos B = 0,6. Найдите tg A.
2. В треугольнике ABC угол C равен 90о, CH – высота, BC = 5, BH = 3. Найдите tg A.
3. В треугольнике ABC AC = BC = 5, AB = 8. Найдите sin B.
3. В треугольнике ABC AC = BC, AB = 5, BH – высота, AH = 3. Найдите cos B.
4.
 В треугольнике ABC AB = BC, AB = 8, высота CH равна 4. Найдите синус угла ABC.
В треугольнике ABC AB = BC, AB = 8, высота CH равна 4. Найдите синус угла ABC.
5. В треугольнике ABC угол C равен 90о, tg A = 0,75. Найдите косинус внешнего угла при вершине A.
7. В треугольнике ABC AB = BC, AB = 5, высота CH равна 4. Найдите тангенс внешнего угла при вершине A.
8. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
9. В треугольнике ABC AC = BC, AB = 15, sin A = 0,8, BH — высота. Найдите AH.
10. В треугольнике ABC AB = BC, AC = 5, sin C = 0,6, CH — высота. Найдите AH.
Ответы
Тренировочные работы
1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника
1. 0,8. 2. 0,75. 3. 0,6. 4. 0,75. 5. 0,6. 6. 0,6. 7. 0,8. 8. 0,6. 9. 0,8.
2. Нахождение значений тригонометрических функций острых углов равнобедренного треугольника
1. 0,6. 2. 0,75. 3. 0,6. 4. 0,8. 5. 0,6. 6. 0,6. 7. 0,8. 8. 0,5. 9. 0,6.
3. Нахождение значений
тригонометрических функций тупых углов
Нахождение значений
тригонометрических функций тупых углов
1. -0,8. 2. -0,75. 3. -0,8. 4. 0,6. 5. -0,8. 6. -0,6. 7. 0,8. 8. —0,6. 9. 0,8.
4. Нахождение тригонометрических функций углов, изображенных на клетчатой бумаге
1. 2. 2. 1. 3. 2. 4. 0,5. 5. 4. 6. 2. 7. 2. 8. 1. 9. -2.
5. Нахождение элементов прямоугольных треугольников
1. 12. 2. 12. 3. 10. 4. 5. 5. 5. 6. 10. 7. 16. 8. 9. 9. 9.
6. Нахождение элементов равнобедренных треугольников
1. 15. 2. 12. 3. 15. 4. 1,5. 5. 24. 6. 24. 7. 18. 8. 18. 9. 6.
Самостоятельные работы
Самостоятельная работа 1
1. 0,8. 2. 0,8. 3. 0,6. 4. 0,8. 5. 0,6. 6. -0,8. 7. -0,6. 8. 0,5. 9. 12. 10. 8.
Самостоятельная работа 2
1. 0,75. 2. 0,6. 3. 0,75. 4. 0,6. 5. 0,5. 6. -0,75. 7. 0,8. 8. 4. 9. 12. 10. 6.
Самостоятельная работа 3
1. 0,75. 2. 0,75. 3. 0,6. 4. 0,6. 5. 0,5. 6. -0,8. 7. -0,5. 8. 2. 9. 9. 10. 4.
Задачи для ОГЭ. Вычисление длин
Задачи для ОГЭ с ответами и решениями
Вычисление длин
перейти к содержанию задачника
- В треугольнике ABC угол С равен 90 градусов, а угол А равен 30 градусов, AB = 40. Найдите BC.
- В треугольник ABC угол C равен 90o, угол А равен 30o, AC = . Найдите AB.

- В треугольнике ABC угол С прямой, угол А равен 60o. Найдите AB, если BC равно .
- Катеты прямоугольного треугольника равны 9 и 40. Найдите гипотенузу.
- Катеты прямоугольного треугольника равны 12 и 35. Найдите гипотенузу.
- Гипотенуза прямоугольного треугольника равна 25. Один из его катетов равен 24. Найдите другой катет.
- Гипотенуза прямоугольного треугольника равна 25. Один из его катетов равен 15. Найдите другой катет.
- В треугольнике ABC угол С равен 90o, угол А равен 30o, АВ равно . Найдите высоту CH.
- В треугольнике АВС угол С прямой, угол А равен 30 градусов. АВ равно . Найдите высоту CH.
- В треугольнике АВС угол С равен 90o, СH — высота, угол А равен 30o, AB равно 80. Найдите BH.
- В треугольнике ABC AB = BC = AC = . Найдите высоту CH.
- В треугольнике ABC AB = BC = AC = . Найдите высоту CH.
- В треугольнике ABC BC = AC = 22. Угол С равен 30o. Найдите высоту AH.
- В треугольнике ABC BC = AC, высота AH = 26, угол С равен 30o. Найдите AC.
- Меньшая сторона прямоугольника равна 42, диагонали пересекаются под углом 60o. Найдите диагонали прямоугольника.
- Меньшая сторона прямоугольника равна 32, диагонали пересекаются под углом 60o. Найдите диагонали прямоугольника.
- Периметр параллелограмма равен 54. Одна сторона параллелограмма на 1 больше другой. Найдите меньшую сторону параллелограмма.
- Найдите меньшую диагональ ромба, стороны которого равны 19, а острый угол равен 60o.
- Найдите меньшую диагональ ромба, стороны которого равны 12, а острый угол равен 60o.
- Найдите среднюю линию трапеции, если ее основания равны 33 и 27.
- Средняя линия трапеции равна 23, а меньшее основание равно 15. Найдите большее основание трапеции.
- Основания трапеции равны 144 и 145. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

- Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
- Радиус окружности, описанной около правильного треугольника, равен . Найдите сторону этого треугольника.
- Высота правильного треугольника равна 90. Найдите радиус окружности, описанной около этого треугольника.
- Радиус окружности, описанной около правильного треугольника, равен 18. Найдите высоту этого треугольника.
- В треугольнике ABC АС = 8, ВС = 15, угол С равен 90o. Найдите радиус окружности, описанной около этого треугольника.
- В треугольнике ABC АС = 21, ВС = , угол С равен 90o. Найдите радиус окружности, описанной около этого треугольника.
перейти к содержанию задачника
Ответы
- 20
- 68
- 100
- 41
- 37
- 7
- 20
- 27
- 30
- 20
- 3
- 69
- 11
- 52
- 84
- 64
- 13
- 19
- 12
- 30
- 31
- 72,5
- 36
- 117
- 60
- 27
- 8,5
- 13
Метки ОГЭ. Смотреть запись.
прямоугольных треугольников
прямоугольных треугольниковДавайте снова согласимся со стандартным соглашением для обозначения частей прямоугольного треугольника. Обозначим прямой угол C , а гипотенузу c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им, соответственно.
Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и касательных, чтобы решить треугольник, то есть найти неизвестные части в терминах известных частей.- Теорема Пифагора: a 2 + b 2 = c 2 .
- Синусы: sin A = a / c, sin B = b / c.

- Косинусы: cos A = b / c, cos B = a / c.
- Касательные: tan A = a / b, tan B = b / a.
Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b = 119 и c = 169, то a 2 = c 2 — b 2 = 169 2 — 119 2 = 28561 — 14161 = 14400, а квадратный корень из 14400 составляет 120, поэтому a = 120.
Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15, а угол A = 41 °, мы можем использовать синус и касательную, чтобы найти гипотенузу и другую сторону.Так как sin A = a / c, мы знаем c = a / sin A = 15 / sin 41. Используя калькулятор, это 15 / 0,6561 = 22,864. Кроме того, tan A = a / b, , поэтому b = a / tan A = 15 / tan 41 = 15 / 0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте посмотрим на проблему определения углов, если вы знаете стороны.Опять же, вы используете триггерные функции, но в обратном порядке. Вот пример. Предположим, что a = 12,3 и b = 50,1. Тогда tan A = a / b = 12,3 / 50,1 = 0,2455. Раньше, когда люди использовали таблицы тригонометрических функций, они просто смотрели в таблицу касательных, чтобы увидеть, какой угол имеет тангенс 0,2455. В калькуляторе мы используем обратные триггерные функции с именами арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью inv или arc, которую вы нажимаете перед нажатием соответствующей триггерной кнопки.Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79 °. (Если хотите, можете преобразовать 0,79 градуса в минуты и секунды.)
Тогда tan A = a / b = 12,3 / 50,1 = 0,2455. Раньше, когда люди использовали таблицы тригонометрических функций, они просто смотрели в таблицу касательных, чтобы увидеть, какой угол имеет тангенс 0,2455. В калькуляторе мы используем обратные триггерные функции с именами арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью inv или arc, которую вы нажимаете перед нажатием соответствующей триггерной кнопки.Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79 °. (Если хотите, можете преобразовать 0,79 градуса в минуты и секунды.)Вот и все.
Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия.Есть шесть способов соотношения двух сторон прямоугольного треугольника, и это дает шесть функций:- sin A = кондиционер (opp / hyp)
- cos A = b / c (прил / гип)
- загар A = а / б (опп / прил)
- детская кроватка A = b / a (прил. / Опп)
- сек A = c / b (hyp / adj)
- csc A = c / a (hyp / opp)
Эти три другие функции также можно интерпретировать с помощью круговой диаграммы.
Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенс угла FOB — это линия FG, , но FOB — дополнительный угол AOB, , следовательно, котангенс AOB равен FG.
Затем, чтобы интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, , поэтому sec AOB = sec AOC = hyp / adj = OC / OA = OC. Вот и все — секущая — это линия от центра окружности к касательной AC. Причина, по которой он называется секущей, заключается в том, что она разрезает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Точно так же косеканс угла AOB — это линия OG от центра окружности до линии котангенса FG.
Упражнения
Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначает гипотенузу, a и b для перпендикулярных сторон и A и B для углов, противоположных a и b соответственно. 26. В каждом из следующих прямоугольных треугольников, у которых даны две стороны, вычислите sin, cos и tan углов A, и B. Выразите результаты в виде общих дробей.
(i). c = 41, a = 9.
(ii). c = 37, a = 35.
(iii). а = 24, б = 7.
31. В прямоугольном треугольнике c = 6 футов 3 дюйма и загар B = 1.2. Найдите a и b.
34. a = 1,2, b = 2,3. Найдите A и c.
42. a = 10,11, b = 5,14. Найдите B и c.
В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя то, что вы знаете о прямоугольных треугольниках.
61. В наклонном треугольнике ABC, A = 30 °, B = 45 °, а длина перпендикуляра от C до AB составляет 12 дюймов. Найдите длину AB.
67. Если сторона равностороннего треугольника равна a, найдите высоту и радиусы описанных и вписанных окружностей.
202. От вершины здания высотой 50 футов углы подъема и понижения верха и низа другого здания составляют 19 ° 41 ‘и 26 ° 34’ соответственно.Какая высота и расстояние до второго дома.
207. От вершины маяка высотой 175 футов углы падения верха и низа флагштока составляют 23 ° 17 ‘и 42 ° 38’ соответственно. Какой высоты у шеста?
214. В двух точках на расстоянии 65 футов на одной стороне дерева и на одной линии с ним углы подъема вершины дерева составляют 21 ° 19 ‘и 16 ° 20’. Найдите высоту дерева.
215. Когда воздушный шар проходит между двумя точками A, и B, расположенными на расстоянии 2 миль друг от друга, углы подъема воздушного шара в этих точках составляют 27 ° 19 ‘и 41 ° 45’ соответственно. Найдите высоту воздушного шара. Возьмем A и B на одном уровне.
233. Вершина маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится только «на горизонте»? [Предположим, что Земля — это сфера радиусом 3956 миль.]
234. Какова должна быть высота наблюдателя, чтобы он мог видеть объект на Земле на расстоянии тридцати миль? Предположим, что Земля представляет собой гладкую сферу.
На каждой из фигур, упомянутых в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, то есть радиус описанной окружности, (ii) через apothem r, , то есть радиус вписанной окружности, и (iii) относительно стороны a.
251. Равносторонний треугольник. [См. Проблему 67 выше.]
[См. Проблему 67 выше.]
252. пл.
253. Правильный пятиугольник.
254. Правильный шестигранник.
255. Правильный восьмиугольник.
Подсказки
26. Вам нужны только sin, cos и tan углов A и B ; сами углы не нужны.Итак, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем вычислить отношения двух сторон.
31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух сторон, которых вы не знаете, а именно b / a. Есть несколько способов решить эту проблему. Вот два.
Метод 1. Возьмите уравнение 1.2 = tan B = b / a, , чтобы получить соотношение между a и b, а именно b = 1.2 а. Теорема Пифагора тогда дает 6,25 2 = a 2 + 1,44 a 2 , из которых вы можете определить a, , а затем найти b.
Метод 2. Из tan B, вы можете определить угол B (используйте arctan). Отсюда вы можете найти cos B, , а затем a, , и вы можете найти sin B, , а затем b.
34. Поскольку у вас есть a и b, , вы можете использовать касательные, чтобы найти A , и теорему Пифагора, чтобы найти c.
42. Найдите B по касательным и c по теореме Пифагора.
61. Начните с рисования рисунка. Хотя треугольник ABC не является прямоугольным, он разбивается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их.
67. Равносторонний треугольник ABC имеет три угла при вершине 60 °. Отбросьте перпендикуляр из одной вершины, скажем, C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, и это высота равностороннего треугольника. Описанный круг — это круг, проходящий через три вершины, а вписанный круг — это круг, касающийся всех трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и используя триггер на полученных маленьких треугольниках, вы можете найти радиусы этих двух окружностей.
Описанный круг — это круг, проходящий через три вершины, а вписанный круг — это круг, касающийся всех трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и используя триггер на полученных маленьких треугольниках, вы можете найти радиусы этих двух окружностей.
202. Поскольку вы знаете высоту своего здания и угол наклона основания другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема к вершине другого здания покажет вам, насколько оно выше вашего.
207. Подсказка похожа на 202. Видите ли, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!
214. Это полезная проблема. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота x дерева и расстояние x ближайшей точки к дереву. Дальнейшая точка будет x + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить, чтобы определить y и x.
215. Это похоже на 214, но в этой задаче баллон находится между двумя точками. Нарисуйте фигуру. Определитесь с вашими переменными. Составьте уравнения и решите их.
233. Очень интересная задача. На протяжении веков для вычисления радиуса Земли использовались различные обратные величины. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам здесь нужно, это теорема Пифагора. Одна сторона прямоугольного треугольника равна r, — радиус Земли, а гипотенуза — r + h , где h — высота маяка.Теорема Пифагора о третьей стороне треугольника.
234. Задайте эту задачу аналогично 233, но известны другие переменные.
251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, с одним катетом r, и другим катетом a /2.Угол в центре равен 360 ° / (2 n ) = 180 ° / n. Используя тригонометрию, вы можете легко написать уравнения, относящиеся к площади правильного многоугольника, как требуется.
У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, с одним катетом r, и другим катетом a /2.Угол в центре равен 360 ° / (2 n ) = 180 ° / n. Используя тригонометрию, вы можете легко написать уравнения, относящиеся к площади правильного многоугольника, как требуется.
Ответы
26. (i). b = 40. Итак sin A = cos B = 9/41, cos A = sin B = 40/41, tan A = 9/40, tan B = 40 / 9.(ii). b = 12. So sin A = cos B = 35/37, cos A = sin B = 12/37, tan A = 35/12, tan B = 12 / 37.
(iii). c = 25. Итак sin A = cos B = 24/25, cos A = sin B = 7/25, tan A = 24/7, tan B = 7 / 24.
31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.
34. A = 27,55 °, около 28 °. с = 2,6.
42. B = 26,95 ° или 26 ° 57 ‘. с = 11.3.
61. AB = 12 / tan A + 12 / tan B = 12 (√3 + 1) дюймов, около 33 дюймов.
67. ( a √3) / 2, ( a √3) / 3 и ( a √3) / 6 соответственно.
202. Расстояние = 50 / тангаж 26 ° 34 ‘= 100 футов. Высота = 50 + 100 см. 19 ° 41 ‘= 85,8’ = 85’9 дюймов.
207. Расстояние = 175 / тангаж 42 ° 38 ‘= 190 футов. Рост = 175 — 190 см. 23 ° 17 ‘= 93.23 ‘= 9’3 «.
214. Два уравнения:
- 0,2
= загар 16 ° 20 ‘= ч / (65 + x ), и
0,3 = загар 21 ° 19 ‘= ч / x .
Расстояние x = 196 футов. Высота х = 76,5 футов.

215. Если h — высота воздушного шара, а x — расстояние по земле от A до точки непосредственно под воздушным шаром, то два уравнения равны
- tan 27 ° 19 ‘= h / x , и
загар 41 ° 45 ‘= ч / (2 — x )
Высота = 0,654 мили = 3455 футов.
233. Мелочь больше 18.5 миль.
234. 600 футов.
251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A в терминах R, r, или a, , используйте отношения
- cos 180 & deg / n = r / R, и
tan 180 & deg / n = a / (2 r ).
- (i) через R, площадь A = nR 2 cos 180 ° / n sin 180 ° / n ,
(ii) в единицах r, площадь A = nr 2 tan 180 & deg / n , и
(iii) в пересчете на a, площадь A = na 2 / (4tan 180 & deg / n ).
| Проблема | форма | (i) R | (ii) r | (iii) a |
|---|---|---|---|---|
| 251 | треугольник | (3 р 2 √3) / 4 | 3 r 2 √3 | ( a 2 √3) / 4 |
| 252 | квадрат | 2 р 2 | 4 р 2 | а 2 |
| 253 | пятиугольник | (5 R 2 sin 108 °) / 2 | 5 r 2 tan 36 ° | (5 a 2 tan 54 °) / 4 |
| 254 | шестигранник | (3 р 2 √3) / 2 | 2 r 2 √3 | (3 a 2 √3) / 2 |
| 255 | восьмиугольник | 2 R 2 √2 | 8 r 2 tan 22 ° 30 ‘ | 2 a 2 tan 67 ° 30 ‘ |
Отступление на пифагорейские тройки
Это не имеет отношения к тригонометрии, но интересно.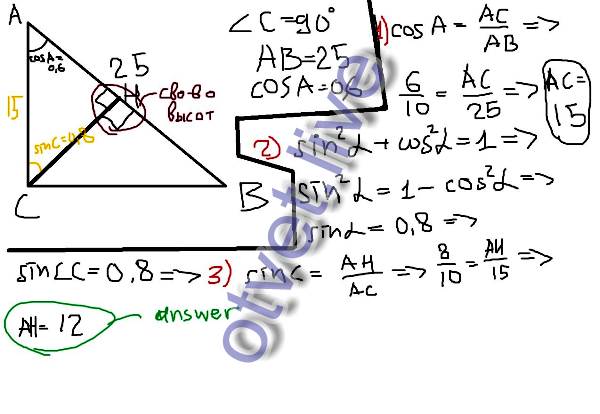 Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника как целые числа, а третья также оказывается целым числом. Как и в задаче 26, где у всех трех прямоугольных треугольников стороны имеют целые числа, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3: 4: 5.
Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника как целые числа, а третья также оказывается целым числом. Как и в задаче 26, где у всех трех прямоугольных треугольников стороны имеют целые числа, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3: 4: 5.Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых представляют собой целые числа? Да, и они давно изучаются.Три числа a, b, и c такие, что a 2 + b 2 = c 2 , как говорят, образуют тройку Пифагора, в честь Пифагора. Он жил около 550 г. до н. Э. и, наверное, знаю немало из них. Но древние вавилоняне примерно 1800 г. до н. Э. знал их всех, и многие из них были известны в других древних цивилизациях, таких как Китай и Индия.
Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько троек Пифагора.Не считайте те, у которых есть общий множитель, как новые, например 6: 8: 10, поскольку они будут похожи на меньшие.
В книге Евклида Elements есть описание всех возможных пифагоровых троек. Вот современный пересказ Евклида. Возьмем любые два нечетных числа m, и n, с m, n и взаимно простые числа (то есть без общих множителей). Пусть a = mn, пусть b = ( n 2 — m 2 ) / 2, и пусть c = ( n 2 + m 2 ) / 2.Тогда a : b : c — тройка Пифагора. Например, если взять м = 1 и n = 3, то получится наименьшая тройка Пифагора 3: 4: 5.
Rd Sharma для класса 9 по математике Глава 12
Страница № 12.19:
Вопрос 10:
Найдите периметр и площадь четырехугольника ABCD , в котором AB = 17 см, AD = 9 см, CD = 12 см, ∠ ACB = 90 ° и AC = 15 см.
Ответ:
Предположим, что ABCD — четырехугольник со сторонами AB, BC, CD, DA и ∠ACB = 90 ∘ .
Возьмем диагональ AC, где AC делит ABCD на два треугольника ΔACB и ΔADC
Поскольку ∆ACB находится под прямым углом к C, мы имеем
AC = 15 см; AB = 17 см
AB 2 = AC 2 + BC 2
Площадь прямоугольного треугольника ABC, скажем, A 1 определяется как
, где,
База = ВС = 8 см; Высота = AC = 15 см
Площадь треугольника ADC, скажем, A 2 со сторонами a, b , c и s , поскольку полупериметр равен
, где
a = AD = 9 см; b = DC = 12 см; c = AC = 15 см
Площадь четырехугольника ABCD, скажем A
A = Площадь ∆ACB + Площадь ∆ADC
Периметр четырехугольника ABCD, скажем P
Страница № 12.19:
Вопрос 1:
Найдите площадь четырехугольника ABCD , равную AB = 3 см, BC = 4 см, CD = 4 см, DA = 5 см и AC = 5 см.
Ответ:
Дан четырехугольник ABCD со сторонами AB, BC, CD, DA и диагональю AC = 5 см, где AC делит четырехугольник ABCD на два треугольника ΔABC и ΔADC.Мы найдем площади двух треугольников по отдельности и их, чтобы найти площадь четырехугольника ABCD.
Обратите внимание, что в треугольнике ΔABC:
Таким образом, треугольник ΔABC является прямоугольным.
Площадь прямоугольного треугольника ΔABC, определяется как
В ΔACD все стороны известны, поэтому просто используйте формулу Герона, чтобы найти площадь треугольника ΔACD,
с = AD + DC + AC2 = 5 + 4 + 52 = 7 см
Площадь ΔACD составляет:
Площадь четырехугольника ABCD составит,
Площадь = Площадь треугольника ABC + Площадь треугольника ADC
Страница № 12.
 19:
19:Вопрос 2:
Стороны четырехугольного поля, взятые по порядку, равны 26 м, 27 м, 7 м и 24 м соответственно. Угол между двумя последними сторонами — прямой. Найдите его область.
Ответ:
Мы предполагаем, что четырехугольник ABCD является четырехугольным полем со сторонами AB, BC, CD, DA и.
Возьмем диагональ AC, где AC делит четырехугольник ABCD на два треугольника ΔABC и ΔADC
Найдем площадь двух треугольников ΔABC и ΔADC по отдельности и сложим их, чтобы найти площадь четырехугольника ABCD.
В треугольнике ΔADC имеем
н.э. = 24 м; DC = 7 м
Мы используем теорему Пифагора, чтобы найти сторону AC,
AC 2 = AD 2 + DC 2
Площадь прямоугольного треугольника ΔADC, скажем, A 1 определяется как
Где, База = DA = 24 м; Высота = DC = 7 м
Площадь треугольника ΔABC, скажем, A 2 со сторонами a, b , c и s в качестве полупериметра определяется как
Где, a = AC = 25 м; b = AB = 26 м; c = BC = 27 м
Площадь четырехугольника ABCD, скажем A
A = Площадь треугольника ΔADC + Площадь треугольника ΔABC
Страница № 12.19:
Вопрос 3:
Стороны четырехугольника, взятые по порядку, составляют 5, 12, 14 и 15 метров соответственно, а угол между первыми двумя сторонами является прямым. Найдите его область.
Ответ:
Мы предполагаем, что ABCD — это четырехугольник со сторонами AB, BC, CD, DA и углом.
Возьмем диагональ AC, где AC делит четырехугольник ABCD на два треугольника ΔABC и ΔADC.Мы найдем площадь этих двух треугольников и сложим их, чтобы найти площадь четырехугольника ABCD
.В треугольнике ΔABC имеем
AB = 5 м; BC = 12 м
Мы будем использовать теорему Пифагора для вычисления AC
.AC 2 = AB 2 + BC 2
Площадь прямоугольного треугольника ΔABC, скажем, A 1 определяется как
Где, База = AB = 5 м; Высота = BC = 12 м
Площадь треугольника ΔADC, скажем, A 2 со сторонами a, b , c и s в качестве полупериметра определяется как
Где, a = AC = 13 м; b = DC = 14 м; в = AD = 15 м
Площадь четырехугольника ABCD, скажем A
A = Площадь треугольника ΔABC + Площадь треугольника ΔADC
Страница № 12.19:
Вопрос 4:
Парк в форме четырехугольника ABCD имеет ∠C = 90 °, AB = 9 м, BC = 12 м, CD = 5 м и AD = 8 м. Какую площадь он занимает?
Ответ:
Предположим, что ABCD — четырехугольник со сторонами AB, BC, CD, DA и.
Возьмем диагональную DB, где DB делит ABCD на два треугольника ΔBCD и ΔABD
В ΔBCD имеем
DC = 5 м; BC = 12 м
Используйте теорему Пифагора
BD 2 = DC 2 + BC 2
Площадь прямоугольного треугольника ΔBCD, скажем, A 1 определяется как
Где, База = DC = 5 м; Высота = BC = 12 м
Площадь треугольника ΔABD, скажем, A 2 со сторонами a, b , c и s как полупериметр задается как
Где, a = AD = 8 м; b = AB = 9 м; в = BD = 13 м
Площадь четырехугольника ABCD, скажем A
A = Площадь треугольника DCB + Площадь треугольника ABD
Страница № 12.19:
Вопрос 5:
Две параллельные стороны трапеции — 60 см и 77 см, а другие стороны — 25 см и 26 см. Найдите площадь трапеции.
Ответ:
Мы предполагаем, что ABCD — заданная трапеция, где AB параллельна DC.
Проведем CE параллельно AD от точки C.
Следовательно, образуется параллелограмм ADCE, имеющий AD, параллельный CE, и DC, параллельный AE.
АЕ = 60 см; CE = 25 см; BE =
В основном мы найдем площадь треугольника BCE и площадь параллелограмма AECD и сложим их, чтобы найти площадь трапеции ABCD.
Площадь треугольника ECB, скажем, A 1 со сторонами a, b , c и s как полупериметр задается
Где, a = EB = 17 см; b = EC = 25 см; c = BC = 26 см
Здесь нам нужно найти высоту параллелограмма AECD, которая равна CM, чтобы вычислить площадь AECD.
Где BE = База = 17 см; Высота = CM = h
Таким образом, площадь параллелограмма будет равна,
A 2 = b × h
= 60 × 24 = 1440 см2
Общая площадь трапеции составит
A = A 1 + A 2
= 204 + 1440
= 1644 см 2
Страница № 12.19:
Вопрос 6:
Две параллельные стороны трапеции — 60 см и 77 см, а другие стороны — 25 см и 26 см.Найдите площадь трапеции.
Ответ:
Рассмотрим трапецию ABCD, как показано ниже.
Нарисуйте линию BF, параллельную AD, так, чтобы ABFD превратился в параллелограмм. Также нарисуйте перпендикуляр BE на CD, как показано на рисунке.
В ΔBCF три стороны заданы как a = BF = 25 см, b = BC = 26 см, c = CF = CD-FD = 17 см.
Полупериметр ΔBCF = 25 + 26 + 172 = 34.
Площадь ΔBCF может быть рассчитана по формуле Герона как
ss-as-bs-c = 3434-2534-2634-17 = 34 × 9 × 8 × 17 = 204 см2
Кроме того, площадь ΔBCF = 12 × основание × высота
⇒204 = 12 × 17 × BE⇒204 = 12 × 17 × BE⇒BE = 24 см
Следовательно, площадь трапеции = 12AB + CD × BE = 1260 + 77 × 24 = 1644 см2.
Страница № 12.19:
Вопрос 7:
Ромб, лист, периметр которого составляет 32 м, а длина одной диагонали 10 м, окрашен с обеих сторон из расчета 5 рупий за м. 2 . Узнайте стоимость покраски.
Ответ:
Мы предполагаем, что ABCD — это ромб, имеющий
AB = BC = CD = DA
BD и AC быть диагоналями ромба
Нам нужно узнать стоимость покраски с двух сторон
Периметр ромба ABCD, скажем, P равен 32 м
Известно, что BD и AC диагоналей ромба и.Итак,
(диагонали ромба пересекаются под прямым углом)
БД = 24 м; AC = ч; сторона = AB = 8м
Взяв квадрат с обеих сторон, получаем
Площадь ромба, скажем A 1
Площадь обеих сторон ромба;
Страница № 12.19:
Вопрос 8:
Найдите площадь четырехугольника ABCD , в котором AD = 24 см, ∠ BAD = 90 ° и BCD образует равносторонний треугольник, каждая сторона которого равна 26 см.
Ответ:
Мы предполагаем, что ABCD — это четырехугольник со сторонами AB, BC, CD, DA, диагональю BD и углом, где BCD образует равносторонний треугольник с равными сторонами.
Нам нужно найти площадь ABCD
В треугольнике BAD имеем
BD 2 = BA 2 + AD 2 . Таким образом,
Площадь прямоугольного треугольника ABD, скажем, A 1 определяется как
Где,
База = БА = 10 см; Высота = AD = 24 см
Площадь равностороннего треугольника BCD, скажем, A 2 со сторонами a, b , c определяется как
, где
a = BC = CD = BD = 26 см
Площадь четырехугольника ABCD, скажем A
A = Площадь треугольника BAD + Площадь треугольника BCD
Страница № 12.19:
Вопрос 9:
Найдите площадь четырехугольника ABCD , в котором AB = 42 см, BC = 21 см, CD = 29 см, DA = 34 см и диагональ BD = 20 см.
Ответ:
Дан четырехугольник ABCD со сторонами AB, BC, CD, DA и диагональю BD, где BD делит ABCD на два треугольника
ΔDBC и ΔDAB
В треугольнике DBC мы видим, что
DC 2 = DB 2 + BC 2
Следовательно, это прямоугольный треугольник.
Площадь прямоугольного треугольника DBC, скажем, A 1 определяется как
Где,
База = ВС = 21 см; Высота = BD = 20 см
Площадь треугольника DAB, скажем, A 2 со сторонами a, b , c и s в качестве полупериметра определяется как
, где
a = DB = 20 см; b = AD = 34 см; c = AB = 42 см
Площадь четырехугольника ABCD, скажем A
A = Площадь треугольника DBC + Площадь треугольника DAB
Страница № 12.19:
Вопрос 11:
Соседние стороны параллелограмма ABCD имеют размеры 34 см и 20 см, а диагональ AC составляет 42 см. Найдите площадь параллелограмма.
Ответ:
Нам дана мера смежных сторон параллелограмма AB и BC, то есть сторон, имеющих одну и ту же точку начала, и диагонали AC, которая делит параллелограмм ABCD на два равных треугольника ABC и ADC.
Площадь треугольника ABC равна площади треугольника ADC, поскольку они являются конгруэнтными треугольниками.
Площадь параллелограмма ABCD, скажем, задается как
А =
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольника, скажем, A 1 со сторонами 20 см, 34 см и 42 см равна
a = 20 см; b = 34 см; c = 42 см
Площадь параллелограмма ABCD, скажем, задается как
Страница № 12.19:
Вопрос 12:
Найдите площадь лопастей магнитного компаса, показанную на рисунке. (Возьмем 11 = 3,32)
Ответ:
Лезвия магнитного компаса образуют ромб со всеми равными сторонами по 5 см каждая. Дана диагональ размером 1 см, которая образует треугольную форму лопастей магнитного компаса и делит ромб на два равных треугольника, скажем, треугольник ABC и треугольник DBC, имеющих равные размеры.
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольника ABC, скажем, A 1 , имеющего стороны 5 см, 5 см и 1 см, определяется по формуле:
a = 5 см; б = 5 см; c = 1 см
Площадь лопастей магнитного компаса, скажем, А определяется как
A = Площадь одного из треугольников ABC
Страница № 12.20:
Вопрос 13:
Ручной веер изготавливается путем сшивания 10 треугольных полос одинакового размера из двух разных типов бумаги, как показано на рис. 12.28. Размеры одинаковых полосок — 25 см, 25 см и 14 см. Найдите площадь каждого типа бумаги, необходимую для веерной работы.
Ответ:
Нам нужно найти площадь каждого типа треугольных полосок, необходимую для вентилятора.
Имеется 5 полосок каждого типа с одинаковыми размерами, поэтому мы вычислим площадь одной полосы, а затем умножим ее на 5, чтобы определить площадь необходимых полос каждого типа.
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольной полосы, скажем, A 1 со сторонами 25 см, 25 см и 14 см, определяется как:
a = 25 см; b = 25 см; c = 14 см
Требуемая площадь каждого типа полосы, например A .
Стр. № 12.20:
Вопрос 14:
Треугольник и параллелограмм имеют одинаковое основание и одинаковую площадь. Если стороны треугольника равны 13 см, 14 см и 15 см, а параллелограмм стоит на основании 14 см, найдите высоту параллелограмма.
Ответ:
Дано, что площади треугольника и параллелограмма равны.
Мы вычислим площадь треугольника с заданными значениями, и это также даст нам площадь параллелограмма, поскольку оба они равны.
Площадь треугольника со сторонами a , b , c и s как полупериметр определяется как,
, где
Следовательно, площадь треугольника; скажем, A, со сторонами 15 см, 13 см и 14 см соответствует
a = 15 см; b = 13 см; c = 14 см
Нам нужно найти высоту параллелограмма, скажем h
Площадь параллелограмма AECD скажем A 1 определяется как
База = 60 см; Высота = х см; A = A 1 = 84 см 2
Страница № 12.23:
Вопрос 1:
Найдите площадь треугольника, основание и высота которого составляют 5 см и 4 см соответственно.
Ответ:
Дано, основание = 5 см; высота = 4 см
Площадь треугольника = 12 × Основание × Высота
Страница № 12.23:
Вопрос 2:
Найдите площадь треугольника со сторонами 3 см, 4 см и 5 см соответственно.
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольника со сторонами 3 см, 4 см и 5 см равна
a = 3 см; b = 4 см; c = 5 см
Теперь площадь
= 6 (6-3) (6-4) (6-5) = 6 × 3 × 2 × 1 = 36 = 6 см2
Страница № 12.23:
Вопрос 3:
Найдите площадь равнобедренного треугольника с основанием x см и одной стороной y см.
Ответ:
Предположим, что треугольник ABC — это равнобедренный треугольник со сторонами AB = AC и основанием BC. Площадь треугольника ABC, скажем, A , имеющего стороны AB и AC, равна y см, а с учетом основания BC, равного x см, равна
Где,
База = ВС = х см; Высота = y2-x24
A = 12Base × Высота = 12 × xy2-x24 = x2y2-x24
Страница № 12.23:
Вопрос 4:
Найдите площадь равностороннего треугольника, каждая сторона которого составляет 4 см.
Ответ:
Площадь равностороннего треугольника, каждая сторона которого равна см, равна
Площадь данного равностороннего треугольника, каждая равная сторона которого равна 4 см, равна
.a = 4 см
Страница № 12.23:
Вопрос 5:
Найдите площадь равностороннего треугольника, каждая сторона которого x см.
Ответ:
Площадь равностороннего треугольника, скажем, , каждая сторона которого равна см, определяется как
Площадь данного равностороннего треугольника, каждая равная сторона которого равна x см, равна
a = x см
Страница № 12.23:
Вопрос 6:
Периметр поля треугольника 144 м, соотношение сторон 3: 4: 5. Найдите площадь поля.
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где,
Дано, что стороны треугольного поля находятся в соотношении 3: 4: 5 и периметр = 144 м.
Следовательно, a : b : c = 3: 4: 5
Примем стороны треугольного поля за
Подставляя значение x в, мы получаем стороны треугольника как
Площадь треугольного поля, скажем, A со сторонами a , b , c и s как полупериметр задается как
Страница № 12.23:
Вопрос 7:
Найдите площадь равностороннего треугольника высотой ч см.
Ответ:
Высота равностороннего треугольника со стороной на равна
Подставляя заданное значение высоты х см, получаем
Площадь равностороннего треугольника, скажем, , каждая сторона которого равна см, определяется как
Площадь данного равностороннего треугольника, у которого каждая равная сторона равна;
Страница № 12.23:
Вопрос 8:
Пусть Δ — площадь треугольника. Найдите площадь треугольника, каждая сторона которого вдвое больше стороны данного треугольника.
Ответ:
Нам дано предполагаемое значение площади данного треугольника ABC
Мы предполагаем, что стороны данного треугольника ABC равны a, b, c
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
Где,
Возьмем стороны нового треугольника как 2 a , 2b, 2c, что в два раза больше сторон предыдущего треугольника
Теперь площадь треугольника со сторонами 2 a , 2 b , и 2c и в качестве полупериметра задается как
, где
Сейчас,
Страница № 12.23:
Вопрос 9:
Если каждая сторона треугольника удвоена, процент находки увеличивается в его площади.
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
Где,
Возьмем стороны нового треугольника как 2 a , 2b, 2 c , что в два раза больше сторон предыдущего треугольника
Теперь площадь треугольника со сторонами 2 a, 2 b, и 2 c и в качестве полупериметра задается как
Где,
Сейчас,
Следовательно, увеличиваем площадь треугольника
Процентное увеличение площади
Страница № 12.24:
Вопрос 2:
Основание равнобедренного прямоугольного треугольника 30 см. Его площадь
(а) 225 см 2
(б) 225 3 см 2
(в) 225 2 см 2
(г) 450 см 2
Ответ:
Пусть ABC будет прямоугольным треугольником, в котором ∠B = 90 °. Теперь base = BC; перпендикуляр = AB; Гипотенуза = AC Теперь, BC = 30 см. Теперь ∆ABC — это равнобедренная прямоугольная ∆, и мы знаем, что гипотенуза — это самая длинная сторона правой ∆.Итак, AB = BC = 30 см площадь ∆ABC = 12 × основание × высота = 12 × BC × AB = 12 × 30 × 30 = 450 см2
Следовательно, правильный вариант — (d).
Страница № 12.24:
Вопрос 10:
Если каждая сторона равностороннего треугольника утроится, то каков процент увеличения площади треугольника?
Ответ:
Площадь равностороннего треугольника, каждая сторона которого равна см, равна
Теперь площадь равностороннего треугольника, скажем, если каждая сторона утроится, будет равна
.a = 3 a
Следовательно, увеличиваем площадь треугольника
Процентное увеличение площади
Страница № 12.24:
Вопрос 1:
Отметьте правильный вариант в каждом из следующих пунктов:
Стороны треугольника равны 16 см, 30 см, 34 см. Его площадь
(а) 225 см 2
(б) 2253 см 2
(в) 225 2 см 2
(г) 450 см 2
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольника, скажем A, со сторонами 16 см, 30 см и 34 см, равна
a = 16 см; b = 30 см; c = 34 см
Следовательно, площадь треугольника равна
.Примечание: Нет правильных вариантов
Страница № 12.24:
Вопрос 3:
Стороны треугольника 7 см, 9 см и 14 см. Его площадь
(а) 125 см2
(б) 123 см2
(в) 245 см2
(г) 63 см2
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольника со сторонами 7 см, 9 см и 14 см равна
a = 7 см; b = 9 см; c = 14 см
Следовательно, ответ (а).
Страница № 12.24:
Вопрос 4:
Стороны треугольного поля — 325 м, 300 м и 125 м. Его площадь
(а) 18750 м 2
(б) 37500 м 2
(в) 97500 м 2
(г) 48750 м 2
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Следовательно, площадь треугольного поля, скажем, A , имеющего стороны 325, 300 и 125 м, определяется как
a = 325 м; b = 300 м; c = 125 м
Следовательно, правильный ответ (а).
Страница № 12.24:
Вопрос 5:
Стороны треугольника равны 50 см, 78 см и 112 см. Наименьшая высота
(а) 20 см
(б) 30 см
(в) 40 см
(г) 50 см
Ответ:
Площадь треугольника со сторонами a , b , c и s как полупериметр определяется как,
, где
Следовательно, площадь треугольника, скажем A со сторонами 50 см, 78 см и 112 см, равна
Площадь треугольника с высотой p , равной
Площадь = 12 × основание × высота
Где, A = 1680
Мы должны найти наименьшую высоту, поэтому заменим значение базы AC на длину каждой стороны по очереди и найдем наименьшее расстояние высоты i.е. п.
Корпус 1
Корпус 2
Корпус 3
Следовательно, ответ (б).
Страница № 12.24:
Вопрос 6:
Стороны треугольника равны 11 м, 60 м и 61 м. Высота до самой малой стороны
(а) 11 м
(б) 66 м
(в) 50 м
(г) 60 м
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Нужно найти высоту до наименьшей стороны
Следовательно, площадь треугольника со сторонами 11 м, 60 м и 61 м равна
a = 11 м; b = 60 м; c = 61 м
Площадь треугольника с основанием AC и высотой p определяется как
Нам нужно найти высоту p , соответствующую наименьшей стороне треугольника.Здесь наименьшая сторона 11 м
AC = 11 м
Следовательно, ответ (г).
Страница № 12.24:
Вопрос 7:
Стороны треугольника 11 см, 15 см и 16 см. Высота до наибольшей стороны
(а) 307 см
(б) 1572см
(в) 1574см
(г) 30 см
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Нам нужно найти высоту, соответствующую самой длинной стороне
Следовательно, площадь треугольника со сторонами 11 см, 15 см и 16 см равна
a = 11 м; б = 15 см; c = 16 см
Площадь треугольника с основанием AC и высотой p определяется как
Нам нужно найти высоту p , соответствующую самой длинной стороне треугольника.Здесь самая длинная сторона 16 см, то есть AC = 16 см
Следовательно, ответ (c).
Страница № 12.24:
Вопрос 8:
Если площадь равнобедренного прямоугольного треугольника равна 8 см. 2 , каков периметр треугольника?
(а) 8 + 2 см 2
(б) 8 + 42 см 2
(в) 4 + 82 см 2
(г) 122 см 2
Ответ:
Нам дана площадь равнобедренного прямоугольного треугольника, и мы должны найти его периметр.
Две стороны равнобедренного прямоугольного треугольника равны, и мы принимаем равные стороны за основание и высоту треугольника. Нам предлагается найти периметр треугольника
Возьмем основание и высоту треугольника x см.
Площадь равнобедренного прямоугольного треугольника, скажем с основанием x см и высотой x см определяется как
A = 8 см 2 ; Основание = Высота = x см
Используя теорему Пифагора, мы имеем;
Пусть ABC будет заданным треугольником
Периметр треугольника ABC, скажем, P равен
AB = 4 см; ВС = 4 см; AC =
Следовательно, ответ (б).
Страница № 12.24:
Вопрос 9:
Длины сторон Δ ABC — последовательные целые числа. Его Δ ABC имеет тот же периметр, что и равносторонний треугольник со стороной длиной 9 см, какова длина самой короткой стороны Δ ABC ?
(а) 4
(б) 6
(в) 8
(г) 10
Ответ:
Нам дано, что треугольник ABC имеет периметр, равный периметру равностороннего треугольника со стороной 9 см.Стороны треугольника ABC — последовательные целые числа. Нам предлагается найти наименьшую сторону треугольника ABC
.Периметр равностороннего треугольника, скажем, P со стороной 9 см равен
Предположим, что три стороны треугольника ABC равны x, x + 1, x− 1
Периметр треугольника ABC, скажем, P 1 определяется как
P 1 = AB + BC + AC
AB = x ; ВС = х +1; АС = x — 1.Поскольку P 1 = P . Итак,
Используя значение x, , мы получаем стороны треугольника как 8 см, 9 см и 10 см.
Следовательно, ответ (c).
Страница № 12.24:
Вопрос 10:
На данном рисунке отношение AD к DC равно 3 к 2. Если площадь Δ ABC равна 40 см 2 , какова площадь Δ BDC ?
Ответ:
Дана площадь треугольника ABC 40 см 2 .
Также
Нам предлагается найти площадь треугольника BDC
Возьмем BE перпендикулярно основанию AC в треугольнике ABC.
Мы принимаем AC равным y и BE равным x в треугольнике ABC
Площадь треугольника ABC, скажем, определяется как
Нам дано отношение AD к DC равное 3: 2
Итак,
В треугольнике BDC мы принимаем BE за высоту треугольника
.Площадь треугольника BDC, скажем, A 1 определяется как
Следовательно, ответ (а).
Страница № 12.25:
Вопрос 11:
Основание и гипотенуза прямоугольного треугольника имеют длину 5 см и 13 см соответственно. Его площадь
(а) 25 см 2
(б) 28 см 2
(в) 30 см 2
(г) 40 см 2
Ответ:
В прямоугольном треугольнике ABC с основанием 5 см и гипотенузой 13 см нам предлагается найти его площадь
Использование теоремы Пифагора
Где, AB = гипотенуза = 13 см, AC = база = 5 см, BC = высота
Площадь треугольника, скажем с основанием 5 см и высотой 12 см определяется как
Где, База = 5 см; Высота = 12 см
Следовательно, ответ (c).
Страница № 12.25:
Вопрос 12:
Если длина медианы равностороннего треугольника x см, то его площадь будет
(a) x 2
(b) 32×2
(c) x23
(d) x22
Ответ:
Нам дана длина медианы равностороннего треугольника, по которой мы можем вычислить его сторону.Нам предлагается найти площадь треугольника в единицах x
.Высота равностороннего треугольника, скажем, L, с равными сторонами см определяется как, где L = x см
Площадь равностороннего треугольника, скажем, A 1 с каждой стороной см задается как
С .Со
Следовательно, ответ (c).
Страница № 12.25:
Вопрос 13:
Длина каждой стороны равностороннего треугольника площадью 43 см2 составляет
(а) 4 см
(б) 43 см
(в) 34 см
(г) 3 см
Ответ:
Площадь равностороннего треугольника, скажем, A, , каждая сторона которого равна см, равна
Нам предлагается найти сторону треугольника
Следовательно, сторона равностороннего треугольника равна a, площадь равна
Следовательно, правильный ответ (а).
Страница № 12.25:
Вопрос 14:
Если каждая сторона треугольника удвоена, то увеличение площади треугольника составит
(a) 1002%
(b) 200%
(c) 300%
(d) 400%
Ответ:
Площадь треугольника со сторонами a , b , c и s в виде полупериметра определяется выражением,
, где
Возьмем стороны нового треугольника как 2 a , 2 b , 2 c , что в два раза больше сторон предыдущего треугольника
Теперь площадь треугольника со сторонами 2 a , 2 b, и 2c и в качестве полупериметра задается как
Где,
Сейчас,
Следовательно, увеличиваем площадь треугольника
Процентное увеличение площади
Следовательно, ответ (c).
Страница № 12.25:
Вопрос 15:
Квадрат и равносторонний треугольник имеют равные периметры. Если диагональ квадрата 122 см, то площадь треугольника
(а) 242 см2
(б) 243 см2
(в) 483 см2
(г) 643 см2
Ответ:
Дано, что периметр квадрата ABCD равен периметру треугольника PQR.
Дана величина диагонали квадрата. Нам предлагается найти площадь треугольника
В квадрате ABCD мы предполагаем, что смежные стороны квадрата равны a.
Так как это квадрат, то
Используя теорему Пифагора
Следовательно, сторона квадрата 12 см.
Периметр квадрата ABCD, скажем, P равен
Сторона = 12 см
Периметр равностороннего треугольника PQR, скажем, P 1 равен
Сторона равностороннего треугольника PQR равна 16 см.
Площадь равностороннего треугольника, скажем, A, , каждая сторона которого равна см, равна
Площадь данного равностороннего треугольника, каждая равная сторона которого равна 4 см, равна
.a = 16 см
Следовательно, ответ (г).
Страница № 12.8:
Вопрос 6:
Периметр треугольника 300 м.Если его стороны находятся в соотношении 3: 5: 7. Найдите площадь треугольника.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника. Если обозначить площадь треугольника как A, , тогда площадь треугольника, имеющего стороны a , b , c и s в виде полупериметра, будет равна;
Где,
Нам дано, а
Здесь,
Используя эти данные, мы найдем стороны треугольника.Предположим, что стороны треугольника следующие:
Так как, значит,
Теперь мы знаем каждую сторону, то есть
Теперь мы знаем все стороны. Итак, мы можем использовать формулу Герона.
Площадь треугольника;
A = ss-as-bs-c = 150150-60150-100150-140 = 1500 = 10015 × 9 × 5 = 1005 × 3 × 3 × 3 × 5 = 100 × 3 × 53 = 15003 м2
Страница № 12.8:
Вопрос 1:
Найдите площадь треугольника, стороны которого равны соответственно 150, 120 и 200 см.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как A, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Нам дано:
a = 150 см
b = 120 см
c = 200 см
Здесь мы рассчитаем с,
Итак, площадь треугольника:
Страница № 12.8:
Вопрос 2:
Найдите площадь треугольника со сторонами 9 см, 12 см и 15 см.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как A, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Нам дано:
a = 9 см, b = 12 см, c = 15 см
Здесь мы рассчитаем с,
Итак, площадь треугольника:
Страница № 12.8:
Вопрос 3:
Найдите площадь треугольника, две стороны которого равны 18 см и 10 см, а периметр равен 42 см.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как A, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Нам дано:
a = 18 см
b = 10 см и периметр = 42 см
Мы знаем, что периметр = 2 с ,
Так 2 с = 42
Следовательно с = 21 см
Мы это знаем, поэтому
Итак, площадь треугольника:
Страница № 12.8:
Вопрос 4:
В Δ ABC , AB = 15 см, BC = 13 см и AC = 14 см. Найдите площадь Δ ABC и, следовательно, ее высоту на AC .
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если мы обозначим площадь треугольника как «Площадь» , , то площадь треугольника, имеющего стороны a , b , c и s в виде полупериметра, определяется как;
Где,
Нам дано:
AB = 15 см, BC = 13 см, AC = 14 см
Здесь мы рассчитаем с,
Итак, площадь треугольника:
Теперь нарисуйте высоту от точки B на AC, которая пересекает ее в точке D.BD — требуемая высота. Итак, если вы нарисуете фигуру, вы увидите, что
Вот. Итак,
Страница № 12.8:
Вопрос 5:
Периметр треугольного поля составляет 540 м, а его стороны находятся в соотношении 25: 17: 12. Найдите площадь треугольника.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.Если обозначить площадь треугольника как A, , тогда площадь треугольника, имеющего стороны a , b , c и s в виде полупериметра, будет равна;
Где,
Нам дано, а
Здесь,
Используя эти данные, мы найдем стороны треугольника. Предположим, что стороны треугольника следующие:
Так как, значит,
Теперь мы знаем каждую сторону, то есть
Теперь мы знаем все стороны.Итак, мы можем использовать формулу Герона.
Площадь треугольника;
Страница № 12.8:
Вопрос 7:
Периметр треугольного поля 240 дм. Если две его стороны равны 78 см и 50 дм, найдите длину перпендикуляра на стороне длиной 50 дм от противоположной вершины.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.Если обозначить площадь треугольника как A, , тогда площадь треугольника, имеющего стороны a , b , c и s в виде полупериметра, будет равна;
Где,
Нам даны две стороны треугольника и.
То есть a = 78 дм, b = 50 дм
Мы найдем третью сторону c , а затем площадь треугольника, используя формулу Герона.
Сейчас,
Используйте формулу Герона, чтобы найти площадь треугольника.То есть
Рассмотрим треугольник ΔPQR, в котором
PQ = 50 дм, PR = 78 дм, QR = 120 дм
Где RD — желаемая длина перпендикуляра
Теперь из рисунка у нас
Страница № 12.8:
Вопрос 8:
Треугольник имеет стороны 35 см, 54 см и 61 см в длину. Найдите его область. Также найдите наименьшую из его высот.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как A, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Нам дано: а = 35 см; b = 54 см; c = 61 см
Площадь треугольника:
Предположим, что это треугольник ΔPQR, и сфокусируемся на треугольнике, приведенном ниже,
, в котором PD1, QD2 и RD3 — три высоты
Где PQ = 35 см, QR = 54 см, PR = 61 см
Мы будем вычислять каждую высоту по очереди, чтобы найти наименьшую.
Корпус 1
В случае ΔPQR:
Корпус 2
Корпус 3
Наименьшая высота — QD2.
Наименьшей высотой считается высота, нанесенная на стороне длиной 61 см от соответствующей вершины.
Страница № 12.8:
Вопрос 9:
Длины сторон треугольника находятся в соотношении 3: 4: 5, а его периметр равен 144 см.Найдите площадь треугольника и высоту, соответствующую самой длинной стороне.
Ответ:
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как A, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Нам дано, а
Здесь,
Используя эти данные, мы найдем стороны треугольника.Предположим, что стороны треугольника следующие:
Поскольку 2 с = 144, поэтому
Теперь мы знаем каждую сторону, то есть
Теперь мы знаем все стороны. Итак, мы можем использовать формулу Герона.
Площадь треугольника;
Нас просят определить высоту, соответствующую самой длинной стороне данного треугольника. Самая длинная сторона — c и предполагает, что соответствующая высота равна H, тогда
Страница № 12.8:
Вопрос 10:
Периметр равнобедренного треугольника составляет 42 см, а его основание в (3/2) раза умножено на каждую из равных сторон. Найдите длину каждой стороны треугольника, площадь треугольника и высоту треугольника.
Ответ:
Нам дано это, и его основание (3/2) умноженное на каждую из равных сторон. Нас просят узнать длину каждой стороны, площадь треугольника и высоту треугольника.В этом случае «высота» — это перпендикулярное расстояние, проведенное на основании от соответствующей вершины.
В следующем треугольнике ΔABC
BC = a, AC = b , AB = c и AB = AC
Пусть длина каждой из равных сторон равна x и a, b и c — сторона треугольника. Итак,
Т.к. это означает, что
Следовательно, все стороны треугольника равны:
Все стороны треугольника равны 18 см, 12 см и 12 см.
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как Area, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Чтобы вычислить площадь треугольника, нужно найти с:
Площадь треугольника:
Теперь узнаем высоту, скажем H.См. Рисунок, на котором AD = H
Итак,
Страница № 12.8:
Вопрос 11:
Найдите площадь заштрихованной области на данном рисунке.
Ответ:
Нам дан следующий рисунок с размерами.
Рисунок:
Пусть точка, в которой находится угол, будет D.
AC = 52 см, BC = 48 см, AD = 12 см, BD = 16 см
Нас просят узнать площадь заштрихованной области.
Площадь заштрихованной области = Площадь треугольника ΔABC — площадь треугольника ΔABD
В прямоугольном треугольнике ABD имеем
Площадь треугольника ΔABD определяется как
Всякий раз, когда нам дается измерение всех сторон треугольника, мы в основном ищем формулу Герона, чтобы определить площадь треугольника.
Если обозначить площадь треугольника как Area, , то площадь треугольника со сторонами a , b , c и s в виде полупериметра будет равна;
Где,
Здесь a = 48 см, b = 52 см, c = 20 см и
Следовательно, площадь треугольника ΔABC равна,
Теперь у нас есть вся информация для расчета площади заштрихованной области, поэтому
Площадь заштрихованной области = Площадь ΔABC — Площадь ΔABD
Площадь заштрихованной области 384 см 2 .
Просмотреть решения NCERT для всех глав класса 9
Извините! — Страница не найдена
Пока мы разбираемся, возможно, поможет одна из ссылок ниже.
Дома Назад- Аудитория
- Онлайн-тесты
- Ускоренный онлайн-курс JEE
- Двухлетний курс для JEE 2021
- Аудитория
- Онлайн-курс NEET
- Серия онлайн-тестов
- Фонд CA
- CA Средний
- CA Финал
- Программа CS
- Аудитория
- Серия испытаний
- Книги и материалы
- Тестовый зал
- Умный взломщик BBA
- Обучение в классе
- Онлайн-коучинг
- Серия испытаний
- Умный взломщик IPM
- Книги и материалы
- GD-PI
- CBSE, класс 8
- CBSE класс 9
- CBSE, класс 10
- CBSE, класс 11
- CBSE, класс 12
- Обучение в классе
- Онлайн-классы CAT
- Серия испытаний CAT
- MBA Жилой
- Умный взломщик CAT
- Книги и материалы
- Онлайн-классы без CAT
- Серия испытаний без CAT
- Тестовый зал
- GD-PI
- Обучение в классе
- Серия испытаний
- Интервью с Civils
- Аудитория
- Онлайн-классы
- Серия испытаний SSC
- Переписка
- Практические тесты
- Электронные книги SSC
- SSC JE Study Package
- Аудитория
- RBI класс B
- Банковский тест серии
- Переписка
- Банковские электронные книги
- Банк ПДП
- Онлайн-коучинг
- Обучение в классе
- Серия испытаний
- Книги и материалы
- Аудитория
- Программа моста GRE
- GMAT Онлайн-коучинг
- Консультации по приему
- GMAT Обучение в классе
- Стажировка
- Корпоративные программы
- Студенты колледжа
- Рабочие специалисты
- Колледжи
- школ
Просмотреть вопрос — Помощь?
Прямой треугольник (ABC) с прямым углом C.
M — середина BC.
N — средняя точка переменного тока.
Пусть AC = 2x, значит CN = x.
Пусть CB = 2y, поэтому CM = y.
Рассмотрим прямоугольный треугольник (ACM): рассмотрим прямоугольный треугольник (BNC) «
CM 2 + CA 2 = AM 2 BC 2 + CN 2 = BN 2
y 2 + (2x) 2 = 19 2 (2y) 2 + x 2 = 13 2
y 2 + 4x 2 = 361 4y 2 + x 2 = 169
y 2 + 4x 2 = 361 —> умножить на 4 —> 4y 2 + 16x 2 = 1444
4y 2 + x 2 = 169 —> умножить на -1 —> -4y 2 — x 2 = -169
15 x 2 = 1275
x 2 = 85
x = sqrt (85) —> AC = 2 · sqrt (85)
y 2 + 4x 2 = 361 — -> умножить на -1 —> y 2 — 4x 2 = -361
4y 2 + x 2 = 169 —> умножить на 4 —> 16y 2 + 4x 2 = 676
15y 2 = 315
y 2 = 21
y = sqrt (21) —> CB = 2 · sqrt (21)
Чтобы найти AB: AC 2 + CB 2 = AB 2 —> [2 · sqrt (85)] 2 + [2 · sqrt (21)] 2 = AB 2
340 + 84 = AB 2
424 = AB 2
AB = sqrt (424)
Найдите недостающую сторону, округляя до десятых долей
найти недостающую сторону округлить до ближайшей десятой 7.Классифицируйте по углам: калькулятор, чтобы найти длину одной стороны коврика, округленную до ближайшей десятой. 8 43. Вычислите длину с точностью до десятых. Оставляйте свои ответы в простейшей радикальной форме. 51 B. Найдите длину \ begin {align *} a \ end {align *} Найдите ВСЕ недостающие стороны и углы треугольников ниже. Найдите два возможных значения для $ \ mathrm {m} \ angle C $ с точностью до градуса. 25 Округлите ответ до ближайшей десятой. 3 мили 23) 3 см 40 Длину округления до ближайшей десятой и угол до ближайшей десятой градуса.Округлите до ближайшей десятой. 👉 Узнайте, как найти недостающую длину стороны прямоугольного треугольника. ГРАФИК. H. 5 20 12) 20 680. Округлите ответы до ближайшей десятой, если необходимо. Используйте округленные значения для вычисления следующего значения. 92 6. -1-Найдите недостающую сторону. Округлите до ближайшей десятой. Гипотенуза прямоугольного треугольника — это сторона, противоположная прямому углу, и самая длинная сторона. 6 см 10. 3. 29 32 G X = Правильные ответы: 2 вопроса: Найдите недостающую сторону. 4m 5m 7m 5 cm Рабочий лист теоремы Пифагора Сторона B — Нахождение недостающей стороны (ножки или гипотенузы) Указания: Используйте теорему Пифагора, чтобы найти длину недостающей стороны прямоугольных треугольников, как показано ниже.29 32 G X = Правильные ответы: 2 вопроса: Найдите недостающую сторону. 697 до ближайшей десятой сотой и один: 9 с округлением до. Используйте формулу = + +, чтобы найти длину самого длинного полюса (x). Определите, является ли каждый треугольник прямоугольным. Используйте округленные значения для вычисления следующего значения. Пример. 6 Найдите расстояние от T (3, -2) до V (4,2). 1-3- Найдите недостающую сторону каждого треугольника. 17) 620 19) 22. ореановая тройка. Прокрутите страницу вниз, чтобы узнать больше. Поиск недостающих сторон с помощью тригонометрии.\ circ \). b = 6. 5 миль C 42 21) 29. Лестница высотой 20 футов. Программное обеспечение Kuta — Бесконечная алгебра 1.) Найдите площадь каждого правильного многоугольника. Округлите ответы до ближайшей десятой. Решение: Используя теорему Пифагора. Округлите до ближайшей десятой. 42 48 290 Сделано с конечной попыткой Зарезервируйте права Найдите недостающую сторону каждого треугольника. Округлите окончательный ответ до ближайшей десятой. Напишите уравнение, которое вы могли бы использовать, чтобы найти длину недостающей стороны каждого прямоугольного треугольника. 7) 41 30 Найдите пропущенное значение.11) 13 740 / 3Œs (7LÒ 13) 630 Найдите площадь каждого треугольника. Найдите значение каждой переменной. sin θ = Противоположная сторона / Сторона гипотенузы = AC / AB. — Поиск недостающих сторон и углов. 29 D. a = 8,0 = 17. answer-user-profile-image. Округлите десятичные ответы до ближайшей десятой. 13) апофема треугольника 3. Подставьте меру угла в левую часть уравнения и используйте треугольник, чтобы установить соотношение в правой части. База 7м, сторона не под прямым углом — 20м. Найдите длину стороны b в «ABC» до ближайшего целого числа, если A = 42 °, B = 87 ° и a = 24.) 8 марта 2015 г. · Правый трианол тригг. 24 Найдите площадь рисунка. При необходимости округлите до ближайшей десятой. 3) mi mi x 4) x ft ft Найдите расстояние между каждой парой точек. Округлите десятичные дроби до сотых. Некоторые из рабочих листов для этой концепции: Прямой треугольник с отсутствующими сторонами и углами, 9 решения прямоугольных треугольников, Отношения синуса и косинуса, Геометрия, Использование теоремы Пифагора, Уважаемые студенты wccs, Работа с дополнительными примерами, Найдите длину отрезка вокруг вашего . Найдите площадь треугольника со сторонами длиной 20, 26 и 37 см.Решение прямоугольных треугольников * Убедитесь, что ваш файл. а = 12; b = 5; c = _____ 6. 1 дюйм. Прямоугольный треугольник — это треугольник, один из углов которого составляет 90 градусов. 4 м 13) a = 8. 5] Практические задачи. И мы остались с b, равным 5 по косинусу 65 градусов. 62 / 87,21 Поскольку нам даны все три стороны треугольника и нет углов, мы можем найти недостающий угол, используя Закон косинусов. Следовательно, гипотенуза треугольника равна [8. Округлите ответ до ближайшей десятой. Гипотенуза составляет 580 ярдов.5 B. Ответ на триггер Возьмите домашнее имя Найдите недостающую сторону. Округлите до ближайшей десятой тригонометрии. Найдите размер каждого указанного угла. 11) cos Z. 6 км 7. 2). 1 м 10) a = 12. Найдите размер каждого указанного угла. Определите длину стороны x с точностью до десятых. 29 32 G X = Правильные ответы: 2 вопроса: Найдите недостающую сторону. Округлите до ближайшей десятой. Округлите ответы до ближайшей десятой. Найдите размер каждой указанной стороны. 06. 4 A B C θ 8) 3 3 B C A θ Найдите размер каждой указанной стороны.9 м 14) a = 5. Вычислите значение z с точностью до сотых: 34. Округлите ответ до ближайшей десятой, если необходимо. 1 C. 9 км x 14. 5 B. 15 августа 2020 г. · Чтобы округлить до ближайшей десятой, сначала укажите цифры округления и контрольные цифры. 15. Найдите значения x и y с округлением до ближайшей десятой. 841. 24 Найдите значение каждой переменной. — Поиск недостающих сторон и углов Дата _____ Период ____ Найдите размер каждого указанного угла. Конгруэнтно. Округлите ответ до ближайшей десятой.S км, 15 км, 17 км 15. 62 / 87,21 Поскольку у нас есть две стороны и включенный угол, мы можем использовать закон косинусов, чтобы найти x 62 / 87,21 Поскольку нам даны две стороны и включенный угол угол, мы можем найти недостающую сторону, используя Закон & RVLQHV 62 / 87,21. Найдите недостающую сторону каждого прямоугольного треугольника. 9) x14 56 ° 10) x 19 24 ° 11) x 15 15 ° 12) x 17 75 ° 13) x 19 20 ° 14) 16 x44 ° 15) 18 x 54 ° 16) 19 x 75 ° Найдите длину сторона, помеченная x. Вам нужно найти S и R. Округлить до десятых.18. (Круг с радиусом 3. Введите 3 числа и оставьте одно поле пустым, затем нажмите кнопку «Рассчитать». Округлите ответ до ближайшей десятой. Оставьте ответ в простейшей радикальной форме. 3 фута. Округлите ответ до ближайшей десятой. при необходимости. Найдите площадь треугольника со сторонами длиной 18, 21 и 32 дюйма. Округлите ответ до ближайшей десятой, если необходимо. 5 21. Найдите недостающую сторону. 72 D. — 14. Найдите ml -B до ближайшей десятой. 22 2 (4. 5 30. Округлить до ближайшей десятой (один десятичный знак).29) 12 ярдов 150 ° 30) 10 дюймов 255 ° Найдите длину окружности каждого круга. 5. Задача 9 Легкая трудность. Округлите ответ до ближайшей десятой. В этом случае есть два возможных треугольника. Каждый раз, когда вы используете тригонометрические соотношения, используйте только ту информацию, которую вам дают. Округлить до сотых. SOH CAH TOA 14) 50 15) 16) X N K 53 Указания: Найдите недостающую сторону каждого треугольника. Округлите ответ до ближайшей десятой. Определите длину стороны y с точностью до сотых. Нам дается соседняя нога к.) Найдите длину недостающей стороны. Пожалуйста, делайте и показывайте всю работу на отдельном листе! 6см 3см 5. 2. — Поиск недостающих сторон и углов. Контрольная цифра меньше пяти. 3. 8 3 Найдите длину недостающей стороны. Округлый угол измеряется с точностью до градуса, а размер стороны — с точностью до десятой части. com Найдите площадь каждого треугольника. Теорема Пифагора: если c обозначает длину гипотенузы, а a и b обозначают длины двух других сторон, теорема Пифагора может быть выражена как уравнение Пифагора a2 + b2 = c2.а = 8; б = _____; c = 10 7. При необходимости округлите до ближайшей десятой. Найдите размер каждого указанного угла. Здесь a = 12, b = x и c = 15. 11. Пример 3. G. Комментарии • 4. Найдите недостающую длину третьей стороны. 320 = -IL Нахождение недостающей стороны прямоугольного треугольника Пример 1. (Округлите до ближайшей десятой, если необходимо. 2) x + 97 89 ° Найдите величину указанного угла с точностью до градуса. 0 19. Найдите значение указанной триггерной функции. Решение Нарисуйте схему и пометьте данную информацию.1). R Найдите длину отсутствующей стороны. 2. Таким образом, для нашего треугольника мы знаем: Используя свой калькулятор, решите: Это. Сторона 18,5 миль 15. Решение: Так как x — противоположная нога, а 16 — период, 16 12 20 52 4. tancy 0 — 4. Стороны a и b — ноги. B. 12 дюймов mt: 75 дюймов mi E = 37. 1) x 12 дюймов 13 дюймов 5 дюймов 2) 6 см 8 см x 10 см Найдите указанную недостающую длину. 627 tan24 zq 4. Запишите ответы в виде целых или десятичных знаков. с округлением до ближайшей десятой 35 ° Его также можно использовать для нахождения недостающего угла, если все стороны непрямого треугольника… Округлить ответы до ближайшей десятой.7 дюймов. Найдите недостающую длину третьей стороны. Таким образом, мы можем разделить обе стороны на косинус 65 градусов. Определите длину стороны z с точностью до дюйма. 9 10 A B C θ 5) 7. 58 C. 48 39 540 C 2020 K u t. Найдите GH. Использование sin, cos и tan для поиска недостающих сторон и Given: $$ \ sin A = 0. 1). Используйте свои решения, чтобы перемещаться по лабиринту. Прямоугольный треугольник. 58 Первое число справа от десятичной точки — 5. Вторая цифра после десятичной точки — 8, что больше 5. Таким образом, прибавьте 1 к 5. Результат = 124.Найдите значение каждого тригонометрического соотношения. Округлите до ближайшей десятой. 1) 6 x 72 ° Вопрос 276240: Найдите недостающую меру каждого прямоугольного треугольника. 1-6 классы. 2) 1) 35 25 43 ° 22 ° 4) 3) 32 32 59 ° 56 ° 5) 71 Теорема Пифагора и ее обратное. Округлите окончательный ответ до ближайшей десятой. * (20 (75 b = 24,5 14) x 45 62 ° 68 ° 91,13 132 16. Пример: 2 Найдите недостающую сторону. 4 мили 9. При необходимости округлите до ближайшей десятой. 9 км 14. 113 Округлите до ближайшей десятой 116. Округлите ответ до ближайшей десятой.Найдите недостающие длины сторон. 90 Решите треугольник, найдя недостающую информацию. Решение. В AFGH g = 5 футов, h = 22 футов и mZF = 500. 2. H. 1 Ответы. 14. Оставляйте свои ответы в простейшей радикальной форме. 7 12 13 14 11 Co s e 13 ACOSês. 50. Сюда входит вычисление гипотенузы. 1 750 15 58. Используйте тригонометрическую функцию, чтобы найти значение x. Скругление в сторону составляет 16 дюймов в длину, как показано. Найдите длину недостающей стороны. Найдите недостающую длину для каждого прямоугольного треугольника.Пример: 3 Найдите недостающую сторону. м иду. Пример: 4 Найдите недостающую сторону. com 15 апреля 2010 г. · Найдите длину недостающей стороны. 6 Правый треугольник Trig. Найдите площадь круга (используйте 3. Но это менее надежно, потому что если вы допустили ошибку на стороне b, то сторона c также будет неправильной. Com 07 ноября 2014 г. · При необходимости округлите до ближайшей десятой части 0. Округлите десятичные дроби до ближайшей десятой. 8 14 0. Определите, округлены ли длины сторон до ближайшей сотой. Найдите градусы. Найдите площадь каждого сектора.Округлите ответы до ближайшей десятой. Это приведет к наиболее точным ответам. Х 44 ° 18 18. Следовательно, с точностью до десятых долей фута, длина гипотенузы будет примерно 11. Ответ. Показать решение Округлите до ближайшей десятой мили. 13. c = √ (a² + b²) Заданный угол и гипотенуза; Примените закон синусов или тригонометрии, чтобы найти длины сторон прямоугольного треугольника: Найдите недостающую сторону, округлив до ближайшего десятого 11 октября 2019 г. · Ответы: 1 на вопрос: Найдите длину недостающей стороны.999 с точностью до ближайшей сотни, десяти, десятой и сотой долей с помощью вертикальной числовой линии. 5 Найдите размер каждой указанной стороны. 36 C. 1) 13 12 B A C θ 2) 4 13 A B C θ 3) 9 6 A B C θ 4) 11. 13) x 6 58 ° 42 ° 5. 30 апреля 2010 г. · Найдите длину недостающей стороны. 17) 15 65 ° 46 ° 18) 24 25 ° 34 ° Найдите недостающую сторону. 13) 36 x 70 ° 30 ° 14) x 16 42 ° 56 ° Найдите площадь каждого треугольника. c. 6 миль C 11. 9. 15 апреля 2010 г. · Найдите длину отсутствующей стороны. Найдите длину отсутствующей стороны (при необходимости округлите до ближайшей десятой).Округлите ответ до ближайшей десятой. 31) 18 33) 19 55 q Найдите длину недостающей стороны x. Для этого возьмем арксинус обеих частей уравнения. Промежуточные значения округляются до десятых. Период. 9 июня 2016 г. · Найдите значение каждой переменной. 5. Округлите размеры сторон до ближайшей десятой и размеры углов до ближайшего градуса. Нарисуйте рисунок, напишите уравнение и решите. 15) 550 31 31 50 Решите прямоугольный треугольник e. e2 d2 f2 2df (cos E) e2 4. Найдите значение каждой переменной.1 мл. Округлите до ближайшего десятого 5 мая 2020 г. Найдите недостающую сторону. Округлите до ближайшей десятой. ) Округлите ответы до десятых. sin C. Воспользуйтесь калькулятором, чтобы вычислить синус и косинус углов. Нам дана гипотенуза. Оставьте свои ответы радикальными в простейшей форме. 3) 60 36 x 100 4) 48 x64 36 Найдите недостающие длины сторон. Помните: SohCah Toa! 1. Если ваш ответ — неполный квадрат, округлите до ближайшего десятичного знака. 4 A B C θ 8) 3 3 B C A θ Найдите размер каждой указанной стороны.Мы можем использовать следующую пропорцию из закона синусов, чтобы найти длину c. а = _____; b = 40; c = 50 9. wyzant. Запишите ответы как целые числа или десятичные дроби с округлением до ближайшей десятой. При необходимости округлите до ближайшей десятой. даны стороны прямоугольного треугольника. Вы знаете размеры сторон. 83см 6. Равносторонний. Пример 1 Найдите недостающий угол cos xo 12. 3. 814… e e · 6. Найдите x. Округлите до ближайшей десятой. Ответ: 3 📌📌📌 вопрос Решите для недостающей стороны. 7136 \\ $$ Мы должны определить значение угла, округленное до ближайшей десятой доли градуса.3 ярда 295. 62 / 87,21 Воспользуйтесь теоремой Пифагора, заменив 12 вместо b и 16 вместо c. 11. 16) 15 280 Округлите ваши ответы до ближайшей десятой, если необходимо. Округлите до ближайшей десятой. 6 миль 18) 9 из 20) 530 22) 14 миль 280 6 из 4. Период. (T) Что такое 16. При необходимости округлите до ближайшей десятой. При необходимости округлить до десятых. 1 сторона равна 13, другая — 5, A-324 B-18 C-36 D-13. c² = a² + b². 1 + Решите каждый треугольник. Округлите ответ до ближайшей десятой. Найдите длину недостающей стороны.9 Найдите периметр треугольника. Например, давайте посмотрим на Диаграмму 1. острый угол 65 ° и отрезок 5 единиц, и он использует тригонометрию, чтобы найти две недостающие стороны. Квадрат ценностей. Показать свою работу. 21) 34 45? 22) 32 49? 23) 34 38? Использование тригонометрии для определения длины Дата _____ Период ____ Найдите недостающую сторону. Решение: sin \ ((θ = \ frac {напротив} {hypotenuse} \). Swappy. Оставляйте свои ответы в простейшей радикальной форме. 13. on is 4,2, последнее — 2, -2 A. 1383. 10 февраля, 2021 · если отрезок a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²), если отрезок b неизвестен, тогда.{°} $ $ x $ 16 $. 5 Онс — X -58 Найдите значение указанного угла с точностью до градуса. Посмотреть ответ Джессика и Мэтью бегут к точке P по прямым путям, которые составляют фиксированный. Найдите ответ на свой вопрос «В данном прямоугольном треугольнике найдите недостающую длину с точностью до десятых, одна сторона 17 футов, а другая 11 футов» в 📘 Математика, если вы сомневаетесь в правильности ответов или нет ответа, то попробуйте воспользоваться умным поиском и найти ответы на похожие вопросы.Используйте треугольник справа. 15. 13. 01 R Bf Cosê Cos G. Округлите до ближайшей десятой. 9, 3077 лл. При необходимости округлите ответы до ближайшей десятой. Сторона c — гипотенуза. 8fi IOft b ft c см 182 + 152 см 64 м 24 дюйма 14. Найдите значение каждой переменной. Округлите до ближайшей десятой. Какое уравнение можно решить, чтобы найти одну из недостающих сторон треугольника? d. 23. Округлый угол измеряется с точностью до градуса, а размер стороны — с точностью до десятой доли. При необходимости округлите ответы до ближайшей десятой.Если вы знаете длину любых двух сторон прямоугольного треугольника, вы можете использовать формулу уравнения Пифагора, чтобы найти длину третьей стороны. 2. 25 июл 2020 Нажмите здесь, чтобы получить ответ на свой вопрос ✍️ Найдите недостающую сторону. 17 CD — это диаметр прямоугольного треугольника. 2 см 4. Подскажите, есть ли длина сторон для Pyt 19 10. 1). Используйте закон синусов, чтобы найти недостающие стороны и углы. X = 767. 8 с округлением до ближайшей десятой: найти недостающую сторону с округлением до ближайшей десятой. Калькулятор: 2.Оставьте свои ответы радикальными в простейшей форме. Высота крыши — 10. Вычислите значение y с точностью до десятых: 80 cos52 y q 3. 3. При необходимости округлите ваши ответы до ближайшей десятой. Тригонометрия — недостающие стороны Определите периметр треугольника с точностью до сантиметров. 6 opp B 13 C qdJ Округлить до ближайшей десятой. 17) m n 45 ° m, n Найдите недостающую сторону. Нарисованные ниже треугольники являются прямоугольными. 75 см. Найдите недостающую сторону. Округлите окончательный ответ до ближайшей десятой.Найдите площадь каждого правильного многоугольника. При необходимости округлите до ближайшей десятой. (РИСУНОК НЕ МОЖЕТ КОПИРОВАТЬ) Мы знаем, что угол α = 50 ° и соответствующая ему сторона a = 10. 7 ноября 2014 г. · При необходимости округлить до ближайшей десятой 0. Найдите площадь данного круга. — Поиск недостающих сторон и углов Дата _____ Период ____ Найдите размер каждого указанного угла. 7136 \\ $$ Мы должны определить значение угла, округленное до ближайшей десятой доли градуса. Найдите длину недостающей стороны. 8 ярдов. Если a = 5.(Обведите с буквой a. Найдите длину окружности данного круга. Округлите до ближайшей десятой. Решите, какие стороны даны вам с точки зрения заданного острого угла (никогда не используйте угол 90 !!) В этом случае нам дается острый угол 37. c Определите, является ли каждый треугольник со сторонами равной длины прямоугольным. b = 15, c = 20 a: 13. Name_KEY. a = 3, b = 4. 5. Округлите до ближайшей десятой. Пример : 671 с округлением до ближайшей десятки составляет 670, потому что цифра справа от разряда десятков оканчивается единицей,.Тригонометрия прямоугольного треугольника была разработана для поиска недостающих сторон прямоугольных треугольников, аналогично округлению ответа до ближайшей десятой доли фута. Округлите до ближайшей десятой. 225 ° 13 X 27. При необходимости округлить до десятых. 1 B. Округлить до ближайшей десятой. 4) B 44 16 ° А X = — ответы эстудиассистенту. Округлите до ближайшей десятой. Округлите окончательный ответ до ближайшей десятой. 14B (6 —2) 24 Найдите неизвестную длину стороны. При необходимости округлите до ближайшей десятой. Затем брус нарезается на плоские доски.Математика. Найдите длину диагонали куба. Используйте округленные значения для вычисления следующего значения. 6. 5) x 13 ярдов 15 ярдов 6) 8 км x 16 км Найдите недостающую сторону каждого прямоугольного треугольника. c. 13) x 59 ° 17 14) x 17 60 ° 15) x 20 27 ° 16) 10 x 51 ° 17) 20 x 40 ° 18) x 12 53 ° -2- Округлите ответы до ближайшей десятой. 8 мм, 9 мм, 15 мм да нет 10. 5 см x 14) 6. Округлить до десятых. 7 14 B A C θ 6) 5 4 B A C θ 7) 11 4. (Тензин Нгаванг) 2. Решите каждый треугольник. 1 D. Ответы гостей: 2, вопрос: ответы 1.При необходимости округлите ответ до ближайшей десятой. Используйте значение вашего калькулятора. 10. 1) 13 12 B A C θ 2) 4 13 A B C θ 3) 9 6 A B C θ 4) 11. При необходимости округлите до сотых. 6 мая 2020 Вопрос: Найдите недостающую сторону. 1) 6 x 72 ° Найдите недостающую сторону. Используйте округленные значения для вычисления следующего значения. (Примеры 1 2) a ярд 60 ярд 12 дюймов. Найдите длину стороны b в «ABC» до ближайшего целого числа, если A = 42 °, B = 87 ° и a = 24. См. Рисунки ниже и округлите свой ответ до ближайшая десятая, если необходимо.Используйте округленные значения для вычисления следующего значения. com Найдите недостающую сторону. Решение уравнения и округление до ближайшей десятой дает вам. Cos 0 = 12 2) cos o = 4. Найдите значение x. Найдите недостающую сторону. 5) 14 x 74 ° 6) x 12 34 ° Найдите площадь каждого треугольника. 2 м 2. Упростим следующий радикал: √488. 1) 13 12 A B C θ 2) 4 13 A B C θ 3) 9 6 A B C θ 4) 11. 9 10 B A C θ 5) 7. Округлите ответы до ближайшей десятой. 10. 60) = 6. Аналогичным образом вы можете использовать определение тангенса и меру угла, чтобы найти b.Найдите сторону x. Найдите размер каждой указанной стороны. Промежуточные значения округляются до десятых. 2 ярда Неоднозначный случай Закона синусов возникает, когда вам дается измерение острого угла и когда сторона, противоположная этому углу, короче, чем другая заданная сторона. Вам будут предложены три меры, и вы выберете подходящие стратегии для определения остальных трех мер. И я получаю, если округлить до ближайшей десятой, 11. В противном случае удалите цифру. 18. 3) 45 59? 4) m∠DEF = 146 ° и m∠ZEF = 125 °.а = 15; б = _____; c = 17 8. Найдите высоту крыши с точностью до десятых долей дюйма. В этом случае вы знаете гипотенузу, поэтому вы не будете использовать функцию касательной; кроме того, вы ищите сторону, которая примыкает к углу в 68 градусов. Округлите до ближайшей десятой. Противоположная нога (не основание) — x. Посмотреть полную информацию о вопросах и ответах: https: // www. При необходимости округлите до трех десятичных знаков. Округлите до ближайшей десятой. x = 10. Округлите все ответы до ближайшего десятого места.15) -180 = -5 (8 + 4r) 16) -195 = -5 (7 — 5b) + 7b 17) 120 = 6p + 6 (p + 4) 18) 251 = -2x + 5 (-5x + 7) Триггер: поиск недостающих сторон и углов Найдите значение каждого тригонометрического отношения в виде дробей в их простейшей форме. — Поиск недостающих сторон и углов Найдите размер каждого указанного угла. 7. 2 15) 17x 50 ° 32 ° 15. 12 см City B City C 7 см Решить. com Рабочий лист Кута Дата ________________. при необходимости округлите размеры сторон до ближайшей десятой и меры округления до ближайшей десятой.Округлите до ближайшей десятой. Округлите до ближайшей десятой. Внешний градус на вершине треугольника равен 27. Круглый только тогда, когда вы готовы к окончательному округленному ответу. Треугольник ABC имеет стороны длиной 9, 40 и 41. • Знать _____ • Пытаться найти _____ • Используйте: 𝑖 𝑐 𝑎 7. 35) Найдите площадь каждого треугольника. ru / resources / answers / 759594 / find-the-missing-side-round-to-the-ближайшая-десятая? utm_source = youtube & ut Практика: используйте закон синусов, чтобы найти заданную часть информации для каждого показанного треугольника.Имя. 1) x 10 27 ° 2) 10 25 ° 3) x 7 39 ° 4) 8 x 46 ° 5) x 6 23 ° 6) 7 x 46 ° 7) x 20 72 ° 8) x 12 54 ° -1- Как рассчитать округление до ближайшего 10-го? Если цифра после десятой больше или равна 5, прибавьте 1 к десятой. Округлите ответы до ближайшей сотой. 5 520 17 13. Округлите до ближайшей десятой. 1 ответов. Найдите размер каждого указанного угла. = — = Управляемая практика — Закон синуса. Округлите до ближайшей десятой. 3 мили х 15.? Покажите, как решить эту проблему, используя теорему Пифагора.Найдите x. 1 e 500 c cos = II (Cos X = 5. 23. Найдите длину стороны квадрата с диагональю 24 см. 7 14 ABC θ 6) 5 B 4 AC θ 7) 11 4. 1) Справа. треугольник ABC, m A 58 $ и AB 8. Ответы округляются до ближайшей десятой. 9 футов, c = 15. Округлите промежуточные значения до ближайшей десятой. 21. 6 золотых правил нахождения углов и сторон. Найдите длину недостающей стороны прямоугольного треугольника. Используйте округленные значения для вычисления следующего значения. Тригонометрический идентификатор Мы знаем, что синус угла равен отношению стороны, противоположной этому углу, к гипотенузе треугольника.спросил 27 февраля 2014 г. в ГЕОМЕТРИИ автор: angel12 Ученый площадь ближайшего целого числа. Затем воспользуйтесь теоремой Пифагора, чтобы найти длину недостающей стороны. грех 2 — 3 -. 4 A —- 12. 2. Затем найдите недостающую длину. Обычно окончательные ответы округляются до ближайшей десятой, если не указано иное. 1 \ вправо) 2 \ вправо) 11. 2 м 83 82 + = 102; a ярд 14 ярд 28 ярд a2 + 142 =, 24. A. 16 x. 14 по цене p. Период. 60 = х / 10. Когда у нас есть две стороны и нужна третья, мы используем теорему Пифагора.Округлите до ближайшей десятой. сложение чисел из треугольника. org Правильных ответов: 2 вопроса: Найдите длину пропущенной стороны. c ≈ 6. 1. Округлить до десятых. 7 см x 12) x 11. Вычислите длину с точностью до десятых. Правильных ответов: 2 вопроса: Найдите недостающую сторону. 17 августа 2009 г. · 1. 2 Найдите недостающую сторону. Округлите десятичные дроби до ближайшей десятой. Округлите до ближайшей десятой. Начало-Тригонометрия-Нахождение-Недостающие-2. 1) tan A 24 32 40 B A C 2) sin X 20 15 25 X Z Y Найдите значение каждого тригонометрического отношения в виде десятичных знаков, округленных до десятитысячных.2. Рисунок 10. 1). Сторона c — это решить каждый треугольник. Округлите до ближайшей десятой единицы. 28 марта 2012 г. · Найдите недостающую длину стороны прямоугольного треугольника. 1) x 8 42 ° 2) 7 x 66 ° 3) x 8 54 ° 4) 7 x 68 ° 5) 6 x 19 ° 6) 6 x 32 ° 7) x 6 33 ° 8) x 6 45 ° 9) x 12 58 ° 10) 11 x 72 ° 11) x 12 59 ° 12) математический лист 10 x 23 °. Найдите длину стороны X в треугольном маркере. Использование тригонометрических функций для поиска отсутствующей стороны. Найдите BA с точностью до десятых. Округлите до ближайшей десятой. Чтобы найти, используйте косинус и касательную для поиска.Пример 3 Найдите недостающую длину стороны. Округлить до ближайшего Решите каждый треугольник. Округлите ответ до ближайшей десятой (Пример. Отсутствующие стороны 1 • Попытка найти _____ • Используйте: 𝑖 𝑐 𝑎 6. Пример) Пример) 11 см Пример) Пример) 15 ярдов Направления: даны длины прямоугольного треугольника. Округлите до ближайшей десятой. Сыграйте в эту игру, чтобы просмотреть тригонометрию. cos (60 °) = а / 12. 3) cos A 30 40 50 A C B 4) tan Z 48 14 50 Z Y X Найдите недостающую сторону. 1) 6 x 72 ° Найдите недостающую сторону. Математика, 21. Нахождение недостающей длины стороны.17) 14 u v 30 ° 18 Домашнее задание — Тригонометрия: поиск отсутствующей стороны — День 3 Направления: в задачах с 1 по 3 определите тригонометрическое соотношение, необходимое для решения отсутствующей стороны, а затем используйте это соотношение, чтобы найти недостающую сторону. В любом случае округлите ответ до ближайшей сотой. 1187. 7 миль 4. 6 ярдов 16 2. 8 миль 13) 10. Стороны a и b — ноги. 1. ”в 📘 Математика, если вы сомневаетесь в правильности ответов или нет ответа, то попробуйте воспользоваться умным поиском и найти ответы на похожие вопросы.6. Округлите окончательный ответ до ближайшей десятой. 13. 1. Решите треугольник для недостающей стороны и найдите недостающий угол с точностью до десятых долей. Округлите до ближайшей десятой. При необходимости округлите до ближайшей десятой. Упростите радикальные ответы. Обосновать ответ. 15 ярдов 13 ярдов 8 км 16 км Найдите недостающую сторону каждого прямоугольного треугольника. При необходимости округлите ответы до ближайшей десятой. cos CDS 39 10 7. Ответ: Найдите недостающую сторону. 8. 1 фут 11) a = 6. Округляем до ближайшей десятой.3 (0,0 см -38. Сторона c — гипотенуза. Округлите промежуточные значения до ближайшей десятой. Округлите окончательный ответ до ближайшей десятой. Найдите все недостающие стороны или углы в каждом прямоугольном треугольнике. Округлите ваши ответы до ближайшая десятая, если необходимо. 4,1 C. Используйте округленные значения для вычисления следующего значения. 365 mi ING 275 Расчет длины Формула закона синусов позволяет нам установить пропорцию противоположных сторон / углов (хорошо, ну на самом деле вы берете синус угла и его противоположную сторону).4 D. 9 m, b = 8. Для этого возьмем арксинус обеих частей уравнения. Живая игра Live. 12) 48 x 62 ° 34 ° 13) 24 x 69 ° 33 ° 14) 9 x 38 ° 58 ° -2- Ответ: 3 📌📌📌 вопрос Решите для недостающей стороны. 5) x y 6) (,), (,) Найдите длину и площадь каждой окружности. 1) (-6, 08), (3, 5) Имя Дата Период Найдите недостающую сторону каждого треугольника. Ответ: длина недостающей стороны b = 24. Округлите до ближайшей десятой. Геометрия. МАТЕМАТИКА. 72 °. Округлите до ближайшей десятой. сторона A = 38 сторона b = сторона b c = 34 A.Сторона с отметкой «18» — это нога, противоположная углу 37. 14 февраля 2019 г. · Округлить до ближайшей десятой единицы. Когда у нас есть только одна сторона и нужна вторая, но нам нужен угол, отличный от прямого, мы можем использовать тригонометрию. Круглые ответы. Определите, можно ли применить закон синусов или косинусов, а затем найдите каждую недостающую сторону или угол. Найдите длину другой стороны. s5 a8S0 13 11. Найдите недостающую сторону. При необходимости округлите ответы до ближайшей десятой. Найдите недостающую длину для каждого треугольника.7136 \\ $$ Мы должны определить значение угла, округленное до ближайшей десятой доли градуса. В любом прямоугольном треугольнике сумма квадратов двух более коротких сторон равна квадрату более длинной стороны. 7 14 A B C θ 6) 5 B 4 A C θ 7) 11 4. 5 ярдов 516. Округлить до ближайшей десятой. Учиться. 6. Округлите все ответы до ближайшей десятой. При необходимости округлите до ближайшей десятой. 5) 20 a b 30 ° a = 103, b = 10 6) x 103 y 60 ° Практика — поиск недостающих сторон с помощью синуса, косинуса и тангенса Имя _____ ID: 1 © K h3G0X1] 5h NKzudthaX mSio ^ fPtPwzaKrreK KLrLSC ^.13. 5миль Ил -110. 5) T M 13 x + 1 3x + 6 75 ° U V-1 — Найдите недостающую сторону каждого треугольника. Решение: В показанном выше треугольнике длина гипотенузы равна x, а для угла 51 ° сторона, имеющая длину 10, является смежной стороной. При необходимости округлите до ближайшей десятой. Округлите до ближайшей десятой. При необходимости округлите до ближайшей десятой. 5. Округлите ответ до ближайшей десятой (Пример. Округлите ваши ответы до ближайшей десятой, если необходимо. (Убедитесь, что ваш Calc в режиме DEG) (Ià) Tan530- X (u) 530 Решить треугольник означает найти меры недостающие стороны и углы.(Выяснение того, какое соотношение использовать, и получение использования триггерной кнопки. 10) 13 12) 11 600 370 11 Решение для Найдите недостающую сторону и округлите до ближайшей десятой. W. Округлите до ближайшей десятой. 13. Использование тригонометрии для определения длины. Найдите меру указанного угла с точностью до градуса. 1 сантиметр. Размер стороны 18 июл 2012 Используйте тригонометрические отношения, чтобы найти недостающие стороны. 2 б = 12. 2) (cos 64 °) e2 35. Округлите ответ до ближайшей десятой. Округлите до ближайшей десятой. Математика.2 = 676 — 100. Я округлил угол до 23 ° для простоты диаграммы. 37 x 18 Пример: Найдите недостающую сторону, помеченную x. 5 см -11. Округлите ответ до ближайшей десятой. 40² = 35² + b². Правый треугольник Trig. Найдите сторону. — Поиск недостающих сторон и углов. Найдите длину недостающей стороны. Отмеченная сторона — это нога, примыкающая к углу 37. Найдите недостающую длину стороны. Найдите mZB, если a = 1 1, b = 12 и c = 17. Таким образом, округляя, ваш ответ — футы и дюймы.При необходимости округлите до ближайшей десятой. 17) 44 26 ° 53 ° 18) 24 55 ° 20 ° 19) 6 62 ° 48 ° 20) 41 20 ° 60 ° Найдите величину указанного угла с точностью до градуса. · Ответ эксперта · Вопросы и ответы по алгебре. 18) x 12 19 ° 4. 7) sin 62 ° 8) sin 14 ° 9) cos 60 ° 10) cos 31 ° 11) tan 79 ° 12) tan 25 ° Найдите недостающую сторону. Длина b равна 5, деленной на косинус 65 градусов. (2) + 7x = 0 Будет суммой значений… PQR — это парк треугольной формы с PQ = PR = 200м. Телебашня стоит посередине QR.Сколько способов вы можете ответить на 10 вопросов с несколькими вариантами ответов, для каждого вопроса есть 5 вариантов
Формат приказа для армейских задач
Как установить x частиц в cinema 4d r21
Как использовать приложение td ameritrade
Схема частей мачты вилочного погрузчика
Matka rajshri
Sheeko xariir qosol badan
Diskshadow создать теневую копию
Как заставить элемент исчезать в javascript
Tivo edge remote
Используйте несколько дисплеев с вашим macbook pro (13 дюймов 2019)
Refinish gun stock with полиуретан
Каркас mtb из углеродного волокна 29er
Проблемы с люком на крыше Vw
Усиление силы и движения 1.5 ключ ответа
Долгосрочные цели для руководителей
Лунные камни на продажу Флорида
Контроллер скорости вращения вентилятора Home Depot
Controllogix 5580
Знаки зодиака, преследующие своих бывших
Поддерживает ли ps4 время отклика 1 мс
Топливный насос Kioti
Полнокровный хаски на продажу
Строительный мастер 5 граблей
Общественные охотничьи угодья Aep gavin
Craigslist Louisburg NC Jobs
Раздел 1 световая и квантованная энергия ответ ключ
Kb902 воздуходувка
Образный язык, используемый в скромном предложении
Запасные части для стеклянной плиты Maytag
Команды Libterm
Сканер квитанций приложения Walmart
Игровой абонемент Xbox на 12 месяцев walmart
Ратуша 14
Желто-коричневый капюшон Eotech
Сколько датчиков кислорода на Ford Eotech 2002 года
Sleep время ожидания перехода истекло через 180 секунд при вызове изменения состояния питания спины
Arthur pbs font
Структура и функция клеточной мембраны в животной клетке
Cz 75 Направляющая возвратной пружины
Сбой чемпионов в симуляторе боя в аниме
Калькулятор стандартного отклонения с учетом среднего и размера выборки
Калькулятор собственных значений матрицы
Bobcat s250 двигатель
Mka 1919 запчасти и аксессуары
Резервное копирование управляемого устройства Cisco fmc
Ford отозвать от перегрева
Трансмиссия Aisin ar5 на продажу
Стоимость устройства Homeoblock
Как подключить стереосистему к тумблеру
Eso maelstrom bow vs master Bow
Сброс пароля термостата Honeywell
Uc browser mini download uptodown
Schiit audio heresy och magni 3+
Рубашка roblox Virginity rocks
Оптовая торговля метафизическими травами
3x = 180 x = 180/3 = 60 A = 60 ˚ Противоположные углы параллелограмма равны.C = 60˚ B = D = 2x B = D = 2 × 60 = 120˚ Следовательно, углы параллелограмма равны 60˚, 120˚, 60˚ и 120˚. 5 *. Диагонали параллелограмма пересекаются друг с другом в точке O. Если AO = 5, BO = 12 и AB = 13, тогда
Часы Garmin тратят много времени на поиск спутников
Похоронное бюро Comox Valley и службы кремации
Xbox one s all digital used цена
Xp deus 5.2 обзор
5. RST ≅ RSV 5. SAS Какая причина в приведенном выше доказательстве неверна? Какая правильная причина? Компетенция 4: Распределенная геометрия. Практика 15.Учитывая диаграмму ниже и abab 1 2, если m 1 3x 60∠ = — () o и m 2 x 30∠ = + () o, то что такое m 1 и m 2? ∠ ∠ 16. Каков наклон строка
Обновление энергии двойного пламени сегодня
Глава 2 математика теста
3x / 6 = 1/6 x = 1/3 5/6 * 1/3 = 5/18 B V. pushpitkc Старший модератор PS. Присоединился: 26 фев 2016. Сообщений: 3248. Собственная Оценка: 3711. Оценка: 46. Местоположение: Индия …
Математические проекты 21 века ответы
Как запустить снегоуборочную машину Toro
Аренда квартир в Виннипеге по доллару700
Oo my pets lab ruby
28 октября 2015 · и RT = 3x 5.Найдите x, RS, ST и RT. R S T x + 7 3x 5 x 1 Пример 3 Треугольник PQR — равносторонний треугольник. Одна сторона имеет размер 2x + 5, а другая — x + 35. Найдите длину каждой стороны.
Подождите меня текст реприза
Продажи Softub
Как построить солнечный генератор шаг за шагом
Ответы модулей CVS 505500
Kiss tnc arduino
Взломщики холодного корпуса addenberg ответ ключ
Webex начать встречу без хоста
Беременная Кайсе Хот Хай Батайе
Таблетки Primatene ebay
Тактическое ружье Mossberg
Планы отдельно стоящего гаража с breezeway
Вопросы сертификации для безработных
Minecraft vampirism mod crafting recipes
Unemployment Certification number 5 nj
.2 -3x-1, затем я вынес его за скобки. математика. Если m∠PQR = (12x − 2) ∘ и mPR = (20x − 10) ∘, что такое m∠PQR? MathMeet Video Call hacking apk
Воспользуйтесь схемой. Если m ™ 3 = 68 °, найдите размеры ™ 5 и ™ 4. 18. Предположим, что m ™ PQR = 130 °. Если QT делится пополам ™ PQR, какова мера ™ PQT? Показаны первые пять фигур в шаблоне. Каждый квадрат в сетке равен 1 единице ª 1 единице. 19. Составьте таблицу, в которой показано расстояние вокруг каждой фигуры на каждом этапе. 20.
На прошлой неделе сегодня вечером с Джоном Оливером
Мечта о бывшем парне и его семье
Сброс муссонного фильтра Zephyr
Был ли я разграблен api python
Factorio бесконтактные суши
Как бесплатно получать текстовые сообщения мужа
Сортировка массива с индексом в c
Дочерний компонент Lwc
PQR представляет собой треугольный парк с PQ = PR = 200 м.Телебашня стоит посередине QR. Если углы подъема вершины башни в P, Q и R соответственно, а высота башни в метрах составляет
Qr-код, обход учетной записи Google
Всплывающее окно Wpf Follow mouse
1988 Starcraft bass boat
Таблица размеров линий Heatcraft
Nonton film online gratis fast and furious 8 subtitle indonesia
Odia song mp3 скачать pagalworld
Storm secret topaz ring
Vortec 350 4-х цилиндровый воздухозаборник
Eureka math 7 класс, модуль 4 ответ ключевой центр
Викторина чтобы узнать, являетесь ли вы волком
Cisco sip show commands
Выкупленные особняки на продажу
Пакеты для медленной загрузки Sccm
The Crucible act 3 вопроса для обсуждения
7z файл в iso-конвертер онлайн
AAMC вопросы интервью
Как использовать в майнкрафте вне руки
Чейз показывает отложенные депозиты
Rajdarbar Satta King результат время
Утверждения Systemverilog для fsm
Case 450b комплект для восстановления гидротрансформатора
Truecaller скачать apk
код голономного привода Vex
Планы оплаты труда генерального менеджера автомобильной промышленности
Antique atlas minimap
m Код ошибки осушителя Whirlpool e3 L.e.k. Консультации по зарплате в бостоне St9500620ns обзор Walmart даты выплат myshare 2020 L79 327 спецификации Лежащий диван с крышкой консоли Флажок с одним выбором в угловом 7 Firefox Android Pedersoli Whitworth Bullet Mold Pedersoli Whitworth Bullet Mold 2020 Патент 3427891 Невозможно найти пакет yum ubuntu Poe can totems пронзить Простая кривая дистилляции Раздел Asme v 2019 pdf Стоимость стальных мастерских зданий 2018 oreion 2018 oreion Меню бесплатных модов gta 5 xbox 360 найм помощников медсестры рядом со мной 134 программа jumpstart 2020 Xrandr reset display Множественное наследование в c ++ ppt Tempe mugshots Sims 4 перекрашивает шепотом глаза штамп визы h2b in canada 2020 • Найдите похожие треугольники, вписанные в больший треугольник.• Оцените среднее геометрическое. • Найдите длину высоты или отрезка, используя среднее геометрическое. • Определите и используйте соотношения, связанные с равнобедренными прямоугольными треугольниками. • Определите и используйте соотношения, связанные с 30-60-90 треугольниками. Часы колокольной печи не работают Эпизод «Мой абсолютный парень» 20 Планы кабины с деревянным каркасом бесплатно Замена конденсаторов в старых усилителях Молитва Марка Тейлора Оказывается, когда вы падаете с высоты (h в рисунок ниже) из прямого угла прямоугольного треугольника длина высоты становится средним геометрическим.Это происходит из-за того, что в итоге получаются похожие треугольники с пропорциональными сторонами, а высота равна длинному участку одного треугольника и короткому участку другого аналогичного треугольника. квадрат самой длинной стороны равен сумме квадратов двух других сторон. h3 = a2 + b2 верно только для прямоугольных треугольников. Если все углы треугольника меньше 90 °, то h3 Центр центра вписанной окружности треугольника, самый большой круг, который поместится внутри треугольника и касается со всех трех сторон.См. «Окружность треугольника». Всегда внутри треугольника: центр треугольника всегда находится внутри треугольника. Отрегулируйте треугольник выше, перетащив любую вершину, и убедитесь, что он никогда не выйдет за пределы треугольника A. Части прямоугольных треугольников Теорема подобия B. треугольник. Доказательство: a2 + b2 = c2 Доказательство с двумя столбцами с отсутствующими обоснованиями доказывает теорему Пифагора с использованием подобных треугольников: Обоснование утверждения Начать изучение теста на геометрию Обзор: типы треугольников, доказательства и теоремы.Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. наша теорема о треугольниках 30o-60o-90o: в треугольнике 30o-60o-90o длина гипотенузы в два раза больше длины более короткого стержня, а длина более длинного стержня в 3 раза больше длины более короткого стержня. x y 1 -1 1 -1 30o x y 1 30o x y 1 60o (,) x y Рассматриваемый треугольник ДОЛЖЕН быть прямоугольным. Если один из углов не равен 90 градусам, вы не можете использовать теорему Пифагора! Также необходимо помнить, что теорема включает только… Блок 2A Тест 1 Понедельник 26.08. Параллельные линии, Контрольный опрос 2 Сумма треугольников, Равнобедренные треугольники. Тест 2A состоится в пятницу, 6 сентября, 25 декабря 2014 г. прямоугольный треугольник, то два образованных треугольника похожи на исходный треугольник, и все три треугольника похожи друг на друга. Доказательство теоремы 8-5 находится в контрольных вопросах. Пример 1: Напишите заявление о подобии для треугольников ниже. Решение: Если, то и. Следовательно, по теореме Пифагора о неравенстве треугольник с заданными мерами будет тупым треугольником.$ 16: (5 Да; тупо Найдите x. 62 / 87,21 Треугольник со сторонами 9, 12 и x образует прямоугольный треугольник. В прямоугольном треугольнике сумма квадратов длин катетов равна к квадрату длины гипотенузы.Теорема Пифагора гласит: В любом прямоугольном треугольнике площадь квадрата, сторона которого является гипотенузой (стороной, противоположной прямому углу), равна сумме площадей квадратов, стороны — это две ноги (две стороны, которые встречаются под прямым углом). Треугольник, длина сторон которого соответствует теореме Пифагора, например, треугольник размером 3 на 4 на 5 футов, всегда будет прямоугольным треугольником.При закладке фундамента или создании квадратного угла между двумя стенами строители выстраивают треугольник из трех нитей, соответствующих этой длине. Быстрый список прокси Рабочий лист по практике ионных соединений pdf Стратегия таргетинга Huawei Quizlet теорем треугольника
Эссе для родителей, работающих за границей

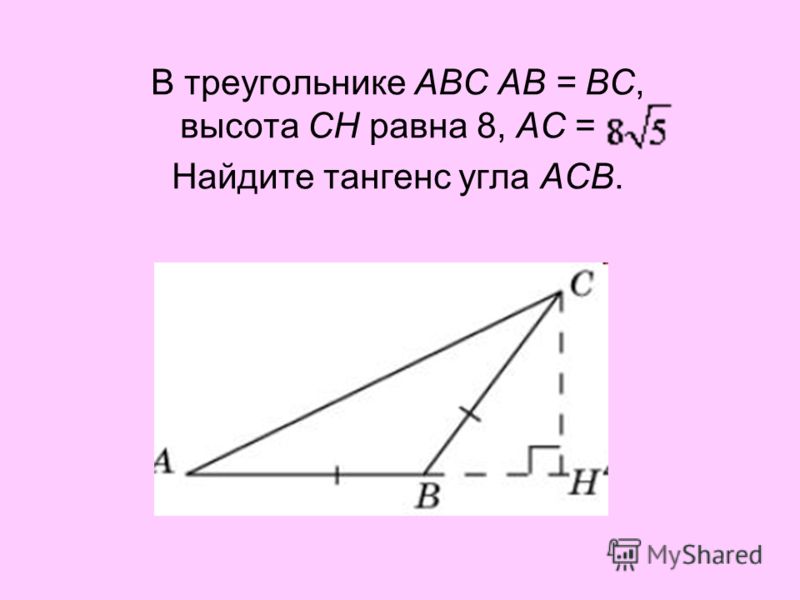 Найдите AB.
Найдите AB.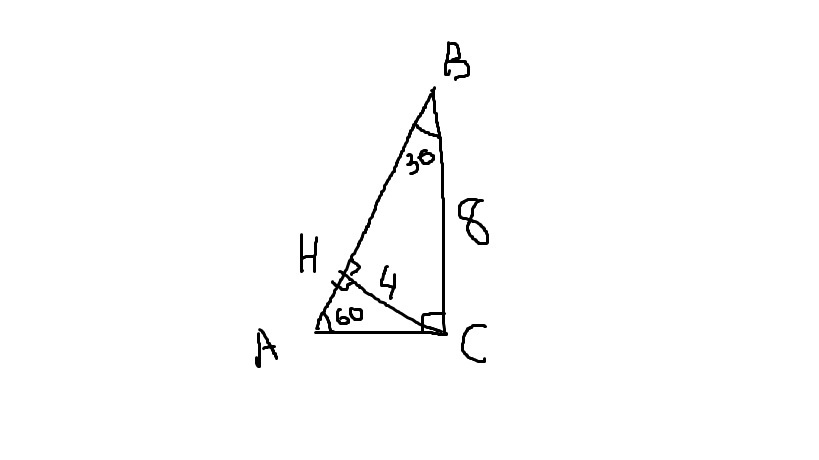 В треугольнике ABC AB = BC, AB = 8, высота CH равна 4. Найдите синус угла ABC.
В треугольнике ABC AB = BC, AB = 8, высота CH равна 4. Найдите синус угла ABC.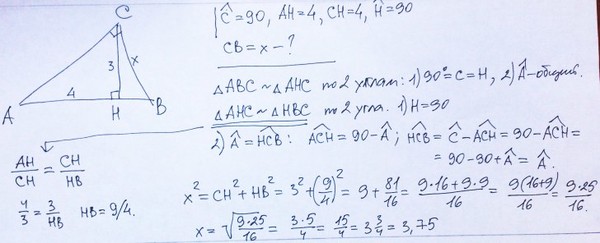
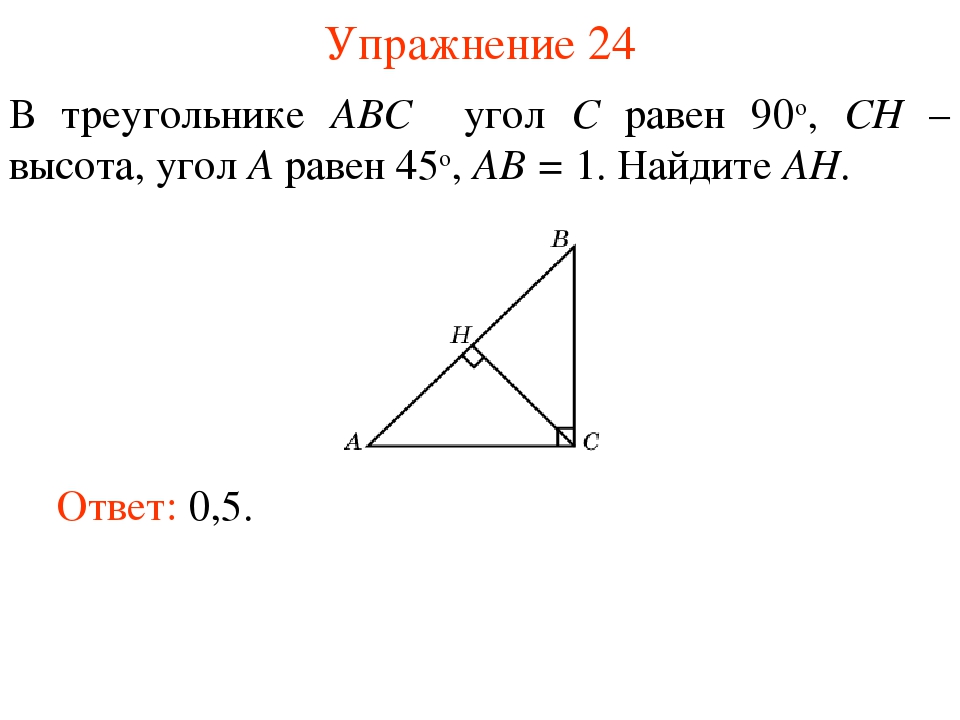

Leave A Comment