В треугольнике авс угол с равен 90 ас равен 3 вс равен 4: В треугольнике АВС угол С=90,АС=3,ВС=4.Найти радиус описанной окружности этого треугольника

3. В треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок СВ… 7 класс А.П. Ершова Геометрия. КП-4 Вариант В-1

3. В треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок СВ… 7 класс А.П. Ершова Геометрия. КП-4 Вариант В-1 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

3.

 
В треугольнике АВС угол С
равен 90°, а угол В равен 70°.
На катете АС отложен отрезок СВ, равный СВ. Найдите
углы треугольника АВD.

ответы

ответ

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

1. Доказать: ∆АВС — равнобедренный. Геометрия 7 класс А.П. Ершова. СП-6 Вариант В-1

(Подробнее…)

ГДЗЕршова А.П.7 классГеометрия

Геометрия. 10 Класс

1. Через середину М сторони АВ трикутника АВС проведено площину, яка паралельна, прямій АС і перетинає сторону ВС у точці N. Довести NM (Подробнее…)

ГеометрияУчителяДосугОГЭЭкзаменыЕГЭГИАВыпускнойГДЗУчебники

Какие два числа надо поменять местами, чтобы квадрат стал магическим? ГДЗ по математике 3 класс Моро Часть 1 стр 30 задание 15

Всем привет) А как вы думаете?)
Какие два числа надо поменять местами, чтобы квадрат стал магическим?
 6  9  2 (Подробнее. ..)

ГДЗ3 классМатематикаМоро М.И.

№ 569. ГДЗ Математика 5 класс Никольский. Помогите доказать!

Докажите, что длина ломаной ABС больше длины ломаной АDС (рис. 118).
  (Подробнее…)

ГДЗМатематика5 классНикольский С.М.

2. Один из внутренних углов треугольника в 3 раза больше другого, а внешний угол, смежный… А.П. Ершова Геометрия 7 класс. СП-9 Вариант Б-2

2.
Один из внутренних углов
треугольника в 3 раза больше другого, а внешний угол, (Подробнее…)

ГДЗГеометрияЕршова А.П.7 класс

Теорема Пифагора — формула, доказательство, задачи

Поможем понять и полюбить математику

Начать учиться

485.6K

Сложно представить, но в научной литературе существует 367 доказательств теоремы Пифагора. В школьной программе мы проходим гораздо меньше — в этом материале познакомимся с главными формулами и их доказательствами.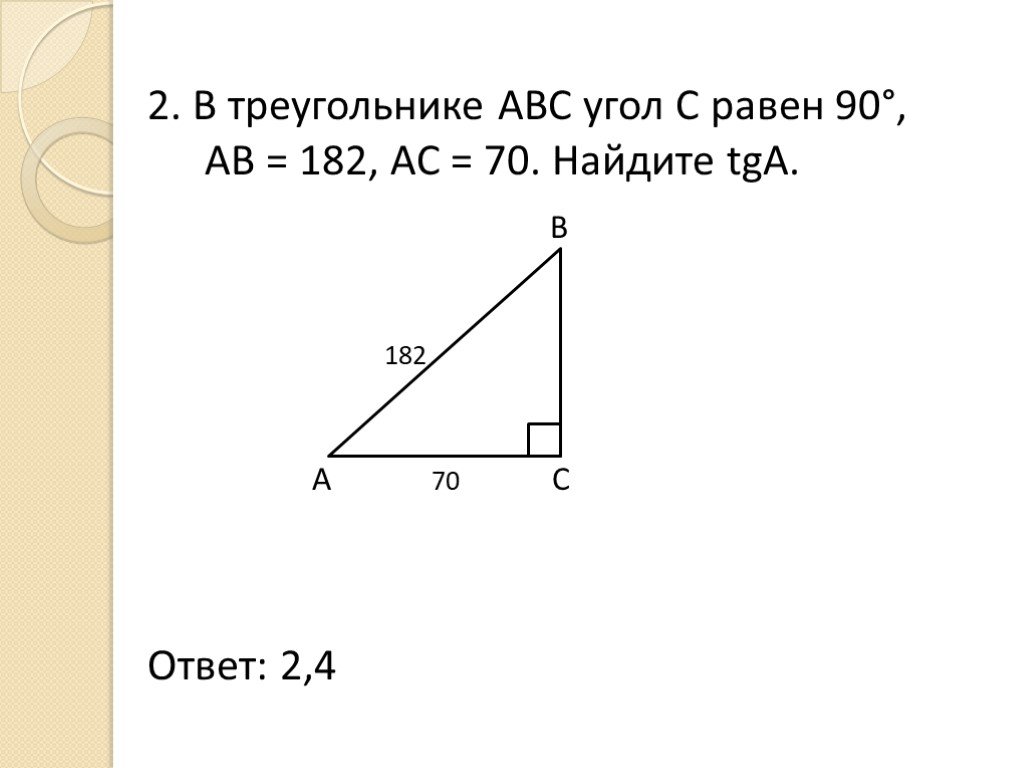

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

a² + b² = c²,

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c² − b²
• b = √c² − a²
• c = √a² + b²

Запоминаем

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c² < a² + b², значит угол, противолежащий стороне c, является острым.
• если c² = a² + b², значит угол, противолежащий стороне c, является прямым.
• если c² > a² +b², значит угол, противолежащий стороне c, является тупым.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a² + b² = c².

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

∠ACB =∠CHA = 90º,

∠A — общий.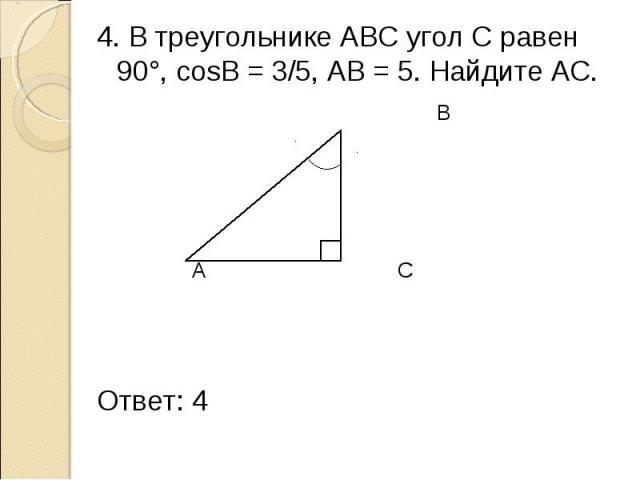

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

∠ACB =∠CHB = 90º,

∠B — общий.

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a² = c * HB, b² = c * AH.
• Сложим полученные равенства:

a² + b² = c * HB + c * AH

a² + b² = c * (HB + AH)

a² + b² = c * AB

a² + b² = c * c

a² + b² = c²

Теорема доказана.

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано:

∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁² = A₁C₁² + B₁C₁².
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

• Пусть катеты a = 6 и b = 8.

• По теореме Пифагора c² = a² + b².

• Подставим значения a и b в формулу:
  c² = 6² + 8² = 36 + 64 = 100
  c = √100 = 10.

Ответ: 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

Как решаем:

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

11² = 8² + 9²

121 ≠ 145

Ответ: треугольник не является прямоугольным.

---

---

 

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

200.1K

Как найти радиус окружности

К следующей статье

233.1K

Как найти периметр треугольника

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Q10 Построить треугольник ABC, если BC 3 см, AC 4 см и AB 5 см.

Измерить угол ACB. Дайте специальное имя…

Перейти к

• Упражнение 26 (А)
• Упражнение 26(Б)
• Повторное упражнение

• Система счисления (закрепление чувства числа)
• Оценка
• Числа в Индии и международной системе (со сравнением)
• Место Значение
• Натуральные числа и целые числа (включая шаблоны)
• Отрицательные числа и целые числа
• Номер строки
• HCF и LCM
• Игра с числами
• Наборы
• Соотношение
• Доля (включая словесные задачи)
• Унитарный метод
• Фракции
• Десятичные дроби
• Процент (Процент)
• Представление о скорости, расстоянии и времени
• Основные понятия (алгебра)
• Основные операции (связанные с алгебраическими выражениями)
• Замена (включая использование скобок в качестве группирующих символов)
• Обрамление алгебраических выражений (включая вычисление)
• Простые (линейные) уравнения (включая текстовые задачи)
• Основные понятия (геометрия)
• Углы (с их типами)
• Свойства углов и линий (включая параллельные линии)
• Треугольники (включая типы, свойства и конструкцию)
• четырехугольник
• Полигоны
• Круг
• Повторное упражнение по симметрии (включая построения по симметрии)
• Распознавание твердых тел
• Периметр и площадь плоских фигур
• Обработка данных (включая пиктограмму и гистограмму)
• Среднее и медиана

Главная > Селина Солюшнс Класс 6 Математика > Глава 26 — Треугольники (включая типы, свойства и конструкцию) > Упражнение 26(Б) > Вопрос 10

Вопрос 10 Упражнение 26(B)

Q10) Постройте треугольник ABC, если:

BC = 3 см, AC = 4 см и AB = 5 см.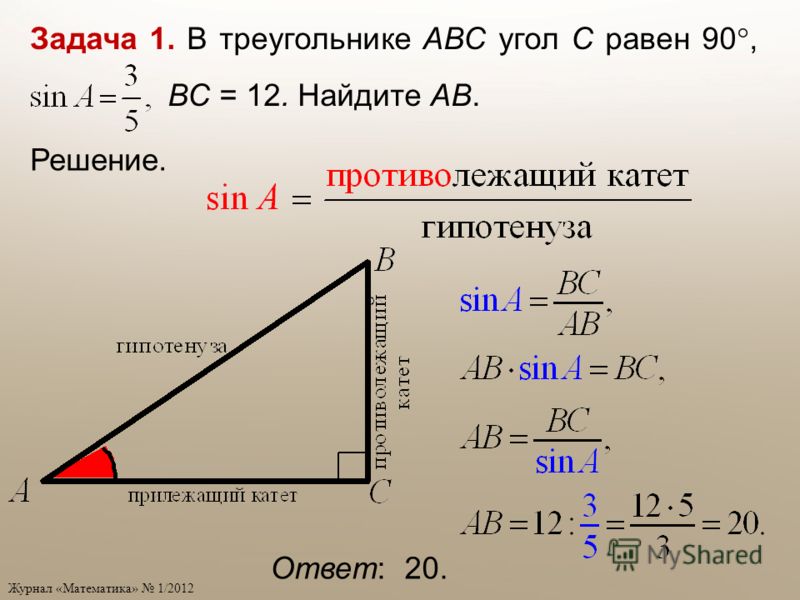 Измерьте угол ACB. Дайте специальное имя этому треугольнику.

Ответ:

Решение:

1. Проведите отрезок AB = 5 см
2. Из А с помощью циркуля отрежьте дугу АС = 4 см
3. Из точки В отрезаем дугу ВС = 3 см
4. Присоединиться к AC и BC
5. ABC требуется прямоугольный треугольник.

Измерение\угол ACB=90\степень

Стенограмма видео

«привет добро пожаловать в Лидо домашняя работа сегодня мы увидим построенный треугольник азбука когда bc равно трем сантиметрам, ac равно четырем сантиметры, а b равно пяти сантиметрам измерь углы abc ладно что делать Делай сейчас Итак, сначала мы собираемся нарисовать b be что-либо сначала возьми это за основу, я собираюсь основание в пять сантиметров хорошо, позвольте мне попробовать и разместить некоторые файлы здесь это делается успешно, то вода следующий следующий, он просит, мне нужно взять один транспортир пройди вот так, ладно, извини возьми это, и я должен нарисовать одну вещь что сделает что-то вроде это четыре сантиметра Хорошо, нарисуйте одну линию, которая включает в себя перекресток Хорошо, используя имплантат, просто используйте два четыре сантиметры [Музыка] нарисовать что-то вроде этого да что делать дальше мне нужно нарисовать то, что будет на другой линии 3 сантиметра я оставлю это здесь мне нужно настроить это на 3 сантиметра [Музыка] ой, извини [Музыка] это будет так хорошо, теперь мы можем сделать вывод, что это будет точка над там и он должен соединить эти две части все в порядке, позвольте мне нарисовать эту штуку [Музыка] снова [Музыка] теперь то, что мы собираемся сделать, это нарисуй вот такую ​​линию также я должен забыть это снова да извини да продукт из еще хорошо, теперь все в порядке с вещь помните это для этого, а также теперь, если вы измерите эти углы, это будет 5 это будет 4 это будет быть 3 хорошо также измерить эти углы также приведены углы это примерно 40 хорошо угол 40. когда вы ищете другую вещь здесь это будет о да угол равен 34 минутам, если мы получим s44 ладно ладно примите это как извинение да одна вторая угол acv 90 градусов в порядке измерения угла acb играть с б это 90 градусов ладно, вот что, если вы видите здесь будет 90 градусов так что это будет прямоугольный треугольник под прямым углом треугольник, я надеюсь, вы поняли это видео подписаться на этот канал эффектор обновления спасибо за просмотр этого видео»

Связанные вопросы

Q1) Постройте треугольник ABC, если: AB = 6 см, BC = 8 см и AC = 4 см.

Q2) Постройте треугольник ABC, если: AB = 3,5 см, AC = 4,8 см и BC = 5,2 см.

Q3) Постройте треугольник ABC, если: AB = BC = 5 см и AC = 3 см. Измерьте углы A и C. Является ли ∠A = ∠C…

Q4) Постройте треугольник ABC, если: AB = BC = CA = 4,5 см.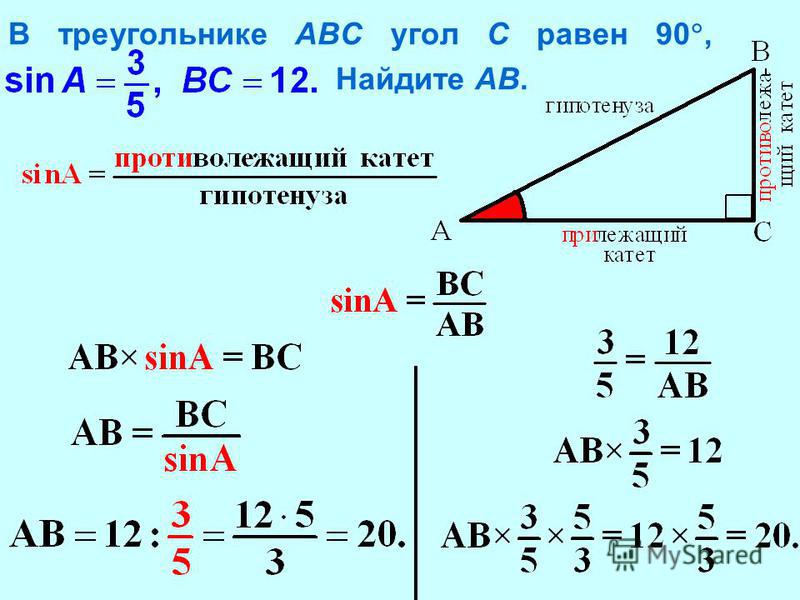 Измерьте все углы треугольника. Ар…

Q5) Постройте треугольник ABC, если: AB = 3 см, BC = 7 см и ∠B = 90°.

Q6) Постройте треугольник ABC, если: AC = 4,5 см, BC = 6 см и ∠C = 60°.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 26(А)

Упражнение 26(B)

Повторное упражнение

Главы

Система счисления (закрепление смысла числа)

Оценка

Числа в Индии и международной системе (с сравнением) Числа (включая шаблоны)

Отрицательные числа и целые числа

Числовая строка

HCF и LCM

Игра с числами

Наборы

Соотношение

Пропорция (включая проблемы слов)

Unitary Method

Фракции

Десятичные дробные фракции

процент (процент)

Идея скорости, расстояния и времени

Фундаментальные концепции (алгебра)

Фундаментальные операции (связанные с аллспрессовыми выражениями. )

Подстановка (включая использование скобок в качестве группирующих символов)

Обрамление алгебраических выражений (включая вычисление)

Простые (линейные) уравнения (включая текстовые задачи)

Фундаментальные концепции (геометрия)

углы (с их типами)

Свойства углов и линий (включая параллельные линии)

Треугольники (включая типы, свойства и конструкция)

Четырехтовые

Полигоны

9000 2

Повторное упражнение по симметрии (включая построения по симметрии)

Распознавание твердых тел

Периметр и площадь плоских фигур

Обработка данных (включая пиктограммы и гистограммы)

Среднее и медиана

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

[Решено] В вопросе прямоугольный треугольник ABC, BD перпендикулярен гипотенузе A

9 задано в

CDS 01/2022: предыдущая статья по математике (состоялась 10 апреля 2022 г. )

Просмотреть все статьи CDS >

1. 12 см
2. 12,2 см
3. 12,4 см
4. 12,6 см

Вариант 4: 12,6 см

Бесплатно

Электрические заряды и закон Кулона (базовый)

84,9 тыс. пользователей

10 вопросов

10 баллов

10 минут

Понятие:

Критерии подобия треугольников:

Угол-Угол-Угол: Если в двух треугольниках соответствующие углы равны, то их соответствующие стороны находятся в одинаковом отношении (или пропорции) и следовательно, эти два треугольника подобны.

Теорема Pythagoras: В прямоугольной треугольнике

гипотенуза ^{. ∠A = общий}

∠ABC = ∠BDA  = 90°

Следовательно, Δ ABC подобен Δ ABD. Следовательно, оба треугольника имеют одинаковое отношение соответствующих сторон

⇒ \(\frac{AD}{AB}=\frac{AB}{AC}\)

⇒ AB ²  = AD × AC

⇒ AB2 = 4 × 9 = 36

⇒ AB = 6 unit

In and Δ ABC, using Pythagoras theorem

⇒ AC ²  = AB ²  + BC ²

⇒ 81 = 36 + BC ²

⇒ BC = √45 = 3√5

⇒ AB + BC = 6 + 3√5

⇒ AB + BC = 6 + 3 × 2,23

∴ AB + BC ≈ 12,6

Дополнительная информация

SSS (бок-бок-бок): Если в двух треугольниках стороны одного треугольника пропорциональны сторонам другого треугольника, то их соответствующие углы равны и, следовательно, эти два треугольника подобны.

SAS (сторона-угол-сторона):  Если один угол треугольника равен одному углу другого треугольника, а стороны, включающие эти углы, пропорциональны, то два треугольника подобны.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления CDS

Последнее обновление: 17 января 2023 г.

UPSC CDS (I) 2022 Отмечены! Окончательные результаты UPSC CDS (I) 2022 OTA были опубликованы 12 января 2022 г. Ранее даты подачи заявок на UPSC CDS 2023 были продлены до 12 января 2023 г. до 18:00!   UPSC CDS Новое уведомление отправлено 21 декабря 2022 года. Всего была открыта 341 вакансия, и кандидаты смогут подавать заявки онлайн с 21 декабря 2022 года по 10 января 2023 года. Кандидаты должны будут пройти процесс отбора, который будет пройти письменный тест, а затем пройти собеседование. Согласно официальному уведомлению, письменный экзамен планируется провести 16 апреля 2023 года.