В треугольнике ABC проведена биссектриса
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-11-06
Теория для решения данных задач задач в предыдущей статье.
27445. В треугольнике АВС угол С равен 118о, АС = ВС. Найдите угол А. Ответ дайте в градусах.
Рассмотрим равнобедренный треугольник AВC.
По свойству равнобедренного треугольника:
По теореме о сумме углов треугольника:
Ответ: 31
27747. В треугольнике ABC АС = ВС. Внешний угол при вершине B равен 122о. Найдите угол C. Ответ дайте в градусах.
Рассмотрим равнобедренный треугольник AВC. Углы АВС и DBC смежные, то есть их сумма равна 180 градусам. Найдём угол АВС:
По свойству равнобедренного треугольника:
По теореме о сумме углов треугольника она равна 180о.
Получаем уравнение:
Ответ: 64
27751. Сумма двух углов треугольника и внешнего угла к третьему равна 40о. Найдите этот третий угол. Ответ дайте в градусах.
Сумма двух углов треугольника и внешнего угла к третьему равна 40о. Найдите этот третий угол. Ответ дайте в градусах.
Рассмотрим равнобедренный треугольник AВC.
По теореме о сумме углов треугольника:
Сумма смежных углов равна 180 градусам. Углы АВС и CBD смежные, значит:
Следовательно:
*Если вы помните свойство внешнего угла в треугольнике, то можете сразу его записать, в противном случае его всегда можно вывести.
В условии сказано, что сумма двух углов треугольника и внешнего угла к третьему равна 40о. Это означает, что на сумму углов
Значит
Таким образом,
Ответ: 160
27757. В треугольнике ABC угол A равен 30о, CH — высота, угол BCH равен 22о. Найдите угол ACB. Ответ дайте в градусах.
По свойству острых углов прямоугольного треугольника их сумма равна 90 градусам, то есть:
Найдём угол АСН:
Теперь можем найти угол АСВ:
Ответ: 38
27768.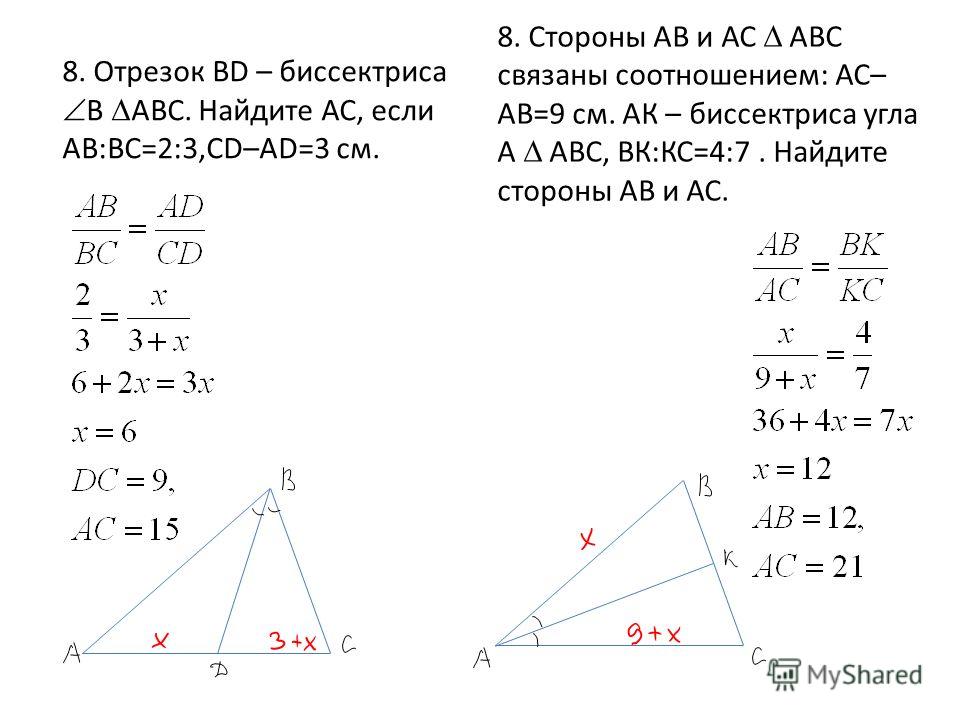 В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
В данном треугольнике не дано ни одного угла. Это значит, что необходимо обозначить какой-либо угол через переменную х, и далее используя свойство биссектрисы и теорему о сумме углов треугольника решить задачу. Пусть угол С равен х градусов, тогда
так как треугольник ADC равнобедренный (AD = DC по условию).
Далее:
так как AD биссектриса. Значит угол САВ равен 2х.
Известно, что внешний угол треугольника равен сумме двух внутренних углов несмежных с ним, то есть:
Так как треугольник BAD равнобедренный (AD = AB по условию), то
Получили, что
По теореме о сумме углов треугольника:
Получили, что меньший угол равен 36 градусам. Два других равны по 72 градуса.
*Обратите внимание! Не смотря на то, что дан эскиз равнобедренного треугольника, в условии не сказано, что он таковым является.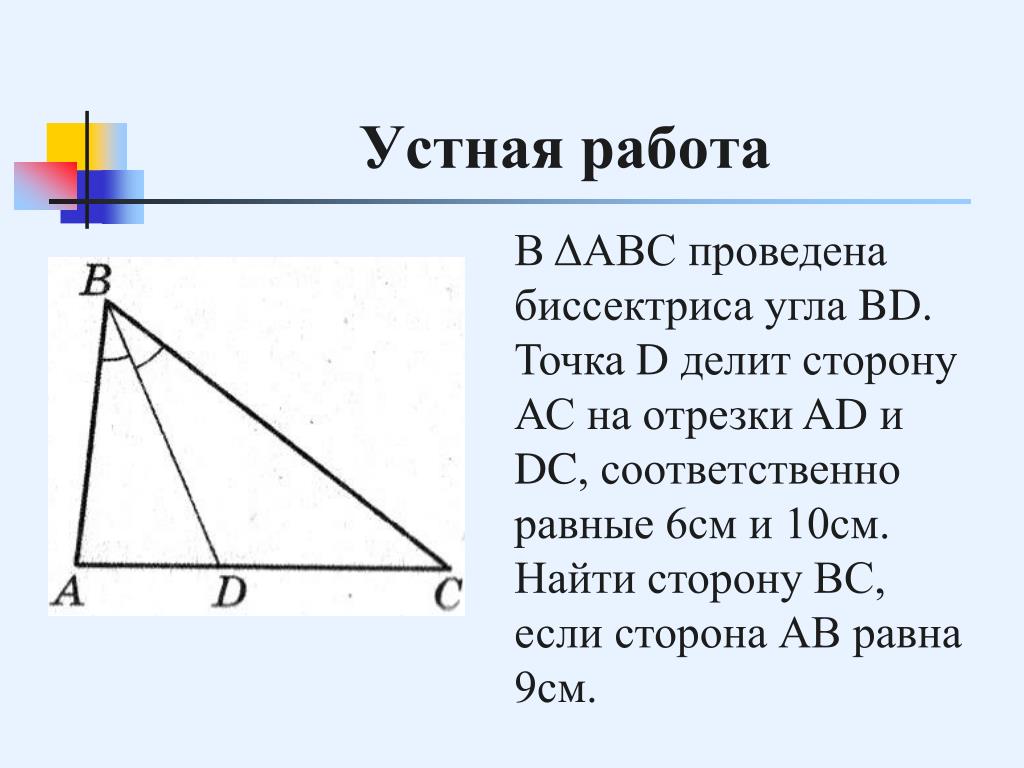 Мы в ходе решения мы, конечно, это установили. Но сразу, без обоснования, принимать его за равнобедренный нельзя. Используйте известные вам свойства для решения.
Мы в ходе решения мы, конечно, это установили. Но сразу, без обоснования, принимать его за равнобедренный нельзя. Используйте известные вам свойства для решения.
В треугольнике ABC угол A равен 40о, внешний угол при вершине B равен 102о. Найдите угол C. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC угол A равен 38о, AC = BC. Найдите угол С. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC АС = ВС, угол С равен 52о. Найдите внешний угол CBD. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC AB = BC. Внешний угол при вершине B равен 138о . Найдите угол C. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC угол C равен 90о, CH — высота, угол A равен 34о. Найдите угол BCH. Ответ дайте в градусах.
Найдите угол BCH. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC AD — биссектриса, угол C равен 50о, угол CAD равен 28о. Найдите угол B. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC AD — биссектриса, угол C равен 30о, угол BAD равен 22о. Найдите угол ADB. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC АС = ВС, AD — высота, угол BAD равен 24о. Найдите угол C. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC CD — медиана, угол ACB равен 90о, угол В равен 58о. Найдите угол ACD. Ответ дайте в градусах.
Посмотреть решение
Какие можно дать рекомендации?
1. Необходимо знать теорему о сумме углов треугольника.
Необходимо знать теорему о сумме углов треугольника.
2. Если в задаче сразу не увидели как выстроить решение, то следуйте принципу – «что можно найти исходя из данных».
3. Если стоит вопрос о нахождении углов и в условии нет никаких числовых величин, то смотрите, что (какой угол) можно обозначить переменной, и далее используйте известные вам свойства опираясь на данные в условии.
4. При решении подобных задач удобно на сделанном эскизе подписывать полученные углы, вычисления без особых затруднений проводятся устно.
В будущем мы продолжим рассматривать задачи связанные с суммой углов треугольника (здесь представлены не все типы), не пропустите! На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Решение треугольников | ЕГЭ-№1Треугольник
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Задание 3 ЕГЭ по математике (профиль) часть 4
Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на нахождение углов в параллелограммах и треугольниках, углы, связанные с комбинацией высот, медиан и биссектрис. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
27823. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
27808. Диагональ параллелограмма образует с двумя его сторонами углы 26º и 34º. Найдите больший угол параллелограмма. Ответ дайте в градусах.
27743. В треугольнике ABC угол A равен 40º, внешний угол при вершине B равен 102º. Найдите угол C. Ответ дайте в градусах.
27746. В треугольнике ABC стороны AC и BC равны, угол C равен 52º, угол CBD — внешний.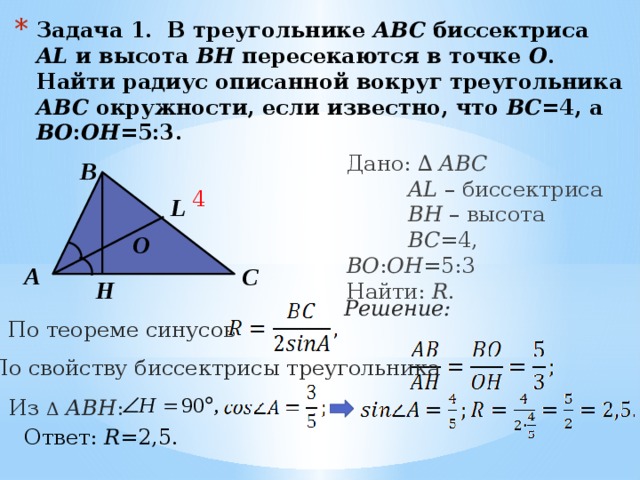 Найдите угол CBD. Ответ дайте в градусах.
Найдите угол CBD. Ответ дайте в градусах.
27747. В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине Bравен 122º. Найдите угол C. Ответ дайте в градусах.
27748. В треугольнике ABC AB = BC. Внешний угол при вершине B равен 138º. Найдите угол C. Ответ дайте в градусах.
27744. В треугольнике ABC угол A равен 38º, стороны AC и BC равны. Найдите угол C. Ответ дайте в градусах.
27745. В треугольнике ABC угол C равен 118º, стороны AC и BC равны. Найдите угол A. Ответ дайте в градусах.
27750. Больший угол равнобедренного треугольника равен 98º. Найдите меньший угол. Ответ дайте в градусах.
27769. В треугольнике ABC угол A равен 44º, угол C равен 62º. На продолжении стороны AB отложен отрезок BD = BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
27757. В треугольнике ABC угол A равен 30º, CH — высота, угол BCH равен 22º. Найдите угол ACB. Ответ дайте в градусах.
27762. В остроугольном треугольнике ABC угол A равен 65º. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
27763. Два угла треугольника равны 58º и 72º. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
27779. В треугольнике ABC угол A равен 60º, угол B равен 82º. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
27760. В треугольнике ABC AC = BC, AD — высота, угол BAD равен 24º. Найдите угол C. Ответ дайте в градусах.
27768. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
27776. В треугольнике ABC угол B равен 45º, угол C равен 85º, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.
27777. В треугольнике ABC угол A равен 30º, угол B равен 86º, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.
27758. В треугольнике ABC угол C равен 50º, AD — биссектриса, угол CAD равен 28º. Найдите угол B. Ответ дайте в градусах.
27759. В треугольнике ABC угол С равен 30º, AD — биссектриса, угол BAD равен 22º. Найдите угол ADB. Ответ дайте в градусах.
27764. В треугольнике ABC угол C равен 58 градусов, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Найдите угол AOB. Ответ дайте в градусах.
27778. В треугольнике ABC угол A равен 60º, угол B равен 82º. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
27765. Острый угол прямоугольного треугольника равен 32º. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
27766. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
27761. В треугольнике ABC угол ACB равен 90º, угол B равен 58º, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
27767. В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения прямых CH и AD, угол BAD равен 26º. Найдите угол AOC. Ответ дайте в градусах.
27770. Один из углов прямоугольного треугольника равен 29º. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Один из углов прямоугольного треугольника равен 29º. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
27771. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21º. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
27772. Острые углы прямоугольного треугольника равны 24º и 66º. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
27773. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40º. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
27774. Острые углы прямоугольного треугольника равны 24º и 66º. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Ответ дайте в градусах.
27775. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14º. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Понравилось это:
Нравится Загрузка…
Видео-вопрос: Построение биссектрисы угла для нахождения длины в равностороннем треугольнике
Учитывая, что 𝐴𝐵𝐶 — равносторонний треугольник со стороной 4 см, с помощью линейки и циркуля начертите треугольник 𝐴𝐵𝐶 и разделите ∠𝐴, ∠𝐵 и ∠𝐶 пополам лучом биссектрисы 𝐴𝐷, лучом 𝐵𝐷 и лучом 𝐶, который пересекает 𝐶 в точке 𝐷. Если луч 𝐶𝐷 пересекает отрезок 𝐴𝐵 в точке 𝑀, с помощью линейки измерьте длину отрезка 𝐷𝑀 до ближайшего десятичного знака.
Стенограмма видео
Учитывая, что 𝐴𝐵𝐶 является равносторонним
треугольника со стороной четыре сантиметра, с помощью линейки и циркуля начертите
треугольник 𝐴𝐵𝐶 и биссектриса угла 𝐴, угла 𝐵 и угла 𝐶 лучом биссектрисы
𝐴𝐷, луч 𝐵𝐷 и луч 𝐶𝐷, пересекающиеся в точке 𝐷. Если луч 𝐶𝐷 пересекает отрезок
𝐴𝐵 в точке 𝑀, линейкой измерьте длину отрезка 𝐷𝑀 до
ближайший десятичный.
Если луч 𝐶𝐷 пересекает отрезок
𝐴𝐵 в точке 𝑀, линейкой измерьте длину отрезка 𝐷𝑀 до
ближайший десятичный.
Начнем с построения описан равносторонний треугольник со стороной четыре сантиметра. Начнем с наброска одной стороны треугольник длиной четыре сантиметра с помощью линейки. Мы называем эту сторону 𝐶𝐵. Мы знаем, что равносторонний треугольник имеет стороны одинаковой длины. Итак, мы используем компас, чтобы проследить окружность с центром в точке 𝐶 радиусом четыре сантиметра. Затем мы повторяем этот процесс с компас с центром в точке 𝐵. Пересечение этих кругов радиусом четыре сантиметра — третья вершина равностороннего треугольника, точка 𝐴. С помощью линейки соединяем вершины, образующие требуемый треугольник.
Далее нас просят разделить каждую пополам
внутренний угол треугольника 𝐴𝐵𝐶. Чтобы разделить угол 𝐴 пополам, мы сначала используем
циркуль, чтобы нарисовать окружность с центром в 𝐴, которая пересекает стороны угла. Затем делаем то же самое для углов 𝐵
и 𝐶. Чтобы закончить первый шаг, мы
отметьте точки пересечения, как показано на рисунке. На втором этапе мы прослеживаем два
окружности одного радиуса с центром в каждой точке пересечения, найденной в
предыдущий шаг. Итак, окружности пересекаются на
внутренность угла 𝐶𝐴𝐵. Затем мы можем использовать нашу линейку, чтобы нарисовать
линия, соединяющая эту точку с вершиной 𝐴. это биссектриса угла
𝐴.
Чтобы разделить угол 𝐴 пополам, мы сначала используем
циркуль, чтобы нарисовать окружность с центром в 𝐴, которая пересекает стороны угла. Затем делаем то же самое для углов 𝐵
и 𝐶. Чтобы закончить первый шаг, мы
отметьте точки пересечения, как показано на рисунке. На втором этапе мы прослеживаем два
окружности одного радиуса с центром в каждой точке пересечения, найденной в
предыдущий шаг. Итак, окружности пересекаются на
внутренность угла 𝐶𝐴𝐵. Затем мы можем использовать нашу линейку, чтобы нарисовать
линия, соединяющая эту точку с вершиной 𝐴. это биссектриса угла
𝐴.
Далее мы можем следовать тому же
разделить угол 𝐵 пополам. Мы используем компас, чтобы проследить два
окружности одного радиуса с центрами в точках пересечения, найденных в первой
шаг. Затем отмечаем пересечение ул.
эти две окружности и провести биссектрису угла из вершины 𝐵 через эту точку
пересечение.
Наконец, построим угол биссектрису 𝐶, используя те же инструменты и шаги. Биссектриса третьего угла выглядит так этот. Как известно, биссектрисы угла треугольник всегда будет параллельным. Другими словами, они пересекаются в единственная точка. В этом случае точка параллелизм называется 𝐷.
Итак, мы построили луч 𝐴𝐷, биссектриса угла 𝐴; луч 𝐵𝐷, биссектриса угла 𝐵; и Рэй 𝐶𝐷, биссектриса угла 𝐶. Нам говорят, что луч 𝐶𝐷 пересекает сторону 𝐴𝐵 в точке 𝑀.
Теперь, когда мы закончили рисовать диаграмма согласно направлениям, мы готовы измерить длину линии сегмент 𝐷𝑀. Если мы измерим эту длину с линейки, получаем 𝐷𝑀, равный примерно одной и двум десятым сантиметра. С точностью до десятичной дроби это измерение составляет 1,2 сантиметра.
Решения по математике, часть II, для класса 10 по математике, глава 1
- Решения для учебников
- Класс 10
- Математика
- сходство
Решения по математике, часть II Решения для 10 класса по математике, глава 1, сходство представлены здесь с простыми пошаговыми пояснениями. Эти решения для подобия чрезвычайно популярны среди учащихся 10 класса для математических решений для подобия, которые пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги решений по математике, часть II, глава 1 по математике для класса 10, предоставляются здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для класса 10 по математике подготовлены экспертами и на 100% точны.
Эти решения для подобия чрезвычайно популярны среди учащихся 10 класса для математических решений для подобия, которые пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги решений по математике, часть II, глава 1 по математике для класса 10, предоставляются здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для класса 10 по математике подготовлены экспертами и на 100% точны.
Страница № 5:
Вопрос 1:
Основание треугольника равно 9, а высота 5. Основание другого треугольника равно 10, а высота 6. Найдите отношение площадей этих треугольников.
Ответ:
Пусть ABC и PQR — два прямоугольных треугольника с AB ⊥ BC и PQ ⊥ QR.
Дано:
BC = 9, AB = 5, PQ = 6 и QR = 10.
∴A△ABCA△PQR=AB×BCPQ×QR=5×96×10=34
Страница № 6:
Вопрос 2:
На данном рисунке BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, тогда найдите A∆ABCA∆ADB.
Ответ:
Дано:
BC = 4
AD = 8
∴A △ ABCA △ ADB = AB × BCAB × AD = BCAD ∵BC = 4 и AD = 8 = 48
= 12
Страница № 6 :
Вопрос 3:
На следующем рисунке сегмент PS ⊥ сегмент RQ сегмент QT ⊥ сегмент PR. Если RQ = 6, PS = 6 и PR = 12, то найти QT.
Ответ:
Дано:
PS ⊥ RQ
QT ⊥ PR
RQ = 6, PS = 6 и PR = 12 и высота PS, A△PQR=12×QR×PS
∴A△PQRA△PQR=12×PR×QT12×QR×PS⇒1=PR×QTQR×PS⇒PR×QT=QR×PS
⇒QT=QR×PSPR=6×612=3
Следовательно, мера стороны QT составляет 3 единицы.
Страница № 6:
Вопрос 4:
На следующем рисунке AP ⊥ BC, AD || до н.э., затем найти A(∆ABC) : A(∆BCD).
Ответ:
Дано:
AP ⊥ BC
AD || BC
∴A△ABCA△BCD=AP×BCAP×BC=11
Следовательно, отношение A(∆ABC) и A(∆BCD) равно 1 : 1.
Страница № 6:
Вопрос 5:
На соседнем рисунке PQ ⊥ BC, AD⊥ BC найдите следующие соотношения.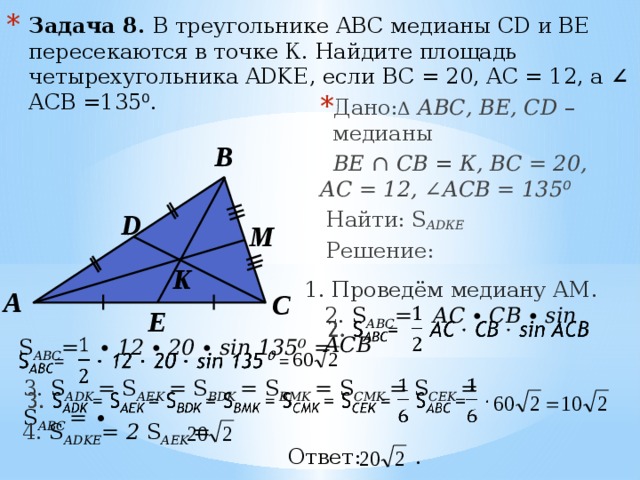
(i) A∆pqba∆pbc
(ii) APbca∆Abc
(iii) APryabca∆Adc
(iv) APQU.
Ответ:
( i)
A△PQBA△PBC=PQ×BQPQ×BC=BQBC
(ii)
A△PBCA△ABC=PQ×BCAD×BC=PQAD
(iii)
A△ABCA△ADC=AD×BCAD×DC =BCDC
(iv)
A△ADCA△PQC=AD×DCPQ×QC
Страница № 13:
Вопрос 1:
Ниже приведены некоторые треугольники и длины отрезков. Определите, на каких фигурах луч PM является биссектрисой ∠QPR.
(1)
(2)
(3)
Ответ:
(1)
В
Согласно теореме, обратной теореме о биссектрисе угла, луч PM является биссектрисой ∠QPR.
(2)
In △QMP, QMQP=810=45
In △MRP,MRRP=67
∴QMQP≠MRRP
Следовательно, луч PM не является биссектрисой ∠QPR.
(3)
In △QMP, QMQP=3,69=25
In △MRP,MRRP=410=25
∴QMQP=MRRP
Согласно теореме, обратной теореме о биссектрисе, луч PM является биссектрисой ∠QPR.
Страница № 13:
Вопрос 2:
В ∆PQR, PM = 15, PQ = 25, PR = 20, NR = 8. Укажите, параллельна ли линия NM стороне RQ. Дайте повод.
Укажите, параллельна ли линия NM стороне RQ. Дайте повод.
Ответ:
Дано:
PM = 15,
PQ = 25,
PR = 20 и
NR = 8 − PM
= 25 − 15
= 10
В △PRQ, PRNR=128=32
Кроме того, PMMQ=1510=32
∴PRNR=PMMQ
Согласно обратной теореме о пропорциональности, NM параллелен стороне RQ или NM | | РК.
Страница № 14:
Вопрос 3:
В ∆MNP NQ является биссектрисой ∠N. Если MN = 5, PN = 7, MQ = 2,5, то найти QP.
. Ответ:
.
Страница № 14:
Вопрос 4:
На рисунке даны меры некоторых углов. Докажите, что APPB=AQQC
Ответ:
Дано:
∠APQ = 60 ∘
∠ABC = 60 ∘
Так как соответствующие углы ∠APQ и ∠APC равны.
Следовательно, строка PQ || ДО Н.Э.
В △ABC, PQ∥BCAPPB=AQQC По основной теореме пропорциональности
Страница № 14:
Вопрос 5:
В трапеции ABCD, сторона AB || сторона PQ || сторона ∆C, AP = 15, PD = 12, QC = 14, Найти BQ.
Ответ:
Построение: Соединить BD с пересечением PQ в точке X.
В △ABD, PX || AB
DPPA=DXXB …1 По основной теореме пропорциональности
В △BDC, XQ||DC
DXXB=CQQB …2 По основной теореме пропорциональности
Из (1) и (2) получаем :
Вопрос 6:
Найдите QP, используя данные на рисунке.
. Ответ:
.
Страница № 14:
Вопрос 7:
На данном рисунке, если AB || компакт-диск || FE, затем найти x и AE.
Ответ:
Построение: Соединить AFпересечение CD в точке X.
В △ABF, DX || AB
FDDB = FXXA … 1 по базовой теореме пропорциональности
в △ AEF, XC || FE
FXXA = ECCA … 2 по базовой теореме пропорциональности
от (1) и (2), мы получаем
FDDB = ECCA. ⇒48=x12⇒x=6
Теперь AE = AC + CE
= 12 + 6
= 18
Страница № 15:
Вопрос 8:
В ∆LMN луч MT делит пополам ∠LMN Если LM = 6, MN = 10, TN = 8, то Найдите LT.
Ответ:
В △LNM, LTNT=LMNM По теореме о биссектрисах угла⇒LT8=610
⇒LT=8×610=4,8
Следовательно, мера LT равна 4.8.LT равна 4.8.
Страница № 15:
Вопрос 9:
В ∆ABC отрезок BD делит пополам ∠ABC. Если AB = х , ВС = х + 5, AD = х — 2, DC = х + 2, то найдите значение х.
Ответ:
в △ abc, ↑ABD = ↑DBC
ADDC = ABCB By Ange Biscection Теорема равила x-2x+2 = XX+5⇒x2+3x-10 = x2+2x
⇒3x-2x. =10⇒x=10
Страница № 15:
Вопрос 10:
На данном рисунке X любая точка внутри треугольника. Точка X соединена с вершинами треугольника. Сегмент PQ || сегмент DE, сегмент QR || сегмент ЭФ. Заполните пробелы, чтобы доказать, что сегмент PR || сегмент ДФ.
Ответ:
Дано:
Сегмент PQ || сегмент DE
сегмент QR || сегмент EF
В △DXE, PQ || DE
XPPD=XQQE …I По основной теореме пропорциональности
В △XEF, QR || Ef .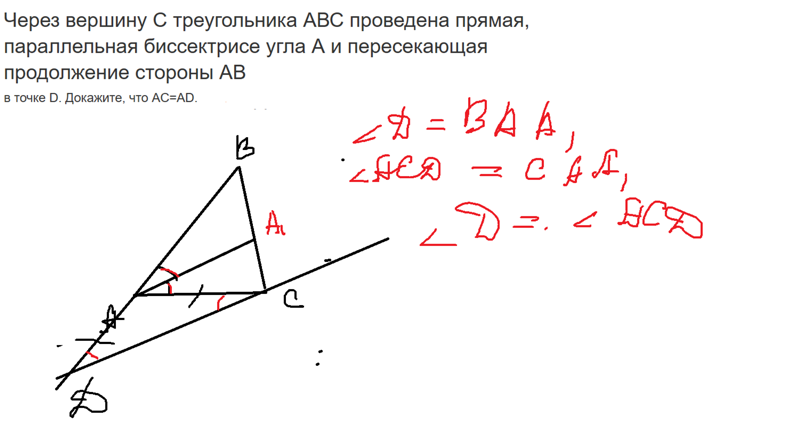 … данный
… данный
∴xqqe = xrrf ….. ii по основной теореме пропорциональности
∴xppd = xrrf из I и II
∴ SEG PR || seg DF (Конверсия основной теоремы о пропорциях)
Страница № 15:
Вопрос 11:
В ∆ABC луч BD делит пополам ∠ABC, а луч CE делит пополам ∠ACB. Если seg AB ≅ seg AC, то докажите, что ED || ДО Н.Э.
Ответ:
Дано:
луч BD делит пополам ∠ABC
луч CE делит пополам ∠ACB.
SEG AB ≅ SEG AC
в △ ABC, ↑ABD = грыти теорема
Из (I) и (II)
ADDC=AEEB ∵seg AB ≅ seg AC
∴ ED || BC (Конверсия основной теоремы о пропорциях)
Страница № 21:
Вопрос 1:
На данном рисунке ∠ABC = 75°, ∠EDC = 75° укажите, какие два треугольника подобны и по какому критерию? Также запишите сходство этих двух треугольников по правильному однозначному соответствию.
ОТВЕТ:
Дано:
ϩabc = 75 °, грытика = 75 °
Теперь, в △ ABC и △ EDC
потряно )
По критерию подобия АА
△ABC ∼ △EDC
Страница № 21:
Вопрос 2:
Подобны ли треугольники на данной фигуре? Если да, то по какому тесту?
Ответ:
Дано:
PQ = 6
PR = 10
QR = 8
LM = 3
LN = 5
MN = 4
Теперь,
PQLM=63=4,N =105=2
∴PQLM=QRMN=RPNL
По критерию подобия SSS
△PQR ∼ △LMN
Страница № 21:
Вопрос 3:
Как показано на данном рисунке, две опоры высотой 8 м и 4 м перпендикулярно земле. Если длина тени меньшего полюса от солнечного света равна 6 м, то какой длины будет в то же время тень от большего полюса?
Если длина тени меньшего полюса от солнечного света равна 6 м, то какой длины будет в то же время тень от большего полюса?
Ответ:
Дано:
PR = 4
RL = 6
AC = 8
в △ PLR и △ ABC
тий PRL = ♂ ACCB (вертикально противоположные углы)
♂ла
По критерию подобия AA
△PLR ∼ △ABC
∴PRAC=LRBC Соответствующие стороны пропорциональны⇒48=6x⇒x=12
.
Страница № 21:
Вопрос 4:
В ∆ABC, AP ⊥ BC, BQ ⊥ AC B–P–C, A–Q – C, затем докажите, что ∆CPA ~ ∆CQB. Если AP = 7, BQ = 8, BC = 12, то Найдите AC.
Ответ:
Дано:
AP ⊥ BC
BQ ⊥ AC
для доказывания: ∆CPA ~ ∆CQB
Доказательство: в ∆CPA и ∆CQB
↑CPA = ↑CQB = 90 ∘
(дано)
(дано)
(дано)
(дано)
(дано)
(дано)
(дано)
(дано)
(дано)
(примерно ∠C = ∠C (Общий)
По критерию сходства АА
∆CPA ~ ∆CQB
Отсюда доказано.
Теперь APBQ=ACBC Соответствующие стороны пропорциональны⇒AC=APBQ×BC=78×12=10,5
Страница № 22:
Вопрос 5:
Дано: В трапеции PQRS, сторона PQ || сторона SR, AR = 5AP, AS = 5AQ, тогда докажите, что SR = 5PQ
Ответ:
Дано:
сторона PQ || сторона SR
AR = 5AP,
AS = 5AQ
Чтобы доказать: SR = 5PQ
Доказательство: В ∆APQ и ∆ARS
∠PAQ = ∠RAS (Вертикально противоположные углы)
∠PQA = ∠RSA угол || сторона SR и QS является поперечной линией)
По критерию подобия АА
∆APQ ~ ∆ARS
PQSR=APAR Соответственные стороны пропорциональны⇒PQSR=15 AR=5AP⇒SR=5PQ
Отсюда доказано.
Страница № 22:
Вопрос 6:
В трапеции ABCD, сторона AB || сторона DC, диагонали AC и BD пересекаются в точке O. Если AB = 20, DC = 6, OB = 15, то найти OD.
Ответ:
Дано:
сторона AB || сторона DC
AB = 20,
DC = 6,
OB = 15
In △COD и △AOB
∠COD = ∠AOB (вертикально противоположные углы)
потрясение stcdo = ♂ (альтернативные углы, CD || BA и BD — это линия поперечной передачи)
по тесту AA сходства
△ COD ∼ △ AOB
∴CDAB = ODOB Соответствующие стороны являются пропорциональными myty . 620 = od15 = 4.5
620 = od15 = 4.5
Страница № 22:
Вопрос 7:
◻ABCD — параллелограмм, точка E лежит на стороне BC. Прямая DE пересекает луч AB в точке T. Докажите, что DE × BE = CE × TE.
Ответ:
Дано: ◻ABCD — параллелограмм
Доказать: DE × BE = CE × TE
Доказательство: В ∆BET и ∆CED
∠BET = ∠CED (Вертикально противоположные углы)
∠BTE = ∠CDE (Альтернативные углы, AT || CD и DT — поперечная линия)
По критерию сходства AA
∼ ∆CED
∴BECE=ETED Соответствующие стороны пропорциональны⇒BE×ED=CE×ET
Отсюда доказано.
Страница № 22:
Вопрос 8:
На данном рисунке отрезки AC и BD пересекаются в точке P и APCP=BPDP. Докажите, что ∆ABP ~ ∆CDP
Ответ:
Дано: APCP = BPDP
, чтобы доказать: ∆ABP ~ ∆CDP
Доказательство: в ∆ABP и ∆DCP
APCP = BPDP (задано)
потряно сходство
APCP=BPDP
Страница № 22:
Вопрос 9:
На данном рисунке в ∆ABC точка D на стороне BC такова, что ∠BAC = ∠ADC. Докажите, что CA 2 = CB × CD
Докажите, что CA 2 = CB × CD
Ответ:
Дано: ∠BAC = ∠ADC
Чтобы доказать: CA 2 = CB × CD
Доказательство: в ∆ABC и ∆DAC
тнамбак = ϪADC (дано)
Ϫc = Ϫc (общий)
с помощью анализа сходства
∆ABC ± ∆DAC
∴BCAC = ACDC Соответствующие стороны. =BC×DC
Отсюда доказано.
Страница № 25:
Вопрос 1:
Отношение соответствующих сторон подобных треугольников равно 3 : 5; затем найти отношение их площадей.
Ответ:
Согласно теореме площадей подобных треугольников «Если два треугольника подобны, отношение площадей этих треугольников равно отношению квадратов соответствующих сторон».
Следовательно, отношение площадей треугольников =3252
=925
Страница № 25:
Вопрос 2:
Если ∆ABC ~ ∆PQR и AB : PQ = 2 : 3, то заполните пропуски.
A∆ABCA∆PQR=AB2 =2232=
Ответ:
Дано:
∆ABC ~ ∆PQR
AB : Когда PQ = 2 : 3, два треугольника подобны по площади». отношение площадей этих треугольников равно отношению квадратов их соответствующих сторон».
отношение площадей этих треугольников равно отношению квадратов их соответствующих сторон».
∴A∆ABCA∆PQR=AB2PQ2=2232= 4 9
Страница № 25:
Вопрос 3:
затем заполните пробелы.
А∆ABCA∆. . . . = 80125 ∴ ABPQ =
Ответ:
Дано:
∆ABC ~ ∆PQR
A (∆ABC) = 80
A (∆PQR) = 125
в соответствии с теорером сходных треугольц », когда два треугольника аналогично, отношение площадей этих треугольников равно отношению квадратов их соответствующих сторон».
. 4:
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). Если QR = 20, то Найдите MN.
Ответ:
Дано:
∆LMN ~ ∆PQR
9 × A (∆PQR ) = 16 × A (∆LMN)
Рассмотрим, 9 × A (∆PQR ) = 16 × A (∆LMN)
A ∆LMNA∆PQR=916⇒MN2QR2=3242⇒MNQR=34
⇒MN=34×QR⇒MN=34×20 ∵QR=20⇒MN=15
Страница № 25:
Вопрос 5:
Площади двух подобных треугольников равны 225 кв.см. 81 кв.см. Если сторона меньшего треугольника равна 12 см, то найти соответствующую сторону большего треугольника.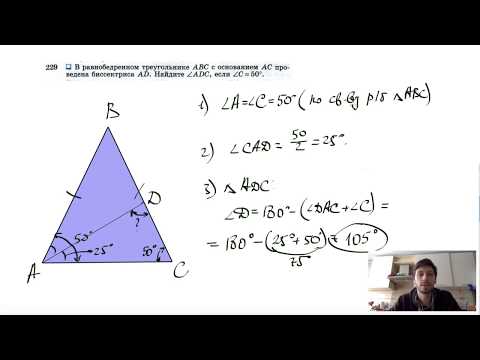
Ответ:
Согласно теореме о площадях подобных треугольников «Если два треугольника подобны, то отношение площадей этих треугольников равно отношению площадей соответствующих сторон».
∴Площадь большего треугольникаПлощадь меньшего треугольника=22581⇒Сторона большего треугольника2Сторона меньшего треугольника2=15292⇒Сторона большего треугольникаСторона меньшего треугольника=159
⇒Сторона большего треугольника=159×Сторона меньшего треугольника⇒Сторона большего треугольника=159×12=20
Следовательно, соответствующая сторона большего треугольника равна 20.
Страница № 25:
Вопрос 6:
Треугольники ∆ABC и ∆DEF равносторонние. Если A(∆ABC) : A (∆DEF) = 1 : 2 и AB = 4, найти DE.
Ответ:
Рассмотрим, A(∆ABC) : A (∆DEF) = 1 : 2
⇒A∆ABCA∆DEF=12⇒AB2DE2=12⇒DE2=2AB2
⇒DE2=2×42 =4⇒DE=32⇒DE=42
Страница № 25:
Вопрос 7:
На приведенном рисунке 1.66, seg PQ || сегмент DE, A(∆PQF) = 20 единиц, PF = 2 DP, затем найдите A(◻DPQE), выполнив следующее задание.
Ответ:
Дано:
seg PQ || seg DE
A(∆PQF) = 20 единиц
PF = 2 DP
Предположим, что DP = x
∴ PF = 2 x
DF=DP+PF=x+2x=3x
In △FDE и △FPQ
∠FDE = ∠FPQ (соответствующие углы)
∠FED = ∠FQP (соответствующие углы)
По критерию сходства АА
△FDE ∼ △FPQ
∴A△FDEA△FPQ=FD2FP2=3x22x2=94A△FDE=94A△FPQ=94×20=45
∴A□DPQE=A△FDE-A△FPQ =45-20=25
Страница № 26:
Вопрос 1:
Выберите подходящий вариант.
(1) В ∆ABC и ∆PQR при однозначном соответствии ABQR=BCPR=CAPQ тогда
(A) ∆PQR ~ ∆ABC
(B) ∆PQR ~ ∆CAB
(C) ∆CBA ~ ∆PQR
(D) ∆BCA ~ ∆PQR
(2) Если в ∆DEF и ∆PQR ∠D ≅ ∠Q, ∠R ≅ ∠E, то какое из следующих утверждений неверно?
(A) EFPR=DFPQ (B) DEPQ=EFRP
(C) DEQR=DFPQ (D) EFRP=DEQR
(3) В ∆ABC и ∆DEF ∠B = ∠E, ∠F = ∠C и AB = 3DE, то какое из утверждений относительно двух треугольников верно?
(B) Треугольники подобны, но не равны.
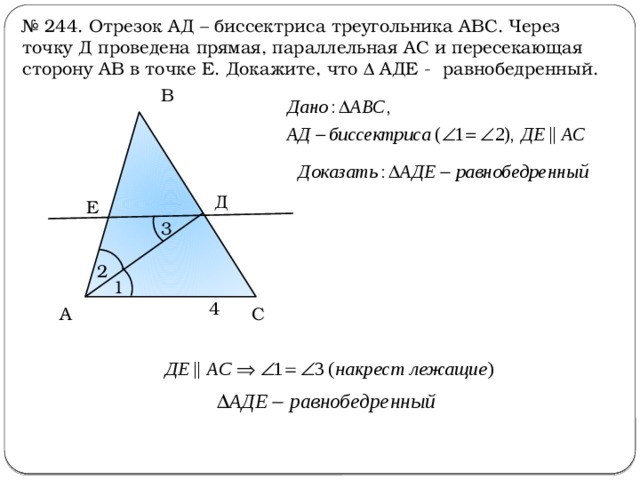
(C) Треугольники равны и подобны.
(D) Ни одно из приведенных выше утверждений не верно.
(4) ∆ABC и ∆DEF равносторонние треугольники, A (∆ABC) : A (∆DEF) = 1 : 2
Если AB = 4, то какова длина DE?
(A) 22
(B) 4
(C) 8
(D) 42
(5) На данном рисунке сегмент XY || seg BC, то какое из следующих утверждений верно?
(A) ABAC=AXAY (B) AXXB=AYAC
(C) AXYC=AYXB (D) ABYC=ACXB
Ответ:
(1)
Дано: ABQR=BCPR=4CAPQ S 90 тест подобия
∆PQR ~ ∆CAB
Следовательно, правильный вариант (B).
(2)
In ∆DEF и ∆PQR
Ϫd ≅ Ϫq
Ϫr ≅ ome
с помощью анализа сходства
∆def ~ ∆pqr
∴depq = efqr = dfpr Соответствующие стороны схоже (Б).
(3)
В ∆ABC и ∆DEF
∠B = ∠E,
∠F = ∠C
По критерию подобия AA
∆ABC ~ ∆DEF
Поскольку не существует критериев конгруэнтности, подобных AA.
Таким образом, ∆ABC и ∆DEF не конгруэнтны.
Следовательно, правильный вариант (B).
(4)
Дано: ∆ABC и ∆DEF равносторонние треугольники.
Построение: Проведите перпендикуляр из вершин A и D на AC и DF в обоих треугольниках.
в ∆ABX и ∆Dey
Ϫb = ↑C = 60 ∘ (∆ABC и ∆DEF — равносторонние треугольники)
↑ксист = ↑dyB (по строительству)
Испытание AA сходства
∆Abx ~ Dey
∴abde = оси, соответствующие сторонам аналогичных треугольников, являются пропорциональными
∴depq ≠ efrp
a △ abca △ def = 12 минут12 × ab × ax12 × de × dy = 12 минут 2 = 12 ∵Abde = Axdy ⇒2 = = DY × 12 минут. 32⇒DE=42
Следовательно, правильный вариант (D).
(5)
Дано: сегмент XY || seg BC
По основной теореме пропорциональности
AXBX=AYYC⇒BXAX+1=YCAY+1⇒BX+AXAX=YC+AYAY
⇒ABAX=ACAY⇒ABAC=AXAY
Следовательно, правильным вариантом является (D).
Страница № 27:
Вопрос 2:
В ∆ABC, B – D – C и BD = 7, BC = 20, затем найдите следующие соотношения. Ответ:
Ответ:
Построение: Проведите перпендикуляр из вершины А к прямой ВС.
(1)
A∆ABDA∆ADC=12×AX×BD12×AX×DC=BDDC=713 DC=BC-BD
(2)
A∆ABDA∆ABC=12×AX×BD12×AX× BC=BDBC=720
(3)
A∆ADCA∆ABC=12×AX×DC12×AX×BC=DCBC=1320 отношение площадей двух равновеликих треугольников равно 2 : 3. Если основание меньшего треугольника равно 6 см, то чему равно основание большего треугольника?
Ответ:
Площадь меньшего треугольникаПлощадь большего треугольника=23⇒12×Высота меньшего треугольника×Основание меньшего треугольника12×Высота большего треугольника× Основание большего треугольника=23⇒6 Основание большего треугольника ⇒ 9 ⇒ 3B большего треугольника=23 больший треугольник=32×6=9
Страница № 27:
Вопрос 4:
На данном рисунке ∠ABC = ∠DCB = 90° AB = 6, DC = 8, тогда A ∆ABCA ∆DCB=?
Ответ:
Дано:
∠ABC = ∠DCB = 90°
AB = 6
DC = 8
Теперь A ∆ABCA ∆DCB=12×AB×BC12×DC×BC=68=34
Страница № 27:
Вопрос 5:
На данном рисунке PM = 10 см A(∆PQS) = 100 кв. см A(∆QRS) = 110 кв.см, тогда Найдите NR.
см A(∆QRS) = 110 кв.см, тогда Найдите NR.
Ответ:
Дано:
PM = 10 см
A(∆PQS) = 100 кв.см
A(∆QRS) = 110 кв.см
×QS12×RN×QS=1011
⇒10RN=1011⇒RN=11 см
Страница № 27:
Вопрос 6:
∆MNT ~ ∆QRS. Длина высоты, проведенной из точки T, равна 5, а длина высоты, проведенной из точки S, равна 9.. Найдите отношение A∆MNTA∆QRS.
Ответ:
Площади двух подобных треугольников пропорциональны квадратам их соответствующих высот.
∴A∆MNTA∆QRS=592=2581
Страница № 28:
Вопрос 7:
На данном рисунке A – D– C и B – E – C сегмент DE || сторона AB Если AD = 5, DC = 3, BC = 6,4, то найти BE.
Ответ:
Дано:
AD = 5,
DC = 3,
BC = 6,4
In △ABC, DE || AB
∴CDDA=CEEB По основной теореме пропорциональности ⇒35=6,4-xx⇒3x=32-5x
⇒8x=32⇒x=4
Страница № 28:
Вопрос 8:
На данном рисунке отрезки PA, отрезки QB, отрезки RC и отрезки SD перпендикулярны прямой AD. AB = 60, BC = 70, CD = 80, PS = 280, затем найдите PQ, QR и RS.
AB = 60, BC = 70, CD = 80, PS = 280, затем найдите PQ, QR и RS.
Ответ:
Дано:
AB = 60,
BC = 70,
CD = 80,
PS = 280
Теперь AD = AB + BC + CD
= 60 + 70 + 80 2010490
0 теорема о пересечении, мы имеем
PQAB=QRBC=RSCD=PSAD⇒PQ60=QR70=RS80=280210⇒PQ60=QR70=RS80=43
∴PQ=43×60=80QR=43×70=2803RS=43×80=3203
Страница № 28:
Вопрос 9:
В сегменте ∆PQR PM является медианой. Биссектрисы углов ∠PMQ и ∠PMR пересекают стороны PQ и стороны PR в точках X и Y соответственно. Докажите, что XY || QR.
Ответ:
В △PMQ луч MX является биссектрисой △PMQ.
∴PXXQ=MQMP ……… (I) теорема о биссектрисе угла.
В △PMR луч MY является биссектрисой △PMR.
∴PYYR=MRMP ……… (II) теорема о биссектрисе угла.
ButMPMQ=MPMR ……… M — средняя точка QR, поэтому MQ = MR.
∴PXXQ=PYYR
∴XY || QR . ……… Обратное из основной теоремы пропорциональности.
……… Обратное из основной теоремы пропорциональности.
Страница № 29:
Вопрос 10:
На данном рисунке биссектрисы ∠B и ∠C отрезка ∆ABC пересекаются в точке X. Прямая AX пересекает сторону BC в точке Y. AB = 5, AC = 4, ВС = 6, тогда найдите AXXY.
Ответ:
в △ aby, omybx = omxba
axxy = abby … I по углу теорема
в △ acy, omycx = retxca
Axxy = Accy … ii By Angle Bisector теорема
Из (I) и (II)
ACCY=ABBY⇒ACBC-BY=ABBY⇒46-BY=5BY
⇒4BY=30-5BY⇒9BY=30⇒BY=103
Из (I) имеем
AXXY=5103=32
Страница № 29:
Вопрос 11:
В ▢ABCD, сегмент AD || сегмент до нашей эры. Диагональ AC и диагональ BD пересекаются в точке P. Затем покажите, что APPD=PCBP
Ответ:
Дано: ▢ABCD является параллелограммом
Доказать: APPD=PCBP
Доказательство: В △APD и △CPB
∠ APD = ∠CPB (вертикально противоположные углы)
ϪPAD = Ϫpcb (альтернативные углы, AD || BC и BD — это линия поперечной передачи)
С помощью AA теста сходства
△ APD ∼ △ CPB
EAPPC = PDPB соответствующие стороны являются пропорциональными NAPPD = PCPB
DED.

Leave A Comment