В треугольнике абс аб бс ас 16 высота сн 4: В треугольнике ABC, AB=BC, AC=16, высота CH равна 4. Найдите синус угла ACB.

Задание №15 базового уровня. Равнобедренный треугольник: вычисление углов

Практикум №2 по решению
планиметрических задач
(базовый уровень)
Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной Геннадьевной
Задание №15 базового уровня
Равнобедренный треугольник:
вычисление углов

3. Содержание

Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
•Задачи для сам. решения

4. Задача №1

В равнобедренном треугольнике ABC боковые
стороны AB = BC = 5, медиана BM = 4. Найдите cos∠BAC.
Решение. В равнобедренном треугольнике медиана
опущенная на основание является высотой и
биссектрисой. Рассмотрим прямоугольный
треугольник ABM. По теореме Пифагора
найдём AM:
AM=3. Найдём cos∠BAC:

5. Задача №2

В треугольнике АВС АС=BС=8, АВ=8 . Найдите cosA .
Решение.
Треугольник АВС равносторонний, значит,
высота СН делит
основание АВ пополам.

6. Задача №3

В треугольнике АВС АС=ВС, высота СН равна 7, АВ=48.
Найдите sinA.
Решение.
Треугольник АВС равнобедренный, значит,
высота СН делит основание АВ пополам.

7. Задача №4

В треугольнике ABC известно, что AB = BC = 20, АС =
32 . Найдите синус угла ВАС.
Решение.
Треугольник ABC равнобедренный, так как AB = BC,
найдём по теореме Пифагора высоту, выходящую из вершины В,
она будет равна:
ВН² = АВ² — АН² = 400 – 256 = 144 = 12²
Синус — это отношение противолежащего катета к
гипотенузе: sinBAC = BH:AB = 12:20 = 0,6

8. Задача №5

В треугольнике АВС АС=ВС=4√5, высота СН равна 4.
Найдите tgA .
Решение.

9. Задача №6

В треугольнике АВС АВ=ВС, АН – высота, sinBAC=7/5.
Найдите sinBAH.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.

10. Задача №7

В треугольнике АВС АВ=ВС, АН – высота, sinBAC=0,1.
Найдите cosBAH.
Решение.
Треугольник ABC равнобедренный,
значит, углы BAC и ABH равны как углы
при его основании.

11. Задача №8

В треугольнике АВС АВ=ВС, АН – высота, sinBAC=4/√17.
Найдите tgBAH.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.
.

12. Задача №9

В треугольнике АВС АВ=ВС, АН – высота и равна 20,
AB=25. Найдите cosBAC.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.

13. Задача №10

В тупоугольном треугольнике АВС АC=ВС=8,
высота АН равна 4. Найдите sinACB .
Решение.
Выразим площадь треугольника двумя
способами:
Значит

14. Задача №11

В тупоугольном треугольнике АВС АC=ВС=25,
высота АН равна 20. Найдите cosACB .
Решение.
.

15. Задача №12

В тупоугольном треугольнике АВС АC=ВС=25, АН-высота,
СН=20. Найдите sinACB .
Решение.
.

16. Задача №13

В тупоугольном треугольнике АВС АC=ВС, высота АН=4,
СН=8. Найдите tgACB.
Решение.

17. Задача №14

В треугольнике АВС АС=ВС, высота АН равна 24, ВН=7.
Найдите cosBAC.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.

18. Задача №15

В треугольнике АВС АС=ВС=25, AB=40. Найдите синус
внешнего угла при вершине А.
Решение.
Синусы смежных углов равны, поэтому

19. Задача №16

В треугольнике АВС АС=ВС=8, AB=8. Найдите косинус
внешнего угла при вершине А.
Решение.

20. Задача №17

В треугольнике АВС АС=ВС=√17, AB=8. Найдите тангенс
внешнего угла при вершине А.
Решение.

21. Задача №18

Один угол равнобедренного треугольника на 90° больше
другого. Найдите меньший угол. Ответ дайте в градусах.
Решение.
Т.к. треугольник равнобедренный, то углы при его основании равны.
Обозначим за х меньший угол, тогда больший угол равен (х+90).
Значит 2х+(х+90)=180 => 3х=90 ; х=30
Задачи
для самостоятельного
решения

23. Задача №2 Решите самостоятельно

1)
2)
3)
4)
5)
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
АС=BС=20, АВ=10. Найдите cosA .
АС=BС=5, АВ=4. Найдите cosA .
АС=BС=12, АВ=18. Найдите cosA .
АС=BС=9√5, АВ=18 . Найдите tgA .
АС=BС=9√2, АВ=18 . Найдите tgA .

24. Задача №3 Решите самостоятельно

1) Задание 15 № 32641. В треугольнике ABC
10, АВ=10√21. Найдите sinA.
2) Задание 15 № 32645. В треугольнике ABC
АВ=12√6. Найдите sinA.
3) Задание 15 № 32653. В треугольнике ABC
45, АВ=10√19 . Найдите sinA.
4) Задание 15 № 32663. В треугольнике ABC
3, АВ=2√7 . Найдите sinA .
, высота CH равна
, высота CH равна 3,
, высота CH равна
, высота CH равна

25.

Задача №5 Решите самостоятельно1) В треугольнике АВС
Найдите tgA .
2) В треугольнике АВС
Найдите tgA .
3) В треугольнике АВС
Найдите tgA .
4) В треугольнике АВС
Найдите tgA .
АС=ВС=5√5, высота СН равна 5.
АС=ВС=2√61, высота СН равна 12.
АС=ВС=√5, высота СН равна 2.
АС=ВС=7√5, высота СН равна 14.

26. Задача №6 Решите самостоятельно

1) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=√3/2.
Найдите sinBAH.
2) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√51/10. Найдите sinBAH.
3) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√19/10. Найдите sinBAH.
4) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√91/10. Найдите sinBAH.

27. Задача №7 Решите самостоятельно

1) В треугольнике АВС
Найдите cosBAH.
2) В треугольнике АВС
Найдите cosBAH.
3) В треугольнике АВС
Найдите cosBAH.
4) В треугольнике АВС
Найдите cosBAH.
АВ=ВС, АН – высота, sinBAC=0,51.
АВ=ВС, АН – высота, sinBAC=0,27.
АВ=ВС, АН – высота, sinBAC=0,99
АВ=ВС, АН – высота, sinBAC=0,18.

28. Задача №8 Решите самостоятельно

1) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=5/13.
Найдите tgBAH.
2) В треугольнике АВС АВ=ВС, АН –
высота, sinBAC=40/41. Найдите tgBAH.
3) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=4/5.
Найдите tgBAH.
4) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=2/√13.
Найдите tgBAH.

29. Задача №10 Решите самостоятельно

1) В тупоугольном треугольнике АВС АC=ВС=5,
высота АН равна 1. Найдите sinACB
2) В тупоугольном треугольнике АВС АC=ВС=14,
высота АН равна 7. Найдите sinACB
3) В тупоугольном треугольнике АВС АC=ВС=20,
высота АН равна 5. Найдите sinACB

30. Задача №15 Решите самостоятельно

1) В треугольнике АВС АС=ВС=25, AB=48. Найдите синус
внешнего угла при вершине А.
2) В треугольнике АВС АС=ВС=5, AB=2√21. Найдите синус
внешнего угла при вершине А.
3) В треугольнике АВС АС=ВС=2, AB=2√3. Найдите синус
внешнего угла при вершине А.

31. Задача №18 Решите самостоятельно

1) Один угол равнобедренного треугольника на 141°
больше другого. Найдите меньший угол. Ответ дайте в
градусах.
2) Один угол равнобедренного треугольника на 165°
больше другого. Найдите меньший угол. Ответ дайте в
градусах.
3) Один угол равнобедренного треугольника на 96°
больше другого. Найдите меньший угол. Ответ дайте в
градусах.

32. Интернет источники

Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
• https://fotki.yandex.ru/next/users/nata-komiati/album/159853/view/688546?page=5
• https://fotki.yandex.ru/next/users/nata-komiati/album/159853/view/688553?page=5
• https://fotki.yandex.ru/next/users/nata-komiati/album/158683/view/665734?page=3
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016. jpg
http://asa.my1.ru/_pu/0/90580308.png

Mathematics_part_ _II_(решения) для 10-го класса по математике, глава 2

Mathematics_part_ _II_(решения) Решения для 10-го класса по математике, глава 2 Теорема Пифагора представлена ​​здесь с простым пошаговым объяснением. Эти решения для теоремы Пифагора чрезвычайно популярны среди учащихся 10 класса по математике. Решения для теоремы Пифагора пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Mathematics_part_ _II_(solutions) Book of Class 10 Math Chapter 2 предоставляются здесь для вас бесплатно. Вам также понравится отсутствие рекламы в Mathematics_part_ _II_(solutions) Solutions от Meritnation. Все решения Mathematics_part_ _II_(solutions) для класса 10 Math подготовлены экспертами и на 100% точны.

Стр. № 38:

Вопрос 1:

Объясните, какие из следующих троек являются пифагорейскими.
(i) (3, 5, 4)
(ii) (4, 9, 12)
(iii) (5, 12, 13)
(iv) (24, 70, 74)
(v) (10 , 24, 27)
(vi) (11, 60, 61)

Ответ:

(i) В тройке (3, 5, 4)
3 ² = 9, 5 ² = 25 , 4 ² = 16 и 9 + 16 = 25

Квадрат наибольшего числа равен сумме квадратов двух других чисел.

∴ (3, 5, 4) — пифагорейская тройка.

(ii) В тройке (4, 9, 12),
4 ² = 16, 9 ² = 81, 12 ² = 144 и 16 + 81 = 97 ≠ 144 90 003

Площадь наибольшее число не равно сумме квадратов двух других чисел.

∴ (4, 9, 12) не является пифагоровой тройкой.

(iii) В тройке (5, 12, 13),
5 ² = 25, 12 ² = 144, 13 ² = 169 и 25 + 144 = 169

Квадрат наибольшего числа равен сумме квадратов двух других чисел.

∴ (5, 12, 13) — пифагорейская тройка.

(iv) В тройке (24, 70, 74),
24 ² = 576, 70 ² = 4900, 74 ² = 5476 и 576 + 4900 = 54 76

Площадь самой большой число равно сумме квадратов двух других чисел.

∴ (24, 70, 74) — пифагорейская тройка.

(v) В тройке (10, 24, 27),
10 ² = 100, 24 ² = 576, 27 ² = 729 и 100 + 576 = 676 ≠ 729

Квадрат наибольшего числа не равен сумме квадраты двух других числа.

∴ (10, 24, 27) не является пифагоровой тройкой.

(vi) В тройке (11, 60, 61),
11 ² = 121, 60 ² = 3600, 61 ² = 3721 и 121 + 3600 = 37 21

Площадь самого большого число равно сумме квадратов двух других чисел.

∴ (11, 60, 61) — пифагорейская тройка.

Страница № 38:

Вопрос 2:

На данном рисунке ∠MNP = 90°, seg NQ ⊥seg MP, MQ = 9, QP = 4, найти NQ.

Ответ:

Мы знаем, что
В прямоугольном треугольнике отрезок, перпендикулярный гипотенузе из противоположной вершины, является средним геометрическим отрезков, на которые делится гипотенуза.

∴ QN2=MQ×QP             =9×4             =36QN=36      =6

Следовательно, NQ = 6.

Страница № 38:

Вопрос 3:

На данном рисунке ∠QPR = 90°, отрезок PM ⊥ отрезок QR и Q–M–R, PM = 10, QM = 8 , найти QR.

Ответ:

Мы знаем, что
В прямоугольном треугольнике отрезок, перпендикулярный гипотенузе из противоположной вершины, является средним геометрическим отрезков, на которые делится гипотенуза.

Здесь, сегмент PM ⊥ сегмент QR

∴ PM2=QM×MR⇒102=8×MR⇒100=8×MR⇒MR=1008⇒MR=252Now,QR=QM+MR      =8+252      =16+ 252      =412      =20,5

Следовательно, QR = 20,5

Страница № 39:

Вопрос 4:

На приведенном рисунке. Найдите RP и PS, используя информацию, приведенную в ∆PSR.

Ответ:

In ∆PSR,
∠S = 90 ^∘ , ∠P = 30 ^∘ , ∴ ∠R = 60 ^∘

К 30 ^∘ − 60 ^∘ − 90 ^∘ теорема,

RS=12×RP⇒6=12×RP⇒6×2=RP⇒RP=12           …1PS=32×RP      =32×12      =63           …2

90 002 Следовательно, RP = 12 и PS = 63,

Страница № 39:

Вопрос 5:

Чтобы найти AB и BC с помощью информации, представленной на рисунке, выполните следующие действия.

AB = BC ……….           

∴∠BAC=          ∴AB=BC=         ×AC                               =          ×22                    =         

Ответ:

В ∆ABC,
∠B = 90 ^∘ , AC = 8, AB = BC, ∴ ∠A = ∠C = 45 ^∘

By 45 ^∘ − 45 ^∘ − 90 ^∘ теорема,

AB=BC=12×AC  =2

Следовательно, AB = 2 и BC = 2.

Следовательно, завершенный активность

AB = BC ……….    данные    

∴∠BAC=    45°   ∴AB=BC=   12   ×AC                              =   12   ×8                    =   12   ×22                    =   2   

Страница № 39:

Вопрос 6:

Найдите сторону и периметр квадрата, диагональ которого равна 10 см.

Ответ:

Дано, что ABCD — квадрат.

∴ AB = BC = CD = DA = a (скажем)

Согласно теореме Пифагора, в ∆ABD

AB2+AD2=BD2⇒a2+a2=102⇒2a2=100⇒a2=50 ⇒а =50⇒a=52 см

Следовательно, сторона квадрата равна 52 см.

Итак,
Периметр квадрата = 4×сторона
                                 = 4×a 52
                                  = 202 см

Следовательно, периметр квадрата равен 202 см.

Страница № 39:

Вопрос 7:

На данном рисунке ∠DFE = 90°, FG ⊥ ED, Если GD = 8, FG = 12, найти (1) EG (2) FD и (3) EF

Ответ:

Мы знаем, что
В прямоугольном треугольнике отрезок, перпендикулярный гипотенузе из противоположной вершины, является средним геометрическим отрезков, на которые делится гипотенуза.

Здесь сегмент GF ⊥ сегмент ED

∴ GF2=EG×GD⇒122=EG×8⇒144=EG×8⇒EG=1448⇒EG=18

Отсюда EG = 18.

Теперь
Согласно теореме Пифагора, в ∆DGF

DG2+GF2=FD2⇒82+122=FD2⇒64+144=FD2⇒FD2=208⇒FD=41 3

In ∆EGF

EG2+GF2=EF2⇒182+122=EF2⇒324+144=EF2⇒EF2=468⇒EF=613

Следовательно, FD = 413 и EF = 613.

Страница № 39: 90 005

Вопрос 8:

Найдите диагональ прямоугольника, длина которого 35 см, а ширина 12 см.

Ответ:

Согласно теореме Пифагора, в ∆ABC

AB2+BC2=AC2⇒352+122=AC2⇒1225+144=AC2⇒AC2=1369⇒AC=37 см

Следовательно, длина диагонали равна 37 см.

Страница № 39:

Вопрос 9:

На данном рисунке M является серединой QR. ∠PRQ = 90°. Докажите, что PQ ² = 4PM ² – 3PR ²

Ответ:

Согласно теореме Пифагора,

In ∆PRM

PR2+RM2=PM2⇒RM2=PM2-PR2        … 1

In ∆PRQ

PR2+RQ2=PQ2⇒PQ2=PR2+RM+MQ2⇒PQ2=PR2+RM+RM2⇒PQ2=PR2+2RM2⇒PQ2=PR2+4RM2⇒PQ2=PR2+4PM2-PR2         из 1⇒PQ2=PR2+4PM2-4PR2⇒PQ2=4PM2-3PR2

Следовательно, PQ ² = 16:00 ² – 3PR ² .

Страница № 39:

Вопрос 10:

Стены двух зданий по обеим сторонам улицы параллельны друг другу. Лестница длиной 5,8 м поставлена ​​на улице так, что ее вершина едва достает до окна здания на высоте 4 м. При переворачивании лестницы на другую сторону улицы ее вершина касается окна другого здания на высоте 4,2 м. Найдите ширину улицы.

Ответ:

Пусть длина лестницы 5,8 м.

Согласно теореме Пифагора, в ∆EAB

EA2+AB2=EB2⇒4,22+AB2=5,82⇒17,64+AB2=33,64⇒AB2=33,64-17,64⇒AB2=16⇒AB=4 м          …1

В ∆DCB

DC2+CB2=DB2⇒42+CB2=5,82⇒16+CB2=33,64⇒CB2=33,64-16⇒CB2=17,64⇒CB=4,2 м          …2

Из (1) и (2) ), получаем

AB+BC=4+4,2 м              =8,2 м

Следовательно, ширина улицы 8,2 м.

Страница № 43:

Вопрос 1:

В ∆PQR точка S является средней точкой стороны QR. Если PQ = 11, PR = 17, PS = 13, найти QR.

Ответ:

 

В ∆PQR точка S является серединой стороны QR.

QS=SR=12QR

PQ2+PR2=2PS2+2QS2     по теореме Аполлония ⇒ 112+172=2132+2QS2⇒121+289=2169+2QS2⇒410=338+2QS2⇒2 QS2=410-338⇒2QS2= 72⇒QS2=36⇒QS=6∴ QR=2×QS           =2×6           =12

Следовательно, QR = 12.

Страница № 43:

Вопрос 2:

В ∆ABC AB = 10, AC = 7, BC = 9, затем найдите длину медианы, проведенной из точки C в сторону AB АБ.

AD = BD = 12AB = 5

CA2+CB2 = 2DC2+2AD2 по Apollonius Theoroemœ 72+92 = 2DC2+252,49+81 = 2DC2+225,130 = 2DC2+50,2DC2 = 130-50 минут. 2DC2=80⇒DC2=40⇒DC=210

Следовательно, длина медианы, проведенной из точки C в сторону AB, равна 210.

Страница № 43:

Вопрос 3:

На данном рисунке seg PS является медианой ∆PQR и PT ⊥ QR. Докажите, что

(1) PR2=PS2+QR×ST+QR22

(2) PQ2=PS2-QR×ST+QR22

Ответ:

Согласно теореме Пифагора, в ∆PTQ

PQ2= PT2+QT2          …1

In ∆PTS

PS2=PT2+TS2          …2

In ∆PTR

PR2=PT2+RT2         . ..3 9 0003

В ∆PQR точка S является средней точкой стороны QR.

QS=SR=12QR      …4

PQ2+PR2=2PS2+2QS2     по теореме Аполлония⇒PR2=2PS2+2QS2-PQ2⇒PR2=PS2+PS2+QS2+QS2-PQ2⇒PR2=PS2+PT 2+ TS2+QS2+QR22-PT2+QT2      От 1, 2 и 4⇒PR2=PS2+QR22+PT2+TS2+QS2-PT2-QT2⇒PR2=PS2+QR22+QS2+TS2-QT2⇒PR2=PS2+QR22+ QS2+TS+QTTS-QT⇒PR2=PS2+QR22+QS2+QSTS-QT⇒PR2=PS2+QR22+QS2+QS×TS-QS×QT⇒PR2=PS2+QR22+QS×TS+QS2-QS× QT⇒PR2=PS2+QR22+QS×TS+QSQS-QT⇒PR2=PS2+QR22+QS×TS+QS×TS⇒PR2=PS2+QR22+2QS×TS⇒PR2=PS2+QR22+QR×TS

Следовательно, PR2=PS2+QR×ST+QR22.

Теперь,

PQ2+PR2=2PS2+2QS2     по теореме Аполлония ⇒PQ2=2PS2+2QS2-PR2⇒PQ2=PS2+PS2+QS2+QS2-PR2⇒PQ2=PS2+PT2+TS2+QS2+QR22- ПТ2 +RT2      От 2, 3 и 4⇒PQ2=PS2+QR22+PT2+TS2+QS2-PT2-RT2⇒PQ2=PS2+QR22+QS2-RT2-TS2⇒PQ2=PS2+QR22+QS2-TS+RTRT-TS ⇒PQ2=PS2+QR22+QS2-TS+RTRS⇒PQ2=PS2+QR22+QS2-TS+RTQS⇒PQ2=PS2+QR22+QS2-QS×TS-QS×RT⇒PQ2=PS2+QR22-QS×TS +QS2-QS×RT⇒PQ2=PS2+QR22-QS×TS-QSRT-QS⇒PQ2=PS2+QR22-QS×TS-QSRT-SR⇒PQ2=PS2+QR22-QS×TS-QS×TS⇒PQ2 =PS2+QR22-2QS×TS⇒PQ2=PS2+QR22-QR×TS

Следовательно, PQ2=PS2-QR×ST+QR22.

Страница № 43:

Вопрос 4:

В ∆ABC точка M является серединой стороны BC.
Если, АВ ² + АС ² = 290 см ² , АМ = 8 см, найти ВС.

Ответ:

В ∆ABC точка M является серединой стороны BC.

BM=MC=12BC

AB2+AC2=2AM2+2BM2     по теореме Аполлония ⇒290=282+2BM2⇒290=264+2BM2⇒290=128+2BM2⇒2BM2=290-128⇒2BM 2=162⇒BM2= 81⇒BM=9∴ BC=2×BM           =2×9=18 см

Следовательно, ВС = 18 см.

Страница № 43:

Вопрос 5:

На данном рисунке точка T находится внутри прямоугольника PQRS. Докажите, что TS ² + TQ ² = TP ² + TR 90 020 2 (Как показано на рисунке, нарисуйте отрезок AB || сторону SR и A-T-B)

Ответ:

Согласно теореме Пифагора, в ∆PAT

PT2=PA2+AT2          …1

In ∆АТС

TS2=AT2+AS2         …2

In ∆QBT

QT2=QB2+BT2         …3

In ∆BRT

TR2=BT2+BR2         . ..4

Сейчас,
TS2+TQ2=AS2+AT2+QB2+BT2         От 2 и 3⇒TS2+TQ2=BR2+AT2+PA2+BT2         ∵ AS=BR и PA=QB⇒TS2+TQ2=BR2+BT2+PA2+AT2⇒TS2+TQ2=TR2+PT2         От 1 и 4⇒TS2+TQ2 =TR2+PT2

Следовательно, TS ² + TQ ² = TP ² + TR ² .

Страница № 43:

Вопрос 1:

Даны некоторые вопросы и варианты ответов на них. Выберите правильную альтернативу.
(1) Что из следующего является пифагорейской тройкой?

(А) (1, 5, 10) (Б) (3, 4, 5) (В) (2, 2, 2) (Г) (5, 5, 2)

(2) В прямоугольном треугольнике, если сумма квадратов сторон, составляющих прямой угол, равна 169, то какова длина гипотенузы?

(А) 15 (Б) 13 (В) 5 (Г) 12

(3) Из дат, приведенных ниже, какая дата составляет пифагорейскую тройку?

(А) 15.08.17 (Б) 16.08.16 (В) 3/5/17 (Г) 4/9/15

(4) Если a, b, c стороны треугольника и a ² + b ² = c ² , назовите тип треугольника.

(A) Тупоугольный треугольник (B) Остроугольный треугольник (C) Прямоугольный треугольник (D) Равносторонний треугольник

(5) Найдите периметр квадрата, если его диагональ равна 102 см.

(A)10 см (B) 402 см (C) 20 см (D) 40 см

(6) Высота на гипотенузе прямоугольного треугольника делит его на две части длиной 4 см и 9 см. Найдите длину высоты.

(A) 9 см (B) 4 см (C) 6 см (D) 26 см

(7) Высота и основание прямоугольного треугольника равны 24 см, а 18 см найдите длину его гипотенузы.

(A) 24 см (B) 30 см (C) 15 см (D) 18 см

(8) В ∆ABC AB = 63 см, AC = 12 см, BC = 6 см. Найдите меру ∠A.

(A) 30° (B) 60° (C) 90° (D) 45°

Ответ:

(1) (A) В тройке (1, 5, 10),
1 ² = 1, 5 ² = 25, 10 ² = 100 и 1 + 25 = 26 ≠ 100

Квадрат наибольшего числа не равен сумме квадратов двух других чисел.

∴ (1, 5, 10) не является пифагорейской тройкой.

(Б) В тройке (3, 4, 5),
3 ² = 9, 4 ² = 16, 5 ² = 25 и 9 + 16 = 25

Квадрат самый большой число равно сумме квадратов двух других чисел.

∴ (3, 4, 5) — пифагорейская тройка.

(C) В тройке (2, 2, 2),
2 ² = 4, 2 ² = 4, 2 ² = 4 и 4 + 4 = 8 ≠ 4

Квадрат из наибольшее число не равно сумме квадратов двух других чисел.

∴ (2, ​​2, 2) не является пифагорейской тройкой.

(D) В тройке (5, 5, 2),
2 ² = 4, 5 ² = 25, 5 ² = 25 и 4 + 25 = 29 ≠ 25

90 002 Площадь наибольшее число не равно сумме квадратов двух других чисел.

∴ (5, 5, 2) не является пифагоровой тройкой.

Следовательно, правильный вариант (B).

(2) Согласно теореме Пифагора,
Сумма квадратов сторон, составляющих прямой угол, равна квадрату третьей стороны.

∴ 169 = квадрат гипотенузы
⇒ Длина гипотенузы = 169
                                             = 13

Следовательно, правильный вариант ( Б).

(3) (А) В тройке 15.08.17,
15 ² = 225, 8 ² = 64, 17 ² = 289 и 225 + 64 = 289 900 03

Площадь г. наибольшее число равно сумме квадратов двух других чисел.

∴ 15.08.17 — пифагорейская тройка.

(Б) В тройке 16.08.16,
16 ² = 256, 8 ² = 64, 16 ² = 256 и 256 + 64 = 320 ≠ 256

Квадрат наибольшего числа не равен сумме квадратов два других числа.

∴ 16.08.16 не является пифагорейской тройкой.

(C) В тройке 05.03.17,
3 ² = 9, 5 ² = 25, 17 ² = 289 и 9 + 25 = 34 ≠ 289

Площадь самого большого число не равно сумме квадратов двух других чисел.

∴ 05.03.17 не является пифагорейской тройкой.

(D) В тройке 09.04.15,
4 ² = 16, 9 ² = 81, 15 ² = 225 и 16 + 81 = 97 ≠ 225 9000 3

Площадь самого большого число не равно сумме квадратов двух других чисел.

∴ 09.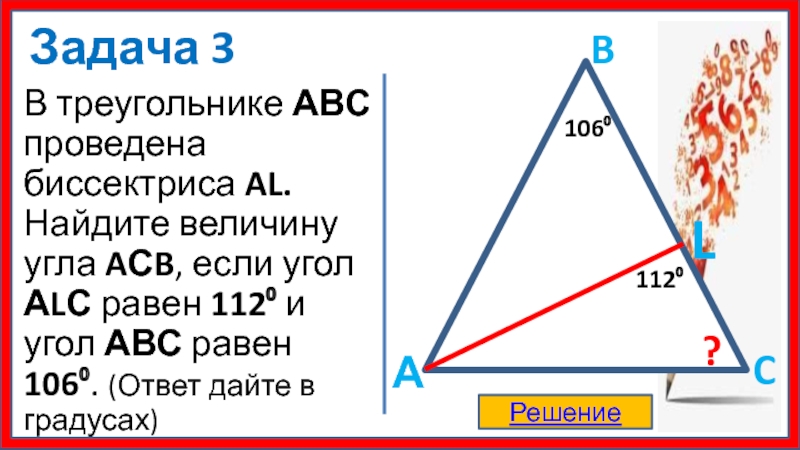 04.15 не является пифагорейской тройкой.

Следовательно, правильный вариант (А).

(4) В треугольнике, если квадрат одной стороны равен сумме квадратов двух оставшихся сторон, то треугольник является прямоугольным.

Следовательно, правильный вариант (C).

(5)

Дан квадрат ABCD.

∴ AB = BC = CD = DA = x (скажем)

Согласно теореме Пифагора, в ∆ABD

AB2+AD2=BD2⇒x2+x2=1022⇒2×2=200⇒x2=1 00⇒ х =100⇒x=10 см

Следовательно, сторона квадрата равна 10 см.

Итак,
Периметр квадрата = 4×сторона
                                 = 4×x
                                  = 4× 10
                                  = 40 см

Следовательно, правильный вариант (D).

(6)

Мы знаем, что
В прямоугольном треугольнике отрезок, перпендикулярный гипотенузе из противоположной вершины, является средним геометрическим отрезков, на которые делится гипотенуза.

∴ AD2=CD×DB             =4×9             =36⇒AD=6 см

Следовательно, правильный вариант (C).

(7) Согласно теореме Пифагора,

Гипотенуза2=Основание2+Высота2                        =182+242                                                   =900∴ Гипотенуза=30

Следовательно, правильный вариант (B).

(8) В ∆ABC, AB = 63 см, AC = 12 см, BC = 6 см.

АВ ² = (63) ² = 108
АС ² = (12) ² = 144
ВС ² = (6 ) ² = 36

108 + 36 = 144

В треугольнике, если квадрат одной стороны равен сумме квадратов двух оставшихся сторон, то треугольник является прямоугольным.

В прямоугольном треугольнике, если одна сторона равна половине гипотенузы, то угол, противолежащий этой стороне, равен 30°.
Здесь ВС составляет половину АС.

Таким образом, мера ∠A равна 30°

Следовательно, правильный вариант (A).

Страница № 44:

Вопрос 2:

Решите следующие примеры.
(1) Найдите высоту равностороннего треугольника со стороной 2 a .
(2) Стороны 7 см, 24 см, 25 см образуют прямоугольный треугольник? Дайте повод.
(3) Найдите длину диагонали прямоугольника со сторонами 11 см и 60 см.
(4) Найдите длину гипотенузы прямоугольного треугольника, если остальные стороны равны 9см и 12 см.
(5) Сторона равнобедренного прямоугольного треугольника равна x. Найдите его гипотенузу.
(6) В ∆PQR; PQ = 8, QR = 5, PR = 3. Является ли ∆PQR прямоугольным треугольником? Если да, то какой угол равен 90°?

Ответ:

(1)
 

Так как треугольник ABC равносторонний, то AD является серединным перпендикуляром к BC.

Теперь, согласно теореме Пифагора,
In ∆ABD

AB2=AD2+BD2⇒2a2=AD2+a2⇒4a2-a2=AD2⇒AD2=3a2⇒AD=3a

Значит, высота равностороннего треугольника равна 3а.

(2) В тройке (7, 24, 25),
7 ² = 49, 24 ² = 576, 25 ² = 625 и 49 + 576 = 625

Площадь самого большого число равно сумме квадратов двух других чисел.

∴ Стороны 7 см, 24 см, 25 см образуют прямоугольный треугольник. по теореме Пифагора АС=61 см

Следовательно, длина диагонали прямоугольника равна 61 см.

(4) В прямоугольном треугольнике

Согласно теореме Пифагора.

Гипотенуза2=Основание2+Высота2                        =92+122                       =81+144                          =225∴ Гипотенуза=15 см

Следовательно, длина гипотенузы равна 15 см.

(5) Дана сторона равнобедренного прямоугольного треугольника, равная х.

Тогда другая сторона треугольника тоже х.

По теореме Пифагора.

Гипотенуза2=x2+x2                        =2×2∴ Гипотенуза=2x

Следовательно, его гипотенуза равна 2x.

(6) В ∆PQR PQ = 8, QR = 5, PR = 3.
 (8) ² = 8,  (5) ² = 5,  (3) + 5 = 8

Квадрат наибольшего числа равен сумме квадратов двух других чисел.

∴ ∆PQR образуют прямоугольный треугольник, где угол R равен 90°.

Страница № 44:

Вопрос 3:

В ∆RST, ∠S = 90°, ∠T = 30°, RT = 12 см, затем найдите RS и ST.

Ответ:

In ∆RST,
∠S = 90 ^∘ , ∠T = 30 ^∘ , ∴ ∠R = 60 ^{∘ 9002 1}

К 30 ^∘ − 60 ^∘ − 90 ^{∘ Теорема} ,

RS=12×RT⇒RS=12×12⇒RS=6 см          …1ST=32×RT⇒ST=32×12⇒ST=63 см           …2

Следовательно, RS = 6 см и СТ = 63 см.

Страница № 44:

Вопрос 4:

Найдите диагональ прямоугольника, длина которого 16 см, а площадь 192 кв.см.

Ответ:

Известно, что площадь прямоугольника равна 192 кв.см.

Площадь=Длина×Ширина⇒192=16×BC⇒BC=19216⇒BC=12 см           …1

Согласно теореме Пифагора,

In ∆ABC

AB2+BC2 =AC2⇒162+122= AC2⇒256+144=AC2⇒AC2=400⇒AC=20 см

Следовательно, длина диагонали прямоугольника равна 20 см.

Страница № 44:

Вопрос 5:

Найдите длину стороны и периметр равностороннего треугольника, высота которого 3 см.

Ответ:

Так как треугольник ABC равносторонний, CD является серединным перпендикуляром треугольника AB.

Теперь по теореме Пифагора
In ∆ACD

AC2=AD2+CD2⇒2a2=a2+32⇒4a2-a2=3⇒3a2=3⇒a2=1⇒a=1 см

Следовательно, длина стороны равностороннего треугольника равна 2 см.

Теперь
Периметр треугольника = (2 + 2 + 2) см
                                      = 6 см

Следовательно, периметр равностороннего треугольника равен 6 см.

Страница № 44:

Вопрос 6:

В сегменте ∆ABC AP является медианой. Если BC = 18, AB ^{2 + AC 2 = 260 Найти AP.}

Ответ:

В ∆ABC точка P является серединой стороны BC.

BP=PC=12BC=9

AB2+AC2=2AP2+2BP2     по теореме Аполлония ⇒ 260=2AP2+292⇒260=2AP2+281⇒260=2AP2+162⇒2AP2=260-162⇒ 2АП2=98⇒AP2=49⇒AP=7

Следовательно, AP = 7.

Страница № 45:

Вопрос 7:

Треугольник ∆ABC равносторонний. Точка P находится на основании BC, так что PC = 13 BC, если AB = 6 см, найдите AP.

Ответ:

∆ABC — равносторонний треугольник.

Дано, что
PC=13BC⇒PC=13×6⇒PC=2 см⇒BP=4 см

Поскольку треугольник ABC равносторонний, OA является серединным перпендикуляром к BC.
∴ OC = 3 см
⇒ OP = OC − PC
           = 3 − 2
           = 1             …(1)

Теперь, согласно теореме Пифагора,
В ∆AOB,

AB2=AO2+OB2⇒62=AO2+32⇒36-9=AO2⇒AO2=2 7⇒АО=33 см          …2

In ∆AOP,

AP2=AO2+OP2⇒AP2=332+12            Из 1 и 2⇒AP2=27+1⇒AP2=28⇒AP=27 см

90 002 Следовательно, АР = 27 см.

Страница № 45:

Вопрос 8:

Из информации, представленной на рисунке, докажите, что PM = PN = 3 × a

Ответ:

Поскольку ∆PQR — равносторонний треугольник, PS — серединный перпендикуляр к QR.
∴ QS = SR = a2       …(1)

Теперь, согласно теореме Пифагора,
In ∆PQS,

PQ2=QS2+PS2⇒a2=a22+PS2⇒PS2=a2-a24⇒PS2=4a2 -a24⇒PS2=3a24⇒PS=3a2          . ..2

В ∆PMS,

PM2=MS2+PS2⇒PM2=a+a22+32a2⇒PM2=3a22+32a2⇒PM2=9a24+3a24 ⇒PM2= 12a24⇒PM2=3a2⇒PM=3a         …3

В ∆PNS,

PN2=NS2+PS2⇒PN2=a+a22+32a2⇒PN2=3a22+32a2⇒PN2=9a24+3a24 ⇒PN2=12a24 ⇒PN2=3a2⇒PN=3a          …4

Из (3) и (4) получаем
PM = PN = 3 × a

Следовательно, PM = PN = 3 × a.

Страница № 45:

Вопрос 9:

Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Ответ:

Диагонали параллелограмма делят друг друга пополам.
, т.е. О – середина АС и BD.

В ∆ABD точка O является серединой стороны BD.

BO=OD=12BD

AB2+AD2=2AO2+2BO2     по теореме Аполлония       …1

В ∆CBD точка O является серединой стороны BD.

BO=OD=12BD

CB2+CD2=2CO2+2BO2     по теореме Аполлония        …2

Складывая (1) и (2), получаем

AB2+AD2+CB2+CD2=2AO2 +2BO2+ 2CO2+2BO2⇒AB2+AD2+CB2+CD2=2AO2+4BO2+2AO2       ∵OC=OA⇒AB2+AD2+CB2+CD2=4AO2+4BO2⇒AB2+AD2+CB2+CD2=2AO2+2BO2⇒AB2+AD2+ CB2+CD2=AC2+BD2⇒AB2+AD2+CB2+CD2=AC2+BD2

Следовательно, сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Страница № 45:

Вопрос 10:

Пранали и Прасад пошли на восток и на север соответственно, из одной и той же точки и с одинаковой скоростью. Через 2 часа расстояние между ними составило 152 км. Найдите их скорость в час.

Ответ:

Известно, что Пранали и Прасад имеют одинаковую скорость.
Таким образом, они преодолевают одинаковое расстояние за 2 часа.
т.е. OA = OB

Пусть скорость будет х км в час.

Согласно теореме Пифагора,
In ∆AOB

AB2=AO2+OB2⇒1522=AO2+OA2⇒450=2AO2⇒AO2=4502⇒AO2=225⇒AO=15 км⇒BO=15 км

Скорость=РасстояниеВремя            =152            =7,5 км на час

Значит, их скорость 7,5 км в час.

Страница № 45:

Вопрос 11:

В ∆ABC ∠BAC = 90°, отрезок BL и отрезок CM являются медианами ∆ABC. Затем докажите, что:
4(BL ² + CM ² ) = 5 BC ²

Ответ:

Согласно теореме Пифагора,
В ∆ABC

AB2+AC2=CB2        . ..1

В ∆ABC точка M является серединой стороны BD.

BM=MA=12AB

AC2+BC2=2CM2+2AM2     по теореме Аполлония       …2

В ∆CBA точка L является серединой стороны AC.

CL=LA=12AC

CB2+AB2=2BL2+2AL2     по теореме Аполлония        …3

Складывая (2) и (3), получаем 2AM2+ 2BL2+2AL2⇒2CM2+2BL2=AC2+BC2+CB2+AB2-2AM2-2AL2⇒2CM2+BL2=AC2+2BC2+AB2-2AM2-2AL2⇒2CM2+BL2=AC2+AB2+2BC2-212AB2-212AC2⇒2CM2+ BL2=BC2+2BC2-12AB2-12AC2            От 1⇒2CM2+BL2=3BC2-12AB2+AC2⇒2CM2+BL2=3BC2-12BC2⇒4CM2+BL2=23BC2-12BC2⇒4CM2+BL2=6BC2-BC2⇒4CM2+BL2= 5BC2

Следовательно, 4(BL ² + CM ² ) = 5 BC ² .

Страница № 45:

Вопрос 12:

Сумма квадратов смежных сторон параллелограмма равна 130 кв.см, а длина одной из его диагоналей равна 14 см. Найдите длину другой диагонали.

Ответ:

Дано, что
AB ² + AD ² = 130 кв. см
BD = 14 см

Диагонали параллелограмма bi секты друг друга.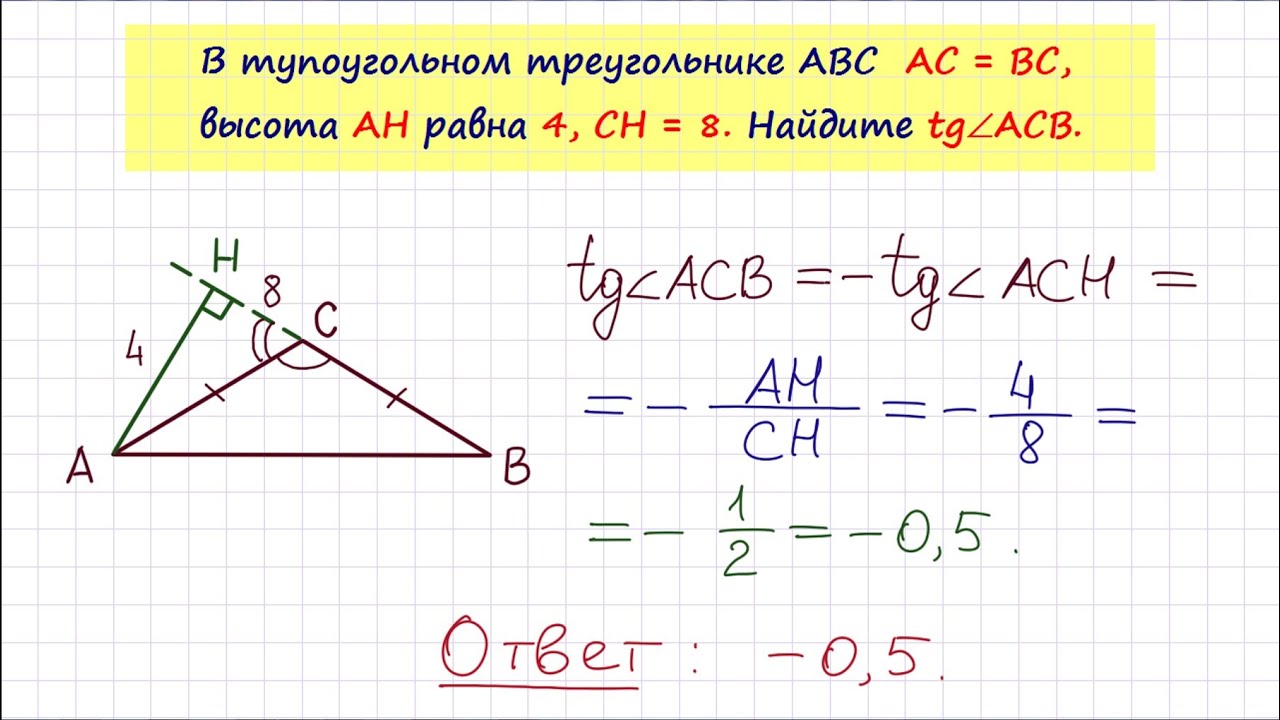
т. е. O — средняя точка AC и BD.

В ∆ABD точка O является серединой стороны BD.

BO=OD=12BD=7 см

AB2+AD2=2AO2+2BO2     по теореме Аполлония ⇒130=2AO2+272⇒130=2AO2+2×49⇒130=2AO2+98⇒2AO2=130-98 ⇒2АО2 =32⇒AO2=16⇒AO=4 см

Sinec, точка O — середина стороны AC.

∴ AC=2AO=8 см

Значит, длина другой диагонали 8 см.

Страница № 45:

Вопрос 13:

В ∆ABC сегмент AD ⊥ сегмент BC DB = 3CD. Докажи, что:
2AB ² = 2AC ² + BC ²

Ответ:

Дано, что
DB = 3 CD

∴ BC = 4 CD        ….(1)

Согласно Теорема Пифагора. От 2 ⇒AC2=AB2 -3CD2+CD2       Дано⇒AC2=AB2-9CD2+CD2⇒AC2=AB2-8CD2⇒AB2=AC2+8CD2⇒AB2=AC2+8BC42          От 1⇒AB2=AC2+BC22⇒2AB2=2AC2+BC2

Следовательно, 2AB ² = 2AC ² + BC ² .

Страница № 45:

Вопрос 14:

В равнобедренном треугольнике длина равных сторон равна 13 см, а основание равно 10 см. Найдите расстояние между вершиной, противоположной основанию, и центроидом.

Ответ:

Площадь треугольника = ss-as-bs-cs=a+b+c2   =13+13+102   =362   =18 смПлощадь треугольника = 1818-1318-1318-10                                  = 2 × 3 ×3×5×5×2×2×2                                 = 60 кв.0003

Центр тяжести находится на расстоянии двух третей расстояния от любой вершины треугольника.

∴ Расстояние между вершиной и центром тяжести=23×12=8 см

Следовательно, расстояние между вершиной, противоположной основанию, и центром тяжести равно 8 см.

Страница № 46:

Вопрос 15:

В трапеции ABCD, отрезок AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, Если AD = 15, BC = 15 и AB = 25. Найдите A(▢ABCD)

Ответ:

 
Согласно теореме Пифагора,
In ∆ABD

AB2=AD2+DB2⇒252=152+BD2⇒625=225+BD2⇒BD2=625-225⇒BD2=400⇒BD=20

Теперь
Площадь треугольника ABD= s с- as-bs-cs=a+b+c2   =20+25+152   =602   =30Площадь треугольника = 3030-2530-2030-15                                   = 30×5×10×15                                 = 150 кв.  единицТакже площадь треугольника = 12×основание×высота⇒150=12×25×DP⇒DP=30025⇒DP=12

Следовательно, высота трапеции = 12.

Теперь
Согласно теореме Пифагора,
In ∆ADP

AD2=AP2+DP2⇒152=122+AP2⇒225=144+AP2⇒AP2=225-144⇒AP2=81⇒AP=9

∴ AP = QB = 9

∴ КД = PQ = 25 − (9 + 9) = 7
Площадь трапеции = 12 × сумма параллельных сторон × высота                                =12×32×12                              =32×6                               =192 кв. единиц

Отсюда , A(▢ABCD) = 192 кв.ед.

Страница № 46:

Вопрос 16:

На данном рисунке ∆PQR представляет собой равносторонний треугольник. Точка S находится на отрезке QR так, что
QS = 13 QR.
Докажите, что: 9 PS ² = 7 PQ ²

Ответ:

Пусть сторона равностороннего треугольника ∆PQR равна x .
PT – высота ∆PQR.

Мы знаем, что в равностороннем треугольнике высота делит основание на две равные части.
∴ QT = TR = 12QR=x2

Дано: QS = 13 QR = x3

∴ ST=QT-QS=x2-x3=x6

Согласно теореме Пифагора,
In ∆PQT

PQ2=QT2+ PT2⇒x2=x22+PT2⇒x2=x24+PT2⇒PT2=x2-x24⇒PT2=3×24⇒PT=3×2

In ∆PST

PS2=ST2+PT2⇒PS2=x62+3×22⇒PS2=x236+3×24⇒PS2=x2+27×236⇒PS2=28×236⇒PS2=7×29⇒9PS2=7PQ2

Следовательно, 9 ПС ² = 7 ПК ² .

Страница № 46:

Вопрос 17:

Seg PM является медианой ∆PQR. Если PQ = 40, PR = 42 и PM = 29, найдите QR.

Ответ:

В ∆PQR точка M является серединой стороны QR.

QM=MR=12QR

PQ2+PR2=2PM2+2QM2     по теореме Аполлония ⇒ 402+422=2292+2QM2⇒1600+1764=1682+2QM2⇒3364-1682=2QM2 ⇒1682=2QM2⇒QM2=841⇒ КМ=29⇒QR=2×29⇒QR=58

Следовательно, QR = 58.

Страница № 46:

Вопрос 18:

Сегмент AM является медианой ∆ABC. Если AB = 22, AC = 34, BC = 24, найдите AM

Ответ:

В ∆ABC точка M является серединой стороны BC.

BM=MC=12BC=12

AB2+AC2=2AM2+2BM2     по теореме Аполлония ⇒ 222+342=2AM2+2122⇒484+1156=2AM2+288⇒1640-288=2AM2⇒13 52=2AM2⇒AM2= 676⇒AM=26

Следовательно, AM = 26.

Математика 9-го класса sa 2 Вопросник 2023

25 апреля 2023 г. 25 апреля 2023 г. по om

Математика 9-го класса sa 2 Вопросник 2023 / AP 9-й класс математики sa 2 Экзамен с итоговой оценкой Ответ на вопросник 2023 Pdf

ПРИСОЕДИНЯЙСЯ

Математика 9-го класса sa 2 Вопросник 2023: ap board был проведен экзамен в классе на основе Суммативное оценивание 2 Экзамен по математике для 9-го класса sa 2 Лист с вопросами 2023 PDF

Содержание

AP 9-й класс sa 2 Суммативное оценивание экзамена Контрольный лист с ответами на вопросы 2023 Pdf

Класс: IX]
Инструкции:
1.
2.
3.
4.
5.
ИТОГОВАЯ ОЦЕНКА-III-2023
МАТЕМАТИКА – Бумага – II
(Английский Средний)
P АРТ-А и Б
( Максимум баллов: 40)
Примечание:
баллов: 30]
42
При продолжительности 2 часа. 45 мин. Первые 15 минут
отведены исключительно на чтение и понимание вопросника
1. Ответьте на все вопросы.
2. Каждый вопрос оценивается в 1 балл.
4×1-4
1. Внутренние углы треугольника равны (x-10p. (3x+10y). (3. Найдите углы
2. Запишите любую точку, лежащую на 07 (положительная ось Y), и любую точку, лежащую на t
(отрицательная ось X)
Примечание:
Вопросник состоит из трех разделов I, II, III.
Все вопросы являются обязательными.
3. Напишите все пары вертикально противоположных ангелов по схеме.

Общего выбора нет. Однако существует внутренний выбор
вопросов в разделе III.
Части A и B следует задавать только в начале экзамена.
[Время: 2-00 часов.
4. На данном рисунке ‘U – центр окружности.
AB — это аккорд. В AOAB покажите, что
Zoab-Loba
10.
Примечание:
42
Часть A

9-й класс Maths SA 2 Вопросной документ 2023

Раздел 1
1. Ответьте на все вопросы.
2. Каждый вопрос оценивается в 2 балла.
5×2=10
5. Для несгруппированных данных 10, 15, 20, 25, 15 медиана и мода равны. Найдите
x, а также среднее значение для приведенных выше данных.
6. На приведенном рисунке 4LEA. BE LED и BD LCD
Найдите площадь пятиугольника ABCDE
7. Прочитайте утверждение. Посмотрите на диаграмму, затем напишите «Дано» и R.T.P.
Утверждение: равные хорды окружности образуют равные углы в центре.
8. Выбрав наугад натуральное число до 100, найдите вероятность того, что число
будет идеальным кубом.
9. Веса 40 учеников в классе приведены в таблице.
Вес в кг)
Кол-во учащихся (5)
Найдите средний вес 40 учащихся
Секция – II
30
847
10
Вес в кг (x)
Кол-во студентов (
50
25
35
Раздел-III
[Время: 2-45 часов.
14
11. На данном рисунке AB CD. Найдите значения
x и y
65
1. Ответить на все вопросы
2. Ответить на любой из внутренних вариантов каждого вопроса
3. Каждый вопрос приносит 4 балла
34
40
10
[Перевернуть
В на данном рисунке B CD EF на равных расстояниях и AF является трансвегальным
GH перпендикулярно IAB-4,5 см, GH-4 см и FB-8см найдите
область
AGDE
(OR)
Нанесите на график точки A (2.2) B (6,2) C (8,5) и D (4.5). Соедините все
точек, чтобы получился параллелограмм. Найдите его площадь
75
38
(ИЛИ)
Ниже приведены веса посылок в транспортной конторе. Если средний вес частоты
, распределение в 85 кг, найдите значение Y’, а также медиану для данных
[Продолжение на 3-й странице…
90
45
T
6
110
4×4-16
47 900 09 120

ТД 9th Class maths sa 2 Вопросник 2023

12. PQRS и ABRS — параллеграммы, а
X — точка сбоку —
Покажите, что &AAS w
(OR)
В соседнем круге AB — это n хорда с центром O.
CD — диаметр, перпендикулярный AB.
Показать этот AD-BD.
13. Построить описанную окружность треугольника ABC, где AB-5 см, BC 28-75 и
-7 см. Напишите этапы строительства.
(OR)
Построить AABC с учетом BC-5см, AB+AC-8 см и LABC-60° и
также напишите этапы строительства.
Class: IX]
Q. No 1
Баллы
Итого

ОБЩАЯ ОЦЕНКА-III-2023 МАТЕМАТИКА – Бумага – II 9-я математика

(английский средний)
ЧАСТЬ-B
(Макс. Оценка: 10)
AS -1
10
Имя студента:
ar PORS
Инструкции:
1. Каждый Вопрос имеет оценку.
2. Каждый вопрос имеет 4 варианта ответа. Выберите правильный ответ в данной скобке
.
3. За переписывание ответов баллы не начисляются.
14. На данном рисунке АС-5,4 см, BD-5,8 см и
AD-84 см, ВС =
А) 2,6 см
15. На данном рисунке m и p — секущей.
Ifx:y= 3: 7
A) 126, 54°
C) 54,126
42 A
[Время: % час.
AS-11
AS-III AS-IV AS-V
A)
ABCD
B) 2,8 см C) 3,0 см
B) 120,60
D) 60°, 20⁰
A)-14,-16, -18
C)-13,-15, -17
L
10
B) (4,5)
16. Точка на расстоянии 4 ед. от оси x и 5 ед. от оси y
равна
A) (5,4)
[Перевернуть
C) (5,6)
2
Номер рулона:…………………….…..
42 A
17. Среднее из трех последовательных четных числа 16. Числа (3)
B) 13, 15, 17
D) 14, 16, 18
C)
D) 3,2 см
10. Ниже приведены длины хорд окружности. Среди этих
одна хорда проходит через центр. Определите длину хорды
, проходящей через центр.
A) 7 см
B) 7,5 см C) 8 см
9
100
D) 6,5 см
19. Вероятность случайного выбора двузначного числа, у которого
единицы и десятки имеют одинаковые цифры
D) (4,6)
23. Ifx>
A)Q,
B) Q₂
C)Q,
D)
[Turn Ov
1
100
B) 10
20. Если дополнительный угол равен дополнительному
этого дополнительного угла, то угол равен
A) 135
B) 45
C) 90
21. Из приведенного рисунка площадь AABC равна
A) AC-BC
B) AB=BC\
C) ABAC
D)*ABBC AC
22. Что из следующего не является вероятностью какого-либо события
A)0
C)-0,2
D) 0,75
D) 60⁰
D)Q,
( )
(

Как скачать ключи ответов 2023 9 класс математика ап

24. На данном рисунке AC диаметр
O центр полукруга
B точка на полуокружности
Если ZC 48°
A) 48⁰
, затем ЗОБА-
B) 42⁰
C) 90⁰
D) 32⁰
25. Какое из следующих событий является примером невозможного события
i) Выпадение 7 при броске игральной кости
ii) Выпадение орла при подбрасывании монеты
iii) Выбор пики из колоды игральных карт
iv) Выпадение четного простого числа меньше 2
A ) Оба (i) и (ii)
C) Оба (i) и (iv)
28. На данной фигуре
1
B) = bh
2
27. Площадь параллелограмма, основание которого равно b. ед., высота ‘h’
ед. (в кв. ед.)
A) bh
3
LCDE-112°, тогда ZAFE =
(Примечание: во вписанном четырехугольнике
противоположных углов являются
дополнительными). :
A) 112°

9-й класс по математике sa 2 Контрольный лист 2023 PDF

AP sa 2 9-й экзаменационный лист по математике 2023 ключи ответов PDF

26. В каком из следующих случаев ордината в два раза больше абсциссы ( )
A) (-2),4) B) (4,2)
C) (4,-2)
D) (2,4)

B) 68°
B) Оба (i) и (iii)
D) Оба (ii) и (iii)
A) ==
4
30. Из приведенного рисунка ZDOC=
B) 60⁰
D) 180°
0
C) xdxd, D) xh(a+b)
C) 78°

Щелкните здесь 9th maths sa 2 Вопросник 2023 PDF

32. В данном круге «О» является центром.
LABC+ZAOC= 2 правых ангела.
Тогда ЗАОД=
A) 120⁰
C) 90⁰
D) I
48
42 A
29. В экзитполе на выборах в собрание победа человека
50%. Тогда вероятность его проигрыша равна
A) 25%
B) 75%
C) 100%
D) 168°