Задача 12 ЕГЭ математика база



Задача 12 ЕГЭ математика база

MATHM >> ЕГЭ >> ЕГЭ базовый >>

Задача 12

ЗАДАЧА 12
сортировка
по сложности

Сложность 1
Сложность 2
Сложность 3

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене, более сложные встретятся если «не повезло».

Сложность 1 (легкие задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

    13. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

    24. посмотреть ответ

    25. посмотреть ответ

    26. посмотреть ответ

    27. посмотреть ответ

    28. посмотреть ответ

    29. посмотреть ответ

    30. посмотреть ответ

    31. посмотреть ответ

    32. посмотреть ответ

    33. посмотреть ответ

    34. посмотреть ответ

    35. посмотреть ответ

    36. посмотреть ответ

    37. посмотреть ответ

    38. посмотреть ответ

    39. посмотреть ответ

    40. посмотреть ответ

Сложность 2 (немного более сложные задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

    13. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

Сложность 3 (более сложные задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

    13. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

Задание 3 ЕГЭ по математике (профиль) часть 1

Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на прямоугольный треугольник, использование тригонометрических функций. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.

 

 

 

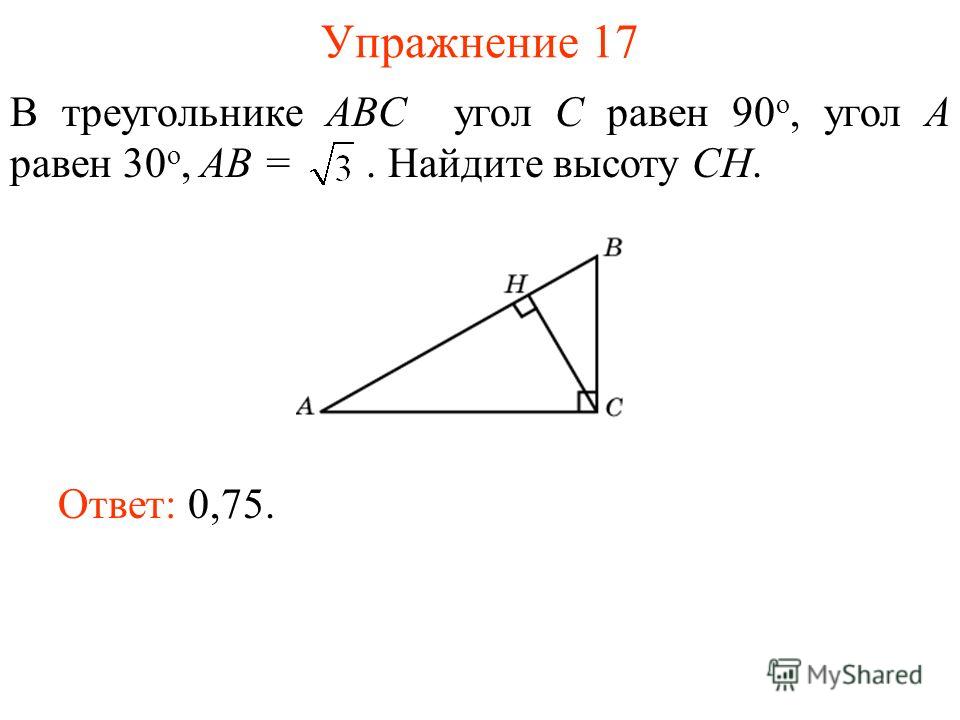
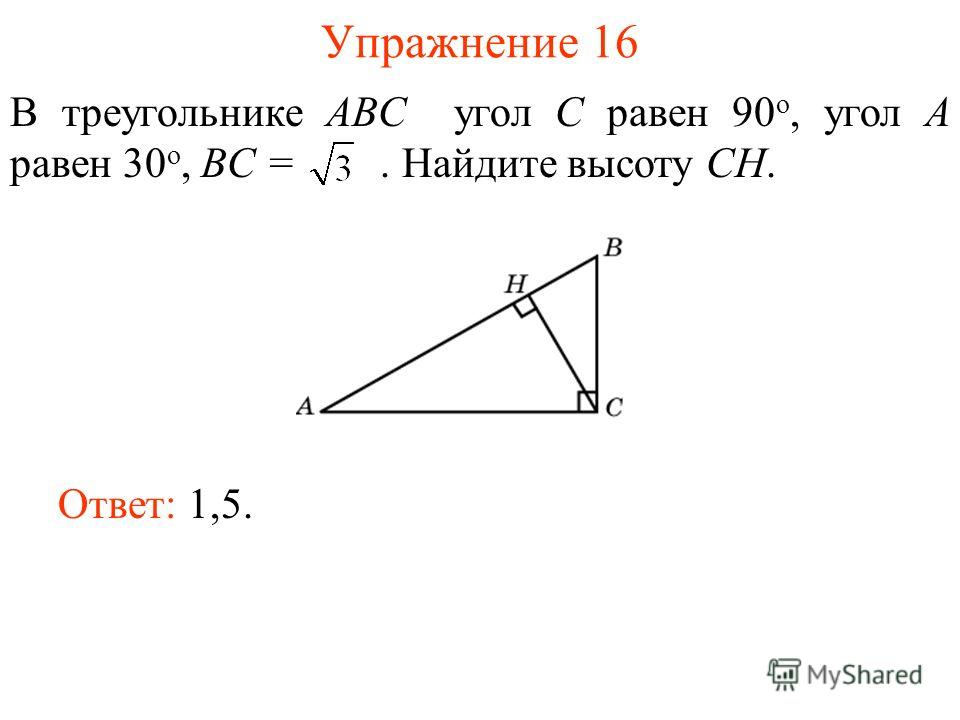
27238. В треугольнике ABC угол C равен 90º, AC = 4,8, . Найдите AB.

 

 

27244. В треугольнике ABC угол C равен 90º, BC = 4, sin A = 0,5. Найдите AB.

 

 

27242. В треугольнике ABC угол C равен 90º, AC = 4,  Найдите AB.

 

 

27240. В треугольнике ABC угол C равен 90º, AC = 4, cos A = 0,5. Найдите AB.

 

 

27249. В треугольнике ABC угол C равен 90º, BC = 4, tg A = 0,5. Найдите AC.

 

 

27247. В треугольнике ABC угол C равен 90º, BC = 2,   Найдите AC.

 

 

27243. В треугольнике ABC угол C равен 90º, AC = 8, tg A = 0,5. Найдите BC.

 

 

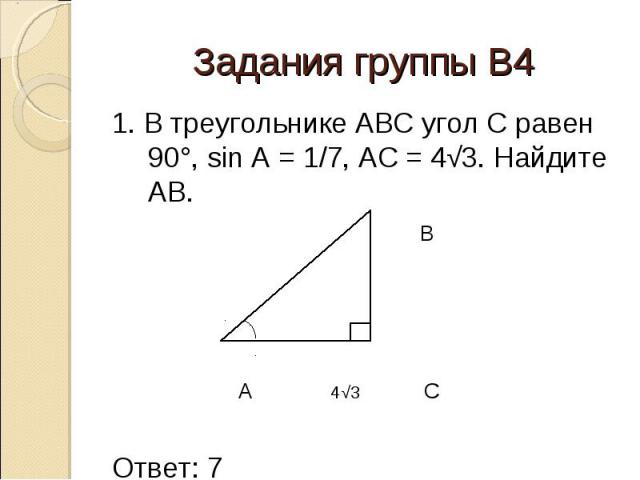
27250. В треугольнике ABC угол C равен 90º, AC = 24, BC = 7. Найдите sin A.

 

 

27268. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, Найдите AH.

 

 

27269. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, sin A = 0,5. Найдите BH.

 

 

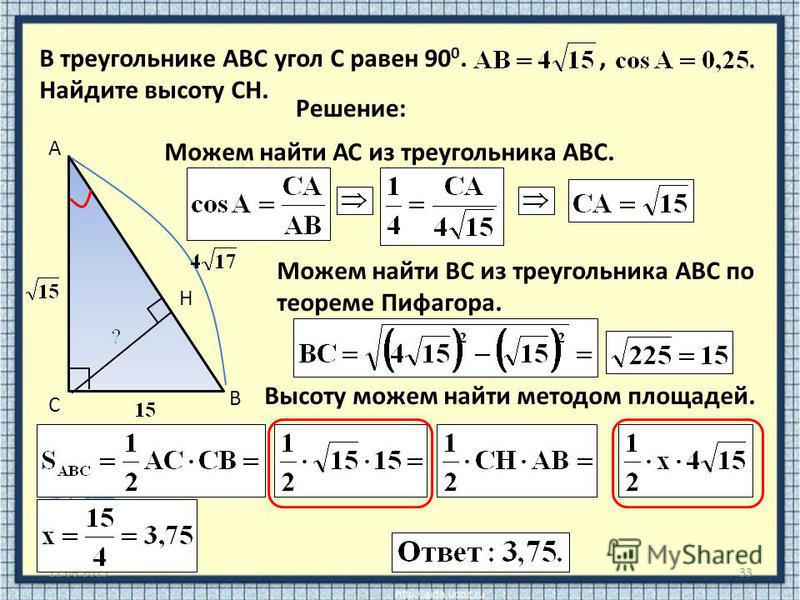
27270. В треугольнике ABC угол C равен 90º, BC = 5, . Найдите высоту CH.

 

 

27277. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, Найдите BH.

 

 

27336. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, BH = 4. Найдите sin A.

 

 

27339. В треугольнике ABC угол C равен 90º, высота CH равна 20, BC = 25. Найдите sin A.

 

 

27342. В треугольнике ABC угол C равен 90º, высота CH равна 24, BH = 7. Найдите sin A.

 

 

27431. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, sin A = 2/3.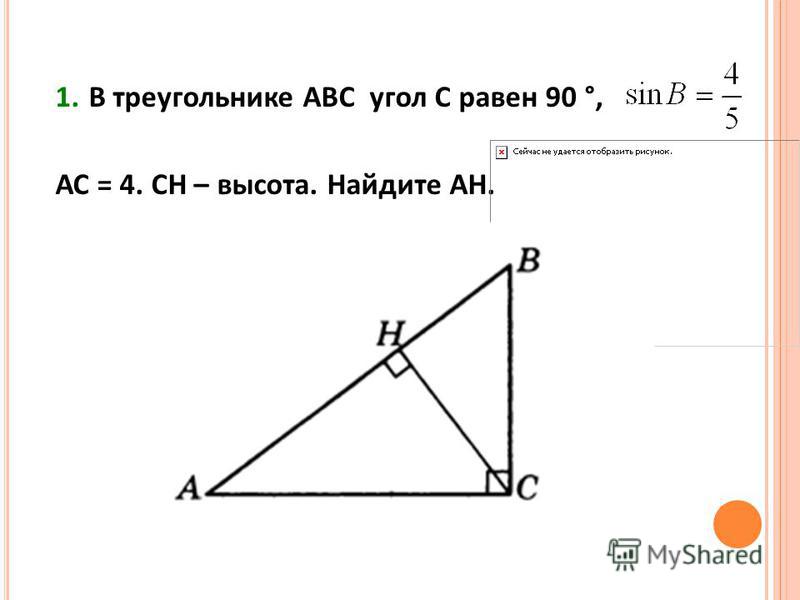 Найдите AB.

 

 

27271. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, . Найдите AH.

 

 

27272. В треугольнике ABC угол C равен 90º, CH — высота, BC = 5, cos A = 7/25. Найдите BH.

 

 

27273. В треугольнике ABC угол C равен 90º, BC = 8, cos A = 0,5. Найдите высоту CH.

 

 

27280. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, cos A =1/6. Найдите BH.

 

 

27337. В треугольнике ABC угол C равен 90º, CH — высота, BC = 25, BH = 20. Найдите cos A.

 

 

27340. В треугольнике ABC угол C равен 90º, высота CH равна 4, BC = 8. Найдите cos A.

 

 

27343. В треугольнике ABC угол C равен 90º, высота CH равна 7, BH = 24. Найдите cos A.

 

 

27432. В треугольнике ABC угол C равен 90º, CH — высота, AH = 12, cos A = 2/3. Найдите AB.

 

 

27265. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A =1/5. Найдите AH.

 

 

27266. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A = 5. Найдите BH.

 

 

27267. В треугольнике ABC угол C равен 90º, AB = 13, tg A = 1/5. Найдите высоту CH.

 

 

27341. В треугольнике ABC угол C равен 90º, высота CH равна 4, Найдите tg A.

 

 

27344. В треугольнике ABC угол C равен 90º, высота CH равна 8, BH = 4. Найдите tg A.

 

 

27357. В треугольнике ABC угол C равен 90º, CH — высота, AH = 27, tg A = 2/3. Найдите BH.

 

 

27358. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, tg A = 2/3. Найдите AH.

 

 

27789. В треугольнике ABC угол C равен 90º, угол A равен 30º, Найдите высоту CH.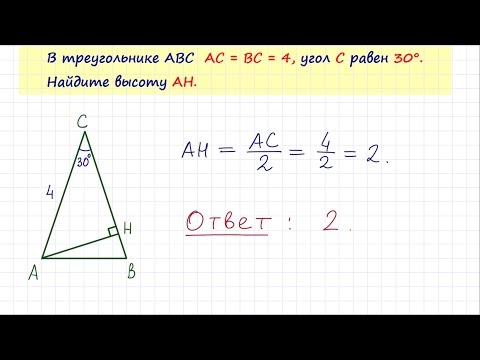

 

 

27790. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 2. Найдите AH.

 

 

27791. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 4. Найдите BH.

 

 

 

 

Понравилось это:

Нравится Загрузка…

30-60-90 Треугольник — Правила, Формула, Теорема, Стороны, Примеры

Треугольник 30-60-90

является особым прямоугольным треугольником, так как углы треугольника относятся как 1:2:3 . Существуют различные типы треугольников, такие как тупоугольные, равнобедренные, остроугольные, равносторонние и так далее. Но только несколько типов треугольников считаются особыми треугольниками. Эти треугольники особенные, поскольку их стороны и углы постоянны и предсказуемы. Их свойства можно использовать для решения различных задач геометрии или тригонометрии. А 30-60-90-треугольник — произносится как «тридцать шестьдесят девяносто» — действительно является одним из таких очень особых типов треугольников.

В этом уроке мы рассмотрим концепцию треугольника 30-60-90 и узнаем все о нем, включая его формулу, определение, стороны, площадь и правила, применимые к этому треугольнику.

1. Что такое треугольник 0-60-90?
2. 30-60-90 Стороны треугольника
3. 30-60-90-Теорема о треугольнике
4. 30-60-90 Треугольная защита
5. 30-60-90 Правило треугольника
6. Площадь треугольника 30-60-90
7. Часто задаваемые вопросы по треугольнику 30-60-90

Что такое треугольник 30-60-90?

Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Здесь под прямоугольным треугольником понимается любой треугольник, содержащий 9угол 0°. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°. Вот несколько вариантов треугольника 30-60-90. Треугольники ABC и PQK составляют 30-60-90 треугольников.

Здесь в треугольнике ABC ∠ C = 30°, ∠ A = 60° и ∠ B = 90°, а в треугольнике PQK ∠ °4, P = ∠ К = 60° и ∠ Q = 90°

30-60-90 Стороны треугольника

Треугольник 30-60-90 является особым треугольником, поскольку длины его сторон всегда находятся в постоянном соотношении друг с другом.

В приведенном ниже треугольнике ABC 30-60-90 ∠ C = 30°, ∠ A = 60° и ∠ B = 90°. Мы можем понять отношение между каждой из сторон из следующих определений:

  • Сторона, противоположная углу 30°, AB = y, всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике
  • Сторона, противоположная углу 60°, BC = y × √ 3 = y √ 3 будет средней длиной, потому что 60° — средний угол в градусах в этом треугольнике
  • На стороне, противоположной углу 90°, гипотенуза AC = 2y будет наибольшей стороной, поскольку 90° является наибольшим углом.

Стороны треугольника 30-60-90 всегда находятся в соотношении 1:√3:2. Это также известно как формула треугольника 30-60-90 для сторон y: y√3: 2y. Давайте узнаем происхождение этого 9Соотношение 0003 в секции доказательства треугольника 30-60-90. Эту формулу можно проверить с помощью теоремы Пифагора.

Рассмотрим несколько примеров треугольника 30-60-90 градусов со следующими длинами сторон:

Здесь, в треугольнике 30-60-90 DEF

∠ F = 30°, ∠ D = 60° и ∠ Е = 90°

  • Сторона, противоположная углу 30°, DE = y = 2
  • Сторона, противоположная углу 60°, BC = y √ 3 = 2 √ 3
  • Сторона, противоположная углу 90°, гипотенуза AC = 2y = 2 × 2 = 4

Здесь, в треугольнике 30-60-90 PQR

∠ R = 30°, ∠ P = 60° и ∠ Q = 90°

  • Сторона, противоположная углу 30°, AB = y = 7
  • Сторона, противоположная углу 60°, BC = y √ 3 = 7 √ 3
  • Сторона, противоположная углу 90°, гипотенуза AC = 2y = 2 × 7 = 14

30-60-90-Теорема о треугольнике

Формулировка теоремы 30-60-90-треугольника дается как,

Утверждение: Длина гипотенузы в два раза больше длины самой короткой стороны, а длина другой стороны в √3 раза больше длины самой короткой стороны в 30-60-90-треугольник.

Формула 30-60-90-треугольника

Вышеупомянутая теорема может быть математически записана как формула 30-60-90-треугольника как 1:√3:2, которая является отношением трех сторон 30-60- 90-треугольник. Другая формула для этого особого треугольника 1:2:3, которая является отношением трех углов треугольника 30-60-90.

30-60-90-Triangle Proof

Рассмотрим равносторонний треугольник ABC с длиной стороны, равной ‘a’.

Теперь проведите перпендикуляр из вершины A на сторону BC в точке D треугольника ABC. Перпендикуляр в равностороннем треугольнике делит другую сторону пополам.

Треугольники ABD и ADC — это два треугольника 30-60-90. Оба треугольника подобны и прямоугольные треугольники. Следовательно, мы можем применить теорему Пифагора, чтобы найти длину AD.

(AB) 2 = (AD) 2 + (BD) 2

A 2 = (AD) 2 + (A/2) 2

A 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 — (a/2) 2 = (AD) 2

3a 2 /4 = (AD) 2

(a √ 3)/2 = AD

AD = (a √ 3)/2

BD = a/2

AB = a

Эти стороны также подчиняются тому же соотношению a/2 : (a√3) /2: a

Умножить на 2 и разделить на ‘a’,

(2a)/(2a) : (2a√3)/(2a): (2a/a)

Получаем 1:√3: 2. Это теорема треугольника 30-60-90.

30-60-90 Правило треугольника

В треугольнике 30-60-90 меру любой из трех сторон можно узнать, зная меру хотя бы одной стороны треугольника. Это называется 30-60-90 правило треугольника. В приведенной ниже таблице показано, как найти стороны треугольника 30-60-90, используя правило треугольника 30-60-90:

.
Основание равно Дан перпендикуляр Гипотенуза дана

Предполагается, что основание треугольника BC равно ‘a’.

Предполагается, что перпендикуляр DE треугольника равен ‘a’.

Предполагается, что гипотенуза PR треугольника равна ‘a’.

Перпендикуляр треугольника ABC равен AB = (a /√3)

Гипотенуза треугольника ABC равна AC = (2a)/√3

Основание треугольника DEF равно EF = √3a.

Гипотенуза треугольника DEF равна DF = 2a.

Основание треугольника PQR равно QR = (√3a)/2.

Перпендикуляр треугольника PQR равен PQ = (a/2).

Площадь треугольника 30-60-90

Формула для вычисления площади треугольника: = (1/2) × основание × высота. В прямоугольном треугольнике высота есть перпендикуляр треугольника. Таким образом, формула для вычисления площади прямоугольного треугольника = (1/2) × основание × перпендикуляр

Давайте узнаем, как применить эту формулу, чтобы найти площадь треугольника 30-60-90.

Основание BC треугольника принимается равным а, а гипотенуза треугольника ABC равна АС. В предыдущем разделе мы узнали, как найти гипотенузу, зная основание.

Применим изученную формулу.

Таким образом, перпендикуляр треугольника = a/√3

Площадь треугольника = (1/2) × основание × перпендикуляр

Площадь = 1/2 × a × a/√3

Таким образом, площадь треугольника 30-60-90, когда основание (сторона средней длины) обозначена как «а», составляет: Треугольники

  • Равнобедренные треугольники
  • Тупоугольные треугольники
  • Остроугольный треугольник
  • Периметр треугольника

    • Важные примечания о треугольнике 30-60-90

    Вот несколько моментов, которые следует помнить при изучении треугольника 30-60-9. 0 треугольников:

    • Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3, а стороны в соотношении 1:√3:2
    • Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°
    • Все стороны треугольника 30-60-90 можно вычислить, если известна любая сторона. Это называется правилом треугольника 30-60-90.

    Часто задаваемые вопросы по телефону 30-60-90 Треугольник

    Что такое треугольник 30-60-90?

    Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°.

    Каков периметр треугольника 30-60-90?

    Периметр треугольника 30 60 90 с наименьшей стороной, равной а, является суммой всех трех сторон. Две другие стороны равны a√3 и 2a. Периметр треугольника равен а+а√3+2а = 3а+а√3 = а√3(1+√3).

    Есть ли какие-нибудь советы по запоминанию правил треугольника 30-60-90?

    Этот метод можно использовать для запоминания правила треугольника 30-60-90. Можно запомнить его как 1, 3, 2; это может напоминать соотношение сторон, все, что нужно помнить, это то, что средний член равен √3

    . Каковы длины сторон треугольника 30-60-90?

    Стороны треугольника 30-60-90 имеют заданный узор. Сторона, противоположная углу 30°, y всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике. Сторона, противоположная углу 60°, y√3, будет средней длиной, потому что 60° — это средний угол в градусах в этом треугольнике. Сторона, лежащая напротив 9.Угол 0 °, 2y будет наибольшей стороной, потому что 90 ° — самый большой угол.

    Каковы правила для треугольника 45-45-90?

    Треугольник 45-45-90 имеет прямой угол и два угла по 45 градусов. Две стороны треугольника 45-45-90 всегда равны, а гипотенуза треугольника всегда противоположна прямому углу.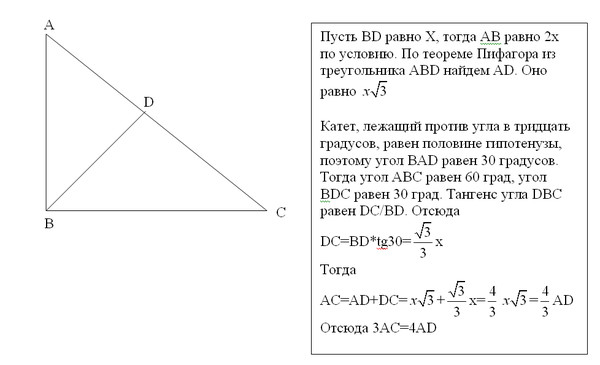

    В чем сходство между треугольниками 30-60-90 и треугольниками 45-45-90?

    Вот некоторые сходства между треугольником 30-60-90 и треугольником 45-45-9.0 треугольник: оба треугольника не остроугольные, оба треугольники прямоугольные, оба треугольники не тупоугольные, квадрат гипотенузы равен сумме квадратов двух других сторон обоих треугольников и сумме внутренних углов треугольника. оба 180°.

    Какая ветвь является длинной в треугольнике 30-60-90?

    Длинный катет треугольника 30-60-90 — это катет, длина которого больше кратчайшего катета и меньше гипотенузы. Длина длинной ноги в √3 раза больше длины самой короткой ноги.

    Как найти угол в прямоугольном треугольнике?

    Треугольники представляют собой трехсторонние замкнутые многоугольники, образованные пересечением трех линий. В повседневной жизни встречается очень часто. Это одна из основных фигур геометрии. У него три стороны, три угла и три вершины. Прямоугольный треугольник – это треугольник, у которого один из углов всегда равен 90°. Для прямоугольных треугольников выведена теорема Пифагора, которая гласит, что квадрат гипотенузы (наибольшая сторона) равен сумме квадратов основания и перпендикуляра.

    Зная длину по крайней мере двух сторон прямоугольного треугольника, мы можем найти значение любого угла прямоугольного треугольника. Для этого мы используем различные тригонометрические функции, такие как синус, косинус, тангенс, котангенс, сек и косек. Они помогают нам связать углы прямоугольного треугольника с его сторонами.

    Свойства

    • Среди трех вершин есть прямоугольная
    • Сторона, противоположная прямоугольной вершине, называется гипотенуза .
    • Длина сторон следует теореме Пифагор, в которой говорится

    Hypotenuse 2 = Основание 2 + Высота 2

    • . .
    • Углы, отличные от прямого угла, являются острыми, так как значение меньше 90 o

    Тригонометрические функции

    ABC – прямоугольный треугольник, в котором ∠B – прямой угол

    • cosθ: Это дает отношение основания к гипотенузе прямоугольного треугольника.

    cosθ = основание / гипотенуза

    • sinθ: Это дает отношение высоты к гипотенузе прямоугольного треугольника.

    sinθ = высота / гипотенуза

    • tanθ: Это отношение высоты к основанию прямоугольного треугольника.

    tanθ = высота / база

    • Cotθ: Это обратный Tanθ
    • Secθ: Это обратное Cosθ
    • COSECθ: IT IS Inverse of Cosθ
    • COSECθ: IT IS Inverse of Cosθ
    • COSECθ: IT IS inperse of Cosθ
    • COSECθ: IT IS IS IS Inverse of Cosθ
    • COSECθ: IT IS IS Inverse of COSO
    • COSECθ: .

      Чтобы найти углы прямоугольного треугольника, мы можем взять обратное тригонометрическое отношение данных сторон треугольника.

      Пример:

      Если sinθ = x, то мы можем записать

      θ = sin -1 х.

      Возвращает угол, для которого значение синуса угла равно x.

      Точно так же существует COS -1 θ, TAN -1 θ, COT -1 θ, SEC -1 θ и COSEC -1 θ

      . И выборки

      θ

      . 1. Дан прямоугольный треугольник, основание которого равно 10 см, а гипотенуза равна 20 см. Найдите значение угла при основании.

      Решение:

      Дано, Основание = 10 см

      Гипотенуза = 20 см

      Пусть значение угла при основании равно θ. Мы можем написать

      cosθ = основание / гипотенуза = 10/20 = 1/2

      θ = cos -1 (1/2) = 60 o

      Таким образом, значение угла при основании равно 60 о .

      Вопрос 2. Найдите величину углов прямоугольного треугольника, если один из острых углов в 2 раза больше другого.

      Решение:

      Поскольку мы знаем, что сумма всех трех углов треугольника равна 180 o .

      Поскольку один из углов равен 90 o , а один из острых углов в два раза больше другого, мы можем рассматривать их как θ и 2θ.

      Таким образом, мы можем написать

      90 O + θ + 2θ = 180 O

      3θ = 180 O — 90 O

      3θ = 909203 O

      3θ = /3 = 30 или

      2θ = 2 × 30 O = 60 O

      Итак, углы 30 O , 60 O , и 90 O .

      Вопрос 3. Найдите значение угла подъема лестницы длиной 5м, если основание лестницы находится на расстоянии 3м от стены.

      Решение:

      Поскольку лестница действует как гипотенуза прямоугольного треугольника, а расстояние до основания равно 3 м, мы можем написать

      Гипотенуза = 5 м

      Основание = 3 м

      Пусть угол возвышения равен θ. Таким образом, мы можем записать

      cosθ = основание / гипотенуза = 3/5

      θ = cos -1 (3/5)

      θ = 53 o

      Таким образом, значение угла места равно 53 или .

      Вопрос 4. Найдите значение гипотенузы, если высота равна 8 м, а угол при основании равен 30 o .

      Решение:

      Учитывая, что угол основания равен 30 o , а высота равна 8 м, мы можем применить функцию синуса, чтобы найти длину гипотенузы.

      sin30 o = высота / гипотенуза

      гипотенуза = высота / sin30 o

      ) = 2 × высота

      Таким образом, гипотенуза = 2 × 8 = 16 м

      Таким образом, длина гипотенузы равна 16 м.