www.abcege.ru — Разбор заданий
-
Задание 1
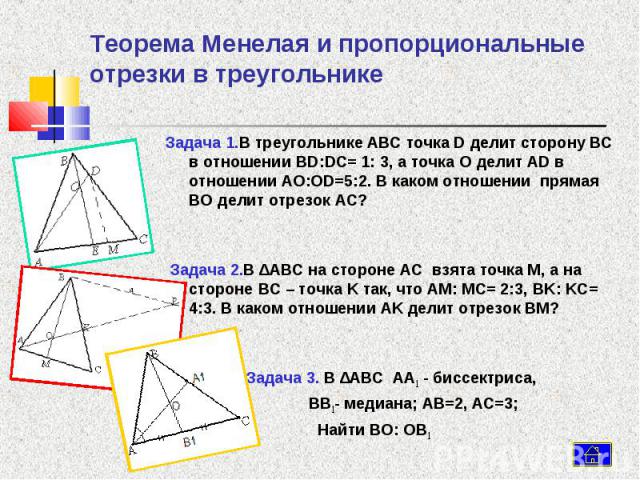
В треугольнике ABC на стороне BC выбрана точка D так, что BD : DC = 1 : 2. Медиана CE пересекает отрезок AD в точке F. Какую часть площади треугольника ABC составляет площадь треугольника AEF?
Разбор задания Свернуть
Пояснение
В условии задачи имеются соотношения на отрезки; чтобы их использовать, необходимо воспользоваться подобием.

Ответ:
-
Задание 2
Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Обе окружности лежат по одну сторону от общей касательной. Третья окружность касается обеих окружностей и их общей касательной. Найдите радиус третьей окружности.
Разбор задания Свернуть
ПОЯСНЕНИЕ
Научимся считать длину общей внешней касательной для двух произвольных окружностей радиуса r и R, чьи центры находятся на расстоянии a.

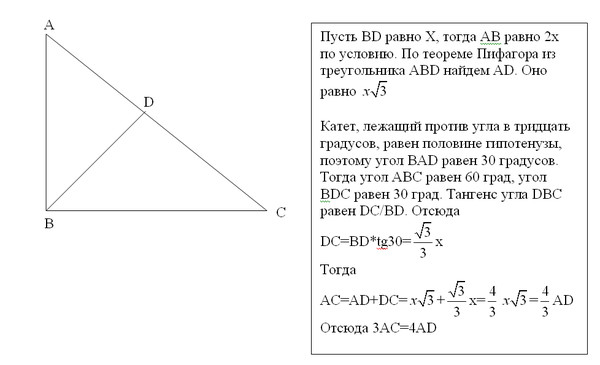
Проведём перпендикуляр из центра первой окружности к прямой , пусть он пересекает в точке Q. Тогда — прямоугольник, значит,
Находим по теореме Пифагора: . Так как , получаем:
Вернёмся к решению задачи. Пусть радиус третьей окружности равен x. Рассмотрим два случая: когда третья окружность находится между первой и второй, и когда это не так. В первом случае (см. рисунок) имеем: AC + CB = AB. При этом, по выведенной ранее формуле,
(расстояние между центрами в случае AC и BC мы сумели вычислить, так как, по условию, окружности касаются между собой, а, значит, расстояние между центрами равно сумме радиусов).
Итак, получаем уравнение:
Во втором случае (см. рисунок) все формулы для длин остаются те же, но теперь CB — AC = AB, что приводит к уравнению:
Ответ:
-
Задание 3
Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4.
 Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Введём обозначения, как показано на рисунке, пусть M, H, N — точки касания. Касательные, проведённые к окружности из одной точки равны: AM = AN, CM = CH, HB = BN. Поэтому:
откуда p = AM.

б) Для определения площади треугольника используем формулу, связывающую её с полупериметром, стороной и радиусом вневписанной окружности, касающейся этой стороны и продолжений двух других сторон треугольника:
Ответ:
-
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Точки A2, B2 и C2 — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A1B2C1A2B
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Шестиугольник разбивается отрезками медиан на 6 треугольников; рассмотрим один из них, например, . Заметим, что (высота к стороне MB общая, а длина стороны в 2 раза меньше по условию). Аналогично для шести оставшихся треугольников. «Большие» треугольники в сумме составляют весь ABC, поэтому утверждение доказано.

б) Обозначим длины сторон BC, AC, AB треугольника ABC через a, b, c.
Докажем, что квадрат медианы AA1 равен Для доказательства на продолжении отрезка за точку отложим отрезок . Получим параллелограмм ACPB со сторонами AC = PB = b и AB = CP = c и диагоналями BC = a и
Теперь выразим стороны шестиугольника через отрезки медиан. Отрезок C1A2 — средняя линия треугольника ABM, значит,
Рассуждая аналогично, мы получим, что стороны шестиугольника втрое меньше медиан треугольника ABC:
Следовательно, сумма квадратов сторон шестиугольника равна
Ответ:
-
Задание 5
Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.
б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Пусть две хорды равны 3x и 3y. По теореме о произведении пересекающихся хорд 2x · x = 2y · y. Отсюда находим, что x = y, значит, эти хорды равны. Аналогично докажем, что третья хорда равна каждой из первых двух.
б) Равные хорды равноудалены от центра окружности, поэтому центр равностороннего треугольника с вершинами в точках попарного пересечения хорд совпадает с центром данной окружности.
 Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.
Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.Через точку T проведём прямую, параллельную AD, через точку P — прямую, параллельную CF, а через точку Q — прямую, параллельную BE. Эти прямые и хорды AD, BE и CF разбивают шестиугольник ABCDEF на 13 одинаковых равносторонних треугольников.
Обозначим PQ = 2a. Тогда
Отсюда находим, что a = 3, значит, PQ = 2a = 6,
Следовательно,
Ответ:
-
Задание 6
В остроугольном треугольнике ABC проведены высоты AP и CQ.

а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и .
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Заметим, что если мы проведём окружность из середины AC с радиусом, равным половине AC, то точки A и C будут лежать на ней (по построению), а также будут лежать точки Q и P (прямой угол, опирающийся на диаметр). В таком случае углы PAC и PQC равны, как опирающиеся на одну дугу.
б) Нам уже известен угол в треугольнике; если мы найдём сторону AC, то сможем воспользоваться формулой Для поиска AC воспользуемся подобием: (обратите внимание на правильный порядок написания вершин).
 Отсюда (первое равенство — определение подобия, второе — определение косинуса угла в прямоугольном треугольнике) Отсюда выражаем длину AC: Тогда радиус R окружности, описанной около треугольника ABC равен
Отсюда (первое равенство — определение подобия, второе — определение косинуса угла в прямоугольном треугольнике) Отсюда выражаем длину AC: Тогда радиус R окружности, описанной около треугольника ABC равенОтвет:
-
Задание 7
Медианы , и треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан и , если известно, что AC = 12.
Разбор задания Свернуть
Пояснение
а) Известно, что медианы треугольника точкой пересечения делятся в отношении 2 : 1, считая от вершины.
 Значит,
Значит,Если медиана равна половине стороны, к которой она проведена, то треугольник прямоугольный с прямым углом, из которого исходит медиана. Доказать это можно, например, построив окружность с центром из середины стороны и радиусом, равным медиане. Тогда на ней окажутся все три вершины треугольника, то есть эта окружность — вписанная, сторона — диаметр, а угол, опирающийся на диаметр — прямой. Доказано.
б) Треугольник прямоугольный с прямым углом B. Поэтому
Аналогично, из прямоугольного треугольника находим:
Сложим полученные равенства:
Ответ: 180.
-
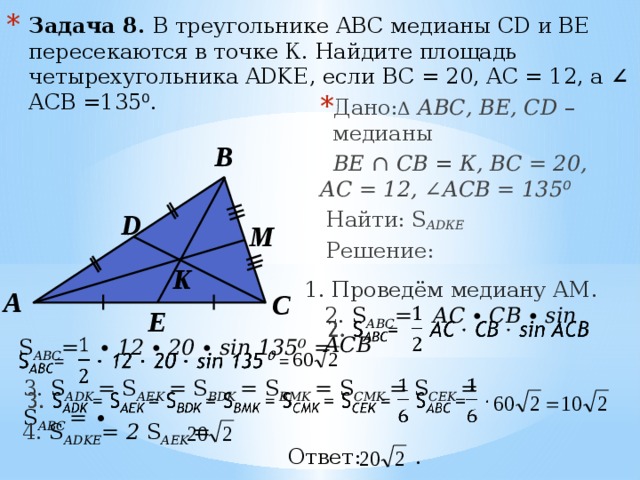
Задание 8
В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 15, BC = 8.
 Окружность радиуса 2,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.
Окружность радиуса 2,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.а) Докажите, что радиус второй окружности меньше, чем длины катета
б) Найдите радиус второй окружности.
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Пусть Q — центр второй окружности, M и N — её точки касания со сторонами AB и AC соответственно, а точка H — проекция точки Q на BC. Имеем: следовательно, Тогда Поэтому что и требовалось доказать.
б) Пусть x — радиус второй окружности.
 Рассмотрим прямоугольный треугольник OHQ:
Рассмотрим прямоугольный треугольник OHQ:По теореме Пифагора откуда:
Условию удовлетворяет только Кстати, отсюда следует, что точки O и H совпадают.
Ответ:
-
Задание 9
Точка О — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку О отмечена точка K так, что
а) Докажите, что четырехугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус окружности, описанной около треугольника АBC равен 12, а
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Пусть тогда где H — проекция О на BC.
 Поэтому Из условия следует, что Тогда (опираются на хорду ОС). Тогда по признаку, связанным со свойством вписанных углов, точки О, В, К, С лежат на одной окружности, ч. т. д.
Поэтому Из условия следует, что Тогда (опираются на хорду ОС). Тогда по признаку, связанным со свойством вписанных углов, точки О, В, К, С лежат на одной окружности, ч. т. д.б) тогда Рассмотрим Из пункта а) тогда так как четырехугольник OBKC вписанный.
Воспользуемся формулой:
тогда
Рассмотрим треугольник KBC:
Ответ:
-
Задание 10
Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.

а) Докажите, что отрезок BK больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 18 и BN = 17.
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Проведём медиану AE к основанию BC, поскольку треугольник ABC — равнобедренный, медиана AE является биссектрисой и высотой. Проведём MK, заметим, что , т. к. он вписанный и опирается на диаметр окружности. Поэтому MK перпендикуляр к ВС. Тогда MK — средняя линия AEС (так как параллельна одной стороне и исходит из середины другой), и тогда КС = EК.
 Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.
Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.б) Пусть Тогда и пусть тогда По свойству секущих имеем:
Подставляя значение для 2y во второе уравнение, получаем квадратное уравнение на искомое x:
Из условия x>17 остаётся только корень x=18.
Ответ:
-
Задание 11
В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD = R.
а) Докажите, что треугольник ABC прямоугольный.
б) Вписанная окружность касается сторон AB и BC в точках E и F.
 Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10.
Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10.Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Пусть O — центр вписанной окружности треугольника ABC.
Центр окружности, вписанной в угол, лежит на его биссектрисе, значит, AO — биссектриса угла BAC. Треугольник AOD прямоугольный и равнобедренный, поэтому . Следовательно,
б) Обозначим BF = x. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки, AE = AD = 2, CF = CD = 10 и BE = BF = x.
 По теореме Пифагора , или . Из этого уравнения находим, что x = 3. Тогда
По теореме Пифагора , или . Из этого уравнения находим, что x = 3. Тогда Следовательно,
Ответ:
-
Задание 12
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что .
б) Найдите BC, если и
Разбор задания Свернуть
Пояснение
а) Заметим, что четырёхугольник можно вписать в окружность (так как ).
 Тогда
Тогда(*)
(как опирающиеся на одну дугу).
С другой стороны, вокруг четырёхугольника тоже можно описать окружность (с центром в середине BC и радиусом, равным половине BC). Тогда имеем, по теореме об углах в окружности, . С другой стороны, по свойству смежных углов, . Совмещая, получаем
(**)
Комбинируя равенство (*) и (**), получаем искомое.
б) Воспользуемся доказанным в предыдущем пункте. Исходя из этого, а также равенства прямых углов, имеем подобие:
(обратите внимание на порядок букв в записи). Записывая соотношение сторон, имеем:
(последнее равенство — согласно определение тангенса угла в прямоугольном треугольнике).
Угол BAC мы знаем, это позволяет вычислить его тангенс и найти ВС:
Ответ: 24.
-
Задание 13
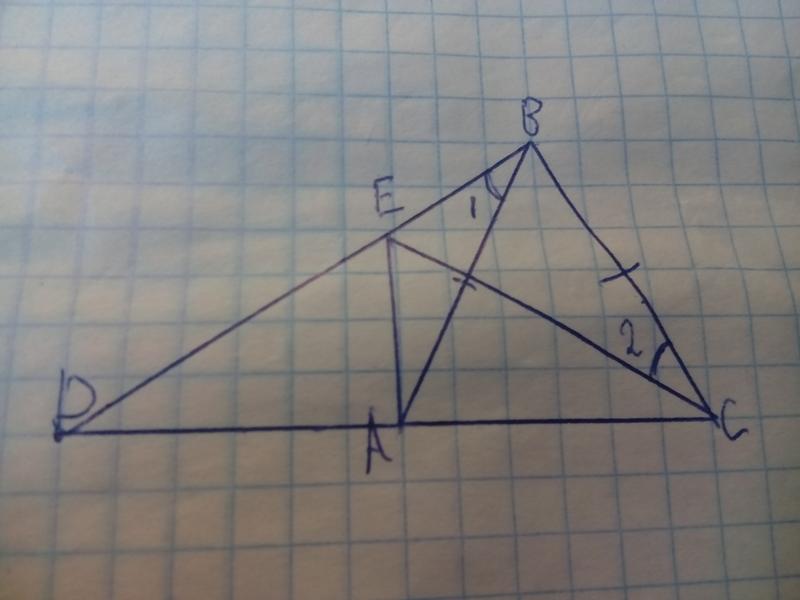
В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.

а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 1, а радиус окружности, описанной около треугольника ABC равен 4.
Разбор задания Свернуть
ПОЯСНЕНИЕ
а) Пусть . Углы BAC и KHB равны, как углы с взаимно перпендикулярными сторонами. Рассмотрим четырёхугольник BKHM , следовательно, четырёхугольник BKHM вписан в окружность. Значит, углы KHB и KBM — вписанные, опирающиеся на одну и ту же дугу, следовательно, они равны.
 Таким образом, . Треугольники ABC и MBK имеют общий угол B и , значит, эти треугольники подобны по двум углам.
Таким образом, . Треугольники ABC и MBK имеют общий угол B и , значит, эти треугольники подобны по двум углам.б) Из прямоугольного треугольника BKH находим, что Для треугольника ABC справедливо равенство Учитывая, что получаем: Стороны BC и BK — сходственные в подобных треугольниках ABC и MBK, следовательно, их коэффициент подобия Найдём отношение площади треугольника MBK к площади четырёхугольника AKMC:
Ответ:
В треугольнике ABC на стороне BC выбрана точка D , так что BD:DC=1:2 . Найти площадь треугольника ABD, если площадь треугольника ABC равна 18см
Последние вопросы
Геометрия
47 минут назад
3. [4 балла] Дана функция у = x² + 4x-5. Не строя графика,
найдите:
а) область определения функции.
b) нули функции.
с) наименьшее значение функции.
[4 балла] Дана функция у = x² + 4x-5. Не строя графика,
найдите:
а) область определения функции.
b) нули функции.
с) наименьшее значение функции.Геометрия
57 минут назад
17.29. Найдите диагональ прямоугольного параллелепипеда ABCD A1 B1 D1 C1 если а = 5 cm, b = 10 cm, c = 12 cmГеометрия
2 часа назад
CH- висота, проведена з вершини прямого кута трикутника FCD (див. рис.). кут F = 60º, FD = 16 см. Знайти довжини вiдрiзкiв FH i HD.Геометрия
2 часа назад
Указати правильне твердження. а) Якщо гіпотенуза і гострий кут одного прямокутного трикутника дорiвнюють гіпотенузі й гострому куту іншого прямокутного трикутника, то такі трикутники не рiвнi б) катет прямокутного трикутника, який лежить проти кута 30°, удвічі більший за гіпотенузу; в) точка, яка лежить на бісектрисi кута, рiввiддав його сторін; г) висоти, проведенi до бічних сторін рівнобедреного трикутника, не рiвні.
Геометрия
3 часа назад
B треугольнике ОАВ проведена медиана ОС. Определите координаты точки С, если А (-1;3) и В (5;4). Геометрия
5 часов назад
правильний трикутник зі стороною √12 см вписаний у коло. знайдіть сторону квадрата, вписаного у це коло.Геометрия
6 часов назад
Геометрия. 9 класс. Помогите, пожалуйста, решить заданиеГеометрия
6 часов назад
Молю решите, хоть одноГеометрия
7 часов назад
Геометрия, найти площадь трапецииГеометрия
8 часов назад
Всем привет, решите задачку по геометрии 🙂Геометрия
8 часов назад
Осталось 25 минут, надеюсь поможетеГеометрия
8 часов назад
Решите пожалуйста геометрию! 10 классГеометрия
8 часов назад
ОЧЕНЬ СРОЧНО УМОЛЯЮ ПОМОГИТЕ 30 МИНУТ ОСТАЛОСЬГеометрия
9 часов назад
помогите пожалуйста, очень надо !!: У прямокутному трикутнику катет дорівнює 0,2 гіпотенузи. Знайдіть гострі кути трикутника.
Знайдіть гострі кути трикутника.Геометрия
9 часов назад
Геометрия, 8 класс
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
биссектрис в треугольнике
Горячая математикаБиссектриса
биссектриса
стороной треугольника называется прямая, перпендикулярная стороне и проходящая через ее середину.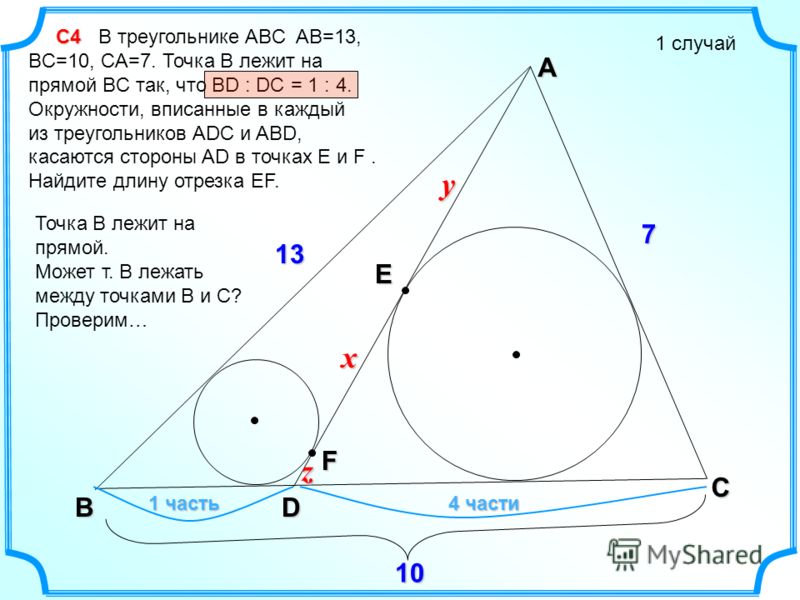
Три перпендикулярные биссектрисы сторон треугольника пересекаются в одной точке, называемой центр окружности . Точка, в которой пересекаются три или более линий, называется точкой параллелизма. Итак, центр описанной окружности — это точка пересечения серединных перпендикуляров треугольника.
Здесь, О является центром окружности Δ Икс Д Z .
Центр описанной окружности равноудален от вершин треугольника. (См. теорему о центре окружности .) То есть Икс О «=» Д О «=» Z О . Окружность, проведенная с центром описанной окружности в качестве центра и радиусом, равным этому расстоянию, проходит через все три вершины и называется описанный круг . Это наименьшая окружность, в которую можно вписать треугольник.
Центр описанной окружности лежит внутри треугольника для остроугольных треугольников, на гипотенузе для прямоугольных треугольников и лежит вне треугольника для тупоугольных треугольников. Центр описанной окружности совпадает с серединой гипотенузы, если это равнобедренный прямоугольный треугольник.
Центр описанной окружности совпадает с серединой гипотенузы, если это равнобедренный прямоугольный треугольник.
Пример 1:
Дома Натхи, Хирена и Джо представляют собой три неколлинеарные точки на координатной плоскости. Если они хотят встретиться в общем месте, так что каждый должен будет пройти одинаковое расстояние от своего дома, как вы определите место встречи?
Поскольку точки, представляющие дома, не лежат на одной прямой, три точки образуют треугольник.
Теперь, если вы рассматриваете центр описанной окружности треугольника, он будет равноудален от вершин. То есть, если в качестве точки встречи выбрать центр описанной окружности треугольника, образованного тремя домами, то каждый из них должен будет пройти одинаковое расстояние от своего дома.
Пример 2:
Найдите значение Икс .
Здесь,
О
точка пересечения трех серединных перпендикуляров сторон
Δ
К
л
М
.
Так, О является центром описанной окружности треугольника.
Центр описанной окружности равноудален от вершин. Затем, О М «=» О К .
То есть, 6 Икс + 1 «=» 19.
Решить для Икс .
6 Икс + 1 − 1 «=» 19 − 1 6 Икс «=» 18 6 Икс 6 «=» 18 6 Икс «=» 3
Биссектриса угла
биссектриса угла
угла треугольника – это прямая, которая делит угол на два равных угла.
Три биссектрисы углов треугольника сходятся в одной точке, называемой центр .
Здесь, я находится в центре Δ п Вопрос р .
Центр вписанной равноудален от сторон треугольника. То есть, п я «=» Вопрос я «=» р я . Окружность, нарисованная с центром вписанной окружности и радиусом, равным этому расстоянию, касается всех трех сторон и называется обвести или вписанную окружность треугольника. Этот круг является самым большим кругом, который поместится внутри треугольника.
В равностороннем треугольнике центр вписанной окружности и центр описанной окружности совпадают.
Пример 3:
У Мисти есть треугольный участок заднего двора, где она хочет построить бассейн. Как ей найти самый большой круглый бассейн, который можно там построить?
Максимально возможный круглый бассейн будет иметь тот же размер, что и самый большой круг, который можно вписать в треугольный задний двор. Самая большая окружность, которую можно вписать в треугольник, — это вписанная окружность. Это можно определить, найдя точку совпадения биссектрис каждого угла заднего двора, а затем сделав круг с этой точкой в качестве центра и кратчайшим расстоянием от этой точки до границы в качестве радиуса.
Самая большая окружность, которую можно вписать в треугольник, — это вписанная окружность. Это можно определить, найдя точку совпадения биссектрис каждого угла заднего двора, а затем сделав круг с этой точкой в качестве центра и кратчайшим расстоянием от этой точки до границы в качестве радиуса.
Пример 4:
Найдите длину Дж О .
Здесь, О является точкой пересечения трех биссектрис угла Δ л М Н и, следовательно, является инцентром. Центр вписанной равноудален от сторон треугольника. То есть, Дж О «=» ЧАС О «=» я О .
У нас есть размеры двух сторон прямоугольного треугольника.
Δ
ЧАС
О
л
, значит можно найти длину третьей стороны.
Здесь, О является точкой пересечения трех биссектрис угла Δ л М Н и, следовательно, является инцентром. Центр вписанной равноудален от сторон треугольника. То есть, Дж О «=» ЧАС О «=» я О .
У нас есть размеры двух сторон прямоугольного треугольника. Δ ЧАС О л , значит можно найти длину третьей стороны.
Используя теорему Пифагора, найдите длину ЧАС О .
ЧАС О «=» ( л О ) 2 − ( ЧАС л ) 2 «=» 13 2 − 12 2 «=» 169− 144 «=» 25 «=» 5
С
Дж
О
«=»
ЧАС
О
, длина
Дж
О
также равно
5
единицы измерения.


 Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.

 Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.
Пусть хорды BE и CF пересекают хорду AD в точках P и Q соответственно, хорды BE и FC пересекаются в точке T, а H — проекция центра O на хорду AD. Тогда H — общая середина отрезков AD и PQ, а OH — радиус вписанной окружности равностороннего треугольника PQT со стороной PQ.
 Отсюда (первое равенство — определение подобия, второе — определение косинуса угла в прямоугольном треугольнике) Отсюда выражаем длину AC: Тогда радиус R окружности, описанной около треугольника ABC равен
Отсюда (первое равенство — определение подобия, второе — определение косинуса угла в прямоугольном треугольнике) Отсюда выражаем длину AC: Тогда радиус R окружности, описанной около треугольника ABC равен Значит,
Значит, Окружность радиуса 2,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.
Окружность радиуса 2,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. Рассмотрим прямоугольный треугольник OHQ:
Рассмотрим прямоугольный треугольник OHQ: Поэтому Из условия следует, что Тогда (опираются на хорду ОС). Тогда по признаку, связанным со свойством вписанных углов, точки О, В, К, С лежат на одной окружности, ч. т. д.
Поэтому Из условия следует, что Тогда (опираются на хорду ОС). Тогда по признаку, связанным со свойством вписанных углов, точки О, В, К, С лежат на одной окружности, ч. т. д.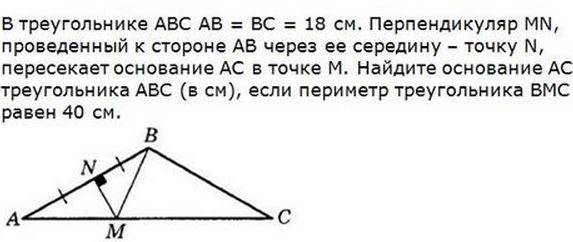
 Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.
Поскольку CE = 2CK, имеем: BK = 3CK, что и требовалось доказать.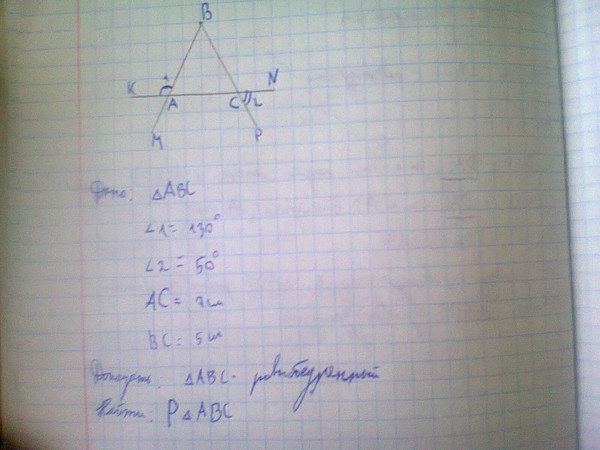 Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10.
Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10. По теореме Пифагора , или . Из этого уравнения находим, что x = 3. Тогда
По теореме Пифагора , или . Из этого уравнения находим, что x = 3. Тогда  Тогда
Тогда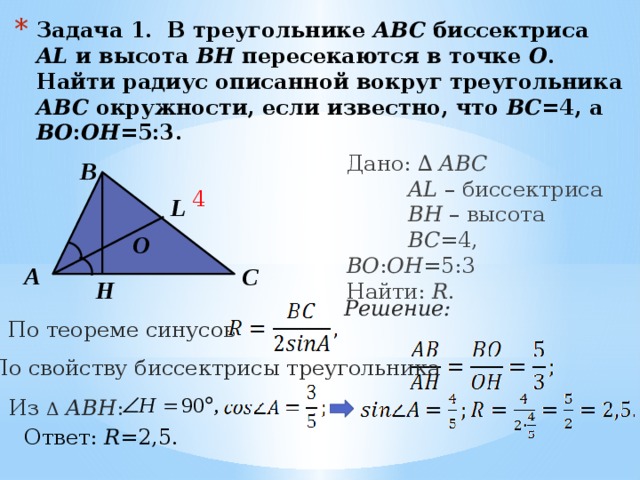
 Таким образом, . Треугольники ABC и MBK имеют общий угол B и , значит, эти треугольники подобны по двум углам.
Таким образом, . Треугольники ABC и MBK имеют общий угол B и , значит, эти треугольники подобны по двум углам. [4 балла] Дана функция у = x² + 4x-5. Не строя графика,
найдите:
а) область определения функции.
b) нули функции.
с) наименьшее значение функции.
[4 балла] Дана функция у = x² + 4x-5. Не строя графика,
найдите:
а) область определения функции.
b) нули функции.
с) наименьшее значение функции.
 Знайдіть гострі кути трикутника.
Знайдіть гострі кути трикутника.
Leave A Comment