Симметричную монету бросают 4 раза найти вероятность. Задачи по теории вероятности
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n . В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n ;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность: p = k : n .
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось k = 2. Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где C n k — число сочетаний из n элементов по k , которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
Задача.
Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k . Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть p 1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:
Теперь найдем p 2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p
1 и p
2 . Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.
Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять
перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Задача 3 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
Из таблицы видим, что число возможных элементарных исходов n=8. Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Решка | Орел | |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Орел | Решка |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | |
| 6 | Орел | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16. Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение . При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6 . Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4. Результат округлите до тысячных.
Результат округлите до тысячных.
Решение . При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
Решение задач по теории вероятностей. Учитель математики МБОУ Нивнянская СОШ, Нечаева Тамара Ивановна
2 слайд
Описание слайда:
Цели урока: рассмотреть разные виды задач по теории вероятностей и методы их решения. Задачи урока: обучить распознавать различные разновидности задач по теории вероятностей и совершенствовать логическое мышление школьников.
3 слайд
Описание слайда:
Задача 1.В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
4 слайд
Описание слайда:
Задача 2.Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
5 слайд
Описание слайда:
Задача 3.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Для того чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем из них выбрать благоприятные исходы (благоприятные исходы – это исходы удовлетворяющие требованиям задачи). В нашем случае, благоприятными будут те исходы, в которых при двух бросаниях симметричной монеты, орел выпадет только один раз. Вероятность события вычисляется как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двух кратном бросании симметричной монеты орел выпадет только один раз, равна: Р=2/4=0,5=50% Ответ: вероятность того, что в результате проведения вышеописанного эксперимента орел выпадет только один раз равна 50%. Номер эксперимента 1-ый бросок 2-ой бросок Сколько раз выпал орел 1 Орел Орел 2 2 Решка Решка 0 3 Орел Решка 1 4 Решка Орел 1
Номер эксперимента 1-ый бросок 2-ой бросок Сколько раз выпал орел 1 Орел Орел 2 2 Решка Решка 0 3 Орел Решка 1 4 Решка Орел 1
6 слайд
Описание слайда:
Задача 4. Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4. Решение: Случайный эксперимент – бросание кубика. Элементарное событие – число на выпавшей грани. Ответ:1/3 Всего граней: 1, 2, 3, 4, 5, 6 Элементарные события: N=6 N(A)=2
7 слайд
Описание слайда:
Задача 5. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А={попал, попал, попал, промахнулся, промахнулся} По формуле умножения вероятностей Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02 Ответ: 0,02
8 слайд
Описание слайда:
Задача 6.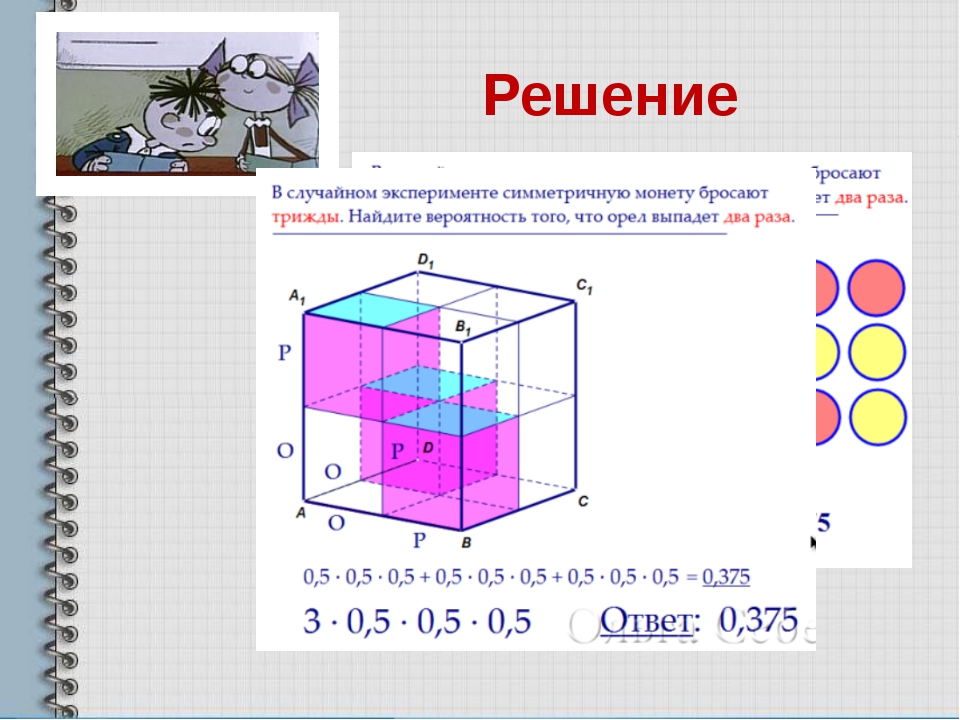 В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых Решение: Элементарный исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют количеству очков на первом кубике, столбцы –на втором кубике. Всего элементарных событий п = 36. Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 элементарных исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых Решение: Элементарный исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют количеству очков на первом кубике, столбцы –на втором кубике. Всего элементарных событий п = 36. Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 элементарных исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
9 слайд
Описание слайда:
Формула вероятности Теорема Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: Где Cnk — число сочетаний из n элементов по k, которое считается по формуле:
10 слайд
Описание слайда:
Задача 7. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. Решение По условию задачи, всего бросков было n =4. Требуемое число орлов: k =3. Подставляем n и k в формулу: С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же. Ответ: 0,25
Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. Решение По условию задачи, всего бросков было n =4. Требуемое число орлов: k =3. Подставляем n и k в формулу: С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же. Ответ: 0,25
11 слайд
Описание слайда:
Задача 8. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу. Решение Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению. Поэтому C30 = 1. Ответ: 0,125
12 слайд
Описание слайда:
Задача 9.В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка. Решение: Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий. Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
Найдем вероятность каждого из этих событий. Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
13 слайд
Описание слайда:
Задача 10.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий.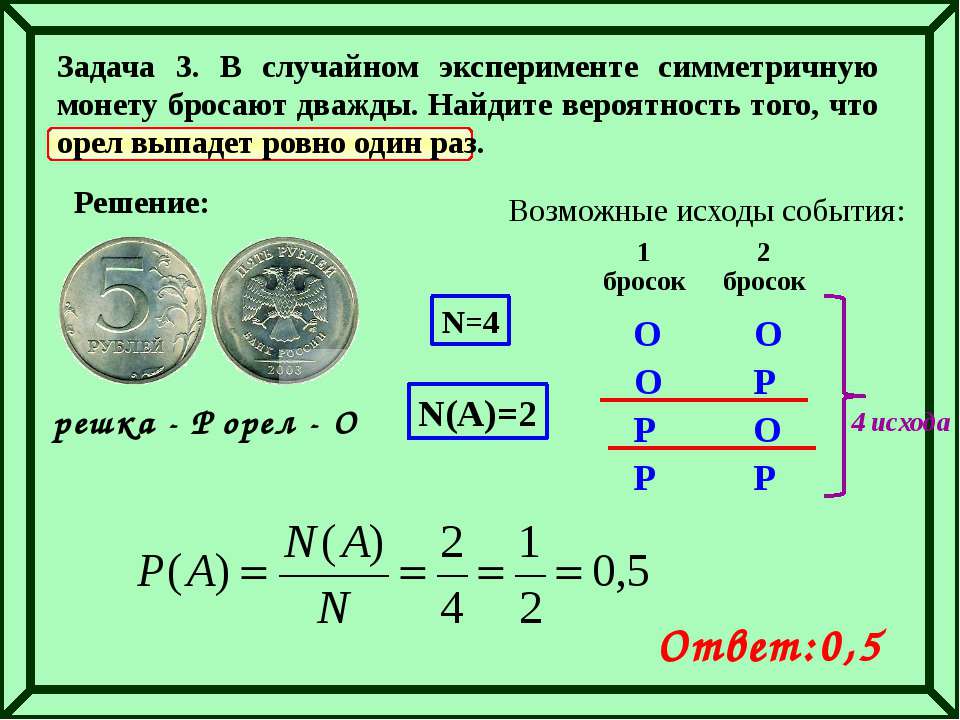 Вероятность каждого из них равна 0,5, откуда нахо дим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
Вероятность каждого из них равна 0,5, откуда нахо дим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
Условие
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
Решение
- Данную задачу будем решать по формуле:
Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.
- Применим данную теорию к нашей задаче:
А – событие, когда во второй раз выпадет то же, что и в первый;
Р(А) – вероятность того, что во второй раз выпадет то же, что и в первый.
- Определим m и n:
m — число благоприятствующих этому событию исходов, то есть число исходов, когда во второй раз выпадет то же, что и в первый. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы во второй раз выпадет то же, что и в первый, а это возможно тогда, когда выпадут следующее комбинации: ОО или РР, то есть получается, что
m = 2, так как возможно 2 варианта, когда во второй раз выпадет то же, что и в первый;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды. Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
Условие
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет хотя бы один раза.
Решение
- Данную задачу будем решать по формуле:
Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.
- Применим данную теорию к нашей задаче:
А – событие, когда орел выпадет хотя бы 1 раза;
Р(А) – вероятность того, что орел выпадет хотя 1 раза.
- Определим m и n:
m — число благоприятствующих этому событию исходов, то есть число исходов, когда орел выпадет 1 раза. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы выпал орел хотя бы один раз, а это возможно тогда, когда выпадут следующее комбинации: ОР, РО и ОО, то есть получается, что
m = 3, так как возможно 3 варианта выпадения хотя бы 1-го орла;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды. Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
Понравилась статья? Поделись с друзьями:
Мой мир
Вконтакте
Google+
Самое интересное:
Монету бросают два раза. В случайном эксперименте симметричную монету бросают дважды
Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
P = 3 / 4 = 0.75
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p
— искомая вероятность, k
— число устраивающих нас событий, n
— общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n . В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР.
 Число таких комбинаций — это n
;
Число таких комбинаций — это n
; - Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность: p = k : n .
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось k = 2. Находим вероятность:
Задача.
Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где C n k — число сочетаний из n элементов по k , которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k . Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза.
Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть p 1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:
Теперь найдем p 2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p 1 и p 2 . Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
Ответ: 0,25. 34. Решение. Всего 4 варианта: о; о о; р р; р р; о. Благоприятных 1: о; р. Вероятность равна 1/4 = 0,25. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй – решка).
Слайд 35 из презентации «Решение заданий В6» . Размер архива с презентацией 1329 КБ.
Размер архива с презентацией 1329 КБ.Математика 11 класс
краткое содержание других презентаций«Решение заданий В6» — Купленная сумка. Вероятность произведения независимых событий. Частота рождения девочек. Исход. Жребий. Возможность выиграть. Участник. Качественные тарелки. Иностранный язык. Команда. Ситуация. Искомая вероятность. Человек. Комбинации. Кофе. Батарейка. События. Магазин. Вопрос по ботанике. Механические часы. Карточки с номерами групп. Вероятность уцелеть. Насос. Пристрелянный револьвер. Спортсмен.
«Подготовка к экзамену по математике» — Информационно-методическое пространство учителей математики. Сборник к ЕГЭ по математике. Решение большого количества задач из «Банка заданий». Рекомендации выпускникам по подготовке к ЕГЭ. Из опыта подготовки к итоговой аттестации немотивированных учащихся. Рабочие тетради по математике B1-B12, С1 – С6 к ЕГЭ 2011. Результаты ЕГЭ. Информационная поддержка Единого государственного экзамена. Учебно-тренировочные тесты к ЕГЭ 2011 по математике.
«Решение текстовых задач по математике» — В разделе прототипов блока B12 всего 82 прототипа задач. Задачи на движение. Движение объектов навстречу друг к другу. Бригада маляров красит забор длиной 240 метров. Задачи на работу. Прототип задания B12. Задачи на работу и производительность. Четыре рубашки дешевле куртки на 8%. Задачи на «концентрацию, смесей и сплавов». Общие подходы к решению задач. Движение велосипедистов и автомобилистов. Движение лодки по течению и против течения.
«Варианты заданий ЕГЭ по математике» — Корни иррациональны. Сюжетные задачи. Укажите график функции, заданной формулой. Простейшие виды уравнений и неравенств. Анализ содержания заданий по математике ЕГЭ. Геометрические фигуры и их свойства. Задания второй и третьей части (форма В и С). Студенческая бригада. Значение выражения. Найдите значение выражения. Сколько корней имеет уравнение. Структура работы по математике. Основные содержательные темы по математике.
«Структура ЕГЭ по математике» — Тренировочные работы. Структура КИМ ЕГЭ. Пример КИМ ЕГЭ по математике 2012. Советы психолога. Типовые экзаменационные варианты. ЕГЭ-2012 математика. Полезные приемы. Бланки ответов. Шкалирование. Оценка работ ЕГЭ по математике. Рекомендации по заучиванию материала. Изменения в ЕГЭ по математике 2012. Структура варианта КИМ. Типовые тестовые задания. Алгебра.
Структура КИМ ЕГЭ. Пример КИМ ЕГЭ по математике 2012. Советы психолога. Типовые экзаменационные варианты. ЕГЭ-2012 математика. Полезные приемы. Бланки ответов. Шкалирование. Оценка работ ЕГЭ по математике. Рекомендации по заучиванию материала. Изменения в ЕГЭ по математике 2012. Структура варианта КИМ. Типовые тестовые задания. Алгебра.
«Задание B1 в ЕГЭ по математике» — Флакон шампуня. Подготовка к ЕГЭ по математике. Содержание задания. Проверяемые требования. Теплоход. Реальные числовые данные. Лимонная кислота. Спасательная шлюпка. Задания для самостоятельного решения. Лимонная кислота продается в пакетиках. Памятка ученику. Наибольшее число. Прототип задания.
Условие
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
Решение
- Данную задачу будем решать по формуле:
Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.
- Применим данную теорию к нашей задаче:
А – событие, когда во второй раз выпадет то же, что и в первый;
Р(А) – вероятность того, что во второй раз выпадет то же, что и в первый.
- Определим m и n:
m — число благоприятствующих этому событию исходов, то есть число исходов, когда во второй раз выпадет то же, что и в первый. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы во второй раз выпадет то же, что и в первый, а это возможно тогда, когда выпадут следующее комбинации: ОО или РР, то есть получается, что
m = 2, так как возможно 2 варианта, когда во второй раз выпадет то же, что и в первый;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды. Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
Получается, что
Понравилась статья? Поделись с друзьями:
Мой мир
Вконтакте
Google+
Самое интересное:
Определение вероятности в задачах про монету и игральную кость
› вернуться в Часть 1
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n, где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.

Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Задача 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно 1 раз.
Решение.
Возможные варианты двух бросаний монеты (все возможные комбинации орлов
и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок |
| 1 | Орел | Орел |
| 2 | Орел | Решка |
| 3 | Решка | Орел |
| 4 | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение. Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Находим вероятность события Р(А)=m/n=1/4=0,25
Задача 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение. Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок |
| 1 | Орел | Орел | Орел |
| 2 | Орел | Решка | Решка |
| 3 | Решка | Орел | Решка |
| 4 | Решка | Решка | Орел |
| 5 | Орел | Орел | Решка |
| 6 | Орел | Решка | Орел |
| 7 | Решка | Орел | Орел |
| 8 | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=8. Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4. В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение. Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Орел | Решка | Орел |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Орел | Решка |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | Орел |
| 6 | Орел | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16. Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение. При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6. Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4. Результат округлите до тысячных.
Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4. Результат округлите до тысячных.
Решение. При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение. Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать
следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6.
Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в
виде таблицы из 6-ти строк и 6-ти столбцов:
Все случаи представим в
виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение. Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение. Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
Другие статьи по данной теме:
Список использованных источников
- Алимов А.Ш., Колягин Ю.М., Ткачева М.В. и др. Алгебра и начала математического анализа. 10-11 классы. Базовый и углубленный уровни / Учебник. — 3-е изд. — М.: Просвещение, 2016;
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
- Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
- Семёнычев В.
 К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
К. Теория вероятности и математическая статистика: Лекции /Самара, 2007; - Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008;
- Яковлев И. В. Комбинаторика-олимпиаднику — MathUs.ru.
В случайном эксперименте симметричную монету бросают дважды – как решать
Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
Решение:
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
Осталось лишь подсчитать вероятность выпадения этой комбинации. Для этого нужно поделить количество интересующих нас комбинаций на количество всех возможных комбинаций:
Ответ: 0.25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение:
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
Осталось лишь подсчитать вероятность выпадения этой комбинации. Для этого нужно поделить количество интересующих нас комбинаций на количество всех возможных комбинаций:
Для этого нужно поделить количество интересующих нас комбинаций на количество всех возможных комбинаций:
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Решение:
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).
Осталось лишь подсчитать вероятность выпадения этой комбинаций. Для этого нужно поделить количество интересующих нас комбинаций на количество всех возможных комбинаций:
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Решение:
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
Осталось лишь подсчитать вероятность выпадения этой комбинаций. Для этого нужно поделить количество интересующих нас комбинаций на количество всех возможных комбинаций:
Ответ: 0.75
Задачи B6 с монетами
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n. В этом и состоит вся сложность.
Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n. В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи.
 Считаем отмеченные комбинации — получаем число k;
Считаем отмеченные комбинации — получаем число k; - Осталось найти вероятность: p = k : n.
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
OO OP PO PP
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
OP PO
Таких вариантов оказалось k = 2. Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где Cnk — число сочетаний из n элементовпо k, которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же.
Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C30 = 1.
Поэтому C30 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4,k = 3. Имеем:
Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4,k = 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
p = p1 + p2 = 0,25 + 0,0625 = 0,3125
Смотрите также:
- Правила комбинаторики в задаче B6
- Комбинаторика в задаче B6: легкий тест
- Метод Гаусса
- Радианная и градусная мера угла
- Показательные функции в задаче B15
- Задачи на проценты: стандартный расчет с помощью пропорций
Монету бросают два раза.
 В случайном эксперименте симметричную монету бросают дважды. Специальная формула вероятности
В случайном эксперименте симметричную монету бросают дважды. Специальная формула вероятностиФормулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
P = 3 / 4 = 0.75
Ответ: 0,25. 34. Решение. Всего 4 варианта: о; о о; р р; р р; о. Благоприятных 1: о; р. Вероятность равна 1/4 = 0,25. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй – решка).
Слайд 35 из презентации «Решение заданий В6» . Размер архива с презентацией 1329 КБ.Математика 11 класс
краткое содержание других презентаций«Решение заданий В6» — Купленная сумка. Вероятность произведения независимых событий. Частота рождения девочек. Исход. Жребий. Возможность выиграть. Участник. Качественные тарелки. Иностранный язык. Команда. Ситуация. Искомая вероятность. Человек. Комбинации. Кофе. Батарейка. События. Магазин. Вопрос по ботанике. Механические часы. Карточки с номерами групп. Вероятность уцелеть. Насос. Пристрелянный револьвер. Спортсмен.
Батарейка. События. Магазин. Вопрос по ботанике. Механические часы. Карточки с номерами групп. Вероятность уцелеть. Насос. Пристрелянный револьвер. Спортсмен.
«Подготовка к экзамену по математике» — Информационно-методическое пространство учителей математики. Сборник к ЕГЭ по математике. Решение большого количества задач из «Банка заданий». Рекомендации выпускникам по подготовке к ЕГЭ. Из опыта подготовки к итоговой аттестации немотивированных учащихся. Рабочие тетради по математике B1-B12, С1 – С6 к ЕГЭ 2011. Результаты ЕГЭ. Информационная поддержка Единого государственного экзамена. Учебно-тренировочные тесты к ЕГЭ 2011 по математике.
«Решение текстовых задач по математике» — В разделе прототипов блока B12 всего 82 прототипа задач. Задачи на движение. Движение объектов навстречу друг к другу. Бригада маляров красит забор длиной 240 метров. Задачи на работу. Прототип задания B12. Задачи на работу и производительность. Четыре рубашки дешевле куртки на 8%. Задачи на «концентрацию, смесей и сплавов». Общие подходы к решению задач. Движение велосипедистов и автомобилистов. Движение лодки по течению и против течения.
Общие подходы к решению задач. Движение велосипедистов и автомобилистов. Движение лодки по течению и против течения.
«Варианты заданий ЕГЭ по математике» — Корни иррациональны. Сюжетные задачи. Укажите график функции, заданной формулой. Простейшие виды уравнений и неравенств. Анализ содержания заданий по математике ЕГЭ. Геометрические фигуры и их свойства. Задания второй и третьей части (форма В и С). Студенческая бригада. Значение выражения. Найдите значение выражения. Сколько корней имеет уравнение. Структура работы по математике. Основные содержательные темы по математике.
«Структура ЕГЭ по математике» — Тренировочные работы. Структура КИМ ЕГЭ. Пример КИМ ЕГЭ по математике 2012. Советы психолога. Типовые экзаменационные варианты. ЕГЭ-2012 математика. Полезные приемы. Бланки ответов. Шкалирование. Оценка работ ЕГЭ по математике. Рекомендации по заучиванию материала. Изменения в ЕГЭ по математике 2012. Структура варианта КИМ. Типовые тестовые задания. Алгебра.
«Задание B1 в ЕГЭ по математике» — Флакон шампуня. Подготовка к ЕГЭ по математике. Содержание задания. Проверяемые требования. Теплоход. Реальные числовые данные. Лимонная кислота. Спасательная шлюпка. Задания для самостоятельного решения. Лимонная кислота продается в пакетиках. Памятка ученику. Наибольшее число. Прототип задания.
Подготовка к ЕГЭ по математике. Содержание задания. Проверяемые требования. Теплоход. Реальные числовые данные. Лимонная кислота. Спасательная шлюпка. Задания для самостоятельного решения. Лимонная кислота продается в пакетиках. Памятка ученику. Наибольшее число. Прототип задания.
Условие
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
Решение
- Данную задачу будем решать по формуле:
Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.
- Применим данную теорию к нашей задаче:
А – событие, когда во второй раз выпадет то же, что и в первый;
Р(А) – вероятность того, что во второй раз выпадет то же, что и в первый.
- Определим m и n:
m — число благоприятствующих этому событию исходов, то есть число исходов, когда во второй раз выпадет то же, что и в первый. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы во второй раз выпадет то же, что и в первый, а это возможно тогда, когда выпадут следующее комбинации: ОО или РР, то есть получается, что
В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы во второй раз выпадет то же, что и в первый, а это возможно тогда, когда выпадут следующее комбинации: ОО или РР, то есть получается, что
m = 2, так как возможно 2 варианта, когда во второй раз выпадет то же, что и в первый;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды. Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что
ЕГЭ. Задача 4. Теория вероятностей
Подготовка к единому государственному экзамену по математике. Полезные материалы и видеоразборы задач по теории вероятностей.
Полезные материалы
Видеоразборы задач
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Найдите вероятность того, что обе девочки будут сидеть рядом.
В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 28 марта, погода в Волшебной стране хорошая. Найдите вероятность того, что 1 апреля в Волшебной стране будет отличная погода.
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 8 прыгунов из России и 10 прыгунов из Мексики. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что пятнадцатым будет выступать прыгун из России.
На рисунке изображен лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому еще не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придет к выходу D.
Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому еще не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придет к выходу D.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Подборка задач
- В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
- Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия.
 Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? - В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: $$1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.$$ Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
- Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Максимова окажется запланированным на последний день конференции?
- В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

- Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
- Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
- В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орел, а во второй — решка.
- В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
- В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

- На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
- В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
- В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
- Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
- Если гроссмейстер Антонов играет белыми, то он выигрывает у гроссмейстера Борисова с вероятностью 0,52.
 Если Антонов играет черными, то Антонов выигрывает у Борисова с вероятностью 0,3. Гроссмейстеры Антонов и Борисов играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что Антонов выиграет оба раза.
Если Антонов играет черными, то Антонов выигрывает у Борисова с вероятностью 0,3. Гроссмейстеры Антонов и Борисов играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что Антонов выиграет оба раза. - В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
- Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
- При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.

- Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
- Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнет игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
- В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
- По отзывам покупателей Иван Иванович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8.
 Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. - Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых
- Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
- На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет.
 Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. - Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятость того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
- Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
- Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков.
 Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. - В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
- В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Артем хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Артем пойдет в магазин?
- Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трех предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трех предметов — математика, русский язык и обществознание.
 Вероятность того, что Петров получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что Петров сможет поступить хотя бы на одну из двух упомянутых специальностей
Вероятность того, что Петров получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что Петров сможет поступить хотя бы на одну из двух упомянутых специальностей - При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
В ходе случайного эксперимента было брошено четыре монеты. В случайном эксперименте симметричная монета бросается дважды. Определение вероятности в задачах игры в кости
Постановка задачи: В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что орел (решка) не выпадет ни разу (выпадет ровно / как минимум 1, 2 раза).
Задача входит в экзамен по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Посмотрим, как решаются похожие задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что орла никогда не выпадут.
OO OR RO
руб.Всего таких комбинаций 4. Нас интересуют только те из них, в которых нет ни единого орла. Есть только одна такая комбинация (ПП).
P = 1/4 = 0,25
Ответ: 0,25
Пример задачи 2:
В случайном эксперименте симметричная монета бросается дважды.Найдите вероятность того, что выпадет ровно две головы.
Рассмотрим все возможные комбинации, которые могут возникнуть, если монета брошена дважды. Для удобства будем обозначать головы буквой O, а решки буквой P:
.OO OR RO
руб. Всего таких комбинаций 4. Нас интересуют только те из них, у которых голова падает ровно 2 раза. Есть только одна такая комбинация (ОО).
Есть только одна такая комбинация (ОО).
P = 1/4 = 0,25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что решка выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут возникнуть, если монета брошена дважды. Для удобства будем обозначать головы буквой O, а решки буквой P:
.OO OR RO
руб.Всего было 4 таких комбинации. Нас интересуют только те из них, у которых голова выпала ровно 1 раз.Таких комбинаций всего две (ОП и РО).
Ответ: 0,5
Пример задачи 4:
В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что он выпадет орлом хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут возникнуть, если монета брошена дважды. Для удобства будем обозначать головы буквой O, а решки буквой P:
.OO OR RO
руб. Всего было 4 таких комбинации. Нас интересуют только те из них, в которые хотя бы 1 раз падает голова. Таких комбинаций всего три (OO, OP и RO).
Нас интересуют только те из них, в которые хотя бы 1 раз падает голова. Таких комбинаций всего три (OO, OP и RO).
P = 3/4 = 0,75
Состояние
В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что второй раз будет таким же, как и первый.
Решение
- Решим эту задачу по формуле:
Где P (A) — вероятность события A, m — количество благоприятных исходов для этого события, n — общее количество всех возможных исходов.
- Давайте применим эту теорию к нашей проблеме:
А — событие, когда второй раз выпадает так же, как и первый;
P (A) — вероятность того, что второй раз будет таким же, как и первый.
- Определим m и n:
м — количество исходов, благоприятных для данного события, то есть количество исходов, когда второй тайм выпадает так же, как и первый. В эксперименте дважды бросается монета, у которой две стороны: решка (P) и решка (O). Нам нужно второй раз выпадать так же, как и первый, а это возможно при выпадении следующих комбинаций: OO или PP, то есть получается
Нам нужно второй раз выпадать так же, как и первый, а это возможно при выпадении следующих комбинаций: OO или PP, то есть получается
м = 2, так как возможны 2 варианта, когда второй раз выпадет то же самое, что и первый;
n — это общее количество всех возможных исходов, то есть для определения n нам нужно найти количество всех возможных комбинаций, которые могут возникнуть при двойном бросании монеты. При первом бросании монеты могут выпасть либо решка, либо орел, то есть возможны два варианта.При подбрасывании монеты во второй раз возможны точно такие же варианты. Оказывается,
Состояние
В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что он выпадет орлом хотя бы один раз.
Решение
- Решим эту задачу по формуле:
Где P (A) — вероятность события A, m — количество благоприятных исходов для этого события, n — общее количество всех возможных исходов.
- Давайте применим эту теорию к нашей проблеме:
A — событие, когда головы выпадают хотя бы 1 раз;
P (A) — вероятность выпадения орлов хотя бы 1 раз.
- Определим m и n:
м — количество исходов, благоприятных для данного события, то есть количество исходов, когда орел выпадает 1 раз. В эксперименте дважды бросается монета, у которой две стороны: решка (P) и решка (O). Нам нужно хоть раз получить орел, а это возможно при выпадении следующих комбинаций: OP, RO и OO, то есть получается
м = 3, так как возможны 3 варианта минимум 1 головы;
n — это общее количество всех возможных исходов, то есть для определения n нам нужно найти количество всех возможных комбинаций, которые могут возникнуть при двойном бросании монеты.При первом бросании монеты могут выпасть либо решка, либо орел, то есть возможны два варианта. При подбрасывании монеты во второй раз возможны точно такие же варианты. Оказывается,
Описание презентации для отдельных слайдов:
1 слайд
Описание слайда:
Решение задач теории вероятностей. Учитель математики МБОУ Нивнянская общеобразовательная школа, Нечаева Тамара Ивановна
2 слайда
Описание слайда:
Цели урока: Рассмотреть разные типы задач теории вероятностей и методы их решения. Задачи урока: научить распознавать разные типы задач теории вероятностей и улучшить логическое мышление школьников.
Задачи урока: научить распознавать разные типы задач теории вероятностей и улучшить логическое мышление школьников.
3 слайда
Описание слайда:
Задача 1: В произвольном эксперименте симметричная монета бросается 2 раза. Найдите вероятность того, что выпадет одинаковое количество орлов и решек.
4 слайда
Описание слайда:
Задача 2: монета бросается четыре раза.Найдите вероятность того, что решка никогда не выпадет.
5 слайдов
Описание слайда:
Задача 3: В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что выпадет орел ровно один раз. Решение: чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем выбрать из них благоприятные исходы (благоприятные исходы — это результаты, которые удовлетворяют требованиям задачи).В нашем случае благоприятными будут те исходы, при которых при двух подбрасываниях симметричной монеты орел выпадает только один раз. Вероятность события рассчитывается как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двукратном подбрасывании симметричной монеты орла выпадут только один раз, равна: P = 2/4 = 0,5 = 50%. Ответ: вероятность того, что в результате вышеизложенного Эксперимент головы выпадет только раз — 50%.Номер эксперимента 1-й бросок 2-й бросок Сколько раз выпадало орлов 1 голова голова 2 2 головы головы 0 3 головы головы 1 4 головы головы 1
Вероятность события рассчитывается как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двукратном подбрасывании симметричной монеты орла выпадут только один раз, равна: P = 2/4 = 0,5 = 50%. Ответ: вероятность того, что в результате вышеизложенного Эксперимент головы выпадет только раз — 50%.Номер эксперимента 1-й бросок 2-й бросок Сколько раз выпадало орлов 1 голова голова 2 2 головы головы 0 3 головы головы 1 4 головы головы 1
6 слайдов
Описание слайда:
Задача 4. Кость был брошен один раз. Какова вероятность того, что количество очков больше 4. Решение: случайный эксперимент — бросание кубика. Элементарное событие — число на выпавшей грани. Ответ: 1/3 Всего лиц: 1, 2, 3, 4, 5, 6 Элементарные события: N = 6 N (A) = 2
7 слайдов
Описание слайда:
Задача 5.Биатлонист пять раз стреляет по мишеням. Вероятность поражения цели одним выстрелом 0,8. Найдите вероятность того, что биатлонист попадет в мишени первые три раза и пропустит два последних. Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А = (попадание, попадание, попадание, промах, промах) По формуле умножения вероятностей P (A) = 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 P (А) = 0,512 ∙ 0,04 = 0.02048 ≈ 0,02 Ответ: 0,02
Найдите вероятность того, что биатлонист попадет в мишени первые три раза и пропустит два последних. Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А = (попадание, попадание, попадание, промах, промах) По формуле умножения вероятностей P (A) = 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 P (А) = 0,512 ∙ 0,04 = 0.02048 ≈ 0,02 Ответ: 0,02
8 слайд
Описание слайда:
Задача 6: В произвольном эксперименте бросаются два кубика. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых. Решение: элементарный результат этого эксперимента — упорядоченная пара чисел. Первое число выпадет на первом кубике, второе — на втором. Многие элементарные исходы удобно представлять в виде таблицы.Строки соответствуют количеству очков на первом кубике, столбцы — на втором кубике. Всего элементарных событий n = 36. Запишем сумму выпавших точек в каждой ячейке и закрасим ячейки, где сумма 6. Их 5. Есть 5. Это означает, что событие A = (сумма выпавших точек равна 6 ) способствует 5 элементарным результатам. Следовательно, m = 5. Следовательно, P (A) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
Есть 5. Это означает, что событие A = (сумма выпавших точек равна 6 ) способствует 5 элементарным результатам. Следовательно, m = 5. Следовательно, P (A) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
9 слайдов
Описание слайда:
Теорема о формуле вероятности Пусть монета будет брошена n раз.Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: где Cnk — количество комбинаций из n элементов по k, которое рассчитывается по формуле:
10 слайдов
Описание слайда:
Задача 7. Монета бросается четыре раза. Найдите вероятность того, что выпадет решка ровно три раза. Решение По условию задачи общее количество бросков было n = 4. Требуемое количество голов: k = 3.Подставим n и k в формулу: Точно так же можно посчитать количество хвостов: k = 4 — 3 = 1. Ответ будет таким же. Ответ: 0,25
11 слайдов
Описание слайда:
Задача 8. Монета бросается трижды. Найдите вероятность того, что решка никогда не выпадет. Решение Снова выпишите числа n и k. Так как монета брошена 3 раза, n = 3. А так как решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению.Следовательно, C30 = 1. Ответ: 0,125
Монета бросается трижды. Найдите вероятность того, что решка никогда не выпадет. Решение Снова выпишите числа n и k. Так как монета брошена 3 раза, n = 3. А так как решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению.Следовательно, C30 = 1. Ответ: 0,125
12 слайдов
Описание слайда:
Задача 9: В произвольном эксперименте симметричная монета бросается 4 раза. Найдите вероятность того, что орел выпадет чаще, чем решка. Решение: чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда будет 1 решка), либо 4 (тогда решки не будет). Найдем вероятность каждого из этих событий. Пусть p1 — вероятность того, что орел выпадет 3 раза.Тогда n = 4, k = 3. Имеем: Теперь находим p2 — вероятность того, что орел выпадет все 4 раза. В данном случае n = 4, k = 4. Имеем: Для получения ответа осталось сложить вероятности p1 и p2. Помните, что вы можете добавлять вероятности только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
13 слайдов
Описание слайда:
Задача 10. Перед началом волейбольного матча капитаны команд проводят честную жеребьевку, чтобы определить, какая команда начнет игру с мячом.Команда Stator по очереди играет с командами Rotor, Motor и Starter. Найдите вероятность того, что Статор запустит только первую и последнюю игры. Решение. Требуется найти вероятность наступления трех событий: «Статор» запускает первую игру, не запускает вторую игру, начинает третью игру. Вероятность возникновения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5 · 0,5 · 0.5 = 0,125. Ответ: 0,125.
В качестве предисловия.
Всем известно, что у монеты есть две стороны — орел и решка.
Нумизматы считают, что у монеты три стороны — аверс, реверс и край.
И среди них, и среди других мало кто знает, что такое симметричная монета. Но те, кто готовится к ЕГЭ, об этом знают (ну или должны знать :).
Но те, кто готовится к ЕГЭ, об этом знают (ну или должны знать :).
В общем, в данной статье речь пойдет о необычной монете, не имеющей ничего общего с нумизматикой, но, в то же время, самой популярной среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и т.д. В результате такая монета также не имеет ребра, то есть действительно имеет только две стороны. Главное свойство симметричной монеты — в таких условиях вероятность выпадения орла или решки абсолютно одинакова. И они придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой: «В случайном эксперименте симметричная монета брошена дважды (трижды, четыре раза и т. Д.).). Требуется определить вероятность того, что одна из сторон выпадет определенное количество раз.
Решение задачи с симметричной монетой
Понятно, что в результате подбрасывания монета выпадет орлом или решкой. Сколько раз зависит от того, сколько бросков вы сделаете. Вероятность выпадения орла или решки вычисляется путем деления количества удовлетворительных результатов на общее количество возможных результатов.
Сколько раз зависит от того, сколько бросков вы сделаете. Вероятность выпадения орла или решки вычисляется путем деления количества удовлетворительных результатов на общее количество возможных результатов.
Один бросок
Здесь все просто.Выпадут орел или решка. Те. у нас есть два возможных исхода, один из которых нас удовлетворяет — 1/2 = 50%
Двойной бросок
На два броска может выпасть следующее:
два орла
две головы
решка затем решка
решка затем решка
Те . возможны только четыре варианта. Проблемы с более чем одним рулоном проще всего решить, составив таблицу возможных вариантов. Для простоты обозначим орла как «0», а решки как «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, вам нужно найти вероятность того, что выпадет орел один раз, вам просто нужно посчитать количество подходящих вариантов в стол — я.е. те строки, где орел встречается один раз. Таких линий две. Это означает, что вероятность выпадения одной орла при двух подбрасываниях симметричной монеты составляет 2/4 = 50%
Это означает, что вероятность выпадения одной орла при двух подбрасываниях симметричной монеты составляет 2/4 = 50%
Вероятность того, что орел при двух подбрасываниях выпадет дважды, составляет 1/4 = 25%
Три Роска
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные цифры от «0» до «7».Так проще не запутаться с опциями.
Решим задачу из предыдущего пункта — посчитаем вероятность того, что орел выпадет один раз. Есть три строки, где «0» встречается один раз. Это означает, что вероятность выпадения одной головы за три броска симметричной монеты составляет 3/8 = 37,5%
Вероятность того, что орла при трех бросках выпадут дважды, составляет 3/8 = 37,5%, т.е. абсолютно одинаковая .
Вероятность того, что орел при трех бросках выпадет три раза, составляет 1/8 = 12.5%.
Четыре броска
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
110251
1100
110251
что головы поднимутся один раз. Есть только три строки, где «0» встречается один раз, как и в случае трех бросков. Но вариантов уже шестнадцать. Это означает, что вероятность выпадения одной головы за четыре подбрасывания симметричной монеты составляет 3/16 = 18.75%
Есть только три строки, где «0» встречается один раз, как и в случае трех бросков. Но вариантов уже шестнадцать. Это означает, что вероятность выпадения одной головы за четыре подбрасывания симметричной монеты составляет 3/16 = 18.75%
Вероятность того, что орел при трех бросках выпадет дважды, составляет 6/8 = 75%.
Вероятность того, что орел при трех бросках выпадет три раза, составляет 4/8 = 50%.
Так что с увеличением количества бросков принцип решения задачи не меняется вообще — только в соответствующей прогрессии количество вариантов увеличивается.
1200 симметричная монета в случайном эксперименте. Задачи теории вероятностей
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и визуализировать предлагаемую ситуацию.К таким проблемам относятся большинство проблем с подбрасыванием монеты и костей. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению количества исходов, благоприятных для этого события, к общему количеству всех равно возможных несовместимых элементарных исходов: P (A) = m / n где:
- m — количество результатов элементарного теста, которые способствуют возникновению события A;
- n — общее количество всех возможных результатов элементарного теста.

Количество возможных исходов элементарного теста и количество благоприятных исходов в рассматриваемых задачах удобно определять путем перечисления всех возможных вариантов (комбинаций) и прямого вычисления.
Из таблицы видим, что количество возможных элементарных исходов n = 4. Благоприятные исходы события A = (выпадение орлов 1 раз) соответствуют вариантам №2 и №3 эксперимента, их два такие варианты m = 2.
Находим вероятность события P (A) = m / n = 2/4 = 0,5
Задача 2 … В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что он никогда не выпадет орлом.
Решение … Так как монета брошена дважды, то, как и в Задаче 1, количество возможных элементарных исходов n = 4. Благоприятные исходы события A = (орла не выпадут ни разу) соответствуют варианту 4 опыта (см. Таблицу в задании 1).Такой вариант всего один, поэтому m = 1.
Находим вероятность события P (A) = m / n = 1/4 = 0,25
Задача 3 . .. В случайном эксперименте симметричная монета бросается три раза. Найдите вероятность выпадения орла ровно 2 раза.
.. В случайном эксперименте симметричная монета бросается три раза. Найдите вероятность выпадения орла ровно 2 раза.
Решение … Возможные варианты трех подбрасываний монеты (все возможные комбинации орла и решки) представлены в виде таблицы:
Из таблицы видим, что количество возможных элементарных исходов n = 8.Благоприятные исходы события A = (выпадение головы 2 раза) соответствуют вариантам 5, 6 и 7 эксперимента. Таких вариантов три, поэтому m = 3.
Находим вероятность события P (A) = m / n = 3/8 = 0,375
Задача 4 … В случайном эксперименте симметричная монета бросается четыре раза. Найдите вероятность того, что орел выпадет ровно 3 раза.
Решение … Возможные варианты четырех подбрасываний монеты (все возможные комбинации орла и решки) представлены в виде таблицы:
| № опции | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | Опция № | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Хвосты | Орел | Хвосты | Орел |
| 2 | Орел | Хвосты | Хвосты | Хвосты | 10 | Орел | Хвосты | Орел | Хвосты |
| 3 | Хвосты | Орел | Хвосты | Хвосты | 11 | Орел | Хвосты | Хвосты | Орел |
| 4 | Хвосты | Хвосты | Орел | Хвосты | 12 | Орел | Орел | Орел | Хвосты |
| 5 | Хвосты | Хвосты | Хвосты | Орел | 13 | Хвосты | Орел | Орел | Орел |
| 6 | Орел | Орел | Хвосты | Хвосты | 14 | Орел | Хвосты | Орел | Орел |
| 7 | Хвосты | Орел | Орел | Хвосты | 15 | Орел | Орел | Хвосты | Орел |
| 8 | Хвосты | Хвосты | Орел | Орел | 16 | Хвосты | Хвосты | Хвосты | Хвосты |
Из таблицы видим, что количество возможных элементарных исходов n = 16. Благоприятные исходы события A = (орла упадут 3 раза) соответствуют вариантам 12, 13, 14 и 15 эксперимента, поэтому m = 4.
Благоприятные исходы события A = (орла упадут 3 раза) соответствуют вариантам 12, 13, 14 и 15 эксперимента, поэтому m = 4.
Найдите вероятность события P (A) = m / п = 4/16 = 0,25
Задача 5 … Определите вероятность того, что при броске кубика выпадет более 3 очков (правильный кубик).
Решение … При броске кубика (правильного кубика) любая из его шести граней может выпасть, т.е. произойдет любое из элементарных событий — падение с 1 до 6 очков (очков). Следовательно, количество возможных элементарных исходов n = 6.
Событие А = (выпало более 3 баллов) означает, что выпало 4, 5 или 6 баллов (баллов). Следовательно, количество благоприятных исходов m = 3.
Вероятность наступления события Р (А) = m / n = 3/6 = 0.5
Задача 6 . .. Определите вероятность того, что при бросании кубика количество очков не больше 4. Результат округлите до тысячных.
.. Определите вероятность того, что при бросании кубика количество очков не больше 4. Результат округлите до тысячных.
Решение … При броске кубика может выпасть любая из шести его граней, т.е. произойдет любое из элементарных событий — падение с 1 до 6 очков (очков). Следовательно, количество возможных элементарных исходов n = 6.
Событие А = (выпало не более 4 баллов) означает, что выпало 4, 3, 2 или 1 балл (балл).Следовательно, количество благоприятных исходов m = 4.
Вероятность наступления события P (A) = m / n = 4/6 = 0,6666 … ≈0,667
Проблема 7 … кости бросаются дважды. Найдите вероятность того, что оба раза выпало число меньше 4.
Решение … Поскольку игральные кости (игральные кости) бросаются дважды, рассуждаем следующим образом: если на первой кости есть одно очко, то вторая может получить 1, 2, 3, 4, 5, 6.Получаем пары (1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6) и так далее с каждой гранью. Все кейсы представлены в виде таблицы из 6 строк и 6 столбцов:
Все кейсы представлены в виде таблицы из 6 строк и 6 столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события A = (оба раза выпало число меньше 4) (они выделены жирным шрифтом), вычисляем и получаем m = 9.
Найдите вероятность события P (A) = m / n = 9/36 = 0,25
Задача 8 … кости бросаются дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Округлите ответ до ближайшей тысячи.
Решение … Все возможные исходы двух бросков костей представлены в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что количество возможных элементарных исходов n = 6 * 6 = 36.
Благоприятные исходы события A = (наибольшее из двух выпавших чисел 5) (они выделены жирным шрифтом) будем рассчитаны и получим m = 8.
Находим вероятность события P (A) = m / n = 8/36 = 0,2222 … ≈0,222
Задача 9 … кости бросаются дважды. Найдите вероятность того, что хотя бы раз выпало число меньше 4.
Решение … Все возможные исходы двух бросков костей представлены в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что количество возможных элементарных исходов n = 6 * 6 = 36.
Фраза «хотя бы один раз выпало число меньше 4» означает «один или два раза выпало число меньше 4», затем количество благоприятных исходов события A = (хотя бы один раз число меньше 4 выпали) (они выделены жирным шрифтом) m = 27.
Найти вероятность события P (A) = m / n = 27/36 = 0,75
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
Решение задач теории вероятностей.Учитель математики МБОУ Нивнянская общеобразовательная школа, Нечаева Тамара Ивановна
2 слайда
Описание слайда:
Задачи урока: рассмотреть разные типы задач теории вероятностей и методы их решения. Задачи урока: научить распознавать разные типы задач теории вероятностей и улучшить логическое мышление школьников.
3 слайда
Описание слайда:
Задача 1: В произвольном эксперименте симметричная монета бросается 2 раза.Найдите вероятность того, что выпадет одинаковое количество орлов и решек.
4 слайда
Описание слайда:
Задача 2: монета бросается четыре раза. Найдите вероятность того, что решка никогда не выпадет.
5 слайдов
Описание слайда:
Задача 3: В случайном эксперименте симметричная монета бросается дважды. Найдите вероятность того, что выпадет орел ровно один раз.Решение: чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем выбрать из них благоприятные исходы (благоприятные исходы — это результаты, которые удовлетворяют требованиям задачи). В нашем случае благоприятными будут те исходы, при которых при двух подбрасываниях симметричной монеты орел выпадает только один раз. Вероятность события рассчитывается как отношение количества благоприятных исходов к общему количеству исходов.Следовательно, вероятность того, что при двукратном подбрасывании симметричной монеты орла выпадут только один раз, равна: P = 2/4 = 0,5 = 50%. Ответ: вероятность того, что в результате вышеизложенного Эксперимент головы выпадет только раз — 50%. Номер эксперимента 1-й бросок 2-й бросок Сколько раз орлов 1 голова голова 2 2 головы головы 0 3 головы головы 1 4 головы головы 1
Ответ: вероятность того, что в результате вышеизложенного Эксперимент головы выпадет только раз — 50%. Номер эксперимента 1-й бросок 2-й бросок Сколько раз орлов 1 голова голова 2 2 головы головы 0 3 головы головы 1 4 головы головы 1
6 слайдов
Описание слайда:
Задача 4.Игра в кости была брошена один раз. Какова вероятность того, что количество очков больше 4. Решение: случайный эксперимент — бросание кубика. Элементарное событие — число на выпавшей грани. Ответ: 1/3 Всего лиц: 1, 2, 3, 4, 5, 6 Элементарные события: N = 6 N (A) = 2
7 слайдов
Описание слайда:
Задача 5. Биатлонист пять раз стреляет по мишеням. Вероятность поражения цели одним выстрелом 0,8. Найдите вероятность того, что биатлонист попадет в мишени первые три раза и пропустит два последних.Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А = (попадание, попадание, попадание, промах, промах) По формуле умножения вероятностей P (A) = 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 P (A) = 0,512 ∙ 0,04 = 0,02048 ≈ 0,02 Ответ: 0,02
8 слайд
Описание слайда:
Задача 6: В произвольном эксперименте бросаются два кубика. Найдите вероятность того, что сумма выпавших баллов равна 6.Округлите ответ до ближайшей сотой. Решение. Элементарный результат этого эксперимента — упорядоченная пара чисел. Первое число выпадет на первом кубике, второе — на втором. Многие элементарные исходы удобно представлять в виде таблицы. Строки соответствуют количеству очков на первом кубике, столбцы — на втором кубике. Всего элементарных событий n = 36. Запишем сумму выпавших точек в каждой ячейке и закрасим ячейки, в которых сумма равна 6.Их 5. Есть 5. Это означает, что событие A = (сумма выпавших очков 6) благоприятствует 5 элементарным исходам. Следовательно, m = 5. Следовательно, P (A) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
Найдите вероятность того, что сумма выпавших баллов равна 6.Округлите ответ до ближайшей сотой. Решение. Элементарный результат этого эксперимента — упорядоченная пара чисел. Первое число выпадет на первом кубике, второе — на втором. Многие элементарные исходы удобно представлять в виде таблицы. Строки соответствуют количеству очков на первом кубике, столбцы — на втором кубике. Всего элементарных событий n = 36. Запишем сумму выпавших точек в каждой ячейке и закрасим ячейки, в которых сумма равна 6.Их 5. Есть 5. Это означает, что событие A = (сумма выпавших очков 6) благоприятствует 5 элементарным исходам. Следовательно, m = 5. Следовательно, P (A) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
9 слайдов
Описание слайда:
Теорема о формуле вероятности Пусть монета будет брошена n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: где Cnk — количество комбинаций из n элементов по k, которое рассчитывается по формуле:
10 слайдов
Описание слайда:
Задача 7. Монета бросается четыре раза. Найдите вероятность того, что выпадет решка ровно три раза. Решение По условию задачи общее количество бросков было n = 4. Требуемое количество голов: k = 3. Подставим n и k в формулу: Точно так же можно посчитать количество решек: k \ u003d 4 — 3 = 1. Ответ будет таким же. Ответ: 0,25
Монета бросается четыре раза. Найдите вероятность того, что выпадет решка ровно три раза. Решение По условию задачи общее количество бросков было n = 4. Требуемое количество голов: k = 3. Подставим n и k в формулу: Точно так же можно посчитать количество решек: k \ u003d 4 — 3 = 1. Ответ будет таким же. Ответ: 0,25
11 слайдов
Описание слайда:
Задача 8. Монета бросается трижды.Найдите вероятность того, что решка никогда не выпадет. Решение Снова выпишите числа n и k. Так как монета брошена 3 раза, n = 3. А так как решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению. Следовательно C30 = 1. Ответ: 0,125
12 слайдов
Описание слайда:
Задача 9: В произвольном эксперименте симметричная монета бросается 4 раза.Найдите вероятность того, что орел выпадет чаще, чем решка. Решение: чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда будет 1 решка), либо 4 (тогда решки не будет). Найдем вероятность каждого из этих событий. Пусть p1 — вероятность трехкратного выпадения орла. Тогда n = 4, k = 3. Имеем: Теперь находим p2 — вероятность того, что орел выпадет все 4 раза. В данном случае n = 4, k = 4. Имеем: Для получения ответа осталось сложить вероятности p1 и p2.Помните, что вы можете добавлять вероятности только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
Найдем вероятность каждого из этих событий. Пусть p1 — вероятность трехкратного выпадения орла. Тогда n = 4, k = 3. Имеем: Теперь находим p2 — вероятность того, что орел выпадет все 4 раза. В данном случае n = 4, k = 4. Имеем: Для получения ответа осталось сложить вероятности p1 и p2.Помните, что вы можете добавлять вероятности только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
13 слайдов
Описание слайда:
Задача 10: Перед началом волейбольного матча капитаны команд проводят честную жеребьевку, чтобы определить, какая команда начнет игру с мячом. Команда Stator по очереди играет с командами Rotor, Motor и Starter. Найдите вероятность того, что Статор запустит только первую и последнюю игры.Решение. Требуется найти вероятность наступления трех событий: «Статор» запускает первую игру, не запускает вторую игру, начинает третью игру. Вероятность возникновения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5 · 0,5 · 0,5 = 0,125. Ответ: 0,125.
Вероятность каждого из них равна 0,5, откуда находим: 0,5 · 0,5 · 0,5 = 0,125. Ответ: 0,125.
В качестве предисловия.
Всем известно, что у монеты есть две стороны — орел и решка.
Нумизматы считают, что у монеты три стороны — аверс, реверс и край.
И среди них, и среди других мало кто знает, что такое симметричная монета. Но те, кто готовится к ЕГЭ, об этом знают (ну или должны знать :).
В общем, в данной статье речь пойдет о необычной монете, не имеющей ничего общего с нумизматикой, но, в то же время, самой популярной среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и т. Д.В результате у такой монеты тоже нет ребра, то есть действительно есть только две стороны. Главное свойство симметричной монеты — в таких условиях вероятность выпадения орла или решки абсолютно одинакова. И они придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой: «В случайном эксперименте симметричную монету бросают дважды (трижды, четыре раза и т. Д.). Требуется определить вероятность того, что одна из сторон выпадет. определенное количество раз.
Д.). Требуется определить вероятность того, что одна из сторон выпадет. определенное количество раз.
Решение задачи с симметричной монетой
Понятно, что в результате подбрасывания монета выпадет орлом или решкой. Сколько раз зависит от того, сколько бросков вы сделаете. Вероятность выпадения орла или решки вычисляется путем деления количества удовлетворительных результатов на общее количество возможных результатов.
Один бросок
Здесь все просто. Выпадут орел или решка. Те. у нас есть два возможных исхода, один из которых нас удовлетворяет — 1/2 = 50%
Двойной бросок
На два броска может выпасть следующее:
два орла
две головы
решка затем решка
решка затем решка
Те .возможны только четыре варианта. Проблемы с более чем одним рулоном проще всего решить, составив таблицу возможных вариантов. Для простоты обозначим орла как «0», а решки как «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, вам нужно найти вероятность того, что выпадет орел один раз, вам просто нужно посчитать количество подходящих вариантов в таблице. table — т.е. те строки, где орел встречается один раз. Таких линий две.Это означает, что вероятность выпадения одной орла при двух подбрасываниях симметричной монеты составляет 2/4 = 50%
table — т.е. те строки, где орел встречается один раз. Таких линий две.Это означает, что вероятность выпадения одной орла при двух подбрасываниях симметричной монеты составляет 2/4 = 50%
Вероятность того, что орел при двух подбрасываниях выпадет дважды, составляет 1/4 = 25%
Three Roska
Составляем таблицу опций:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, куда мы пришли. 🙂 Да, это двоичные цифры от «0» до «7». Так проще не запутаться с опциями.
Давайте решим задачу из предыдущего пункта — посчитаем вероятность того, что орел выпадет один раз. Есть три строки, где «0» встречается один раз. Это означает, что вероятность выпадения одной головы за три броска симметричной монеты составляет 3/8 = 37,5%
Вероятность того, что орла при трех бросках выпадут дважды, составляет 3/8 = 37,5%, т.е. абсолютно одинаковая .
Вероятность того, что орел при трех бросках выпадет три раза, составляет 1/8 = 12,5%.
Четыре броска
Составляем таблицу опций:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
110251
1100
110251
Вероятность что головы поднимутся один раз.Есть только три строки, где «0» встречается один раз, как и в случае трех бросков. Но вариантов уже шестнадцать. Это означает, что вероятность выпадения одной головы за четыре броска симметричной монеты составляет 3/16 = 18,75%
Вероятность того, что орел при трех бросках выпадет дважды, составляет 6/8 = 75%.
Вероятность того, что орел при трех бросках выпадет три раза, составляет 4/8 = 50%.
Так что с увеличением количества бросков принцип решения задачи не меняется вообще — только в соответствующей прогрессии количество вариантов увеличивается.
В задачах по теории вероятностей, которые представлены в экзамене №4, кроме того, есть задачи по подбрасыванию монеты и по бросанию кости.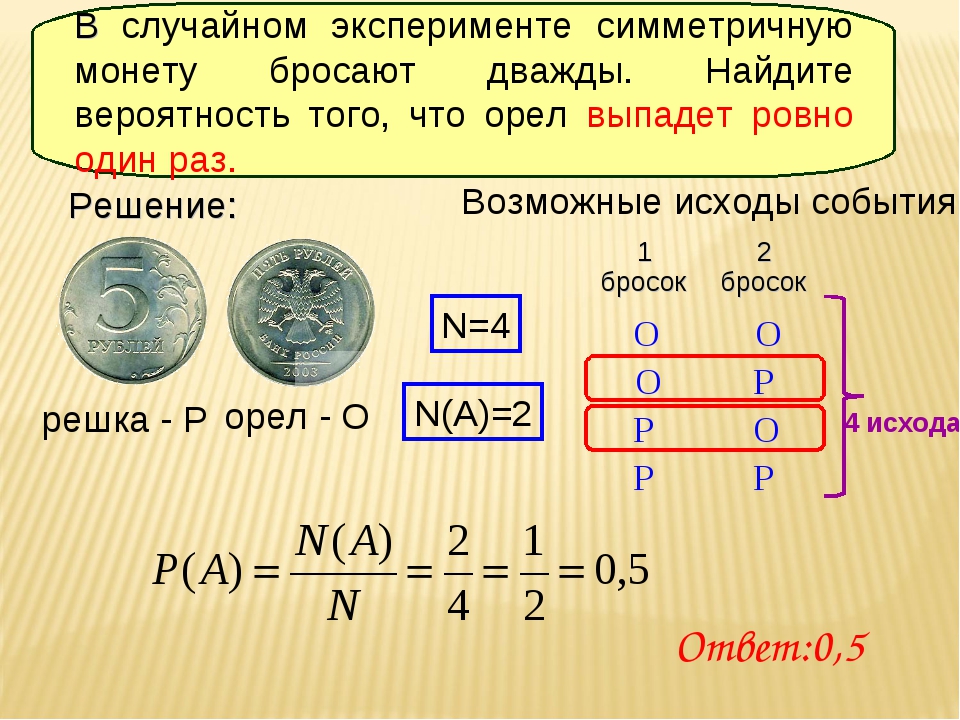 Сегодня мы их разберем.
Сегодня мы их разберем.
Проблемы с подбрасыванием монет
Задача 1. Симметричная монета бросается дважды. Найдите вероятность того, что решка выпадет ровно один раз.
В таких задачах удобно записывать все возможные исходы, записывая их буквами P (решки) и O (решетки).Итак, исход OP означает, что при первом броске выпадает решка, а при втором — решка. В рассматриваемой задаче возможны 4 исхода: PP, RO, OP, OO. Два исхода в пользу события «решка выпадет ровно один раз»: RO и OP. Искомая вероятность равна.
Ответ: 0,5.
Задача 2. Трижды бросается симметричная монета. Найдите вероятность того, что орел будет брошен ровно два раза.
Возможны 8 исходов: RRP, RRO, ROR, ROO, ORR, ORO, OOR, LLC.В пользу события «ровно два раза выпадут головы» три исхода: ROO, ORO, OOR. Искомая вероятность равна.
Ответ: 0,375.
Задача 3.
Перед началом футбольного матча судья подбрасывает монетку, чтобы определить, какая команда начнет игру с мячом. Команда «Изумруд» сыграет три матча с разными командами. Найдите вероятность того, что Изумруд выиграет жеребьевку ровно один раз в этих играх.
Эта задача аналогична предыдущей.Пусть каждый раз, когда выпадает решка, Изумруд выигрывает лот (это предположение не влияет на расчет вероятностей). Тогда возможны 8 исходов: RRR, RRO, ROR, ROO, ORR, ORO, OOR, LLC. Три исхода в пользу события «решка выпадет ровно один раз»: ROO, ORO, OOR. Искомая вероятность равна.
Ответ: 0,375.
Задача 4 … Симметричная монета брошена трижды. Найдите вероятность того, что исход ROO наступит (решка в первый раз, решка во второй и третий).
Как и в предыдущих задачах, здесь 8 исходов: PPR, PPO, POR, ROO, ORR, ORO, OOR, LLC. Вероятность наступления исхода РОО составляет.
Ответ: 0,125.
Проблемы с броском кубиковЗадача 5.
Кости бросаются дважды. Сколько элементарных исходов опыта благоприятствует событию «сумма баллов 8»?
Задача 6 … Две кости бросаются одновременно.Найдите вероятность получения 4 баллов. Результат округлите до сотых.
В общем, если кости брошены, то возможны равные результаты. Такое же количество результатов получается, если один и тот же кубик бросается один раз подряд.
Событию «всего 4» благоприятствуют следующие исходы: 1 — 3, 2 — 2, 3 — 1. Их количество равно 3. Желаемая вероятность равна.
Для расчета примерного значения дроби удобно использовать деление на угол.Таким образом, оно примерно равно 0,083 …, округляем до сотых, имеем 0,08.
Ответ: 0,08
Задача 7 … Три кубика бросаются одновременно. Найдите вероятность того, что сумма будет 5 баллов. Результат округлите до сотых.
Результатом будет три числа: очки, выпавшие на первом, втором и третьем кубиках. В общем, есть одинаково возможные исходы. Событию «5 всего» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1.Их количество 6. Желаемая вероятность. Для расчета примерного значения дроби удобно использовать деление уголком. Примерно получаем 0,027 …, округляем до сотых, получаем 0,03. Источник «Подготовка к ЕГЭ. Математика. Теория вероятности «. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
В общем, есть одинаково возможные исходы. Событию «5 всего» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1.Их количество 6. Желаемая вероятность. Для расчета примерного значения дроби удобно использовать деление уголком. Примерно получаем 0,027 …, округляем до сотых, получаем 0,03. Источник «Подготовка к ЕГЭ. Математика. Теория вероятности «. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
случайных экспериментов | Образец пространства | Испытания
1.3.1 Случайные эксперименты
До того, как бросить кубик, вы не знаете результат.Это пример случайного эксперимента .
В частности, случайный эксперимент — это процесс, с помощью которого мы наблюдаем нечто неопределенное. После
эксперимент, результат случайного эксперимента известен. Результат — результат
случайный эксперимент. Набор всех возможных результатов называется пространством выборки . Таким образом, в
В контексте случайного эксперимента примерное пространство — это наш универсальный набор .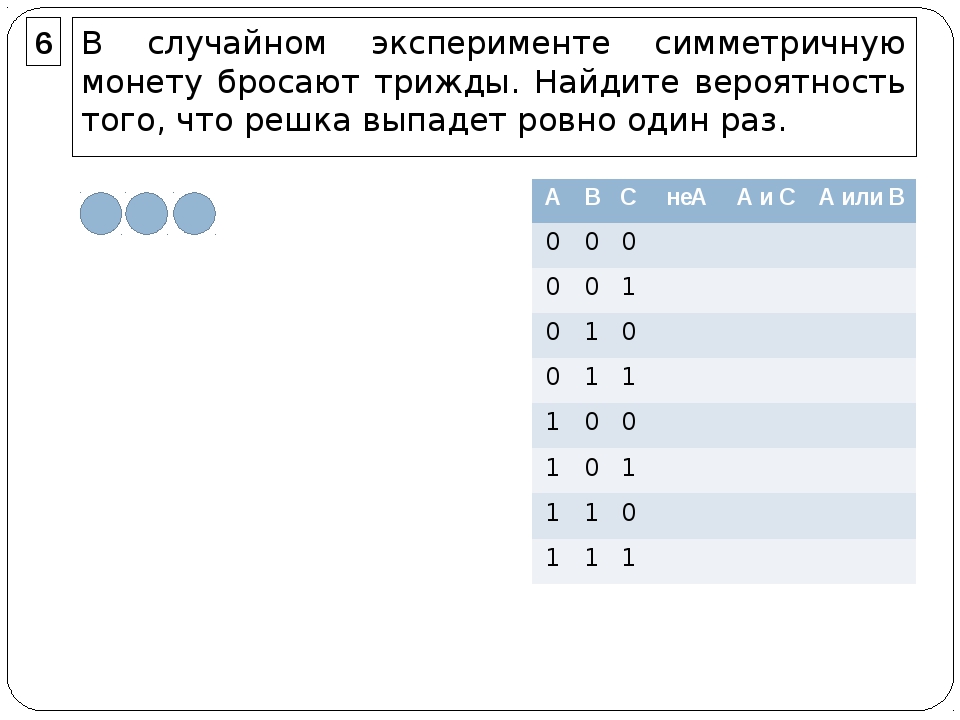 Вот некоторые
примеры случайных экспериментов и их выборочные пространства:
Вот некоторые
примеры случайных экспериментов и их выборочные пространства:
- Случайный эксперимент: подбросить монету; пробел: $ S = \ {Heads, Tails \} $ или, как мы обычно пишем, $ \ {H, T \} $.
- Случайный эксперимент: бросьте кубик; образец пространства: $ S = \ {1, 2, 3, 4, 5, 6 \} $.
- Случайный эксперимент: посмотрите количество iPhone, проданных в магазине Apple в Бостон в $ 2015; образец пространства: $ S = \ {0, 1, 2, 3, \ cdots \} $.
- Случайный эксперимент: наблюдайте за количеством голов в футбольном матче; образец пространства: $ S = \ {0, 1, 2, 3, \ cdots \} $.
Когда мы повторяем случайный эксперимент несколько раз, мы называем каждый из них испытанием .Таким образом, испытание
это частный спектакль случайного эксперимента. В примере с подбрасыванием монеты каждое испытание будет
в результате либо орел, либо решка. Обратите внимание, что пространство выборки определяется на основе того, как вы определяете свой случайный
эксперимент.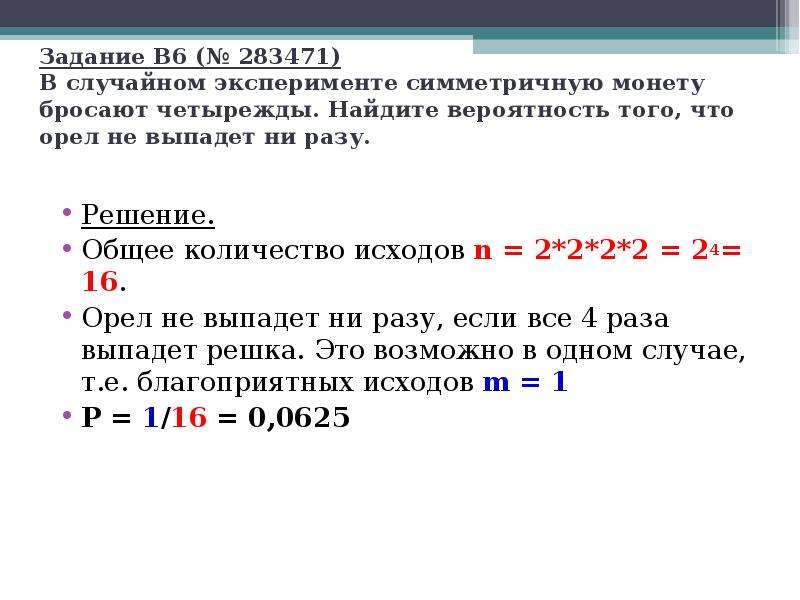 Например,
Например,
Пример
Трижды подбрасываем монету и наблюдаем последовательность орла / решки. Пространство выборки здесь может быть определено как
$$ S = \ {(H, H, H), (H, H, T), (H, T, H), (T, H, H), (H, T, T), (T, H , Т), (Т, Т, Н), (Т, Т, Т) \}.
Наша цель — присвоить вероятность некоторым событиям . Например, предположим, что мы хотели бы
знать вероятность того, что результат броска справедливого кубика будет четным числом. В этом случае наше мероприятие
— множество $ E = \ {2, 4, 6 \} $. Если результат нашего случайного эксперимента принадлежит множеству $ E $, мы говорим, что
произошло событие $ E $. Таким образом, событие — это набор возможных результатов. Другими словами, событие
— это подмножество выборочного пространства, которому мы назначаем вероятность.Хотя мы еще не обсуждали, как
чтобы найти вероятность события, вы можете угадать, что вероятность $ \ {2, 4, 6 \} $ равна
$ 50 $ процентов, что совпадает с $ \ frac {1} {2} $ в соглашении теории вероятностей.
Результат: результат случайного эксперимента.
Пространство образца: набор всех возможных результатов.
Событие: подмножество пробного пространства.
Объединение и пересечение: Если $ A $ и $ B $ являются событиями, то $ A \ cup B $ и $ A \ cap B $ также являются событиями.Помня определение объединения и пересечения, мы замечаем, что $ A \ cup B $ встречается, если $ A $ или $ B $ происходить. Аналогично, $ A \ cap B $ возникает, если встречаются и $ A $ , и $ B $. Аналогично, если $ A_1, A_2, \ cdots, A_n $ события, то событие $ A_1 \ cup A_2 \ cup A_3 \ cdots \ cup A_n $ происходит, если хотя бы одно из Встречается $ A_1, A_2, \ cdots, A_n $. Событие $ A_1 \ cap A_2 \ cap A_3 \ cdots \ cap A_n $ происходит, если встречаются все $ A_1, A_2, \ cdots, A_n $.Полезно помнить, что ключевые слова «или» и «по крайней мере» соответствуют объединениям, а ключевые слова «и» и «все из» соответствуют пересечениям.
Вероятность | Безграничная алгебра
Основы теории вероятностей
Вероятность — это раздел математики, который имеет дело с вероятностью наступления определенных результатов. Есть пять основных правил, или аксиом, которые нужно понять, изучая основы вероятности.
Есть пять основных правил, или аксиом, которые нужно понять, изучая основы вероятности.
Цели обучения
Объясните самые основные и самые важные правила определения вероятности события
Ключевые выводы
Ключевые моменты
- Вероятность — это число, которое может быть присвоено исходам и событиям. Он всегда больше или равен нулю и меньше или равен единице.
- Сумма вероятностей всех исходов должна равняться [латекс] 1 [/ латекс].
- Если два события не имеют общих исходов, вероятность того, что то или иное произойдет, является суммой их индивидуальных вероятностей.
- Вероятность того, что событие не произойдет, равна [latex] 1 [/ latex] минус вероятность того, что событие действительно произойдет.
- Два события [latex] A [/ latex] и [latex] B [/ latex] независимы, если знание того, что одно происходит, не изменяет вероятность того, что другое произойдет.
Ключевые термины
- событие : подмножество выборочного пространства.

- пространство выборки : набор всех результатов эксперимента.
- эксперимент : то, что делается, что дает измеримые результаты, называемые результатами.
- результат : один из индивидуальных результатов, которые могут быть получены в эксперименте.
В дискретной вероятности мы предполагаем хорошо определенный эксперимент , такой как подбрасывание монеты или бросание кости. Каждый индивидуальный результат, который мог произойти, называется исходом . Набор всех результатов называется выборкой пространством , а любое подмножество выборочного пространства называется событием .
Например, рассмотрим эксперимент по подбрасыванию монеты два раза.Есть четыре индивидуальных результата, а именно [латекс] HH, HT, TH, TT. [/ Latex] Таким образом, пробелом является [latex] \ {HH, HT, TH, TT \}. [/ Latex] Событие «в выпадет хотя бы одна решка »будет набором [латекс] \ {HH, HT, TH \}. [/ latex] Если бы монета была обычной монетой, мы бы присвоили вероятность [латекс] 1/4 [/ latex] к каждому исходу.
[/ latex] Если бы монета была обычной монетой, мы бы присвоили вероятность [латекс] 1/4 [/ latex] к каждому исходу.
В теории вероятностей вероятность [латекс] P [/ латекс] некоторого события [латекс] E [/ латекс], обозначаемого [латекс] P (E) [/ латекс], обычно определяется таким образом, что [латекс ] P [/ latex] удовлетворяет ряду аксиом или правил.Ниже перечислены самые основные и самые важные правила.
Правила вероятности
- Вероятность — это число. Он всегда больше или равен нулю и меньше или равен единице . Это можно записать как [латекс] 0 \ leq P (A) \ leq 1 [/ latex]. Невозможное событие или событие, которое никогда не произойдет, имеет вероятность [latex] 0 [/ latex]. Событие, которое происходит всегда, имеет вероятность [latex] 1 [/ latex]. Событие с вероятностью [латекс] 0,5 [/ латекс] произойдет в половине случаев.
- Сумма вероятностей всех возможностей должна равняться [латекс] 1 [/ латекс]. В каждом испытании должен быть какой-то результат, и сумма всех вероятностей составляет 100%, или в данном случае [латекс] 1 [/ латекс].
 Это можно записать как [latex] P (S) = 1 [/ latex], где [latex] S [/ latex] представляет все пространство сэмплов.
Это можно записать как [latex] P (S) = 1 [/ latex], где [latex] S [/ latex] представляет все пространство сэмплов. - Если два события не имеют общих исходов, вероятность того, что одно или другое произойдет, является суммой их индивидуальных вероятностей . Если одно событие происходит в [latex] 30 \% [/ latex] испытаний, другое событие происходит в [latex] 20 \% [/ latex] испытаний, и эти два события не могут происходить вместе (если они не пересекаются) , то вероятность того, что то или иное произойдет, составляет [латекс] 30 \% + 20 \% = 50 \% [/ латекс].Иногда это называют правилом сложения, и его можно упростить следующим образом: [латекс] P (A \ \ text {или} \ B) = P (A) + P (B) [/ latex]. Слово «или» в математике означает то же самое, что и союз, в котором используется следующий символ: [латекс] \ чашка [/ латекс]. Таким образом, когда [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, мы имеем [latex] P (A \ cup B) = P (A) + P (B) [/ latex].
- Вероятность того, что событие не произойдет, равна [латекс] 1 [/ latex] минус вероятность того, что событие действительно произойдет .
 c [/ latex] является дополнением к [latex] A [/ latex].
c [/ latex] является дополнением к [latex] A [/ latex]. - Два события [латекс] A [/ латекс] и [латекс] B [/ латекс] являются независимыми, если знание того, что одно происходит, не изменяет вероятность того, что другое произойдет . Это часто называют правилом умножения. Если [латекс] A [/ latex] и [latex] B [/ latex] независимы, то [latex] P (A \ \ text {and} \ B) = P (A) P (B) [/ latex] . Слово «и» в математике означает то же самое, что и пересечение, в котором используется следующий символ: [латекс] \ крышка [/ латекс].Следовательно, когда A и B независимы, мы имеем [latex] P (A \ cap B) = P (A) P (B). [/ Latex]
Расширение примера
Продолжая описанный выше пример подбрасывания двух монет, присвойте вероятность [latex] 1/4 [/ latex] каждому из результатов [latex] 4 [/ latex]. Мы рассматриваем каждое из пяти правил выше в контексте этого примера.
1. Обратите внимание, что каждая вероятность составляет [латекс] 1/4 [/ латекс], что находится между [латекс] 0 [/ латекс] и [латекс] 1 [/ латекс]. c) = \ frac {1} {4} = 1 — \ frac {3} {4} = 1-P (A).[/ латекс]
c) = \ frac {1} {4} = 1 — \ frac {3} {4} = 1-P (A).[/ латекс]
5. Если [latex] A [/ latex] — это событие, когда первый флип — это решка, а [latex] B [/ latex] — это событие, когда второй флип — это хедсы, то [latex] A [/ latex ] и [латекс] B [/ латекс] независимы. У нас есть [латекс] A = \ {HT, HH \} [/ latex] и [latex] B = \ {TH, HH \} [/ latex] и [латекс] A \ cap B = \ {HH \}. [/ latex] Обратите внимание, что [латекс] P (A \ cap B) = \ frac {1} {4} = \ frac {1} {2} \ cdot \ frac {1} {2} = P (A) P (B). [/ Латекс]
Кубик: Игральные кости часто используются при изучении правил вероятности.
Союзы и пересечения
Объединение и пересечение — два ключевых понятия в теории множеств и вероятности.
Цели обучения
Приведите примеры пересечения и объединения двух или более множеств
Ключевые выводы
Ключевые моменты
- Объединение двух или более наборов — это набор, который содержит все элементы двух или более наборов.
 Союз обозначается символом [латекс] \ чашка [/ латекс].
Союз обозначается символом [латекс] \ чашка [/ латекс]. - Общее правило сложения вероятностей для объединения двух событий гласит, что [латекс] P (A \ cup B) = P (A) + P (B) -P (A \ cap B) [/ latex], где [latex ] A \ cap B [/ latex] — это пересечение двух наборов.
- Правило сложения может быть сокращено, если наборы не пересекаются: [латекс] P (A \ cup B) = P (A) + P (B) [/ latex]. Это может быть даже расширено на большее количество множеств, если все они не пересекаются: [латекс] P (A \ cup B \ cup C) = P (A) + P (B) + P (C) [/ latex].
- Пересечение двух или более наборов — это набор элементов, общих для каждого набора. Символ [латекс] \ крышка [/ латекс] используется для обозначения пересечения.
- Когда события независимы, мы можем использовать правило умножения для независимых событий, которое гласит, что [latex] P (A \ cap B) = P (A) P (B) [/ latex].
Ключевые термины
- независимый : Не зависит от чего-либо еще.

- непересекающиеся : не имеющие общих членов; имеющий пересечение, равное пустому множеству.
Введение
Вероятность использует математические идеи множеств, как мы видели в определении как выборочного пространства эксперимента, так и в определении события. Чтобы выполнить базовые вычисления вероятности, нам необходимо рассмотреть идеи теории множеств, относящиеся к операциям объединения, пересечения и дополнения множеств.
Союз
Объединение двух или более наборов — это набор, который содержит все элементы каждого из наборов; элемент входит в объединение, если он принадлежит хотя бы к одному из множеств. Символ объединения — [латекс] \ чашка [/ латекс] и связан со словом «или», потому что [латекс] A \ чашка B [/ latex] — это набор всех элементов, которые находятся в [латексе] A [/ latex] или [latex] B [/ latex] (или оба). Чтобы найти объединение двух наборов, перечислите элементы, которые находятся в одном (или обоих) наборах. В терминах диаграммы Венна объединение наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано как два полностью заштрихованных взаимосвязанных круга.
В терминах диаграммы Венна объединение наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано как два полностью заштрихованных взаимосвязанных круга.
Объединение двух наборов: Закрашенная диаграмма Венна показывает объединение набора [латекс] A [/ латекс] (круг слева) с набором [латекс] B [/ латекс] (круг справа). Это может быть сокращено как [латекс] A \ чашка B [/ латекс].
В символах, поскольку объединение [latex] A [/ latex] и [latex] B [/ latex] содержит все точки, которые находятся в [latex] A [/ latex] или [latex] B [/ latex] или оба, определение союза:
[латекс] \ Displaystyle A \ чашка B = \ {x: x \ in A \ text {или} \ x \ in B \} [/ латекс]
Например, если [латекс] A = \ {1, 3, 5, 7 \} [/ латекс] и [латекс] B = \ {1, 2, 4, 6 \} [/ латекс], то [латекс ] A \ cup B = \ {1, 2, 3, 4, 5, 6, 7 \} [/ латекс].Обратите внимание, что элемент [latex] 1 [/ latex] не указан дважды в объединении, хотя он присутствует в обоих наборах [latex] A [/ latex] и [latex] B [/ latex]. Это приводит нас к общему правилу сложения для объединения двух событий:
Это приводит нас к общему правилу сложения для объединения двух событий:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) — P (A \ cap B) [/ латекс]
Где [латекс] P (A \ cap B) [/ latex] — пересечение двух наборов. Мы должны вычесть это, чтобы избежать двойного счета включения элемента.
Если наборы [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, то событие [latex] A \ cap B [/ latex] не имеет результатов и представляет собой пустой набор, обозначенный как [latex] \ emptyset [/ latex], вероятность которого равна нулю.Таким образом, приведенное выше правило может быть сокращено только для непересекающихся множеств:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) [/ латекс]
Это может быть даже расширено на большее количество наборов, если все они не пересекаются:
[латекс] \ Displaystyle P (A \ чашка B \ чашка C) = P (A) + P (B) + P (C) [/ латекс]
Перекресток
Пересечение двух или более наборов — это набор элементов, общих для каждого из наборов. Элемент находится в пересечении, если он принадлежит всем множествам. Символ пересечения — [латекс] \ cap [/ latex] и связан со словом «и», потому что [latex] A \ cap B [/ latex] — это набор элементов, которые находятся в [latex] A [ / latex] и [latex] B [/ latex] одновременно.Чтобы найти пересечение двух (или более) наборов, включайте только те элементы, которые перечислены в обоих (или во всех) наборах. В терминах диаграммы Венна пересечение двух наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано в заштрихованной области в середине двух взаимосвязанных кругов.
Элемент находится в пересечении, если он принадлежит всем множествам. Символ пересечения — [латекс] \ cap [/ latex] и связан со словом «и», потому что [latex] A \ cap B [/ latex] — это набор элементов, которые находятся в [latex] A [ / latex] и [latex] B [/ latex] одновременно.Чтобы найти пересечение двух (или более) наборов, включайте только те элементы, которые перечислены в обоих (или во всех) наборах. В терминах диаграммы Венна пересечение двух наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано в заштрихованной области в середине двух взаимосвязанных кругов.
Пересечение двух наборов: Набор [латекс] A [/ latex] — круг слева, набор [латекс] B [/ latex] — круг справа, а пересечение [латекса] A [/ латекс] и [латекс] B [/ латекс] или [латекс] A \ cap B [/ latex] — это заштрихованная часть в середине.
В математической записи пересечение [латекса] A [/ latex] и [latex] B [/ latex] записывается как [latex] A \ cap B = \ {x: x \ in A \ \ text {и} \ x \ in B \} [/ латекс]. Например, если [латекс] A = \ {1, 3, 5, 7 \} [/ латекс] и [латекс] B = \ {1, 2, 4, 6 \} [/ латекс], то [латекс] A \ cap B = \ {1 \} [/ latex], потому что [latex] 1 [/ latex] — единственный элемент, который присутствует в обоих наборах [latex] A [/ latex] и [latex] B [/ latex].
Например, если [латекс] A = \ {1, 3, 5, 7 \} [/ латекс] и [латекс] B = \ {1, 2, 4, 6 \} [/ латекс], то [латекс] A \ cap B = \ {1 \} [/ latex], потому что [latex] 1 [/ latex] — единственный элемент, который присутствует в обоих наборах [latex] A [/ latex] и [latex] B [/ latex].
Когда события независимы, то есть результат одного события не влияет на результат другого события, мы можем использовать правило умножения для независимых событий, которое гласит:
[латекс] \ Displaystyle P (A \ cap B) = P (A) P (B) [/ латекс]
Например, предположим, что мы дважды подбрасывали монету и хотим узнать вероятность того, что выпадет две орла.Поскольку первый бросок не влияет на второй, события независимы. Скажем, это событие, когда первый бросок — орел, а [латекс] B [/ latex] — это событие, когда второй бросок — это орел, тогда [латекс] P (A \ cap B) = \ frac {1} {2 } \ cdot \ frac {1} {2} = \ frac {1} {4} [/ latex].
Условная вероятность
Условная вероятность события — это вероятность того, что событие произойдет, при условии, что произошло другое событие.
Цели обучения
Объясните значение теоремы Байеса для манипулирования условными вероятностями
Ключевые выводы
Ключевые моменты
- Условная вероятность [latex] P (B \ vert A) [/ latex] события [latex] B [/ latex], учитывая событие [latex] A [/ latex], определяется следующим образом: [latex] P (B | A) = \ frac {P (A \ cap B)} {P (A)} [/ latex], когда [latex] P (A)> 0 [/ latex].
- Если знание о том, что событие [latex] A [/ latex] происходит, не изменяет вероятность того, что событие [latex] B [/ latex] происходит, то [latex] A [/ latex] и [latex] B [/ latex] являются независимыми событиями, и, таким образом, [latex] P (B | A) = P (B) [/ latex].
- Математически теорема Байеса дает соотношение между вероятностями [латекс] A [/ латекс] и [латекс] B [/ латекс], [латекс] P (A) [/ латекс] и [латекс] P (B) [/ latex] и условные вероятности [latex] A [/ latex] для [latex] B [/ latex] и [latex] B [/ latex] для [latex] A [/ latex], [latex] P (A | B) [/ латекс] и [латекс] P (B | A) [/ латекс].
 В наиболее распространенной форме это: [латекс] P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ latex].
В наиболее распространенной форме это: [латекс] P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ latex].
Ключевые термины
- условная вероятность : вероятность того, что событие произойдет при ограничительном предположении, что произошло другое событие или что произошло сочетание других событий
- независимый : не зависимый; не случайный или зависящий от чего-то еще; свободный.
Вероятность [латекса] B [/ латекса] с учетом того, что [латекс] A [/ латекс] имел место
Наша оценка вероятности события может измениться, если мы узнаем, что произошло какое-то другое событие.Например, вероятность того, что на свернутом кубике будет [латекс] 2 [/ латекс], равна [латекс] 1/6 [/ латекс] без какой-либо другой информации, но если кто-то посмотрит на кубик и скажет вам, что это четный число, теперь вероятность [latex] 1/3 [/ latex], что это [latex] 2 [/ latex]. Обозначение [латекс] P (B | A) [/ latex] указывает условную вероятность, то есть указывает вероятность одного события при условии, что мы знаем, что другое событие произошло. Бар «|» может читаться как «данный», так что [латекс] P (B | A) [/ latex] читается как «вероятность [латекса] B [/ latex] с учетом того, что [latex] A [/ latex] произошло ».
Бар «|» может читаться как «данный», так что [латекс] P (B | A) [/ latex] читается как «вероятность [латекса] B [/ latex] с учетом того, что [latex] A [/ latex] произошло ».
Условная вероятность [latex] \ displaystyle P (B | A) [/ latex] события [latex] B [/ latex], учитывая событие [latex] A [/ latex], определяется следующим образом:
[латекс] \ Displaystyle P (B | A) = \ frac {P (A \ cap B)} {P (A)} [/ латекс]
Когда [латекс] P (A)> 0 [/ латекс]. Обязательно запомните различные роли [латекса] B [/ латекса] и [латекса] A [/ латекса] в этой формуле. Набор после бара — это тот, который, как мы предполагаем, произошел, и его вероятность входит в знаменатель формулы.
Пример
Предположим, что монета подбрасывается 3 раза, что дает пробел:
[латекс] S = \ {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT \} [/ латекс]
Каждый индивидуальный исход имеет вероятность [латекс] 1/8 [/ латекс].Предположим, что [latex] B [/ latex] — это событие, при котором выпадает хотя бы одна голова, а [latex] A [/ latex] — это событие, когда все монеты [latex] 3 [/ latex] одинаковы. Тогда вероятность [latex] B [/ latex] для [latex] A [/ latex] равна [latex] 1/2 [/ latex], поскольку [latex] A \ cap B = \ {HHH \} [/ latex ] с вероятностью [латекс] 1/8 [/ латекс] и [латекс] A = \ {HHH, TTT \} [/ latex] с вероятностью [латекс] 2/8 [/ латекс] и [латекс] \ frac {1/8} {2/8} = \ frac {1} {2}. [/ latex]
Тогда вероятность [latex] B [/ latex] для [latex] A [/ latex] равна [latex] 1/2 [/ latex], поскольку [latex] A \ cap B = \ {HHH \} [/ latex ] с вероятностью [латекс] 1/8 [/ латекс] и [латекс] A = \ {HHH, TTT \} [/ latex] с вероятностью [латекс] 2/8 [/ латекс] и [латекс] \ frac {1/8} {2/8} = \ frac {1} {2}. [/ latex]
Независимость
Условная вероятность [латекс] P (B | A) [/ latex] не всегда равна безусловной вероятности [latex] P (B) [/ latex].Причина в том, что возникновение события [latex] A [/ latex] может предоставить дополнительную информацию, которая может изменить вероятность того, что событие [latex] B [/ latex] произойдет. Если знание о том, что событие [latex] A [/ latex] происходит, не изменяет вероятность того, что событие [latex] B [/ latex] происходит, то [latex] A [/ latex] и [latex] B [/ latex] являются независимые события, и, таким образом, [латекс] P (B | A) = P (B) [/ latex].
Теорема Байеса
В теории вероятностей и статистике теорема Байеса (альтернативно закон Байеса или правило Байеса) является важным результатом при математическом манипулировании условными вероятностями. Его можно вывести из основных аксиом вероятности.
Его можно вывести из основных аксиом вероятности.
Математически теорема Байеса дает соотношение между вероятностями [латекс] A [/ латекс] и [латекс] B [/ латекс], [латекс] P (A) [/ латекс] и [латекс] P (B) [/ latex], а также условные вероятности [латекса] A [/ latex] для [latex] B [/ latex] и [latex] B [/ latex] для [latex] A [/ latex]. В наиболее распространенной форме это:
[латекс] \ Displaystyle P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ латекс]
Это может быть легче запомнить в альтернативной симметричной форме:
[латекс] \ Displaystyle \ frac {P (A | B)} {P (B | A)} = \ frac {P (A)} {P (B)} [/ латекс]
Пример:
Предположим, кто-то сказал вам, что приятно поговорил с кем-то в поезде.Ничего не зная об этом разговоре, вероятность того, что они говорили с женщиной, составляет [латекс] 50 \% [/ латекс]. Теперь предположим, что они также сказали вам, что у этого человека были длинные волосы. Сейчас более вероятно, что они разговаривали с женщиной, поскольку женщины в этом городе чаще имеют длинные волосы, чем мужчины. Теорема Байеса может быть использована для расчета вероятности того, что это женщина.
Теорема Байеса может быть использована для расчета вероятности того, что это женщина.
Чтобы увидеть, как это делается, пусть [latex] W [/ latex] представляет событие, в котором беседа велась с женщиной, а [latex] L [/ latex] обозначает событие, когда беседа велась с длительным — волосатый человек.Можно предположить, что для этого примера женщины составляют половину населения. Итак, не зная ничего другого, вероятность того, что [латекс] W [/ латекс] встречается, равна [латексу] P (W) = 0,5 [/ латекс].
Предположим, также известно, что [латекс] 75% [/ латекс] женщин в этом городе имеют длинные волосы, которые мы обозначаем как [латекс] P (L | W) = 0,75 [/ latex]. Точно так же предположим, что известно, что [латекс] 25 \% [/ латекс] мужчин в этом городе имеют длинные волосы, или [латекс] P (L | M) = 0,25 [/ латекс], где [латекс] M [/ латекс] является дополнительным элементом [латекс] W [/ латекс], т.е.е., событие, при котором беседа велась с мужчиной (при условии, что каждый человек либо мужчина, либо женщина).
Наша цель — вычислить вероятность того, что разговор велся с женщиной, учитывая тот факт, что у человека были длинные волосы, или, в наших обозначениях, [латекс] P (W | L) [/ латекс]. Используя формулу теоремы Байеса, получаем:
[латекс] \ displaystyle \ begin {align} P (W | L) & = \ frac {P (L | W) P (W)} {P (L)} \\ & = \ frac {P (L | W) P (W)} {P (L | W) P (W) + P (L | M) P (M)} \\ & = \ frac {0.c [/ latex] или [latex] \ bar {A} [/ latex].
Ключевые термины
- взаимоисключающие : описание нескольких событий или состояний, при которых возникновение любого из них подразумевает ненаступление всех остальных
- исчерпывающий : включая все возможные элементы
Что такое дополнительные события?
В теории вероятностей дополнением к любому событию [latex] A [/ latex] является событие [latex] [\ text {not} \ A] [/ latex], т. c [/ latex] или [latex] \ bar {A} [/ latex] .
c [/ latex] или [latex] \ bar {A} [/ latex] .
Простые примеры
Типичным примером, используемым для демонстрации дополнительных событий, является подбрасывание монеты. Допустим, монета подбрасывается и предполагается, что она не может упасть на край. Он может приземлиться либо на голову, либо на хвост. Других возможностей нет (исчерпывающие), и оба события не могут происходить одновременно (взаимоисключающие). Поскольку эти два события дополняют друг друга, мы знаем, что [latex] P (\ text {Head}) + P (\ text {tails}) = 1 [/ latex].
Подбрасывание монеты: Часто в спортивных играх, например в теннисе, подбрасывание монеты используется для определения того, кто подаст первым, поскольку орел и решка дополняют друг друга.
Еще один простой пример дополнительных событий — вытаскивание мяча из мешка. Допустим, в пакете три пластиковых мяча. Один синий и два красных. Предполагая, что каждый мяч имеет равные шансы вытащить из мешка, мы знаем, что [latex] P (\ text {blue}) = \ frac {1} {3} [/ latex] и [latex] P (\ текст {красный}) = \ frac {2} {3} [/ latex]. Поскольку мы можем выбрать только синий или красный (исчерпывающий), и мы не можем выбрать оба одновременно (взаимоисключающие), выбор синего и красного являются дополнительными событиями, а [латекс] P (\ text {blue}) + P ( \ text {red}) = 1 [/ latex].
Поскольку мы можем выбрать только синий или красный (исчерпывающий), и мы не можем выбрать оба одновременно (взаимоисключающие), выбор синего и красного являются дополнительными событиями, а [латекс] P (\ text {blue}) + P ( \ text {red}) = 1 [/ latex].
Наконец, давайте рассмотрим не пример дополнительных событий. Если бы вас попросили выбрать любое число, вы могли бы подумать, что это число может быть простым или составным. Ясно, что число не может быть одновременно простым и составным, так что это учитывает взаимоисключающее свойство. Однако быть простым или составным не являются исчерпывающими, потому что число 1 в математике обозначается как «уникальное». ”
Правило добавления
Правило сложения гласит, что вероятность двух событий — это сумма вероятностей того, что одно из них произойдет, минус вероятность того, что оба события произойдут.
Цели обучения
Рассчитайте вероятность события с помощью правила сложения
Ключевые выводы
Ключевые моменты
- Правило сложения: [латекс] P (A \ cup B) = P (A) + P (B) -P (A \ cap B).
 [/ Latex]
[/ Latex] - Последний член учитывался дважды, один раз в [латексе] P (A) [/ latex] и один раз в [латексе] P (B) [/ latex], поэтому его необходимо вычесть один раз, чтобы он не удваивался. -считано.
- Если [латекс] A [/ латекс] и [латекс] B [/ латекс] не пересекаются, то [латекс] P (A \ cap B) = 0 [/ latex], поэтому формула становится [латекс] P (A \ чашка B) = P (A) + P (B).[/ латекс]
Ключевые термины
- вероятность : относительная вероятность того, что событие произойдет.
Закон о добавлении
Закон сложения вероятностей (иногда называемый правилом сложения или правилом сумм) гласит, что вероятность появления [латекс] A [/ латекс] или [латекс] B [/ латекс] является суммой вероятностей того, что [latex] A [/ latex] произойдет, и что [latex] B [/ latex] произойдет, за вычетом вероятности того, что оба [latex] A [/ latex] и [latex] B [/ latex] произойдут.Правило сложения резюмируется формулой:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) -P (A \ cap B) [/ латекс]
Рассмотрим следующий пример. При вытягивании одной карты из колоды игральных карт [latex] 52 [/ latex], какова вероятность получить черву или лицевую карту (король, дама или валет)? Пусть [latex] H [/ latex] обозначает рисование сердца, а [latex] F [/ latex] обозначает рисование лицевой карты. Так как есть [латексные] 13 [/ латексные] червы и в общей сложности [латексные] 12 [/ латексные] лицевые карты ([латекс] 3 [/ латекс] каждой масти: пики, червы, бубны и трефы), но только [latex] 3 [/ latex] лицевых карты червей, получаем:
При вытягивании одной карты из колоды игральных карт [latex] 52 [/ latex], какова вероятность получить черву или лицевую карту (король, дама или валет)? Пусть [latex] H [/ latex] обозначает рисование сердца, а [latex] F [/ latex] обозначает рисование лицевой карты. Так как есть [латексные] 13 [/ латексные] червы и в общей сложности [латексные] 12 [/ латексные] лицевые карты ([латекс] 3 [/ латекс] каждой масти: пики, червы, бубны и трефы), но только [latex] 3 [/ latex] лицевых карты червей, получаем:
[латекс] \ Displaystyle P (H) = \ frac {13} {52} [/ латекс]
[латекс] \ Displaystyle P (F) = \ frac {12} {52} [/ латекс]
[латекс] \ displaystyle P (F \ cap H) = \ frac {3} {52} [/ latex]
Используя правило сложения, получаем:
[латекс] \ displaystyle \ begin {align} P (H \ cup F) & = P (H) + P (F) -P (H \ cap F) \\ & = \ frac {13} {52} + \ frac {12} {52} — \ frac {3} {52} \ end {align} [/ latex]
Причина вычитания последнего члена состоит в том, что в противном случае мы будем считать среднюю часть дважды (поскольку [латекс] H [/ латекс] и [латекс] F [/ латекс] перекрываются).
Правило сложения для непересекающихся событий
Предположим, что [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, их пересечение пусто. Тогда вероятность их пересечения равна нулю. В условных обозначениях: [латекс] P (A \ cap B) = 0 [/ латекс]. Затем закон сложения упрощается до:
[латекс] P (A \ cup B) = P (A) + P (B) \ qquad \ text {when} \ qquad A \ cap B = \ emptyset [/ latex]
Символ [latex] \ emptyset [/ latex] представляет собой пустой набор, который указывает, что в этом случае [latex] A [/ latex] и [latex] B [/ latex] не имеют общих элементов (они имеют не перекрывать).
Пример:
Предположим, что карта взята из колоды из 52 игральных карт: какова вероятность получить короля или королеву? Пусть [latex] A [/ latex] представляет событие, когда вытаскивается король, а [latex] B [/ latex] представляет событие, когда вытаскивается ферзь. Эти два события не пересекаются, поскольку нет королей, которые также были бы королевами. Таким образом:
Таким образом:
[латекс] \ displaystyle \ begin {align} P (A \ cup B) & = P (A) + P (B) \\ & = \ frac {4} {52} + \ frac {4} {52} \\ & = \ frac {8} {52} \\ & = \ frac {2} {13} \ end {align} [/ latex]
Правило умножения
Правило умножения гласит, что вероятность того, что [latex] A [/ latex] и [latex] B [/ latex] встречаются, равна вероятности того, что [latex] B [/ latex] встречается, умноженная на условную вероятность того, что [latex] ] A [/ latex] встречается при условии, что встречается [latex] B [/ latex].
Цели обучения
Примените правило умножения, чтобы вычислить вероятность того, что [latex] A [/ latex] и [latex] B [/ latex] встречаются.
Ключевые выводы
Ключевые моменты
- Правило умножения можно записать так: [latex] P (A \ cap B) = P (B) \ cdot P (A | B) [/ latex].
- Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.
Ключевые термины
- пробел : Набор всех возможных результатов игры, эксперимента или другой ситуации.

Правило умножения
В теории вероятностей правило умножения гласит, что вероятность того, что [латекс] A [/ latex] и [latex] B [/ latex] встречается, равна вероятности того, что [латекс] A [/ latex] встречается, умноженная на условную вероятность что [latex] B [/ latex] встречается, учитывая, что мы знаем, что [latex] A [/ latex] уже произошло. Это правило можно записать:
[латекс] \ Displaystyle P (A \ cap B) = P (B) \ cdot P (A | B) [/ латекс]
Переключая роли [latex] A [/ latex] и [latex] B [/ latex], мы также можем записать правило как:
[латекс] \ Displaystyle P (A \ cap B) = P (A) \ cdot P (B | A) [/ латекс]
Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.То есть в уравнении [латекс] \ displaystyle P (A | B) = \ frac {P (A \ cap B)} {P (B)} [/ latex], если мы умножим обе стороны на [латекс] P (B) [/ latex], получаем Правило умножения.
Правило полезно, когда мы знаем оба [латекс] P (B) [/ latex] и [латекс] P (A | B) [/ latex], или оба [латекс] P (A) [/ latex] и [ латекс] П (В | А). [/ латекс]
[/ латекс]
Пример
Предположим, что мы вытягиваем две карты из колоды карт и пусть [latex] A [/ latex] будет событием, когда первая карта является тузом, а [latex] B [/ latex] будет событием, что вторая карта туз, то:
[латекс] \ Displaystyle P (A) = \ frac {4} {52} [/ латекс]
А:
[латекс] \ displaystyle P \ left ({B} | {A} \ right) = \ frac {3} {51} [/ latex]
Знаменатель во втором уравнении [латекс] 51 [/ латекс], поскольку мы знаем, что карта уже разыграна.Следовательно, всего осталось [латекс] 51 [/ латекс]. Мы также знаем, что первой картой был туз, поэтому:
[латекс] \ displaystyle \ begin {align} P (A \ cap B) & = P (A) \ cdot P (B | A) \\ & = \ frac {4} {52} \ cdot \ frac {3 } {51} \\ & = 0,0045 \ end {align} [/ latex]
Независимое событие
Обратите внимание, что когда [latex] A [/ latex] и [latex] B [/ latex] независимы, мы имеем, что [latex] P (B | A) = P (B) [/ latex], поэтому формула становится [латекс] P (A \ cap B) = P (A) P (B) [/ latex], с которым мы столкнулись в предыдущем разделе. В качестве примера рассмотрим эксперимент по бросанию игральной кости и подбрасыванию монеты. Вероятность того, что мы получим [латекс] 2 [/ latex] на кубике и решки на монете, равна [latex] \ frac {1} {6} \ cdot \ frac {1} {2} = \ frac {1 } {12} [/ latex], поскольку эти два события независимы.
В качестве примера рассмотрим эксперимент по бросанию игральной кости и подбрасыванию монеты. Вероятность того, что мы получим [латекс] 2 [/ latex] на кубике и решки на монете, равна [latex] \ frac {1} {6} \ cdot \ frac {1} {2} = \ frac {1 } {12} [/ latex], поскольку эти два события независимы.
Независимость
Сказать, что два события независимы, означает, что возникновение одного не влияет на вероятность другого.
Цели обучения
Объяснить понятие независимости применительно к теории вероятностей
Ключевые выводы
Ключевые моменты
- Два события являются независимыми, если выполняются следующие условия: [latex] P (A | B) = P (A) [/ latex], [latex] P (B | A) = P (B) [/ latex], и [латекс] P (A \ \ text {and} \ B) = P (A) \ cdot P (B) [/ latex].
- Если хотя бы одно из этих условий верно, то все они верны.
- Если события [latex] A [/ latex] и [latex] B [/ latex] независимы, то вероятность возникновения [latex] A [/ latex] не влияет на вероятность [latex] B [/ latex] происходит и наоборот.

Ключевые термины
- независимость : возникновение одного события не влияет на вероятность наступления другого.
- теория вероятностей : математическое исследование вероятности (вероятность возникновения случайных событий с целью прогнозирования поведения определенных систем).
Независимые мероприятия
В теории вероятностей утверждение, что два события независимы, означает, что возникновение одного не влияет на вероятность того, что другое произойдет. Другими словами, если события [латекс] A [/ латекс] и [латекс] B [/ латекс] независимы, то вероятность возникновения [латекса] A [/ латекса] не влияет на вероятность [латекса] B [ / латекс] и наоборот. Концепция независимости распространяется на коллекции, состоящие из более чем двух событий.
Два события являются независимыми, если выполняется одно из следующих условий:
- [латекс] \ Displaystyle P (A | B) = P (A) [/ латекс]
- [латекс] \ Displaystyle P (B | A) = P (B) [/ латекс]
- [латекс] \ Displaystyle P (A \ \ text {и} \ B) = P (A) \ cdot P (B) [/ латекс]
Чтобы показать, что два события независимы, вы должны показать только одно из перечисленных выше условий. Если любое из этих условий верно, то все они верны.
Если любое из этих условий верно, то все они верны.
Переводя символы в слова, первые два математических утверждения, перечисленные выше, говорят, что вероятность события с условием такая же, как вероятность события без условия. Для независимых событий условие не меняет вероятность события. Третье утверждение говорит, что вероятность возникновения обоих независимых событий [латекс] A [/ latex] и [латекс] B [/ latex] такая же, как вероятность возникновения [latex] A [/ latex], умноженная на вероятность [латекс] Б [/ латекс] встречающийся.
В качестве примера представьте, что вы последовательно выбираете две карты из полной колоды игральных карт. Два выбора не являются независимыми. Результат первого выбора изменяет оставшуюся колоду и влияет на вероятность второго выбора. Это называется выбором «без замены», потому что первая карта не была заменена в колоду до того, как была выбрана вторая карта.
Однако предположим, что вы должны были выбрать две карты «с заменой», вернув свою первую карту в колоду и перетасовав колоду перед тем, как выбрать вторую карту. Поскольку колода карт является полной для обоих вариантов выбора, первый выбор не влияет на вероятность второго выбора. При выборе карт с заменой выбор не зависит.
Поскольку колода карт является полной для обоих вариантов выбора, первый выбор не влияет на вероятность второго выбора. При выборе карт с заменой выбор не зависит.
независимых событий: выбор двух карт из колоды, сначала выбрав одну, затем заменив ее в колоде перед выбором второй, является примером независимых событий.
Рассмотрим роль справедливого кубика, которая представляет собой еще один пример независимых событий. Если человек, играющий роль двоих, умирает, результат первого броска не влияет на вероятность результата второго броска.
Пример
Два друга играют в бильярд и решают подбросить монетку, чтобы определить, кто будет играть первым в каждом раунде. В первых двух раундах монета выпадает орлом. Они решают сыграть в третий раунд и снова подбрасывают монету. Какова вероятность того, что монета снова выпадет орлом?
Во-первых, обратите внимание, что каждое подбрасывание монеты — независимое событие. Сторона, на которую приземляется монета, не зависит от того, что произошло ранее.
При любом подбрасывании монеты существует [latex] {\ frac {1} {2}} [/ latex] шанс, что монета упадет орлом.Таким образом, вероятность того, что монета упадет орлом во время третьего раунда, равна [latex] {\ frac {1} {2}} [/ latex].
Пример
При подбрасывании монеты, какова вероятность получить решки [латекс] 5 [/ латекс] раз подряд?
Напомним, что каждый бросок монеты независим, и вероятность выпадения решки равна [латекс] {\ frac {1} {2}} [/ latex] для любого подбрасывания. Также напомним, что для любых двух независимых событий A и B справедливо следующее утверждение:
[латекс] \ Displaystyle P (A \ \ text {и} \ B) = P (A) \ CDOT P (B) [/ латекс]
Наконец, концепция независимости распространяется на коллекции более чем [latex] 2 [/ latex] событий.
Следовательно, вероятность получить хвосты [латекс] 4 [/ латекс] раза подряд составляет:
[латекс] \ displaystyle {\ frac {1} {2}} \ cdot {\ frac {1} {2}} \ cdot {\ frac {1} {2}} \ cdot {\ frac {1} {2 }} = {\ frac {1} {16}} [/ latex]
Экспериментальные вероятности
Вероятность эксперимента — это отношение количества исходов, при которых происходит событие, к общему количеству испытаний в эксперименте.
Цели обучения
Рассчитать эмпирическую вероятность события на основе данной информации
Ключевые выводы
Ключевые моменты
- В общем смысле экспериментальная (или эмпирическая) вероятность оценивает вероятности на основе опыта и наблюдений.
- В простых случаях, когда результат испытания только определяет, произошло ли указанное событие, может быть целесообразным моделирование с использованием биномиального распределения; тогда эмпирическая оценка является оценкой максимального правдоподобия.
- Если испытание дает больше информации, эмпирическая вероятность может быть улучшена путем принятия дополнительных предположений в форме статистической модели. Если такая модель подобрана, ее можно использовать для получения оценки вероятности указанного события.
Ключевые термины
- биномиальное распределение : Дискретное распределение вероятностей количества успехов в последовательности [латекс] n [/ латекс] независимых экспериментов да / нет, каждый из которых дает успех с вероятностью [латекс] p [/ латекс].

- экспериментальная вероятность : Вероятность того, что произойдет определенный результат, определяемая экспериментально.
- дискретный : отдельный; отчетливый; индивидуальный; прерывистый.
Экспериментальная (или эмпирическая) вероятность относится к данным, взятым из ряда испытаний. Это вероятность, рассчитанная на основе опыта, а не теории. Если наблюдается выборка испытаний [латекс] x [/ латекс], которая приводит к событию [латекс] e [/ латекс], которое происходит [латекс] n [/ латекс] раз, вероятность события [латекс] e [ / латекс] рассчитывается как соотношение [латекс] n [/ латекс] к [латекс] x [/ латекс].
[латекс] \ displaystyle \ text {экспериментальная вероятность события} = \ frac {\ text {количество случаев события}} {\ text {общее количество испытаний}} [/ latex]
Экспериментальная вероятность контрастирует с теоретической вероятностью, чего мы и ожидали.Например, если мы подбросим монету [латекс] 10 [/ латекс] раз, мы можем ожидать, что она упадет на голову [латекс] 5 [/ латекс] раз, или в половине случаев. Мы знаем, что на практике это вряд ли произойдет. Если мы проводим большее количество испытаний, часто случается, что экспериментальная вероятность становится ближе к теоретической. По этой причине обычно ценятся большие размеры выборки (или большее количество испытаний).
Мы знаем, что на практике это вряд ли произойдет. Если мы проводим большее количество испытаний, часто случается, что экспериментальная вероятность становится ближе к теоретической. По этой причине обычно ценятся большие размеры выборки (или большее количество испытаний).
С точки зрения статистики, эмпирическая вероятность — это оценка вероятности.В простых случаях, когда результат испытания только определяет, произошло ли указанное событие, может оказаться целесообразным моделирование с использованием биномиального распределения. Биномиальное распределение — это дискретное распределение вероятностей количества успехов в последовательности [латексных] n [/ латексных] независимых экспериментов да / нет. В таких случаях наиболее вероятной оценкой является эмпирическая вероятность.
Если испытание дает больше информации, эмпирическую вероятность можно улучшить, приняв дополнительные допущения в форме статистической модели: если такая модель подобрана, ее можно использовать для оценки вероятности указанного события. Например, можно легко присвоить вероятность каждому возможному значению во многих дискретных случаях: при броске кубика каждое из шести значений [латекс] 1 [/ латекс] — [латекс] 6 [/ латекс] имеет вероятность [ латекс] \ frac {1} {6} [/ латекс].
Например, можно легко присвоить вероятность каждому возможному значению во многих дискретных случаях: при броске кубика каждое из шести значений [латекс] 1 [/ латекс] — [латекс] 6 [/ латекс] имеет вероятность [ латекс] \ frac {1} {6} [/ латекс].
Преимущества
Преимущество оценки вероятностей с использованием эмпирических вероятностей состоит в том, что эта процедура включает несколько предположений. Например, рассмотрите возможность оценки вероятности среди популяции мужчин, удовлетворяющих двум условиям:
- Они более шести футов в высоту.
- Клубничное варенье они предпочитают малиновому.
Прямая оценка может быть получена путем подсчета количества мужчин, которые удовлетворяют обоим условиям, чтобы дать эмпирическую вероятность комбинированного состояния.
Альтернативная оценка может быть получена путем умножения доли мужчин ростом более шести футов на долю мужчин, которые предпочитают клубничное варенье малиновому джему, но эта оценка основана на предположении, что эти два состояния статистически независимы.
Недостатки
Недостаток использования эмпирических вероятностей заключается в том, что без теории, которая их «осмысляет», легко сделать неверные выводы. Если бросить шестигранный кубик сто раз, вполне возможно, что больше [латекса] \ frac {1} {6} [/ latex] роликов упадет на [латекс] 4 [/ latex]. Интуитивно мы знаем, что вероятность выпадения любого номера должна быть равна вероятности выпадения на следующий. Эксперименты, особенно с меньшим размером выборки, могут подсказать обратное.
Этот недостаток становится особенно проблематичным при оценке вероятностей, которые либо очень близки к нулю, либо очень близки к единице. Например, вероятность выпадения числа от [latex] 1 [/ latex] до [latex] 1000 [/ latex] равна [latex] \ frac {1} {1000} [/ latex]. Если берется [latex] 1000 [/ latex] розыгрышей, и первое выпавшее число — [latex] 5 [/ latex], остается [latex] 999 [/ latex] розыгрышей, чтобы нарисовать [латекс] 5 [/ latex] снова и, таким образом, есть экспериментальные данные, которые показывают вдвое большую ожидаемую вероятность вытягивания [латекса] 5 [/ латекса].
В этих случаях потребуются очень большие размеры выборки, чтобы оценить такие вероятности с хорошим стандартом относительной точности. Здесь могут помочь статистические модели, в зависимости от контекста.
Например, рассмотрите возможность оценки вероятности того, что самая низкая из максимальных дневных температур на участке в феврале за любой год будет ниже нуля градусов Цельсия. Запись таких температур в прошлые годы может быть использована для оценки этой вероятности. Альтернативой, основанной на модели, будет выбор семейства распределений вероятностей и подгонка его к набору данных, содержащему значения прошлых лет.Подобранное распределение предоставит альтернативную оценку желаемой вероятности. Этот альтернативный метод может обеспечить оценку вероятности, даже если все значения в записи больше нуля.
Биномиальное распределение
«Би» означает «два» (как у велосипеда два колеса) . | |
Подбрасывание монеты:
- Получили ли мы головы (H) или
- Хвосты (Т)
Мы говорим, что вероятность выпадения монеты H составляет ½
И вероятность выпадения монеты T составляет ½
Бросок кубика:
- Мы получили четверку…?
- … или нет?
Мы говорим, что вероятность четырех равна 1/6 (одна из шести граней равна четверке)
И вероятность того, что не четыре , составляет 5/6 (пять из шести граней не являются четверкой)
Обратите внимание, что матрица имеет 6 сторон, но здесь мы рассмотрим только два случая : «четыре: да» или «четыре: нет»
Подбросим монетку!
Подбросьте честную монету трижды … каков шанс получить две головы ?
Подбрасывая монету три раза ( H — орел, T решка) можно получить любой из этих 8 результатов :
Какие результаты мы хотим?
«Две головы» могут быть в любом порядке: «HHT», «THH» и «HTH» имеют две головы (и один хвост).
Итак, 3 результата дают «Две головы».
Какова вероятность каждого исхода?
Каждый исход одинаково вероятен, а их 8, поэтому каждый исход имеет вероятность 1/8
Таким образом, вероятность события «Две головы» составляет:
| Количество желаемых результатов | Вероятность каждого исхода | ||
| 3 | × | 1/8 | = 3/8 |
Таким образом, шанс получить две головы составляет 3/8
Мы использовали специальные слова:
- Результат : любой результат трех подбрасываний монеты (8 различных возможностей)
- Событие : «Две головы» из трех подбрасываний монеты (3 исхода имеют это)
3 головы, 2 головы, 1 голова, нет
Расчеты (P означает «Вероятность»):
- P (три головки) = P ( HHH ) = 1/8
- P (две головки) = P ( HHT ) + P ( HTH ) + P ( THH ) = 1/8 + 1/8 + 1/8 = 3/8
- P (одна головка) = P ( HTT ) + P ( THT ) + P ( TTH ) = 1/8 + 1/8 + 1/8 = 3/8
- P (нулевой напор) = P ( TTT ) = 1/8
Мы можем записать это в терминах случайной переменной, X, = «Количество голов при 3 подбрасывании монеты»:
- P (X = 3) = 1/8
- P (X = 2) = 3/8
- P (X = 1) = 3/8
- P (X = 0) = 1/8
А вот как это выглядит в виде графика:
Он симметричный!
Создание формулы
Теперь представьте, что нам нужны шансы выпадения 5 орлов за 9 бросков : перечисление всех 512 исходов займет много времени!
Итак, давайте составим формулу.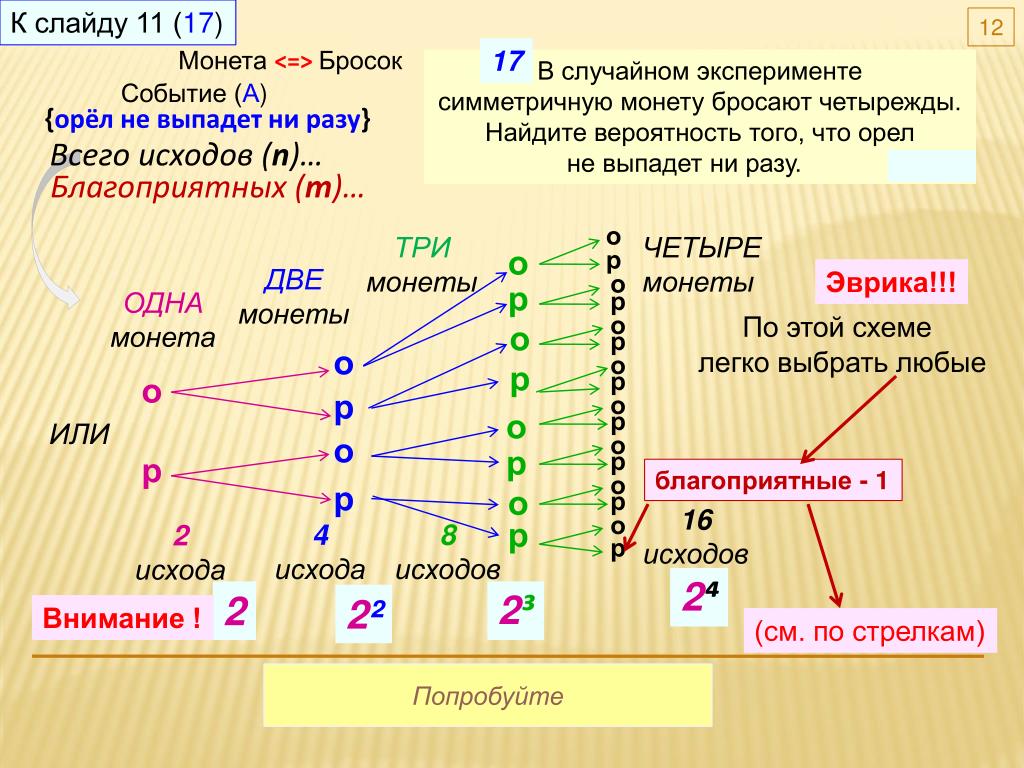
В нашем предыдущем примере, как мы можем получить значения 1, 3, 3 и 1?
Ну, на самом деле они находятся в Треугольнике Паскаля!
Можем ли мы сделать их по формуле?
Конечно, можем, и вот он:
Его часто называют «n choose k»
- n = общее количество
- k = число, которое мы хотим
- знак «!» означает «факториал», например 4! = 1 × 2 × 3 × 4 = 24
Подробнее см. об этом в Комбинации и Перестановки.
Попробуем:
Пример: при 3 бросках, каковы шансы на 2 решки?
У нас есть n = 3 и k = 2 :
н! к! (Н-к)! = 3! 2! (3-2)!
= 3 × 2 × 1 2 × 1 × 1
= 3
Итак, есть 3 исхода с «2 головами»
(Мы это уже знали, но теперь у нас есть формула.)
Давайте ответим на более сложный вопрос:
Пример: при 9 бросках, каковы шансы на 5 бросков?
У нас n = 9 и k = 5 :
н! к! (Н-к)! = 9! 5! (9-5)!
= 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 5 × 4 × 3 × 2 × 1 × 4 × 3 × 2 × 1
= 126
Значит, у 126 исходов будет 5 голов
А для 9 бросков всего 2 9 = 512 исходов, поэтому получаем вероятность:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 126 | × | 1 512 | = | 126 512 |
Итак:
P (X = 5) = 126 512 = 0. 24609375
24609375
Примерно с вероятностью 25% .
(Легче, чем перечислить их все.)
Смещение!
Пока шансы на успех или неудачу равны .
Но что, если монеты смещены (больше на одну сторону, чем на другую) или выбор не равен 50/50.
Пример: вы продаете бутерброды. 70% выбирают курицу, остальные выбирают что-то другое.
Какова вероятность продать 2 бутерброда с курицей следующим 3 покупателям?
Это похоже на пример орла и решки, но с 70/30 вместо 50/50.
Нарисуем древовидную диаграмму:
Ящики «Две курицы» выделены.
Вероятности для «двух цыплят» равны 0,147 , потому что мы умножаем два 0,7 и один 0,3 в каждом случае. Другими словами
0,147 = 0,7 × 0,7 × 0,3
Или, используя экспоненты:
= 0,7 2 × 0,3 1
0,7 — это вероятность каждого выбора, который мы хотим, назовем это p
2 — это количество вариантов, которое мы хотим, назовем его k
А у нас (пока):
= p k × 0. 3 1
3 1
0,3 — вероятность противоположного выбора, так что это: 1 − p
1 — это количество противоположных вариантов, так что это: n − k
Что дает нам:
= p k (1-p) (n-k)
Где
- p — вероятность каждого выбора, который мы хотим
- k — это количество вариантов, которое мы хотим
- n — общее количество вариантов
Пример: (продолжение)
- р = 0.7 (шанс курицы)
- k = 2 (выбор курицы)
- n = 3 (всего вариантов)
Получаем:
p k (1-p) (n-k) = 0,7 2 (1-0,7) (3-2)
= 0,7 2 (0,3) (1)
= 0,7 × 0,7 × 0,3
= 0,147
, что у нас было раньше, но теперь используется формула
Теперь мы знаем, что вероятность каждого исхода равна 0,147
Но мы должны указать, что существует три таких способов: (курица, курица, другое) или (курица, другое, курица) или (другое, курица, курица)
Пример: (продолжение)
Общее количество исходов «два цыпленка»:
н! к! (Н-к)! = 3! 2! (3-2)!
= 3 × 2 × 1 2 × 1 × 1
= 3
И получаем:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 3 | × | 0. 147 147 | = | 0,441 |
Таким образом, вероятность события «2 человека из 3 выбирают курицу» = 0,441
ОК. Это был большой труд для того, что мы уже знали, но теперь у нас есть формула, которую мы можем использовать для более сложных вопросов.
Пример: Сэм говорит: «70% выбирают курицу, поэтому 7 из следующих 10 клиентов должны выбрать курицу» … каковы шансы, что Сэм прав?
Итак имеем:
И получаем:
p k (1-p) (n-k) = 0.7 7 (1-0,7) (10-7)
= 0,7 7 (0,3) (3)
= 0,0022235661
Это вероятность каждого исхода.
И общее количество этих исходов:
н! к! (Н-к)! = 10! 7! (10-7)!
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 7 × 6 × 5 × 4 × 3 × 2 × 1 × 3 × 2 × 1
= 10 × 9 × 8 3 × 2 × 1
= 120
И получаем:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 120 | × | 0. 0022235661 0022235661 | = | 0,266827932 |
Таким образом, вероятность того, что 7 из 10 выберут курицу, составляет всего около 27%
Мораль истории: даже при том, что долгосрочное среднее значение составляет 70%, не ожидайте 7 из следующих 10.
Собираем вместе
Теперь мы знаем, как вычислить сколько :
н! к! (Н-к)!
И вероятность каждого :
п к (1-р) (н-к)
При умножении получаем:
Вероятность k из n способов:
P (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Общая формула биномиальной вероятности
Важные примечания:
- Испытания независимые,
- В каждом испытании есть только два возможных исхода,
- Вероятность «успеха» в каждом испытании постоянна.
Quincunx
Поиграйте с Quincunx (затем прочтите «Quincunx Explained»), чтобы увидеть биномиальное распределение в действии.
Брось кубик
Честный кубик бросается четыре раза. Рассчитайте вероятности получения:
- 0 Двойки
- 1 Два
- 2 пары
- 3 пары
- 4 двойки
В данном случае n = 4 , p = P (Два) = 1/6
X — это случайная переменная «Число двоек из четырех бросков».
Подставьте x = от 0 до 4 в формулу:
P (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Вот так (до 4 знаков после запятой):
- P (X = 0) = 4! 0! 4! × (1/6) 0 (5/6) 4 = 1 × 1 × (5/6) 4 = 0,4823
- P (X = 1) = 4! 1! 3! × (1/6) 1 (5/6) 3 = 4 × (1/6) × (5/6) 3 = 0.3858
- P (X = 2) = 4! 2! 2! × (1/6) 2 (5/6) 2 = 6 × (1/6) 2 × (5/6) 2 = 0,1157
- P (X = 3) = 4! 3! 1! × (1/6) 3 (5/6) 1 = 4 × (1/6) 3 × (5/6) = 0,0154
- P (X = 4) = 4! 4! 0! × (1/6) 4 (5/6) 0 = 1 × (1/6) 4 × 1 = 0,0008
Резюме: «для 4 бросков существует 48% вероятность отсутствия двоек, 39% вероятность 1 два, 12% вероятность 2 двоек, 1. 5% шанс выпадения 3 двоек и крошечный 0,08% шанс того, что все броски будут двойками (но это все равно может случиться!) »
5% шанс выпадения 3 двоек и крошечный 0,08% шанс того, что все броски будут двойками (но это все равно может случиться!) »
На этот раз график несимметричный:
Это несимметрично!
Перекошено, потому что p не равно 0,5
Спортивные мотоциклы
Ваша компания занимается производством спортивных мотоциклов. 90% проходят окончательную проверку (а 10% не проходят и требуют исправления).
Каково ожидаемое среднее значение и отклонение от 4 следующих проверок?
Сначала посчитаем все вероятности.
X — случайная переменная «Число проходов из четырех проверок».
Подставьте x = от 0 до 4 в формулу:
P (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Как это:
- P (X = 0) = 4! 0! 4! × 0,9 0 0,1 4 = 1 × 1 × 0,0001 = 0,0001
- P (X = 1) = 4! 1! 3! × 0,9 1 0.
 1 3 = 4 × 0,9 × 0,001 = 0,0036
1 3 = 4 × 0,9 × 0,001 = 0,0036 - P (X = 2) = 4! 2! 2! × 0,9 2 0,1 2 = 6 × 0,81 × 0,01 = 0,0486
- P (X = 3) = 4! 3! 1! × 0,9 3 0,1 1 = 4 × 0,729 × 0,1 = 0,2916
- P (X = 4) = 4! 4! 0! × 0,9 4 0,1 0 = 1 × 0,6561 × 1 = 0,6561
Резюме: «для следующих 4 велосипедов есть крошечный 0.Вероятность отсутствия передач 01%, вероятность отсутствия передач 0,36%, вероятность 2 передач 5%, вероятность 3 передач 29% и колоссальная вероятность 66%, что все они пройдут проверку «.
Среднее значение, дисперсия и стандартное отклонение
Давайте вычислим среднее значение, дисперсию и стандартное отклонение для проверок спортивных велосипедов.
Для них существуют (относительно) простые формулы. Их немного сложно доказать, но они работают!
Среднее или «ожидаемое значение»:
мк = np
Для спортивных мотоциклов:
μ = 4 × 0. 9 = 3,6
9 = 3,6
Таким образом, можно ожидать, что 3,6 мотоцикла (из 4) пройдут техосмотр.
Действительно имеет смысл … 0,9 шанс для каждого велосипеда умножить на 4 велосипеда равен 3,6
Формула дисперсии:
Отклонение: σ 2 = np (1-p)
Стандартное отклонение — это квадратный корень из дисперсии:
σ = √ (np (1-p))
Для спортивных мотоциклов:
Разница: σ 2 = 4 × 0,9 × 0,1 = 0,36
Стандартное отклонение:
σ = √ (0.36) = 0,6
Примечание: мы также можем вычислить их вручную, составив такую таблицу:
| X | П (Х) | X × P (X) | X 2 × P (X) |
| 0 | 0,0001 | 0 | 0 |
| 1 | 0.0036 | 0,0036 | 0,0036 |
| 2 | 0,0486 | 0,0972 | 0,1944 |
| 3 | 0,2916 | 0,8748 | 2,6244 |
| 4 | 0,6561 | 2,6244 | 10,4976 |
| СУММА: | 3. 6 6 | 13,32 |
Среднее значение — это Сумма (X × P (X)) :
мк = 3,6
Дисперсия равна сумме (X 2 × P (X)) минус Среднее 2 :
Разница: σ 2 = 13,32 — 3,6 2 = 0,36
Стандартное отклонение:σ = √ (0,36) = 0,6
И мы получили те же результаты, что и раньше (ура!)Сводка
теория вероятностей | Определение, примеры и факты
Применение простых вероятностных экспериментов
Фундаментальным элементом теории вероятностей является эксперимент, который можно повторить, по крайней мере, гипотетически, в практически идентичных условиях и который может привести к различным результатам в разных испытаниях.Набор всех возможных результатов эксперимента называется «пробелом». Эксперимент по подбрасыванию монеты один раз приводит к выборке с двумя возможными исходами: «орлом» и «решкой». При подбрасывании двух игральных костей имеется область выборки с 36 возможными исходами, каждый из которых может быть идентифицирован с помощью упорядоченной пары ( i , j ), где i и j принимают одно из значений 1, 2, 3 , 4, 5, 6 и обозначают лица, изображенные на отдельных кубиках. Важно думать, что игральные кости можно идентифицировать (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1).«Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма лиц, показанных на двух кубиках, равна шести», состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).
Важно думать, что игральные кости можно идентифицировать (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1).«Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма лиц, показанных на двух кубиках, равна шести», состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).
Третий пример — вытянуть n шаров из урны, содержащей шары разного цвета. Общий результат этого эксперимента — набор n , где запись i определяет цвет шара, полученного при розыгрыше i ( i = 1, 2,…, n ) .Несмотря на простоту этого эксперимента, глубокое понимание дает теоретическую основу для опросов общественного мнения и выборочных опросов. Например, люди в группе населения, поддерживающие конкретного кандидата на выборах, могут быть идентифицированы с помощью шариков определенного цвета, лица, поддерживающие другого кандидата, могут быть идентифицированы другим цветом и так далее. Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение предназначено для получения сведений об электоральных предпочтениях населения на основе выборки, взятой из этого населения.
Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение предназначено для получения сведений об электоральных предпочтениях населения на основе выборки, взятой из этого населения.
Еще одно применение простых моделей урн — клинические испытания, призванные определить, лучше ли новое лечение болезни, новое лекарство или новая хирургическая процедура, чем стандартное лечение. В простом случае, когда лечение можно рассматривать как успешное или неудачное, цель клинического испытания состоит в том, чтобы выяснить, приводит ли новое лечение к успеху чаще, чем стандартное лечение. Больных можно идентифицировать по шарикам в урне.Красные шары — это те пациенты, которых вылечили с помощью нового лечения, а черные шары — это те пациенты, которые не вылечились. Обычно есть контрольная группа, получающая стандартное лечение. Они представлены второй урной с возможно другой долей красных шаров. Цель эксперимента по извлечению некоторого количества шаров из каждой урны — определить на основе образца, в какой из урн больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины.Возможно, самым крупным и известным примером является испытание вакцины Солка от полиомиелита, проведенное в 1954 году. Оно было организовано Службой общественного здравоохранения США и охватило почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здоровья в промышленно развитых частях мира. Строго говоря, эти приложения являются задачами статистики, основу которых составляет теория вероятностей.
Вариант этой идеи можно использовать для проверки эффективности новой вакцины.Возможно, самым крупным и известным примером является испытание вакцины Солка от полиомиелита, проведенное в 1954 году. Оно было организовано Службой общественного здравоохранения США и охватило почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здоровья в промышленно развитых частях мира. Строго говоря, эти приложения являются задачами статистики, основу которых составляет теория вероятностей.
В отличие от описанных выше экспериментов, многие эксперименты имеют бесконечно много возможных результатов.Например, можно подбрасывать монету до тех пор, пока «орел» не появится впервые. Количество возможных бросков: n = 1, 2,…. Другой пример — крутить спиннер. Для идеализированного прядильщика, сделанного из отрезка прямой линии без ширины и повернутого в его центре, набор возможных результатов представляет собой набор всех углов, которые конечное положение прядильщика образует с некоторым фиксированным направлением, что эквивалентно всем действительным числам в [0 , 2π). Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. Д., Производятся в непрерывных масштабах и, по крайней мере, теоретически включают бесконечно много возможных значений.Если повторные измерения на разных предметах или в разное время на одном и том же предмете могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.
Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. Д., Производятся в непрерывных масштабах и, по крайней мере, теоретически включают бесконечно много возможных значений.Если повторные измерения на разных предметах или в разное время на одном и том же предмете могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.
Из-за их сравнительной простоты сначала обсуждаются эксперименты с конечным пространством выборок. На раннем этапе развития теории вероятностей математики рассматривали только те эксперименты, для которых казалось разумным, исходя из соображений симметрии, предположить, что все результаты эксперимента были «одинаково вероятными.«Затем в большом количестве испытаний все результаты должны происходить примерно с одинаковой частотой. Вероятность события определяется как отношение количества случаев, благоприятных для данного события, то есть количества исходов в подмножестве выборочного пространства, определяющего событие, к общему количеству случаев. Таким образом, 36 возможных исходов при броске двух кубиков считаются равновероятными, а вероятность получения «шести» равна количеству благоприятных случаев, 5, деленному на 36, или 5/36.
Таким образом, 36 возможных исходов при броске двух кубиков считаются равновероятными, а вероятность получения «шести» равна количеству благоприятных случаев, 5, деленному на 36, или 5/36.
Теперь предположим, что монета была подброшена n раз, и рассмотрим вероятность события «орел не выпадет» в n подбрасываниях.Результатом эксперимента является n -й набор, k -я запись которого определяет результат k -го броска. Поскольку существует два возможных результата для каждого броска, количество элементов в пространстве выборки составляет 2 n . Из них только один исход соответствует отсутствию орла, поэтому требуемая вероятность равна 1/2 n .
Немного сложнее определить вероятность «не более одной головы.В дополнение к единственному случаю, когда голова не выпадает, существует n случаев, когда выпадает ровно одна голова, потому что она может произойти при первом, втором,… или n -м броске. Следовательно, существует n + 1 случаев, благоприятных для получения не более одной головы, и желаемая вероятность составляет ( n + 1) / 2 n .
Следовательно, существует n + 1 случаев, благоприятных для получения не более одной головы, и желаемая вероятность составляет ( n + 1) / 2 n .
Пространство выборки — обзор
Схема обоснования Неймана-Пирсона
Согласно теории Неймана-Пирсона, мы разрабатываем проверку гипотез, чтобы минимизировать две ошибки.Основная ошибка, которую мы хотим минимизировать, называемая ошибкой типа I, состоит в том, чтобы отклонить H 0 , тогда как на самом деле H 0 истинно. Если мы достигли разумной минимизации этого типа ошибки, мы также пытаемся минимизировать ошибку, называемую ошибкой типа II, принятия H 0 , когда она ложна, то есть когда H 1 истинно. Однако я не рассматриваю минимизацию ошибок типа II как оправдание для тестов, а, как мы видели в конце раздела 4 предыдущей главы, только как удобную возможность, которая может быть доступна.
Тесты Неймана-Пирсона обычно представляются следующим образом: Рабочая гипотеза H 0 и альтернативная гипотеза H 1 служат для разделения пространства параметров Ω. При H 0 θ лежит в подпространстве Ω ′; при H 1 , θ лежит в дополнительном подпространстве Ω — Ω ′.
H0: θ∈Ω′ и h2: θ∈Ω − Ω ′.
При H 0 θ лежит в подпространстве Ω ′; при H 1 , θ лежит в дополнительном подпространстве Ω — Ω ′.
H0: θ∈Ω′ и h2: θ∈Ω − Ω ′.
Примерное пространство S возможных значений X1,…, Xn, делится процедурой тестирования на два дополнительных подпространства S 0 и S 1 : критическая область и некритическая область, соответственно.Тест выражается предложением φ = [ X ∈ S 0 ] языка с X , так что если x ∈ S 0 встречается в действительности, то φ равен истина, и если x ∈ S 1 получает, то φ ложно. Тест продолжается по политике:
отклонить H 0 , если x ∈ S 0 ; принять H 0 , если x ∈ S 1 .
Обычное обоснование проверок гипотез, выполненное Нейманом и его школой, можно резюмировать следующим образом. Выбор теста { S 0 , S 1 } в основном руководствуется желанием предотвратить неправильное отклонение H 0 , присвоив уровень значимости α как верхний предел для вероятность ошибочного отклонения H 0 . То есть pr θ [ X ∈ S 0 ] ≤ α для всех θ ∈ Ω ′.Таким образом, вероятность, присвоенная Pr θ для θ ∈ Ω ′ предложению [ X ∈ S 0 ], мала. Введено новое измерение теста — его мощность. Мощность теста для θ определяется как 1 — β (θ), где
Выбор теста { S 0 , S 1 } в основном руководствуется желанием предотвратить неправильное отклонение H 0 , присвоив уровень значимости α как верхний предел для вероятность ошибочного отклонения H 0 . То есть pr θ [ X ∈ S 0 ] ≤ α для всех θ ∈ Ω ′.Таким образом, вероятность, присвоенная Pr θ для θ ∈ Ω ′ предложению [ X ∈ S 0 ], мала. Введено новое измерение теста — его мощность. Мощность теста для θ определяется как 1 — β (θ), где
β (θ) = Prθ ([X∈S1]) для θ∈Ω − Ω ′.
В традиционной теории Неймана-Пирсона среди всех тестов с уровнем значимости α выбирается тот, который имеет наибольшую мощность. Фактически, поскольку всегда существует много тестов уровня α, одним из критериев для выбора среди них является мощность теста.Одна из проблем состоит в том, что не может быть одного теста, который имел бы наибольшую мощность для всех θ ∈ Ω — Ω ′. Итак, одна из важных задач математической статистики для школы Неймана-Пирсона состоит в том, чтобы найти условия, при которых существуют эти одинаково наиболее мощные тесты.
Итак, одна из важных задач математической статистики для школы Неймана-Пирсона состоит в том, чтобы найти условия, при которых существуют эти одинаково наиболее мощные тесты.
Продолжим пример. Предположим, мы хотим проверить гипотезу H 0 о том, что некоторая случайная величина X почти нормально распределена со средним μ 0 и дисперсией
σ02.Мы предполагаем, что свидетельство состоит из n независимых наблюдаемых значений X ,
x → = 〈x1, x2,…, xn〉. Вектор
x → рассматривается как точка в пространстве возможных значений отсчетов, S . Проблема тестирования, по замыслу Неймана и Пирсона, заключается в выборе подмножества S 0 из S , так что если наблюдаемое значение
x → ∈S0, то следует отклонить H 0 . Набор S 0 является критической областью. Как мы упоминали выше, Нейман и Пирсон требуют, чтобы S 0 было выбрано так, чтобы минимизировать два типа ошибок (см. , Например, первую совместную работу Неймана и Пирсона [73, с.3]). Ошибка типа I — это ошибка отклонения H 0 , когда это действительно так. Ошибка типа II — это ошибка принятия H 0 , хотя на самом деле она ложна.
, Например, первую совместную работу Неймана и Пирсона [73, с.3]). Ошибка типа I — это ошибка отклонения H 0 , когда это действительно так. Ошибка типа II — это ошибка принятия H 0 , хотя на самом деле она ложна.
Обработка ошибки типа I, которая является наиболее важной из двух, заключается в следующем. Гипотеза H 0 индуцирует распределение вероятностей по S , Pr H 0 . Мы контролируем ошибку типа I, находя низкое значение для Pr H 0 S 0 .Если
PrH0S0 = α,
мы говорим, что используем тест размера α. Проблема здесь в том, что мы можем выбрать большое количество наборов S 0 , так что Pr H 0 S 0 = α. Многие из них будут интуитивно неудовлетворительными в качестве критических регионов. Чтобы исключить эти неудовлетворительные области и получить хорошую критическую область, мы должны, согласно Нейману и Пирсону, учитывать ошибку второго типа. В этом заключается основное отличие моей теории.Вместо того чтобы рассматривать ошибку типа II, я предлагаю использовать наборы отклонений.
В этом заключается основное отличие моей теории.Вместо того чтобы рассматривать ошибку типа II, я предлагаю использовать наборы отклонений.
Именно для того, чтобы лечить ошибку типа II, Нейман и Пирсон вводят набор альтернативных гипотез, так что, если H 0 ложно, одна из этих альтернатив верна. Таким образом, мы начинаем с набора Ω гипотез. Каждая гипотеза полностью определяет распределение вероятностей определенной случайной величины, X . Мы предполагаем, для простоты, что каждая гипотеза определяется значениями набора параметров.В рассматриваемом нами примере это среднее значение μ и дисперсия σ 2 . Таким образом, в этом случае мы рассматриваем почти нормальные распределения со средним значением μ и известной дисперсией σ 2 , где σ> 0. Как и раньше, мы предполагаем пространство выборки, S , и считаем, что проблема заключается в выборе S 0 ⊆ S для проверки нашей гипотезы скажем, что среднее значение μ 0 . Требуется, чтобы S 0 имел некоторый фиксированный размер α, т.е.е., Pr H 0 S 0 = α. Как мы упоминали выше, мы уменьшаем ошибку типа II, делая β (μ) как можно меньшим, для μ ≠ μ 0 , где 1 — β — мощность или тест. Таким образом, мы должны сделать мощность как можно большей.
Требуется, чтобы S 0 имел некоторый фиксированный размер α, т.е.е., Pr H 0 S 0 = α. Как мы упоминали выше, мы уменьшаем ошибку типа II, делая β (μ) как можно меньшим, для μ ≠ μ 0 , где 1 — β — мощность или тест. Таким образом, мы должны сделать мощность как можно большей.
Предположим, что есть только две простые альтернативы, μ 0 и μ 1 . Тогда нам понадобится набор S 0 такой, что
Prμ0S0 = α,
и
Prμ1S0≥Prμ1C,
для любого другого набора C , такой что Prμ0C = α.В случае двух простых альтернатив с почти нормальным распределением Нейман и Пирсон показали, что всегда можно найти такое множество.
Проблема возникает, когда есть много альтернатив, от μ до μ 0 . Тогда нам понадобится набор S 0 такой, что
Prμ0S0 = α, и
PrμS0≥PrμC, для любого другого набора C , такого что Pr μ 0 C = α, и для каждого μ ≠ μ 0 .

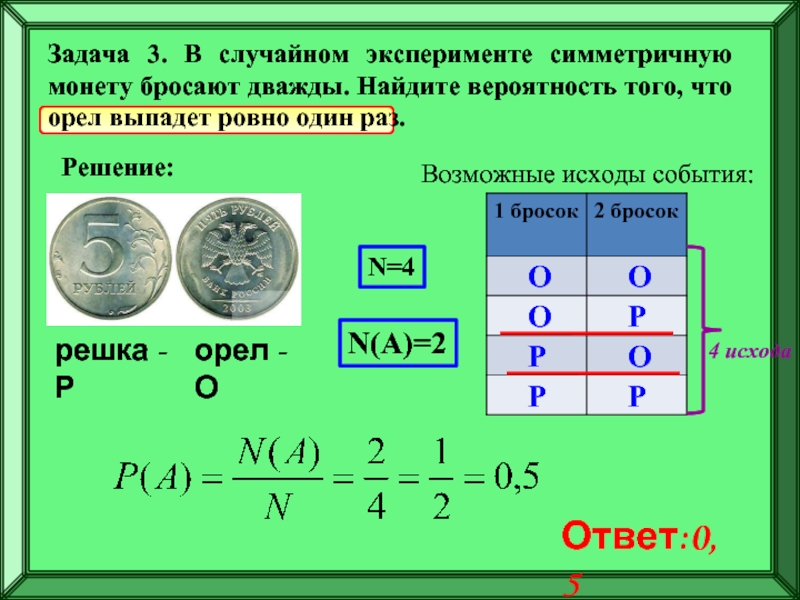

 Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу. Число таких комбинаций — это n
;
Число таких комбинаций — это n
; Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Найдите вероятность того, что орел выпадет больше раз, чем решка.
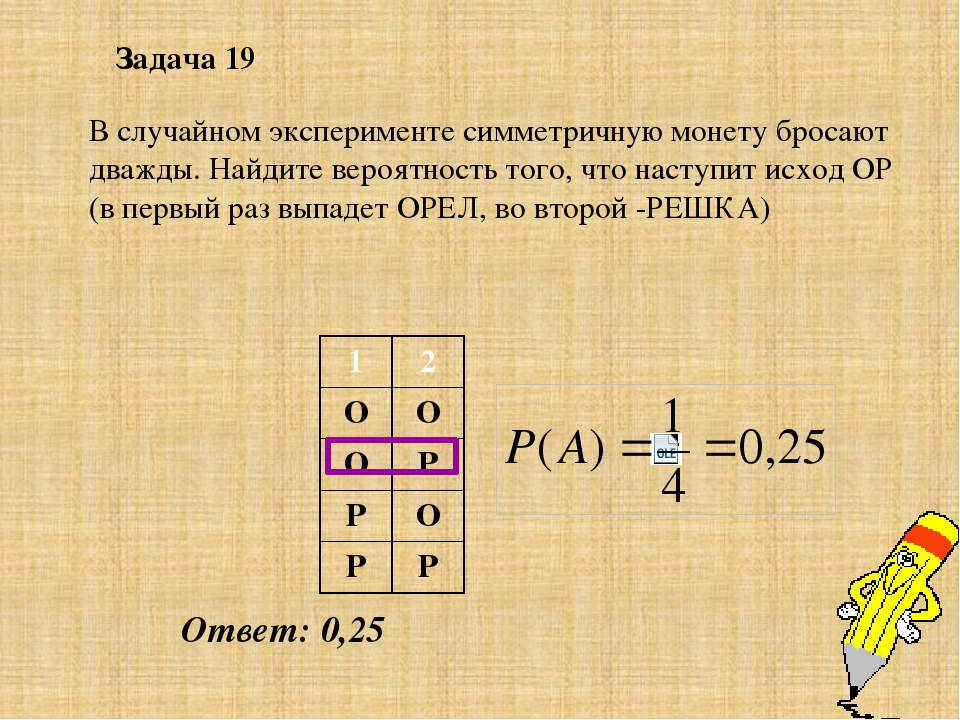 К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
К. Теория вероятности и математическая статистика: Лекции /Самара, 2007; Считаем отмеченные комбинации — получаем число k;
Считаем отмеченные комбинации — получаем число k;
 Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

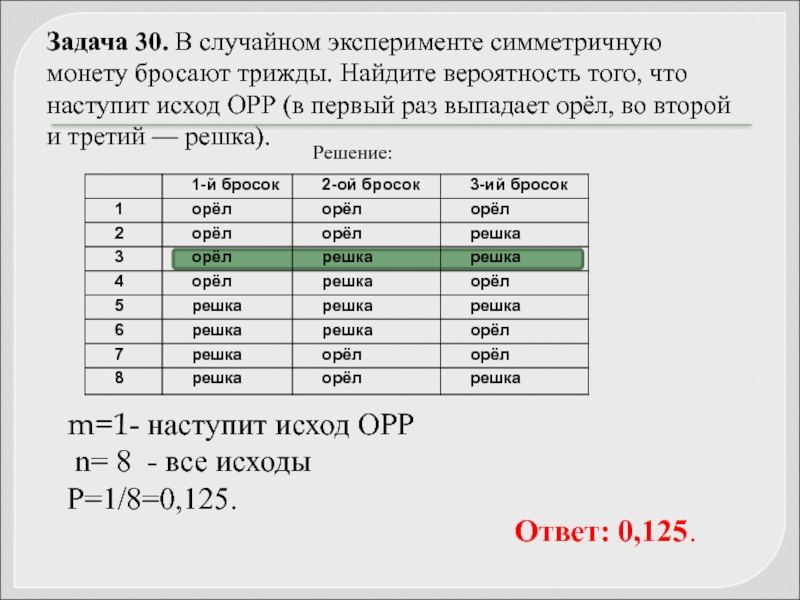 Если Антонов играет черными, то Антонов выигрывает у Борисова с вероятностью 0,3. Гроссмейстеры Антонов и Борисов играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что Антонов выиграет оба раза.
Если Антонов играет черными, то Антонов выигрывает у Борисова с вероятностью 0,3. Гроссмейстеры Антонов и Борисов играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что Антонов выиграет оба раза.
 Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. Вероятность того, что Петров получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что Петров сможет поступить хотя бы на одну из двух упомянутых специальностей
Вероятность того, что Петров получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что Петров сможет поступить хотя бы на одну из двух упомянутых специальностей
 Перед началом футбольного матча судья подбрасывает монетку, чтобы определить, какая команда начнет игру с мячом. Команда «Изумруд» сыграет три матча с разными командами. Найдите вероятность того, что Изумруд выиграет жеребьевку ровно один раз в этих играх.
Перед началом футбольного матча судья подбрасывает монетку, чтобы определить, какая команда начнет игру с мячом. Команда «Изумруд» сыграет три матча с разными командами. Найдите вероятность того, что Изумруд выиграет жеребьевку ровно один раз в этих играх. Кости бросаются дважды. Сколько элементарных исходов опыта благоприятствует событию «сумма баллов 8»?
Кости бросаются дважды. Сколько элементарных исходов опыта благоприятствует событию «сумма баллов 8»?
 Это можно записать как [latex] P (S) = 1 [/ latex], где [latex] S [/ latex] представляет все пространство сэмплов.
Это можно записать как [latex] P (S) = 1 [/ latex], где [latex] S [/ latex] представляет все пространство сэмплов. c [/ latex] является дополнением к [latex] A [/ latex].
c [/ latex] является дополнением к [latex] A [/ latex]. Союз обозначается символом [латекс] \ чашка [/ латекс].
Союз обозначается символом [латекс] \ чашка [/ латекс].
 В наиболее распространенной форме это: [латекс] P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ latex].
В наиболее распространенной форме это: [латекс] P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ latex]. [/ Latex]
[/ Latex]


 ..
..  1 3 = 4 × 0,9 × 0,001 = 0,0036
1 3 = 4 × 0,9 × 0,001 = 0,0036
Leave A Comment