В равнобедренном треугольнике авс с основанием ас внешний угол при вершине с: В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине A равен 140 градусов….

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123 . Найдите величину угла ВАС — вопрос №1404968 — Учеба и наука

Ответы

Наталия Дмитриевна Белова 12. 03.15

Михаил Александров от 0 p. Читать ответы

Андрей Андреевич от 70 p. Читать ответы

Eleonora Gabrielyan от 0 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Ответы нужны очень срочно !!!!!!!!!

Решено

основание прямой призмы ромб с острым углом 60градусов.боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…

вставь пропущенные знаки арифметических действий и расставь скобки так,чтобы равенство стало верным. 6 6 6 6 6 6 6=100

Решено

два самолёта вылетели с аэродрома…

Решено

Из пункта А в пункт В,расположенный ниже по течению реки,отправился плот. Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…

Пользуйтесь нашим приложением

Равнобедренный треугольник. Свойства, признаки, высота

Поможем понять и полюбить математику

Начать учиться

392.5K

В равнобедренном треугольнике прекрасно всё: и три угла, и два симметричных бедра. Полюбуемся этой фигурой, а заодно узнаем ее свойства, признаки и формулы, чтобы решать задачки легко.

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.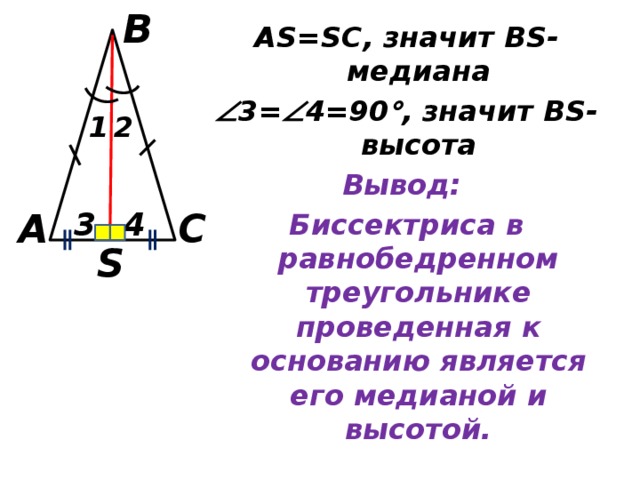

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC —

основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

 

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.


2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.


3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.


4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.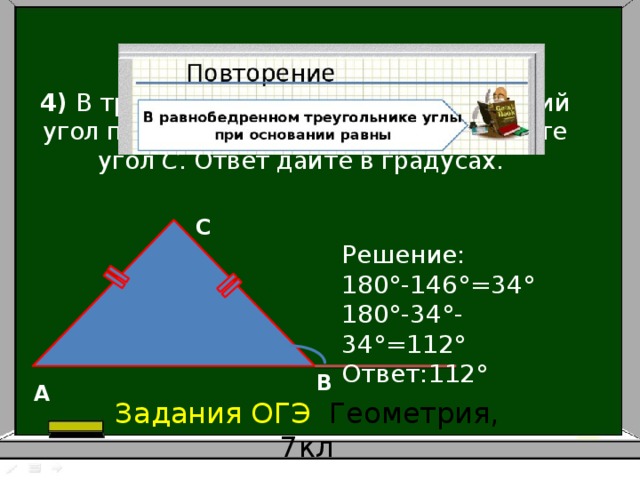

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

1. Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

2. Значит, во-первых, AH = HC и BH — медиана.

3. Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

1. Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

2. Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

3. Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

1. Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

2. Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

3. Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.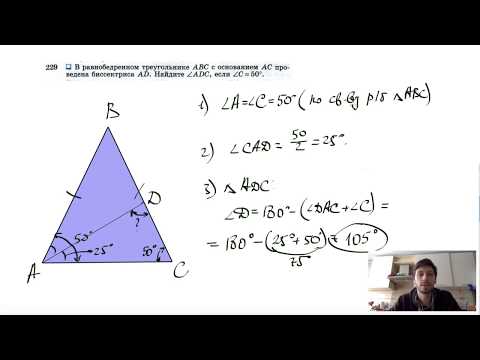

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Ответ: ∠B = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

1. Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

2. А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

3. Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Ответ: 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

122. 2K

Как сокращать алгебраические дроби?

К следующей статье

150.1K

Как найти среднюю линию треугольника?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Геометрия треугольников | mathtestpreparation.com

вернуться к Геометрия

Треугольник

Треугольник — трехсторонняя фигура. У него внутри три угла, и каждый угол соответствует вершине, помеченной буквой.

Теорема о сумме внутренних углов треугольника

Сумма внутренних углов любого треугольника равна 180 градусам.

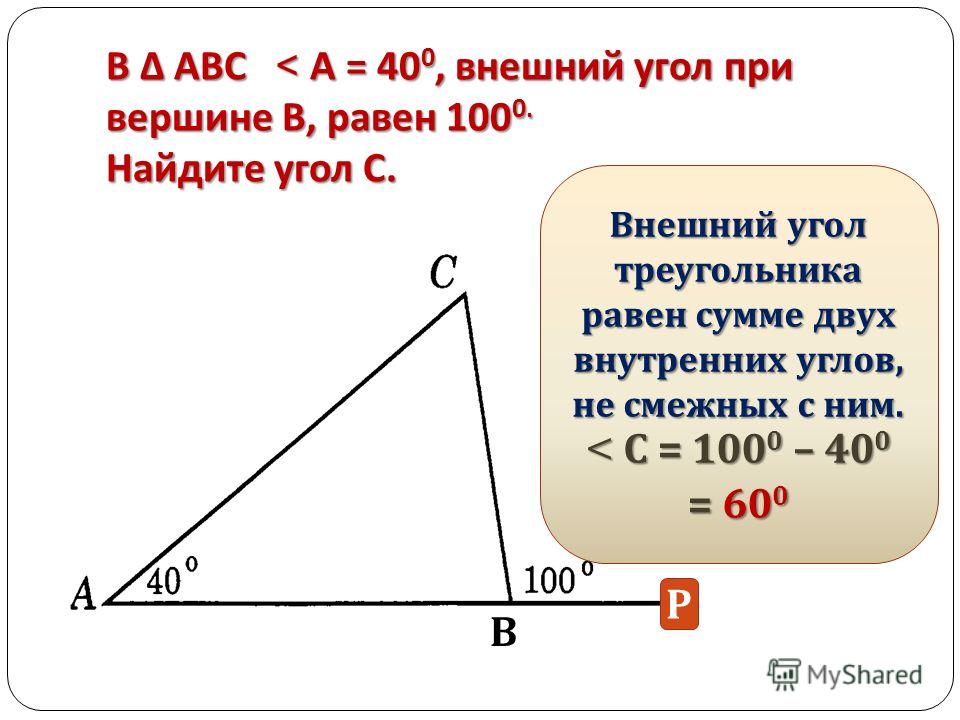
Внешний угол треугольника

Внешний угол треугольника образуется при удлинении одной стороны треугольника. Угол вне треугольника, но примыкающий к внутреннему углу, является внешним углом треугольника

На рисунке выше угол 2 является внешним углом треугольника ABC. Угол 2 примыкает к углу 1, который является внутренним углом треугольника ABC. Одна сторона угла 2 — это CD, которая исходит из продолжения стороны BC.

Теорема о внешнем угле треугольника

Мера внешнего угла треугольника равна сумме мер двух несмежных внутренних углов.

Угол 2 — внешний угол треугольника ABC. Угол А и угол В — два внутренних угла треугольника АВС. Угол 2 не смежный с углом А и углом В

Равносторонний треугольник

Равносторонний треугольник — это треугольник, у которого все три стороны равны по размеру.

Если треугольник ABC равносторонний треугольник, то AB = AC = BC

Равнобедренный треугольник

Равнобедренный треугольник — это треугольник, две стороны которого равны по размеру.

Если треугольник ABC равнобедренный, то AB = AC.

Разносторонний треугольник

Разносторонний треугольник — это треугольник, у которого все три стороны разной величины.

Тупоугольный треугольник

Тупоугольный треугольник — это треугольник, тупой угол которого больше 90 градусов, но меньше 180 градусов.

В треугольнике ABC, так как 90 ^o &lt угол A &lt 180 ^o , то треугольник ABC тупоугольный.

Остроугольный треугольник

Остроугольный треугольник — это треугольник, все углы которого меньше 90 градусов.

На рисунке выше, поскольку угол A < 90 ^o , угол B &lt 90 ^o и угол C &lt 90 ^o , поэтому треугольник ABC остроугольный.

Биссектриса угла в треугольнике

Биссектриса угла в треугольнике представляет собой отрезок, проведенный из вершины и делящий угол пополам.

На рисунке выше, поскольку угол 1 = углу 2, отрезок AD является биссектрисой угла, которая делит угол A пополам.

Медиана треугольника

Медиана треугольника — это отрезок, проведенный от вершины к середине противоположной стороны.

На рисунке выше, поскольку BD = DC, отрезок AD является медианой треугольника ABC. Медиана делит сторону ВС пополам.

Высота и основание

Высота в треугольнике – это перпендикулярный отрезок, проведенный из вершины к его противоположной стороне или к продолжению противоположной стороны.

Теорема о трех сторонах треугольника

В треугольнике сумма двух сторон больше третьей стороны.

AB + BC &gt AC

AB + AC & gt BC

AC + BC &gt AB

Следствие отношения трех сторон треугольника

В треугольнике разность любых двух сторон меньше, чем разность третьей стороны.

|AB — BC| &lt AC

|АВ — АС| &lt до н.э.

|AC — БК| &lt AB

Пример 1

В треугольнике ABC, если угол A : угол B : угол C = 3 : 4 : 5, то какова градусная мера угла A?

Раствор

Пусть угол A = 3x, угол B = 4x, угол C = 5x

В треугольнике ABC угол A + угол B + угол C = 180 ^o

[Теорема: сумма внутренних углов любого треугольника равна 180 градусам. ]

3х + 4х + 5х = 180 ^или

12x = 180 ^или

х = 15 ^или

угол A = 3x = 3 &times 15 ^o = 45 ^o

Следовательно, градусная мера угла А равна 45 ^o .

Пример 2

На рисунке ниже найдите значение x.

Раствор

Так как угол ACD примыкает к углу 1, который является внутренним углом треугольника ABC.

, и поскольку одна сторона угла ACD равна CD, которая является продолженной линией BC

.

Итак, угол ACD является внешним углом треугольника ABC.

[Теорема о внешнем угле треугольника: мера внешнего угла треугольника равна сумме мер двух несмежных внутренних углов.]

Итак, угол ACD = угол A + угол B = 77 ^o + 45 ^o = 122 ^o

На рисунке выше угол ACD = x = 122 ^o

Калькулятор равнобедренного треугольника

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Адена Бенн

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Что такое равнобедренный треугольник?
• Формулы площади и периметра равнобедренного треугольника
• Что такое теорема о равнобедренном треугольнике?
• Калькулятор золотого треугольника
• Как найти площадь с помощью этого калькулятора равнобедренного треугольника?
• Часто задаваемые вопросы

Калькулятор равнобедренного треугольника — лучший выбор, если вы ищете быстрое решение ваших задач по геометрии. Найдите площадь равнобедренного треугольника, его периметр, внутренний радиус, радиус описанной окружности, высоты и углы — все в одном месте. Если вы хотите построить конуру, узнать площадь равнобедренного фронтона греческого храма или просто сделать домашнее задание по математике, этот инструмент для вас. Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника и теореме о равнобедренном треугольнике.

Что такое равнобедренный треугольник?

Равнобедренный треугольник представляет собой треугольник с двумя сторонами одинаковой длины, называемыми катетами. Третья сторона треугольника называется основанием. Угол при вершине — это угол между катетами. Углы, у которых основание является одной из сторон, называются углами при основании.

Вот важнейшие свойства равнобедренных треугольников:

• Имеет ось симметрии по высоте вершины;
• Два угла, противоположные катетам, равны; и
• Равнобедренный треугольник может быть остроугольным, прямоугольным или тупоугольным, но зависит только от угла при вершине (углы при основании всегда острые)

Равносторонний треугольник является частным случаем равнобедренного треугольника. Вы можете узнать обо всех возможных типах треугольников в калькуляторе классификации треугольников. Кроме того, если вы хотите углубиться в характеристики равностороннего треугольника, ознакомьтесь с калькулятором равностороннего треугольника

Формулы площади и периметра равнобедренного треугольника

Для расчета площади равнобедренного треугольника можно использовать множество различных формул. Наиболее популярны уравнения:

1. Данная ножка a и основание b :

   площадь = (1/4) × b × √(4 × a² - b²)

2. Дано h высота от вершины и основания b или h3 высота от двух других вершин и ножки a :

   площадь = 0,5 × h × b = 0,5 × h3 × a

3. При любом угле и катете или основании

   площадь = (1/2) × a × b × sin(base_angle) = (1/2) × a² × sin(vertex_angle)

Кроме того, вы можете проверить наш калькулятор площади треугольника, чтобы найти другие уравнения, которые работают для любого типа треугольника, а не только для равнобедренного.

Чтобы вычислить периметр равнобедренного треугольника, просто сложите все стороны треугольника:
периметр = a + a + b = 2 × a + b

Что такое теорема о равнобедренном треугольнике?

Теорема о равнобедренном треугольнике, также известная как теорема об углах при основании, утверждает, что если две стороны треугольника конгруэнтны, то углы, противоположные этим сторонам, равны .

Также существует обратная теорема, утверждающая, что если два угла треугольника равны, то стороны, противоположные этим углам, равны .

Калькулятор золотого треугольника

Золотой треугольник, который также называют возвышенным треугольником, представляет собой равнобедренный треугольник, в котором катет находится в золотом отношении к основанию:

a / b = φ ~ 1,618

Золотой треугольник обладает некоторыми необычными свойствами:

• Это единственный треугольник с тремя углами в соотношении 2:2:1
• Это форма треугольников, найденных в точках пентаграмм
• Используется для формирования логарифмической спирали

Как найти площадь с помощью этого калькулятора равнобедренного треугольника?

Давайте узнаем, как использовать этот инструмент на простом примере. Посмотрите на это пошаговое решение:

1. Определите первое значение . Предположим, мы хотим проверить свойства золотого треугольника. Введите 1,681 дюйма в поле ноги .
2. Введите второй известный параметр . Например, возьмем основание равное 1 д.
.
3. Все остальные параметры рассчитываются в мгновение ока! Мы проверили, например, что периметр равнобедренного треугольника равен 4,236 дюйма и что углы в золотом треугольнике равны 72° и 36° — отношение действительно равно 2:2:1.

Вы можете использовать этот калькулятор для определения других параметров, чем в примере, но помните, что обычно есть два различных равнобедренных треугольника с заданной площадью и другими параметрами, например, длиной катета. Наш калькулятор покажет одно из возможных решений.

Часто задаваемые вопросы

Как рассчитать площадь равнобедренного треугольника по катету и основанию?

Чтобы вычислить площадь равнобедренного треугольника с катетом a и основанием b , выполните следующие действия:

1. Применить теорему Пифагора к найти высоту : √( a² - b²/4 ) .

2. Примените стандартную формулу площади треугольника , т. е. умножьте основание b на высоту, найденную в шаге 1, а затем разделите на 2 .

3. Вот и все. Окончательная формула у нас есть:

   площадь = ½ × b × √(a² - b²/4) .

Как рассчитать периметр равнобедренного треугольника по катету и основанию?

Периметр равнобедренного треугольника с катетом a и основанием b вычисляем по формуле периметр = 2 × a + b . В этой формуле используется тот факт, что две стороны равнобедренного треугольника имеют одинаковую длину.

Какова площадь равнобедренного треугольника со стороной 4 и основанием 4?

Ответ: 6,93 . Чтобы получить его, мы можем использовать формулу площадь = ½ × b × √(a² - b²/4) с a = b = 4 .

В качестве альтернативы мы можем заметить, что здесь у нас есть равносторонний треугольник : формула площади упрощается до площадь = a² × √3 / 4 с a = 4 .