Некоторые свойства трапеции. Спецкурс по геометрии. 9 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Некоторые свойства трапеции
Спецкурс по геометрии
9 класс

2. Разминка

b
a
Для нахождения каких величин используются формулы?»
c
m
1
a b h
2
1
m a b
2
S
h
d
2
3
1 70
1
4
P a b c d
S mh
P 2m c d
3 4 180
Сумма углов, прилежащих
к боковой стороне трапеции
равна 180
2 110
, то трапеция какого
1 4
Если углы при основании трапеции равны
вида?
2
Равнобедренная
3
Будут ли равны 2 3 ?
1
4
У равнобедренной трапеции
углы при основаниях равны
2
3
1
4
Какую трапецию можно вписать в окружность?
В окружность можно вписать
только
1 3 180
2 3
равнобедренную
1 2 180
трапецию
В какую трапецию можно вписать окружность?
a
r
r
c
a b c d
d
r
h 2r
b
Если в трапецию можно вписать
окружность, то суммы
противоположных сторон равны
Чему равна средняя линия трапеции?
a
3
5
b
a b 3 5 4
m
a b
4
2

4.

Решение задачКакими еще свойствами обладает равнобедренная трапеция?
Задача 1. В равнобедренной трапеции ВК – высота, ВК=6, КD=8.
8-x
B
Найдите площадь трапеции.
C
S
6
A
8
N x
x K
h
m
BC AD
8 x 8 x
BK
6 8 6 48
2
2
D
S h m

5. Задача 2. В равнобедренную трапецию с основаниями a и b вписана окружность. Найти высоту трапеции.

а
B
a b
2
AK DN
C
b a
2
h
A
D
b a K
2
b
АВК :
N
AB CD
a b
2
b a 2 h 2 a b 2
4
4
h ab
Найти площадь равнобедренной трапеции, в которую можно
вписать окружность, если ее основания равны 4см и 9 см
4
a b
a b
S
h
ab
2
2
9
4 9
S
4 9 39
2

6. Задача 3. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 10. Найти ее площадь.

а
В 2
а
N 2 С
О
3 4
А
1
b
2
2
M
b
2
1 2 45 АОМ -равнобедренный
b
ОМ АМ
2
3 4 45
a
ON BN
D
2
a b a b
h OM ON
2 2
2
S
a b
h h3
2
S 102 100
S h3

7.

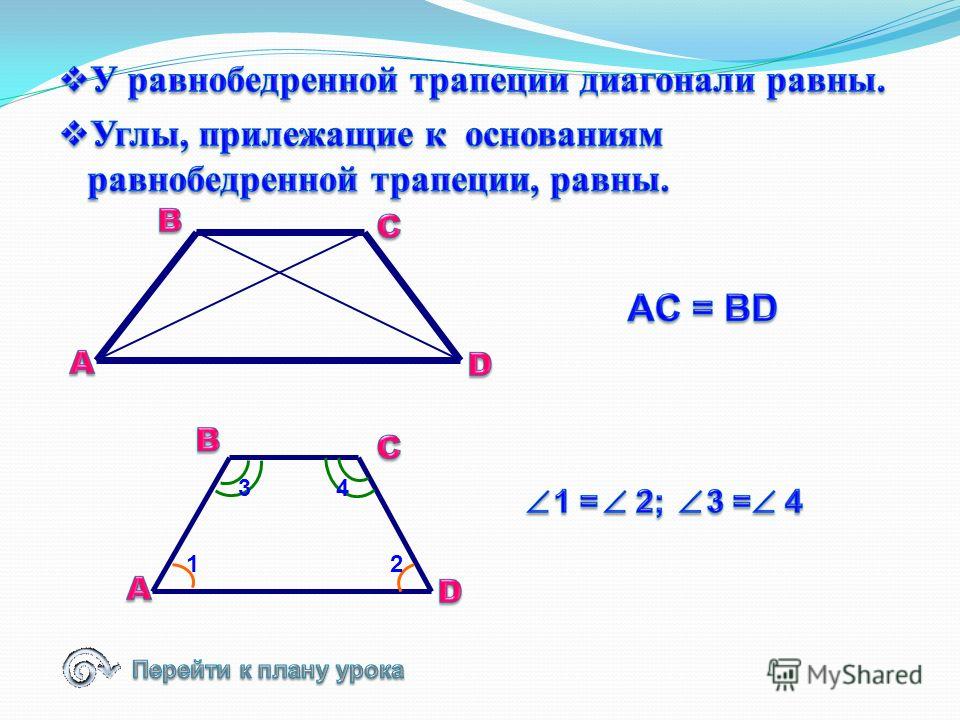Домашняя работа1.Доказать, что в равнобедренной трапеции при пересечении диагоналей
получаются равнобедренные треугольники AOD и BOC , а ABO COD
С
В
O
А
D
2. Для произвольной трапеции ABCD доказать, что BOC подобен DOA ,
а площади всех образовавшихся треугольников можно найти так, как
показано на рисунке.
В
С
S
kS
О
kS
k 2S
А
к – коэффициент подобия
D

8. Тест

Вариант 1
1.
2.
Вариант 2
Найдите среднюю линию трапеции

9. 3. В равнобедренную трапецию вписана окружность

3.
4.
В равнобедренную трапецию вписана окружность
5. В трапеции ABCD AB||BC,
А 90 , С 135 , АВ = 2. Найдите
среднюю линию трапеции, если
одна из ее диагоналей перпендикулярна боковой стороне.
5.В равнобедренной трапеции
диагональ перпендикулярна
боковой стороне, большее
основание равно 12, угол при
основании равен 60 . Найдите
среднюю линию трапеции.

11.

Ответы Вариант 1
Вариант 2
1.
5
5
2.
30
8
3.
2
4
4.
6
3
5.
63
60

English     Русский Правила

Диагонали прямоугольной трапеции взаимно перпендикулярны угол между. Диагонали трапеции

Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать

Ответы.

Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)

Похожие задачи:

1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.

2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.

3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.

1. Найдите сторону квадрата если его диагональ составляет 10 см

2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?

3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого.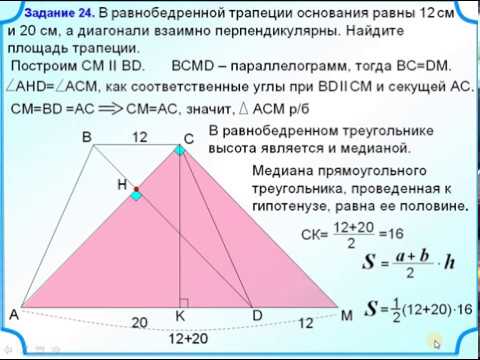 Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?

4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.

1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О

а) Сравните площади треугольников ABD и ACD

б) Сравните площади треугольников ABO и CDO

в) Докажите что OA*OB=OC*OD

2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.

  1. Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
  2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
  3. Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
  4. Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
  5. Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
  6. Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .

Данный отрезок параллелен основаниям трапеции .

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2
или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции


Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными

.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.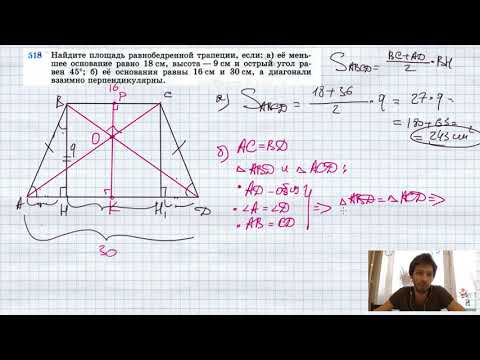

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции


Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.


Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет

совпадать с прямой линией, которая проходит через середины оснований .

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

  • Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
  • Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции


Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON)

будет равно соотношению оснований трапеции (BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции


Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

  • Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
  • Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)


a, b — основания трапеции

c, d — боковые стороны трапеции

d1 d2 — диагонали трапеции

α β — углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований . Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту


Примечание . В данном уроке приведено решение задач по геометрии о трапециях.

Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16

Ответ : 16 см

Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12

Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2

Ответ : площадь трапеции равна 80 см 2 .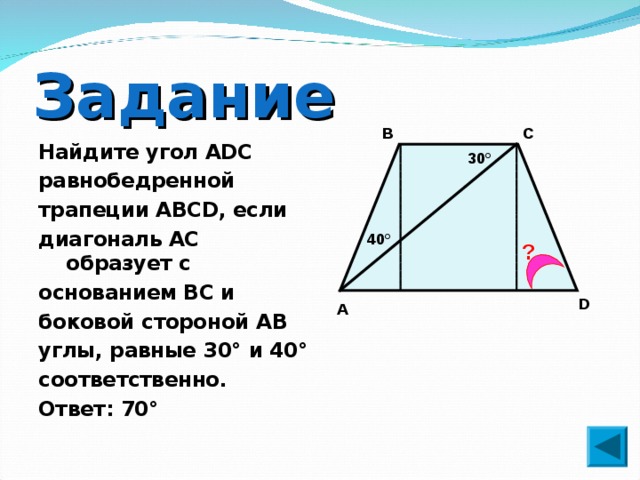

Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.

Четырехугольник BCFD — параллелограмм (BC∥ DF как основания трапеции, BD∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то

что в общем виде можно записать как

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).

Так как площадь трапеции находится по формуле

а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:

4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

геометрия — Найдите площадь трапеции, зная длину диагонали и высоту трапеции.

спросил

Изменено 1 год, 6 месяцев назад

Просмотрено 232 раза

$\begingroup$

В трапеции с перпендикулярными диагоналями длина диагонали равна 5, а высота трапеции равна 4. Найдите площадь трапеции.

Я пытался использовать аналогичные свойства треугольника и теорему Пифагора, но не нашел решения. Я пытался использовать треугольник BPC ~ треугольник APD, но не знал, куда идти после этого.

ОБНОВЛЕНИЕ: я добрался до сути, используя определение высоты треугольника и теорему Пифагора. Но я не знаю, как найти площадь верхнего левого треугольника. введите описание изображения здесь

Я использовал тот факт, что ACF и ABC конгруэнтны ASA, поэтому я получил площадь трапеции 38, но я’ м не уверен, что это правильно

  • геометрия

$\endgroup$

1

$\begingroup$

Подсказка: Используйте этот рисунок, чтобы найти:

1-В трапеции, если диагонали перпендикулярны, то одна сторона равна одной диагонали (AB=BD).

2- В этом случае AD=6 (используйте теорему Пифагора).

3-Используйте конгруэнтность прямоугольных треугольников с вершиной E, чтобы найти меру стороны BC. 9\circ$

$\треугольник AOD \sim \треугольник AFC$ и $\треугольник AOD \sim \треугольник COB$. Если $OC = y, AO = 5 — y$,

$ \displaystyle \frac{BC}{y} = \frac{AD}{5-y} = \frac{5}{3}$

$ \подразумевает \displaystyle BC = \frac{5y}{3}, AD = \frac{25-5y}{3}$

$ \displaystyle BC + AD = \frac{25}{3}$

Площадь трапеция,

$ \displaystyle A = \frac{1}{2} (BC + AD) \cdot CF = \frac{50}{3}$

$\endgroup$

$\begingroup$ 92=EF\times ED$, затем $25=3\times ED=$, $ED=\frac{25}{3}$

$\endgroup$

геометрия — Равнобедренная трапеция спросил

Изменено 12 лет, 1 месяц назад

Просмотрено 3к раз

$\begingroup$

Я решал упражнение на равнобедренную трапецию, диагональ которой была дана, и замечаю, что если я проведу диагональ в равнобедренной трапеции, то у меня получится два треугольника

Для определения площади треугольников я проведу их высоты, которые диагональ.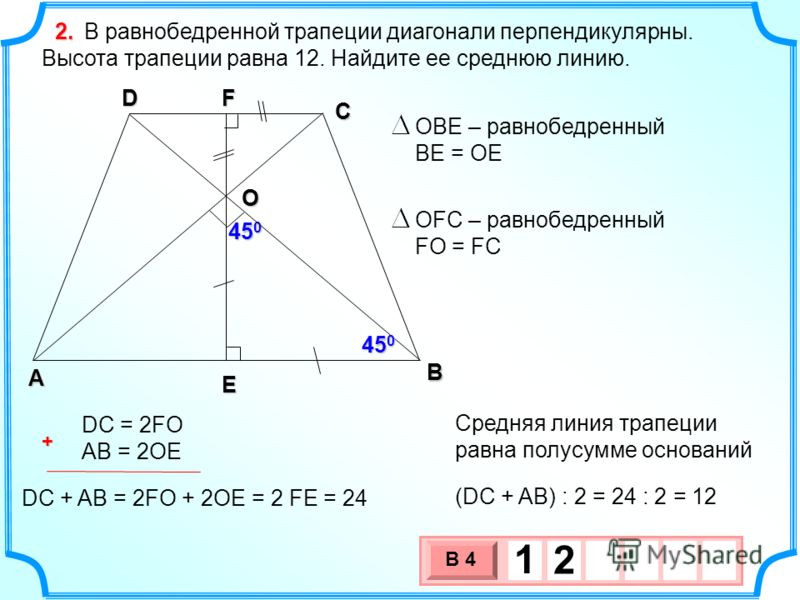 Проблема возникает, когда я предполагаю, что сумма высот двух треугольников равна диагонали. Забавно, что таким образом я получил правильный ответ, однако он был только интуитивным, а не точным.

Но как доказать, что $(a = b + c)$ истинно или ложно?

  • геометрия
  • евклидова геометрия

$\endgroup$

0

$\begingroup$

Ваше утверждение: $a=b+c$ неверно. Поскольку ваша трапеция равнобедренная, два нижних угла равны. Следовательно, две диагонали равны, потому что каждый нижний треугольник, образуемый при делении трапеции, конгруэнтен (по SAS). Тогда по теореме Пифагора, пока два перпендикуляра не лежат на одной прямой, $a>b+c$:

Только когда два перпендикуляра лежат на одной прямой, $a=b+c$, но тогда ваша равнобедренная трапеция будет квадратом. (Как заметил Исаак, два перпендикуляра могут лежать на одной прямой, если равнобедренная трапеция не является квадратом. 2}{2}=5$ вместо $3$

Простой способ увидеть это — представить себе очень широкую трапецию. $b$ и $c$ будут почти вертикальными и не длиннее высоты, но диагональ $a$ очень длинная.

$\endgroup$

$\begingroup$

То, что $a=b+c$ в целом неверно, хорошо освещено в других ответах. Однако есть множество равнобедренных трапеций, для которых это верно.

В любой равнобедренной трапеции $TRAP$, показанной с $TP=RA$, $\triangle TPD\cong\triangle RAD$ и $\triangle RAD$ является отражением $\triangle TPD$ на прямой, проходящей через $D$ перпендикулярно $\overline{TR}$ и $\overline{AP}$.

Обратно, начиная с любого $\треугольника XYZ$ и отражая его по прямой, проходящей через $Z$, для которой острые углы, образованные этой прямой и $\overline{XZ}$ и $\overline{YZ}$, имеют одинаковую меру ‡ в $\треугольник X’Y’Z$ дает равнобедренную трапецию $XX’Y’Y$ с $Z$ на пересечении диагоналей.