8 класс. Медианы, биссектрисы, высоты в прямоугольном треугольнике №1.
Не пропустите весеннюю распродажу инструментов учителя! Доступ ко всем комплектам со скидкой до 90%
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Подготовка к ОГЭ Количество заданий в тесте: 10
Вопрос 1
Один острый угол прямоугольного треугольника на 7o больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Найдите больший острый угол. Ответ дайте в градусах.
Вопрос 2
Один острый угол прямоугольного треугольника в 8 раз больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Вопрос 3
В треугольнике ABC угол C равен 90o, CH — высота, угол A равен 49o. Найдите угол BCH. Ответ дайте в градусах.
Вопрос 4
В треугольнике ABC CD — медиана, угол C равен 90o, угол B равен 24o. Найдите угол ACD. Ответ дайте в градусах.
Вопрос 5
Острый угол прямоугольного треугольника равен 40o. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Вопрос 6
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Вопрос 7
Острые углы прямоугольного треугольника равны 47o и 43o. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Ответ дайте в градусах.
Вопрос 8
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 17o. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Вопрос 9
Острые углы прямоугольного треугольника равны 69oи 21o. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Вопрос 10
Острые углы прямоугольного треугольника равны 56
Пройти тест
Сохранить у себя:
© 2019, Яковлева Ирина Владимировна 379
Острый угол прямоугольного треугольника равен
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-09-21
Для вас несколько заданий — в условии дан прямоугольный треугольник.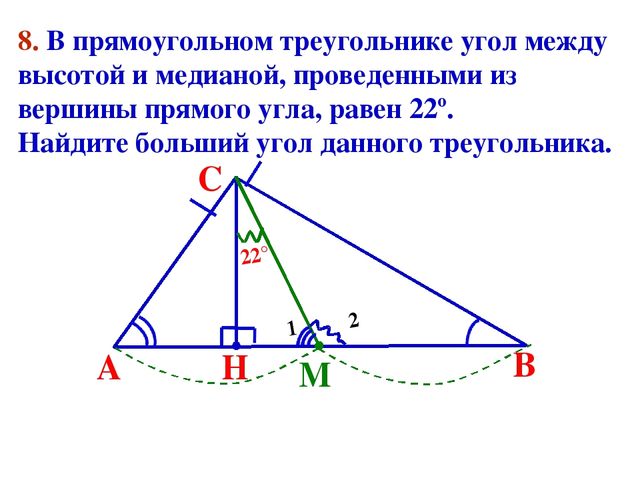 В условии говорится о вычислении углов между высотой и биссектрисой, медианой и биссектрисой, высотой и медианой проведёнными из прямого угла.
В условии говорится о вычислении углов между высотой и биссектрисой, медианой и биссектрисой, высотой и медианой проведёнными из прямого угла.
Это группа заданий входит в состав ЕГЭ по математике. Задачи несложные, требуется знание теоремы о сумме углов треугольника, свойств равнобедренного треугольника и немного логики. Да! Есть один нюанс — задачи, в которых говорится о медиане проведённой к гипотенузе необходимо знать одно свойство, теорию можно посмотреть здесь. Приступим!
Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Обозначим меньший острый угол прямоугольного треугольника через x. Тогда больший острый угол данного треугольника будет равен 4х.
По свойству прямоугольного треугольника сумма его острых углов равна 90о. Отсюда получаем уравнение х + 4х = 90о.
Вычисляем, получим 5х = 90о, х = 18о.
Следовательно больший угол будет равен 18о ∙ 4 = 72о
Ответ: 72
Острый угол прямоугольного треугольника равен 32о. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Нам необходимо найти угол COD. По условию известно, что CE и AD — это биссектрисы (делят углы пополам). Это означает, что угол CAD равен 32о, а угол ACO равен 45о. По теореме о сумме углов треугольника мы можем найти угол AOC, и далее угол COD. Итак, известно, что сумма углов треугольника равна 180о, следовательно
Углы AOC и COD смежные, то есть их сумма равна 180о. Таким образом, искомый угол (острый угол между данными биссектрисами) равен 61 градусу.
Ответ: 61
*Если в подобных задачах вы сразу не видите ход решения, то ищите те элементы, которые можно найти исходя из условия в первую очередь. А далее уже используйте найденные значения.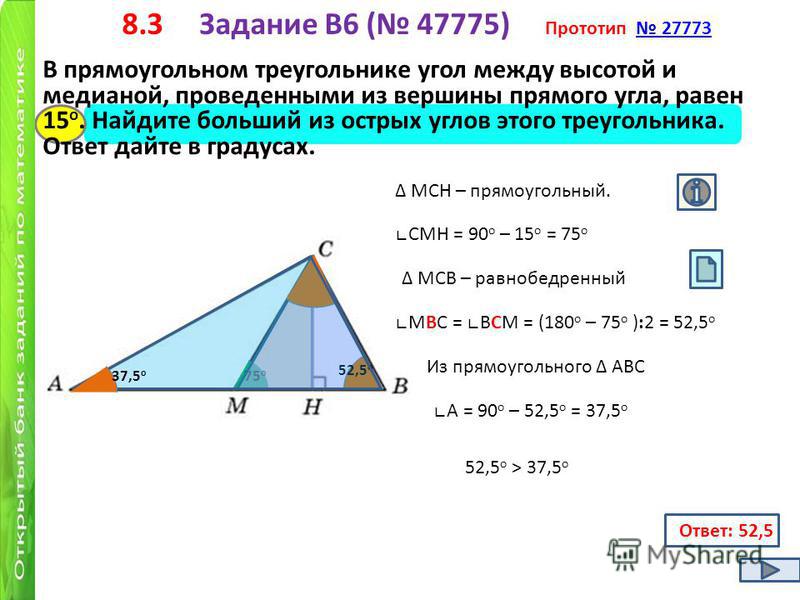
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
В условии нам не даны ни какие величины, кроме того, что угол С прямой. Это говорит о том, что их необходимо ввести, то есть в данном случае мы можем обозначить угол через переменную, а далее использовать свойства прямоугольного треугольника и теорему о сумме углов.
Обозначим угол CAD как х. Тогда угол CBA будет равен 90о – х.
Рассмотрим треугольник AOB:
Можем найти угол AOB:
Значит острый угол между биссектрисами будет равен 45о, так является смежным углу 135о.
Как видите, не всегда нужны численные величины в условии. Достаточно знать свойства, включить логику и задача будет решена.
Ответ: 45
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21о. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Ответ дайте в градусах.
Сразу отметим, что в треугольнике CDH нам известны два угла. Используя теорему о сумме углов треугольника мы можем найти угол CDH. То есть:
Теперь мы можем найти угол В в треугольнике CDВ. Так как CD биссектриса, то угол BCD равен 45о, угол CDB мы нашли.
Значит угол В равен 180о–45о–69о=66о. По свойству прямоугольного треугольника: сумма острых углов в нём равна 90 градусов.
Следовательно другой острый угол будет равен 24о.
Ответ: 24
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14о. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Нам дан угол MCD равный 14о. Так же нам известен угол DCB, он равен 45о, так как CD биссектриса. Можем найти угол MCB: 14о + 45о = 59о.
Как уже сказано, медиана в прямоугольном треугольнике проведённая из прямого угла к гипотенузе равна её половине.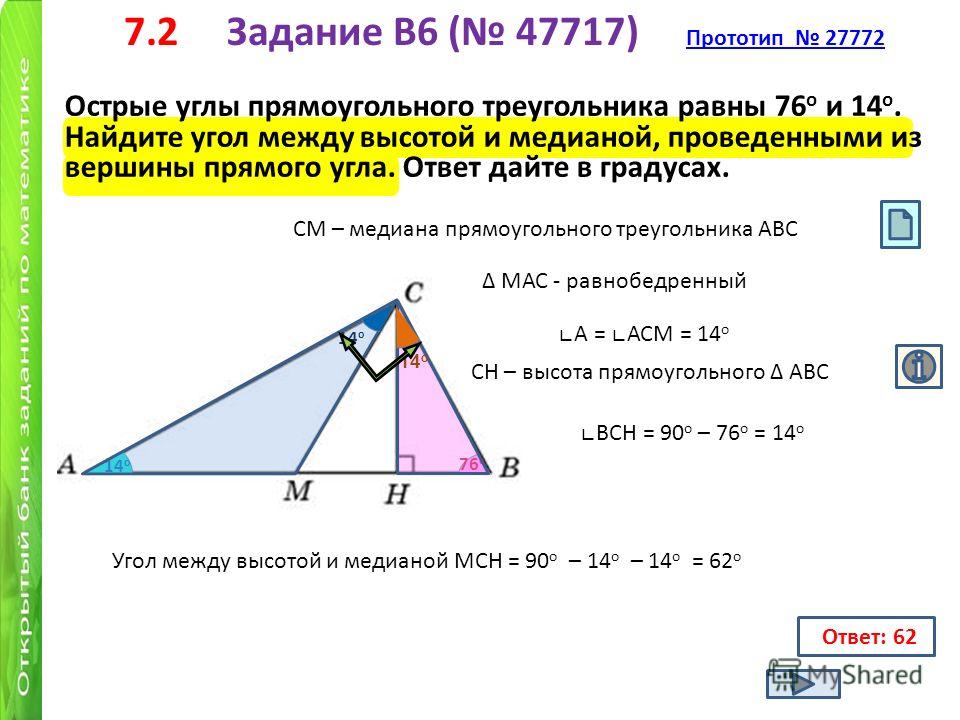 То есть, она разбивает прямоугольный треугольник на два равнобедренных треугольника, в данном случае AMC и BMC. Известно, что в равнобедренном треугольнике углы при основании равны, то есть угол MBC равен углу BCM. Таким образом,
То есть, она разбивает прямоугольный треугольник на два равнобедренных треугольника, в данном случае AMC и BMC. Известно, что в равнобедренном треугольнике углы при основании равны, то есть угол MBC равен углу BCM. Таким образом,
То есть, меньший угол равен 31о.
Ответ: 31
Один острый угол прямоугольного треугольника на 32о больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Посмотреть решение
В треугольнике АВС угол С равен 90о, СН — высота, угол А равен 34о. Найдите угол ВСН. Ответ дайте в градусах.
Посмотреть решение
В треугольнике ABC CD — медиана, угол ACB равен 90о, угол В равен 58о. Найдите угол ACD. Ответ дайте в градусах.
Посмотреть решение
Острые углы прямоугольного треугольника равны 29о и 61о. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Ответ дайте в градусах.
Посмотреть решение
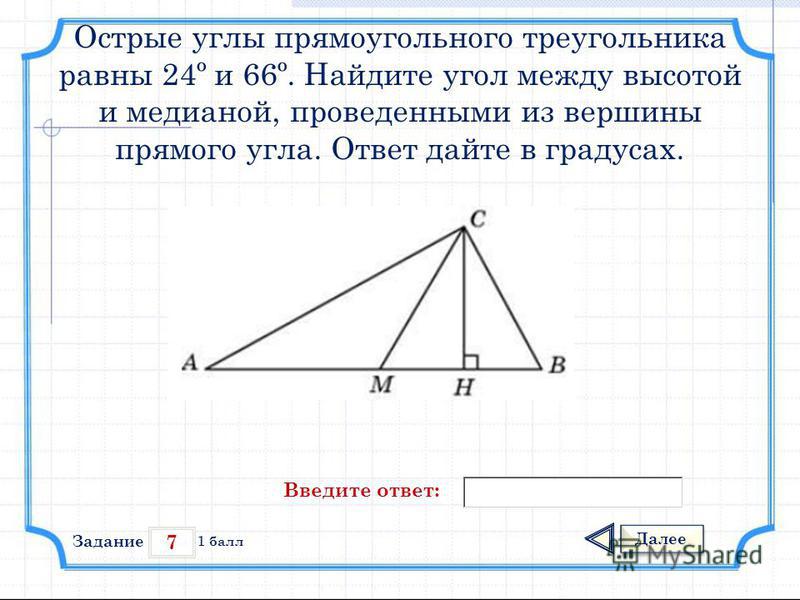
Острые углы прямоугольного треугольника равны 24о и 66о. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Посмотреть решение
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40о. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Посмотреть решение
Острые углы прямоугольного треугольника равны 24о и 66о. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Посмотреть решение
Какие общие рекомендации можно дать?
1. Используйте теорему о сумме углов треугольника. Это одна из основных теорем, связанных с треугольниками, её нужно всегда помнить.
2. Нужно чётко помнить, что такое медиана, биссектриса, высота (не перепутать).
3. Запомните свойство медианы в прямоугольном треугольнике.
4. В задачах, где в условии не даны численные величины углов, обозначайте их переменной(ыми) и далее используйте известные вам свойства.
5. Если не видите каким путём строить решение, и сразу не можете увидеть логическую цепочку рассуждений, то исходя из данных в условии ищите то, что возможно найти. Получив новые величины, также смотрите, что вы можете найти при их использовании.
На этом всё. Успеха Вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Решение треугольников | ЕГЭ-№1ТреугольникУглы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
{\circ}}\].
Полный пошаговый ответ:
Рассмотрим треугольник ABC. Нарисуем AH как высоту от A до BC, которая является серединой длины BC. Из рисунка мы можем сказать, что H лежит между B и M.
Если мы рассмотрим \[\Delta ABH\] и \[\Delta AMH\], мы можем сказать, что
\[\угол AHB=\ угол AHM\], где оба угла прямые.
\[\угол BAH=\угол MAH\], равны, так как говорят, что углы делятся поровну на высоту и медиану.
AH = AH, сторона у обоих треугольников общая.
Таким образом, по критерию подобия ASA мы можем сказать, что два угла и одна сторона \[\Delta ABH\] равны двум углам и одной стороне \[\Delta AMH\]. Таким образом, \[\Delta ABH\] и \[\Delta AMH\] конгруэнтны по критерию подобия ASA.
Таким образом, мы можем сказать, что BH = HM.
\[\поэтому HM=\dfrac{1}{2}BM\], из рис.
Теперь рассмотрим \[\Delta AHC\].
Мы сказали, что АМ — это медиана, но она также делит угол А на равные части. Таким образом, мы можем сказать, что AM делит угол A пополам, поэтому мы получаем отношения из \[\Delta AHC\].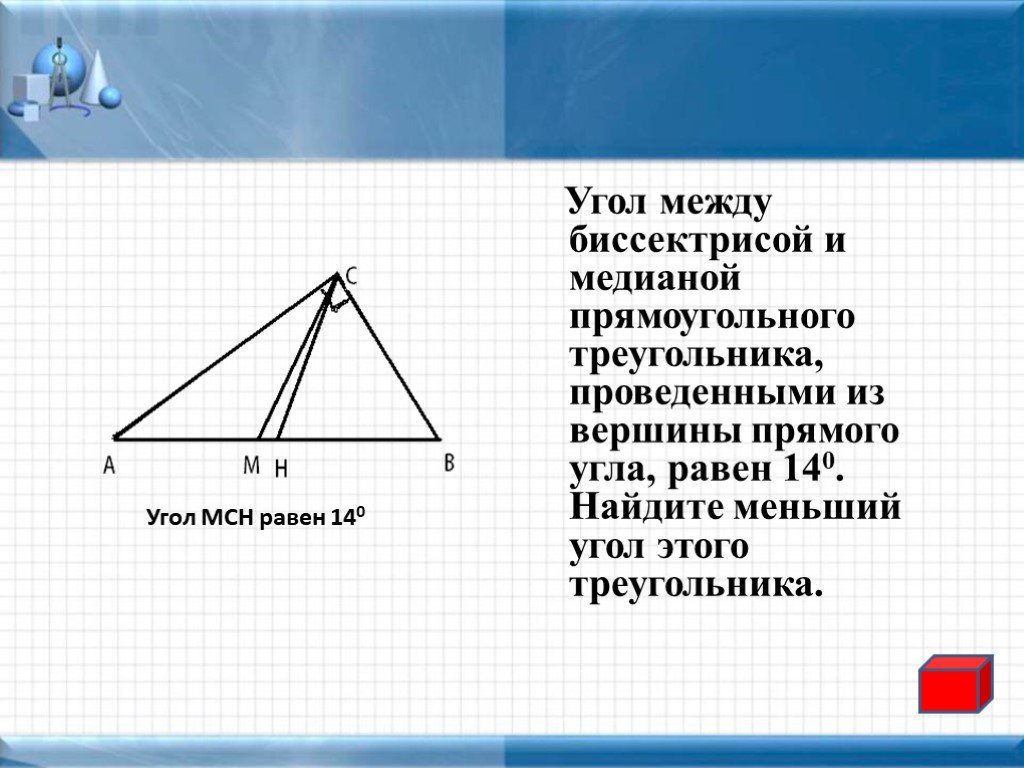
\[\следовательно \dfrac{MH}{MC}=\dfrac{AH}{AC}\]
Мы сказали, что M является серединой BC. Таким образом, мы можем сказать, что BM = CM.
Мы получили, \[MH=\dfrac{1}{2}MB\].
Поставить, МБ=МС.
\[\begin{align}
& \следовательно, MH=\dfrac{1}{2}MC \\
& \Rightarrow \dfrac{MH}{MC}=\dfrac{1}{2} \\
\ end{align}\]
AHC — прямоугольный треугольник с вершиной H.
\[\begin{align}
& \Rightarrow \dfrac{MH}{MC}=\dfrac{1}{2}=\dfrac{AH }{AC} \\
& \Стрелка вправо AC=2AH \\ 9{\circ}}\].
Примечание: Докажите равенство образующихся треугольников. Чтобы найти искомые углы, докажите, что M — середина BC, а H — середина BM. Таким образом, сделайте отношения, связывающие его. Доказательство треугольника даст нам пропорциональные соотношения в \[\Delta AHC\].
Недавно обновленные страницы
Если пружина имеет период T и разрезана на равные n класс 11 физики CBSE
Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE
В любом треугольнике AB2 BC4 CA3 и D является серединой математического класса 11 JEE_Main
В треугольнике ABC 2asin dfracAB+C2 равно IIT Отборочный класс 11 математики JEE_Main
Если в aDelta ABCangle A 45circ угол C 60circ, то класс 11 maths JEE_Main
Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол класса 11 maths JEE_Main
Если пружина имеет период T и разрезана на n равных 11 классов физики CBSE
Планета движется вокруг Солнца в почти круговая орбита класс 11 физика CBSE
В любом треугольнике AB2 BC4 CA3 и D является серединой математического класса 11 JEE_Main
В треугольнике ABC 2asin dfracAB+C2 равно IIT Отборочный класс 11 математики JEE_Main
Если в aDelta ABCangle A 45circ угол C 60circ тогда класс 11 maths JEE_Main
Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и класс угла 11 maths JEE_Main
Трендовые сомнения
Урок Биссектриса угла, проведенная к гипотенузе прямоугольного треугольника
This Lesson (Биссектриса угла, проведенная к гипотенузе прямоугольного треугольника) была создана пользователем ikleyn(47821) : Посмотреть исходный код, Показать
О ikleyn :
Этот урок посвящен углам в прямоугольном треугольнике.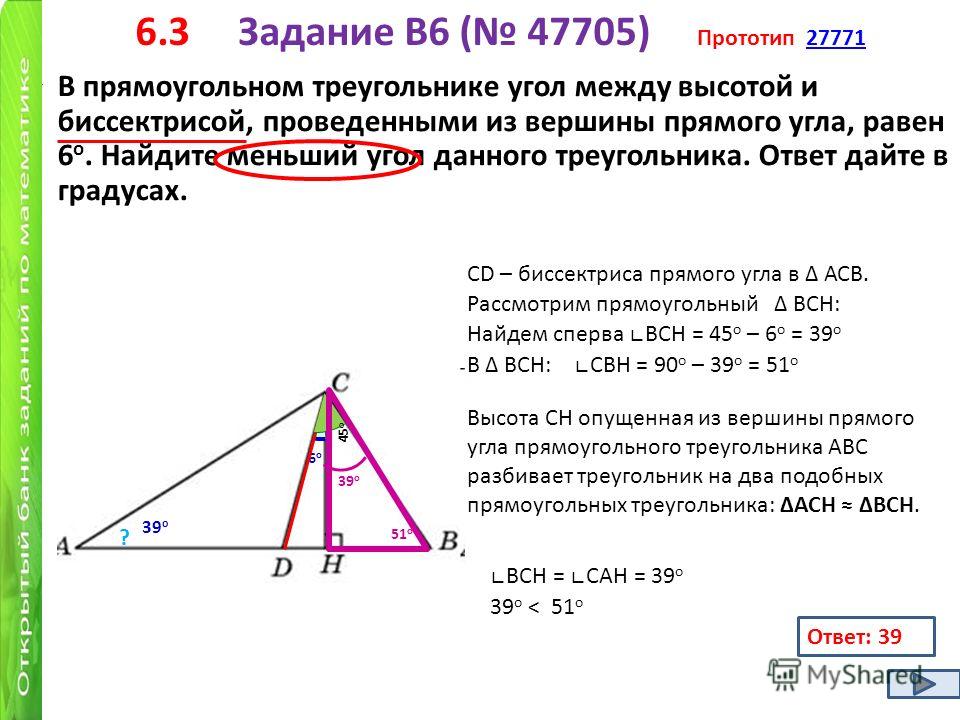
Проблема
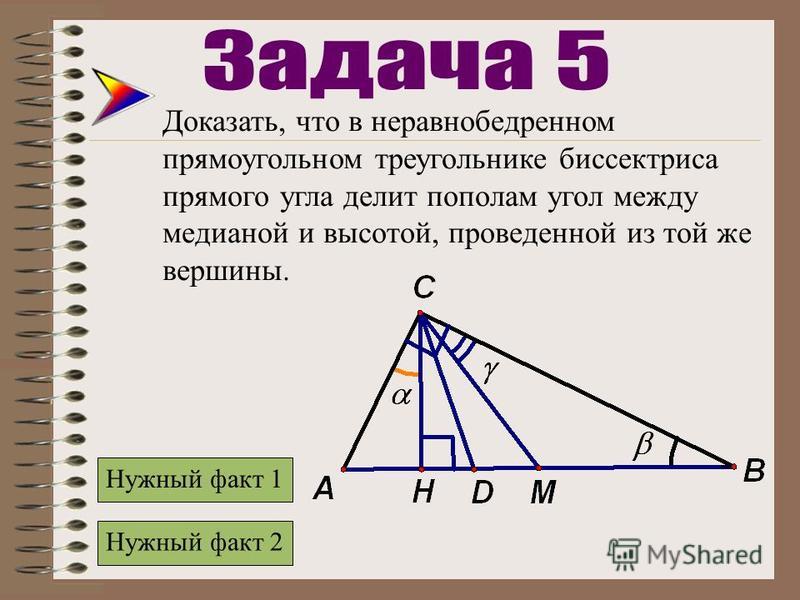
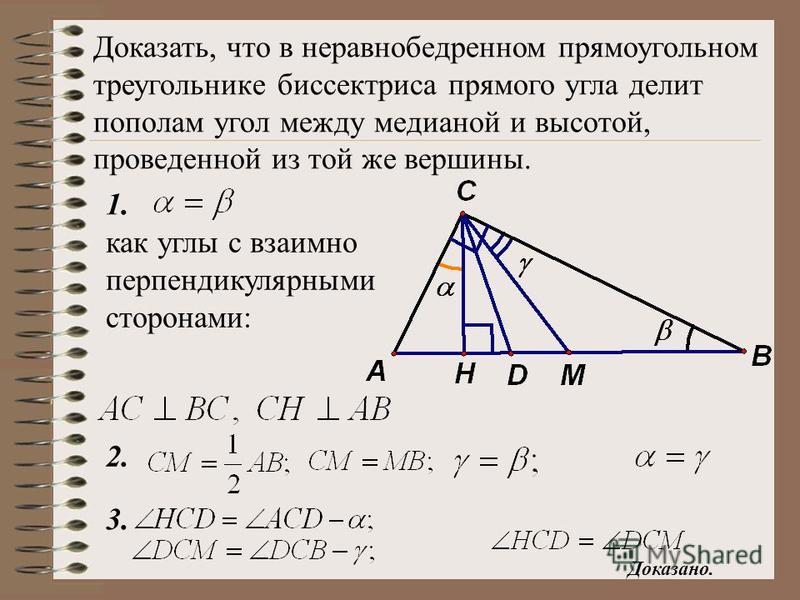
В прямоугольном треугольнике биссектриса угла, высота и медиана проведены от вершины прямого угла к гипотенузе.
Докажите, что биссектриса прямого угла также делит пополам угол между высотой и медианой.
| Раствор На рис. 1 показан прямоугольный треугольник ABC . Угол ACB является прямым угла. Высота AD (красная линия), биссектриса угла AE (синяя линия) и медиана AF (зеленая линия) проведены от вершины прямого угла (точка C ) к гипотенузе AB . Нам нужно доказать, что биссектриса угла также делит пополам угол DCF . Доказательство очень простое ( Рисунок 2 ). | Рисунок 1 . Биссектриса угла и медиана прямоугольного треугольника | Рисунок 2 . К решению проблемы |
В прямоугольном треугольнике ADC угол ACD дополняет угол CAD . Следовательно, угловая мера угла ACD равно 90 — = 90 — (90 — ) = .
Итак, угол ACD равен углу ABC . Вот почему в Рис. 2 мы обозначили угол ACD тем же символом, что и угол ABC .
С другой стороны медиана прямоугольного треугольника делит его на два равнобедренных треугольника. Этот факт был доказан на уроке Медиана в прямоугольном треугольнике, проведенном к его гипотенузе по текущей теме Геометрия раздела

 урок Углы основы
урок Углы основы
Leave A Comment