Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
\[{\Large{\text{Медиана}}}\]
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Доказательство
Пусть \(AD\) и \(BE\) – медианы в треугольнике \(ABC\), \(O\) – точка пересечения \(AD\) и \(BE\).
\(DE\) – средняя линия в треугольнике \(ABC\), тогда \(DE\parallel AB\), значит \(\angle ADE = \angle BAD\), \(\angle BED = \angle ABE\), следовательно, треугольники \(ABO\) и \(DOE\) подобны (по двум углам).
Из подобия треугольников \(ABO\) и \(DOE\): \(\dfrac{BO}{OE} = \dfrac{AB}{DE} = \dfrac{2}{1}\).
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).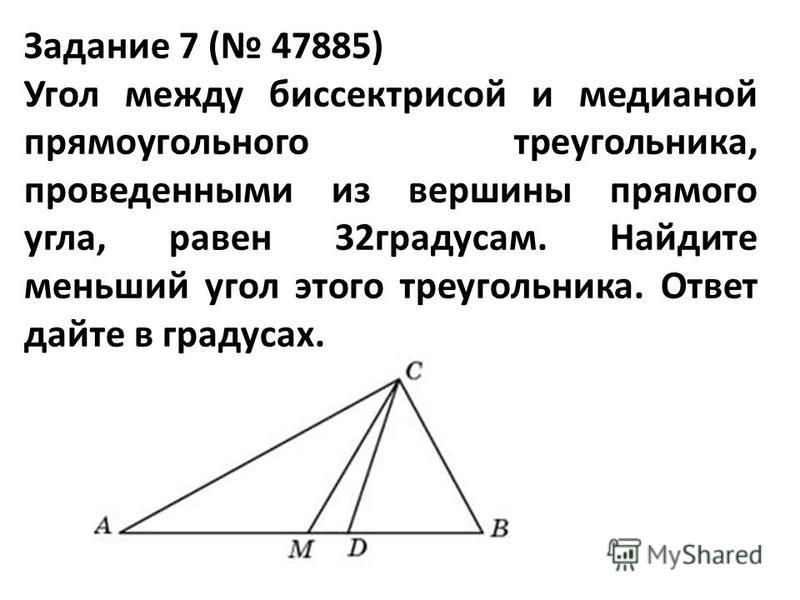
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: \(S_{ABC} = 0,5\cdot AC\cdot h\).
Пусть \(BD\) – медиана в треугольнике \(ABC\), тогда \(AD = DC\).
\(S_{ABD} = 0,5\cdot AD\cdot h\),
\(S_{BCD} = 0,5\cdot DC\cdot h\).
Так как \(AD = DC\), то \(S_{ABD} = S_{BCD}\), что и требовалось доказать.
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
1) Докажем, что если \(\triangle ABC\) – прямоугольный, то \(BM=\frac12AC\), где \(M\) – середина гипотенузы \(AC\).
Достроим треугольник \(ABC\) до прямоугольника \(ABCD\) и проведем диагональ \(BD\).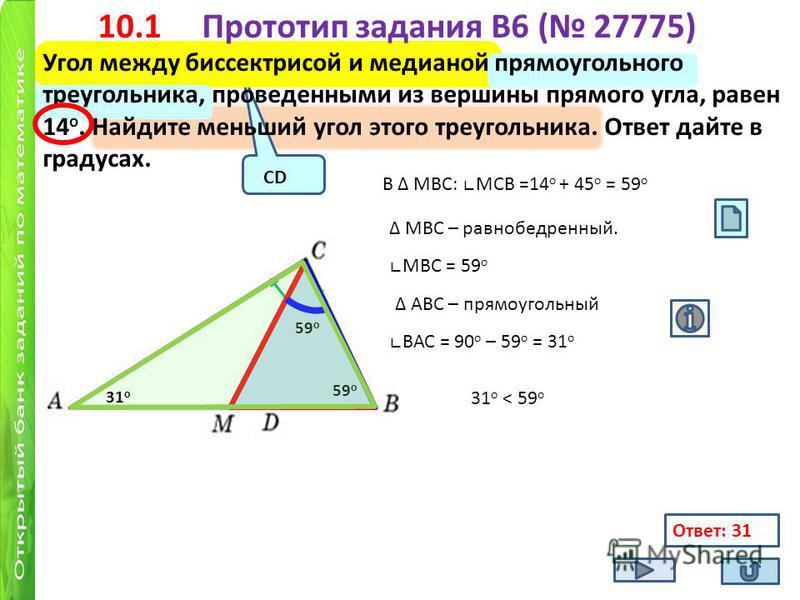
\[{\Large{\text{Биссектриса}}}\]
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC\cdot CD}{CB\cdot CD} = \dfrac{AC}{CB}\]
С другой стороны, \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{0,5\cdot AD\cdot h}{0,5\cdot DB\cdot h}\), где \(h\) – высота, проведённая из точки \(C\), тогда \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AD}{DB}\).
В итоге \(\dfrac{AD}{DB} = \dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC}{CB}\), откуда \(\dfrac{AD}{AC} = \dfrac{DB}{BC}\), что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.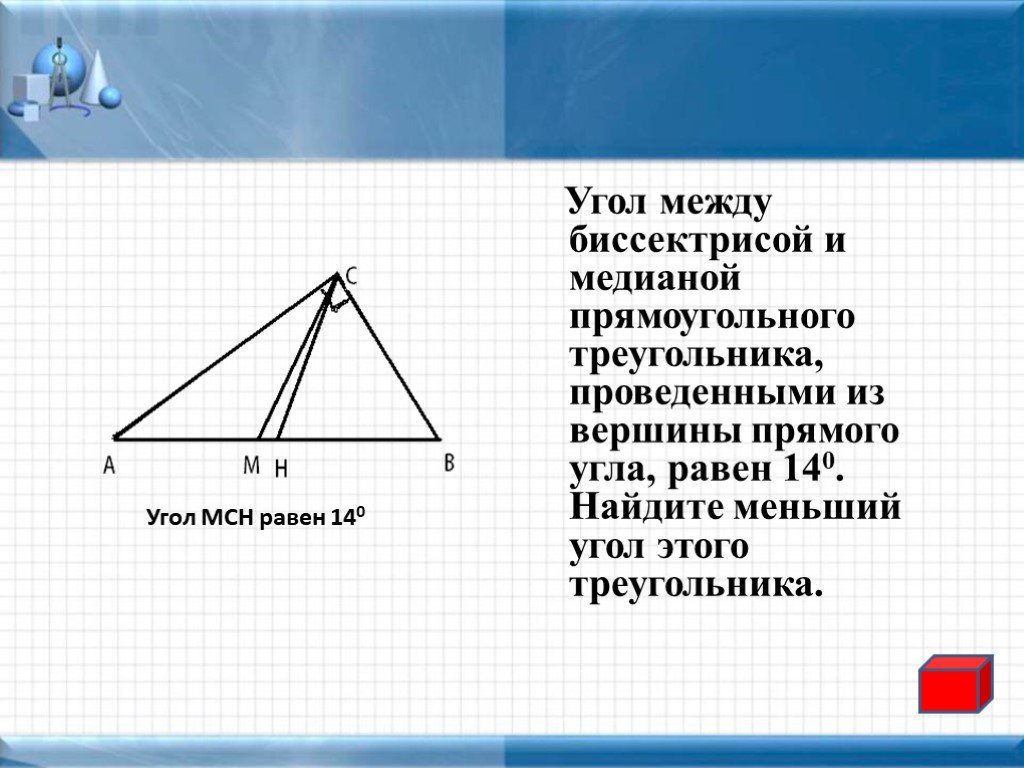
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
1) Докажем, что если \(KA=KB\), то \(OK\) – биссектриса.
2) Докажем, что если \(OK\) – биссектриса, то \(KA=KB\).
Аналогично треугольники \(AOK\) и \(BOK\) равны по гипотенузе и острому углу, следовательно, \(KA=KB\), чтд.
Свойства биссектрисы и медианы треугольника. | Геометрия
Здравствуйте, уважаемые читатели! Сегодня мы приступим к решению задач по
свойствам биссектрисы и медианы треугольника. А для начала давайте вспомним, что такое биссектриса и медиана.Биссектриса — это отрезок CD, который выходит из вершины угла треугольника, делит угол пополам и заканчивается на противоположной стороне.
Медиана – это отрезок СМ, который соединяет вершину треугольника с серединой противоположной стороны.
Поскольку в треугольнике вершин и сторон по три, то биссектрис медиан у него будет тоже три.
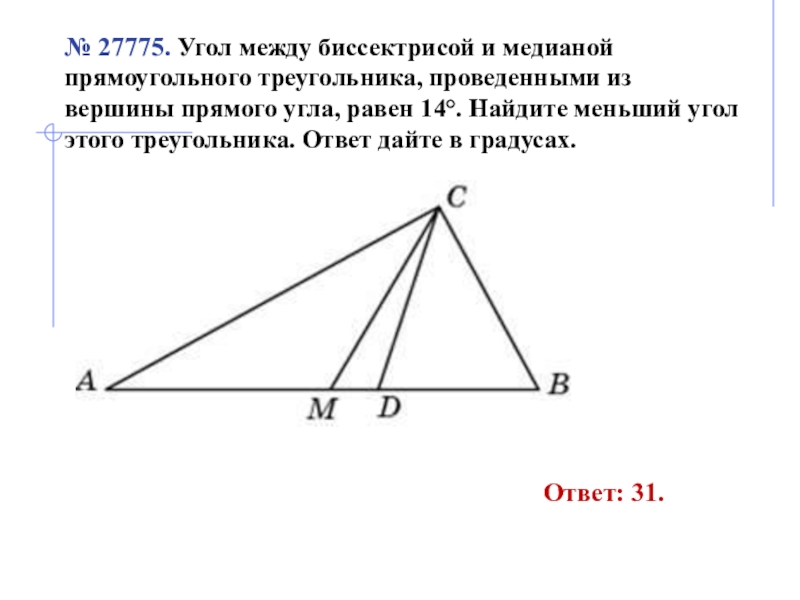
Задача 1. Дан прямоугольный треугольник АВС. Из вершины А к стороне ВС проведены медиана АД и биссектриса АМ. Угол между медианой и биссектрисой равен 17°. Найти острые углы треугольника.
Решение: Поскольку АМ — биссектриса, то угол ВАМ равен углу МАС и они равны 45°. Но угол ДАМ равен 17°. Отсюда, угол ВАД равен разности углов ВАМ и ДАМ, или 45-17 = 28°.
Мы знаем, что медиана, проведённая из вершины прямого угла прямоугольного треугольника, делит этот треугольник на 2 равнобедренных треугольника. А именно треугольники АВД и АДС.
И теперь, поскольку треугольник АВД равнобедренный, то углы при основании у него равны, т.е. угол ВАД равен углу АВД и они оба равны 28°.
А это значит, что в прямоугольном треугольнике угол В равен 28°.
Но сумма острых углов в прямоугольном треугольнике равна 90°. Отсюда, угол С будет равен 90 — 28 = 62°.

Ответ: острые углы в прямоугольном треугольнике равны 28° и 62°.
Задача 2. Докажите, что биссектрисы смежных углов перпендикулярны.
Решение: Мы знаем свойство измерения углов, которое гласит, что если внутри угла провести лучи, то они разобьют его на несколько углов и сумма градусных мер этих углов будет равна градусной мере первоначального угла.
Поэтому мы имеем: α+α+β+β = 180°.
Или 2α+2β = 180°.
Сокращаем правую и левую часть уравнения на 2, получим: α + β = 90°.
Т.е. угол ДВК между биссектрисами ВД и ВК смежных углов ВСЕГДА равен 90° независимо от величин смежных углов.
Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Найти АВ, если АМ = 24, ВМ = 18.
Решение: Из предыдущей задачи мы узнали, что биссектрисы смежных углов всегда образуют угол 90°.
Биссектрисы, проведённые из углов трапеции, прилежащих к боковой стороне тоже образуют угол 90°.
В самом деле: углы А и В трапеции в сумме дают 180°, как односторонние углы при параллельных прямых АД и ВС и секущей АВ.

Значит, половины этих углов в сумме будут равны 90°.
А если в треугольнике 2 угла в сумме равны 90°, то третий угол будет равен 90°, ведь сумма внутренних углов треугольника равна 180°.
Значит, это треугольник — прямоугольный. Нам известно в нём 2 катета, найти гипотенузу можно по теореме Пифагора.
АВ² = АМ² + ВМ² = 24² + 18² = 900. Отсюда, АВ = 30.
Ответ: АВ = 30.
На сегодня мы заканчиваем решать задачи по свойствам биссектрисы и медианы треугольника. В следующий раз мы продолжим решать геометрические задачи.
Оставить комментарий
Объяснение урока: Медианы треугольников
В этом объяснении мы научимся определять медианы треугольника и использовать их свойства пропорциональности, чтобы найти недостающую длину.
Медианы треугольников — это специальные линии с особыми свойствами. Давайте начнем с определением медианы.
Определение: Медиана
Медианы треугольника — это три отрезка, идущие от каждой вершины к
середина противоположной стороны.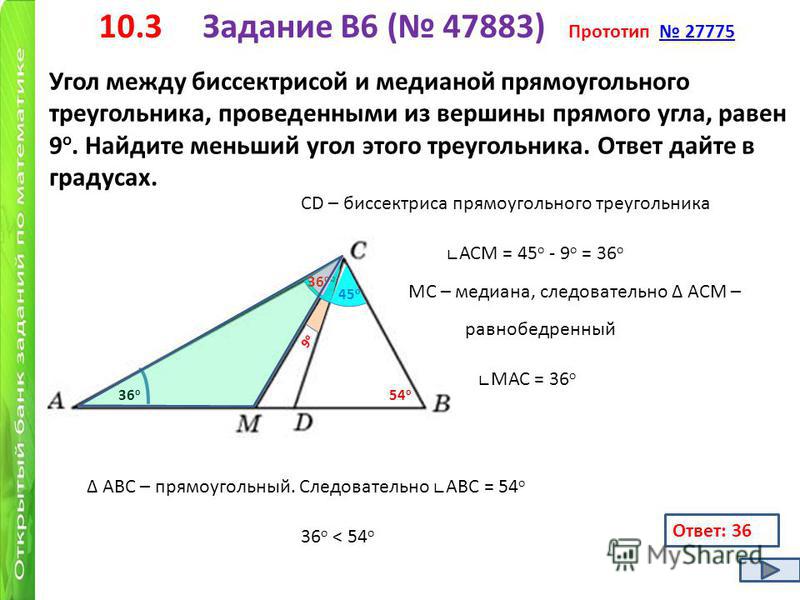
На следующей диаграмме показан пример, содержащий медиану треугольника и две другие линии в треугольнике, которые не являются медианами.
Так как в треугольнике 3 вершины, то и 3 медианы. Когда мы рисуем все мы видим, что все они пересекаются. Это общее свойство медиан которые мы изложим в следующей теореме.
Теорема: совпадение медиан треугольника
Три медианы треугольника пересекаются в одной точке (то есть они параллельны). Точка их пересечения называется точкой совпадение медиан.
Другое свойство медиан треугольника состоит в том, что относительное положение точка пересечения медиан всегда одна и та же. Действительно, точка совпадение расположено на двух третях длины медианы от вершина.
Давайте представим себе это. Мы можем разделить каждую медиану на три трети, как показано на
диаграмма. Две трети находятся между вершиной и точкой пересечения,
и одна треть находится между точкой пересечения и серединой
сторона.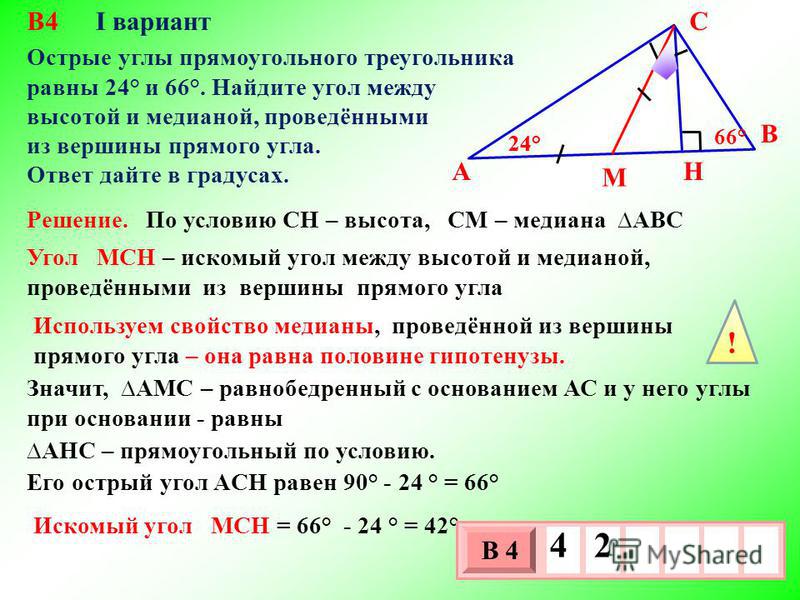
Эквивалентно это означает, что длина сегмента между вершиной и точка совпадения в два раза больше, чем между точкой совпадения и середина противоположной стороны.
Это можно найти и с помощью алгебры.
Если 𝐴𝑃=23⋅𝐴𝐸 и 𝑃𝐸=13⋅𝐴𝐸, то из второго уравнения (умножая обе части на 3) получаем 𝐴𝐸=3𝑃𝐸, и заменив 𝐴𝐸 на 3𝑃𝐸 в первое уравнение, получаем 𝐴𝑃=23⋅3𝑃𝐸, что дает 𝐴𝑃=2𝑃𝐸.
Подведем итоги.
Теорема: положение точки пересечения медиан треугольника
Расстояние от каждой вершины треугольника до точки пересечения его medians составляет две трети длины медианы от этой вершины.
Эквивалентно расстоянию от точки пересечения медиан до вершина в два раза больше, чем расстояние до противоположной средней точки.

Пример 1: Свойства точки пересечения медиан треугольника
В треугольнике 𝐴𝐵𝐶 𝑀 является точкой совпадение его медиан. Если 𝐴𝐷 медиана, тогда 𝐴𝑀=𝑀𝐷.
Ответ
Напомним, что медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. Нарисуем все медианы треугольник 𝐴𝐵𝐶 с точкой 𝑀 совпадение. 𝐴𝐷 — медиана, соединяющая вершину 𝐴 с 𝐷; следовательно, 𝐷 — середина стороны 𝐵𝐶.
Мы знаем из теоремы о точке пересечения трех медиан треугольника, что расстояние от каждой вершины до точки пересечения медиан составляет две трети длины медианы от этой вершины. Это значит у нас тут 𝐴𝑀=23𝐴𝐷.
Это означает, что если мы разрежем 𝐴𝐷 на три равных сегмента, 𝐴𝑀 будет сделан из двух из них. Следует, что 𝑀𝐷 состоит из третьего. Поэтому, 𝐴𝑀 в два раза длиннее 𝑀𝐷.
Следовательно, 𝐴𝑀=2𝑀𝐷.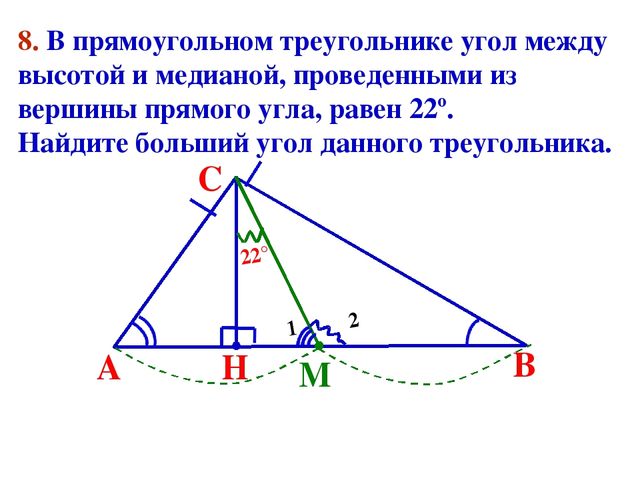
Во втором примере нам нужно определить медианы, а затем использовать свойство точка пересечения медиан, чтобы найти длину от вершины до точки согласия.
Пример 2. Определение медиан и использование свойства их точки пересечения с Найдите недостающую длину
Найдите длину 𝐴𝑀, учитывая, что 𝐴𝐸=54.
Ответ
Глядя на диаграмму, мы видим, что оба 𝐴𝐸 и 𝐶𝐷 — отрезки, соединяющие вершину с середина противоположной стороны. Следовательно, 𝐴𝐸 и 𝐶𝐷 медианы треугольника 𝐴𝐵𝐶. Таким образом, точка 𝑀 является точкой совпадения медиан треугольника 𝐴𝐵𝐶.
Напомним, что длина 𝐴𝑀, т. е. расстояние от вершины до точки пересечения составляет две трети от медианы 𝐴𝐸: 𝐴𝑀=23⋅𝐴𝐸=23⋅54=36.
Таким образом, длина 𝐴𝑀 равна 36.
Теперь рассмотрим пример, где мы используем наши знания о медианах
треугольник, чтобы составить и решить линейное уравнение.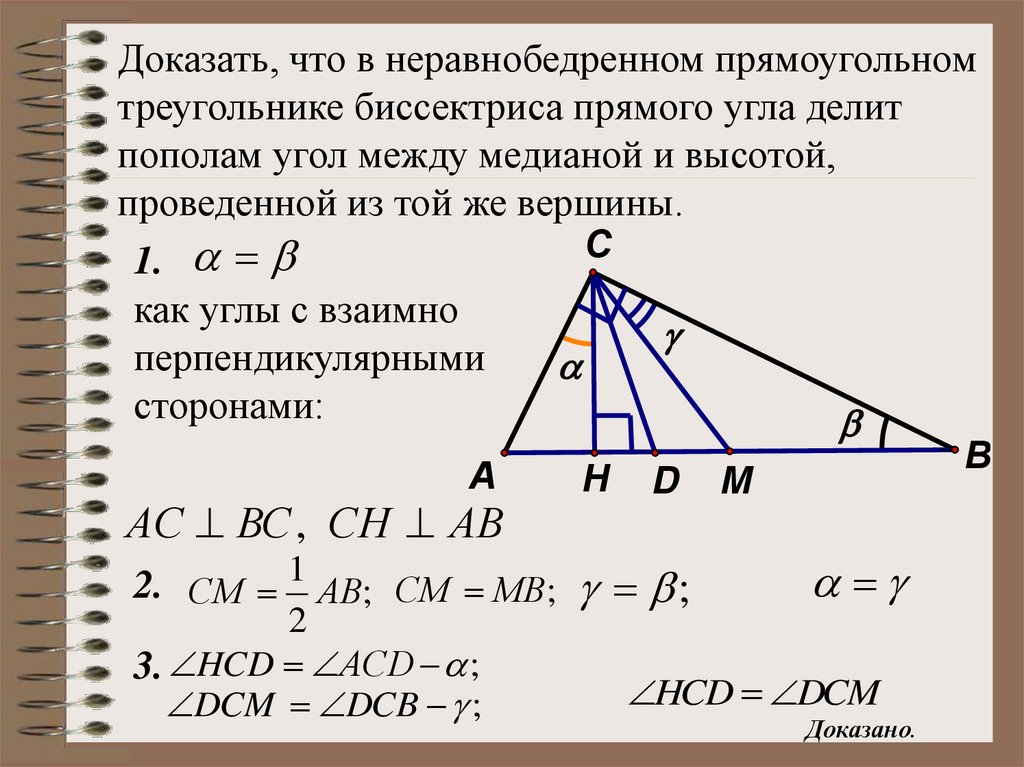
Пример 3. Использование свойств точки пересечения медиан Треугольник для формирования и решения линейного уравнения
В △𝐾𝑀𝐻, 𝐾𝑄=2 и 𝑄𝑃=(5𝑥−7). Найдите 𝑥.
Ответ
В треугольнике 𝐾𝑀𝐻 точка 𝑄 совпадение его медиан. 𝐾 является вершиной и 𝑃 — середина противоположной стороны, 𝐻𝑀. Напомним, что расстояние от каждой вершины треугольника до точки совпадение его медиан составляет две трети общей длины медианы из этой вершины. Следовательно, для медианы 𝐾𝑃 имеем 𝐾𝑄=23𝐾𝑃 и 𝑄𝑃=13𝐾𝑃.
Как 𝐾𝑄=2×13𝐾𝑃, Мы видим, что 𝐾𝑄=2𝑄𝑃.
В вопросе сказано, что 𝐾𝑄=2 и 𝑄𝑃=5𝑥−7.
Отсюда имеем 2=2(5𝑥−7).
Деление обеих частей этого уравнения на 2 дает 1=5𝑥−7.
Прибавление 7 к обеим сторонам дает 8=5𝑥.
И, наконец, разделив обе части на 5, находим, что
𝑥=85=1,6.
Теперь посмотрим на медианы прямоугольного треугольника. Помните, что право треугольник является половиной прямоугольника, как показано на следующей диаграмме, где 𝐴𝐵𝐶𝐷 — прямоугольник, а △𝐴𝐵𝐶 и △𝐶𝐷𝐴 — конгруэнтные прямоугольные треугольники.
В △𝐴𝐵𝐶, 𝐵𝐸 является медианой. В прямоугольнике 𝐴𝐵𝐶𝐷, 𝐵𝐸 составляет половину диагонали. Так как диагонали прямоугольников делят друг друга пополам (это свойство параллелограмма) и равны по длине (это свойство прямоугольники; это происходит от того, что △𝐴𝐵𝐶 и △𝐶𝐷𝐴 конгруэнтны), имеем 𝐵𝐷=𝐴𝐶, поэтому 12𝐵𝐷=12𝐴𝐶, то есть 𝐵𝐸=𝐴𝐸=𝐸𝐶.
Мы доказали следующее свойство.
Теорема: длина медианы прямоугольного треугольника
В прямоугольном треугольнике длина медианы, проведенной из вершины правого треугольника угол равен половине длины гипотенузы треугольника.
Стоит отметить, что одно из следствий этой теоремы состоит в том, что медиана, проведенная
из вершины прямого угла всегда делит прямоугольный треугольник на два
равнобедренные треугольники.
Давайте воспользуемся этой последней теоремой в нашем следующем примере и одновременно обнаружим его следствием в специальном прямоугольном треугольнике, а именно, 30∘-60∘ прямоугольный треугольник.
Пример 4. Определение длины меньшей стороны прямоугольного треугольника с углами 30°-60° с помощью свойства его медианы, проведенной под прямым углом
Определите длины 𝐵𝐷 и 𝐴𝐵.
Ответ
Из диаграммы видно, что △𝐴𝐵𝐶 — прямоугольный треугольник в точке 𝐵, а поскольку 𝐷 — середина 𝐴𝐶, 𝐵𝐷 — медиана △𝐴𝐵𝐶 нарисовано под прямым углом.
Напомним, что в прямоугольном треугольнике длина медианы, проведенной из вершина прямого угла равна половине длины гипотенуза треугольника. Следовательно, у нас есть 𝐵𝐷=12𝐴𝐶=12×49=24.5.cm
Нас также просят найти длину 𝐴𝐵. Мера угла при вершине 𝐶 указана на диаграмме:
это 30∘. Так как угол в
𝐵 — прямой угол, это означает, что мера угла при
вершина 𝐴 равна 180−(30+90)=60∘.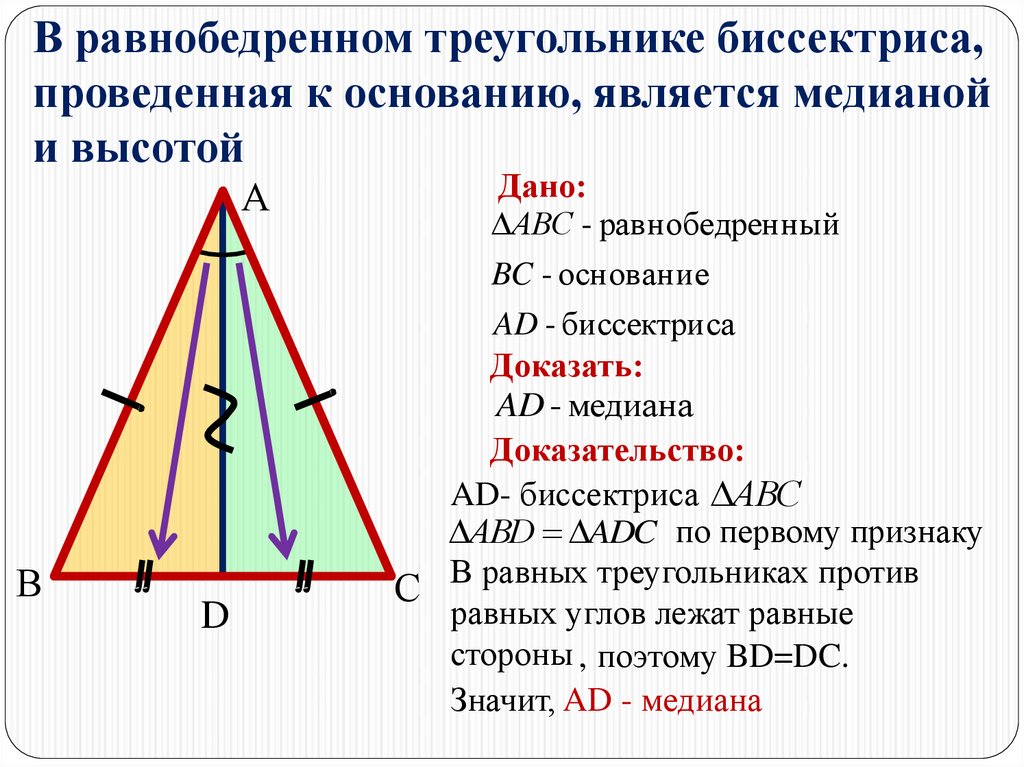 Кроме того,
как мы нашли выше, что 𝐵𝐷=12𝐴𝐶, это означает, что
𝐵𝐷=𝐴𝐷.
Кроме того,
как мы нашли выше, что 𝐵𝐷=12𝐴𝐶, это означает, что
𝐵𝐷=𝐴𝐷.
Значит, △𝐴𝐵𝐷 равнобедренный, значит, два угла, образованные каждой конгруэнтной стороной и третьей стороной, равны, то есть 𝑚∠𝐴𝐵𝐷=𝑚∠𝐴=60.∘
Это означает, что третий угол в △𝐴𝐵𝐷 также имеет меру 60∘ (поскольку 180−(60+60)=60∘), и поэтому △𝐴𝐵𝐷 равносторонний. Таким образом, у нас есть 𝐴𝐵=𝐵𝐷=𝐴𝐷=24.5.cm
Обратите внимание, что в последнем примере мы используем тот факт, что △𝐴𝐵𝐷 равнобедренный, чтобы доказать, что 𝑚∠𝐴𝐵=60∘. Мы могли бы также заметили, что △𝐵𝐷𝐶 равнобедренный, Который означает, что 𝑚∠𝐷𝐵𝐶=𝑚∠𝐶=30.∘
Отсюда, как 𝑚∠𝐴𝐵𝐷=90−30=60.∘
Подытожим наши выводы из последнего примера.
Теорема: Длина меньшей стороны в прямоугольном треугольнике 30°-60°
В треугольнике 30°-60°
прямоугольного треугольника, длина меньшей стороны (т. е.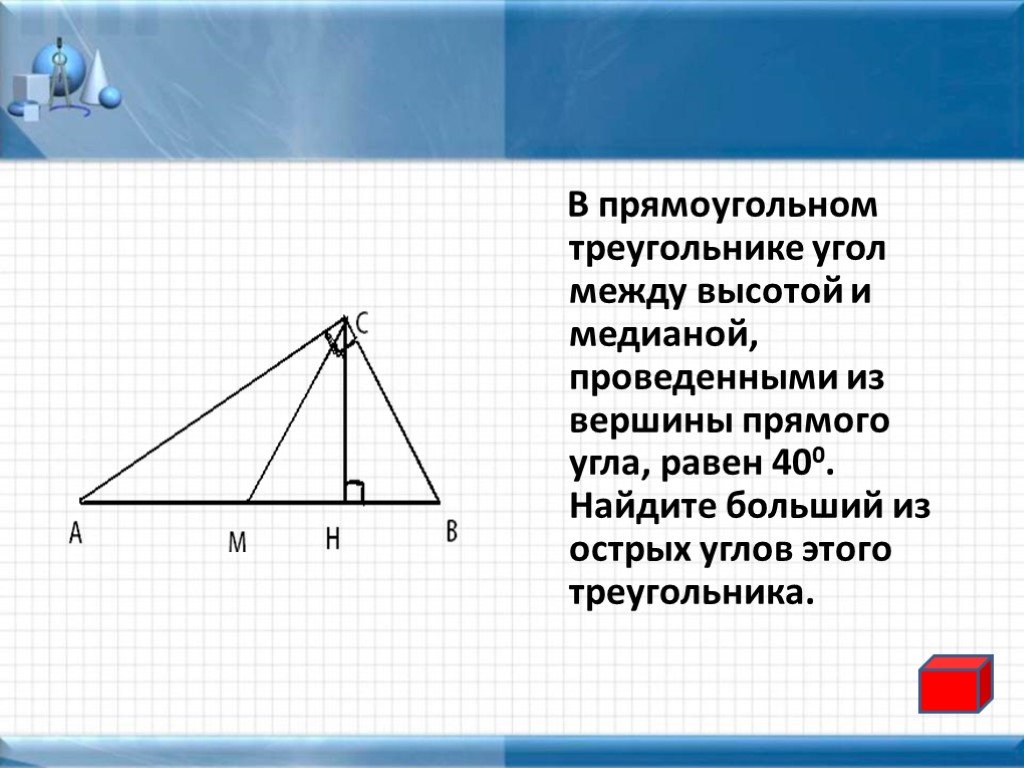 стороны, противоположной
угол 30∘) равен половине
длина гипотенузы треугольника.
стороны, противоположной
угол 30∘) равен половине
длина гипотенузы треугольника.
В нашем последнем примере мы будем использовать свойства медиан и их точку согласие на решение задачи по геометрии.
Пример 5. Нахождение периметра треугольника с помощью медиан треугольника
Учитывая, что 𝐴𝐷=9см и 𝐸𝐵=𝐴𝐵, найдите периметр △𝑀𝐷𝐸.
Ответ
Нас просят найти периметр △𝑀𝐷𝐸. Заметим, что длины 𝐶𝐷 и 𝐷𝐵 отмечены на диаграмме как равны, поэтому 𝐷 является средней точкой. Сходным образом, 𝐶𝐸=𝐸𝐴, поэтому 𝐸 также является средней точкой. Следовательно, 𝐸𝐷 — это отрезок, соединяющий середины двух сторон △𝐴𝐵𝐶, а 𝐴𝐷 и 𝐵𝐸, которые соединяют каждую вершину △𝐴𝐵𝐶 с середина противоположной стороны, две медианы △𝐴𝐵𝐶.
Напомним, что теорема о середине треугольника утверждает, что отрезок, соединяющий
середины двух сторон треугольника параллельны третьей стороне и равны
половину своей длины. 𝐸𝐷 поэтому
параллелен 𝐴𝐵 и составляет половину его длины;
то есть половина от 12 см,
или 6 см.
𝐸𝐷 поэтому
параллелен 𝐴𝐵 и составляет половину его длины;
то есть половина от 12 см,
или 6 см.
Теперь мы можем найти длину 𝑀𝐸 и 𝑀𝐷, вспомнив, что расстояние от каждого вершины треугольника до точки пересечения его медиан составляет две трети длина медианы от этой вершины. Отсюда следует, что расстояние от точки совмещения с серединой одной стороны составляет одну треть длины медиана от вершины, противоположной этой стороне. Следовательно, у нас есть 𝑀𝐸=13𝐸𝐵 и 𝑀𝐷=13𝐴𝐷.
Дано, что 𝐸𝐵=𝐴𝐵 и указано на на схеме 𝐴𝐵=12см. Следовательно, 𝐸𝐵=12см. Нам также дано, что 𝐴𝐷=9см. Подставляя эти значения в приведенные выше уравнения, мы получаем 𝑀𝐸=13×12=4см и 𝑀𝐷=13×9=3.cm
Чтобы найти периметр △𝑀𝐷𝐸, нам нужно
чтобы сложить длины его трех сторон следующим образом:
Периметрсм=𝐸𝐷+𝑀𝐸+𝑀𝐷=6+4+3=13.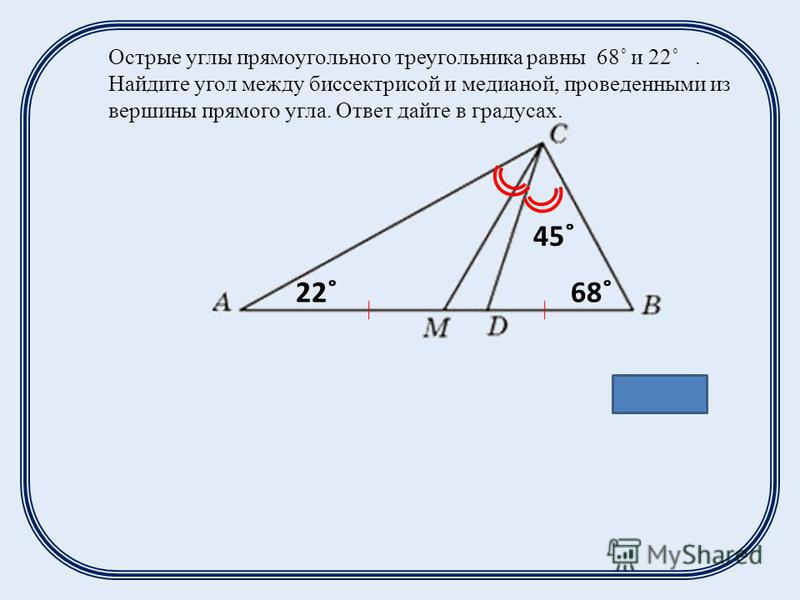
Давайте теперь обобщим то, что мы узнали из этого объяснения.
Ключевые точки
- Медианы треугольника — это три отрезка, идущие от каждой вершины к середина противоположной стороны.
- Три медианы треугольника пересекаются в одной точке: мы говорим, что они одновременны. Точка их пересечения называется точкой совпадение медиан.
- Расстояние от каждой вершины треугольника до точки пересечения его медианы составляют две трети общей длины медианы от этой вершины. То есть расстояние от точки пересечения медиан до вершина в два раза больше, чем расстояние до противоположной средней точки.
- В прямоугольном треугольнике длина медианы, проведенной из вершины Прямой угол равен половине длины гипотенузы треугольника.
- В 30∘-60∘
прямоугольного треугольника, длина меньшей стороны (т. е. стороны, противоположной
угол 30∘) равен половине
длина гипотенузы треугольника.

В $ \Delta ABC,AX $ является медианой. Внутренние биссектрисы углов $\angle AXB$ и $\angle AXC$ пересекают AB и AC в точках L и M соответственно. Докажите, что $ LM||BC $ .\[\]
Дата последнего обновления: 22 апреля 2023
•
Всего просмотров: 262,2 тыс.
•
Просмотров сегодня: 4,32 тыс.
Ответ
3 Подтверждено
3 просмотров 600023
Подсказка: Используем уголок теорема о биссектрисе треугольника ABX для доказательства $ \dfrac{XA}{XB}=\dfrac{AL}{LB} $, и мы получаем теорему о биссектрисе угла в треугольнике ACX для доказательства $ \dfrac{XA}{XB}=\dfrac {AM}{MC} $ . Мы приравниваем правые части к $ \dfrac{AL}{LB}=\dfrac{AM}{LC} $ и используем теорему о пропорциональности в треугольниках, чтобы заключить $ LM||BC $ . \[\]
Полный пошаговый ответ:
Рассмотрим данную схему. \[\]
Нам дано, что в $ \Delta ABC AX $ является медианой. $ХВ=ХС$. Также дано, что внутренние биссектрисы углов $ \angle AXB $ пересекаются с AB в L, что означает
$ХВ=ХС$. Также дано, что внутренние биссектрисы углов $ \angle AXB $ пересекаются с AB в L, что означает
\[\angle BXL=\angle AXL\]
Нам даны внутренние биссектрисы $ \angle AXC $ пересекаются с AC в M что означает
\[\угол AXM=\угол CXM\]
Из теоремы о биссектрисе угла в треугольнике мы знаем, что биссектриса угла делит длину противоположной стороны в отношении, равном длине соответствующих смежных стороны. Мы наблюдаем треугольник AXB, где XL — биссектриса угла $ \ угла AXB $, противоположная сторона которого AB делится на LB и AL. Прилегающей стороной $ \angle AXB $ и соответствующей LB и AL являются XB и XA. Итак, по теореме о биссектрисе угла мы имеем;
\[\dfrac{XB}{XA}=\dfrac{LB}{AL}………\left( 1 \right)\]
Наблюдаем треугольник AXC, где XM — биссектриса угла угла $ \angle AXC $, противоположной стороной которого является AC, разделенный на LM и AM. Прилегающей стороной $ \angle AXC $ и соответствующей MC и AM являются XC и XA. Итак, по теореме о биссектрисе угла мы имеем;
\[\begin{align}
& \Rightarrow \dfrac{XC}{XA}=\dfrac{MC}{AM} \\
& \Rightarrow \dfrac{XB}{XA}=\dfrac{MC}{ AM}\left( \потому что XB=XC \right).


Leave A Comment