Окружность и круг. Угол между касательной и хордой
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
2. Окружность. Круг.
3. Окружность
секущаядиаметр
радиус
О
хорда
касательная
Дуга
4. Центральный угол
Оα
А
В
Угол с вершиной в центре
окружности называется
центральным углом
5. Вписанный угол
αУгол, вершина которого лежит на
окружности, а стороны пересекают
окружность, называется
вписанным углом
6.
 Теорема о центральном углеО
Теорема о центральном углеОА
В
Градусная мера
центрального угла
равна градусной мере
дуги , на которую он
опирается.
AOB AB
7. Теорема о вписанном угле
СВписанный угол
измеряется половиной
дуги, на которую он
опирается
О
А
В
1
ACB AB
2
8. Следствия о вписанных углах
ОВписанные углы,
опирающиеся на одну и
ту же дугу, равны.
Вписанный угол,
опирающийся на
полуокружность – прямой.
О
9. Угол между касательной и хордой
ОВ
А
1
AB
2
α
Угол между касательной и хордой,
проходящей через точку касания, измеряется
половиной заключенной в нем дуги
10. Угол между двумя пересекающимися хордами
1AC BD
2
А
О
D
α
С
В
Угол между двумя пересекающимися
хордами измеряется полусуммой
заключенных между ними дуг
11. Угол между двумя секущими, проведенными из одной точки
1CE BD
2
B
C
О
α
E
D
А
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
12.
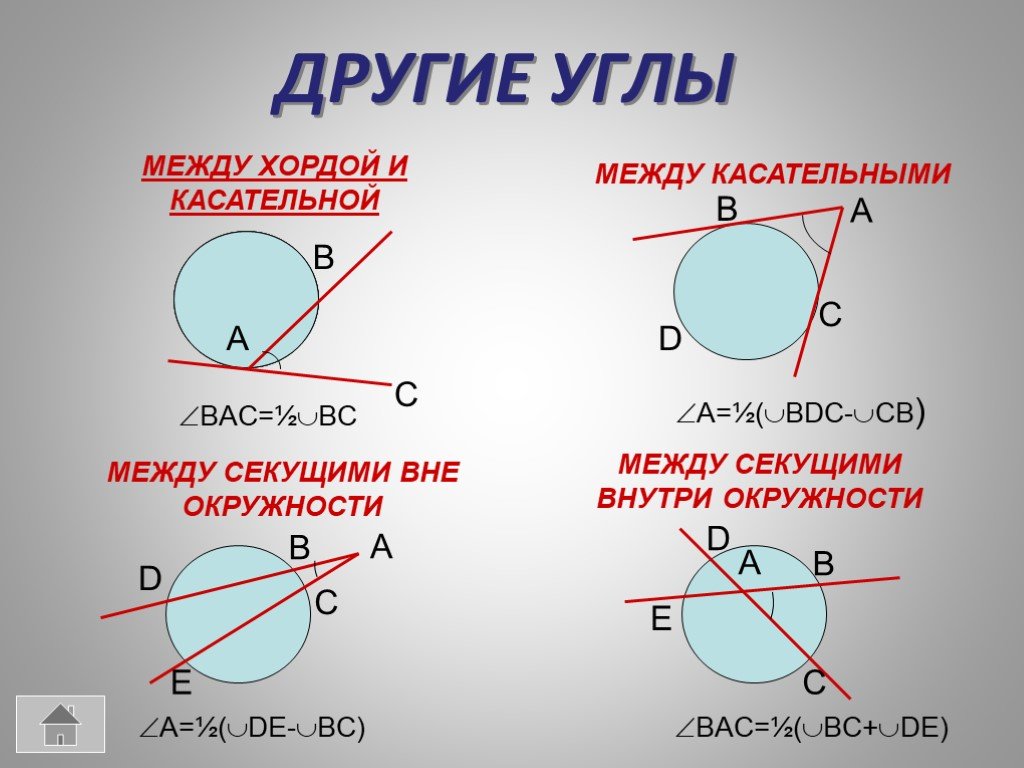 Угол между касательной и секущей, проведенными из одной точкиB
Угол между касательной и секущей, проведенными из одной точкиBО
D
C
1
BD BC
2
α
A
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
13. Угол между двумя касательными, проведенными из одной точки
BО
A
α
0
180 BC
C
Угол между двумя касательными, проведенными
из одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.
1
5
9
13
17
21
25
29
2
6
10
14
18
22
26
30
3
7
11
15
19
23
27
31
4
8
12
16
20
24
28
Литература
Задача 1
A
B
X
C
∠ BAC = 41 15′
0
∪BAC,∪ BXC — ?
Задача 2
A
B
55
0
X
C
∪BXC = 55
0
∠ BAC — ?
Задача 3
A
C
B
О
∠ BAC — ?
B
A
Задача 4
500
O
C
∪AB : ∪ BC = 5 : 8
0
∠ABC = 50
∪AB,∪ BC,∪AC,∠AOC
B
1200
A
Задача 5
700
C
∪AB = 120 ,∠ABC = 70
0
∪BC — ?
0
Задача 6
A
B
X
C
∪BAC : ∪ BXC = 5 : 3
∠ BAC — ?
A
B
Задача 7
O
C
∪AB : ∪ BC : ∪AC = 2 : 7 : 9
∠AOB,∠ BOC,∠AOC
Задача 8
A
B
O
C
AB = AO
∠ CAB — ?
Задача 9
B
A
C
∪AB : ∪ BC : ∪AC = 5 : 6 : 7
∠ACB,∠ BAC,∠ ABC — ?
Задача 10
B
600
A
C
O
∪AB = 60 , OB = 6ñì
0
AC — ?
Задача 11
С
56
0
О
A
В
∠CAB — ?
Задача 12
A
230
С
О
В
∠COB — ?
Задача 13
B
A
C
530
D
∠ ABC — ?
Задача 14
B
A
1250
C
O
∠ ABC — ?
Задача 15
B
C
340
A
∠ ABC — ?
Задача 16
D
54
0
B
A
C
∠ ABC — ?
Задача 17
B
A
120
C
D
O
∠ ABC — ?
Задача 18
A
400
B
220
D
C
O
∠ ABC — ?
Задача 19
A
D
B
600
O
C
200
E
∠ ABC — ?
Задача 20
A
B
490
210
C
O
∠ ABC — ?
Задача 21
D
C
A
320 490
O
B
∠ ABC — ?
Задача 22
A
D
120
B
400
O
C
∠ ABC — ?
Задача 23
A
D
180
B
32
0
O
C
∠ ABC — ?
Задача 24
D
A
C
180
K
350
B
∠ ABC — ?
Задача 25
B
A
D
450
C
890
F
∠ ABC — ?
Задача 26
A
B
280
D
C
1000
F
∪BC — ?
Задача 27
A
32
B
0
D
460
C
F
∪FD — ?
Задача 28
460
A
D
B
C
1030
F
∠ ABC — ?
Задача 29
660
A
D
B
C
530
F
∪FD — ?
Задача 30
B
A
D
330
C
500
F
∠ ABC — ?
Задача 31
D
F
B
C
20
0
300
A
∠ ABC — ?
46.
 Прототип в6Вписанные и описанные углы
Прототип в6Вписанные и описанные углы47. Прототип задания B6 (№ 27884)
Угол ACO равен 240. Его сторона CA касается окружности.Найдите градусную величину большей дуги AD окружности,
заключенной внутри этого угла. Ответ дайте в градусах.
∆АСО –прямоугольный. ∟С = 240 => ∟АОС = 660
Центральный угол измеряется дугой, на
которую опирается. Следовательно меньшая
дуга АВ = ∟АОС = 660
Развернутый угол DОB = 1800
∟DОA = ∟DOB — ∟AOB = 1800 — 660
∟DОA = 1140
∟DОA измеряется дугой АD, на которую опирается
Большая дуга АD окружности, заключенная
внутри ∟АСО равна 1140
27.01.22
Ответ 114
47
48. Прототип задания B6 (№ 27869)
АС и BD— диаметры окружности с центром О.Угол АСВ равен 38о. Найдите угол AOD. Ответ
дайте в градусах.
∆ ВОС равнобедренный. ОС = ОВ = R,
следовательно…
∟ВСО = ∟СВО = 38о
∆ ОСВ : ∟СОВ + ∟ОСВ + ∟СВО = 180о
38о
∟СОВ = 180о – 38о — 38 о
∟СОВ = 104о
∟AOD = ∟COB — как вертикальные
∟AOD =104о
Ответ: 104
27.
 01.22
01.2248
49. Прототип задания B6 (№ 27878)
Угол между хордой AB и касательной BC к окружности равен32о. Найдите величину меньшей дуги, стягиваемой хордой AB.
Ответ дайте в градусах.
Угол, составленный касательной и хордой, измеряется
половиной дуги заключенной внутри него
Следовательно: Искомая меньшая дуга,
стягиваемой хордой АВ равна 32о · 2 = 64о
32о
Ответ 64
27.01.22
49
50. Прототип задания B6 (№ 27863)
Центральный угол на 36о больше острого вписанногоугла, опирающегося на ту же дугу окружности.
Найдите вписанный угол. Ответ дайте в градусах.
Вписанный угол АСВ составляет половину
центрального АОВ, опирающегося на туже дугу АВ
Пусть ∟АСВ = х
х
Тогда ∟АОВ = х + 36о
Так как ∟АОВ = 2∟АСВ, то
х + 36о = 2х
х = 36о
Ответ: 36
27.01.22
50
51. Прототип задания B6 (№ 27857)
Чему равен острый вписанный угол, опирающийся нахорду, равную радиусу окружности? Ответ дайте в
градусах.

По условию задачи АС = R , Следовательно АС = АО = СО
∆ АОС равносторонний => ∟АОС = 60о
В
Центральный угол АОС измеряется дугой АС, на
которую опирается.
Вписанный угол АВС составляет половину
центрального АОС, опирающегося на туже дугу АС
О
∟АВС = ½∟АОС
А
27.01.22
С
∟АВС = 60о : 2 = 30о
Ответ: 30
51
52. Задание B6 (№ 51031)
Найдите хорду, на которую опирается угол 30о ,вписанный в окружность радиуса 28.
Вписанный угол АВС составляет половину центрального
АОС, опирающегося на туже дугу АС
Дуга АС =2·30о = 60о
В
О
R
А
27.01.22
30о
Хорда АС = R = 28
R
R
∟АОС = 60о. Следовательно ∆АОС равносторонний
Ответ: 28
С
52
Дугу ВАС
Дугу ВС
Угол ВОС опирающийся на
дугу ВС
English Русский Правила
Окружность и круг — что это, определение и ответ
Окружность – это множество всех точек плоскости, равноудаленных от данной точки на плоскости.
Круг – это часть плоскости, ограниченная окружностью.
Окружность – это замкнутая линия, а круг – это площадь, находящаяся внутри окружности:
Длина окружности равна:
\(l = 2\pi R = \text{dπ}\)
где \(R\) – это радиус, а \(D\) – диаметр окружности
ЭЛЕМЕНТЫ ОКРУЖНОСТИ:
Центр окружности – точка O.
Радиус окружности – отрезок R, соединяющий точку окружности с центром. Все радиусы одной окружности равны.
Хорда – это отрезок АВ, соединяющий любые две точки окружности.
Диаметр – это хорда d, проходящая через центр окружности. Диаметр равен двум радиусам.
ДУГА И СЕКТОР:
Дуга – это часть окружности, заключенная между точками на ней.
Сектор – площадь круга, ограниченная двумя радиусами и дугой окружности.
Понятия дуга и сектор связаны между собой как круг и окружность. \circ}}\) показывает, какую часть от всей окружности занимает дуга
\circ}}\) показывает, какую часть от всей окружности занимает дуга
КАСАТЕЛЬНАЯ:
Касательная к окружности – это прямая, которая пересекается с окружностью в одной точке.
Свойства касательной:
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания:
\(a\bot OA,\ A \in a,\ OA = R\)
2. Отрезки касательных, проведенных из одной точки, равны до точек касания.
\(CA = CB,\ a,\ b\ –\ касательные\)
ЦЕНТРАЛЬНЫЕ И ВПИСАНЫЕ УГЛЫ:
С окружностью связано два вида углов – вписанные и центральные. Рассмотрим такую окружность:
На данном чертеже угол АОС является центральным, а угол АВС – вписанным.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны являются ее хордами.
Свойства вписанного угла:
1. Измеряется половиной дуги, на которую он опирается.
2. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Вписанный угол, опирающийся на диаметр — прямой.
Центральный угол – угол, образованный двумя радиусами. Его вершина лежит на центре окружности.
Свойства центрального угла:
1. Измеряется дугой, на которую опирается;
2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
КОМБИНАЦИИ ХОРД, КАСАТЕЛЬНЫХ И СЕКУЩИХ:
Секущая – это прямая, которая пересекает окружность в двух точках.
ПЕРЕСЕЧЕНИЕ ХОРД
Хорды AB и CD пересекаются в точке M
1. Произведение длин отрезков пересекающихся хорд равны:
\(AM \bullet MB = CM \bullet MD\)
2. Угол между двумя пересекающихся хорд равен полусумме высекаемых ими дуг:
\(\angle AMD = \angle CMD = \frac{дуга\ AD + дуга\ \text{CB}\ }{2}\)
ХОРДА И КАСАТЕЛЬНАЯ
Прямая AB касается окружности в точке B, BC – хорда. {2}\)
{2}\)
2. Угол между секущей и касательной равен полуразности высекаемых ими дуг:
\(\angle DAC = \frac{дуга\ DC\ –\ дуга\ \text{CB}}{2}\)
УГОЛ МЕЖДУ СЕКУЩИМИ
AD и AE – секущие, выходящие из одной точки, пересекающие окружность в точках В и С соответственно.
Угол между секущими равен полуразности большей и меньшей высекаемых ими дуг:
\(\angle BAC = \frac{дуга\ \text{DE}\ –\ дуга\ \text{BC}}{2}\)
Секанты, аккорды и касательные (видео)
TranscriptPracticeЗдравствуйте! Сегодня мы собираемся исследовать, что может произойти, когда встречаются круг и линия или две линии. Начнем с определения словаря, который нам понадобится. Линия, пересекающая окружность и касающаяся двух точек вне окружности, равна секансе окружности.
Вот пример. Мы можем видеть, что линия пересекает внешнюю сторону круга в двух точках и создает отрезок линии между теми точками, которые выделены красным цветом. Этот отрезок называется хордой .
Этот отрезок называется хордой .
У нас также может быть более одной секущей окружности, взаимодействующей друг с другом, например:
Теперь наши две хорды создали вписанный угол в нашу окружность, которую мы обозначили символом \(x \) и знак степени. Напротив угла находится часть окружности между точками, где хорды пересекают окружность, выделенные желтым цветом. это перехваченная дуга . Мы можем найти меру нашего вписанного угла \(x\), если мы знаем длину дуги, на которую опираемся, в градусах. Перехваченная дуга является той же мерой, что и центральный угол , который использует те же две точки, что и наш вписанный угол, но с вершиной в центре окружности.
Центральный угол равен 120°, поэтому наша дуга, на которую опираются, также имеет размер 120°. Обратите внимание, что центральный угол немного «шире», чем вписанный угол. Это потому что так! На самом деле он ровно в два раза шире. {\circ}\div 2\), или 60°! Центральный угол всегда вдвое больше вписанного угла, когда вершина вписанного угла лежит на самой окружности. Это также означает, что мы можем легко найти центральный угол или дугу, на которую опираемся, если мы знаем меру вписанного угла — все, что нам нужно сделать, это удвоить меру вписанного угла! 9{\circ}\)
{\circ}\div 2\), или 60°! Центральный угол всегда вдвое больше вписанного угла, когда вершина вписанного угла лежит на самой окружности. Это также означает, что мы можем легко найти центральный угол или дугу, на которую опираемся, если мы знаем меру вписанного угла — все, что нам нужно сделать, это удвоить меру вписанного угла! 9{\circ}\)
Мы можем сделать небольшую проверку на здравый смысл, чтобы убедиться, что мы используем правильную версию этой формулы. Если бы мы случайно воспользовались формулой сложения, то получили бы угол, равный 65°, что кажется слишком большим для нашего маленького угла. Однако будьте осторожны. Задачи стандартизированных тестов иногда не соответствуют масштабу — следите за предупреждением об этом в любой задаче, которую вы решаете.
Касательные линии
При взаимодействии линии и окружности секущие иногда не создаются. Если линия проходит через окружность и касается ее только в одной точке, она создает то, что мы называем линией, состоящей из касательной к окружности. Точка, в которой линия и окружность соприкасаются, называется точкой касания .
Точка, в которой линия и окружность соприкасаются, называется точкой касания .
Слово тангенциальный мы иногда встречаем и за пределами математики, описывая тему, которая лишь немного связана с обсуждаемой темой. Здесь это означает линию, которая касается окружности как можно мельчайшим образом – только в одной точке.
В любом случае, если внимательно посмотреть на нашу диаграмму, мы можем увидеть радиус окружности, встречающейся с нашей касательной на 9угол 0°. Чтобы наша линия была действительно касательной, это должно быть правдой. Если наша линия не будет точно перпендикулярна радиусу в точке касания, она на самом деле коснется круга дважды, хотя, возможно, очень близко друг к другу. Это фактически создаст секущую вместо касательной. Мы можем видеть это, увеличив масштаб круга, показывающего углы, которые всего на несколько градусов отличаются от 90°:
происходит, хотя это было бы очень трудно показать на диаграмме!
Надеюсь, это видео о секущих, аккордах и тангенсах было полезным! Спасибо за просмотр и удачной учебы!
Вопрос № 1:
Сопоставьте правильное имя с каждой строкой.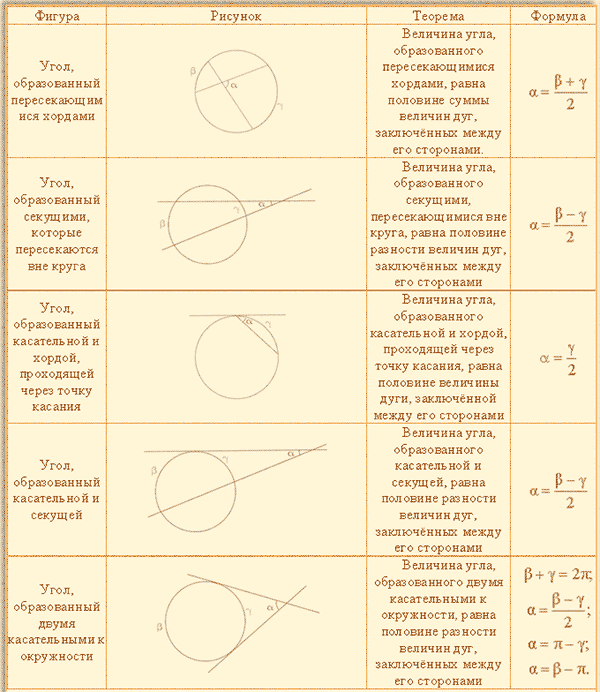
Black-Secant Red-Chord Orange-Tangent
Black-Hord Red-Secant Orange-Tangent
Black-Tangent Red-Chord Orange-Secant
Black-Secant Red-Tangent Orange-Hord
Показать ответ Ответ: Секущая: линия, которая касается двух точек на окружности окружности.
Хорда: отрезок, соединяющий две точки на окружности окружности.
Касательная: Линия, которая касается окружности только один раз.
Каково значение \(x\)?
\(82°\)
\(31°\)
\(42°\)
\(41°\)
Показать ответ Ответ:На рисунке \(x\) является мерой вписанного угла. Вписанный угол составляет половину дуги, на которую опирается. В этом случае пересекаемая дуга равна \(82°\). Половина \(82°\) равна \(41°\). Значит, вписанный угол равен \(41°\).
Скрыть ответ Вопрос №3:
Какова мера внутреннего угла с мерой \(x°\)?
\(125°\)
\(230°\)
\(115°\)
\(46°\)
Показать ответ Ответ: Внутренний угол \(x\) можно определить по формуле \(x=\frac{1}{2}(a°+b°)\), где \(a\) и \(b\) — пересекаемые дуги.
\(x=\frac{1}{2}(92°+138°)\)
\(x=\frac{1}{2}(230°)\)
\(x=115° \)
Фонарик светит в лес в точке \(x°\). Соответствующие перехваченные дуги, образованные сияющим светом, равны \(21°\) и \(162°\). Под каким углом свет падает от фонарика?
\(70,5°\)
\(114°\)
\(39°\)
\(74,5°\)
Показать ответ 900 05 Ответ: Угол \ (x\) можно определить по формуле \(x=\frac{1}{2}(a°-b°)\), где \(a\) и \(b\) представляют пересекаемые дуги.
\(x=\frac{1}{2}(162°-21°)\)
\(x=\frac{1}{2}(141°)\)
\(x=70,5° \)
Угол падения света от фонарика равен \(70,5°\).
Скрыть ответ Вопрос № 5:
Вы привариваете круглые серьги для продажи на местном фермерском рынке. Каждая серьга круглая с двумя стержнями через круг. Вы хотите, чтобы каждая серьга выглядела одинаково, поэтому вам нужно рассчитать точную угловую меру внутреннего угла. Меры двух дуг, пересекаемых стержнями, равны \(72°\) и \(70°\) соответственно. Какова мера угла \(x\)?
Меры двух дуг, пересекаемых стержнями, равны \(72°\) и \(70°\) соответственно. Какова мера угла \(x\)?
\(70°\)
\(71°\)
\(72°\)
\(74°\)
Показать ответ Ответ: Неизвестный угол находится внутри круга, поэтому угол \(x\) можно вычислить по формуле \(x=\frac{ 1}{2}(a°+b°)\), где \(a\) и \(b\) представляют пересекаемые дуги.
\(x=\frac{1}{2}(72°+70°)\)
\(x=\frac{1}{2}(142°)\)
\(x=71° \)
Вернуться к видео о геометрии
Другие ракурсы
Теорема 73: Если касательная и диаметр пересекаются в точке касания, то они перпендикулярны друг другу.
На рисунке 1 диаметр AB пересекается с касательной в точке B . Согласно теореме 73 , AB ⊥ , что означает, что м ∠ ABC = 90° и м ∠ ABD = 90°.
Рисунок 1 Касательная к окружности и диаметр окружности, пересекающиеся в точке касания.
Теорема 74: Если хорда перпендикулярна касательной в точке касания, то это диаметр.
Пример 1: Теорему 74 можно использовать для нахождения центра окружности, если известны две касательные к окружности. На рисунке 2 – касается окружности в точке P , – касается окружности в точке S . Используйте эти факты, чтобы найти центр круга.
Рисунок 2 Нахождение центра окружности, когда известны две касательные к окружности.
Согласно Теореме 74 , если хорда проведена перпендикулярно P , это диаметр, а это значит, что она проходит через центр окружности.
Точно так же, если хорда проведена перпендикулярно точке
Рисунок 3 Аккорды, проведенные перпендикулярно касательным, помогают найти центр окружности.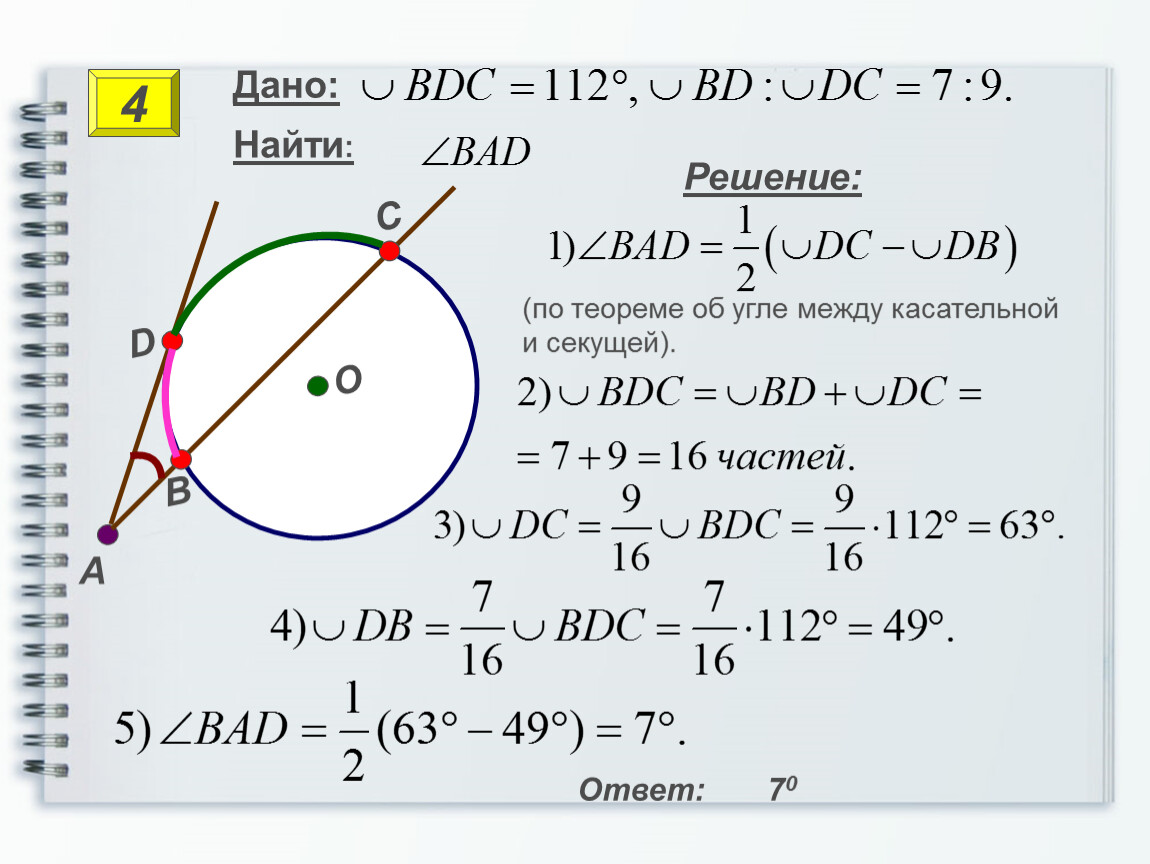
Теорема 75: Мера угла, образованного двумя хордами, пересекающимися внутри окружности, равна половине суммы мер дуг, захваченных этим углом и его вертикальным аналогом угла.
На рисунке 4 хорды AC и BD пересекаются внутри круга в точке
Рисунок 4 Углы, образованные двумя хордами, пересекающимися внутри окружности.
По Теорема 75: ,
Теорема 76: Мера угла, образованного касательной и хордой, пересекающейся в точке касания, равна половине меры дуги, на которую она опирается.
На рис. 5 хорда QR и касательная пересекаются в точке R . По теореме 76 , м ∠1 = 1/2 ( м ) и м ∠ 2 = ½ ( м ).
Рисунок 5 Касательная к окружности и хорда, пересекающиеся в точке касания Теорема 77: Мера угла, образованного двумя секущими, пересекающимися вне круга, равна половине разности мер пересекаемых дуг.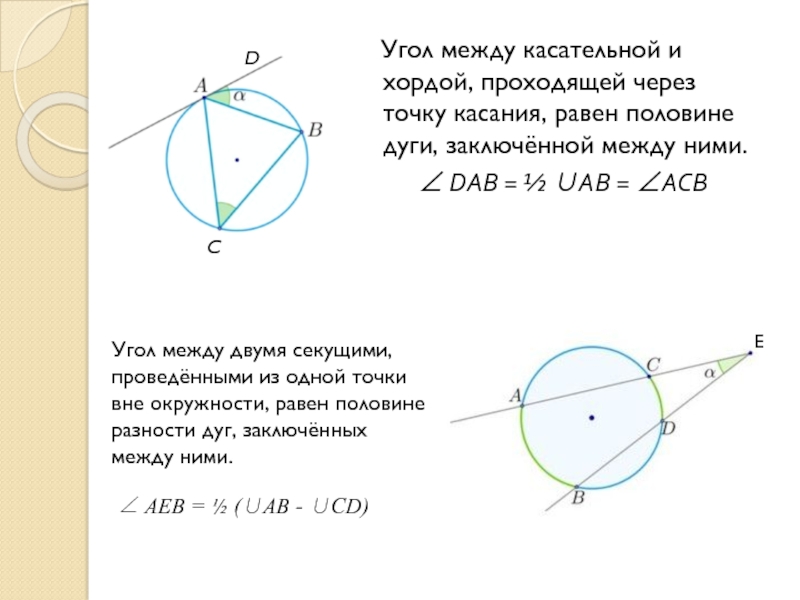

Leave A Comment