Угол между высотой и медианой треугольника
Примечание. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.
| Найдіть кут між медіаною і висотою прямокутного трикутника , які проведені з вершини прямого кута , якщо гострий кут дорівнює 20 градусів | Найдите угол между высотой и медианой прямоугольного треугольника, которые проведены из вершины прямого угла, если острый угол равен 20 градусов |
Решение.
Решим задачу путем дополнительного построения вокруг заданной геометрической фигуры (треугольника), чтобы использовать свойства новой образованной фигуры (прямоугольника) для решения этой задачи по геометрии
Сначала достроим прямоугольный треугольник до прямоугольника.
В результате дополнительного построения катеты прямоугольного треугольника одновременно являются сторонами прямоугольника, а гипотенуза — его диагональю.
Далее учтем следующие свойства треугольника и прямоугольника:
- Сумма углов треугольника равна 180 градусам
- Диагонали прямоугольника в точке пересечения делятся пополам
- Диагонали прямоугольника равны
Величина одного из углов треугольника задана в условии задачи. Поскольку треугольник по условию прямоугольный, то мы можем найти величину третьего угла, зная, что сумма углов треугольника равна 180 градусам.
Поскольку угол CAB = 20°, то угол ABC = 180 — 90 — 20 = 70°
Таким образом, мы нашли градусную меру угла B в треугольнике ABC
Рассмотрим треугольник COA. Он равнобедренный, так как его стороны — это половины диагоналей прямоугольника.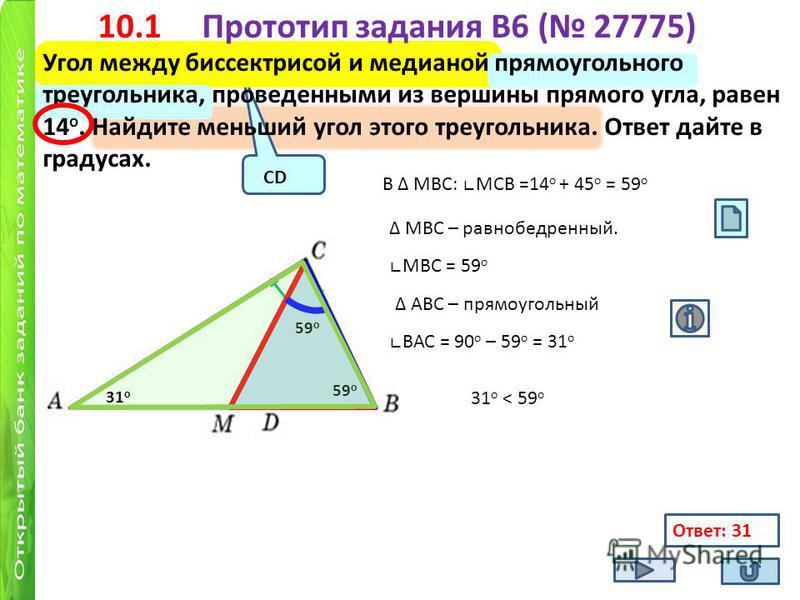 Это следует из свойств прямоугольника. Так как диагонали прямоугольника равны, а в точке пересечения они делятся пополам, то половины равных отрезков будут также между собой равны. Поскольку в равнобедренном треугольнике углы при основании равны, то:
Это следует из свойств прямоугольника. Так как диагонали прямоугольника равны, а в точке пересечения они делятся пополам, то половины равных отрезков будут также между собой равны. Поскольку в равнобедренном треугольнике углы при основании равны, то:
∠OCA = ∠OAC = 20º
Рассмотрим треугольник BKC. CK является высотой треугольника ABC, проведенной к гипотенузе. Значит угол BKC — прямой, то есть равен 90 градусам, а сам треугольник BKC — прямоугольный. Поскольку треугольник BKC — прямоугольный, то угол BCK = 180 — 90 — 70 = 20°. (Это следует из того, что сумма углов треугольника 180 градусов, угол BKC — прямой, а величину угла B мы нашли ранее)
Поскольку угол BCA — прямой, то его градусная мера равна 90 градусов и, одновременно, равна сумме градусных мер составляющих его углов: BCK, KCO и OCA.
Величину угла BCK мы только что нашли, она составляет 20 градусов, величину угла OCA мы также нашли ранее и она тоже составляет 20 градусов.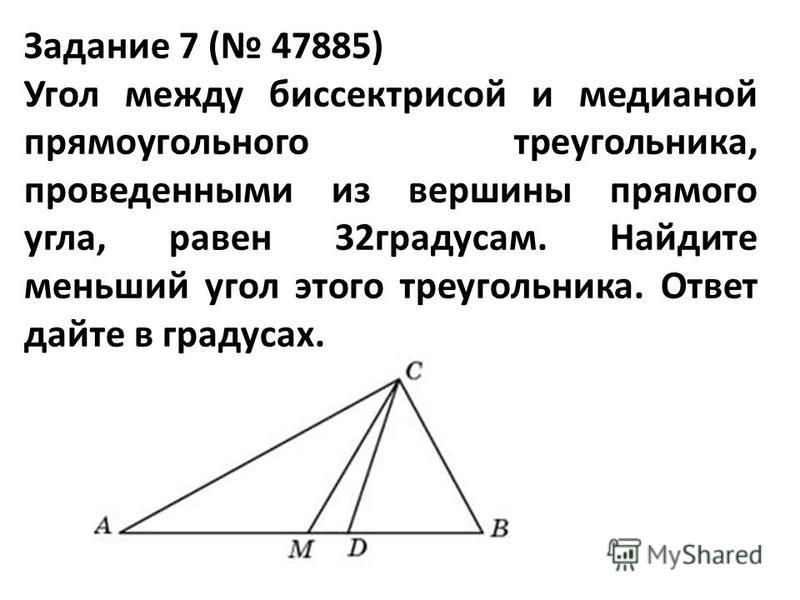
Откуда:
20° + 20° + ∠KCO = 90°
∠KCO = 50°
Ответ: Угол между медианой и биссектрисой заданного прямоугольного треугольника равен 50 градусов.
0
Нахождение площади через медианы | Описание курса | Медиана прямоугольного треугольника
Высоты медианы биссектрисы треугольника — материалы для подготовки к ЕГЭ по Математике
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.
Высотой треугольника называется перпендикуляр,
опущенный из вершины треугольника
на противоположную сторону.
В тупоугольном треугольнике высота
опускается на продолжение стороны.
Три высоты треугольника всегда
пересекаются в одной точке.
В случае тупого угла пересекаются
Медианой треугольника называют отрезок,
соединяющий вершину треугольника с
серединой противоположной стороны.
Три медианы треугольника пересекаются в
одной точке и делятся в ней в отношении
2 : 1 , считая от вершины.
Биссектриса треугольника делит
угол треугольника пополам.
Три биссектрисы пересекаются в одной точке,
которая является центром окружности,
вписанной в треугольник.
Напомним, что высота треугольника

Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.
Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки A на отрезок BC, зато можем опустить его на прямую BC — то есть на продолжение стороны BC.
В этом случае в одной точке пересекаются не сами высоты, а их продолжения.
В прямоугольном треугольнике каждый катет является высотой к другому катету. Три высоты прямоугольного треугольника пересекаются в вершине прямого угла.
Как доказать, что три высоты треугольника пересекаются в одной точке?
Доказательство здесь: Свойство высот треугольника.
Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2 : 1, считая от вершины.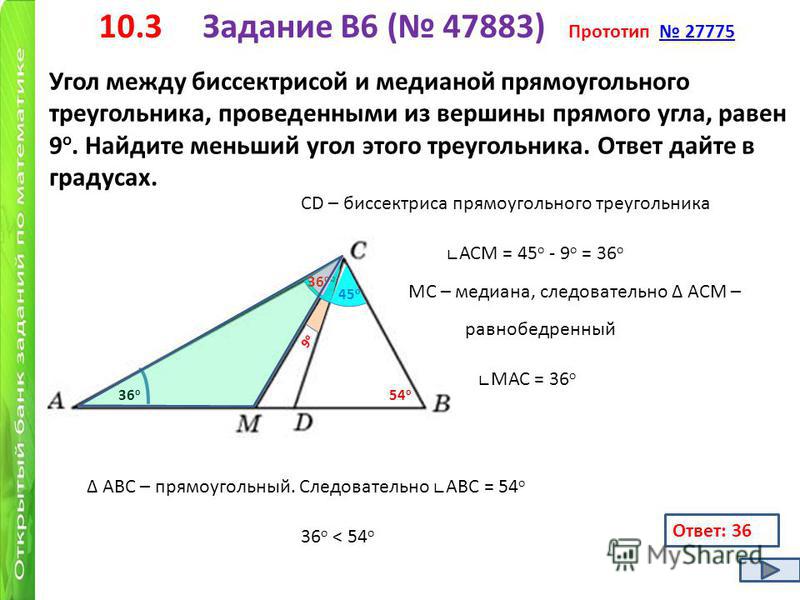
Доказательство этой теоремы смотрите здесь: Свойства медиан треугольника.
Биссектриса треугольника
У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.
Читайте доказательство теоремы о том, что три биссектрисы треугольника пересекаются в одной точке:
Свойства биссектрис треугольника.
Еще одно свойство биссектрисы часто применяется при решении задач.
Теорема. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон:
Доказательство этой теоремы здесь: Свойство биссектрисы треугольника.
Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.
Задача 1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.
Ответ дайте в градусах.
Решение:
Пусть биссектрисы треугольник ABC (в котором угол C равен ) пересекаются в точке M.
Рассмотрим треугольник ABM.
,
, тогда .
Острый угол между биссектрисами на рисунке обозначен .
Угол смежный с углом , следовательно, .
Поскольку треугольник — прямоугольный, то .
Тогда .
Ответ: 45.
Задача 2. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Пусть CH — высота, проведенная из вершины прямого угла C, CK — биссектриса угла C.
Тогда ;
.
Угол между высотой и биссектрисой — это угол .
.
Ответ: 16.
Задача 3. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Рассмотрим треугольник АВС, в котором угол С – прямой, CD – высота, СМ – медиана.
Требуется найти угол МСD.
Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.
Следовательно,
Искомый
Ответ: 42.
Задача 4. Острые углы прямоугольного треугольника равны и . Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Рассмотрим треугольник АВС, в котором угол С – прямой, CL – биссектриса, СМ – медиана.
. Требуется найти угол МСL.
Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.
Следовательно,
т.к. CL – биссектриса.
Искомый
Ответ: 22.
Задача 5. Два угла треугольника равны и . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Решение:
Из треугольника ACH (угол H — прямой) найдем угол CAH. Он равен .
Из треугольника ACK ( K — прямой) найдем угол ACK. Он равен .
В треугольнике AOC известны два угла. Найдем третий, то есть угол AOC, который и является тупым углом между высотами треугольника ABC:
.
Ответ: 130.
Задача 6. В треугольнике ABC угол С равен , AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Решение:
Пусть в треугольнике ABC угол BAC равен A, угол ABC равен B.
Рассмотрим треугольник AOB.
,
, тогда .
Из треугольника ABC получим, что .
Тогда .
Ответ: 119.
Задача 7. В треугольнике ABC угол A равен , угол B равен . AD, BD и CF — биссектрисы, пересекающиеся в точке O.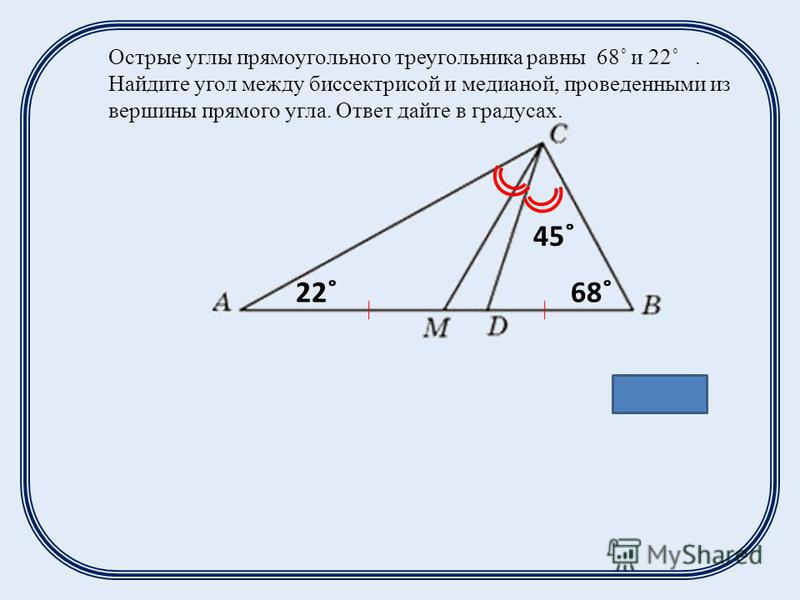 Найдите угол AOF. Ответ дайте в градусах.
Найдите угол AOF. Ответ дайте в градусах.
Решение:
Найдем угол ACB. Он равен
Тогда
Из треугольника ACF найдем угол . Он равен .
Рассмотрим треугольник AOF.
, . Значит .
Ответ: 49.
Задача 8. В треугольнике ABC, CD — медиана, угол ACB равен , угол B равен . Найдите угол ACD. Ответ дайте в градусах.
Решение:
В прямоугольном треугольнике медиана равна половине гипотенузы.
Поэтому
Треугольник ADC равнобедренный, следовательно, углы при основании равны:
Поскольку в прямоугольном треугольнике сумма острых углов равна 90 градусов, получим:
Ответ: 32.
Задача 9. В треугольнике АВС АD — биссектриса, угол С равен . Угол САD равен . Найдите угол В. Ответ дайте в градусах.
Решение:
Поскольку AD – биссектриса, то
Сумма углов треугольника равна , следовательно,
Ответ: 74.
Задача 10. В треугольнике АВС CH – высота, AD – биссектриса, О – точка пересечения прямых CH и AD, угол BAD равен . Найдите угол АОС. Ответ дайте в градусах.
Найдите угол АОС. Ответ дайте в градусах.
Решение:
Угол АОС – внешний в треугольнике АНО, следовательно,
Ответ: 116.
Задача 11. В треугольнике АВС проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника АВС. Ответ дайте в градусах.
Решение:
AD = CD, следовательно, треугольник ADC – равнобедренный и
AD — биссектриса, следовательно,
AB = AD, следовательно, треугольник ABD – равнобедренный и
– внешний в треугольнике ADC, следовательно,
Таким образом, наименьшим углом треугольника АВС является , два других угла – в два раза больше.
Воспользуемся тем, что сумма углов треугольника АВС равна :
, откуда получаем:
Наименьший угол треугольника АВС равен .
Ответ: 36.
Задача 12. Биссектриса треугольника делит противоположную сторону на отрезки 2,8 и 4,2. Периметр треугольника равен 22. Найдите стороны треугольника.
Решение:
Пусть стороны треугольника равны и . Биссектриса делит сторону c на отрезки 2,8 и 4,2.
Биссектриса делит сторону c на отрезки 2,8 и 4,2.
Значит,
В соответствии со свойством биссектрисы:
Или:
Одновременно выполнено условие для периметра:
Тогда
Ответ: 9, 6, 7.
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Элементы треугольника. Высоты, медианы, биссектрисы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 07.02.2023
геометрия — Угол между медианами в прямоугольном треугольнике
спросил
Изменено 7 лет, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
В прямоугольном треугольнике медианы проведены от острых углов к противоположным сторонам. 2}$$
где $\frac ca=s\gt 0$. 92}.$$
Итак, имеем $f(s)\le f(1)=\frac 34$.
2}$$
где $\frac ca=s\gt 0$. 92}.$$
Итак, имеем $f(s)\le f(1)=\frac 34$.
Следовательно, максимальный острый угол равен $\arctan\frac 34$.
$\endgroup$
$\begingroup$
Просто для удовольствия я добавлю ответ, который не требует исчисления. Пусть $A(-1,0)$, $B(1,0)$ и $C(\cos\theta,\sin\theta)$ — вершины прямоугольного треугольника, и пусть $O(0,0) $. Медианы из $A$ и $B$ пересекают медиану $OC$ в такой точке $P$, что $OP=1/3$. Если взять $\alpha=\angle OAP$ и $\beta=\angle OBP$, то легко показать, что $\tan\alpha=(1/3)\sin\theta/(1+(1/ 3)\cos\theta)$ и $\tan\beta=(1/3)\sin\theta/(1-(1/3)\cos\theta)$. Острый угол между медианами равен $\alpha+\beta$, и прямое вычисление дает $\tan(\alpha+\beta)=(3/4)\sin\theta$, что достигает своего максимума $3/4$ для $\ тета=\пи/2$.
$\endgroup$
$\begingroup$
ПОДСКАЗКА. … Ваша ошибка в том, что вы говорите, что градиент $CE$ равен $-\frac{a}{2c}$, тогда как он должен быть….каким?
… Ваша ошибка в том, что вы говорите, что градиент $CE$ равен $-\frac{a}{2c}$, тогда как он должен быть….каким?
$\endgroup$
Высоты Медианы и биссектрисы углов
Так же, как существуют специальные имена для особых типов треугольников, существуют специальные имена для особых отрезков внутри треугольников. Разве это не особенное?
База и высота
Каждый треугольник имеет три оснований (любая из его сторон) и три высот (высот). Каждая высота представляет собой перпендикулярный отрезок от вершины к противоположной стороне (или продолжение противоположной стороны) (рис. 1).
Рисунок 1 Три основания и три высоты одного и того же треугольника.
Высоты иногда могут совпадать со стороной треугольника или иногда могут пересекаться с расширенным основанием за пределами треугольника. На рис. 2, AC — высота до основания BC , а BC — высота до основания AC .
Рисунок 2 В прямоугольном треугольнике каждый катет может служить высотой.
На рисунке 3 AM — это высота до основания BC .
Рисунок 3 Высота тупоугольного треугольника.Интересно отметить, что в любом треугольнике три прямые, содержащие высоты, пересекаются в одной точке (рис. 4).
Рисунок 4 Три линии, содержащие высоты, пересекаются в одной точке,
, который может быть или не быть внутри треугольника.
Медиана
Медиана в треугольнике — это отрезок, проведенный от вершины к середине противоположной стороны. Каждый треугольник имеет три медианы. На рисунке 5 E является средней точкой BC . Следовательно, BE = EC . АЭ — это медиана Δ ABC.
Рисунок 5 Медиана треугольника.
В каждом треугольнике три медианы сходятся в одной точке внутри треугольника (рис. 6).
6).
Биссектриса угла
Биссектриса угла в треугольнике — это отрезок, проведенный из вершины, которая делит пополам (разрезает пополам) этот угол при вершине. У каждого треугольника есть три биссектрисы угла. На рисунке , представляет собой биссектрису угла в Δ азбука.
Рисунок 7 Биссектриса угла.
В каждом треугольнике три биссектрисы угла пересекаются в одной точке внутри треугольника (рис. 8).
Рисунок 8 Биссектрисы трех углов пересекаются в одной точке внутри треугольника. Как правило, высоты, медианы и биссектрисы являются разными отрезками. Однако в некоторых треугольниках они могут быть одними и теми же сегментами. На рисунке можно доказать, что высота, проведенная из угла при вершине равнобедренного треугольника, является медианой, а также биссектрисой угла.

Leave A Comment